28.05.21

Dr inż. Tadeusz BURAK

1

Metody Numeryczne

Metody Numeryczne

ALGORYTMY

28.05.21

Dr inż. Tadeusz BURAK

2

Algorytm definicje

Algorytm definicje



Algorytm jest to sposób postępowania

podczas rozwiązywania zadania



Algorytm – mechaniczna procedura

rozwiązywania problemu obliczeniowego

Gdzie:

problem obliczeniowy to zadanie z para-

metrami, niekoniecznie matematyczne, byle

precyzyjnie określone, tzn. jakie parametry

są dopuszczalne, jakie warunki ma spełniać

rozwiązanie,jakie mają być wyniki.

Parametry to dane wejściowe (INPUT).
Rozwiązanie –dane wyjściowe (OUTPUT).

28.05.21

Dr inż. Tadeusz BURAK

3

Algorytm definicje II

Algorytm definicje II



ALGORYTM, dokładny przepis podający

sposób rozwiązania określonego zadania

w skończonej liczbie kroków; zbiór

poleceń odnoszących się do pewnych

obiektów, ze wskazaniem porządku, w

jakim mają być realizowane.



ALGORYTM zapisany przy pomocy

języka programowania jest

programem.



Wyróżniamy algorytmy numeryczne

(np. Euklidesa)

i nienumeryczne

operujące na obiektach nie liczbowych

(np. dokumenty)

28.05.21

Dr inż. Tadeusz BURAK

4

Algorytm definicje III

Algorytm definicje III



ALGORYTM sekwencyjny
Kolejność czynności jest określona

w sposób jednoznaczny



ALGORYTM niesekwencyjny
Kolejność czynności nie w każdym

przypadku jest jednoznaczna

Np.– Algorytmy równoległe,

współbieżne



ALGORYTMY skończone

28.05.21

Dr inż. Tadeusz BURAK

5

Algorytm formy zapisu:

Algorytm formy zapisu:



Zapis słowny

(np. zbiór przepisów kulinarnych)



Zapis matematyczny -

wzory



Graficzny -

schemat blokowy



Zapis w języku programowania

28.05.21

Dr inż. Tadeusz BURAK

6

Schemat blokowy - elmenty

Schemat blokowy - elmenty

We
A,B,C

START

STOP

WEJŚCIE – WYJŚCIE

PRZETWARZANIE - PROCES

DECYZJA

PROCEDURA

(POWTARZALNY

FRAGMENT ZDEFINIOWANY W INNYM
MIEJSCU)

PRZENIESIENIE

START

STOP

WARUNEK

Tak

Nie

9

9

28.05.21

Dr inż. Tadeusz BURAK

7

Schemat blokowy I (wzór)

Schemat blokowy I (wzór)

)

3

)

2

)

1

)

2

)

2

0

0

0

4

c

c

c

b

a

albo

albo

c

a

b

c

x

b

x

a

y

































Znając parametry a,b,c znajdź miejsce
zerowe funkcji:

a

b

x

a

b

x





















2

2

2

1

a

b

x







2

brak

rozwiązania w

dziedzinie

liczb

rzeczywistych

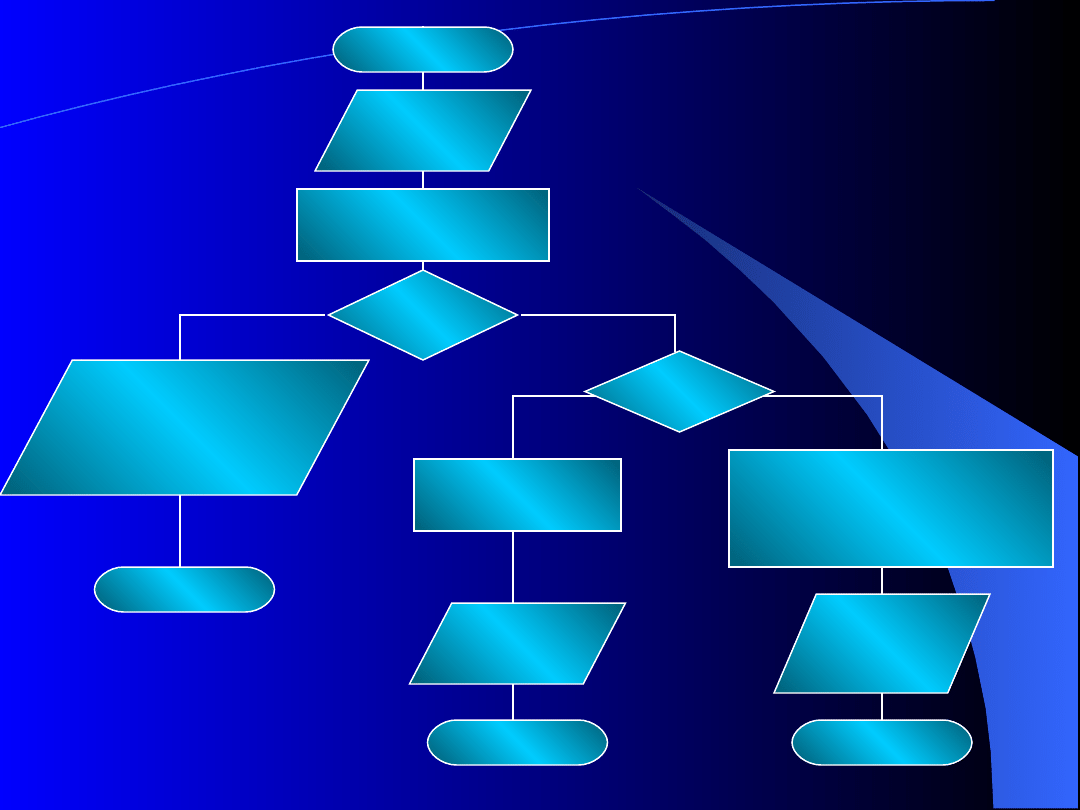
8

Dr inż. Tadeusz BURAK

28.05.21

Start

Start

STOP

STOP

WE:

WE:

A,B,C

A,B,C

D = B2-4*A*C

D = B2-4*A*C

D < 0

D < 0

X = -B/(2*A)

X = -B/(2*A)

WY:

WY:

X

X

D > 0

D > 0

X

X

1

1

= (-B+sqrt(D))/(2*A)

= (-B+sqrt(D))/(2*A)

X2= (-B-sqrt(D))/(2*A)

X2= (-B-sqrt(D))/(2*A)

WY:

WY:

BRAK

BRAK

ROZWIĄZANIA

ROZWIĄZANIA

WY:

WY:

X

X

1

1

, X

, X

2

2

STOP

STOP

STOP

STOP

Tak

Tak

Tak

Tak

Nie

Nie

Nie

Nie

Schemat

Schemat

blokowy

blokowy

II

II

28.05.21

Dr inż. Tadeusz BURAK

9

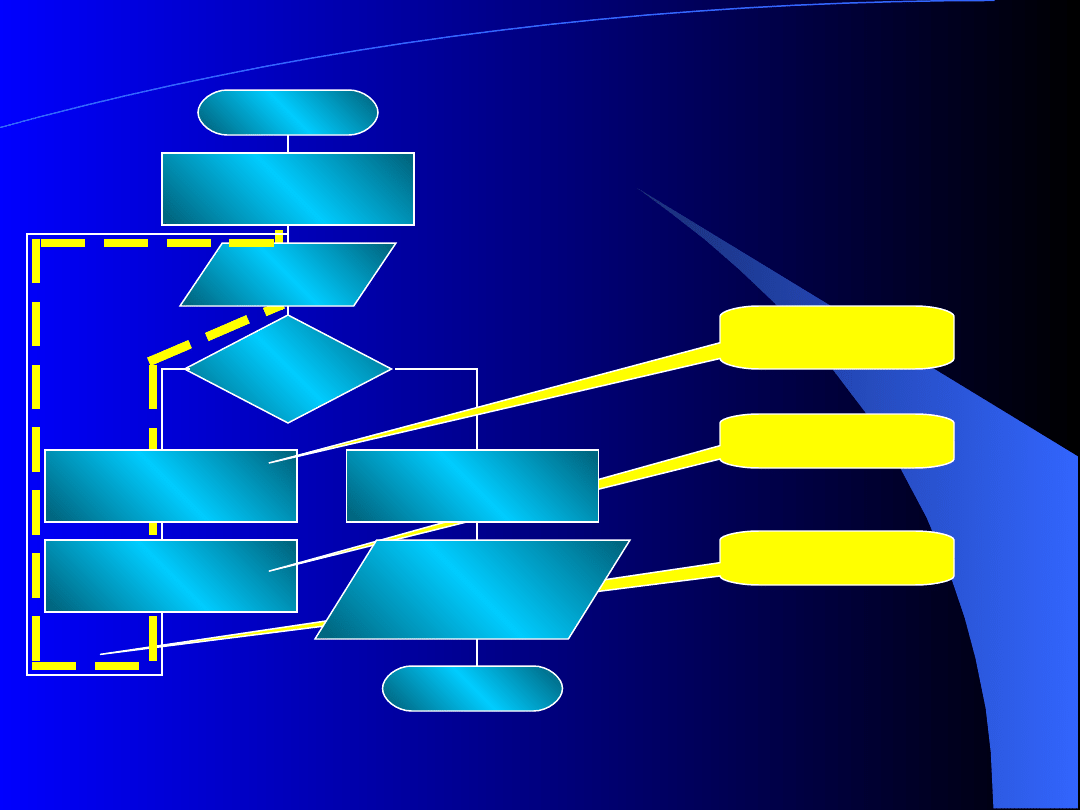
Pętla

I = I+1

I = I+1

Licznik

Schemat

Schemat

blokowy

blokowy

SUMATOR

SUMATOR

Dane:l

1

, l

2

,l

3

,...l

N

,9999 Oblicz

średnią?

STOP

STOP

Start

Start

WE: X

WE: X

I = 0; S=0

I = 0; S=0

X = 9999

X = 9999

S = S+X

S = S+X

WY:

WY:

‘

‘

Średnia =‘ ;

Średnia =‘ ;

S

S

S = S / I

S = S / I

Ta
k

Sumator

Ni
e

28.05.21

Dr inż. Tadeusz BURAK

10

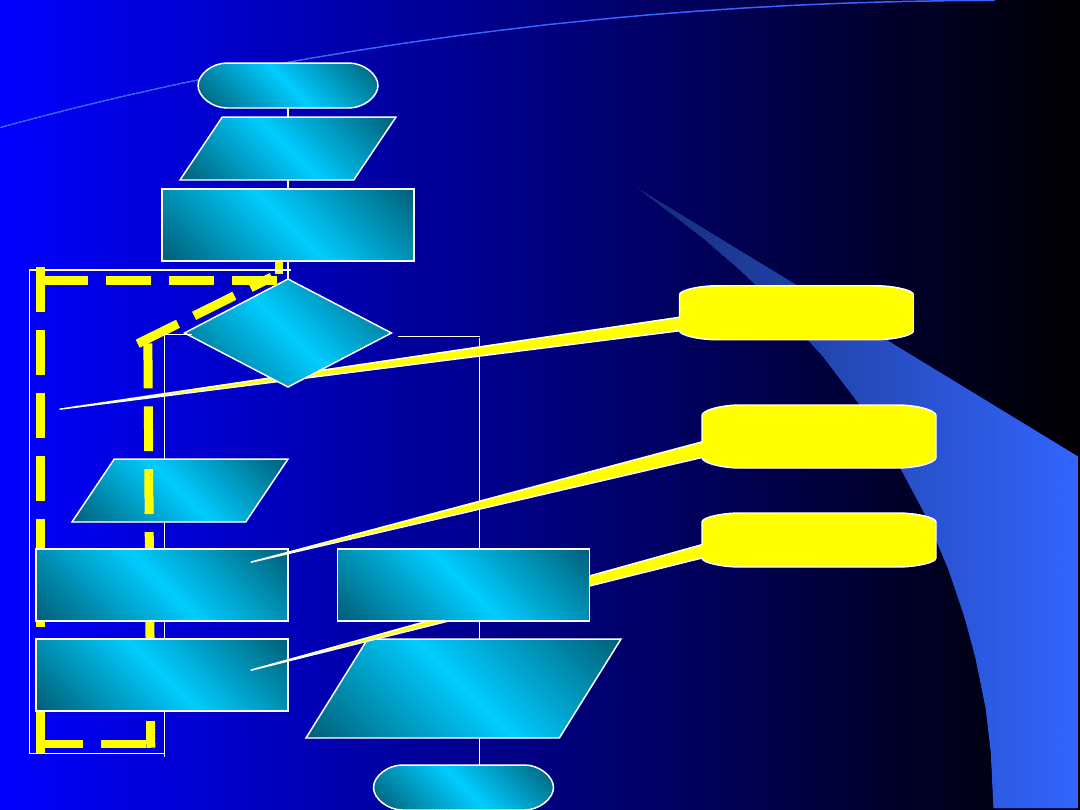
Pętla

Schemat

Schemat

blokowy

blokowy

SUMATOR II

SUMATOR II

Dane:N,l

1

, l

2

,l

3

,...l

N

Oblicz

średnią?

Start

Start

WE: X

WE: X

I = 1; S=0

I = 1; S=0

I = N

I = N

Ta
k

Ni
e

WE: N

WE: N

I = I+1

I = I+1

STOP

STOP

S = S+X

S = S+X

WY:

WY:

‘

‘

Średnia =‘ ;

Średnia =‘ ;

S

S

Licznik

Sumator

S = S / N

S = S / N

28.05.21

Dr inż. Tadeusz BURAK

11

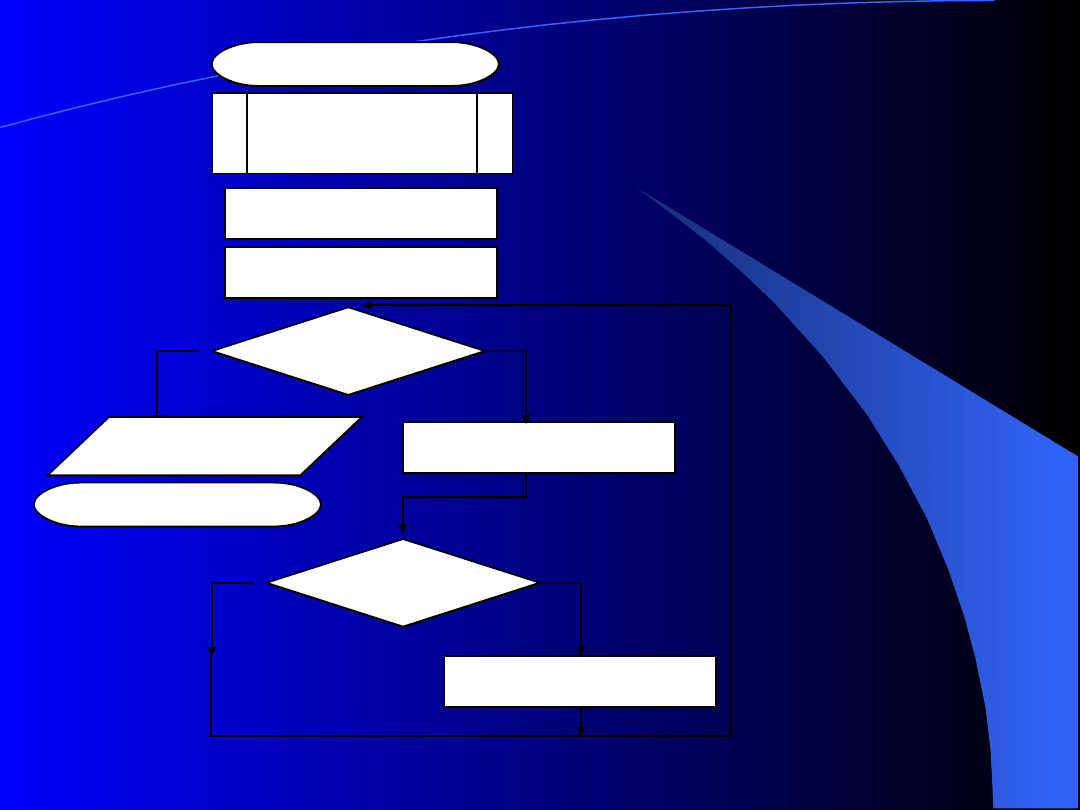
I=I+1

START

We N,

l

1

,l

2

,l

3

,..l

N

Umieść w Tab

A(I)

X= A(1)

I=1

X< A(I)

X= A(I)

I>N

WY X

STOP

    

Dane: N, l

1

, l

2

, l

3

,..l

N

Znajdź największą liczbę

  A(1)=L

1

A(2)=L

2

...

A(N)=L

N

28.05.21

Dr inż. Tadeusz BURAK

12

2.       Procedura zamiany
Dane w tablicy (zmiennej indeksowej):

T(1),T(2),..T(K),..T(L),..T(M)

Zamień wartości T(K) z T(L)

Z = T(K)

PROC.ZAMIEŃ

T(K) =T(L)

T(L) = Z

KONIEC PROC.