dr inż. Tadeusz BURAK

1

Algorytm Euklidesa

Algorytm Euklidesa

Algorytm Euklidesa to algorytm znajdowania

największego wspólnego dzielnika (NWD)

dwóch liczb naturalnych. Nie wymaga on

rozkładania tych liczb na czynniki pierwsze.

Algorytm



dane są dwie liczby naturalne a i b



jeśli b jest równe zeru, to NWD jest równe a



w przeciwnym wypadku oblicz c jako resztę

z dzielenia a przez b



zastąp a przez b, zaś b przez c i zacznij od

początku.

dr inż. Tadeusz BURAK

2

Algorytm Euklidesa

Algorytm Euklidesa

Przykład

Przykład

NWD liczb 1029 i 42 wynosi 21
obliczany jest następująco:

a

   b

   c

1029

42

21

42

21

0

21

0

 

dr inż. Tadeusz BURAK

3

Sortowanie

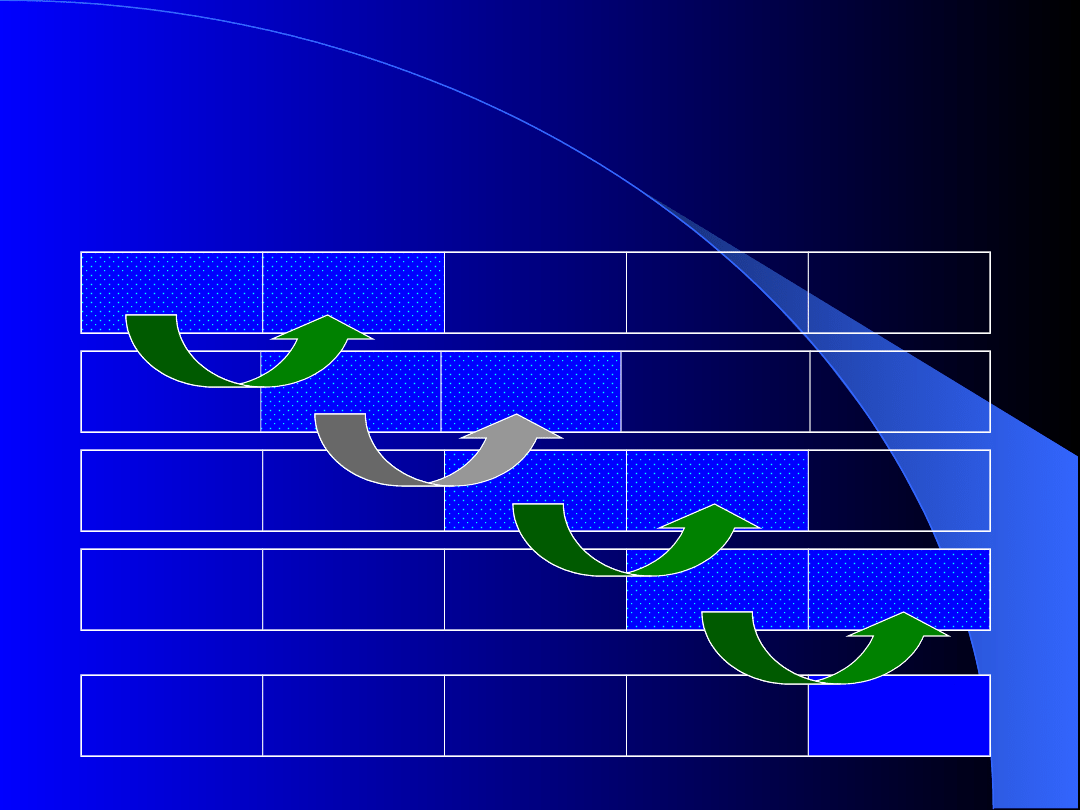
Sortowanie

metodą przez porównanie sąsiednich

metodą przez porównanie sąsiednich

elementów

elementów

32

24

45

-13

26

24

32

45

-13

26

24

32

45

-13

26

24

32

-13

45

26

24

32

-13

26

45

dr inż. Tadeusz BURAK

4

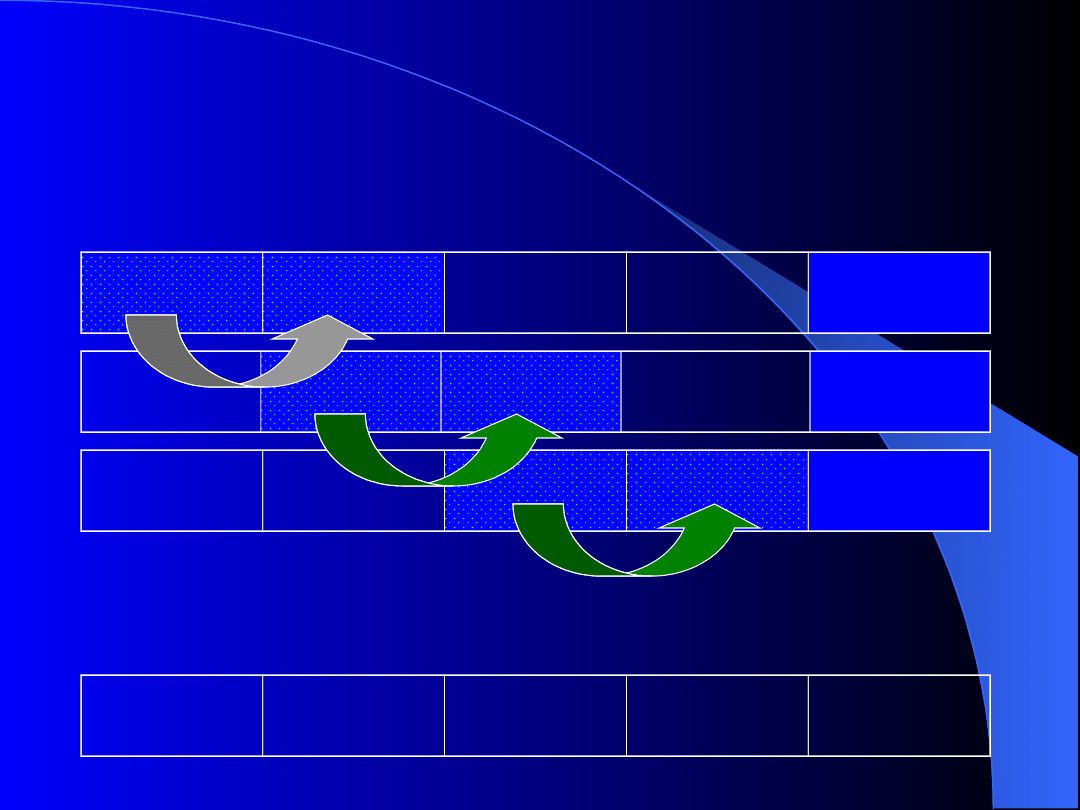
Sortowanie 2

Sortowanie 2

24

32

-13

26

45

24

32

-13

26

45

24

-13

32

26

45

24

-13

26

32

45

dr inż. Tadeusz BURAK

5

Sortowanie 3

Sortowanie 3

24

-13

26

32

45

-13

24

26

32

45

-13

24

26

32

45

dr inż. Tadeusz BURAK

6

Sortowanie 4

Sortowanie 4

-13

24

26

32

45

-13

24

26

32

45

32

24

45

-13

26

Wynik

Dane

wejściowe

dr inż. Tadeusz BURAK

7

Sortowanie schemat

Sortowanie schemat

blokowy

blokowy

START

We: N,L

1

,L

2

...L

N

Do tablicy: (1),A(2),
…,A(N)

J=2

ZAMIEŃ
A(J-1) z A(J)

J > N - I

I = N -1

A(J-1) > A(J)

J =J + 1

I =I + 1

Tak

Nie

Nie

I=1

dr inż. Tadeusz BURAK

8

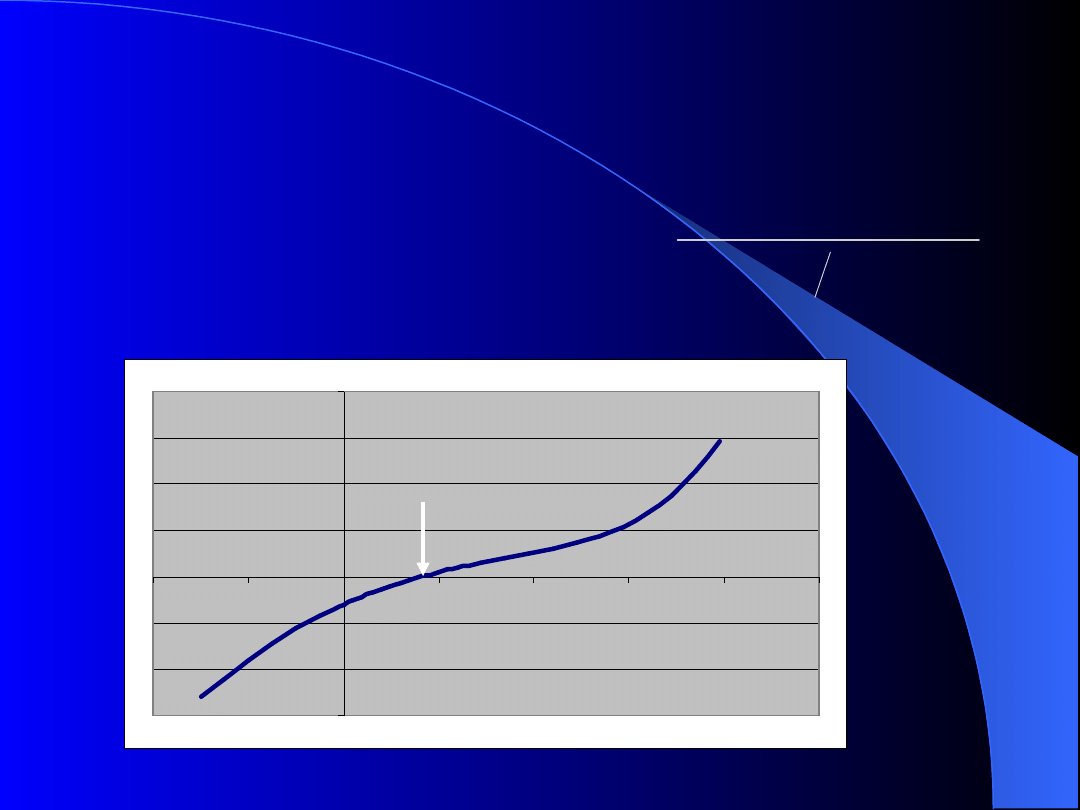
Miejsce zerowe funkcji

Miejsce zerowe funkcji

metoda bisekcji – podziału

metoda bisekcji – podziału

połówkowego

połówkowego

-15

-10

-5

0

5

10

15

20

-4

-2

0

2

4

6

8

10

Dana jest następująca funkcja:

Zadaniem jest znalezienie miejsca zerowego

 

2

2

sin

5

)

cos(

3











x

x

x

y

dr inż. Tadeusz BURAK

9

Miejsce zerowe funkcji

Miejsce zerowe funkcji

(

(

metoda bisekcji)

metoda bisekcji)

ALGORYTM 1

ALGORYTM 1

Założenia:

•Funkcja jest monotoniczna w założonym
przedziale.

•Wartości funkcji na końcach przedziału są
różnego znaku.

( F(Xp) * F(Xk) ) < 0

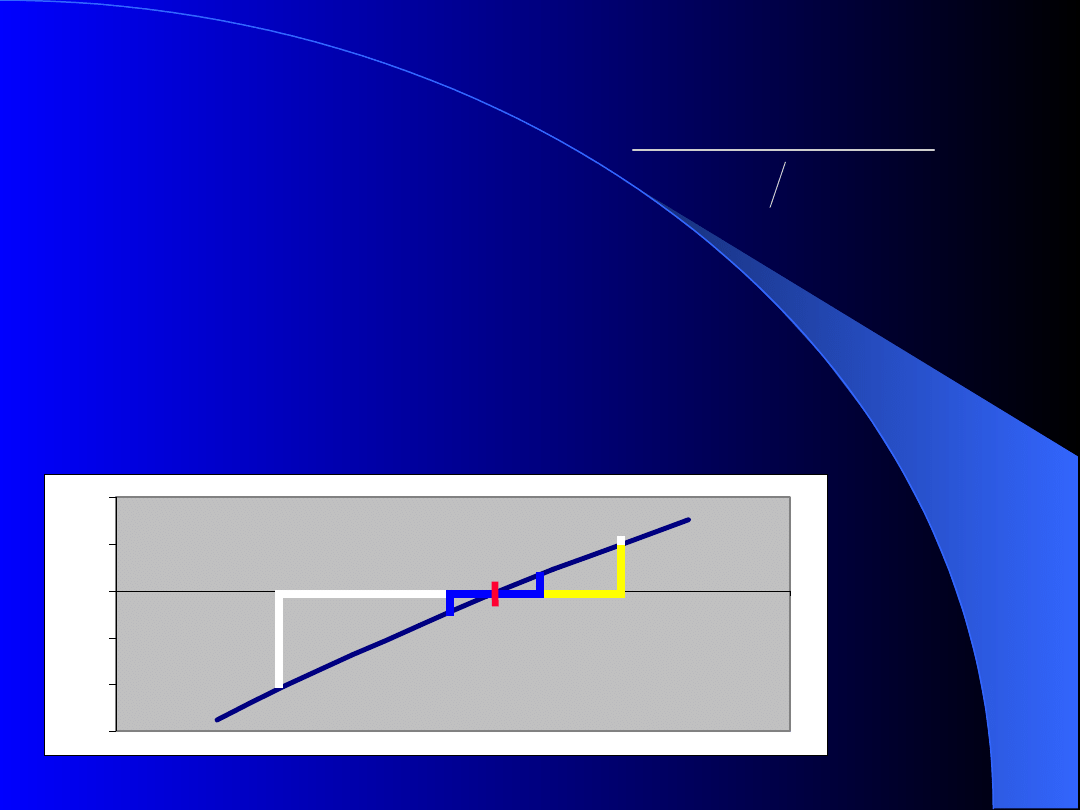
Algorytm:

•znajdujemy wartość funkcji dla połowy długości
przedziału

•Jeżeli wartość funkcji na początku i w środku
przedziału jest tego samego znaku to wybieramy
jako nowy początek przedziału punkt środkowy –
jeśli znaki się różnią to punkt środkowy staje się
nowym końcem przedziału.

dr inż. Tadeusz BURAK

10

Miejsce zerowe funkcji

Miejsce zerowe funkcji

(

(

metoda bisekcji)

metoda bisekcji)

ALGORYTM 2

ALGORYTM 2

 

2

2

sin

5

)

cos(

3











x

x

x

y

Dla danej funkcji:

Przedział początkowy przyjmuje: Xp=1 ,
Xk=2

I odpowiednio Yp= -1,02 ; Yk=0,498

Wyliczone Xs = 1,5 i odpowiednio Ys =
-0,213

-1,5

-1

-0,5

0

0,5

1

0,5

1

1,5

2

2,5

dr inż. Tadeusz BURAK

11

Xp= 1,50

0

Xs= 1,62

5

Xk= 1,75

0

0,250

F(Xp)

=

-

0,21

F(Xs)

=

-

0,02

6

F(Xk)

=

0,15

5

Miejsce zerowe funkcji

Miejsce zerowe funkcji

(

(

metoda bisekcji)

metoda bisekcji)

ALGORYTM 3

ALGORYTM 3

Xp= 1,00

0

Xs= 1,50

0

Xk= 2,00

0

1,000

F(Xp)

=

-

1,02

F(Xs)

=

-

0,21

3

F(Xk)

=

0,49

8

Xp= 1,50

0

Xs= 1,75

0

Xk= 2,00

0

0,500

F(Xp)

=

-

0,21

F(Xs)

=

0,15

5

F(Xk)

=

0,49

8

Xp= 1,63

0

Xs= 1,68

8

Xk= 1,75

0

0,125

F(Xp)

=

-

0,02

6

F(Xs)

=

0,06

5

F(Xk)

=

0,15

5

dr inż. Tadeusz BURAK

12

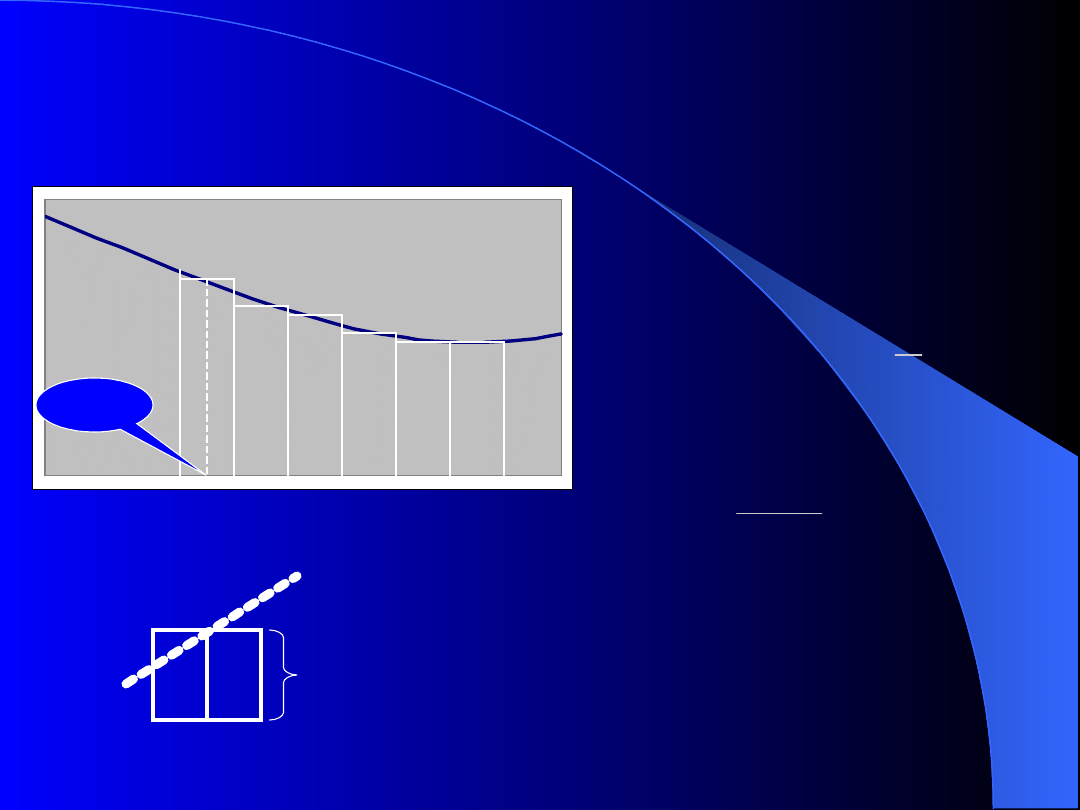
Algorytm obliczania całki

Algorytm obliczania całki

oznaczonej metodą prostokątów

oznaczonej metodą prostokątów

a a+h a+2h ....

b

A+h

/2

N

a

b

h

gdzie

h

i

h

x

f

y

dx

x

f

y

N

i

b

a





















:

)

2

(

)

(

1

a a+h/2 a+h

F(h/2)