Kinetyka

Kinetyka

chemiczna

chemiczna

Kinetyka

chemiczna

zajmuje

się

badaniem przebiegu reakcji chemicznych
w czasie, pomiarem ich szybkości,
czynnikami wpływającymi na szybkość
reakcji. Ostatecznym celem kinetyki
chemicznej jest ustalenie mechanizmu
reakcji na poziomie molekularnym.

Reakcje mogą być :

Homogeniczne

– wszystkie reagenty są

w tej samej fazie np. mieszanina gazowa
lub roztwór

Heterogeniczne

– reagenty występują

w różnych fazach

Z punktu widzenia termodynamicznego
wszystkie reakcje są odwracalne i
zachodzą

aż

do

osiągnięcia

stanu

równowagi.

Reakcje kinetycznie nieodwracalne

to

takie, w których stan równowagi jest
bardzo silnie przesunięty w prawo (w
stronę produktów), a szybkość reakcji
odwrotnej jest znikomo mała

.

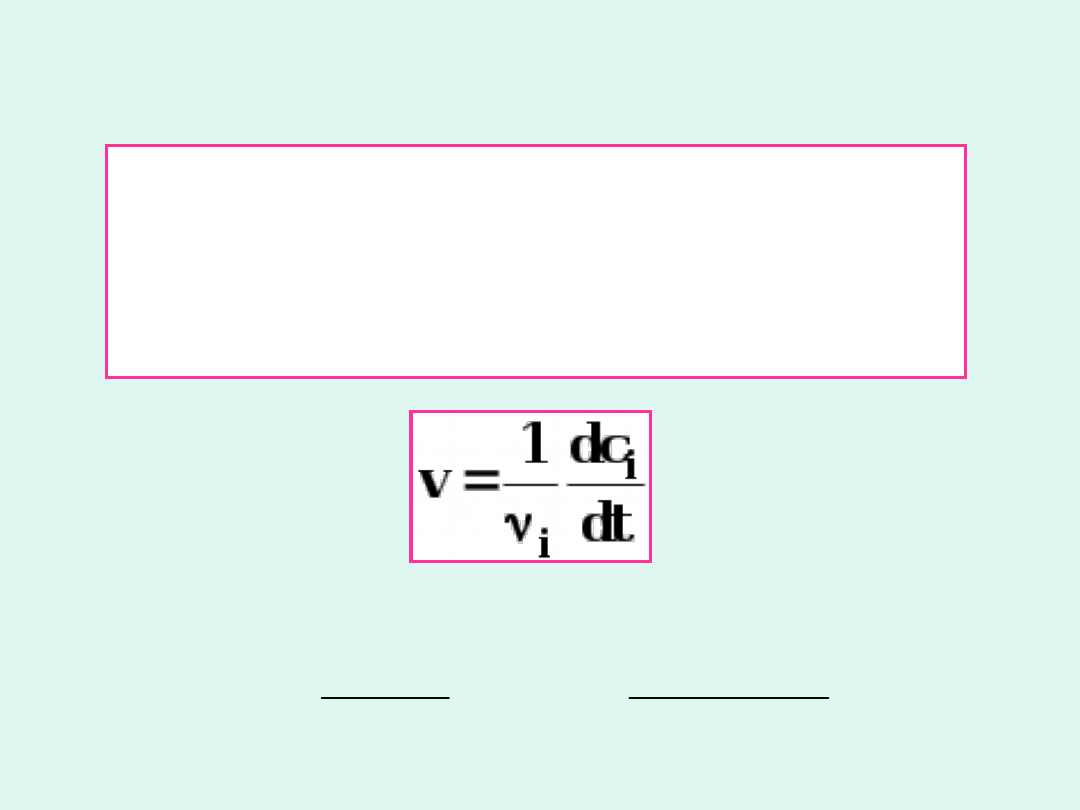
Szybkość reakcji

chemicznej

Szybkość reakcji chemicznej

to

ubytek stężenia molowego substratu
lub

przyrost

stężenia

molowego

produktu do czasu, w jakim nastąpiła
ta zmiana.

Jednostka szybkości reakcji to :

3

3

mol

mol

lub

dm s

dm min

�

�

Metody badania szybkości reakcji

chemicznych

Metody chemiczne

Metody fizykochemiczne

Ponadto istnieją specjalne metody badania
reakcji bardzo szybkich np. fotoliza
błyskowa czy technika „stopped flow”.

W

ustalaniu

mechanizmu

reakcji

chemicznych pomocne są różne techniki
identyfikacji produktów przejściowych.

Przykład

( )

( )

( )

katalizator

1

2

2

2

2 aq

l

2 g

H O

H O

O

�����

�

+

Szybkość tej reakcji można badać w

następujący sposób :

Z mieszaniny reakcyjnej pobierane są próbki, w
których stężenie H

2

O

2

oznaczane jest przez

miareczkowanie jodometryczne.
Z mieszaniny reakcyjnej pobierane są próbki, w
których stężenie H

2

O

2

oznaczane jest

kolorymetrycznie np. z odczynnikiem tytanowym.
Mierzona jest objętość tlenu tworzącego się w
reakcji.
Ponieważ H

2

O

2

silnie absorbuje światło w zakresie

UV, można w sposób ciągły mierzyć jego stężenie
metodą spektrofotometryczną.
Możliwy jest też pomiar elektrochemiczny stężenia
H

2

O

2

i tlenu przy użyciu odpowiednich elektrod

amperometrycznych.

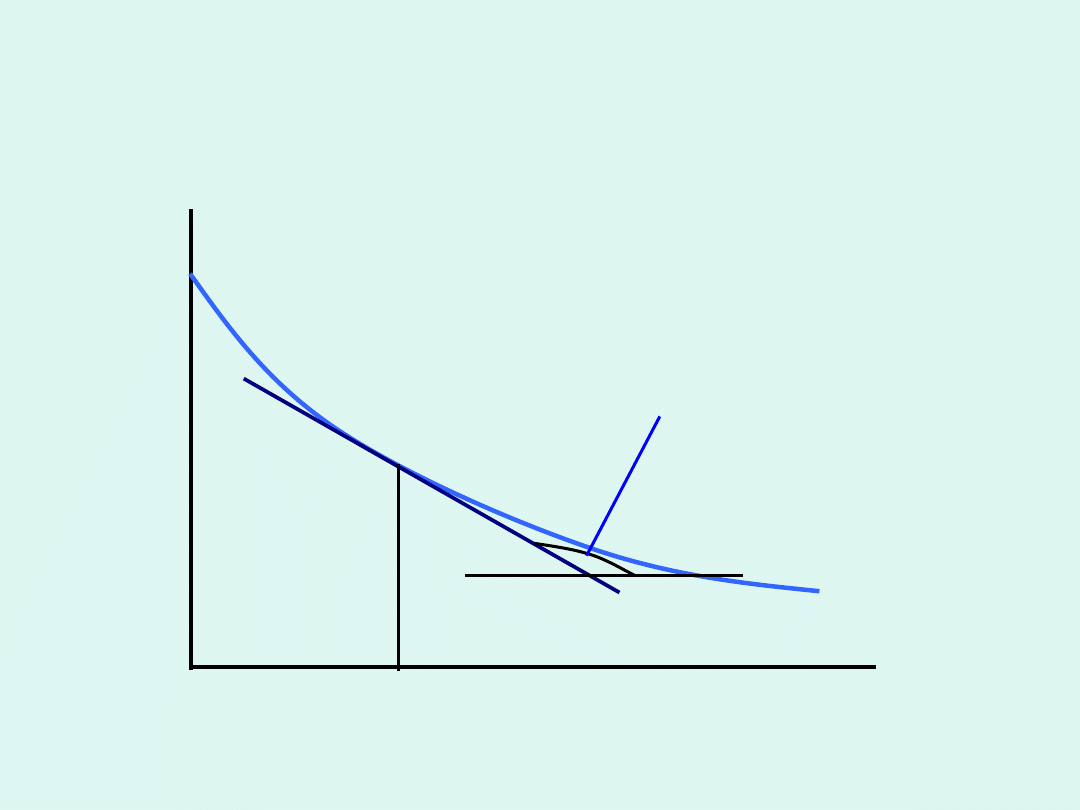
Szybkość reakcji chemicznej –

interpretacja graficzna

stężenie molowe
substratu

czas

t



s

s

v





 tg

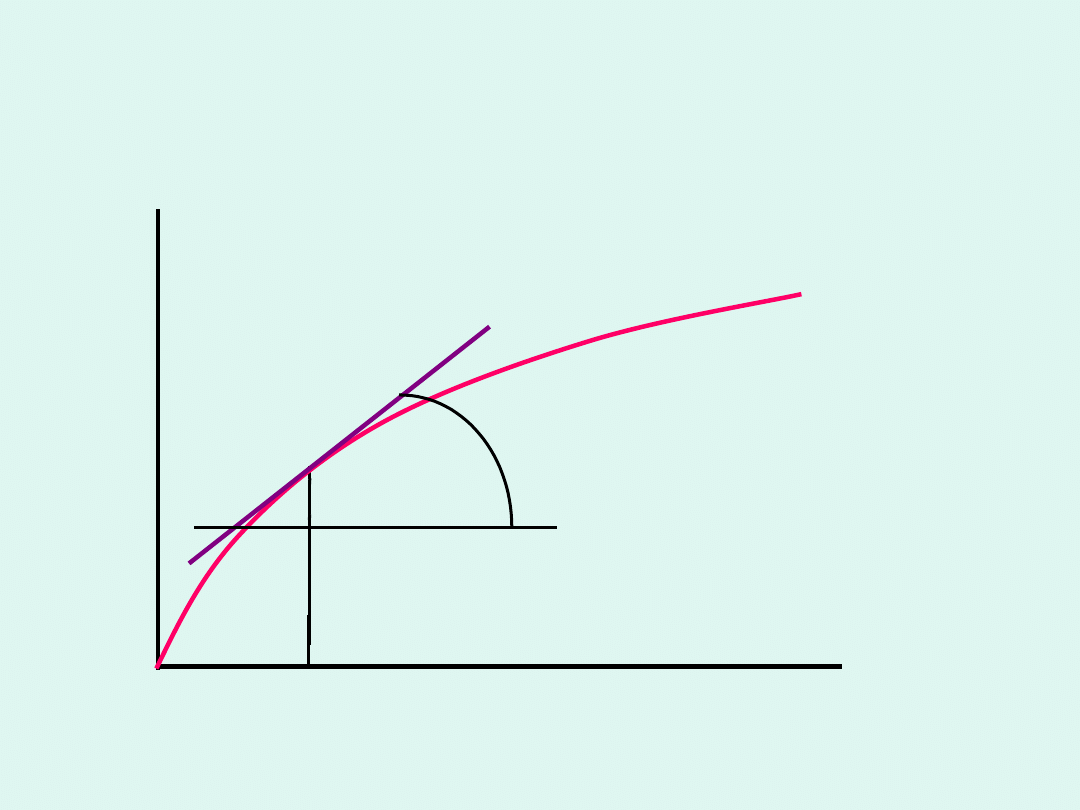
Szybkość reakcji chemicznej –

interpretacja graficzna

stężenie molowe
produktu

czas

t



p

p

v



 tg

Czynniki wpływające na

szybkość reakcji

chemicznych

Stężenie substratów i

produktów

Temperatura
Rodzaj i stężenie katalizatora
Inne : rodzaj rozpuszczalnika,

siła jonowa, ciśnienie, światło,
kształt i rodzaj naczynia, w którym
przebiega reakcja i inne

Pierwsze trzy czynniki wpływają na szybkość każdej
reakcji chemicznej, natomiast czynniki z punktu
czwartego wpływają na szybkość tylko określonych
reakcji.

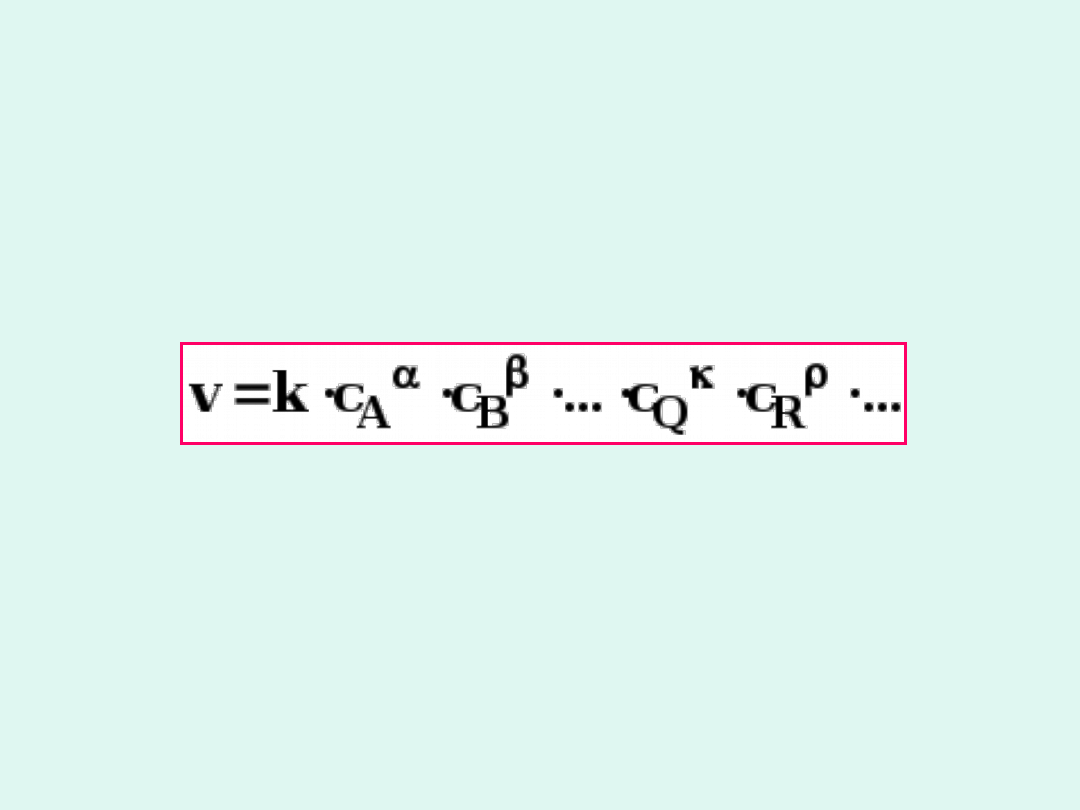
Wpływ stężenia reagentów

aA bB ....

qQ rR ...

+

+ �

+

+

W większości przypadków szybkość
reakcji zależy od stężeń reagentów w
następujący sposób :

Jest to

kinetyczne równanie reakcji

w

postaci różniczkowej.

k

– stała szybkości reakcji (ma stałą

wartość w określonych warunkach
prowadzenia reakcji)



- rząd reakcji względem

odpowiednio reagenta A, B, Q, R
(cząstkowe) (nie mają nic wspólnego ze
współczynnikami stechiometrycznymi a,
b, q, r)

Całkowity rząd reakcji chemicznej

to

suma wykładników potęgowych, w
jakich stoją stężenia reagentów w
kinetycznym równaniu reakcji.

r

...

...

=a +b+ +k+r +

Rząd reakcji może wyrażać się liczbami 0, 1, 2, 3. W
pewnych przypadkach mogą istnieć rzędy ułamkowe
np. ½. Istnieją reakcje, dla których nie można określić
rzędu, gdyż zależność szybkości reakcji od stężenia
reagentów jest bardziej złożona.

Cząsteczkowość

reakcji chemicznej to

liczba cząsteczek biorących udział w
elementarnym akcie reakcji, decydującym
o szybkości całej reakcji.

Czas połowicznej przemiany

jest to

czas, po którym stężenie substratu
maleje o połowę (osiąga połowę
stężenia początkowego).

Reakcja 0 rzędu

k

v

c

k

v

0







t

k

c

c

t

k

c

c

dt

k

dc

k

dt

dc

o

o

t

0

c

c

o

























Szybkość reakcji zerowego rzędu jest stała.

Dla reakcji zerowego rzędu stężenie substratu maleje
liniowo w funkcji czasu.
Z reakcjami zerowego rzędu mamy do czynienia, gdy
szybkość reakcji zależy od jakiegoś innego czynnika, a
nie od stężenia reagentów np. od natężenia światła w
przypadku reakcji fotochemicznych.

k

2

c

k

c

o

2

1

2

1

2

c

o

o

















 

 

min

dm

mol

k

s

dm

mol

k

t

c

c

k

3

3

o











Jednostka stałej szybkości :

Czas połowicznej przemiany :

Czas połowicznej przemiany w przypadku
reakcji zerowego rzędu jest wprost
proporcjonalny do stężenia początkowego
substratu.

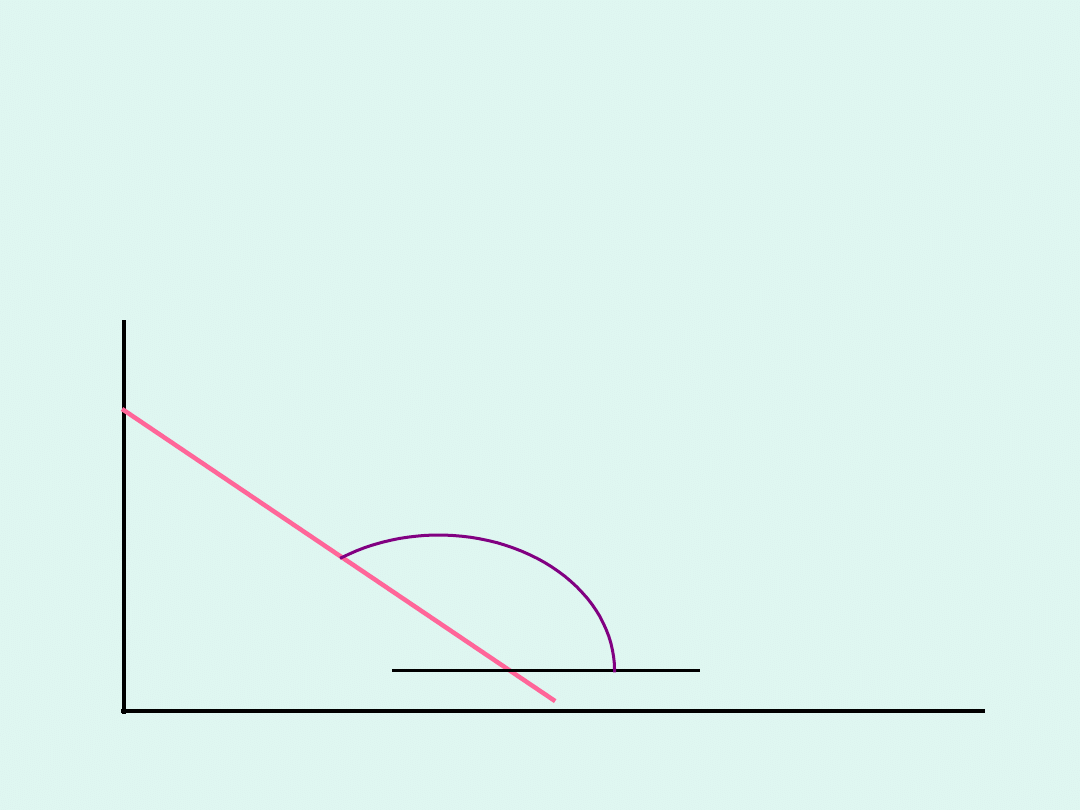
c

t



tg =

-k

Reakcja 0 rzędu - wyznaczanie

stałej szybkości

t

k

c

c

o







Reakcja I rzędu

c

k

dt

dc

c

k

v











kt

o

o

o

t

0

c

c

e

c

c

t

k

c

c

t

k

c

c

dt

k

c

dc

o

























ln

ln

t

k

c

c

o





ln

ln

W przypadku reakcji pierwszego rzędu logarytm
naturalny ze stężenia jest liniową funkcją czasu.

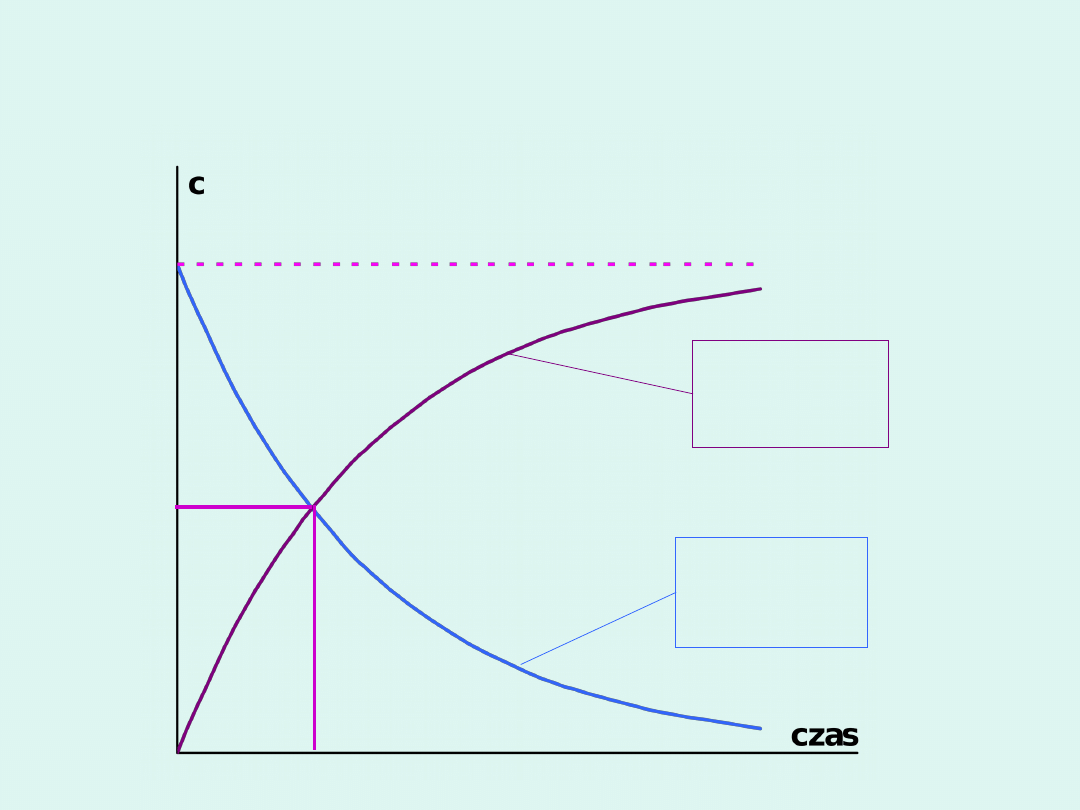
stężenie

substratu

stężenie

produktu

c

o

1/2
c

o



1/2

Reakcja I rzędu

(

)

k t

k t

A

Ao

P

Ao

A

S

c

c

e

c

c

1 e

- �

- �

�

=

�

=

-

 

 

min

1

k

s

1

k

t

k

c

c

o









ln

Jednostka stałej szybkości :

Czas połowicznej przemiany :

Czas połowicznej przemiany w przypadku
reakcji pierwszego rzędu nie zależy od
stężenia początkowego substratu.

k

2

k

2

c

c

2

1

2

1

o

o

ln

ln













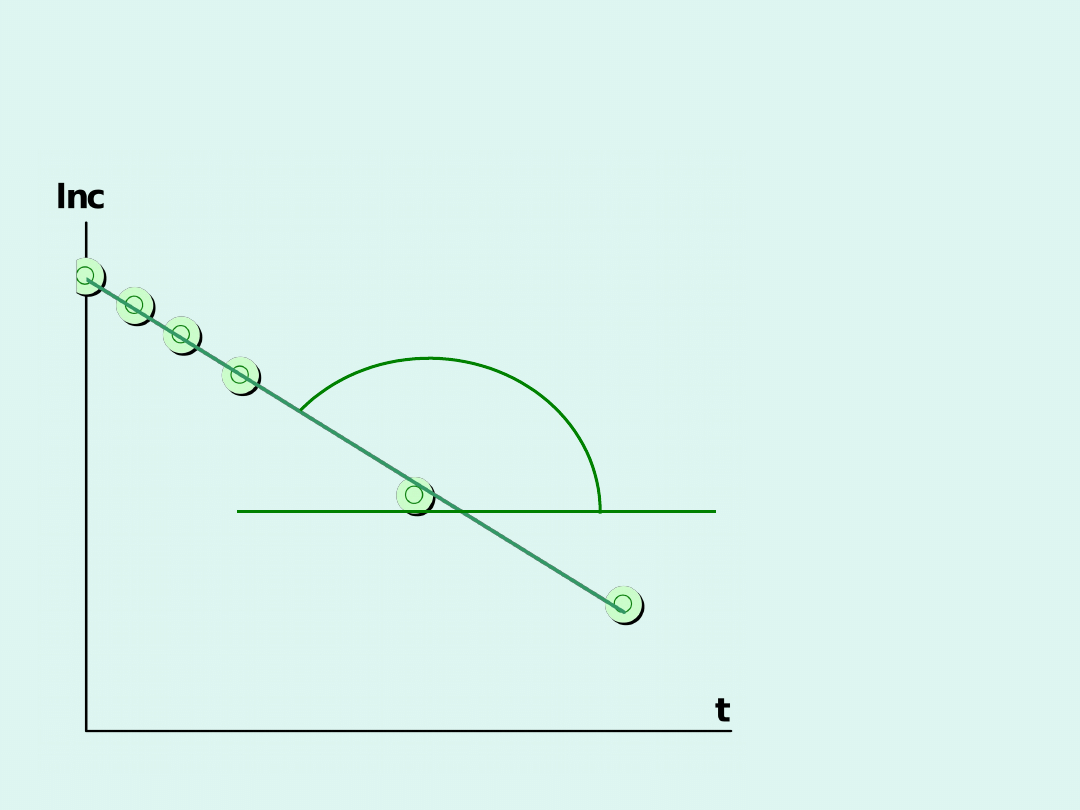
Wyznaczanie stałej szybkości dla

reakcji I rzędu



tg a = -k

t

k

c

c

o





ln

ln

Reakcje pierwszego rzędu są bardzo często
spotykane np. hydroliza estru w środowisku
kwaśnym.

Model kinetyki pierwszego rzędu stosuje się
bardzo często do opisu rozmaitych innych
zjawisk, na przykład :

rozpad izotopów promieniotwórczych

rozpad leku w organizmie po podaniu

śmiertelność mikroorganizmów w wyniku

działania temperatury (pasteryzacja, sterylizacja)

zanik substancji szkodliwych w środowisku

Reakcja II rzędu

2 A

P

A

1.

2.

B

P

�

+ �

2

dc

v

k c

dt

=-

= �

gdy

c

Ao

= c

Bo

gdy

c

Ao

≠ c

Bo

(

) (

)

Ao

Bo

dx

v

k c

x c

x

dt

=

=

-

-

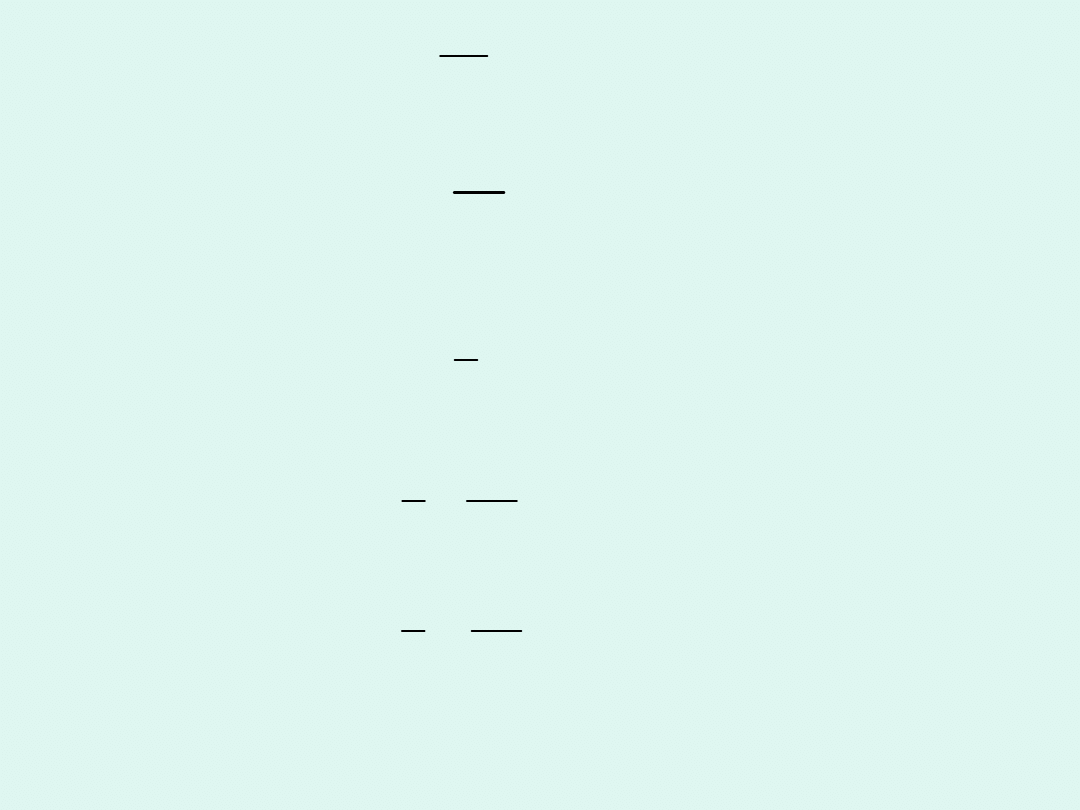
o

o

2

c

t

2

c

0

c

c

o

o

dc

k c

dt

dc

k dt

c

1

k t

c

1 1

k t

c c

1

1

k t

c c

-

= �

-

=

� �

- -

= �

� �

� �

-

= �

=

+ �

�

�

W przypadku reakcji drugiego rzędu odwrotność
stężenia jest liniową funkcją czasu.

[ ]

[ ]

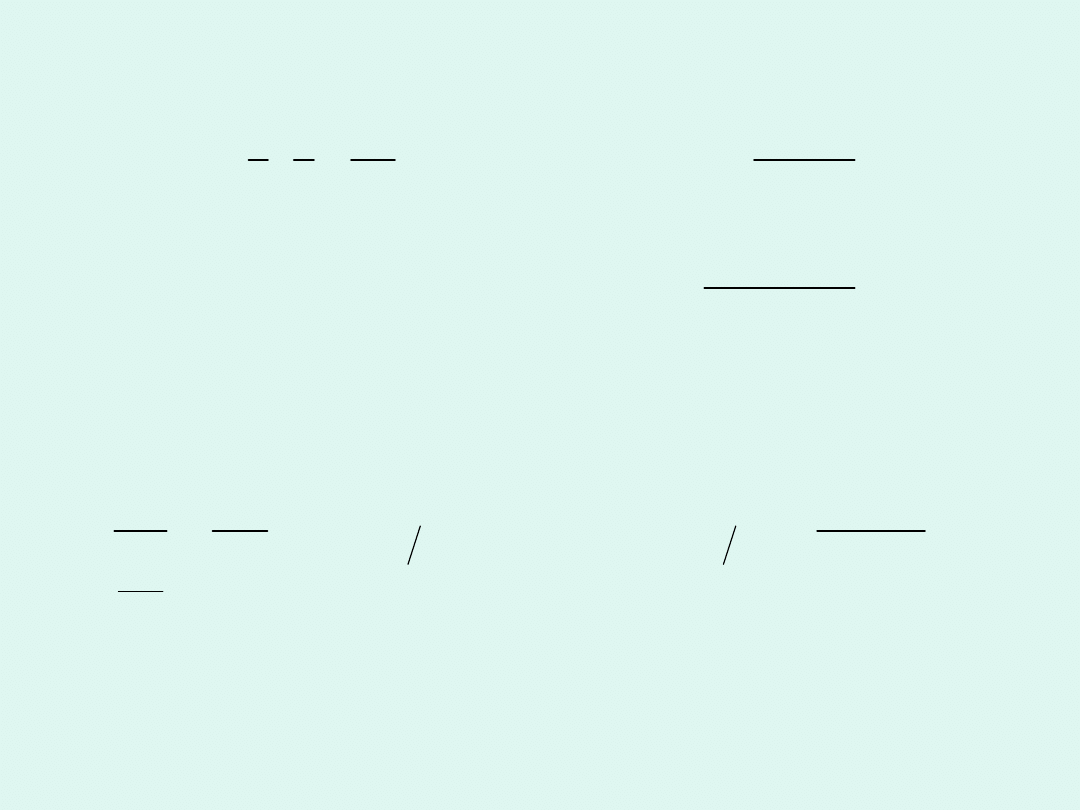
3

o

3

1 1 1

dm

k

k

t c c

s mol

dm

k

min mol

�

�

=

-

�

=

�

�

�

�

�

=

�

Jednostka stałej szybkości :

Czas połowicznej przemiany :

o

1 2

1 2

c

o

o

2

1

1

1

k

c

k c

-

= �

t

�

t

=

�

W przypadku reakcji drugiego rzędu czas
połowicznej przemiany jest odwrotnie
proporcjonalny do stężenia początkowego substratu.

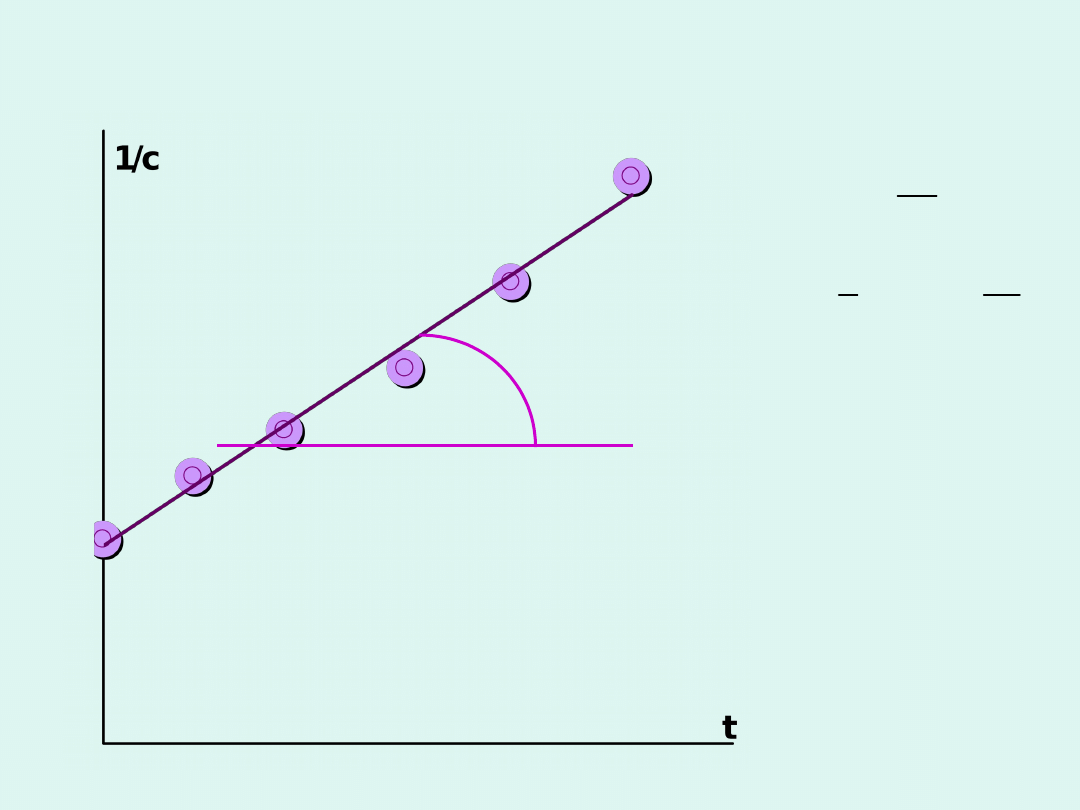
Wyznaczanie stałej szybkości

reakcji II rzędu

2

o

dc

v

k c

dt

1

1

k t

c

c

=-

= �

= �+



tg a = k

1/c

o



 



Bo

Ao

Bo

Ao

c

c

x

c

x

c

k

dt

dx













x

– ubytek stężenia substratu lub przyrost

stężenie produktu

Ao

A

Bo

B

A

Ao

B

Bo

x c

c

c

c

c

c

x c

c

x

=

-

=

-

=

-

=

-



 





 























t

0

x

0

Bo

Ao

Bo

Ao

dt

k

x

c

x

c

dx

kdt

x

c

x

c

dx

Aby wykonać powyższe całkowanie, musimy ułamek
pod całką po lewej stronie rozdzielić na ułamki
proste.



 

 

 





 













 





 





 







Bo

Ao

Bo

Ao

Bo

Ao

Ao

Bo

Ao

Bo

Bo

Ao

Ao

Bo

Bo

Ao

Bo

Ao

Ao

Bo

Bo

Ao

Bo

Ao

Bo

Ao

c

c

1

A

c

c

1

B

1

c

c

B

1

c

B

c

B

B

A

1

c

B

c

A

0

B

A

x

c

x

c

x

B

c

B

x

A

c

A

x

c

x

c

1

x

c

x

c

x

c

B

x

c

A

x

c

x

c

1

x

c

B

x

c

A

x

c

x

c

1

















































































































(

)

(

)

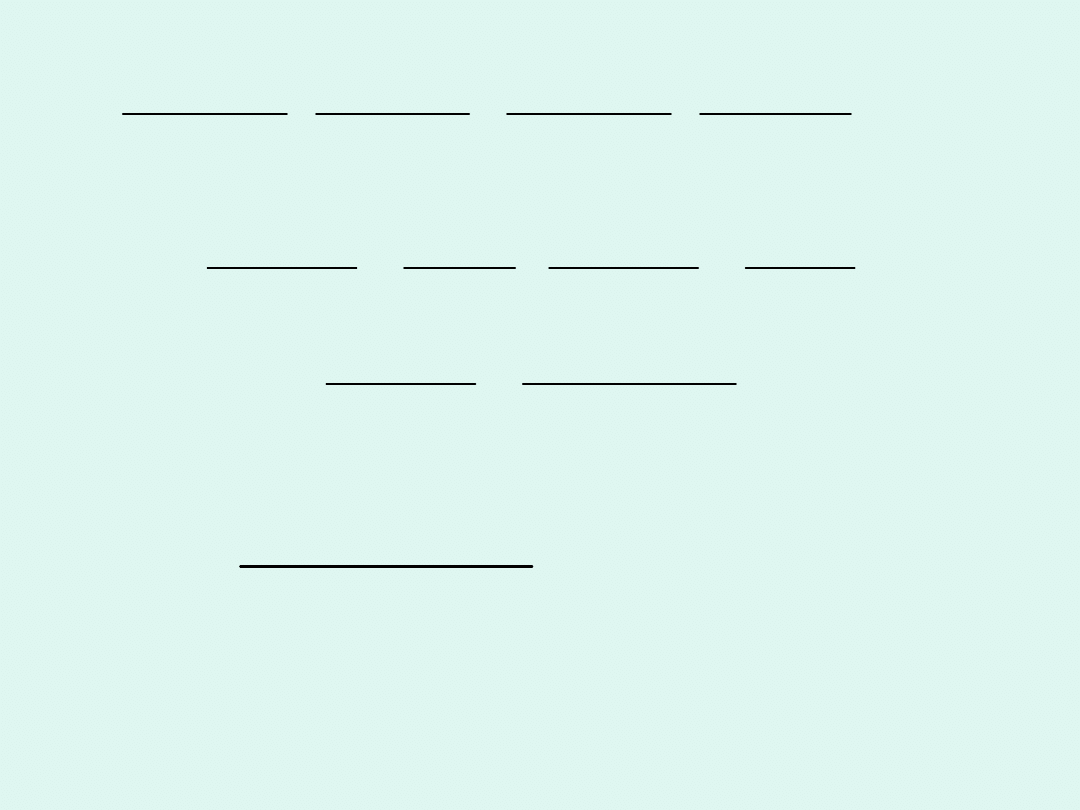
x

x

t

Ao

Bo

Ao

Bo

Ao

Bo

0

0

0

1

dx

1

dx

k dt

c

c

c

c

c

x

c

x

-

+

=

-

-

-

-

�

�

�

(

)

(

)

Ao

Bo

Ao

Bo

Ao

Ao

Bo

Bo

Ao

Bo

Ao

Bo

Ao

Bo

c

x

c

x

1

1

k t

c

c

c

c

c

c

c

x c

1

k t

c

c

c

c

x

ln

ln

ln

-

-

-

= �

-

-

-

�

= �

-

�

-

(

)

(

)

(

)

Ao

Bo

Ao

Bo

Ao

Bo

c

x c

c

c

k t

c

c

x

ln

-

�

=

-

��

�

-

W tym wypadku pojęcie czasu połowicznej przemiany
traci sens.

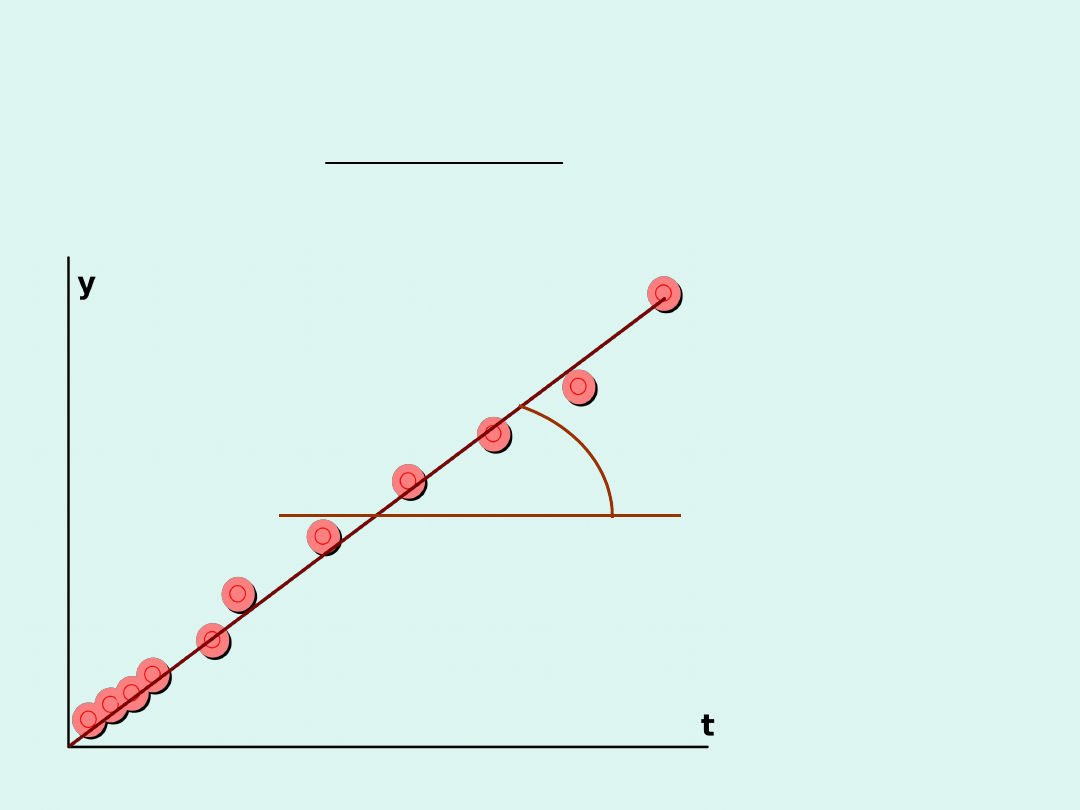
Wyznaczanie stałej szybkości

reakcji II rzędu

(

)

(

)

(

)

Ao

Bo

Ao

Bo

Ao

Bo

c

x c

y

c

c

k t

c

c

x

ln

-

�

=

=

-

��

�

-

0



tg  = (c

Ao

- c

Bo

)·k

Reakcja III rzędu

Rozpatrzymy tylko jeden przypadek, gdy mamy
jeden substrat, lub kilka, ale ich stężenia
początkowe są jednakowe.

C

B

A

B

2

A

3

A

c

c

c

k

v

c

c

k

v

c

k

v



















3

dc

k c

dt

-

= �

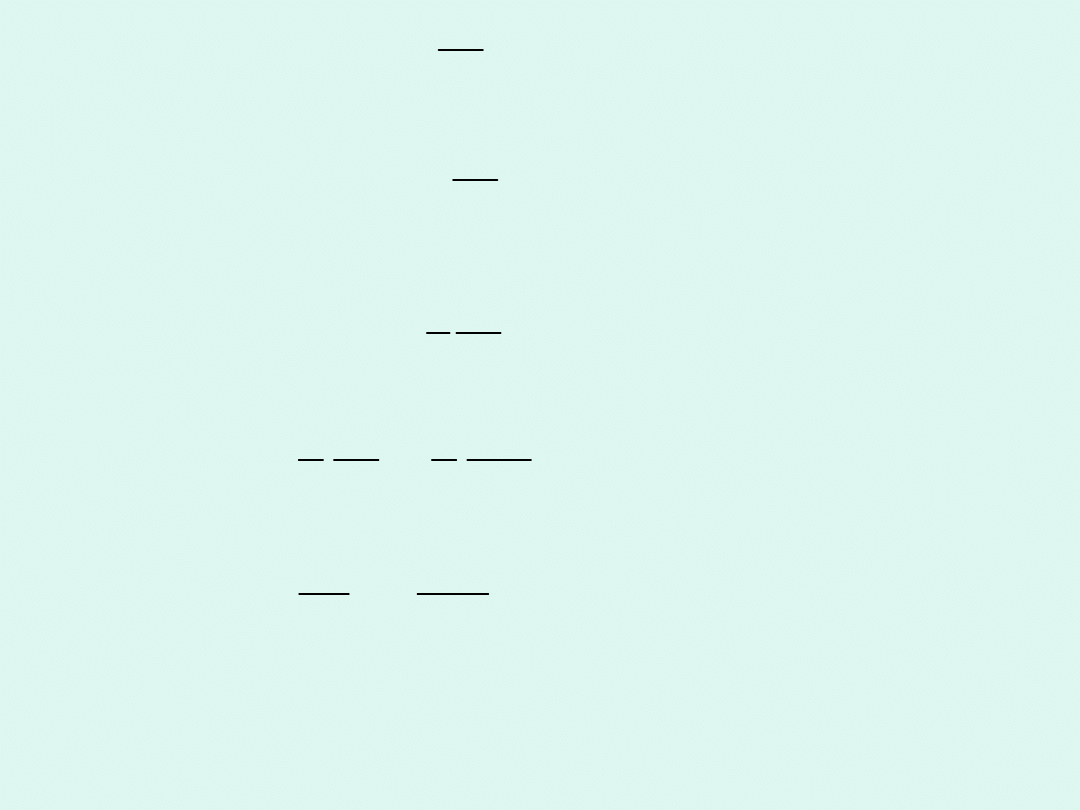
o

o

3

c

t

3

c

0

c

2

c

dc

k dt

c

dc

k dt

c

1 1

k t

2c

-

= �

-

=

�

�

- -

= �

�

�

�

�

�

�

t

k

c

1

2

1

c

1

2

1

2

o

2







t

k

2

c

1

c

1

2

o

2









Dla reakcji trzeciego rzędu odwrotność stężenia
podniesionego do kwadratu jest liniową funkcją
czasu.

[ ]

[ ]

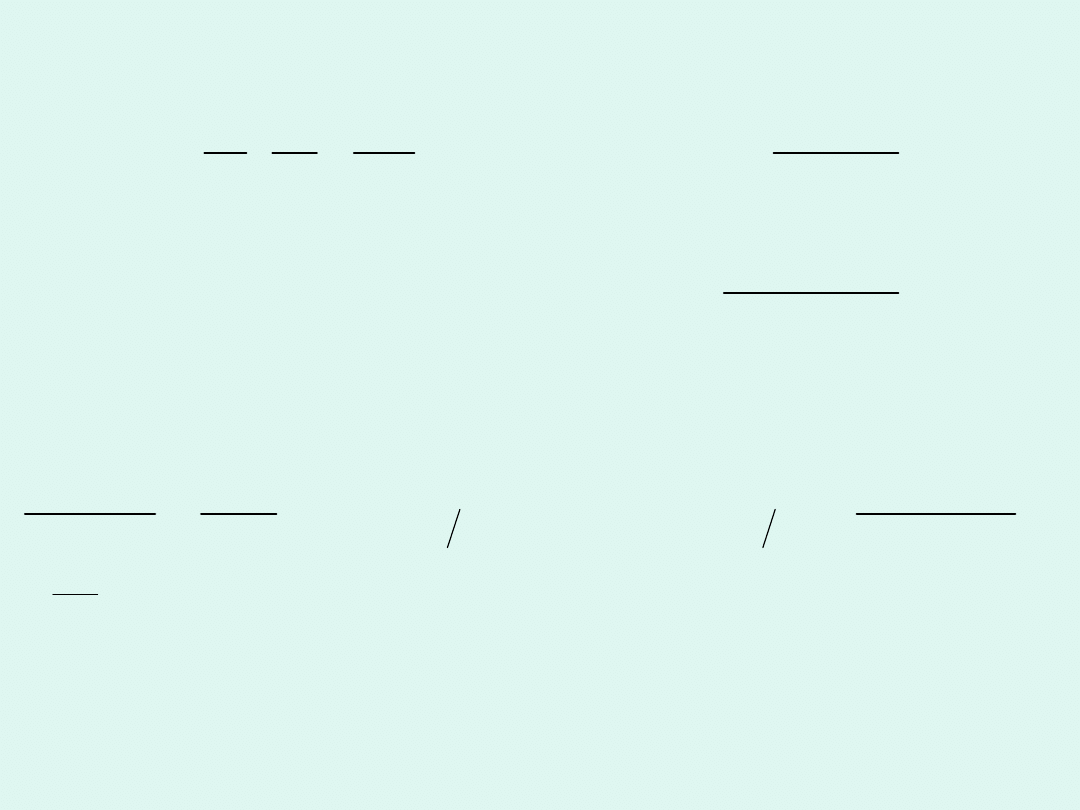
6

2

2

2

o

6

2

1 1

1

dm

k

k

2t c

c

s mol

dm

k

min mol

�

�

�

�

=

-

�

=

�

�

�

�

�

=

�

Jednostka stałej szybkości :

Czas połowicznej przemiany :

o

1 2

1 2

2

2

2

c

o

o

2

1

1

3

2k

c

2k c

-

=

�

t

�

t

=

�

� �

� �

� �

W przypadku reakcji trzeciego rzędu czas
połowicznej przemiany jest odwrotnie
proporcjonalny do stężenia początkowego substratu
podniesionego do kwadratu.

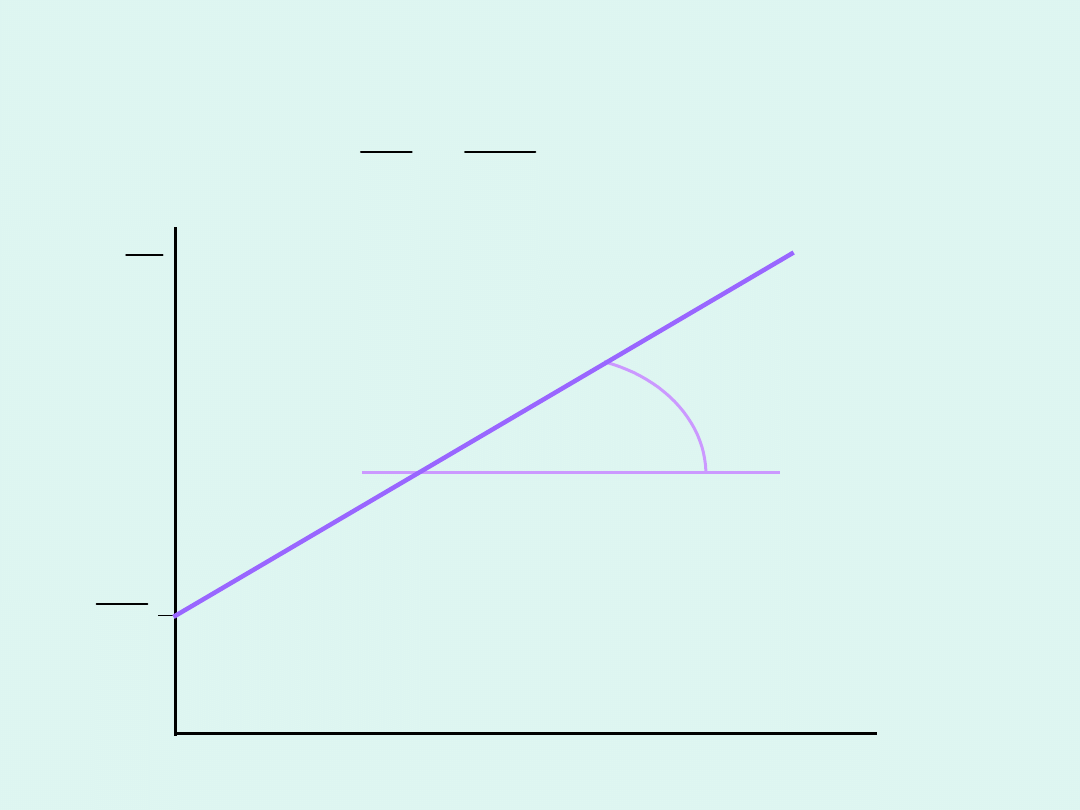
Wyznaczanie stałej szybkości

reakcji III rzędu

2

2

o

1

1

2 k t

c

c

=

+ ��

t



2

1

c

2

o

1

c

tg a = 2 k

Jednostka stałej szybkości reakcji zależy od rzędu

reakcji.

Metody wyznaczania rzędu

reakcji chemicznej

Metoda podstawienia do wzoru
Metoda czasów połowicznej
przemiany
Metoda różniczkowa (van’t
Hoffa)
Metoda izolacyjna Ostwalda –
pozwala na wyznaczenie
cząstkowych rzędów względem
poszczególnych reagentów

Wyznaczanie rzędu reakcji

metodą podstawiania do wzoru

Polega na podstawianiu do równań
scałkowanych danych doświadczalnych i
stwierdzeniu do którego z równań dane
pasują najlepiej. Można to robić w sposób
rachunkowy lub graficzny.

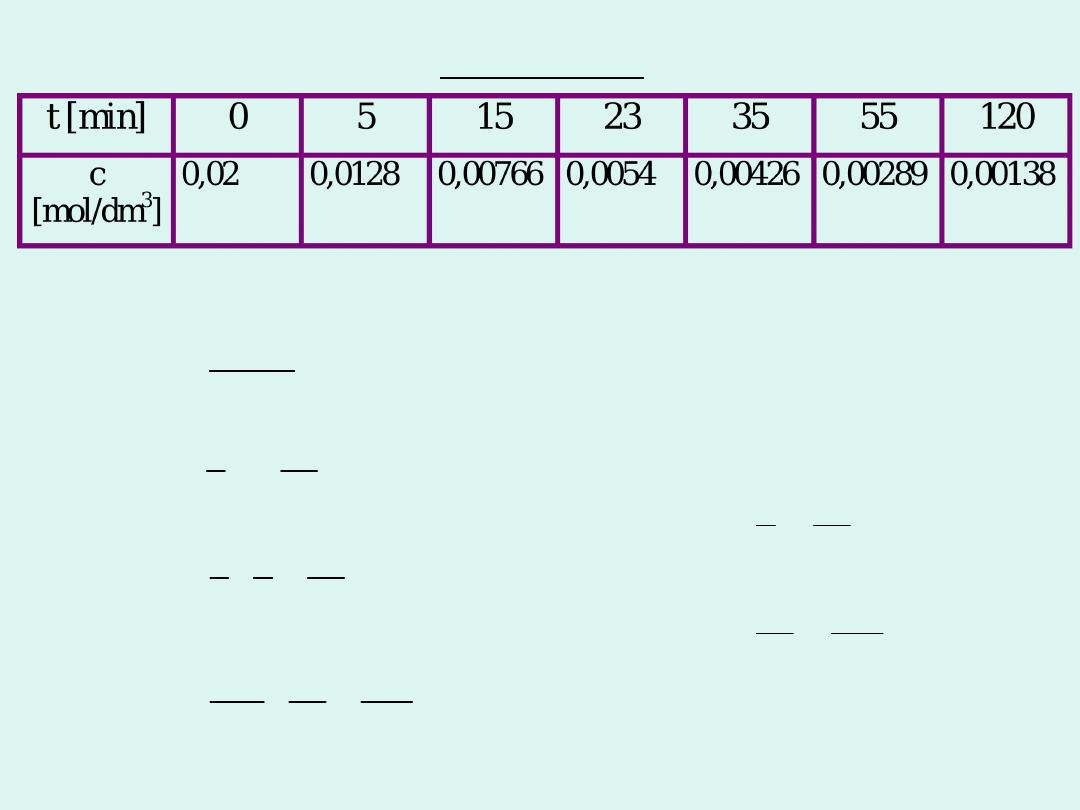
Przykład

o

o

o

2

2

o

0 c c

k t

1 lnc lnc

k t

1 1

2

k t

c c

1

1

3

2 k t

c

c

= - �

=

- �

=

+ �

=

+ ��

o

o

o

2

2

o

c

c

0 k

t

c

1

1 k

ln

t

c

1 1 1

2 k

t c c

1

1

1

3 k

2 t c

c

-

=

= �

�

�

=

-

�

�

�

�

�

�

=

-

�

�

�

�

��

�

sposób rachunkowy
sposób graficzny

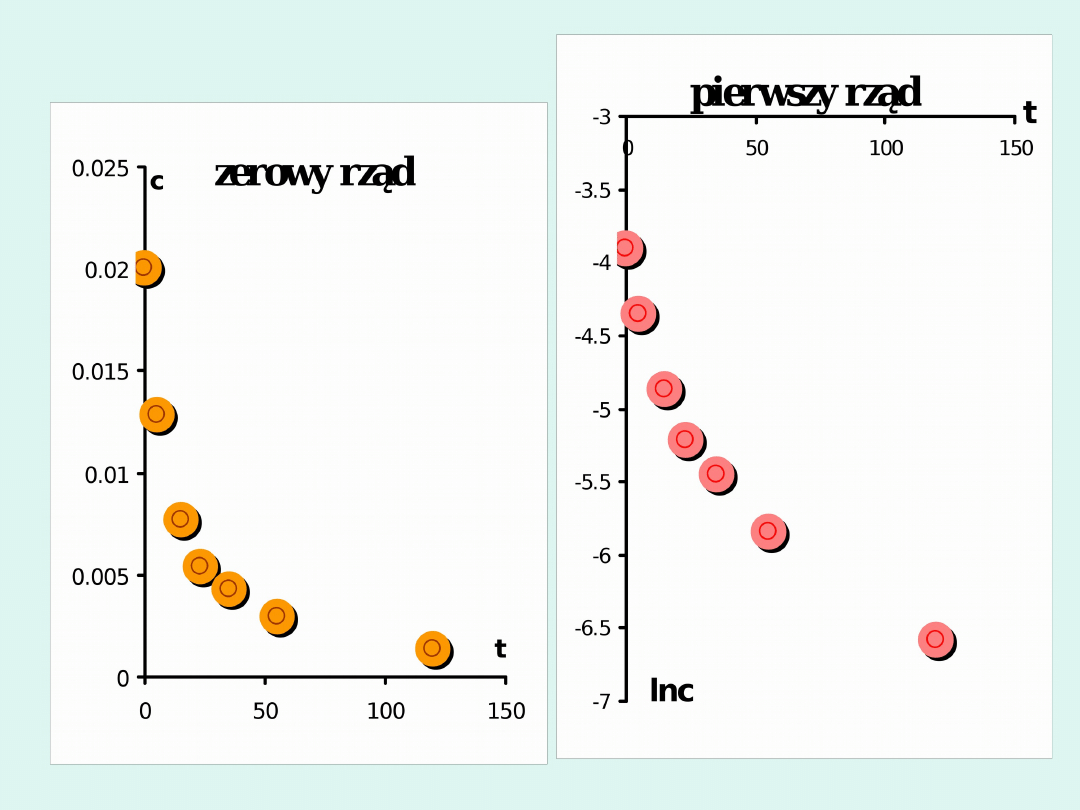
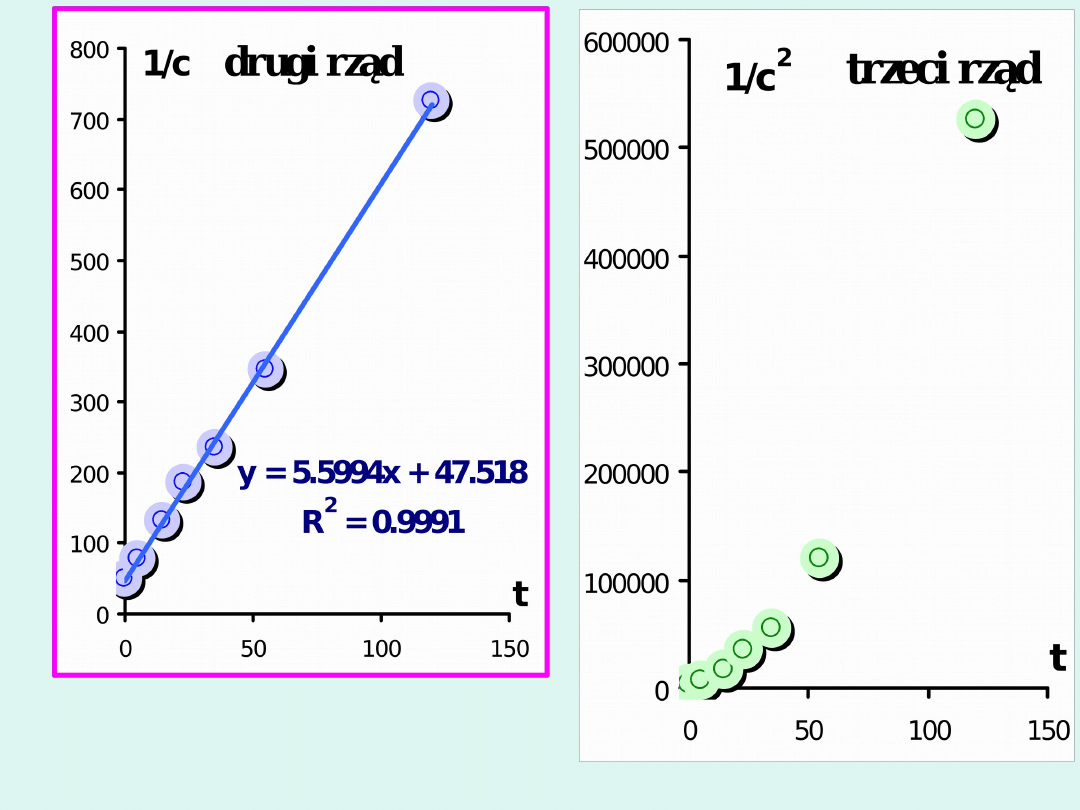
Reakcja jest II rzędu.

Wyznaczanie rzędu reakcji

metodą różniczkową

r

c

k

v





r

1

1

r

2

2

v

k c

v

k c

= �

= �

Dzielimy oba równania stronami i otrzymujemy :

r

r

1

1

1

r

2

2

2

v

k c

c

v

c

k c

�

� �

=

=� �

� �

�

( )

1

1

1

2

2

2

1

2

1

2

r

v

c

c

v

c

c

v

v

c

c

ln

ln

rln

ln

r

ln

=

=

=

Po zlogarytmowaniu stronami otrzymujemy :

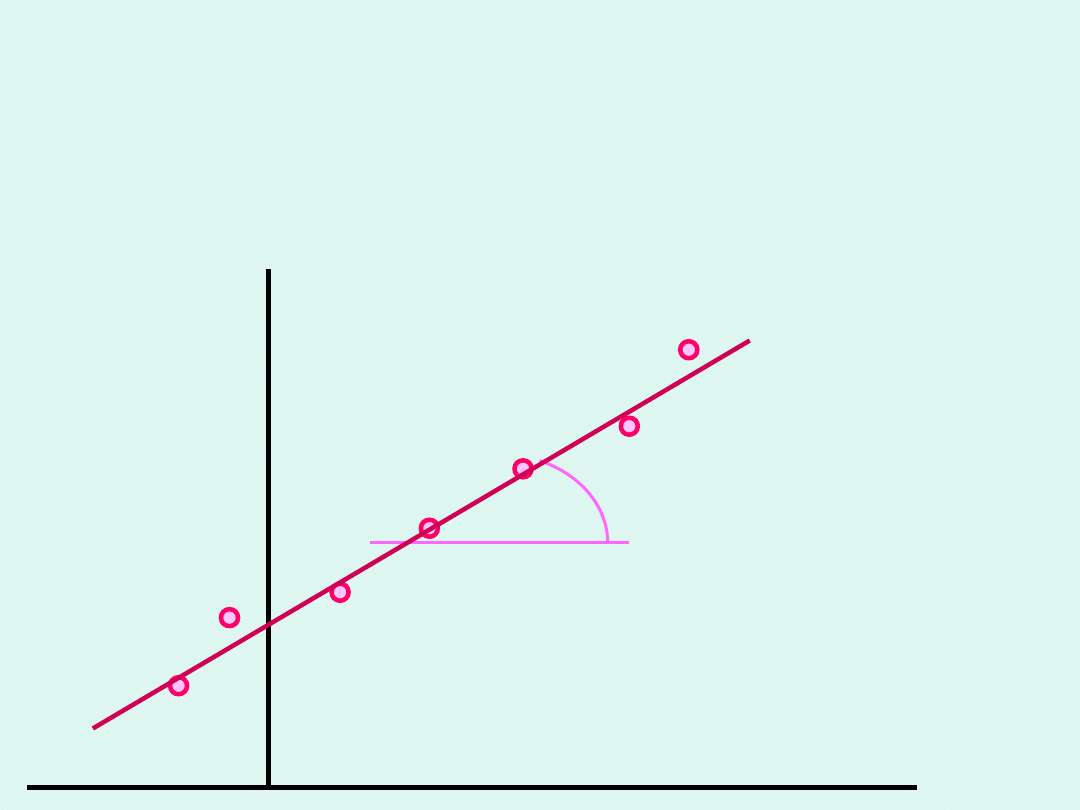
Wyznaczanie rzędu reakcji metodą

różniczkową

r

c

k

v





v

k r

c

ln

ln

ln

=

+ �

ln
v

ln c



tg = r

Po
zlogarytmowaniu
stronami :

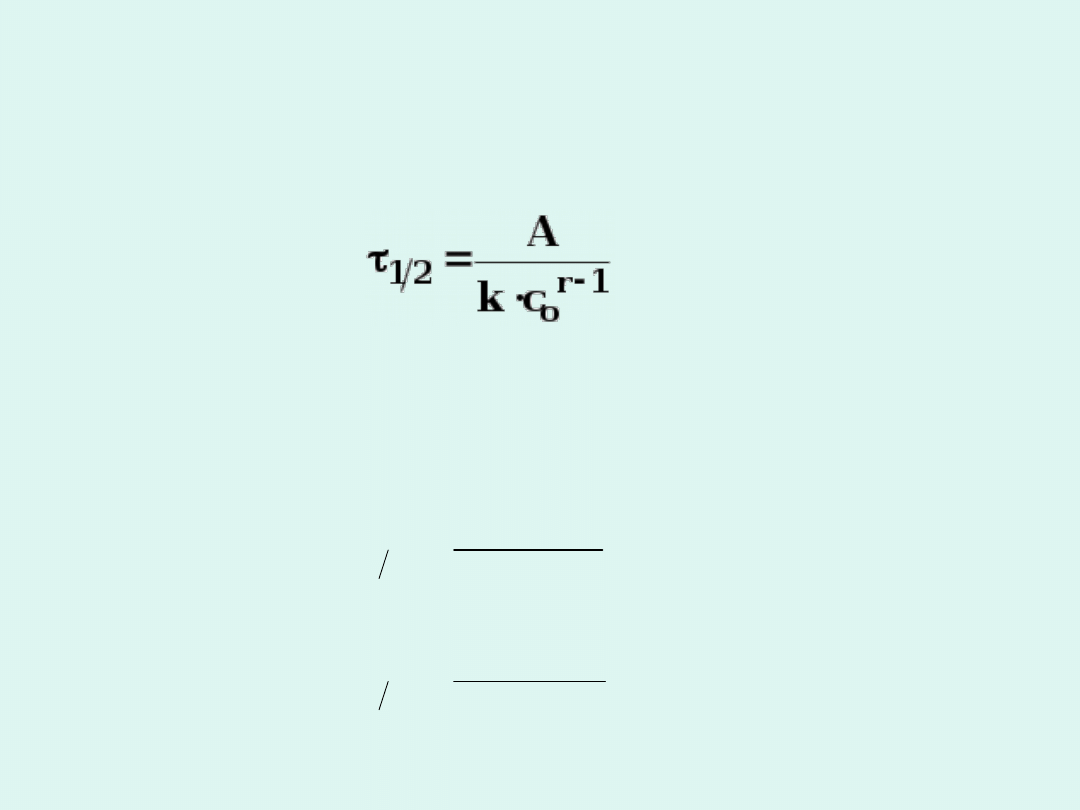
Wyznaczanie rzędu reakcji

chemicznej na podstawie

czasów połowicznej przemiany

Wyznaczamy dwa czasy połowicznej przemiany dla
dwu różnych stężeń początkowych substratu w tej
samej temperaturze.

1

r

2

o

2

1

1

r

1

o

2

1

c

k

A

c

k

A

















''

'

Dzielimy oba wyrażenia stronami :

1

r

1

o

2

o

1

r

1

o

1

r

2

o

c

k

A

c

k

A

2

1

2

1

c

c

c

c

1

r

2

o

1

r

1

o





































''

'

Po zlogarytmowaniu stronami otrzymujemy :





''

'

''

'

ln

ln

''

'

ln

ln

ln

2

1

2

1

2

1

2

1

1

r

c

c

1

r

c

c

1

o

2

o

1

r

1

o

2

o

2

1

2

1





































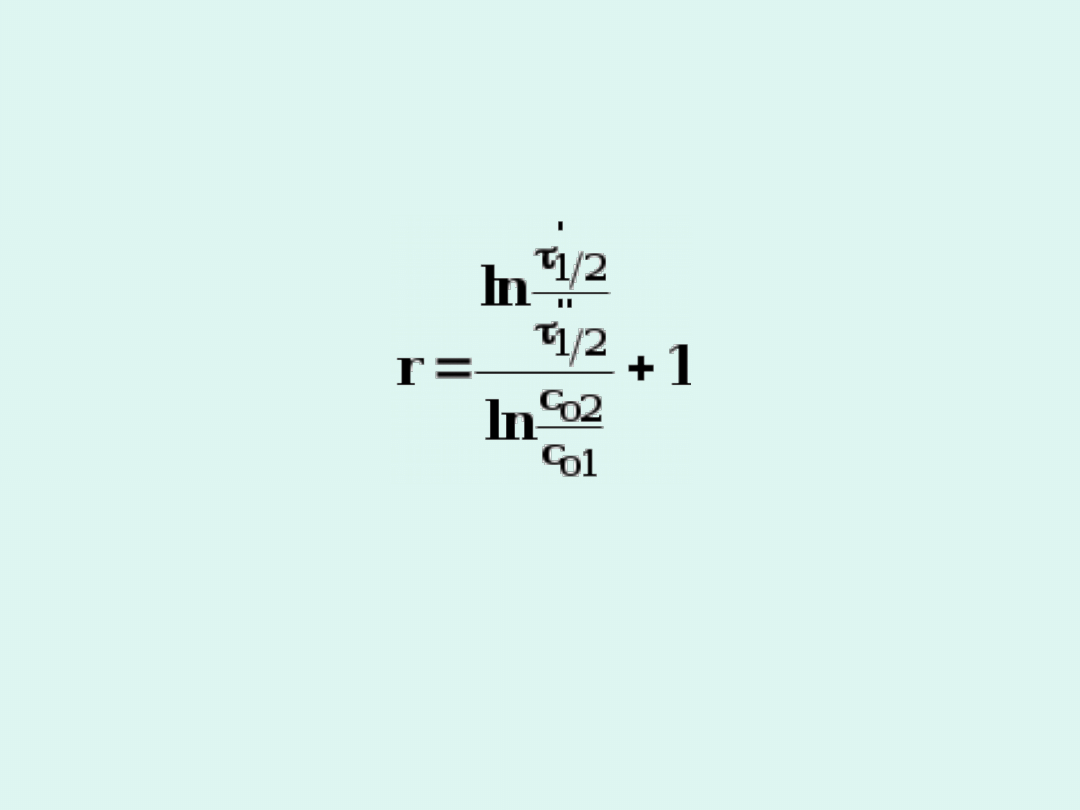
Ostatecznie rząd reakcji chemicznej obliczamy z
równania :

Wyznaczanie rzędu reakcji

chemicznej metodą izolacyjną

Ostwalda

A

B

v k c

c

a

b

= � �

Metoda

ta

pozwala

na

wyznaczenie

indywidualnych

rzędów

reakcji

dla

poszczególnych substratów.

Ustalamy warunki

reakcji tak, aby

c

Ao

>> c

Bo

.

Ustalamy warunki

reakcji tak, aby

c

Ao

<< c

Bo

.

















Ao

'

B

'

Ao

A

A

c

k

k

c

k

v

c

c

const

c

















Bo

''

A

''

Bo

B

B

c

k

k

c

k

v

c

c

const

c

r = 

Rzędy



i



po „izolacji” wyznaczamy którąś z

poprzednio poznanych metod.

1.

Reakcje równoległe

2.

Reakcje odwracalne

3.

Reakcje następcze

Reakcje złożone

A

P

1

P

2

A

P

A

B

C

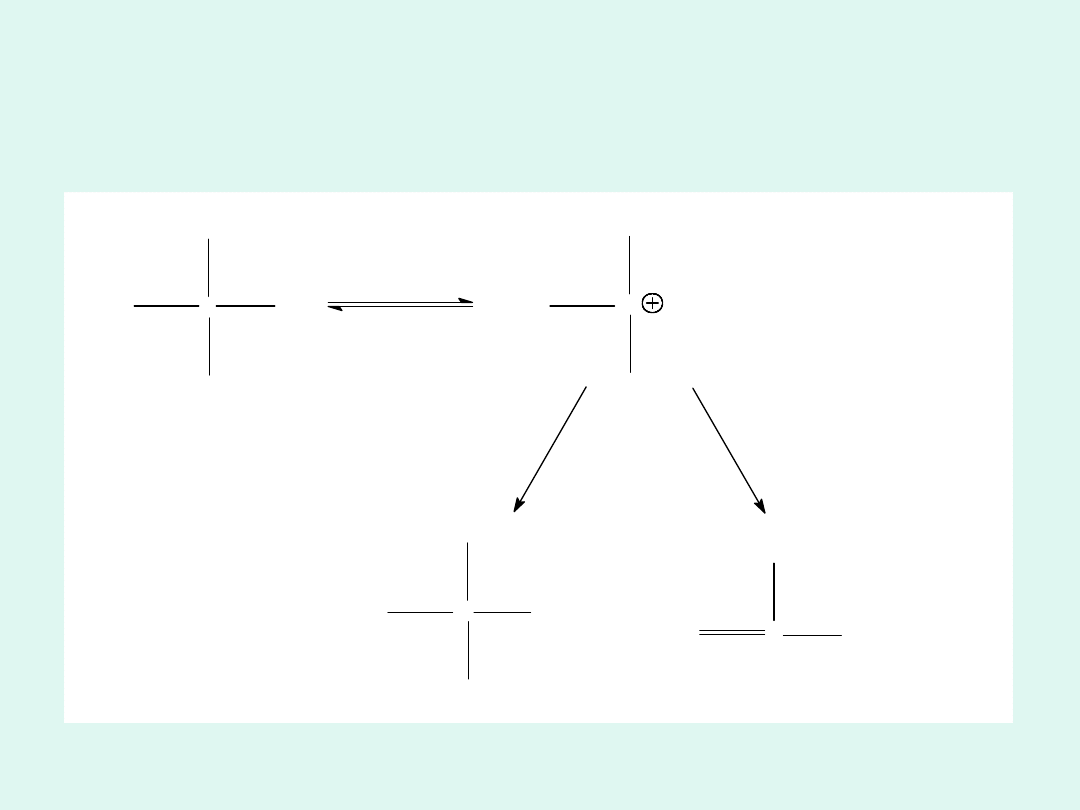
Rzeczywiste reakcje mogą być złożeniem

kilku różnych typów reakcji.

C

CH

3

CH

3

CH

3

Br

+ Br

-

C

CH

3

CH

3

CH

3

+ OH

-

+ OH

-

C

CH

3

CH

3

CH

3

OH

C

CH

3

CH

3

CH

2

+ H

2

O

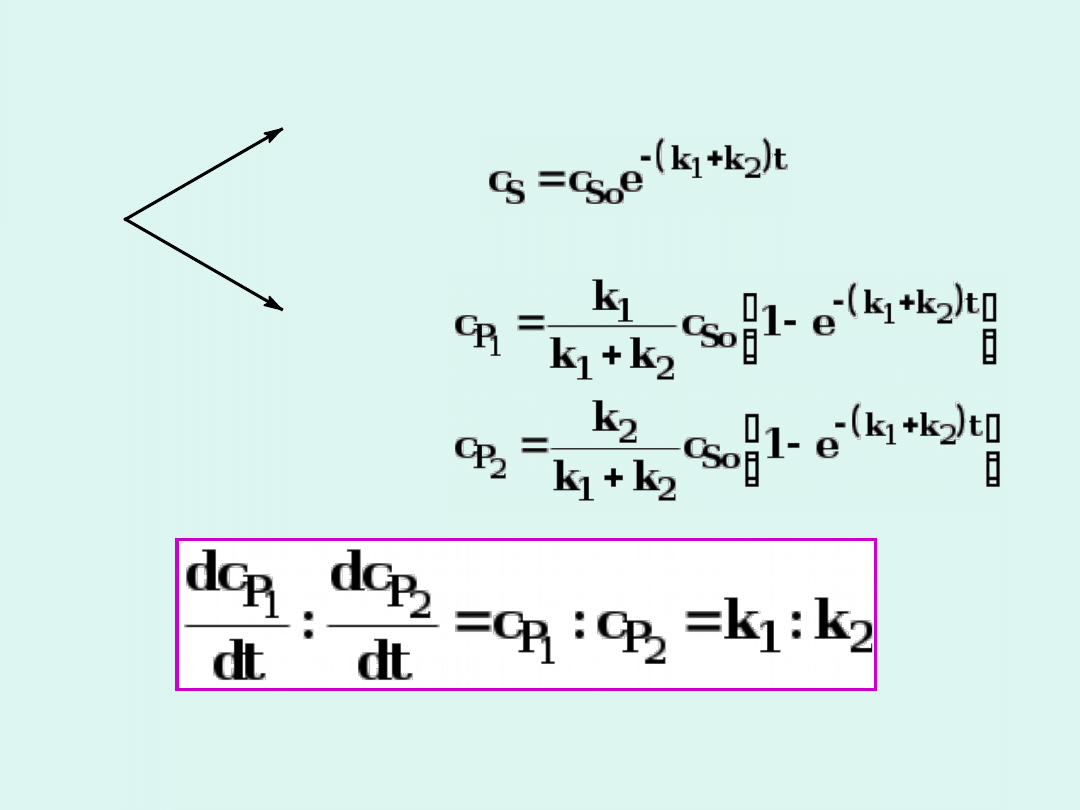
Reakcje równoległe

S

P

1

P

2

k

1

k

2

Stosunek stężeń produktów i szybkości ich tworzenia
mają się do siebie jak ich stałe szybkości.

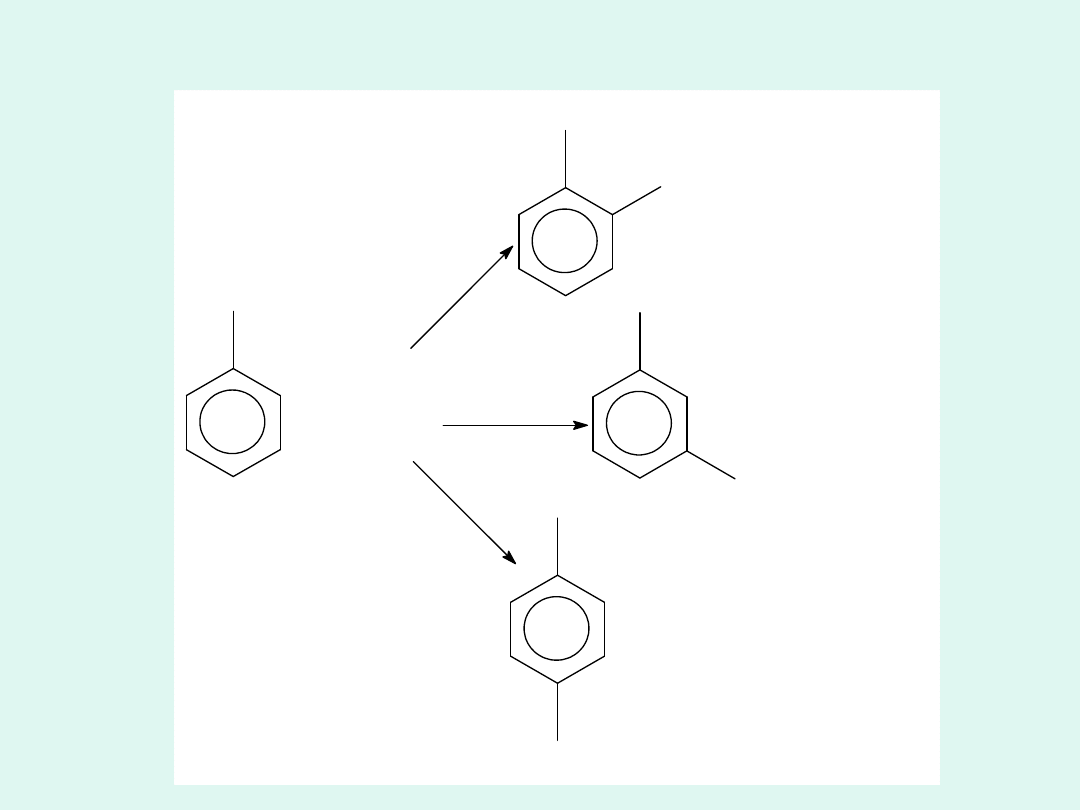
Reakcje równoległe - przykład

CH

3

+ HNO

3

CH

3

NO

2

CH

3

NO

2

CH

3

NO

2

+ H

2

O

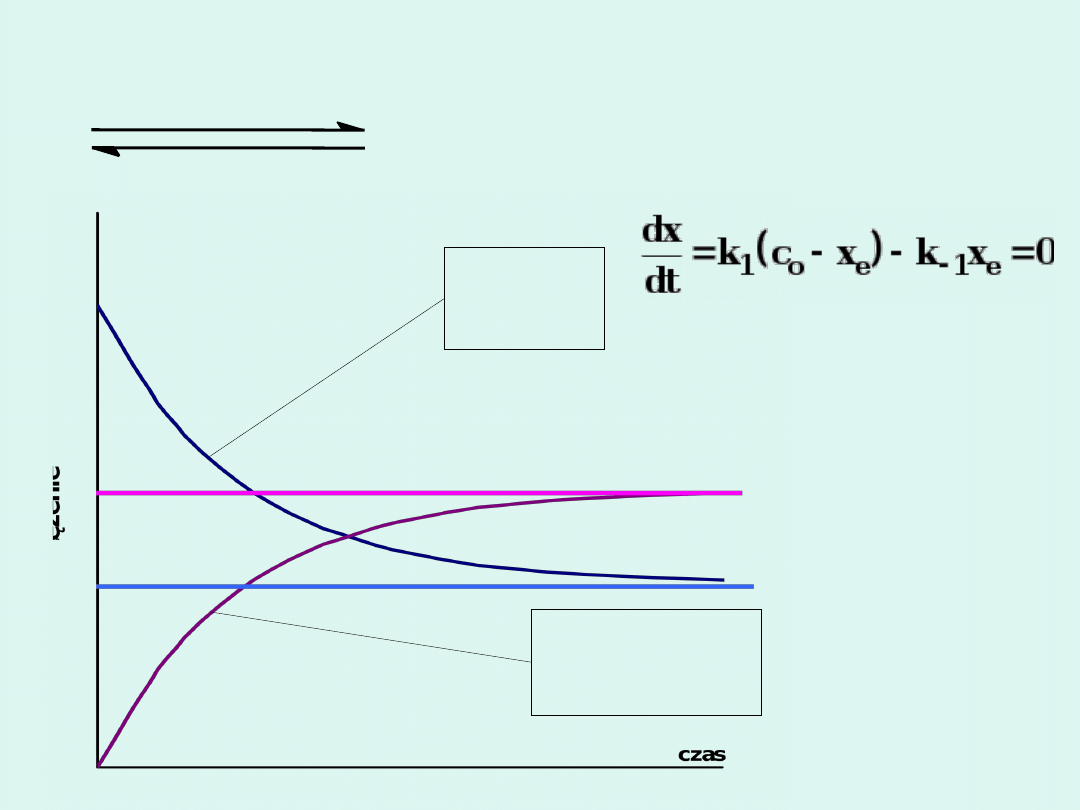
Reakcje odwracalne

A

P

k

1

k

-1

Zakładamy, że w obie strony

reakcja jest pierwszego

rzędu

.

stężeni

e

substra

tu

stężenie

produktu

c

o

- x

e

x

e

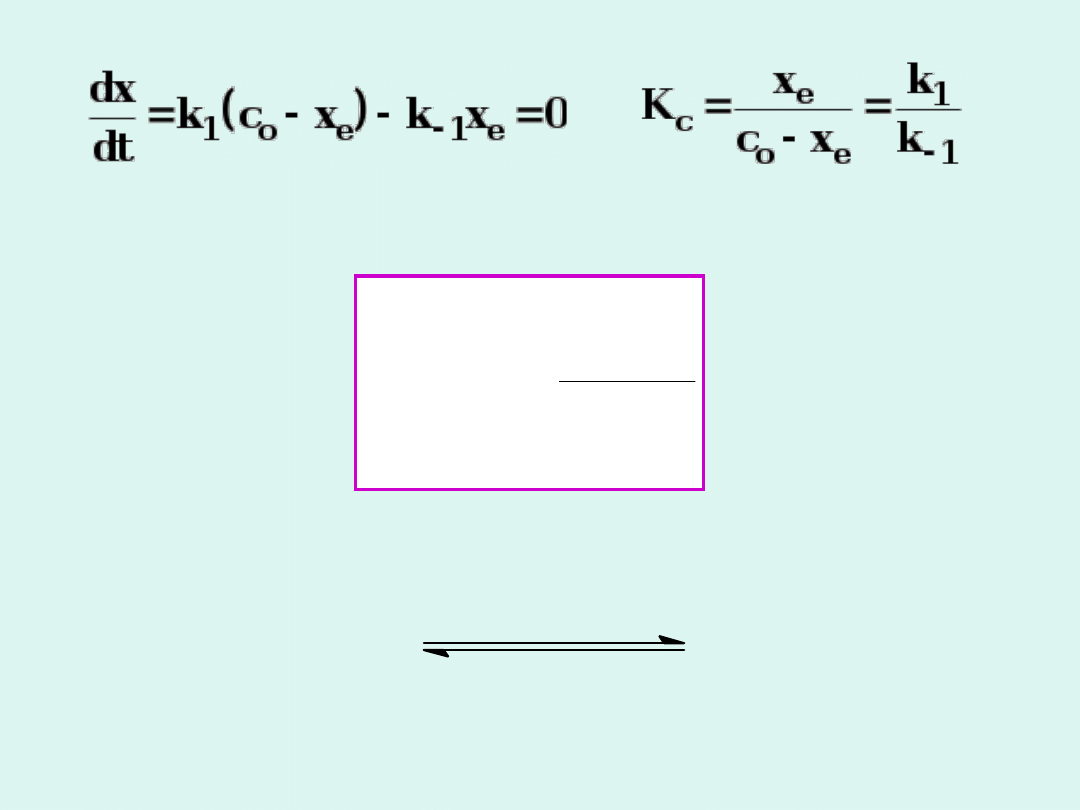
W stanie równowagi :

Wniosek ten jest słuszny dla reakcji
dowolnego rzędu.

1

1

c

k

k

K





Przykład reakcji odwracalnej



-

D

-

g

l

u

k

o

z

a



-

D

-

g

l

u

k

o

z

a

k

1

k

-

1

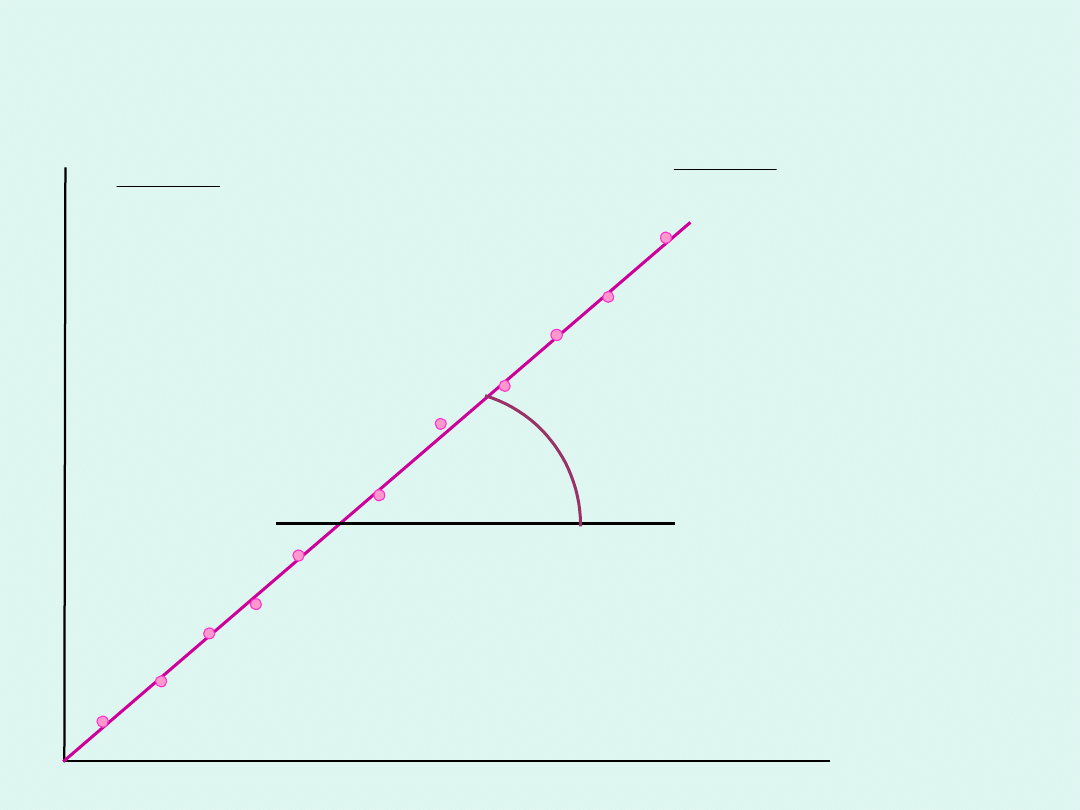
Scałkowane równanie kinetyczne dla

odwracalnej reakcji I rzędu

czas







t

k

k

x

x

x

ln

1

1

e

e











tg  = k

1

+ k

-1

x

x

x

ln

e

e



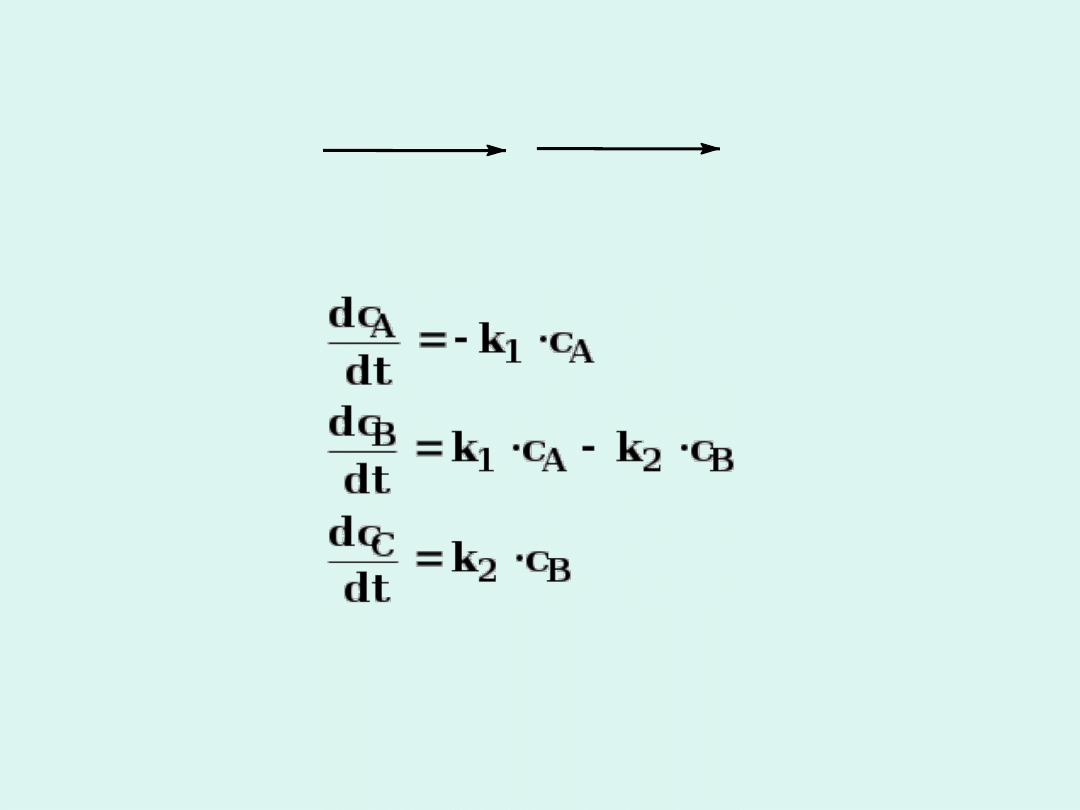
Reakcje następcze

A

B

C

k

1

k

2

Zakładamy, że obie reakcje są pierwszego

rzędu.

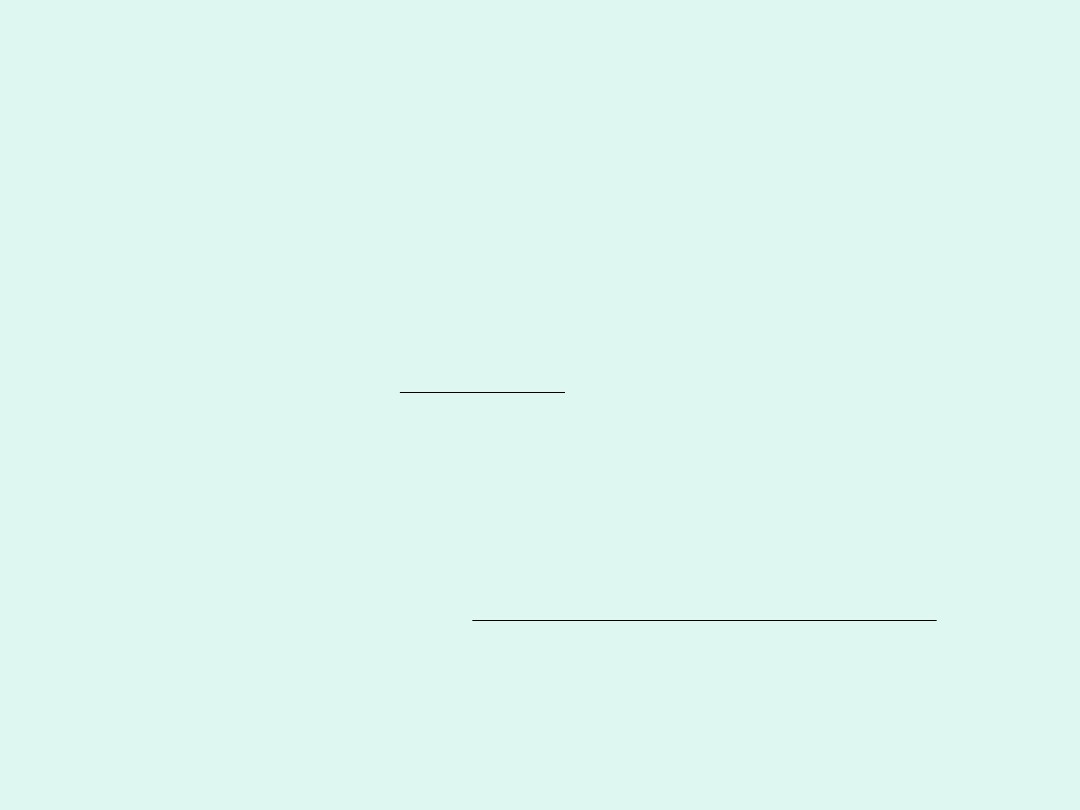
Jeśli stałe szybkości obu etapów są różne,
rozwiązanie układu równań ma postać :







































































1

2

t

k

1

t

k

2

Ao

C

B

A

Ao

C

t

k

t

k

1

2

1

Ao

B

t

k

Ao

A

2

1

k

k

e

k

e

k

1

c

c

c

c

c

c

e

e

k

k

k

c

c

e

c

c

k

k

gdy

2

1

2

1

1

Przykład reakcji następczej

R

COOR'

COOR''

+ H

2

O

COOH

COOR'

R

+ R''OH

R

COOR'

COOH

+ H

2

O

COOH

COOH

R

+ R'OH

k

1

k

2

H

3

O

+

H

3

O

+

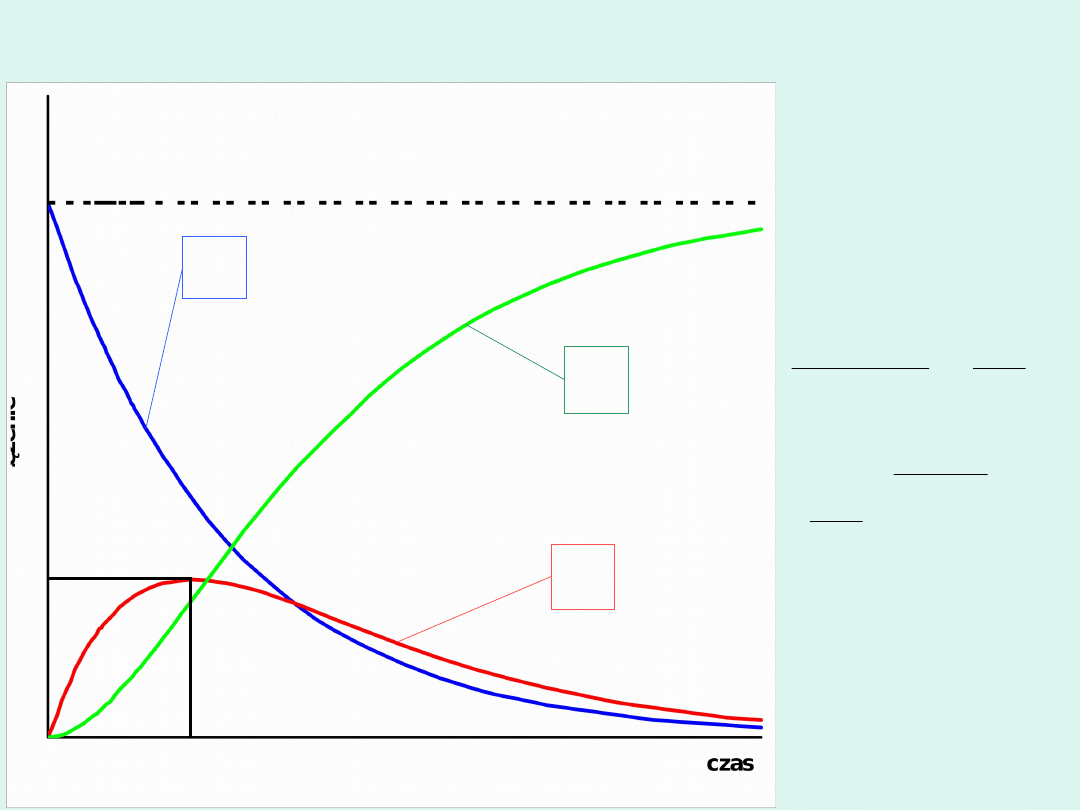
c

A

c

A

c

A

t

ma

x

c

B

max

c

Ao

Zmiany stężeń reagentów w typowej

reakcji następczej

Ao

k

k

k

2

1

max

B

1

2

1

2

max

c

k

k

c

k

k

ln

k

k

1

t

1

2

2























Przypadek graniczny w reakcji

następczej gdy :

k

1

>> k

2

t

k

t

k

2

1

e

e











1

k

1

t 





t

k

Ao

C

t

k

Ao

B

2

2

e

1

c

c

e

c

c

















Wówczas

i po czasie

równania sprowadzają się do
postaci

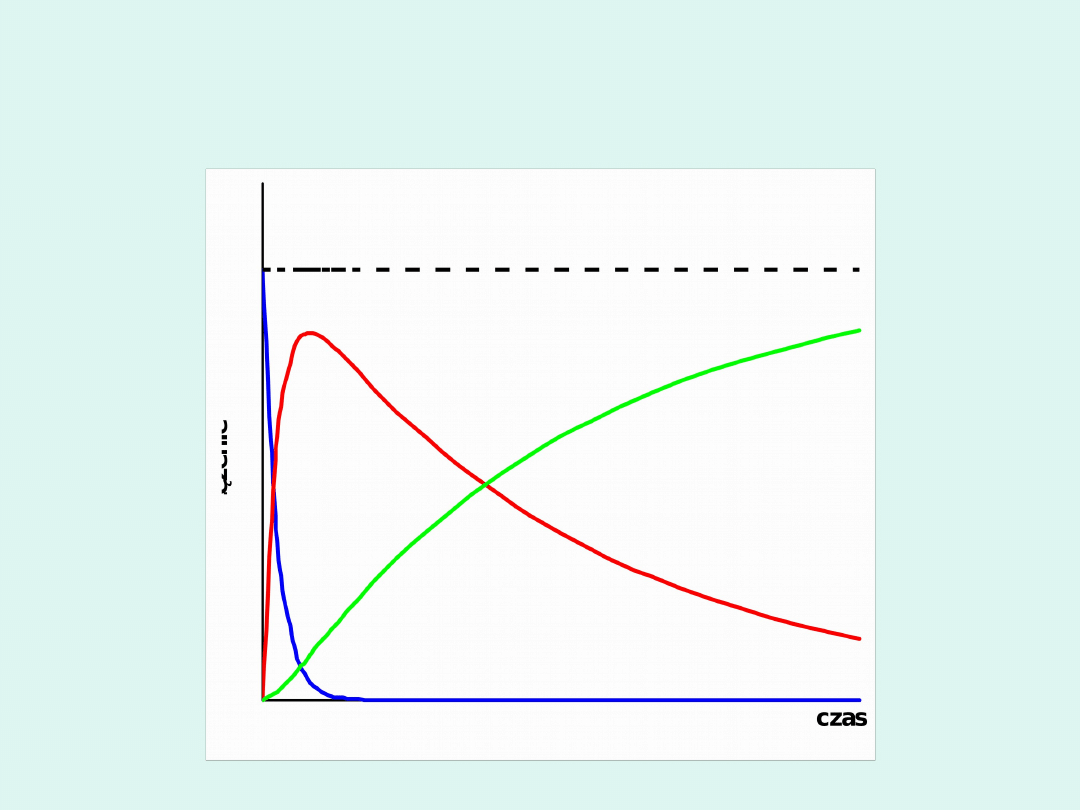
Przypadek graniczny w reakcji

następczej gdy :

k

1

>> k

2

Przypadek graniczny w reakcji

następczej gdy :

k

1

<< k

2

t

k

t

k

2

1

e

e











2

1

A

B

B

2

A

1

B

k

k

c

c

0

c

k

c

k

dt

dc



















t

k

Ao

C

A

1

A

2

1

2

B

2

C

1

e

1

c

c

c

k

c

k

k

k

c

k

dt

dc





















Wówczas

I po krótkim czasie zwanym

czasem

indukcji

równania przybierają postać :

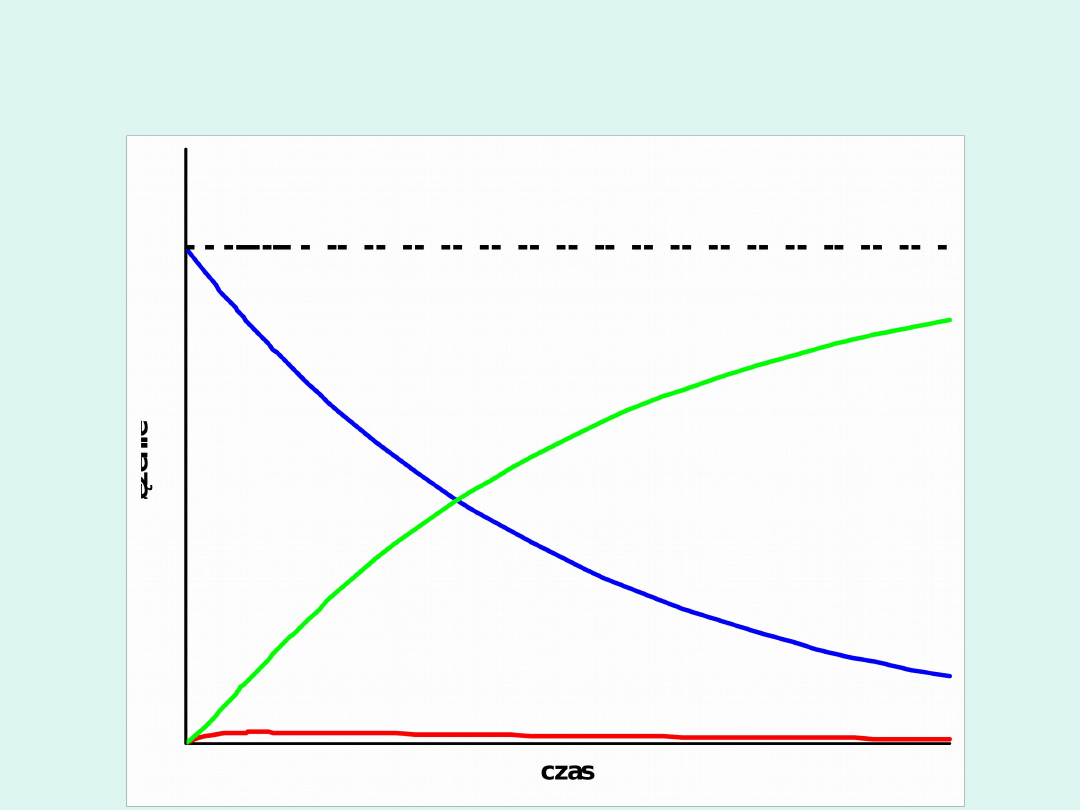
Przypadek graniczny w reakcji

następczej gdy :

k

1

« k

2

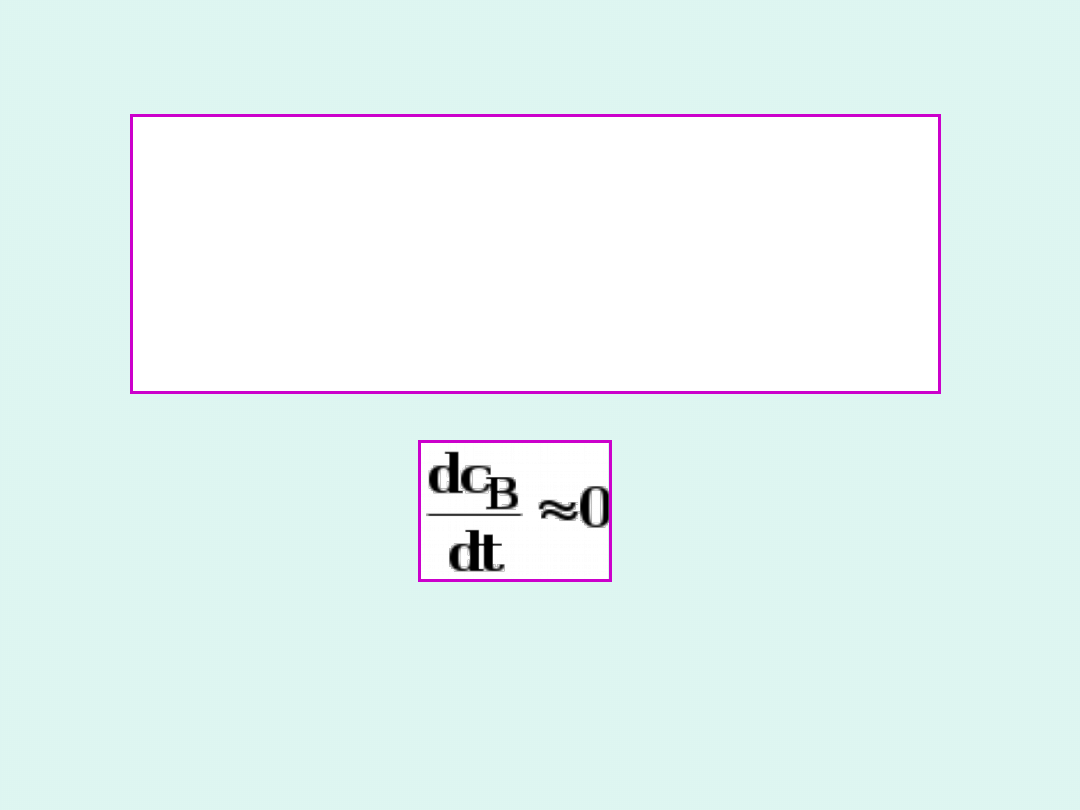
Przybliżenie stanu stacjonarnego

Bodensteina

W reakcji złożonej po pewnym
czasie indukcji stężenie substratu
pośredniego ustala się na niskim, w
przybliżeniu stałym poziomie, a
całkowita szybkość zmian jego
stężenia jest w przybliżeniu równa
zero.

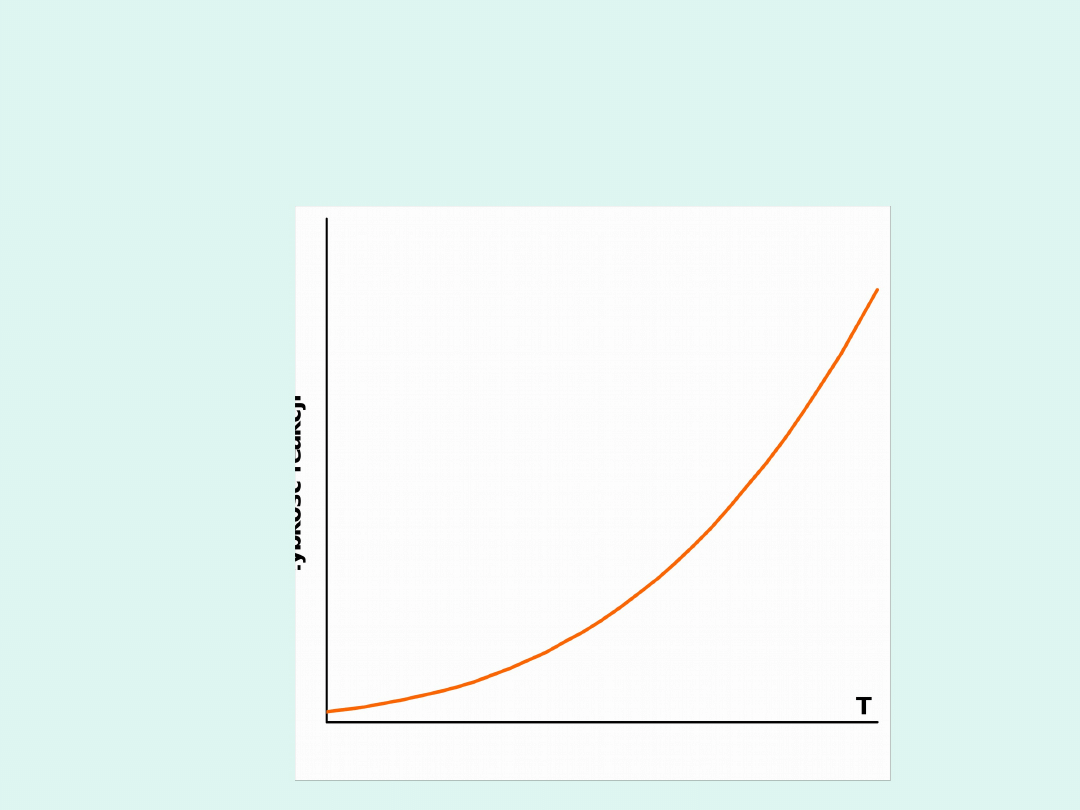
Wpływ temperatury na szybkość

reakcji chemicznych

Dla większości reakcji szybkość rośnie wraz
ze wzrostem temperatury.

Równanie Arrheniusa

Opisuje zależność szybkości reakcji od

temperatury.

Energia aktywacji

to najmniejsza ilość

energii, jaką muszą posiadać substraty,
aby ulec przekształceniu w produkty,
liczona na 1 mol elementarnych aktów
reakcji.

E

A

– energia aktywacji

2

A

RT

E

dT

k

d



ln

o

A

A

2

A

2

A

2

A

k

T

1

R

E

C

T

1

R

E

k

T

dT

R

E

k

d

T

dT

R

E

k

d

RT

E

dT

k

d

ln

ln

ln

ln

ln























RT

E

o

A

e

k

k





k

o

– czynnik przedwykładniczy (czynnik częstości)

Oznacza szybkość reakcji w nieskończenie dużej
temperaturze, gdy wszystkie cząsteczki mają
wystarczającą energię do pokonania bariery
energetycznej na drodze reakcji.

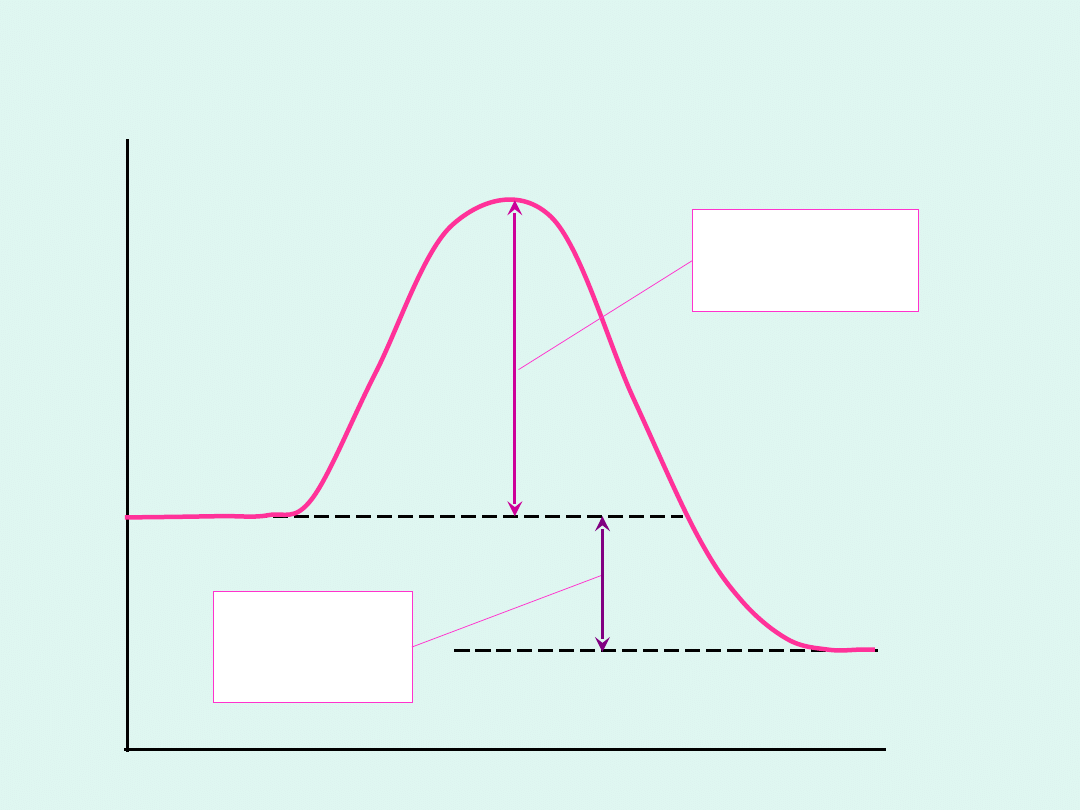
energia

aktywacji

E

A

ciepło

reakcji

Q

substr
aty

produk
ty

komlek

s

aktywn

y

droga
reakcji

energi
a

Energia aktywacji

Jak wyznaczamy energię

aktywacji ?

Trzeba wyznaczyć doświadczalnie stałe
szybkości w co najmniej dwu różnych
temperaturach. Następnie do obliczenia
energii aktywacji korzystamy z równania
Arrheniusa.

1

2

1

2

1

2

A

1

2

1

2

A

1

2

2

1

A

T

T

A

1

2

T

T

2

A

k

k

T

T

k

k

T

T

R

E

T

T

T

T

R

E

k

k

T

1

T

1

R

E

T

1

R

E

k

k

T

dT

R

E

k

d

2

1

2

1

2

1

















































ln

ln

ln

ln

W celu dokładniejszego wyznaczenia energii
aktywacji wyznaczamy stałe szybkości
reakcji w wielu różnych temperaturach, a
następnie wykreślamy zależność

lnk

w

funkcji

1/T

zgodnie z zależnością :

A

o

E

1

lnk lnk

R T

=

-

�



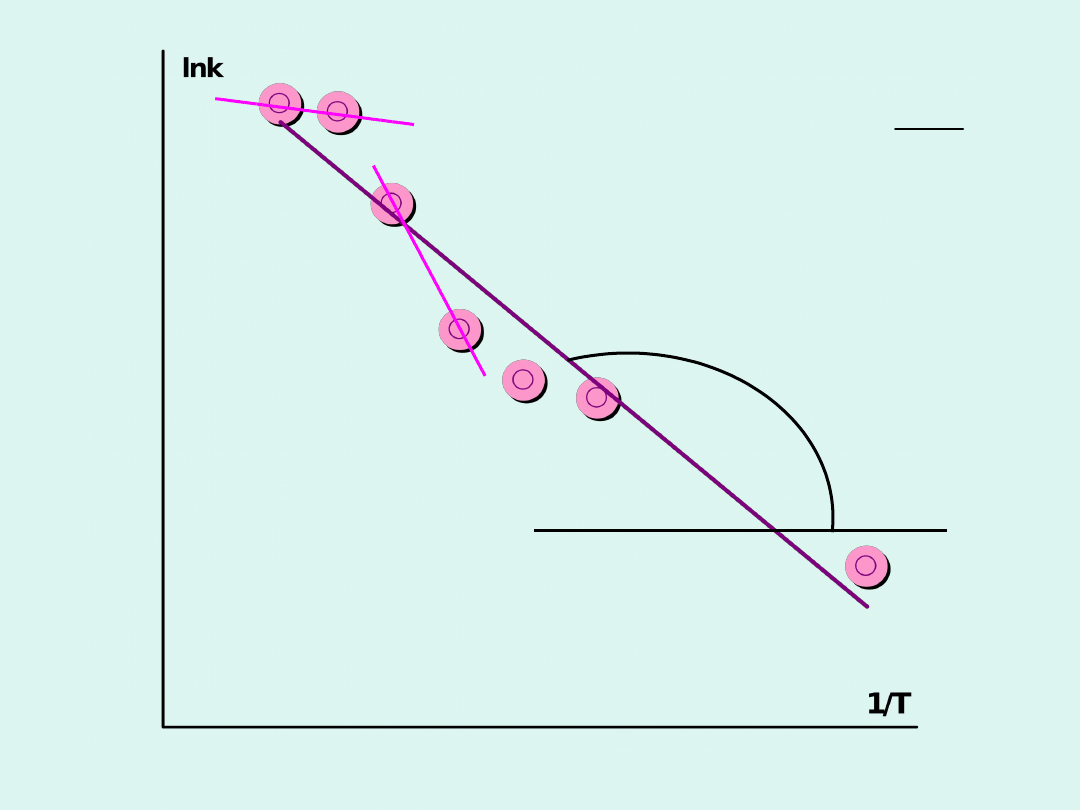
A

A

E

a tg

R

E

R tg

= a =-

=- �a

Teorie szybkości reakcji

chemicznych

Teoria zderzeń aktywnych (starsza)

Teoria kompleksu aktywnego zwana też
teorią absolutnych szybkości reakcji lub
teorią Eyringa-Polanyi’ego (nowsza)

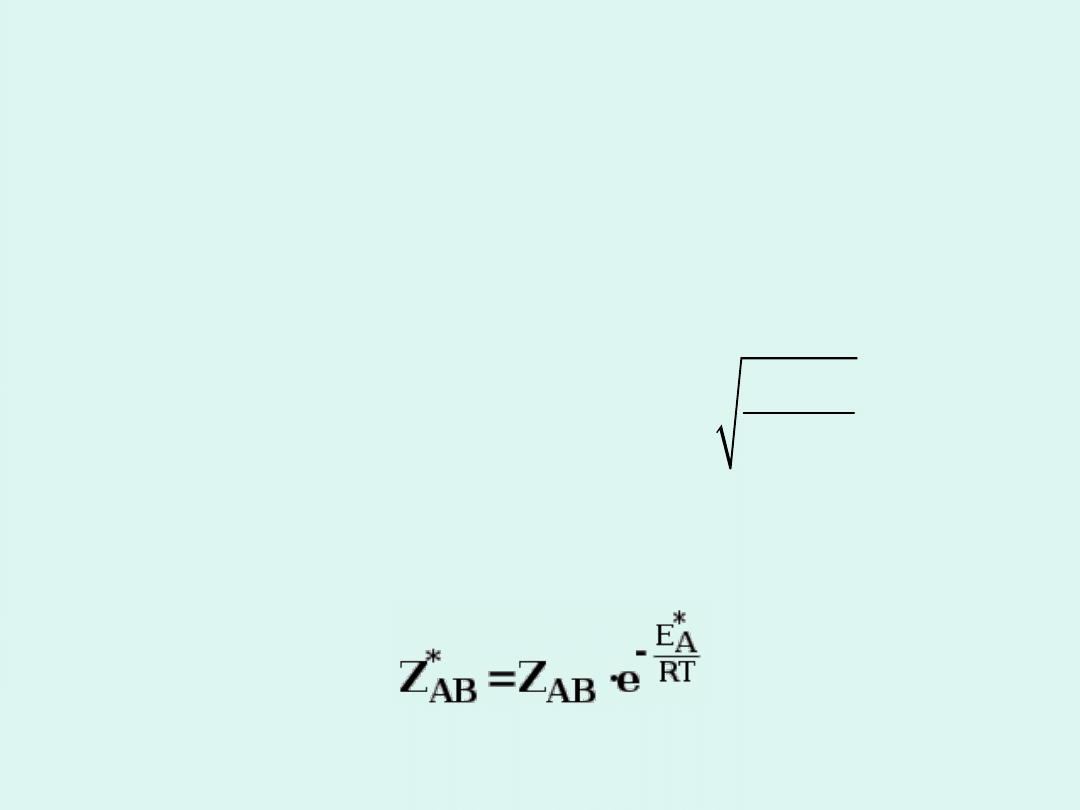
Teoria zderzeń

A B

P

+ �

Szybkość reakcji jest wprost
proporcjonalna do częstości zderzeń
cząsteczek

A

i

B.

(

)

2

AB

A

B

AB

AB

8RT

Z

=

� �

P s

Pm

N

N

Tylko zderzenia, których energia jest
większa od progowej

E

*

A

, prowadzą do

powstania produktu.

Energia progowa

E

*

A

jest wyznaczana

doświadczalnie

i

nie

można

jej

przewidzieć na podstawie teorii zderzeń.
Jest

ona

związana

z

wyznaczaną

doświadczalnie energią aktywacji :

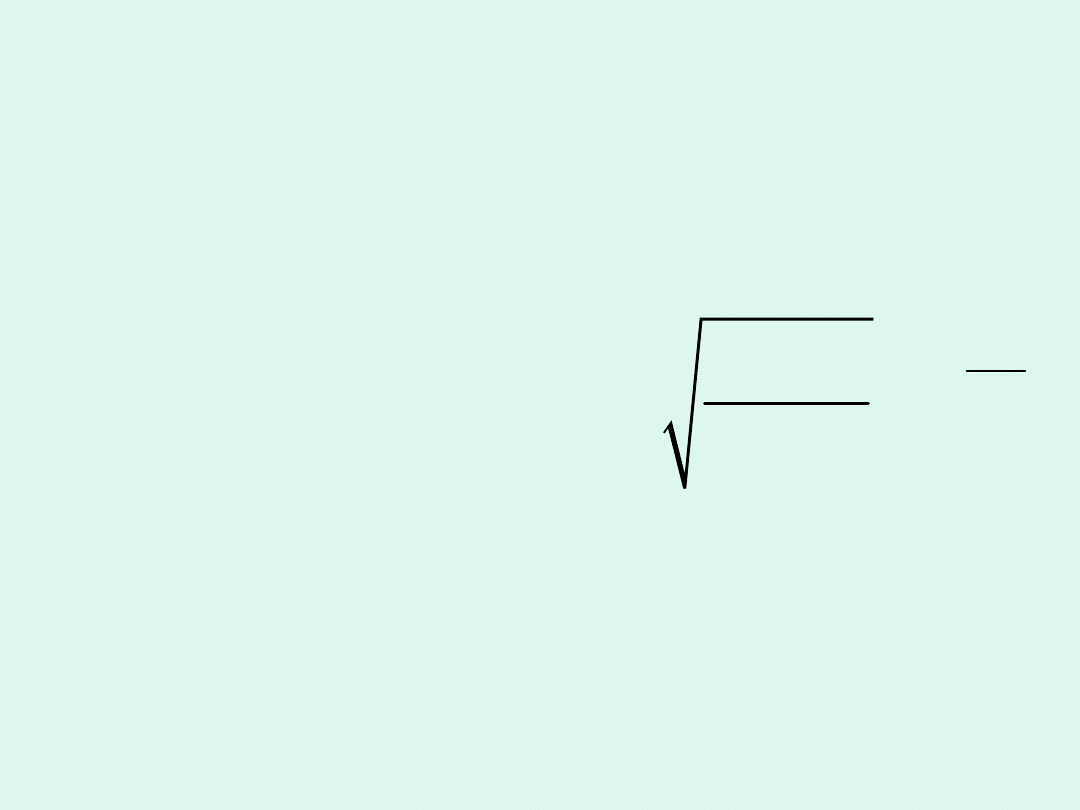
Współczynnik steryczny

Zwykle stała szybkości obliczona z teorii
zderzeń jest większa niż wyznaczona
doświadczalnie.

k

doświadczalna

< k

teoretyczna

(

)

*

EA

RT

2

A

AB

AB

8RT

k

N

e

P

-

= � �

P s

�

Pm

P – współczynnik steryczny

. Określa

prawdopodobieństwo zderzenia się cząsteczek
w taki sposób, aby mogła zajść pomiędzy nimi
reakcja.

P =

k

doświadczalna

/k

teoretyczna

P < 1

(zwykle)

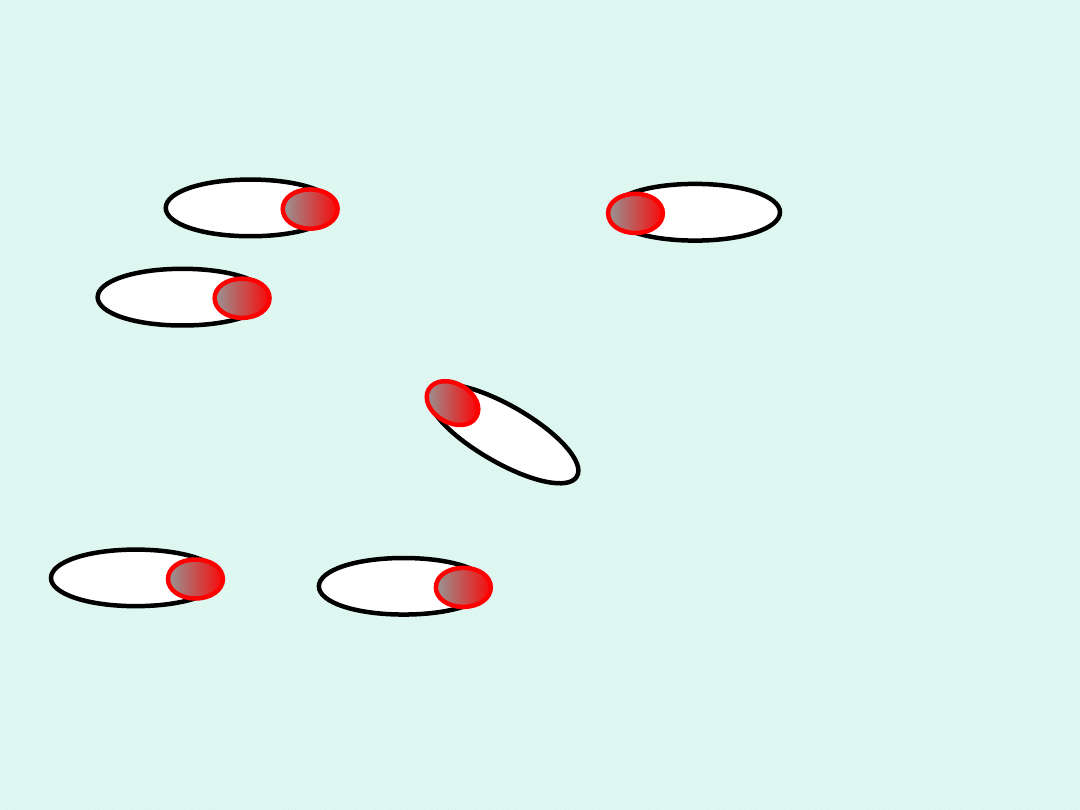
Interpretacja współczynnika

sterycznego

To
zderzenie
prowadzi
do reakcji.

Te zderzenia
są
nieefektywn
e

Im bardziej
złożone są
cząsteczki tym
mniejsza jest
wartość P.

Istnieją reakcje, dla których

P >1

.

Przyczyną jest wymiana elektronu pomiędzy
atomem K i Br

2

. W wyniku tego powstają jony

różnoimienne, które nawzajem się przyciągają i
zwiększają prawdopodobieństwo spotkania się
cząsteczek. Elektron działa jak „harpun” łączący
obie cząsteczki

Zwykle wartość

P > 1

wskazuje na mechanizm

łańcuchowy reakcji.

Wartości współczynnika sterycznego nie można w
zasadzie przewidzieć teoretycznie.

 

 

 

 

8

,

4

P

Br

KBr

Br

K

g

g

g

2

g









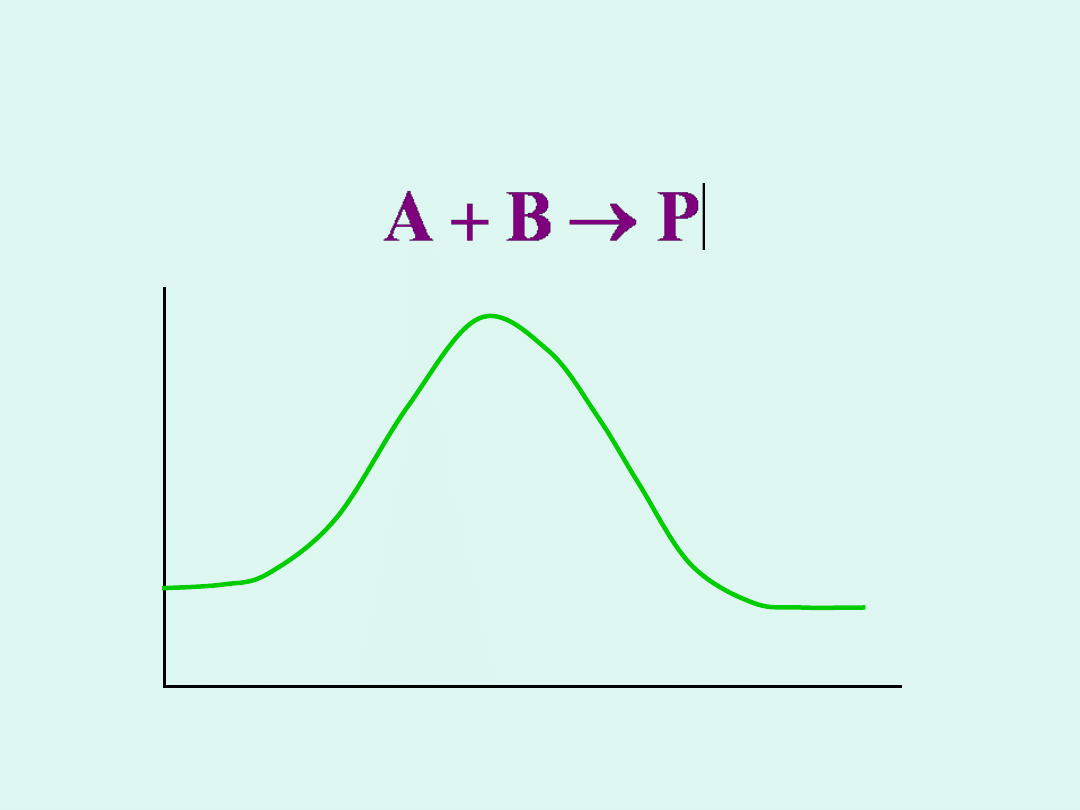
Teoria kompleksu aktywnego

(absolutnej szybkości reakcji,

Eyringa-Polanyi'ego)

A+
B

P

[A

....

B]



- kompleks

aktywny

współrzędna
reakcji

E

Formalnie możemy napisać, że reakcja zachodzi w

dwu etapach :

1.

Odwracalne tworzenie kompleksu aktywnego.

A + B [A

....

B]

#

2.

Rozpad kompleksu aktywnego do produktów.

[A

....

B]

#

 P

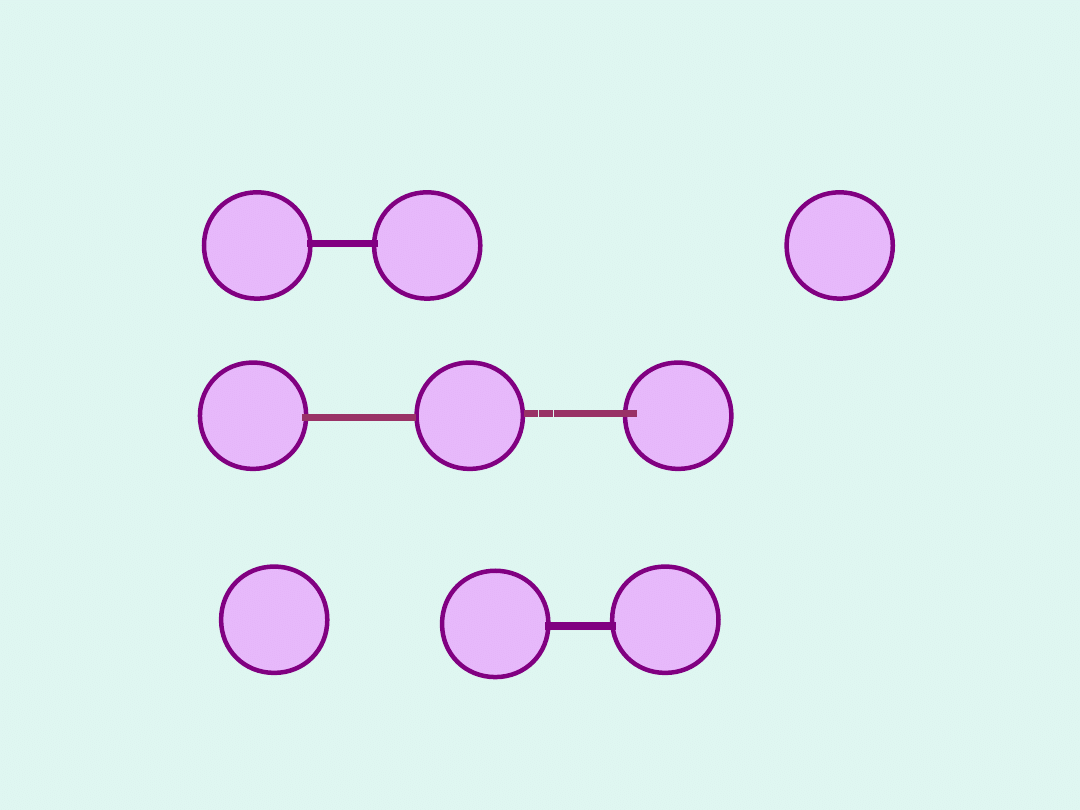
X

X

X

Y

Y

Z

Z

Y

Z

Co się dzieje w trakcie

reakcji ?

komplek
s
aktywny

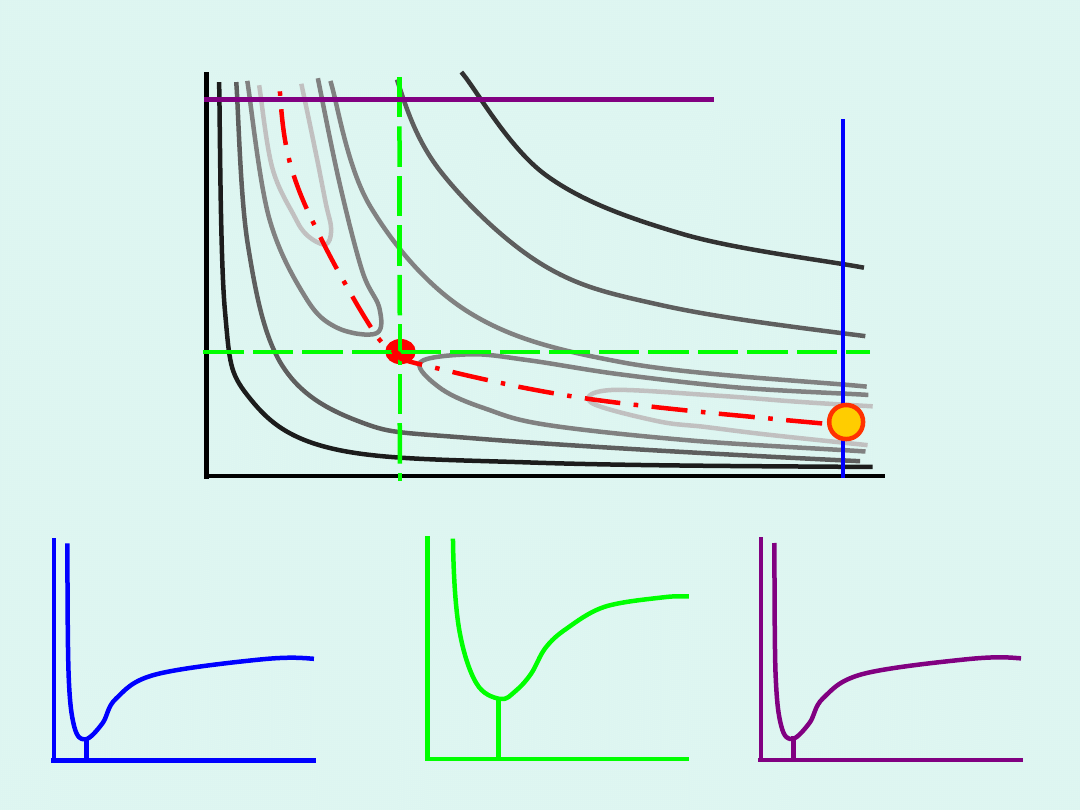
r

XY

r

YZ

D

C

B

#

A

r

XY

E

r

e

r

YZ

E

r

e

r

e

#

r

XY

r

XZ

E

Mapa energetyczna reakcji

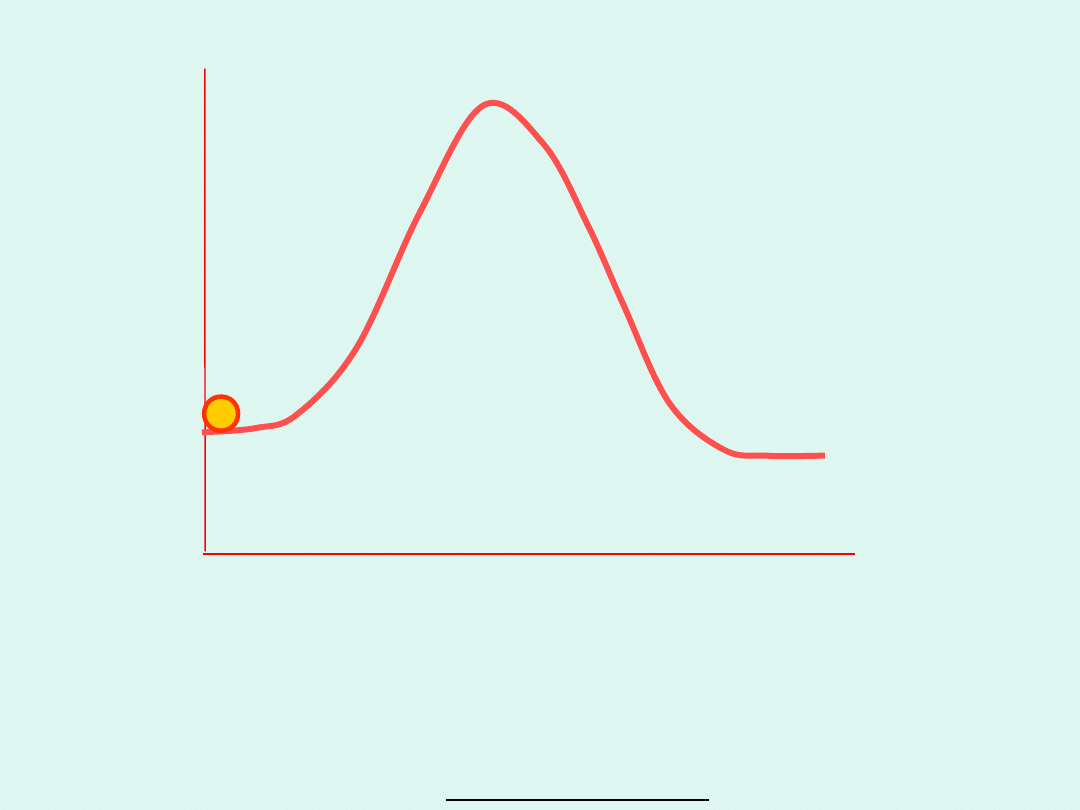
E

XY + Z

#

droga
reakcji

X + YZ

Cała mapę energetyczną reakcji a więc i
zależność energii od drogi reakcji oraz
ostatecznie energię kompleksu aktywnego
można obliczyć teoretycznie na gruncie
mechaniki kwantowej (w sposób przybliżony).

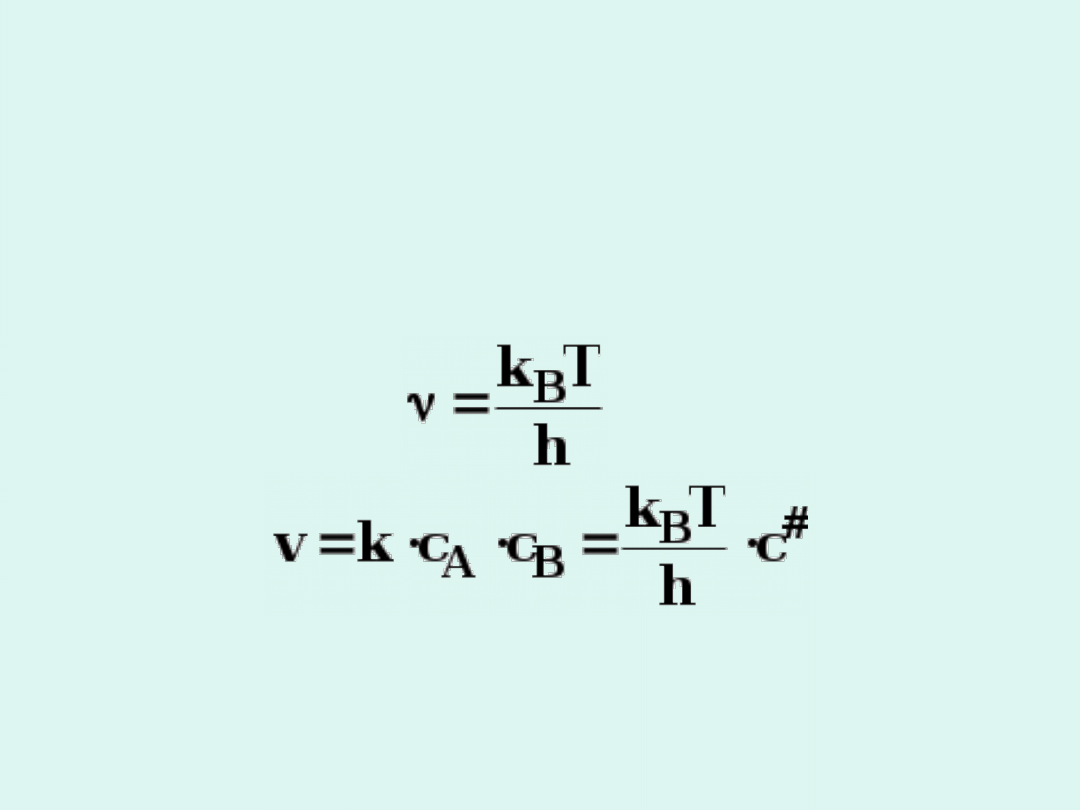
Szybkość reakcji jest wprost proporcjonalna
do stężenia kompleksu aktywnego :

#

v

c

 

i częstości drgań wiązania decydującego o
rozpadzie kompleksu aktywnego w kierunku
produktu

#

#

#

B

c

c

A

B

gdzi

k T

c

k

K

K

h

c c

e

=

=

�

Wielkość stałej równowagi tworzenia
kompleksu

aktywnego

K

c

#

można

wyznaczyć

teoretycznie

metodami

termodynamiki statystycznej i mechaniki
kwantowej.

Równanie Eyringa

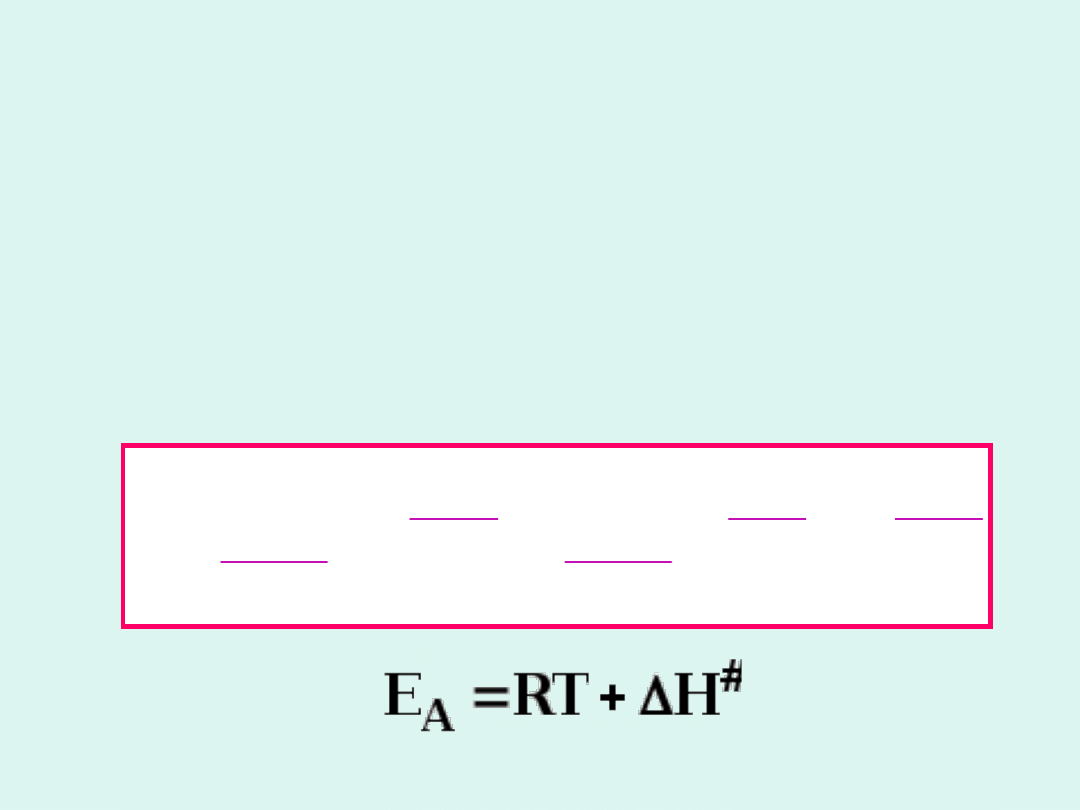
Wielkość stałej równowagi tworzenia
kompleksu

aktywnego

K

c

#

można

powiązać z odpowiednimi funkcjami
termodynamicznymi tworzenia : entalpią
swobodną, entalpią i entropią.

#

#

c

#

#

#

G

RTlnK

G

H

T S

D

=-

D

=D

- D

#

#

#

G

S

H

B

B

RT

R

RT

k T

k T

k

e

e

e

h

h

D

D

D

-

-

=

�

=

�

�

Kataliza i katalizatory

Katalizatory

to substancje, które zwiększają

szybkość reakcji chemicznej, pozornie nie
wchodząc w nią. Po zajściu reakcji pozostają
niezmienione.

Katalizatory ujemne (zmniejszające szybkość
reakcji) to

inhibitory

.

Autokaliza

to przyspieszenie reakcji przez

jej produkty.

Kataliza homogeniczna

– katalizator i

reagenty są w tej samej fazie.

Kataliza heterogeniczna

– katalizator

jest w innej fazie niż reagenty. Zwykle
katalizator jest w tym wypadku ciałem
stałym. Taki typ katalizy nazywamy

katalizą kontaktową

, a katalizator

kontaktem

.

Ponadto

wyróżniamy

katalizę

enzymatyczną

i

fotokatalizę

.

Katalizator powoduje przyspieszenie
reakcji.

Katalizator zwiększa stałą szybkości
reakcji w danej temperaturze.

Obecność katalizatora obniża energię
aktywacji reakcji.

W obecności katalizatora mechanizm
reakcji jest inny niż bez niego.

Katalizator nie ma wpływu na stan
równowagi reakcji ani na jej efekt
cieplny.

Katalizator nie zmienia stałej
równowagi reakcji.

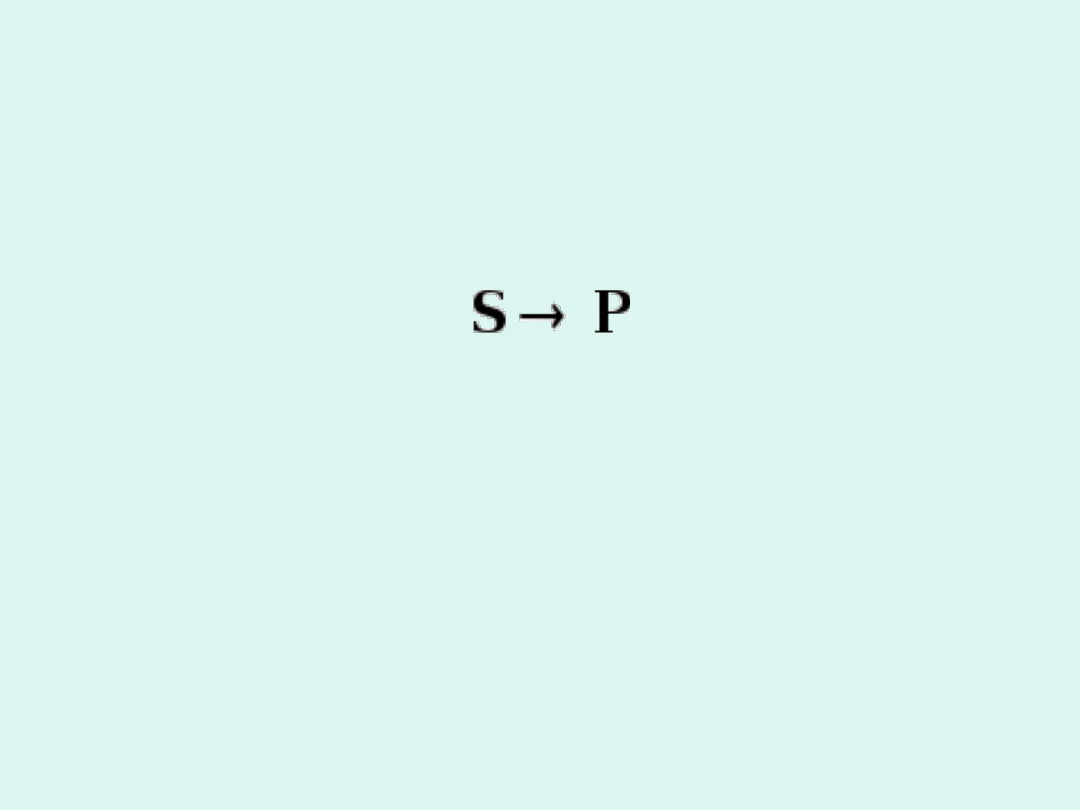
Jak działa katalizator ?

S K

SK

SK

P K

+ �

� +

Reakcja bez katalizatora :

W obecności katalizatora reakcja zachodzi
co najmniej w dwu etapach:

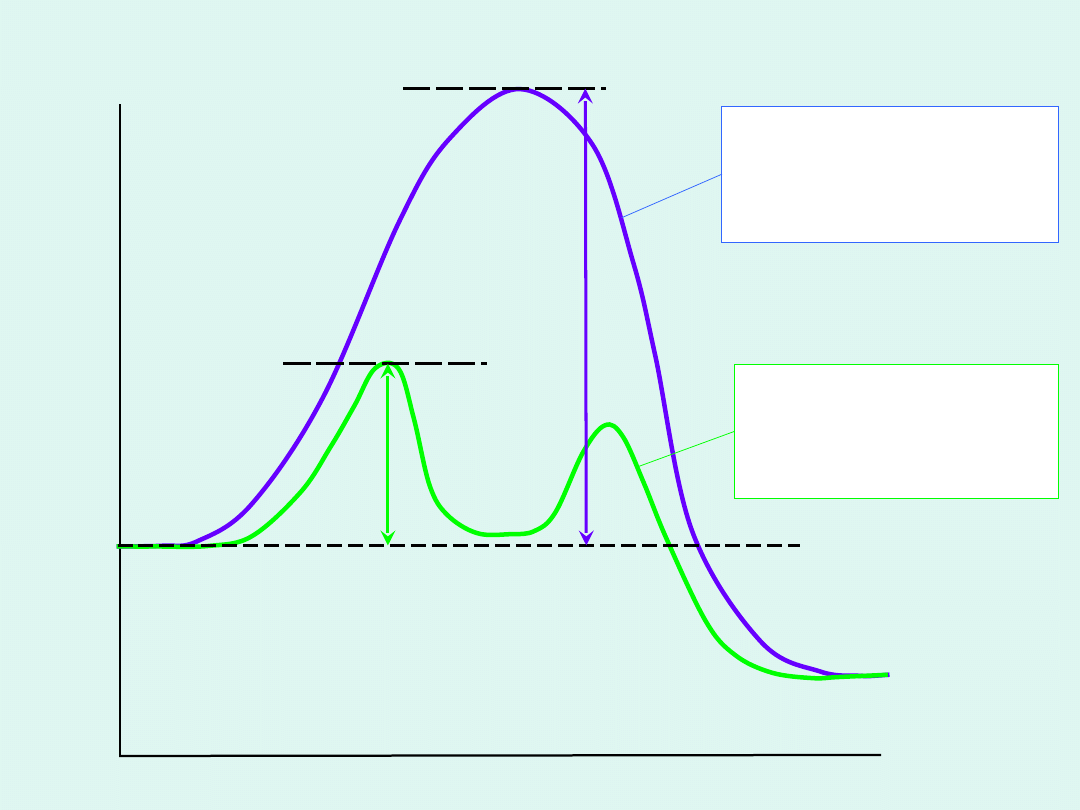
S

P

SK

E

współrzędna reakcji

E

A

'

E

A

Profil

energetyczny

reakcji bez

udziału

katalizatora

Profil

energetyczny

reakcji z

udziałem

katalizatora