1

ELEMENTY LOGIKI

KRYTERIA PRAWDY

1. Kryterium św. Tomasza z Akwinu: „prawda jest to zgodność
rzeczy z rozumem” („veritas est adequatio rei et intellectus”).

2. Kryterium klasyczne (współczesne): za prawdziwe uznajemy te
informacje, które głoszą treści zgodne ze stanem faktycznym,
który odnajdujemy w rzeczywistości.

3. Koherencyjne kryterium prawdy: prawda jest zgodnością myśli
z samą sobą, a ściślej – zgodnością z innymi myślami, wcześniej
uznanymi za prawdziwe.

4. Pragmatyczna koncepcja prawdy: utożsamiała prawdziwość
jakiegoś twierdzenia z jego użytecznością.

ZDANIE I SĄD, WARTOŚĆ LOGICZNA ZDANIA

Zdaniami w sensie logicznym są tylko zdania oznajmujące.

Zdanie oznajmujące – to wyrażenie, które jest prawdziwe bądź
fałszywe. Znaczenie zdania nazywamy sądem. Sąd – to sposób
rozumienia danego zdania.

WYKŁAD 12

2

RODZAJE ZDAŃ
Zdanie proste

jest to zdanie, w którym występują wyłącznie funktory

zdaniotwórcze od argumentów nazwowych. Szczególne znaczenie mają tzw.
zdania kategoryczne. Należą do nich takie zdania, jak: „Ziemia jest planetą”,
„Słońce świeci”, „Słońce przyciąga Ziemię”, „Niektóre ptaki nie latają”,
„Każdy metal jest pierwiastkiem chemicznym”, „Żaden koziorożec nie fruwa”.
Wspólną cechą tych zdań (to jest zdań kategorycznych) jest to, że dadzą się
one rozłożyć na części, z których jedna jest funktorem zdaniotwórczym od
nazw, a pozostałe części są nazwami.

W klasycznej logice formalnej wyróżniało się pewne postacie zdań
kategorycznych,

które

nazywa

się

„

klasycznymi

zdaniami

kategorycznymi

”. Są to zdania, które dają się zapisać w następujących

postaciach:

1. „Każde S jest P”, 2. „Żadne S nie jest P”, 3. „Niektóre S

są P”, 4. „Niektóre S nie są P”.

3

Zdanie złożone

jest to zadnie, w którym występuje funktor od

przynajmniej jednego argumentu zdaniowego. (przynajmniej jedna negacja)

Negacja (zaprzeczenie) zdania

lub : czytamy "nieprawda, że

p ".

Koniunkcja zdań

: czytamy "p i q".

Alternatywa zdań

: czytamy "p lub q".

Implikacja

: czytamy "jeśli p, to q".

Równoważność

: czytamy "p wtedy i tylko wtedy, gdy q".

Alternatywa wykluczająca zdań

: czytamy "p albo q".

p



q

p

q

p

q

p

q

p

q

p

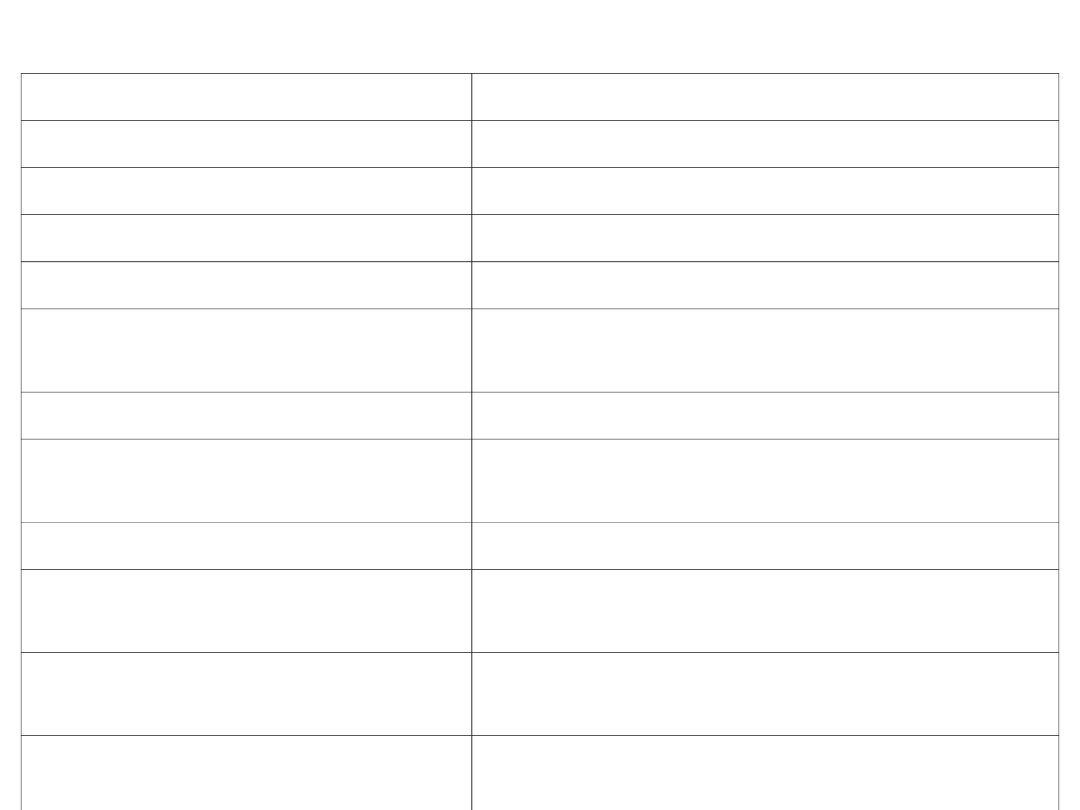
WARTOŚCI LOGICZNE ZDAŃ ZŁOŻONYCH

p

q

1

1

0

1

1

1

1

0

1

0

0

0

1

0

0

1

0

1

1

0

1

1

0

1

0

0

1

0

0

1

1

0

p



q

p

q

p

q

p

q

p

q

p

~
p

4

TAUTOLOGIE RACHUNKU ZDAŃ

~~p <=> p

prawo podwójnego przeczenia

p v (~p)

prawo wyłączonego środka

(p v p) <=> p

prawo idempotentności alternatywy

(p ^ p) <=> p

prawo idempotentności koniunkcji

(p ^ q) <=> (q ^ p)

prawo przemienności koniunkcji

[(p ^ q) ^ r] <=> [p ^ (q ^

r)]

prawo łączności koniunkcji

(

p v q) <=> (q v p)

prawo przemienności alternatywy

[(p v q) v r] <=> [p v (q v

r)]

prawo łączności alternatywy

(p <=> q) <=> (q <=> p)

prawo przemienności równoważności

[p ^ (q v r)] <=> [(p ^ q) v

(p ^ r)]

prawo rozdzielności koniunkcji

względem alternatywy

[p v (q ^ r)] <=> [(p v q) ^

(p v r)]

prawo rozdzielności alternatywy

względem koniunkcji

[(p => q) ^ (q => r)] => (p

=> r)

prawo przechodniości implikacji

[(p <=> q) ^ (q <=> r)]

=> (p => r)

prawo przechodniości

równoważności

5

~(p ^ q) <=> (~p v ~q)

prawo De Morgana zaprzeczenia

koniunkcji

~(p v q) <=> (~p ^ ~q)

prawo De Morgana zaprzeczenia

alternatywy

~(p => q) <=> (p ^ ~q)

prawo zaprzeczenia implikacji

(p => q) <=> (~q => ~p)

prawo kontrapozycji

[(p => q) ^ (q = > p)] => (p

<=> q)

związek między implikacją a

równoważnością

[(p ^ q) => r] <=> [p =>(q =>

r)]

prawo ekstraportacji

(~p => p) => p

prawo Claviusa

(p =>q) <=> [(p ^ ~q) => ~p]

prawo reductio ad absurdum

[p ^ (p => q)] => q

reguła odrywania

[(p => q) ^ (r => s)] => [(p v

r)=>(q v s)]

pierwsze prawo dylematu

konstrukcyjnego

[(p => q) ^ (r => s)] => [(p ^ r)

=> (q ^ s)]

drugie prawo dylematu

konstrukcyjnego

p => (p v q)

prawo wprowadzania alternatywy

(p ^ q) => p

prawo opuszczania koniunkcji

[(p => q) ^ ~q] => ~p

prawo modus tollendo tollens

(zaprzeczenie przy pomocy

zaprzeczenia)

[(p v q) ^ ~p] => q

prawo modus ponendo tollens

(potwierdzenie przy pomocy

zaprzeczenia)

(p q) <=> (p v q) ^ ~(p ^ q)

określenie alternatywy
wykluczającej



6

SPEŁNIALNOŚĆ I TAUTOLOGIE

Mówimy, że

formuła

jest:

•

spełniona,

jeżeli dla danego wartościowania ma wartość logiczną 1,

•

spełnialna

, jeżeli istnieje wartościowanie, przy którym ma wartość

logiczną 1,
•

tautologią,

jeśli ma wartość 1 dla każdego wartościowania

zmiennych (lub — co na jedno wychodzi — nie istnieje wartościowanie, dla
którego ma wartość 0),
•

niespełnialna

(albo

kontrtautologią

), jeżeli ma wartość 0 dla każdego

wartościowania.
O formule spełnionej przez dane wartościowanie będziemy niekiedy mówić,
że jest prawdziwa przy tym wartościowaniu, natomiast formuła nie spełniona
będzie fałszywa.

Przykład:

jest tautologią, jest niespełnialna
p => q jest spełnialna, i jest spełniona przy wartościowaniu takim, że
(p) = 0 i (q) = 1, natomiast nie jest spełniona przy wartościowaniu
takim, że (p) = 1 i (q) = 0.

p

p 



p

p





7

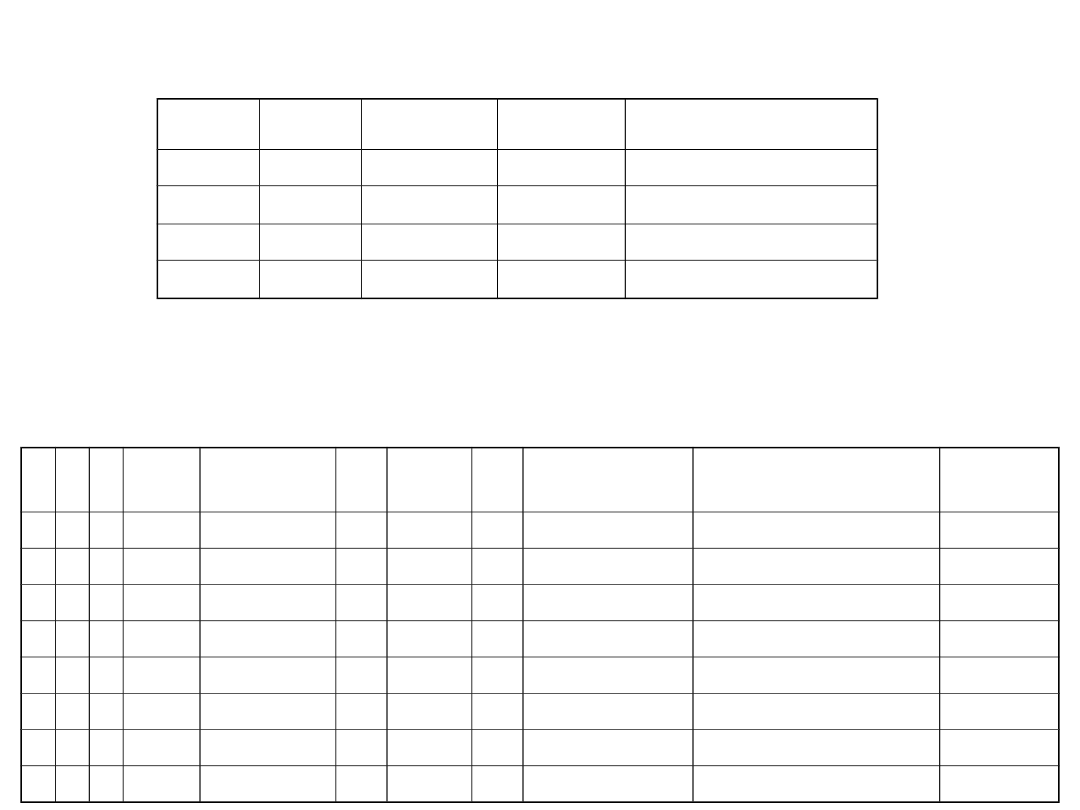
Badamy

metodą

zerojedynkową

, czy wyrażenie (p  q)  (p  q) jest

tautologią.

Ponieważ w ostatniej kolumnie znajdują się same wartości 1
(odpowiadające prawdzie), więc powyższe wyrażenie jest tautologią.
Badamy metodą

zerojedynkową

, czy wyrażenie:

((p  q)  r)  (((p  r)  (~q))  (~p)) jest tautologią.

p

q

p  q

p  q

(p  q)  (p  q)

1

1

1

1

1

1

0

0

1

1

0

1

0

1

1

0

0

0

0

1

p q r

Całe
zdanie

1 1 1

1

1

0

1

0

1

0

0

1 1 0

1

0

0

1

0

1

0

1

1 0 1

0

0

0

0

1

1

0

1

0 1 1

1

1

1

0

0

0

0

0

0 0 1

1

1

1

1

1

1

1

1

0 1 0

1

0

1

0

0

0

0

1

1 0 0

0

0

0

0

1

1

0

1

0 0 0

1

0

1

1

1

1

1

1

q

p

r

q

p



 )

(

p



q

p

q



)

(

)

(

q

q

p







)

(

))

(

)

((

p

q

q

p











8

SKRÓCONA METODA ZEROJEDYNKOWA

[(p  q)  ( p  ~q) ]  (~p  q )

0

0

1

0

)

1

1

(

)

0

0

(

)]

1

1

(

)

0

1

[(

















1

0

0

0

)

1

0

(

0

))

0

0

(

0

(

))

(

(



















q

q

p

p

Sprawdź, które z podanych zdań są tautologiami, a które
kontrtautologiami:

q

q

p

p

q

p

q

p

q

p

q

p

q

p

p

q

q

p

q

p

q

p

q

p

q

p

q

p

q

p

q

p







































































)

(

)

8

)

(

)

7

)

(

)

(

)

6

)

(

)

(

)

5

)

(

)]

(

)

[(

)

4

)

(

)

(

)

3

)

(

)

(

)

2

)

(

)

(

)

1