1

1

Analiza 

Analiza 

zjawisk rynkowych

zjawisk rynkowych

2

2

Program wykładu

Program wykładu

 

 

- szeregi czasowe

- szeregi czasowe

 

 

- metody analizy szeregów czasowych

- metody analizy szeregów czasowych

 

 

- postacie funkcji trendu

- postacie funkcji trendu

 

 

- prognozowanie

- prognozowanie

 

 

- wykorzystanie arkusza Excel

- wykorzystanie arkusza Excel

3

3

Analiza przebiegu zjawisk w czasie polega 

Analiza przebiegu zjawisk w czasie polega 

na wyodrębnieniu składników oddziałujących 

na wyodrębnieniu składników oddziałujących 

na nie i stworzeniu na tej podstawie modelu 

na nie i stworzeniu na tej podstawie modelu 

matematycznego  

matematycznego  

Składowe szeregu czasowego: 

 - tendencje rozwojowe (trend)
 - wahania okresowe (periodyczne, regularne)
 - wahania nieregularne

Metody analizy szeregów czasowych to metody 
ilościowe (obiektywne)

4

4

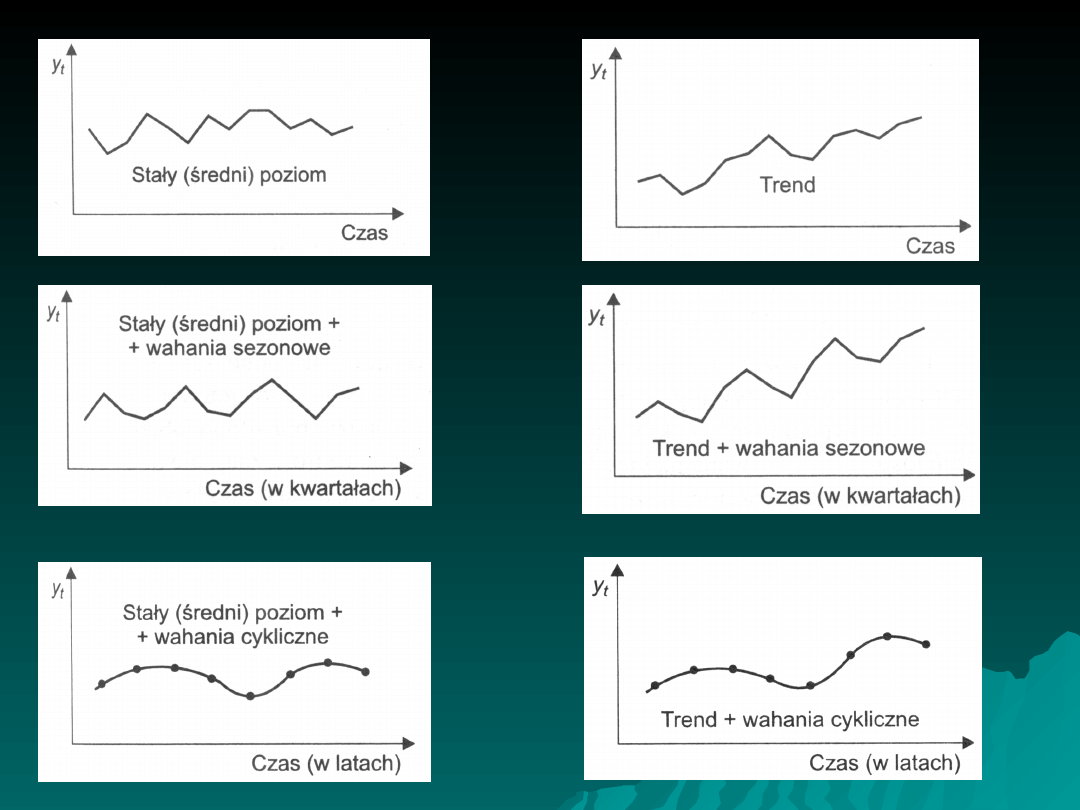
Tendencja rozwojowa

Tendencja rozwojowa (trend): 

    to istotne, trwałe zmiany rozmiarów badanego 

zjawiska,  będące wynikiem oddziaływania 
określonego zespołu przyczyn głównych.

• rosnący
• malejący
• stały lub średni (pozostaje na takim samym 
poziomie)

5

5

6

6

Wahania okresowe

Wahania okresowe

   odzwierciedlają pewien cykl zmian, które mają mniej 

więcej takie same rozmiary i powtarzają się co 
pewien okres.

Wahania periodyczne w skali

• dnia
• tygodnia
• dekady
• miesiąca 
• kwartału
• sezonu
• roku

7

7

Wahania nieregularne

Wahania nieregularne

   odnoszące się do siły, kierunku i częstości 

występowania zjawisk. 

 - przypadkowe (czysto losowe)
 - wahania incydentalne (katastroficzne)

Wahania okresowe

Wahania okresowe uwzględniając długości 
cyklu

• wahania krótkookresowe (

dni, tygodnie, miesiące)

• wahania sezonowe (

roczny okres wahań, przyczyny 

naturalne)

• wahania koniunkturalne (

tzw. cykliczne, > 1 roku)

8

8

Modele opisujące przebieg zjawisk 

rynkowych

Model addytywny                       

Model 

multiplikatywny

 

t

s

c

t

f

y











t

s

c

const

y











t

s

c

const

y











 

t

s

c

t

f

y











f (t) – funkcja trendu
const – stały (średni) poziom 

zjawiska
c – wahania cykliczne
s – wahania sezonowe



 - składnik losowy

Wahania o stałej 

amplitudzie

Wahania o zmiennej 

amplitudzie, ale w 

przybliżeniu o stałym 

stosunku

9

9

Ważne!

Charakterystyczną cechą metod analizy szeregów czasowych jest 

wykorzystywanie tylko jednej zmiennej - 

czasu

.

Należy pamiętać, iż nie jest on bezpośrednią przyczyną zmian, a 

jedynie odzwierciedla wpływ czynników na rozwój zjawiska.

Metody wyodrębniania trendów

Ważne!

Istotne jest, że koszty opracowania analiz opartych na modelu 

szeregów czasowych mogą być niewspółmiernie niższe w 

porównaniu z kosztami zdobycia wiedzy o przyczynach 

wystąpienia zjawiska? 

Cel analizy

Określenie tego, co się zdarzy, a nie wyjaśnienie, dlaczego to się 

zdarzy. 

10

10

 

- metoda średnich ruchomych

 - metoda graficzna 
 - metoda najmniejszych kwadratów

Wygładzanie szeregów czasowych

Rok

Pługi eksport

3-letnie

śr. ruchome

5-letnie

śr. ruchome

2001

347

-

-

2002

560

563,7

-

2003

784

797,3

815,2

2004

1048

1056,3

1081,8

2005

1337

1355,0

1347,8

2006

1680

1635,7

-

2007

1890

-

-

3

3

2

1

2

y

y

y

y







5

5

4

3

2

1

2

y

y

y

y

y

y











Excel

Excel !!!

11

11

Produkcja maszyn dla rolnictwa w 

Produkcja maszyn dla rolnictwa w 

tys. szt.

tys. szt.

rok

ciągniki

pługi

siewni

ki

kosiark

i

stan 

ciągników

1980

57,5

30,0

13,4

11,0

619

1990

35,4

31,1

13

24,2

1185

1995

21,5

19,0

6,4

12,3

1319

2000

7,2

5,3

2,2

6,2

1307

2001

5,7

5,7

1,6

6,2

1309

2002

5,1

6,8

1,7

5,4

1365

2003

5,8

7,7

1,8

5,4

1371

2004

8,3

6,1

2,3

5,1

1365

2005

6,0

5,2

2,0

5,5

1437

2006

6,7

6,7

2,9

5,8

2007

7,4

7,0

2,7

5,9

1553

2008

6,5

4,9

3,8

4,4

1566

2009

3,7

12

12

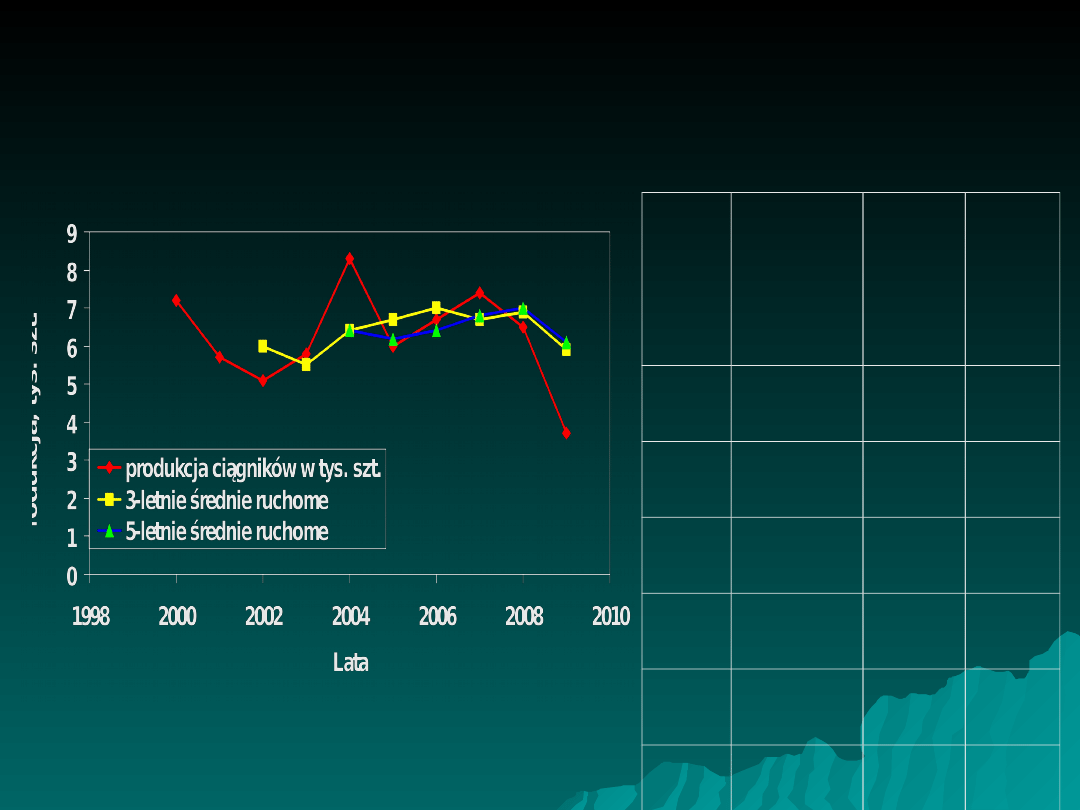
Produkcja ciągników w latach 2000-2009 – 

Produkcja ciągników w latach 2000-2009 – 

trend wyznaczony metodą średnich 

trend wyznaczony metodą średnich 

ruchomych

ruchomych

rok

ciągnik

i

3-

letni

e 

śred.

5-

letni

e 

śred

.

200

0

7,2

200

1

5,7

200

2

5,1

6,0

200

3

5,8

5,5

200

4

8,3

6,4

6,4

200

5

6,0

6,7

6,2

200

6

6,7

7,0

6,4

200

7

7,4

6,7

6,8

200

8

6,5

6,9

7,0

200

9

3,7

5,9

6,1

13

13

Założenie :
 - 

trend jest funkcją liniową

Metoda najmniejszych kwadratów
  

pozwala na minimalizację sumy różnic kwadratów 

odchyleń wartości teoretycznych od wartości 
empirycznych (rzeczywistych), co gwarantuje najlepsze 
dopasowanie funkcji do badanego szeregu, czyli dla 

t

b

a

y







N

t

b

y

a









 

2

2





  







t

t

N

t

y

yt

N

b

Excel

Excel !!!

t

b

a

y























2

min

a

t

b

y

minimalizuje się wyrażenie

14

14

Dobór modelu funkcji 

Metoda empiryczna

 1. Przedstawienie szeregu czasowego w układzie współrzędnym
 2. Analiza otrzymanego wykresu
 3. Formułowanie hipotezy dotyczącej kierunku i natężenia rozwoju 

zjawiska

Uwaga !

Jeśli więcej niż jedna funkcja prawidłowo, tzn. dokładnie (wsp. 

zbieżności), opisuje kształtowanie się tendencji rozwojowych, 

wtedy zwykle wybiera się

 najprostszą postać funkcji. 

15

15

Metoda analityczna

 1. Wyboru funkcji dokonuje się na podstawie przesłanek 

teoretycznych
 2. Wybór zależy od charakteru zjawiska, rodzaju i etapu cyklu życia 

dobra, 
 3. Analiza przyrostu badanej zmiennej w odniesieniu do czasowej 

zmiennej

Funkcja liniowa

 -  

jednakowym przyrostom czasu odpowiadają 

 równe przyrosty zmiennej zależnej

Funkcja wykładnicza

 - 

jednakowym przyrostom czasu 

odpowiadają 

stałe względne przyrosty zmiennej zależnej

Funkcja potęgowa

 - 

względne przyrosty zmiennej zależnej są 

wprost proporcjonalne do względnych 

przyrostów zmiennej czasowej

Funkcja logarytmiczna

 - 

przyrosty zmiennej zależnej są wprost 

proporcjonalne do względnych przyrostów 

czasu









1

1











t

t

c

y

y

t

t









1

1









t

t

c

y

y

t

t

t

t

c

y

y

t

t







 1

t

t

c

y

t







16

16

Zalety wybranych funkcji

Funkcja krzywoliniowa – wykładnicza 

y = ab

t

, 

lub

 

y = ae

bt

  możliwość i łatwość obliczenia średniego rocznego tempa 

rozwoju zjawiska w czasie. Taka informacja jest przydatna przy 

porównywaniu rozwoju wielu różnorodnych zjawisk 

gospodarczych 

I

p

 = b 



 100 - 100

   I

p 

– przeciętne tempo wzrostu lub spadku zjawiska

- Jeśli I

p  

> 0, to tempo wzrostu jest dodatnie,

- Jeśli I

p  

< 0, to tempo wzrostu jest ujemne (średnie tempo 

spadku),

Excel !!!

b

t

a

y

ab

y

t

log

log

log









Parametry funkcji wykładniczej szacuje się metodą 

najmniejszych kwadratów – postać liniowa - 
logarytmowanie:

17

17

Zalety wybranych funkcji

Funkcja krzywoliniowa – potęgowa →  

y = at

b

 - wartość bezwzględna parametru 

b

 mówi o sile elastyczności 

badanego zjawiska względem czasu (przyrost 

t

 o 1% powoduje 

wzrost zjawiska 

y

 o 

b%

)

 - znak przy parametrze 

b

 informuje, czy jest to zależność wprost 

proporcjonalna 

(b>0)

 czy odwrotnie proporcjonalna 

(b<0)

Funkcja krzywoliniowa – paraboliczna →  

y = a + 

bt + ct

2

t

b

a

y

at

y

b

log

log

log









Parametry funkcji potęgowej szacuje się metodą 

najmniejszych kwadratów – postać liniowa - 
logarytmowanie:

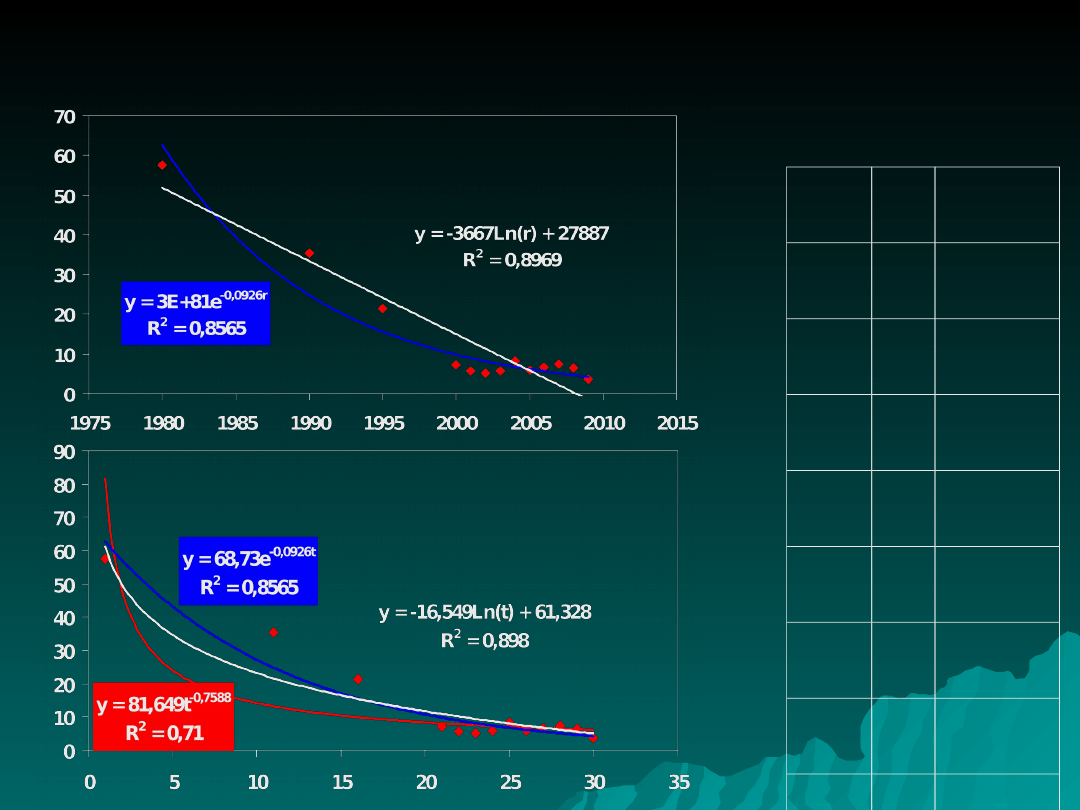
18

18

Produkcja ciągników w latach 2000-2009 – 

Produkcja ciągników w latach 2000-2009 – 

trend wyznaczony za pomocą różnych modeli

trend wyznaczony za pomocą różnych modeli

rok

t

ciągni

ki

198

0

1

57,5

199

0 11

35,4

199

5 16

21,5

200

0 21

7,2

200

1 22

5,7

200

2 23

5,1

200

3 24

5,8

200

4 25

8,3

200

5 26

6,0

200

6 27

6,7

200

7 28

7,4

200

8 29

6,5

200

9 30

3,7

19

19

Przykład 1

Badamy popyt na dobro nowo wprowadzane na rynek, 
które dopiero znajduje się w fazie rozpowszechniania.

Zastosujemy jedną z funkcji:

 - wykładniczą

 - potęgową

 - kwadratową

t

ab

y 

b

at

y 

2

ct

bt

a

y







Wskazówki doboru typu funkcji

Wstęp - graficzna analiza układu danych 
empirycznych

20

20

Przykład 2

Jeśli wzrost analizowanego zjawiska przebiega coraz 
wolniej i dąży do stałego poziomu, czyli mamy 
względne nasycenie rynku, wzrost popytu jest coraz 
wolniejszy (produkty już istniejące na rynku są 
wypierane przez lepsze, konkurencyjne artykuły)
Zastosujemy jedną z funkcji:

 - logarytmiczną

 - potęgową (przy 0 < b < 1)

 - kwadratową

 - wymierną 

 - hiperboliczną 

b

at

y 

2

ct

bt

a

y







b

t

at

y





t

b

a

y





t

b

a

y

ln





Lub inne funkcje, które:

0

,

0

2

2





dt

y

d

dt

dy

21

21

Przykład 3

Zjawiska rynkowe, które charakteryzuje tendencja 
spadkowa należy podzielić na dwie grupy. Grupa I - 
maleje w tempie przyspieszonym, Grupa II - spadek jest 
coraz wolniejszy.

2

ct

bt

a

y







b

at

y 

Paraboliczne

Potęgowe

Logarytmiczne

t

b

a

y

ln





22

22

Funkcja logistyczna  

→

   przebieg zjawisk w dłuższym okresie, analiza całego cyklu 

rozwojowego np. krzywą życia produktu. Przebieg logistyczny 
charakteryzuje wiele zjawisk przyrodniczych i ekonomicznych, 
tych ograniczonych do pewnej przestrzeni. 

  Tak można opisać zjawiska dotyczące popytu na dobra trwałego 

użytku, rozpowszechniania się innowacji oraz naśladownictwa. 

at

be

k

y







1

Zaleta funkcji

 - interpretacja parametru 

k

, w którym momencie 

badane zjawisko zmienia tempo wzrostu z rosnącego na 
malejące - na wykresie jest to punkt przegięcia o współrzędnych

Szacowanie parametrów funkcji jest skomplikowane (metoda 
Hotellinga)  i  polega na podwójnym stosowaniu metody 
najmniejszych kwadratów. 













k

b

a

2

1

,

ln

1

oraz jaki jest jego poziom nasycenia – asymptota pozioma 

y = k

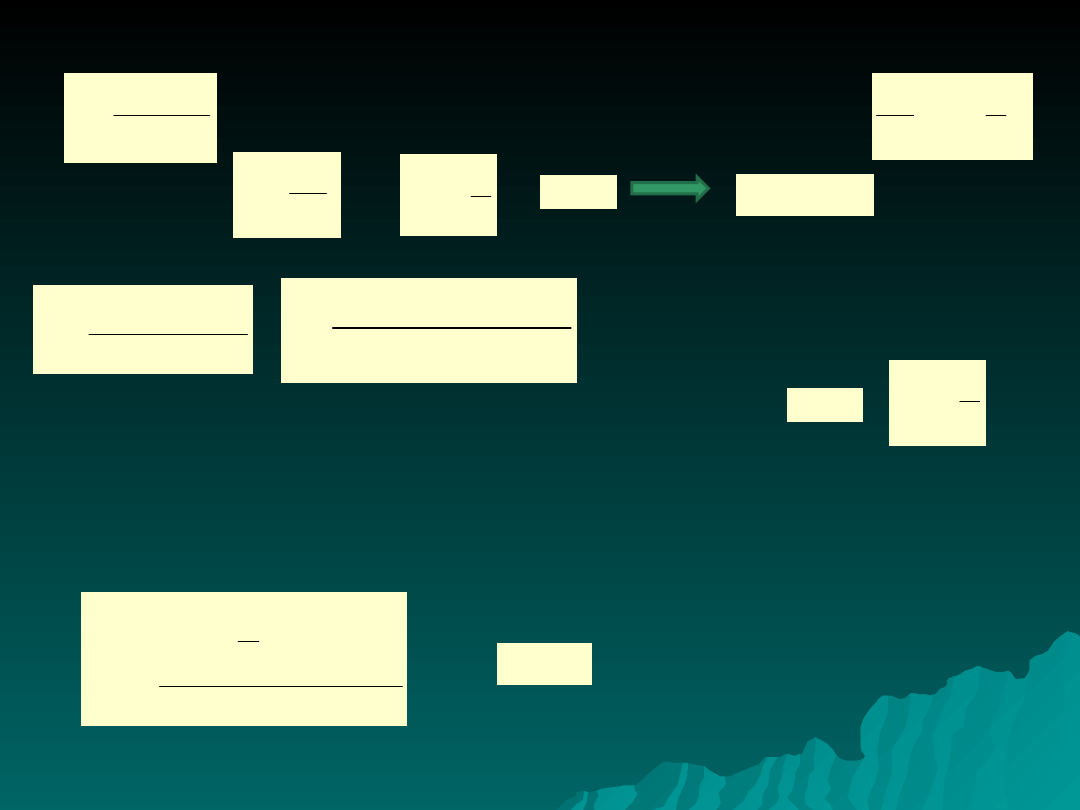
Szacowanie parametrów funkcji logistycznej metoda Hotellinga

Szacowanie parametrów funkcji logistycznej metoda Hotellinga

Różniczkowanie i pomnożenie przez 

Różniczkowanie i pomnożenie przez 

1/

1/

y

y

23

23

at

be

k

y







1

y

k

a

a

y

y







Podstawienia

Podstawienia

y

y

R 



k

a

q 



a

p

qy

p

R





Stosując metodę najmniejszych kwadratów – układ równań

Stosując metodę najmniejszych kwadratów – układ równań

N

y

q

R

p









 



















2

2

y

y

N

y

R

y

N

q

Znając parametry 

Znając parametry 

p

p

 i 

 i 

q

q

, oblicza się parametry 

, oblicza się parametry 

k

k

 i 

 i 

a

a

p

a 

q

a

k 



Parametr 

Parametr 

b

b

 szacuje się przez ponowne zastosowanie metody najmniejszych 

 szacuje się przez ponowne zastosowanie metody najmniejszych 

kwadratów. Bierze się pod uwagę 4 wartości 

kwadratów. Bierze się pod uwagę 4 wartości 

t

t

, dla których 

, dla których 

y

y

 jest bliskie 

 jest bliskie 

1/2

1/2

k

k

n

t

a

y

k

b























1

ln

ln

b

e

b

ln



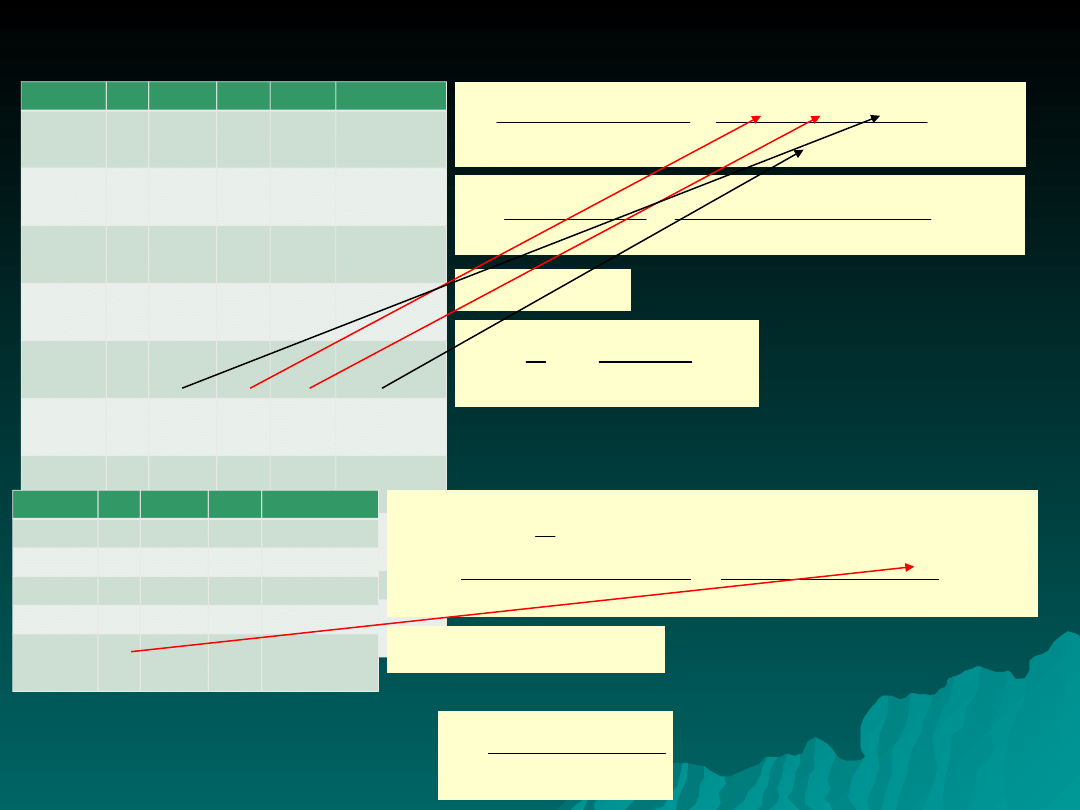
Przykład

Przykład

: wyposażenie gospodarstw rolników (na 100) w 

: wyposażenie gospodarstw rolników (na 100) w 

regionie północno-wschodnim w sam. osobowe w latach 1994-

regionie północno-wschodnim w sam. osobowe w latach 1994-

2002

2002

Lata

t

y

∆y

R

y

2

1994

1 37,4 4,5 0,12

0

1398,76

1995

2 41,9 0,8 0,01

9

1755,61

1996

3 42,7 8,1 0,19

0

1823,29

1997

4 50,8 5,7 0,11

2

2580,64

1998

5 56,5 2,2 0,03

9

3192,25

1999

6 58,7 1,9 0,03

2

3445,69

2000

7 60,6 4,7 0,07

8

3672,36

2001

8 65,3 2,5 0,03

8

4264,09

2002

9

a

67,8

-

-

-

Ogółe

m

413,

9

30,

4

0,62

8

22132,6

9

24

24

a

 Dane z tego okresu służą wyłącznie do obl. ∆y dla poprzedniego okresu. 

Informacji pochodzących z ostatniego okresu nie uwzględnia się przy określaniu liczby 
analizowanych okresów (N) oraz przy sumowaniu (∑y)

 

003

,

0

9

,

413

69

,

22132

8

9

,

413

628

,

0

4

,

30

8

2

2

2



































y

y

N

y

R

y

N

q





234

,

0

8

9

,

413

003

,

0

628

,

0



















N

y

q

R

p

234

,

0



p

a

78

003

,

0

234

,

0













q

a

k

Lata

t

y

k/y ln(k/y-1)

1994

1 37,4 2,09 0,082

1995

2 41,9 1,89 -0,149

1996

3 42,7 1,83 -0,190

1997

4 50,8 1,54 -0,625

Ogółe

m

10 172,

8

-

-0,882

Parametr b, 4 wartości t, 
dla których y = 1/2k, 
czyli y = ½*78=39

365

,

0

4

10

234

,

0

882

,

0

1

ln

ln

































n

t

a

y

k

b

441

,

1

365

,

0

ln







e

e

b

b

t

e

y

234

,

0

441

,

1

1

78

ˆ







Funkcja 
logistyczna

Nasycenie 

k

 

= 78

 sam. na 100 gosp.

Punkt przegięcia 

y

 

= ½*78 = 39

Dalej będzie przyrost 
zmniejszający się

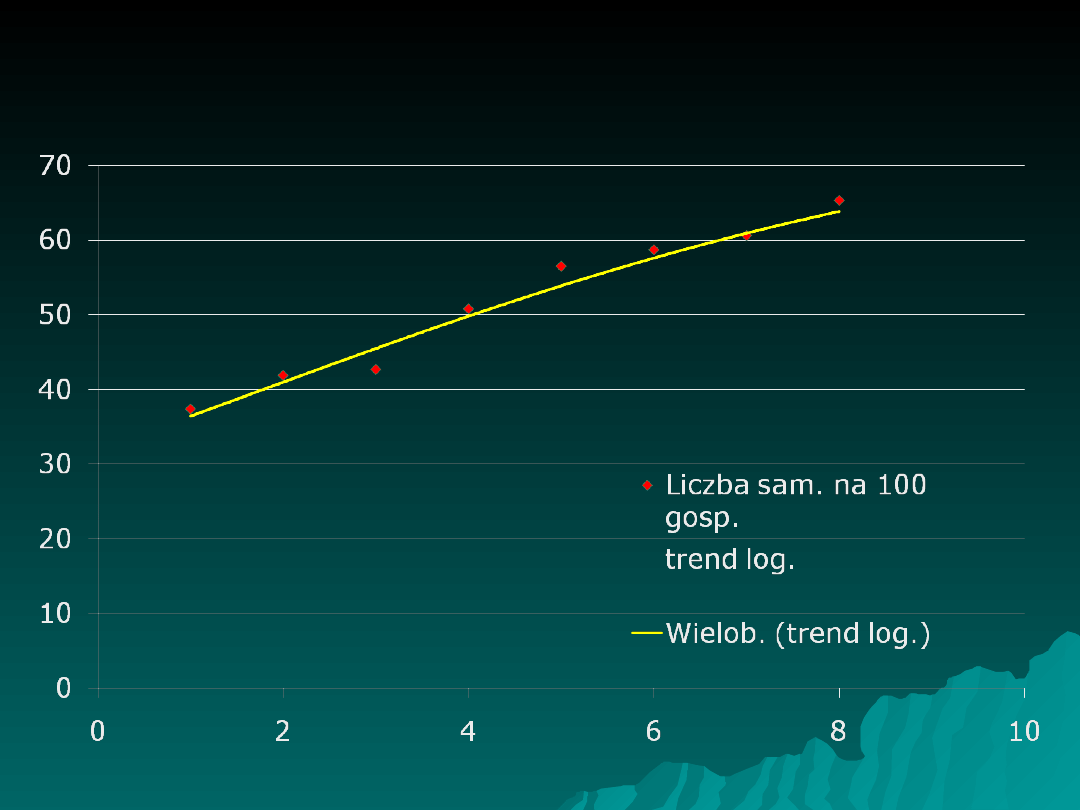
Wyposażenie gospodarstw rolników (na 100) w 

Wyposażenie gospodarstw rolników (na 100) w 

regionie północno-wschodnim w sam. osobowe w 

regionie północno-wschodnim w sam. osobowe w 

latach 1994-2002

latach 1994-2002

25

25

Przykład

Przykład

: stan ciągników w latach 2000-2010

: stan ciągników w latach 2000-2010

26

26

 

05

865

,

3

14346

20682064

10

14346

199

,

0

282

10

2

2

2



































E

y

y

N

y

R

y

N

q

Δ





075

,

0

10

14346

05

865

,

3

1993

,

0





















E

N

y

q

R

p

075

,

0



p

a

1940

05

865

,

3

075

,

0















E

q

a

k

Lata

t

y

k/y ln(k/y-1)

2000

1

1307

1,48 -0,725

2001

2

1309

1,48 -0,730

2002

3

1365

1,42 -0,864

2003

4

1371

1,41 -0,879

Ogółe

m

10 5352 -

-3,199

Parametr b, 4 wartości t, 
dla których y = 1/2k, 
czyli y = ½*1940=970

612

,

0

4

10

075

,

0

199

,

3

1

ln

ln



































n

t

a

y

k

b

542

,

0

612

,

0

ln









e

e

b

b

t

e

y

075

,

0

542

,

0

1

1940







Funkcja logistyczna

Nasycenie 

k

 

= 1940 

stan ciągników

Punkt przegięcia 

y

 

= ½*1940 = 970

Dalej będzie przyrost zmniejszający się

rok

t

y

Δy R

y^2

2000

1

1307 2

0,0015 1708249

2001

2

1309 56 0,0428 1713481

2002

3

1365 6

0,0044 1863225

2003

4

1371 -6

-

0,0044 1879641

2004

5

1365 72 0,0527 1863225

2005

6

1437 58 0,0404 2064969

2006

7

1495 58 0,0388 2235025

2007

8

1553 13 0,0084 2411809

2008

9

1566 12 0,0077 2452356

2009 10 1578 11 0,0070 2490084
2010

1589

ogółem

1434

6 282 0,1993

2068206

4

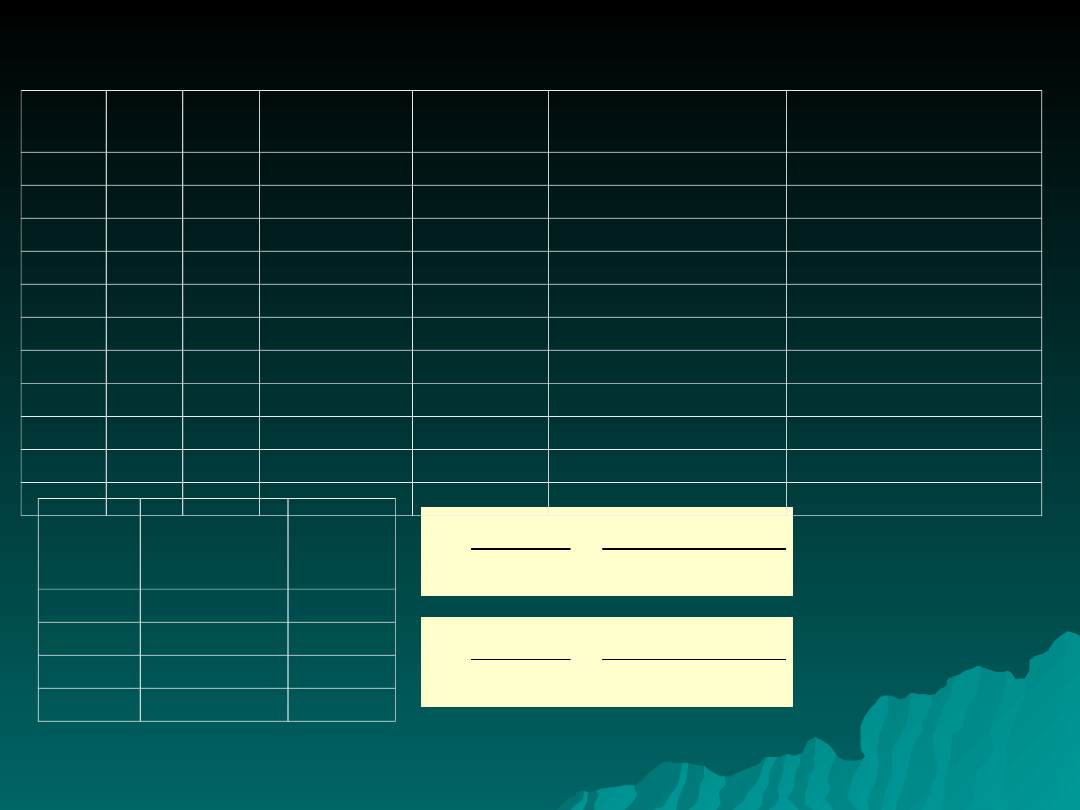
Przykład

Przykład

: stan ciągników w latach 2000-2010

: stan ciągników w latach 2000-2010

27

27

t

at

e

be

k

y

075

,

0

678

,

0

1

2080

1













rok

t

yH

Ei^2

yH^

różnica (yH^-

yH)^2

błąd względny, %

2000

1

1307 895,5794

1277

900

-2,3

2001

2

1309 20,48987

1314

25

0,38

2002

3

1365 247,3472

1349

256

-1,17

2003

4

1371 175,1983

1384

169

0,95

2004

5

1365 2846,085

1418

2809

3,88

2005

6

1437 211,6899

1452

225

1,04

2006

7

1495 125,7451

1484

121

-0,74

2007

8

1553 1442,865

1515

1444

-2,45

2008

9

1566 432,6767

1545

441

-1,34

2009

10 1578 13,61007

1574

16

-0,25

2010

11 1589 177,6787

1602

169

0,82

punkty 

starto

we

k=

2080,622

1940

a=

0,07457

0,07

b=

0,677925

0,5

Suma= 6588,965 min

t

at

e

be

k

y

075

,

0

542

,

0

1

1940

1













metoda Hotellinga

metoda Hotellinga

solver

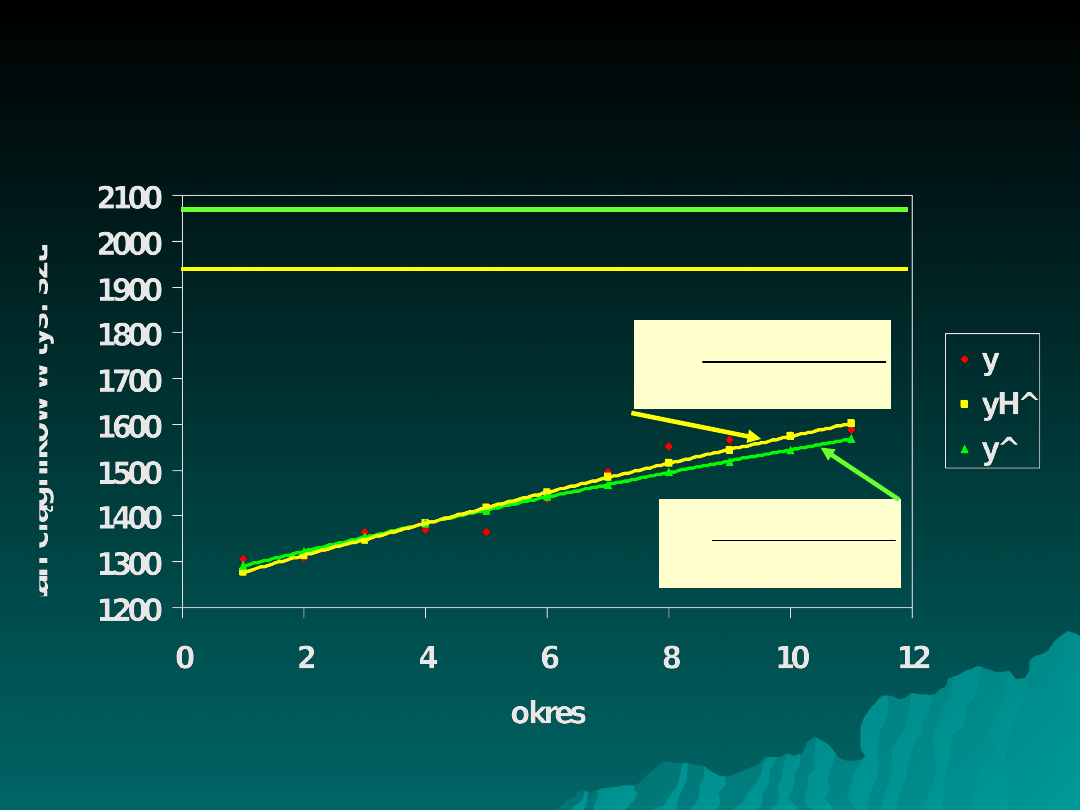
Stan ciągników w latach 2000-2010 – aproksymacja 

Stan ciągników w latach 2000-2010 – aproksymacja 

porównawcza

porównawcza

t

e

y

075

,

0

678

,

0

1

2080







t

H

e

y

075

,

0

542

,

0

1

1940







metoda Hotellinga

metoda Hotellinga

solver

k=1940

k=2080

29

29

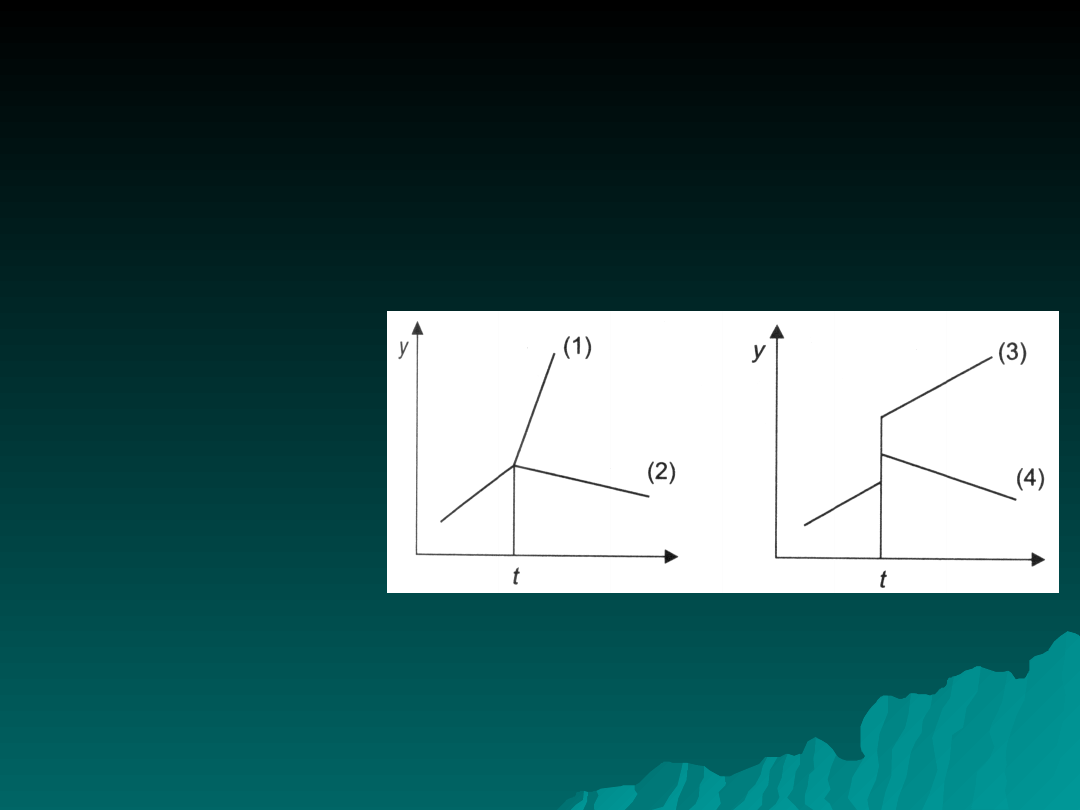
Trend (funkcja) segmentowa

  stosuje się, jeśli trudno określić prawa rozwojowe 

charakteryzujące zjawisko w całym przedziale czasowym

Rozwój zjawiska przebiega segmentowo, obrazem jest funkcja 
wyznaczana sekwencyjne, za pomocą odcinków linii prostej 
pomiędzy punktami zwrotnymi.

1 - zmiana prędkości 

V

2 - zmiana kierunku  

k

3 – uskok const 

V i k

4 – uskok i zmiana 

V i k

30

30

Dopasowanie trendu

• współczynnik zbieżności (zgodności) 

 pozwala ocenić, jaki procent wartości rzeczywistych 

(y)

 

nie został 
 wyjaśniony przez przyjętą funkcję



















2

2

2

ˆ

y

y

y

y



Przy 



2

  

   0

  - zgodność danych empirycznych 

do teoretycznych jest idealna

Przy 



2

  

   1

  - brak zgodność danych 

empirycznych 
z teoretycznymi

31

31

•współczynnik determinacji

 to różnica między jednością a wartością współczynnika 

zbieżności.

























2

2

2

2

ˆ

1

1

y

y

y

y

R



Współczynnik informuje, jaki procent wartości rzeczywistych 

(y)

 

został wyjaśniony przez przyjęty model trendu

Przy 

R

2

  

   0

  - wybrana funkcja trendu jest gorzej 

dopasowana do wartości 
empirycznych

Przy 

R

2

  

   1

  - wybrana funkcja trendu dobrze 

opisuje wartości empiryczne

Excel !!!

32

32

•standardowy błąd szacunkowy

 ocena dopasowania funkcji trendu jest przedstawiana nie 

procentowo, ale w wartościach bezwzględnych, czyli 
informuje o ile dane teoretyczne różnią się od wartości 
rzeczywistych.  

n 

 - liczba obserwacji 

k

  - liczba szacowanych 

parametrów





k

n

y

y

S









2

ˆ

33

33

Prognozowanie

wnioskowanie o zdarzeniach nieznanych na podstawie zdarzeń 

znanych

Prognozowanie powinno być

 - 

racjonalne

 (logiczny proces wnioskowania)

 - 

naukowe

 (sąd o zajściach uzyskany w wyniku reguł i metod 

naukowych)

Prognozowanie w oparciu o techniki ekstrapolacyjne. 

 - przyjmujemy założenie, że nastąpi ilościowe „przedłużenie” 

tendencji na pewien okres w przyszłości, zakładając że dane o 
rozwoju zjawiska w przeszłości są wiarygodne a warunki jego 
kształtowania się będą podobne w przyszłości.

34

34

Prognozowanie zjawisk rynkowych

 - 

model średniej ruchomej

 

- prostej

- ważonej

Ważne !

 

   

Aby prawidłowo wnioskować o przyszłości, należy zebrać 

Aby prawidłowo wnioskować o przyszłości, należy zebrać 

dane 

dane 

z przynajmniej 10 okresów.

z przynajmniej 10 okresów. 

 - 

funkcji 

trendu 
(Mynarski)

 











1

*

1

t

k

t

i

i

t

y

k

y

















1

1

1

*

1

t

k

t

i

k

i

i

t

w

y

k

y

prognoza poziomu zjawiska wyznaczona w czasie t

y

i

 – poziom zjawiska w okresie t,

k – stała wygładzania

*

t

y



































n

k

k

t

t

y

n

n

k

n

y

1

*

1

1

6

4

n – liczba obserwacji

Prognozowanie na podstawie funkcji 

trendu

2

1

*

2









t

t

t

y

y

y

Przyjmując n = 2, 3, …, 7 

3

2

1

*

3

2

3

1

3

4













t

t

t

t

y

y

y

y

4

2

1

*

2

1

2

1













t

t

t

t

y

y

y

y

5

4

3

2

1

*

5

2

10

1

5

1

2

1

5

4





















t

t

t

t

t

t

y

y

y

y

y

y

6

5

4

3

2

1

*

3

1

15

2

15

1

15

4

15

7

6

4

























t

t

t

t

t

t

t

y

y

y

y

y

y

y

7

6

4

3

2

1

*

7

2

7

1

7

1

7

2

7

3

7

4

























t

t

t

t

t

t

t

y

y

y

y

y

y

y

Z rozwinięcia wynikają następujące relacje:

• Wpływ zaobserwowanych wartości w 
poszczególnych okresach na wartość 
prognozowaną jest tym większy, im mniejsza 
jest liczba obserwacji.

• Największy dodatni 
wpływ na wartość 
prognozowaną mają 
wartości pochodzące z 
okresów bezpośrednio 
poprzedzających okres 
prognozowany; później 
wpływ ten stopniowo 
słabnie, a następnie – w 
przypadku najstarszych 
obserwacji – zaczyna 
oddziaływać ujemnie.

36

36

Etapy prognozowanie zjawisk rynkowych

 - analiza tendencji otoczenia makroekonomicznego

 - prognozowanie kierunku i natężenia zmian w nim zachodzących

 - pokazanie trendów dla gałęzi przemysłu

 - prognoza dla możliwych kierunków rozwoju w ujęciu globalnym

 - prognozy dla grup asortymentów

 - określenie perspektywy rozwoju dla określonego produktu 

   (uwzględniamy: podaż, popyt, import, eksport)

 - sporządzamy prognozę dla firmy 

   (uwzględniamy: wielkość produkcji, sprzedaż, poziom kosztów)

Excel – przykład siewniki!!!

Charakterystyka metody ekstrapolacji 

Charakterystyka metody ekstrapolacji 

trendu

trendu



Analizowane wymiary

Analizowane wymiary

37

37



Charakterystyka metody

Charakterystyka metody

Czas

Czas



Horyzont czasowy prognozy

Horyzont czasowy prognozy

raczej krótko- i średnioterminowe 

raczej krótko- i średnioterminowe 

prognozy; istnieje możliwość 

prognozy; istnieje możliwość 

prognozowania długoterminowego

prognozowania długoterminowego



Pilność (czy prognoza będzie 

Pilność (czy prognoza będzie 

potrzebna natychmiast?)

potrzebna natychmiast?)

można szybko uzyskać wyniki, gdy 

można szybko uzyskać wyniki, gdy 

zebrano niezbędne dane

zebrano niezbędne dane



Częstotliwość (czy będzie 

Częstotliwość (czy będzie 

potrzebna i możliwa częsta 

potrzebna i możliwa częsta 

aktualizacja prognoz?)

aktualizacja prognoz?)

prognozy mogą być w łatwy sposób 

prognozy mogą być w łatwy sposób 

systematycznie aktualizowane

systematycznie aktualizowane

Zasoby

Zasoby



Umiejętność posługiwania 

Umiejętność posługiwania 

się metodami statystycznymi

się metodami statystycznymi

wymagany jest podstawowy poziom 

wymagany jest podstawowy poziom 

wiedzy z zakresu statystyki

wiedzy z zakresu statystyki



Sprzęt i oprogramowanie 

Sprzęt i oprogramowanie 

komputerowe

komputerowe

jest konieczne (znacznie przyśpiesza 

jest konieczne (znacznie przyśpiesza 

opracowanie prognozy)

opracowanie prognozy)



Zasoby finansowe

Zasoby finansowe

jeśli niezbędne dane są łatwo dostępne, to 

jeśli niezbędne dane są łatwo dostępne, to 

koszt opracowania prognozy jest 

koszt opracowania prognozy jest 

minimalny

minimalny

Charakterystyka metody ekstrapolacji 

Charakterystyka metody ekstrapolacji 

trendu

trendu



Analizowane wymiary

Analizowane wymiary

38

38



Charakterystyka metody

Charakterystyka metody

Dane wejściowe

Dane wejściowe



Dane o przeszłości

Dane o przeszłości

logicznie powiązane z zadaniem 

logicznie powiązane z zadaniem 

prognostycznym 

prognostycznym 



Zmienność (czy występują istotne 

Zmienność (czy występują istotne 

wahania?)

wahania?)

duże wahania zmniejszają dokładność 

duże wahania zmniejszają dokładność 

prognozy

prognozy



Stabilność (czy nastąpią istotne 

Stabilność (czy nastąpią istotne 

zmiany we wzajemnych 

zmiany we wzajemnych 

powiązaniach między zmiennymi?)

powiązaniach między zmiennymi?)

nie można przewidzieć takich zmian; 

nie można przewidzieć takich zmian; 

jedyną zmienną reprezentującą wpływ 

jedyną zmienną reprezentującą wpływ 

wszystkich czynników jest czas

wszystkich czynników jest czas

Wyniki

Wyniki



Dokładność

Dokładność

możne być mierzona za pomocą 

możne być mierzona za pomocą 

odpowiednich wskaźników

odpowiednich wskaźników



Zdolność wykrywania zmian 

Zdolność wykrywania zmian 

kierunkowych

kierunkowych

brak (nie można określić tzw. punktów 

brak (nie można określić tzw. punktów 

zwrotnych)

zwrotnych)



Forma prezentacji

Forma prezentacji

Prognozy ilościowe

Prognozy ilościowe



Stałość (czy można przewidzieć 

Stałość (czy można przewidzieć 

znaczące zmiany w otoczeniu?)

znaczące zmiany w otoczeniu?)

prognozy nie przewidują takich zmian; 

prognozy nie przewidują takich zmian; 

przyjmuje się pewną konsekwencję w 

przyjmuje się pewną konsekwencję w 

rozwojowi zjawiska

rozwojowi zjawiska