1

Suwałki, 2011 r.

Suwałki, 2011 r.

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Instytut Budownictwa

Instytut Budownictwa

Metody Obliczeniowe

Metody Obliczeniowe

Dr inż. Władysław Ryżyński

Dr inż. Władysław Ryżyński

Wykład Nr 1

Wykład Nr 1

Macierze

i układy równań

liniowych

2

Suwałki, 2011 r.

Suwałki, 2011 r.

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Instytut Budownictwa

Instytut Budownictwa

RACHUNEK MACIERZOWY - DEFINICJE

Macierz A – tablica liczb składająca się z n wierszy i m

kolumn (oznaczana jako A lub [a

ik

] ; i – numer

wiersza, k – numer kolumny)

Macierz kwadratowa – macierz w której n = m

Macierz transponowana A

T

– macierz, w której

zamieniono wiersze i kolumny

Macierz symetryczna – macierz niezmiennicza względem

transpozycji (a

ik

= a

ki

)

Macierz odwrotna A

-1

– pomnożona przez macierz A daje

macierz jednostkową oznaczaną jako I lub E (A A

-1

= I)

3

Suwałki, 2011 r.

Suwałki, 2011 r.

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Instytut Budownictwa

Instytut Budownictwa

Użyteczne reguły

Mnożenie macierzy nie jest przemienne

















































































41

14

31

13

21

12

11

11

44

43

42

41

34

33

32

31

24

23

22

21

14

13

12

11

44

43

42

41

34

33

32

31

24

23

22

21

14

13

12

11

b

a

b

a

b

a

b

a

b

b

b

b

b

b

b

b

b

b

b

b

b

b

b

b

a

a

a

a

a

a

a

a

a

a

a

a

a

a

a

a





j

jk

ij

ik

b

a

c

4

Suwałki, 2011 r.

Suwałki, 2011 r.

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Instytut Budownictwa

Instytut Budownictwa

METODY ROZWIĄZYWANIA

UKŁADÓW RÓWNAŃ LINIOWYCH

1. Metoda wyznaczników Cramera

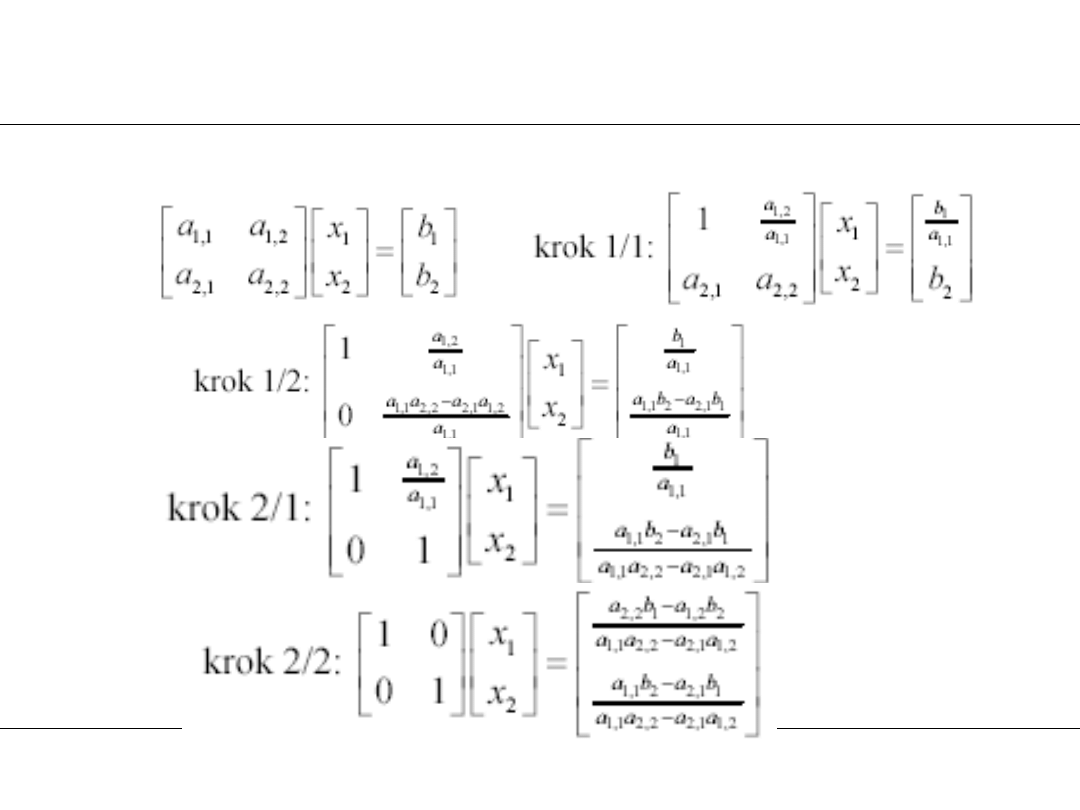
2. Metoda eliminacji Gaussa-Jordana

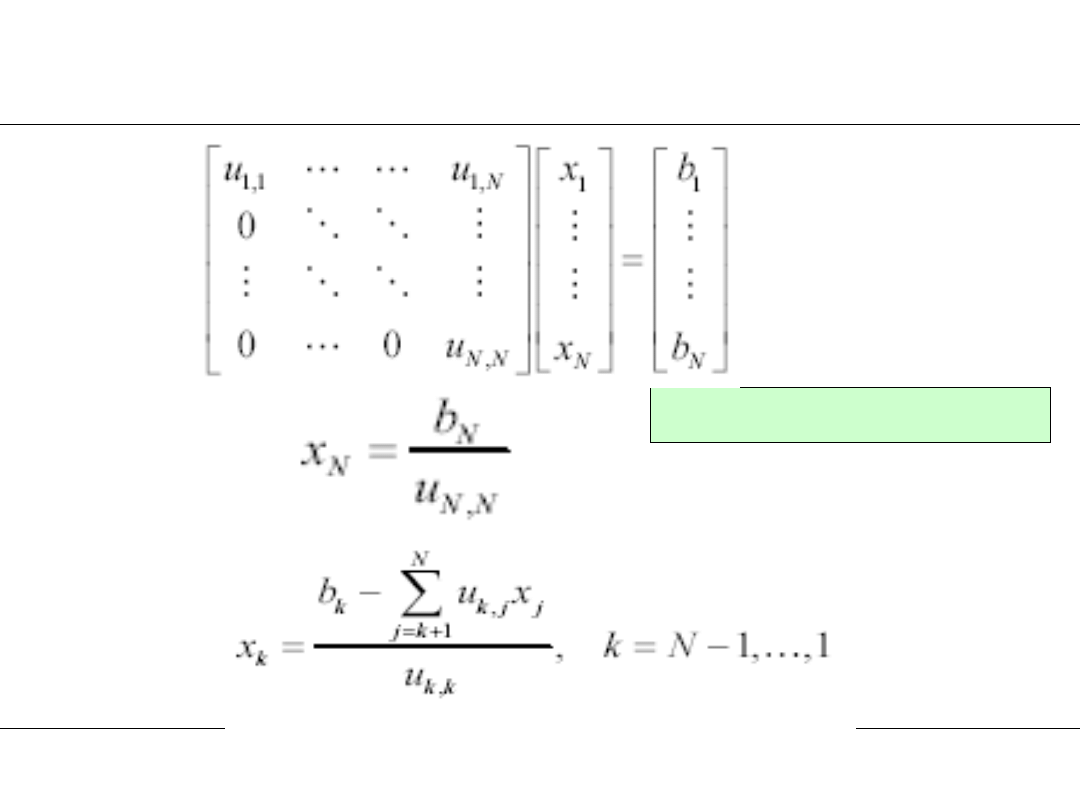
3. Metoda eliminacji Gaussa

5

Suwałki, 2011 r.

Suwałki, 2011 r.

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Instytut Budownictwa

Instytut Budownictwa

6

Suwałki, 2011 r.

Suwałki, 2011 r.

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Instytut Budownictwa

Instytut Budownictwa

PRZYKŁAD

7

Suwałki, 2011 r.

Suwałki, 2011 r.

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Instytut Budownictwa

Instytut Budownictwa

Eliminacja Gaussa

8

Suwałki, 2011 r.

Suwałki, 2011 r.

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Instytut Budownictwa

Instytut Budownictwa

W metodzie dekompozycji LU macierz A jest rozdzielana na

iloczyn dwu macierzy składowych dolnej i górnej trójkątnej,

tzn. A = LU.

Algorytm Crouta

9

Suwałki, 2011 r.

Suwałki, 2011 r.

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Instytut Budownictwa

Instytut Budownictwa

Jeśli macierz A układu równań jest macierzą symetryczną dodatnio
określoną (jest np. macierzą kowariancyjną lub korelacyjną) to jej
dekompozycja LU ma prostszą postać nazywaną

dekompozycją

Choleskiego

– macierz trójkątna górna U ma taką samą zawartość

elementową jak macierz trójkątna dolna L. Wyznaczyć trzeba
dwukrotnie mniej elementów macierzy.

10

Suwałki, 2011 r.

Suwałki, 2011 r.

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Instytut Budownictwa

Instytut Budownictwa

Poszczególne elementy macierzy L są wyznaczane wg zależności

:

11

Suwałki, 2011 r.

Suwałki, 2011 r.

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Instytut Budownictwa

Instytut Budownictwa

Metody dla macierzy specjalnych i rzadkich

Duże

macierze rzadkie

(częsty przypadek przy analizie metodą

różnic i elementów skończonych) i w szczególności macierze
trójprzekątniowe mogą być przetwarzane metodami eliminacji
dużo efektywniej przy wykrywaniu i pomijaniu elementów
zerowych.

Metody iteracyjne – alternatywa dla macierzy rzadkich

Metoda Successive Overrelaxation (SOR)

1. Metoda Jacobiego

2. Metoda Gaussa-Seidla

3. Metoda Successive Overrelaxation (SOR

)

12

Suwałki, 2011 r.

Suwałki, 2011 r.

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Państwowa Wyższa Szkoła Zawodowa w Suwałkach

Instytut Budownictwa

Instytut Budownictwa

Dziękuję za uwagę!