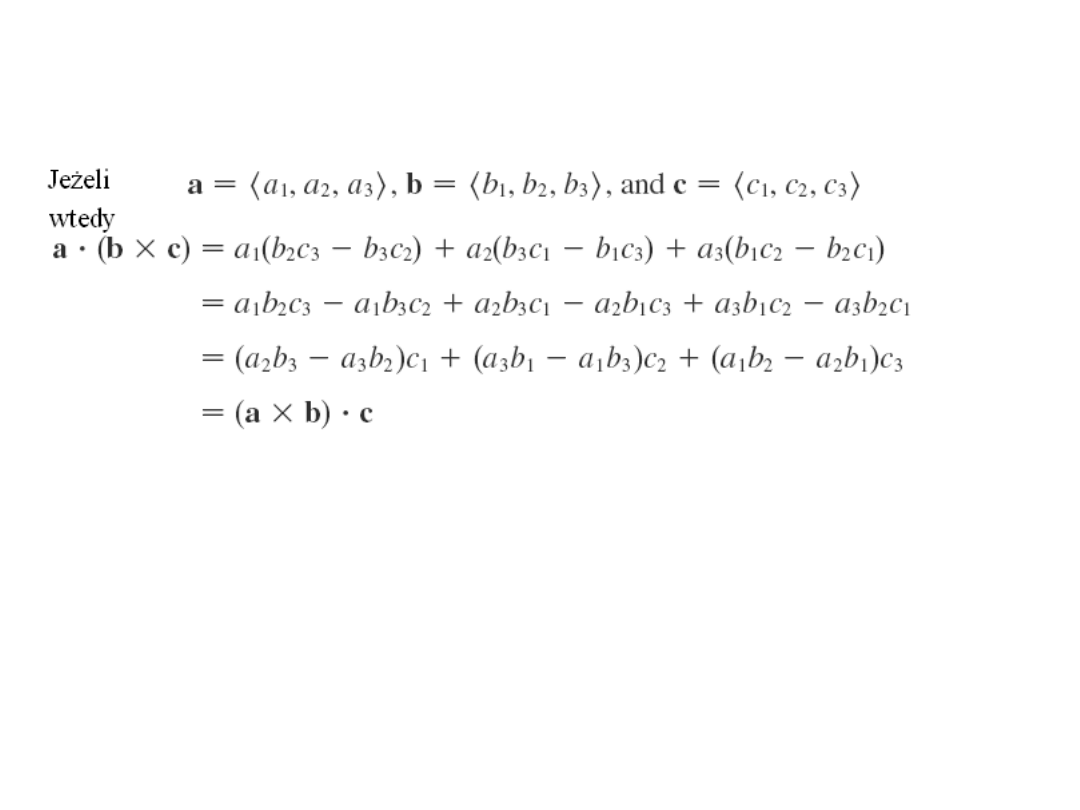
Dowód własności 5 :
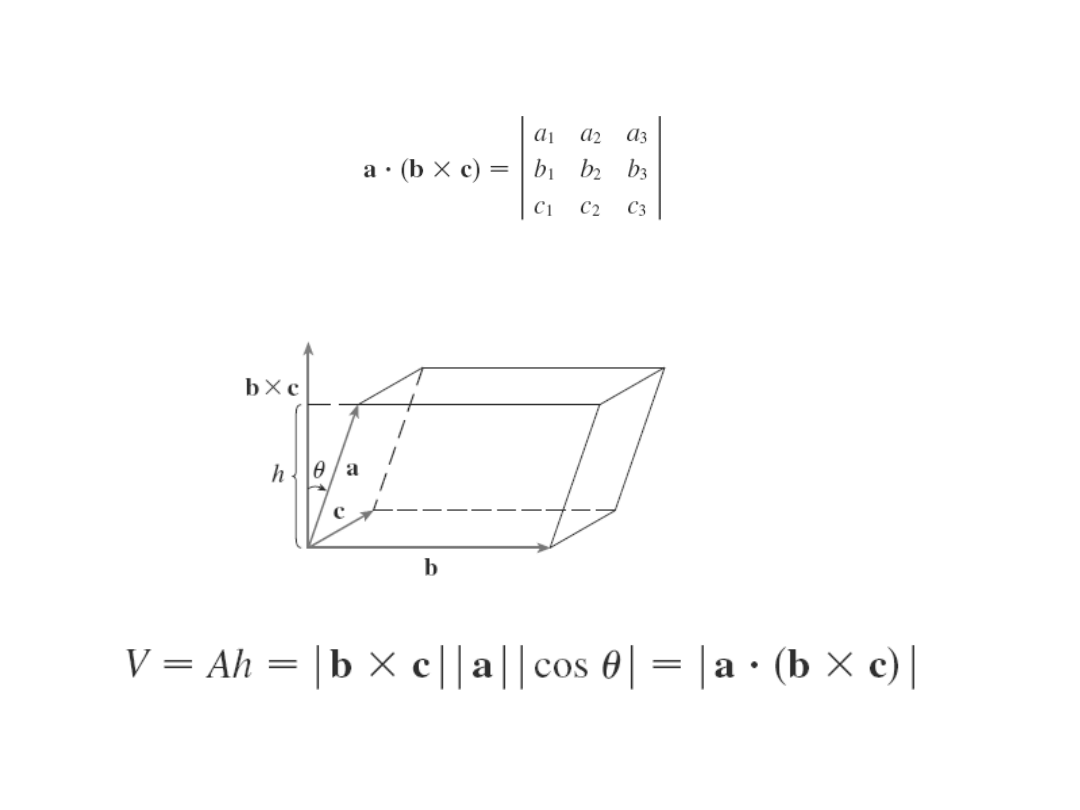
Iloczyn potrójny
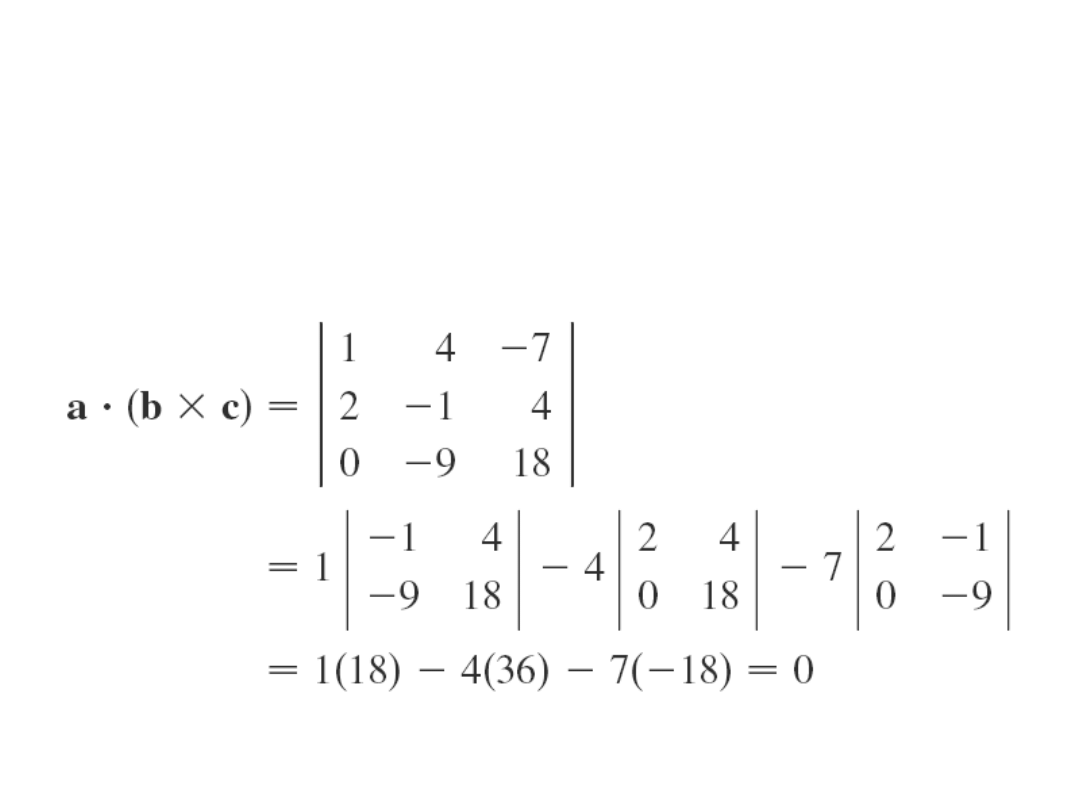
Przykład
Używając iloczynu potrójnego pokazać, że wektory a
= (1,4,-7),
b = (2,-1,4) ,c = (0,-9,18) są współpłaszczyznowe.
Pojęcie iloczynu
wektorowego ma
zastosowanie w fizyce.
Służy do definiowania
momentu siły.
Moment siły, wektor
osiowy,
gdzie: r - promień
wodzący zaczepiony w
pewnym wybranym
punkcie (względem tego
punktu wyznacza się
moment siły), F - wektor
działającej siły, znak ×
oznacza iloczyn
wektorowy.
F
r
Moment siły
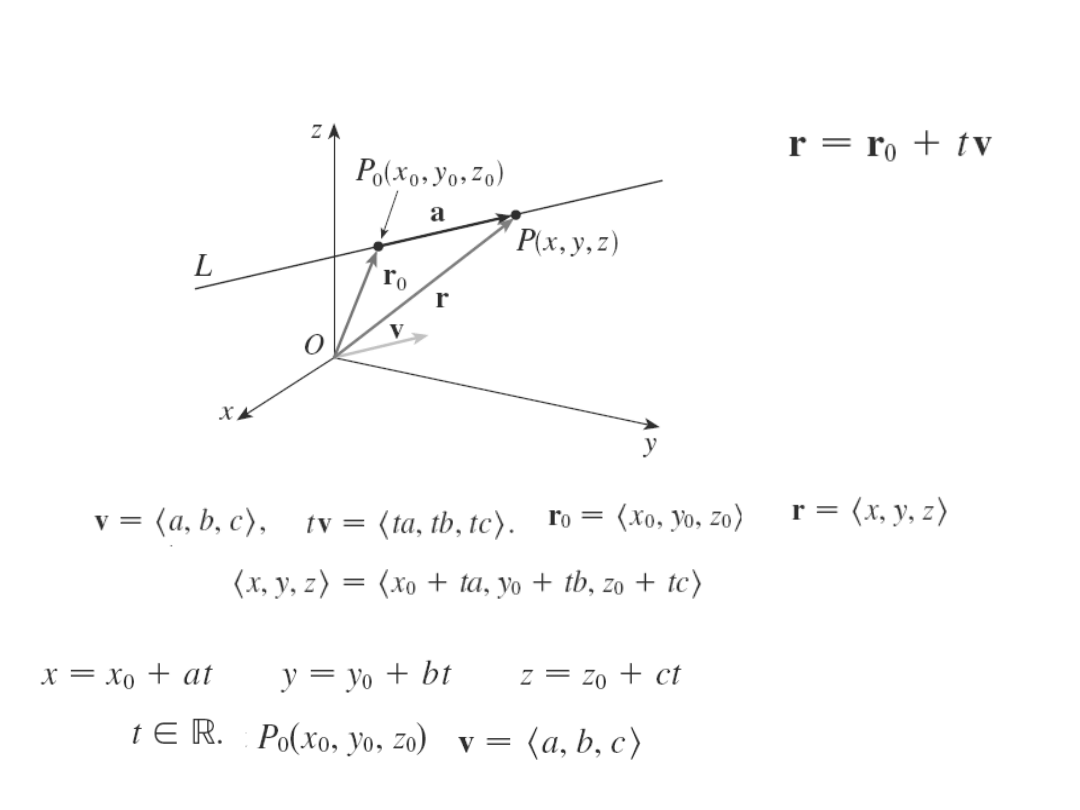
Równanie prostej
Równanie
wektorowe
prostej
Równanie
parametryczn
e
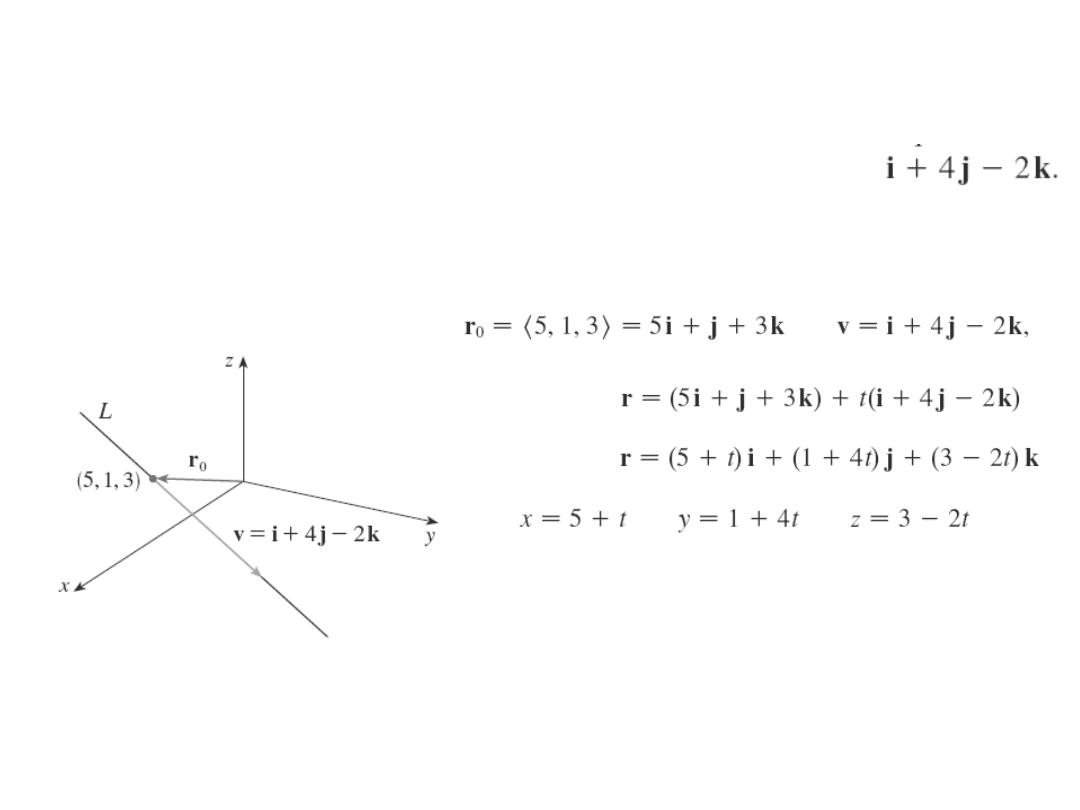
Przykład
Znajdź równanie wektorowe i parametryczne prostej
przechodzącej przez punkt (5,1,3) i równoległej do
wektora
c
z
z
b
y
y
a
x
x
c
z
z
t
b
y
y
t
a
x
x
t
ct
z
z
bt
y
y
at
x
x
0
0
0
0
0
0
0
0
0
Inny sposób opisu prostej otrzymujemy
eliminując z równania parametrycznego
parametr t .
Równanie odcinka
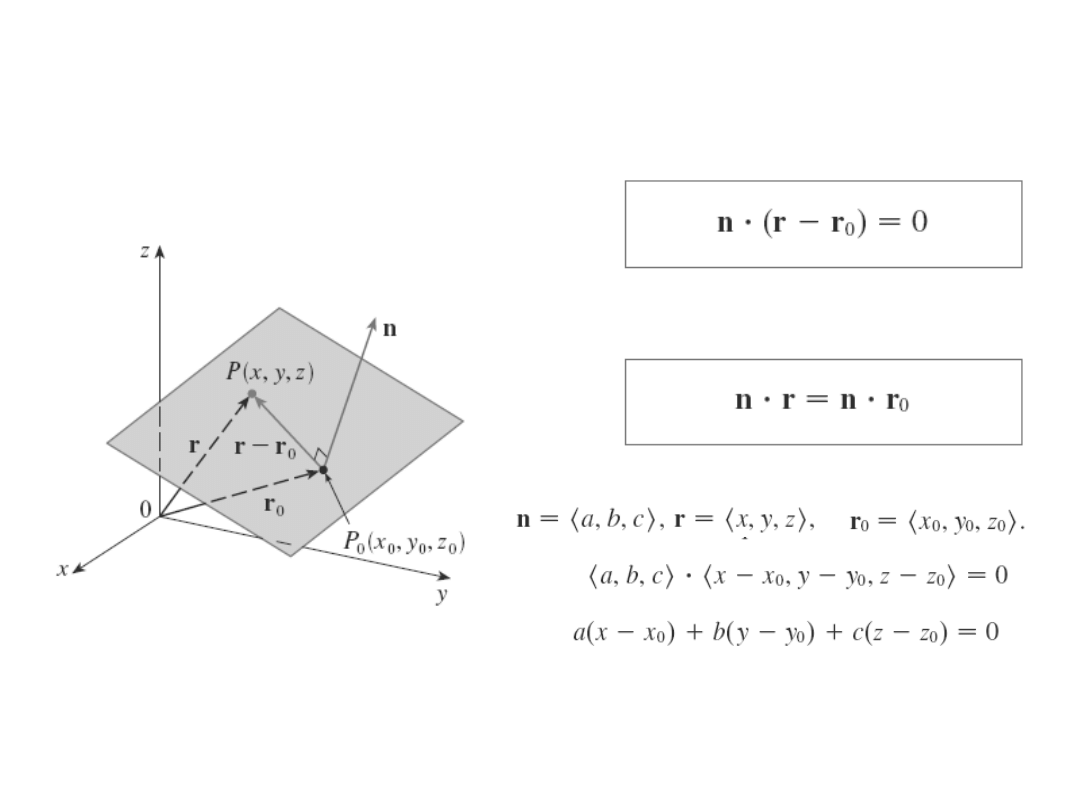
Równanie płaszczyzny
Równanie wektorowe
płaszczyzny
Równanie skalarne
0
d
cz
by
ax
Równanie
liniowe
)
(
0
0
0
cz
by
ax
d
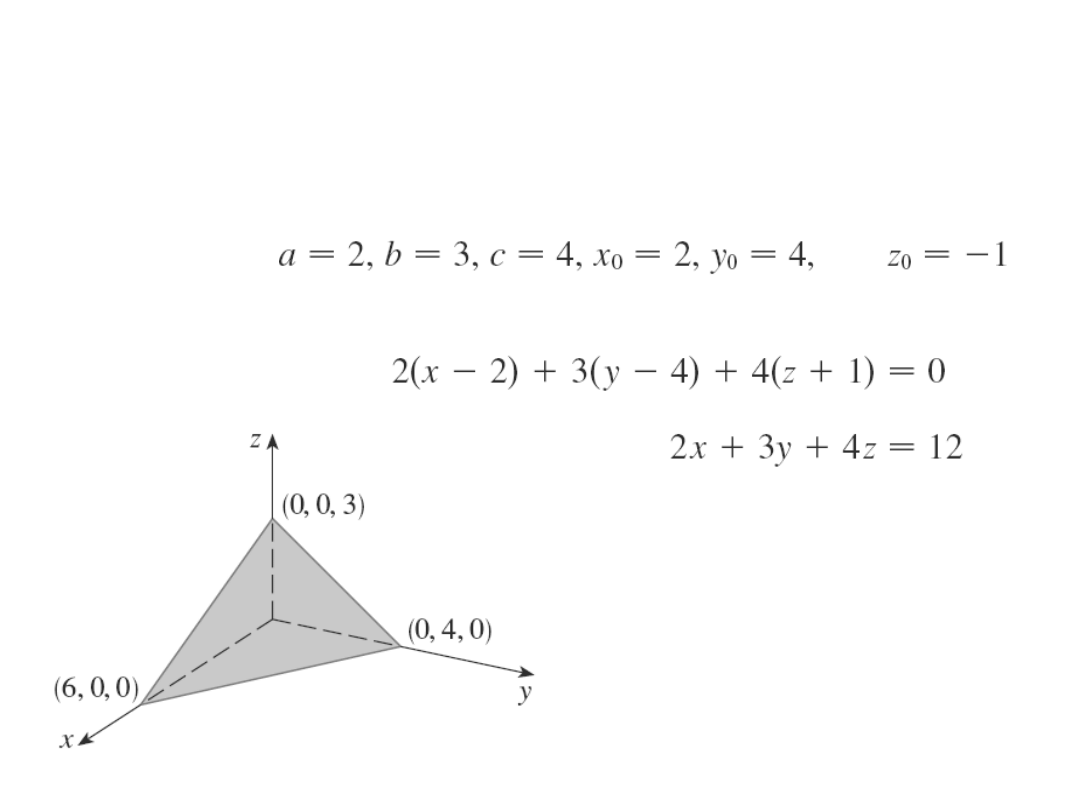
Przykład
Znajdź równanie płaszczyzny o wektorze
normalnym n = (2,3,4) przechodzącej przez punkt
(2,4,-1) .
Przykład
Znajdź równanie płaszczyzny przechodzącej przez
punkty P(1,3,2), Q(3,-1,6), R(5,2,0) .
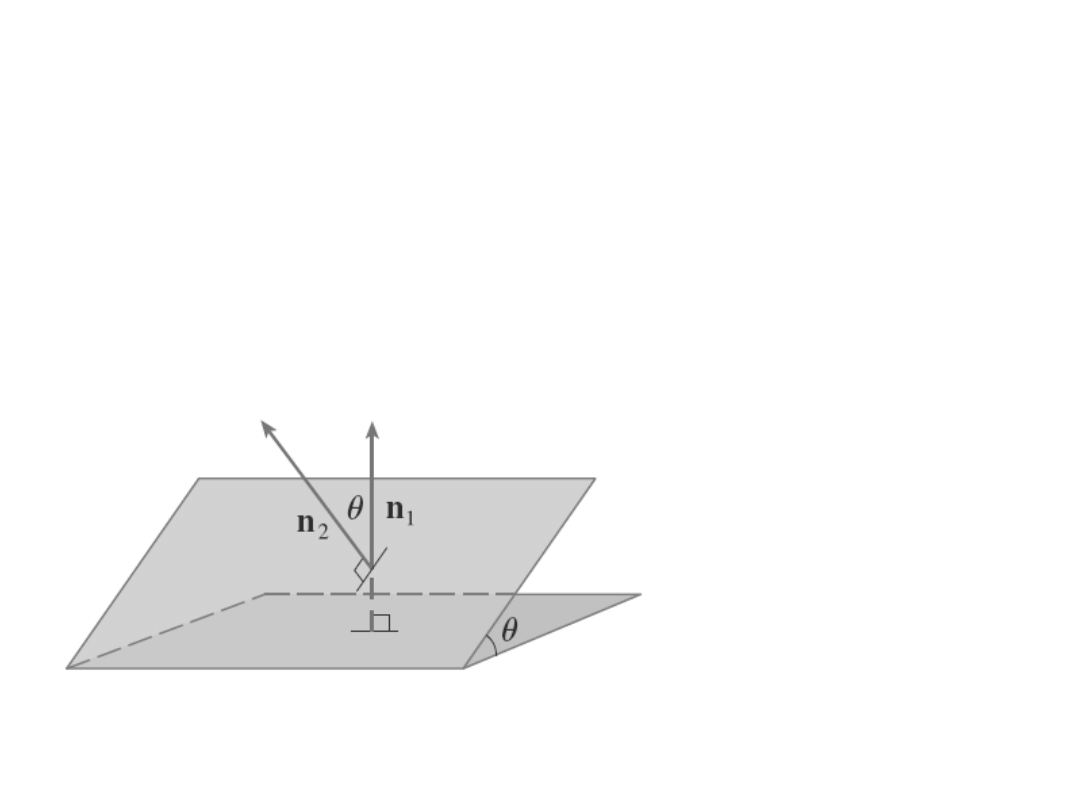
Kąt między płaszczyznami
Dwie płaszczyzny są równoległe jeżeli ich wektory
normalne są równoległe. Na przykład płaszczyzny: x + 2y
3z = 4 i 2x + 4y 6z =3 są równoległe ponieważ ich
wektory normalne: n
1
= (1,2,-3) n
2
= (2,4,-6) spełniają
związek 2n
1
= n
2
. Jeżeli dwie płaszczyzny nie są
równoległe wtedy przecinają się wzdłuż prostej i kąt
między nimi jest zdefiniowany jako kąt między ich
wektorami normalnymi.
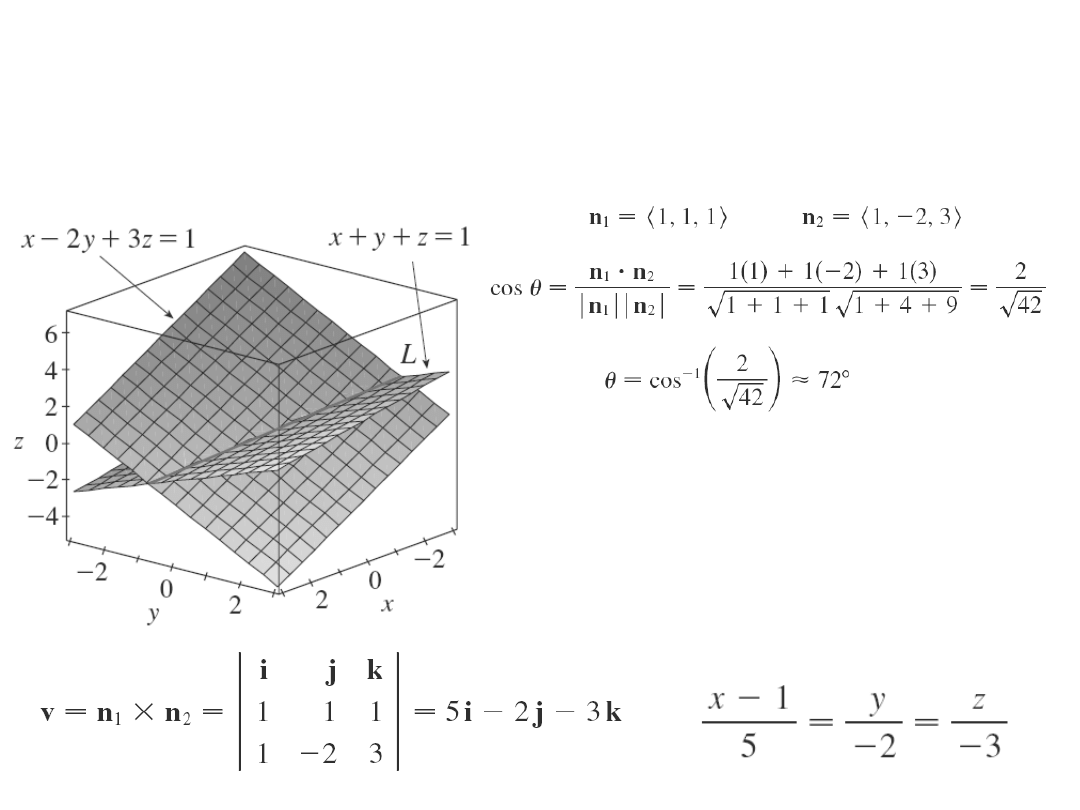
Przykład
a) Zajdź kąt między płaszczyznami x + y + z = 1 i x
– 2y +3z = 1
b) Znajdź równanie prostej wzdłuż której te płaszczyzny
się przecinają.
Ad b) Szukamy
punktu na prostej
np. o współrzędnej z
= 0: x + y = 0 x
2y =1 x = 1 y =
0 .
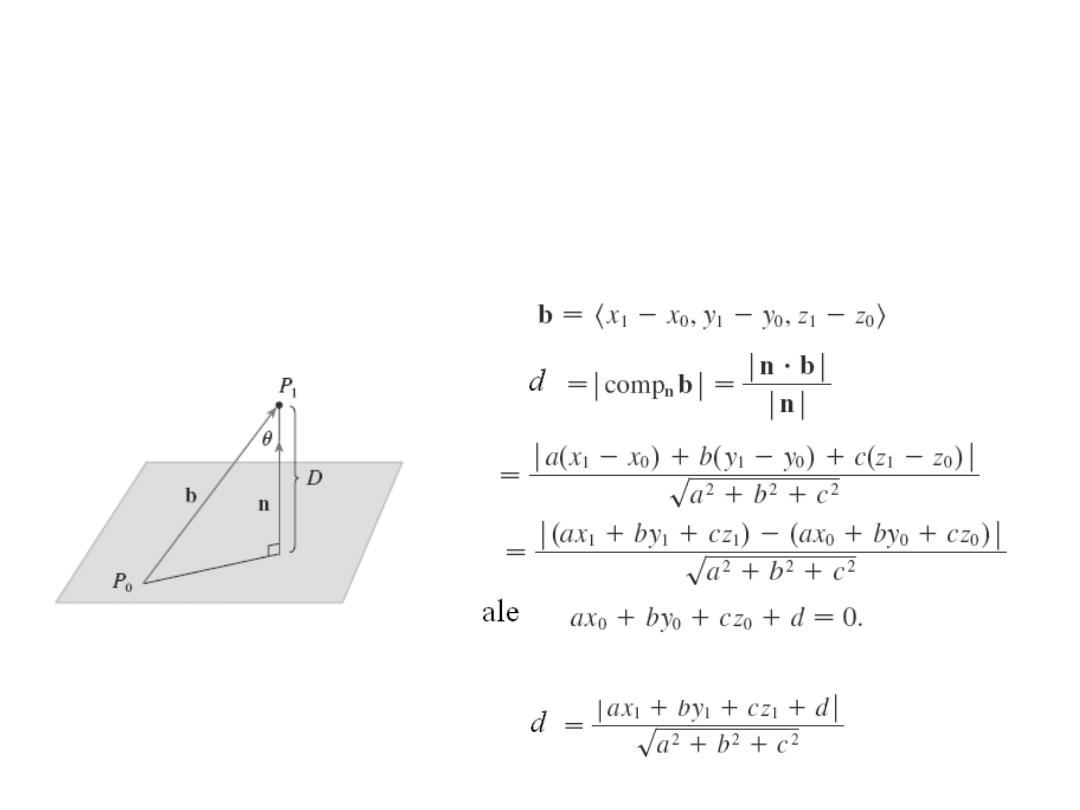
Przykład
Znajdź wzór na odległość d punktu P
1
od
płaszczyzny
ax + by + cz = 0
Niech P
0
(x
o
.y
0
,z
0
) będzie punktem na danej
płaszczyźnie i niech b będzie wektorem P
o
P
1
. Wtedy
Walec i powierzchnia
kwadratowa
z = x
2
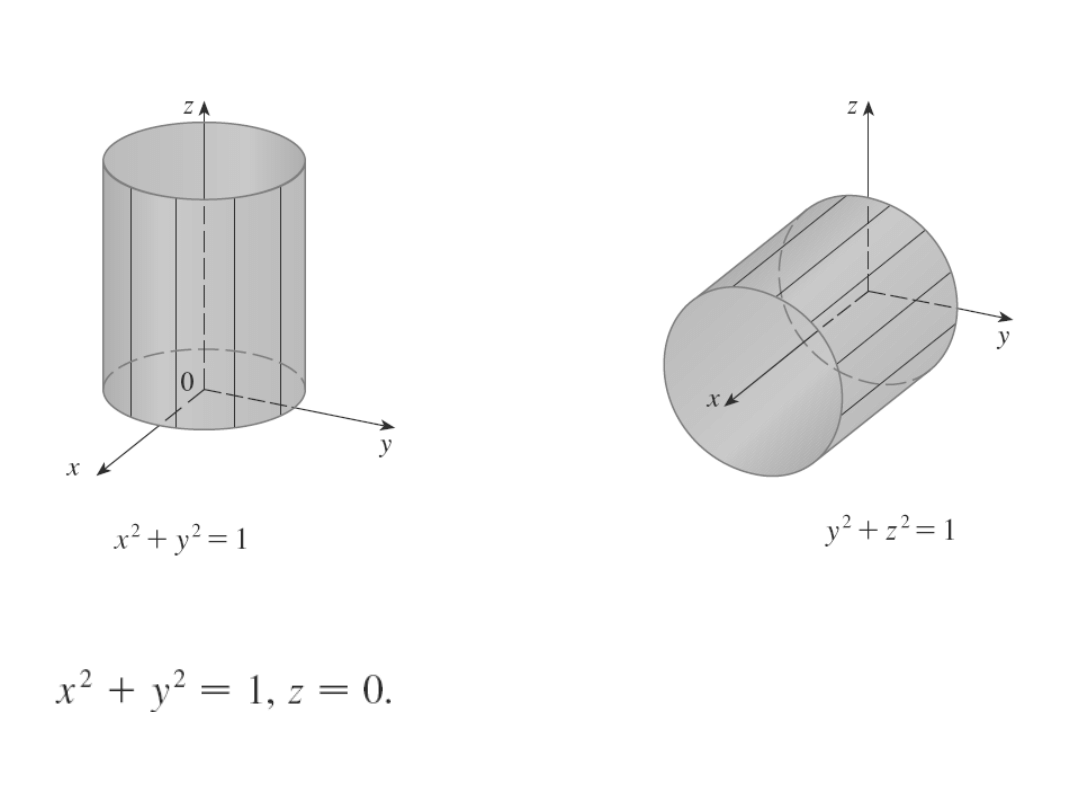
okrąg na płaszczyźnie
xy
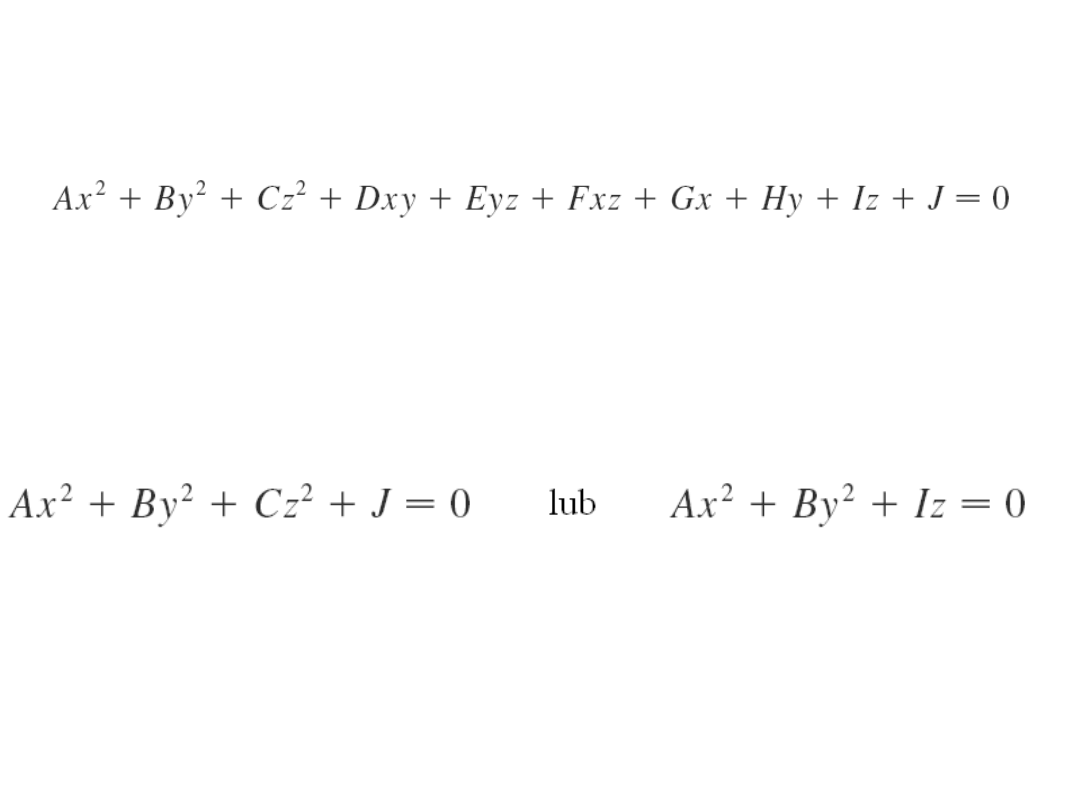
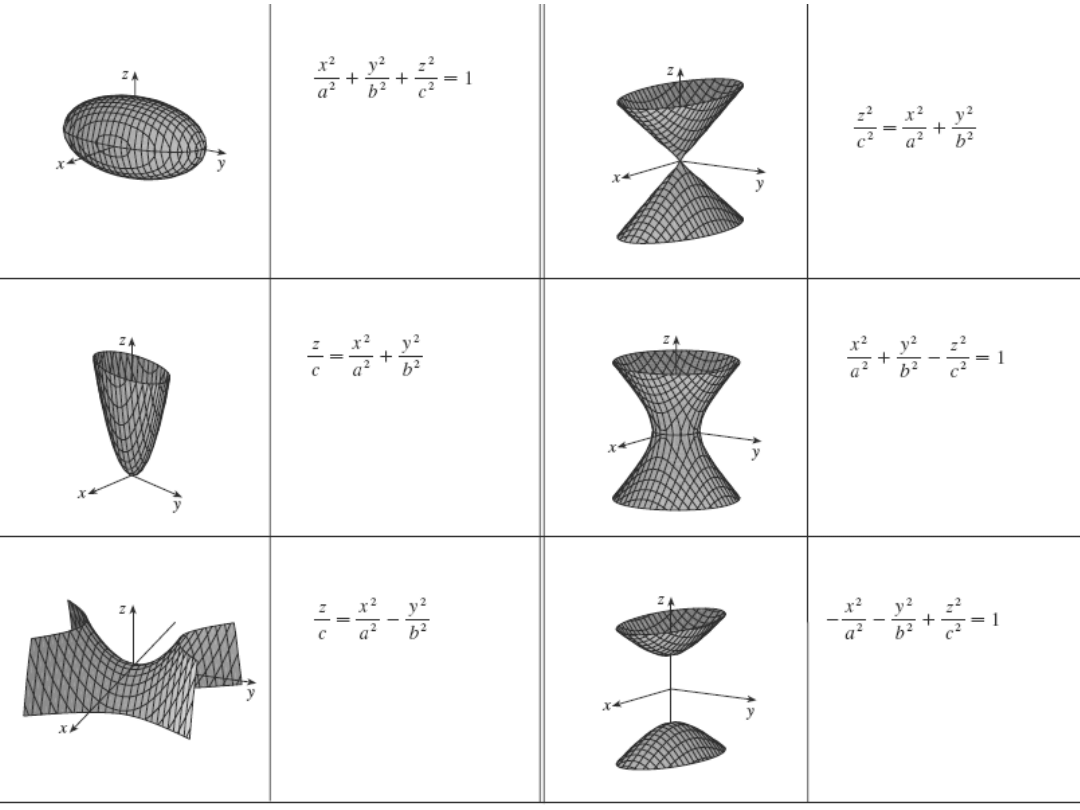
Powierzchnia drugiego stopnia
A,B,...J stałe. Poprzez operacje tranzlacji i obrotu
można otrzymać prostszą postać:
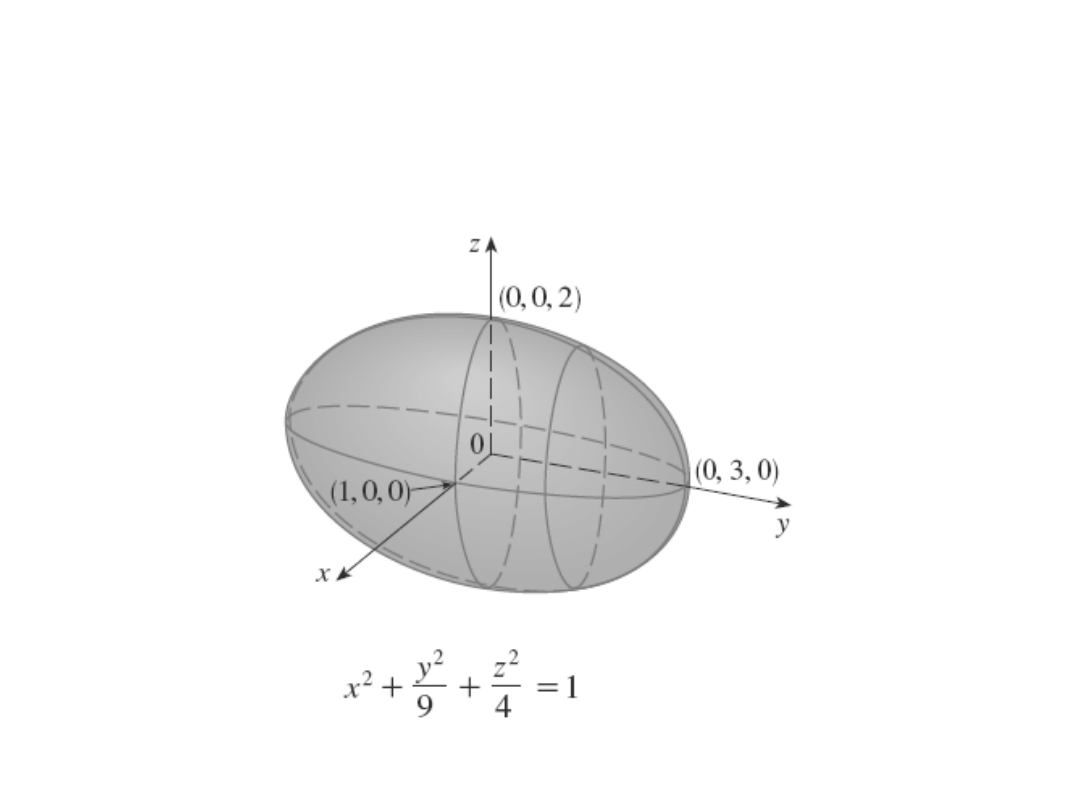
Elipsoida
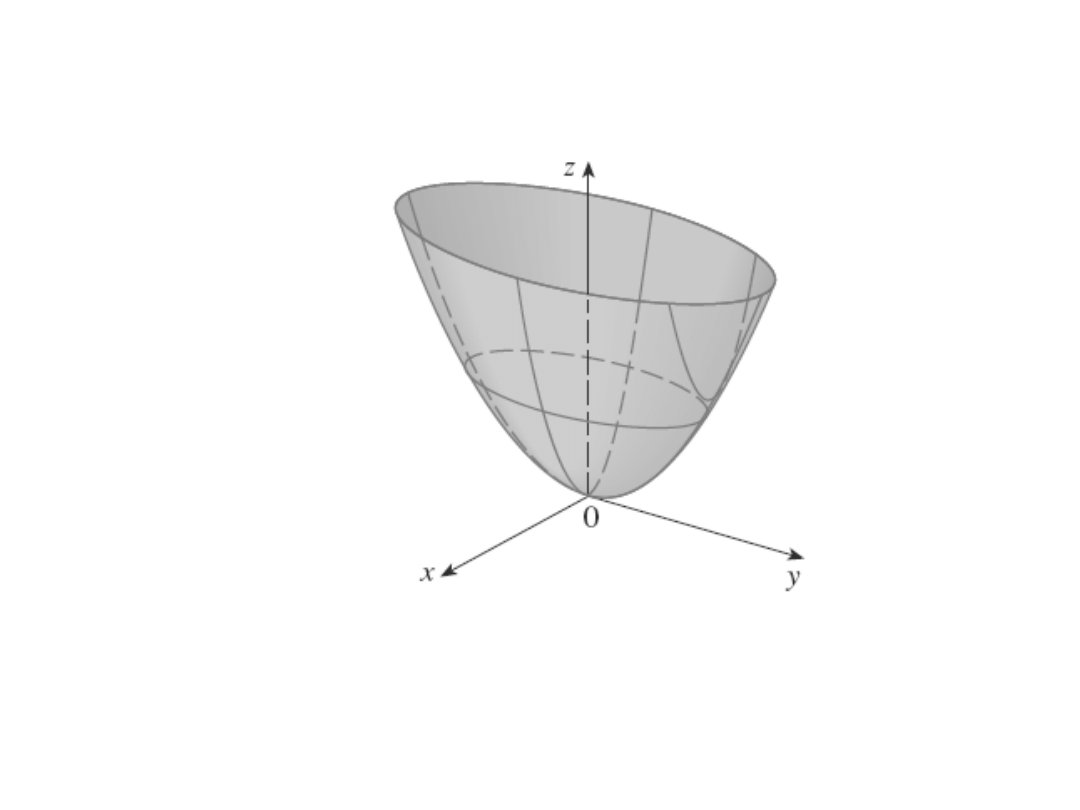
Paraboloida
2
2
4
y
x
z
Paraboloida eliptyczna
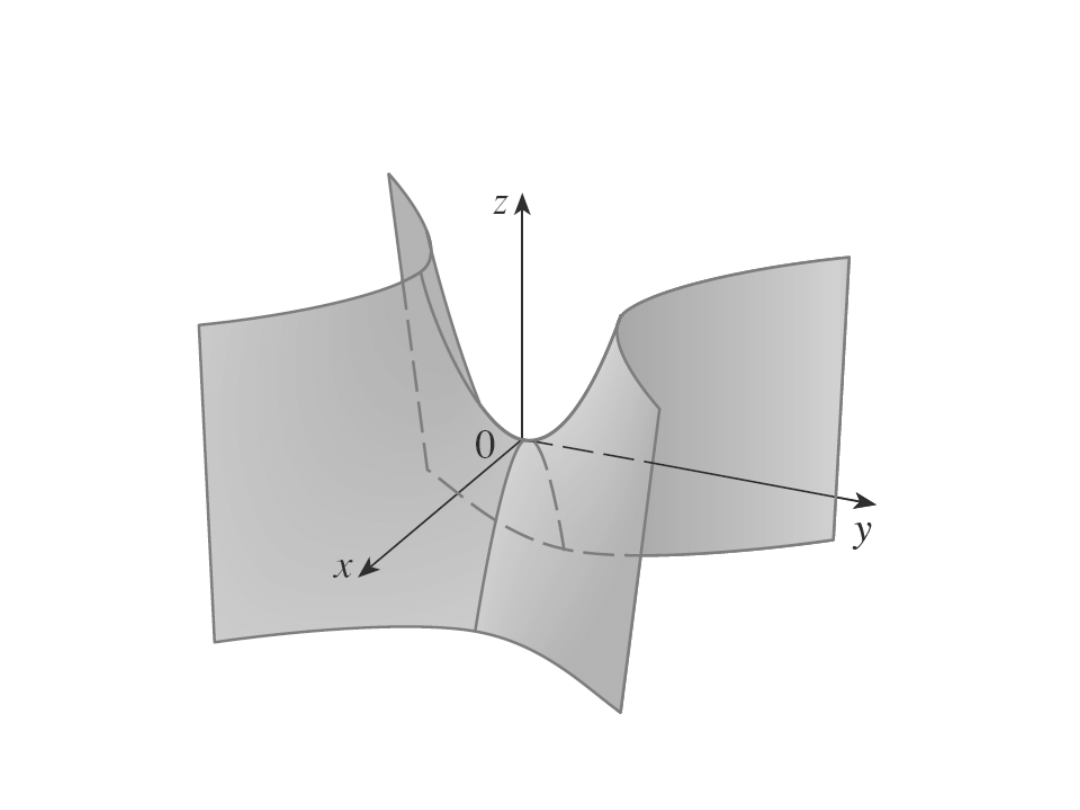
Paraboloida hiberboliczna
2
2
y
x
z
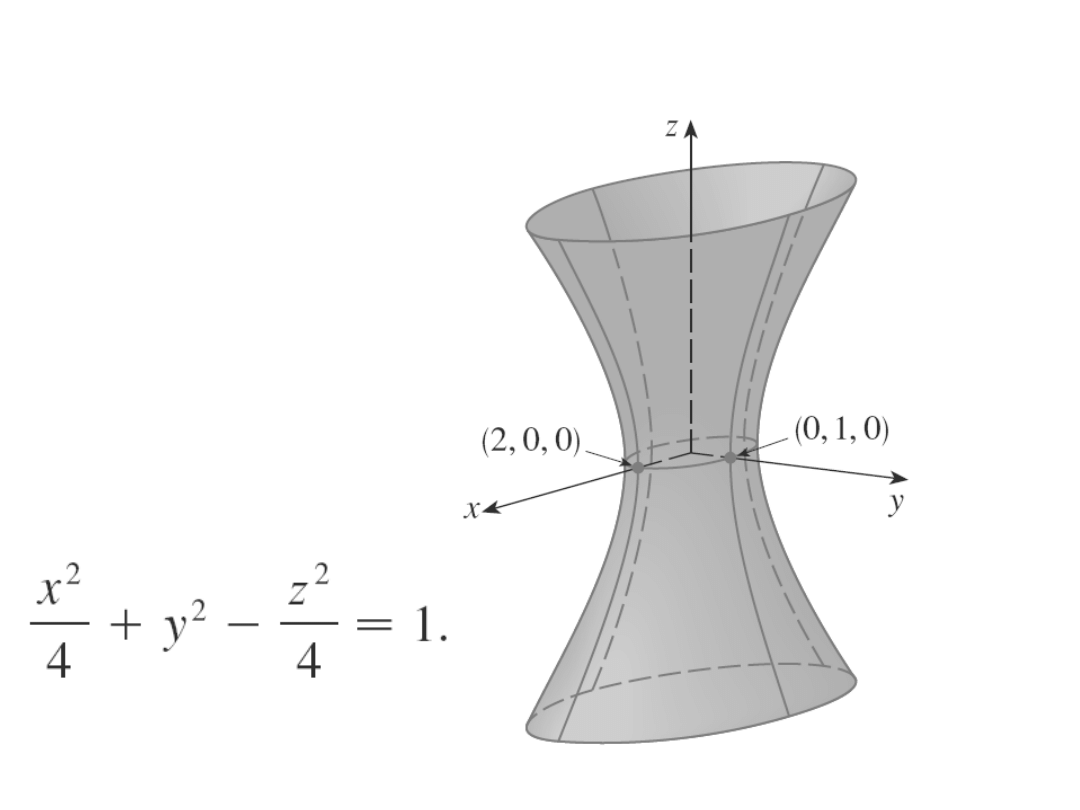
Hipeboloida jednopowłokowa
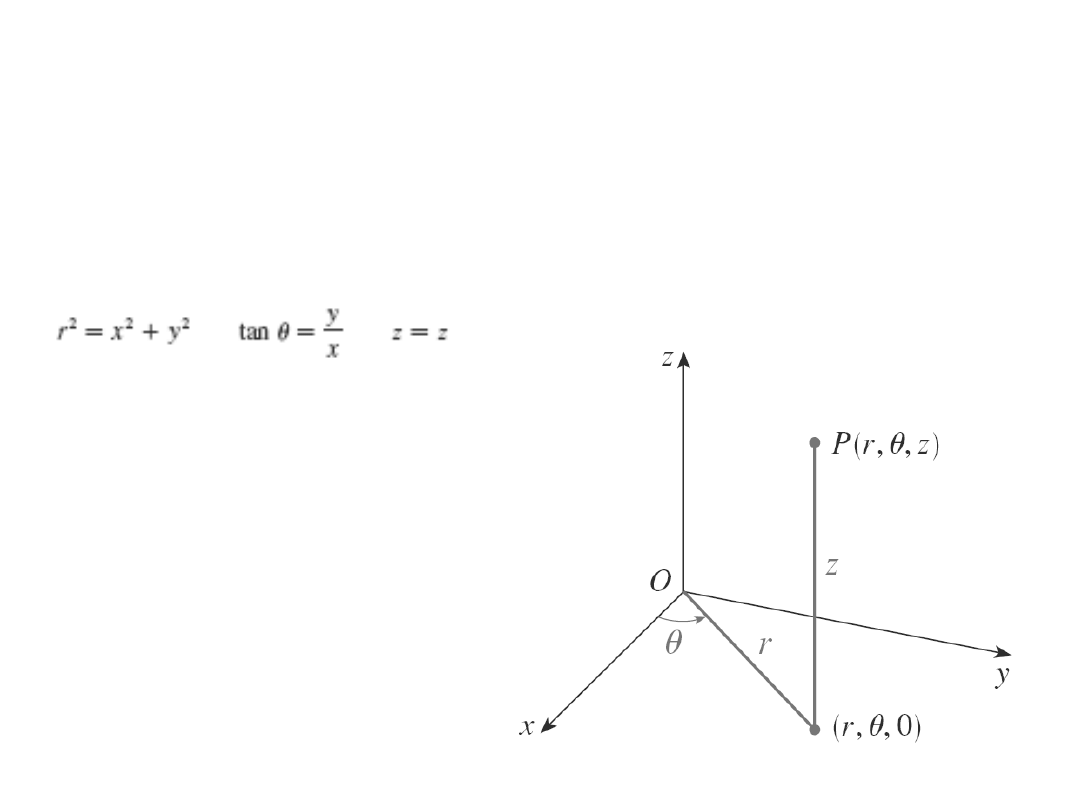
Współrzędne walcowe
z
z
r
y
r
x
,
sin
,
cos
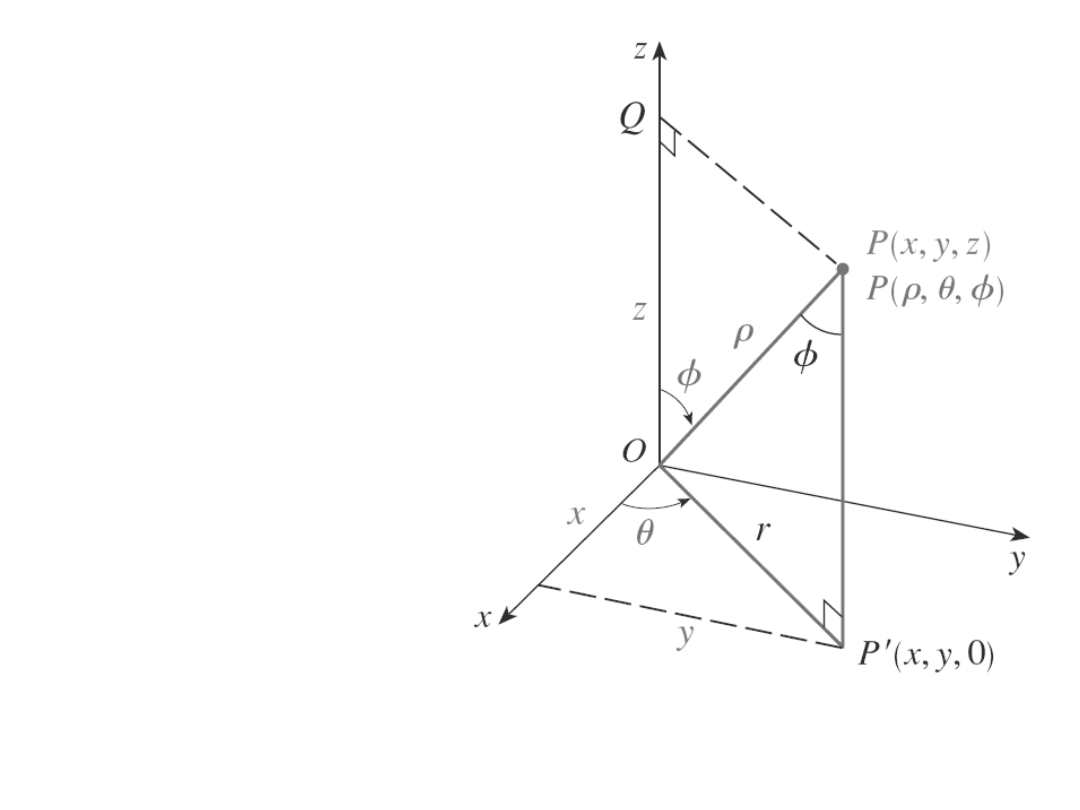
Współrzędne
sferyczne
cos
sin
sin
cos
sin
z
y
x
sin
cos
r
z
Funkcja o wartościach
wektorowych:
Grupą nazywamy taki niepusty zbiór G , w którym
określone jest działanie:
,
:
G
G
G
m
ab
b
a
m
b
a
)
,
(
)
,
(
zwane działaniem grupowym ( albo mnożeniem w G ),
spełniające warunki
a) zawsze zachodzi
( działanie jest łączne)
c
ab
bc
a
)
(
)
(
istnieje element zwany elementem
neutralnym taki, że
dla każdego
G
e
a
ae
ea
G
a
c) dla każdego elementu istnieje taki
element taki, że
G
a
G
a
'
e
aa
a
a
'
'
Jeżeli ponadto jest spełniony warunek
dla dowolnych grupę nazywamy przemienną
albo Abelową
ba
ba
G
b
a
,
Definicja grupy
Zbiór , zawierający co najmniej dwa elementy
nazywamy ciałem , jeżeli określone są dwa działania:
zwane odpowiednio dodawaniem i mnożeniem
spełniające następujące warunki:
ab
b
a
b
a
b
a
K
K
K
)
,
(
,
)
,
(
:
K
(a) jest grupą Abelową z działaniem
dodawaniem;
(b) gdzie oznacza element
neutralny dodawania, jest grupą z działaniem
mnożenia;
( c) mnożenie jest rozdzielne względem dodawania,
tzn.
}
0
{
\
*
K
K
K
}
0
{
ac
ab
c
b
a
)
(
K
c
b
a
,
,
dla
każdego
Definicja ciała
Przestrzeń wektorowa
Niech V będzie dowolnym niepustym zbiorem, a
ustalonym ciałem. Elementy zbioru V będziemy
nazywać wektorami, a ciała – skalarami.
Mówimy, że jest przestrzenią wektorową nad
ciałem (rozpiętą nad ciałem) lub przestrzenią
liniową , jeśli określone są funkcje
zwane odpowiednio dodawaniem wektorów i
mnożeniem wektora przez skalar, takie, że spełnione
są następujące warunki:
•1. V jest grupą Abelową względem
dodawania;
K
K
K
v
u
v
u
V
V
V
)
,
(
:
u
u
V
V
K
)
,
(
:
2
.
3
.
4
.
5
.
v
u
v
u
)
(
u
u
u
)
)
(
u
u
)
(
)
(
u
u
1
Definicja
Niech V będzie przestrzenią wektorową nad ciałem
K .
Niech . Mówimy, że
tworzą układ liniowo niezależny,
jeżeli dla dowolnego ciągu skalarów
z równości :
V
e
e
e
n
,...,
,
2
1
n
e
e
e
,...,
,
2
1
K
n
,...,
,
2
1
0
...
2
2
1
1
n
n
e
e
e
wynika, że
0
...
2
1
n
Definicja
Układ wektorów przestrzeni liniowej nazywamy bazą tej
przestrzeni, jeśli jest on maksymalnym układem wektorów liniowo
niezależnych w tej przestrzeni, tzn. nie można do niego dołączyć
żadnego wektora przestrzeni w taki sposób, aby otrzymany układ
był liniowo niezależny.
Wyrażenie nazywamy
kombinacją liniową
wektorów
n
n
e
e
e
...
2
2
1
1
V
e
e
e
n
,...,
,
2
1
Baza przestrzeni liniowej
Definicja.
Układ wektorów przestrzeni liniowej V nazywamy bazą tej
przestrzeni, jeżeli jest on maksymalnym układem wektorów
liniowo niezależnych w tej przestrzeni, tzn. jeśli nie można do
niego dołączyć żadnego wektora przestrzeni V w taki sposób,
aby otrzymany układ był liniowo niezależny.
n
i
i
i
i
i
n
n
e
e
e
e
e
x
1
2
2
1
1
...
Definicja. Liczbę elementów skończonej bazy przestrzeni
liniowej V nazywamy wymiarem przestrzeni i
oznaczamy ją symbolem .
Jeśli dana przestrzeń nie ma skończonej bazy to mówimy,
że jest nieskończona i piszemy .
V
dim
V
dim
Przekształcenia liniowe
Definicja Niech będą przestrzeniami liniowymi nad
ciałem K .
Odwzorowanie ( funkcja ) : nazywa się
przekształceniem liniowym ( odwzorowaniem liniowym) ,
jeśli ma ono następujące własności:
(addytywność)
(jednorodność)
W
V
i
W
V
:
T
)
(
)
(
)
(
v
T
u
T
v
u
T
V
,
,v
u
)
(
)
(
u
T
u
T
K
V
,
u
inaczej zapiszemy:
)
(
)
(
)
(
v
T
u
T
v
u
T
K
V
,
,
,v
u
Niech wektory i odpowiednio stanowią bazy
w przestrzeniach liniowych .
n
e
e
e
,...,
,
2
1
m
f
f
f
,...,
,
2
1
W
V
i
Przekształcenie liniowe T jest wyznaczone jednoznacznie poprzez
wartości jakie przyjmuje na wektorach bazy przestrzeni :
V
)
(
),...,
(
),
(
n
e
T
e
T
e
T
2
1
Jeśli
bowiem :
to
n
n
e
e
e
x
x
...
2
2
1
1
V
)
(
...
)
(
)
(
)
(
n
n
e
T
e
T
e
T
x
T
2
2
1
1
m
k
k
k
i
k
k
i
m
m
i
i
i
i
f
f
f
f
f
e
T
1
2
2
1
1
...
)
(
Wypisując kolejno współczynniki w poziomym
rzędzie , a następnie pod spodem, w drugim rzędzie
(wierszu) współczynniki
otrzymamy prostokątną tablicę
współczynników z ciała mającą m wierszy
i n kolumn.
1
i
2
i
Macierz przekształcenia T względem baz
m
n
f
f
f
i
e
e
e
,...,
,
,...,
,
2
1
2
1
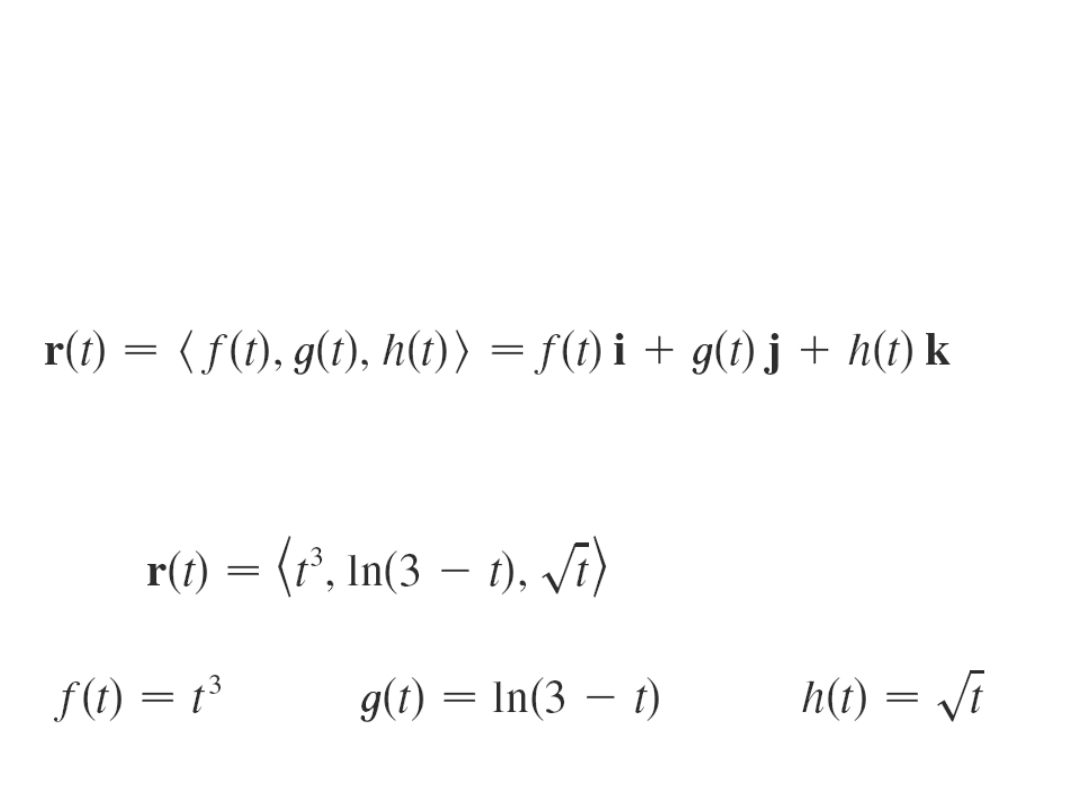
Definicja
a)
ń wektorow
(przestrze
:
V
r
R
Przykład
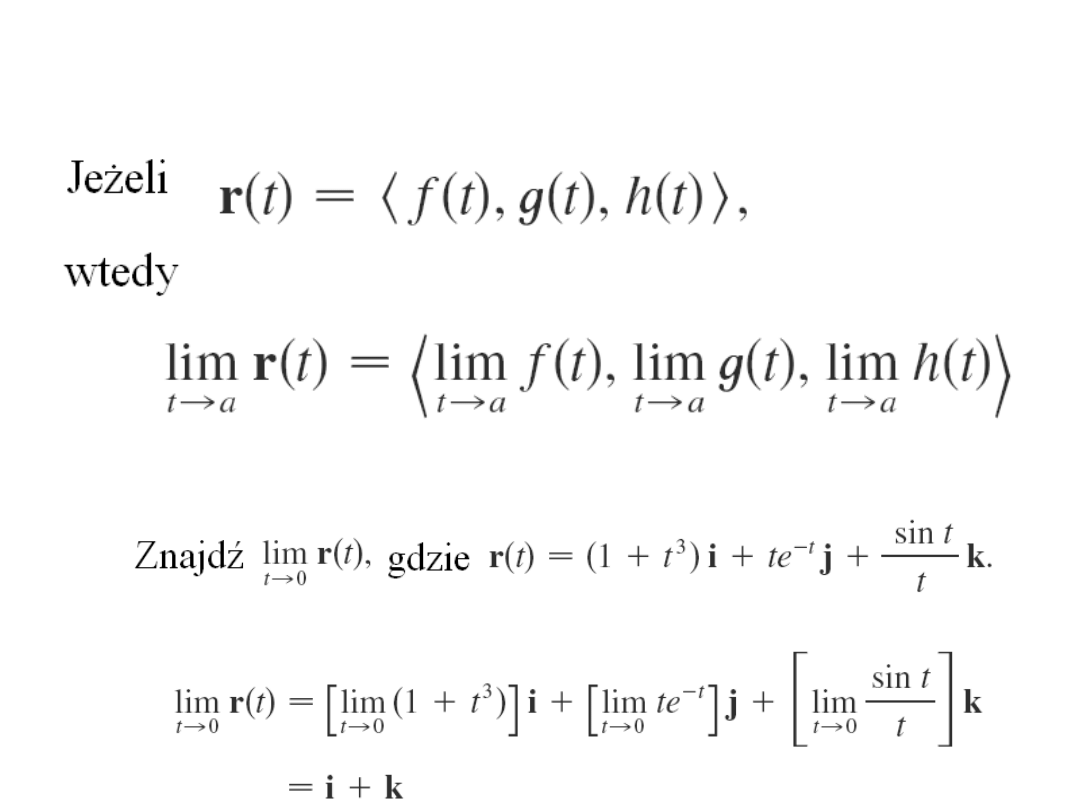
Granica funkcji wektorowej
Przykład
Ciągłość
Funkcja r jest ciągła wtedy i tylko wtedy, gdy
ciągłe są funkcje składowe f, g, h .
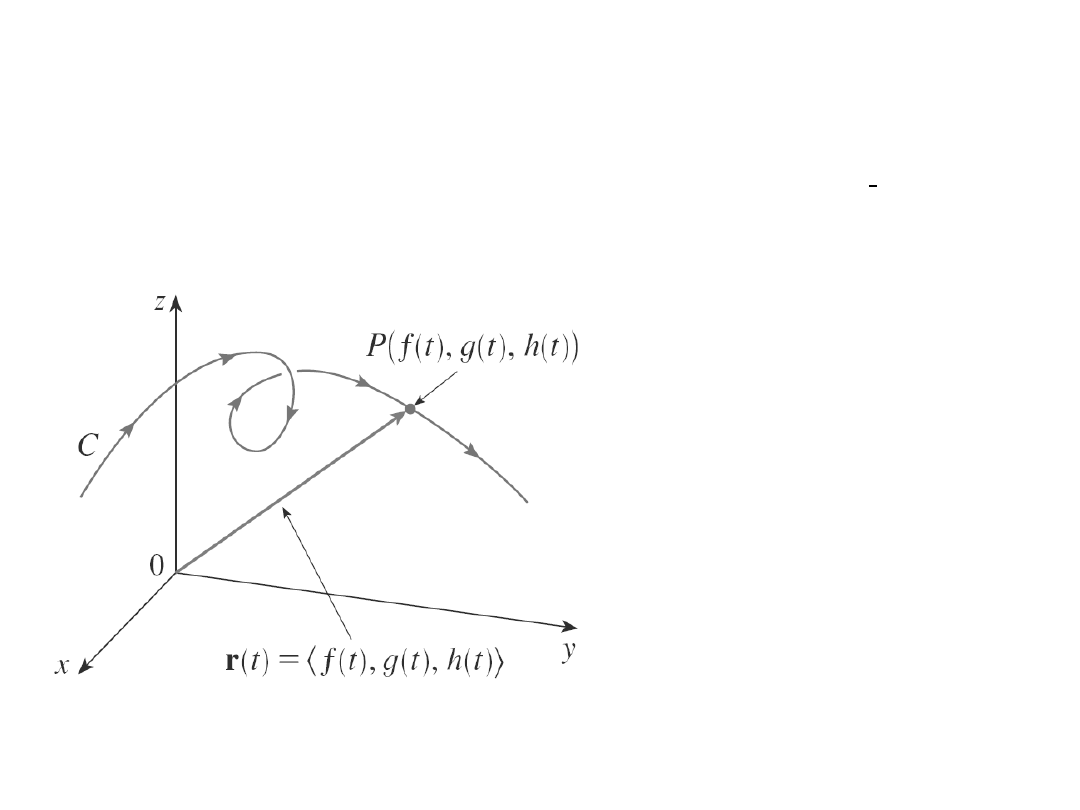
Istnieje związek pomiędzy
ciągła funkcją wektorową i
krzywą przestrzenną.
Załóżmy, że f,g,h są
funkcjami ciągłymi dla t z
przedziału I. Zbiór C
wszystkich punktów (x,y,z)
przestrzeni gdy:
(*) x = f(t), y = g(t) ,
z = h(t)
gdzie t przebiega przedział I
nazywa się krzywą
przestrzenną . Równania (*)
nazywa się
parametrycznymi
równaniami krzywej t -
parametrem. Możemy
pomyśleć o C jak o śladzie
poruszającej się cząsteczki,
której pozycją w chwili t jest
(f(t), g(t), h(t)). Jeżeli
rozpatrzymy wektor r(t)=
(f(t),g(t),h(t)) to r(t) jest
wektorem wodzącym
punktu P.
Wektor wodzący
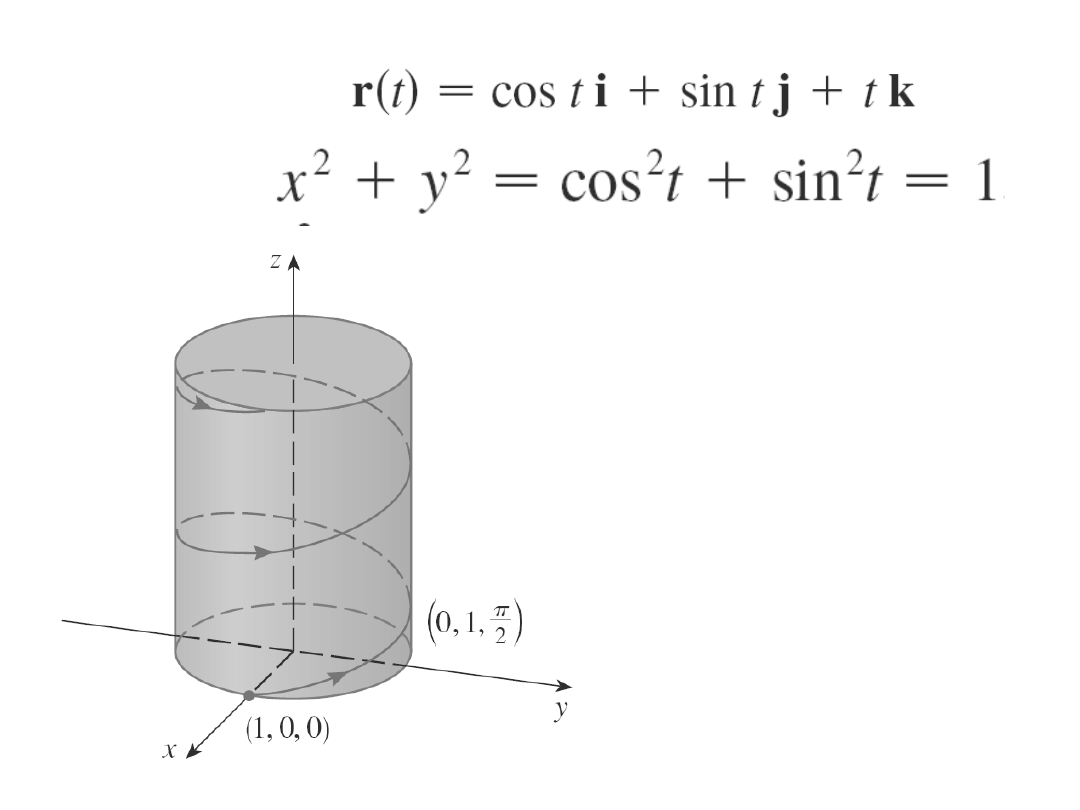
Przykład
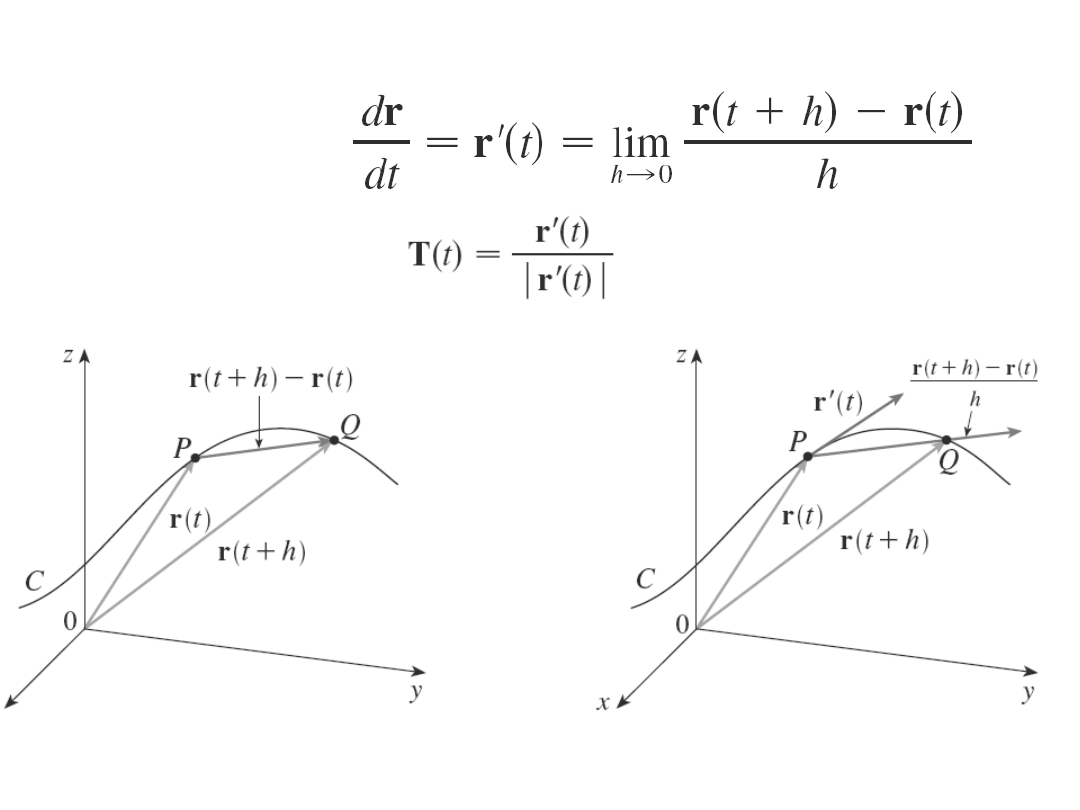
Pochodna
Jednostkowy wektor
styczny
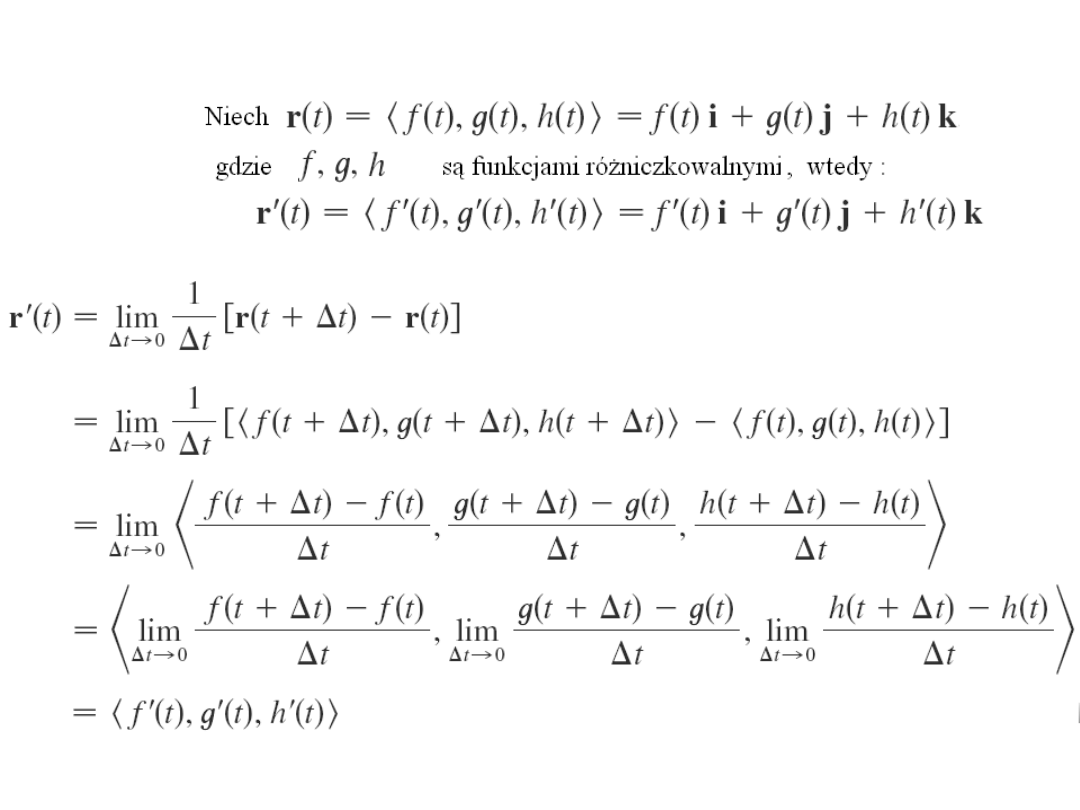
Twierdzenie
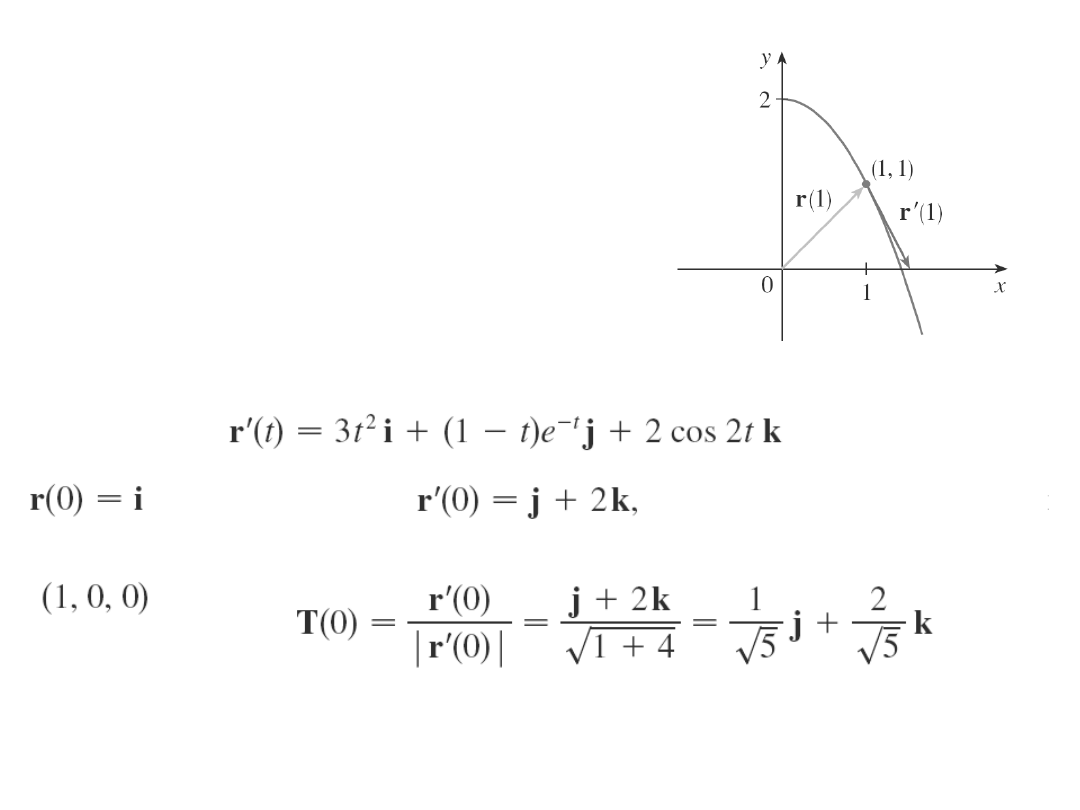
Przykład
a) Znajdź pochodną funkcji
wektorowej
r(t) = (1 + t
3
)i + te
-t
j +sin 2t k
b) Znajdź jednostkowy wektor
styczny
w punkcie dla t = 0 .
Twierdzenie 2
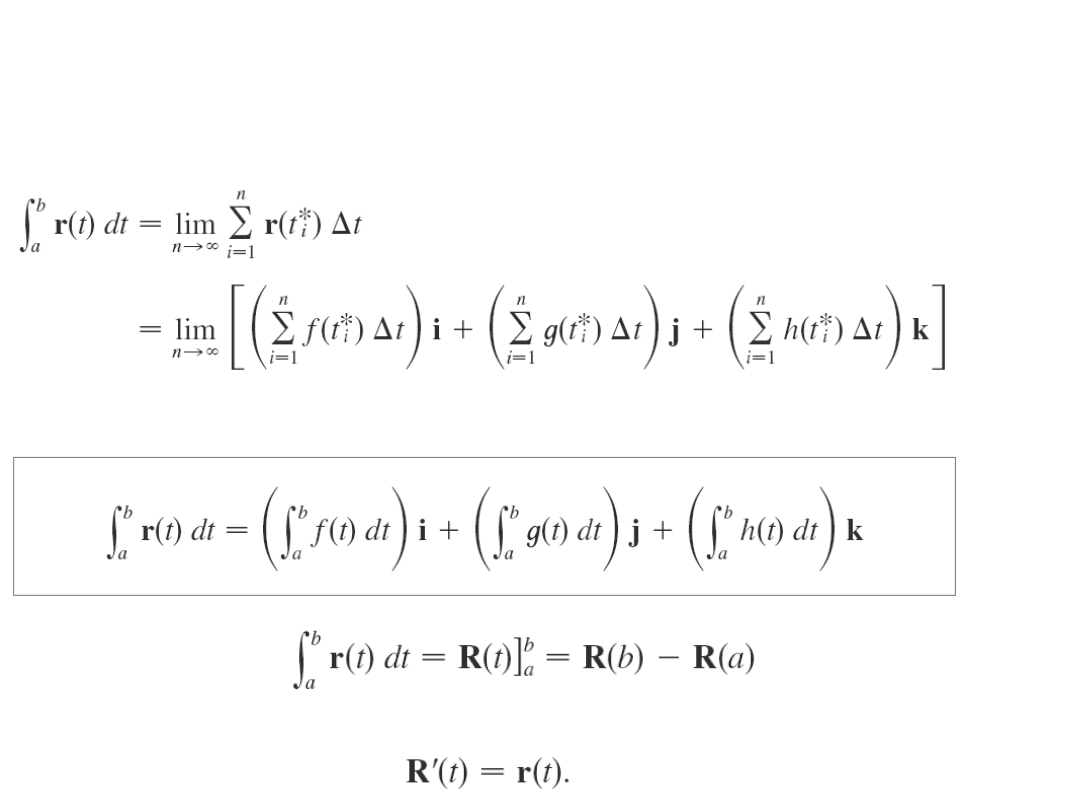
Całkowanie
Całka oznaczona funkcji
wektorowej ciągłej
Długość łuku