1

I

T
P

W

ZPT

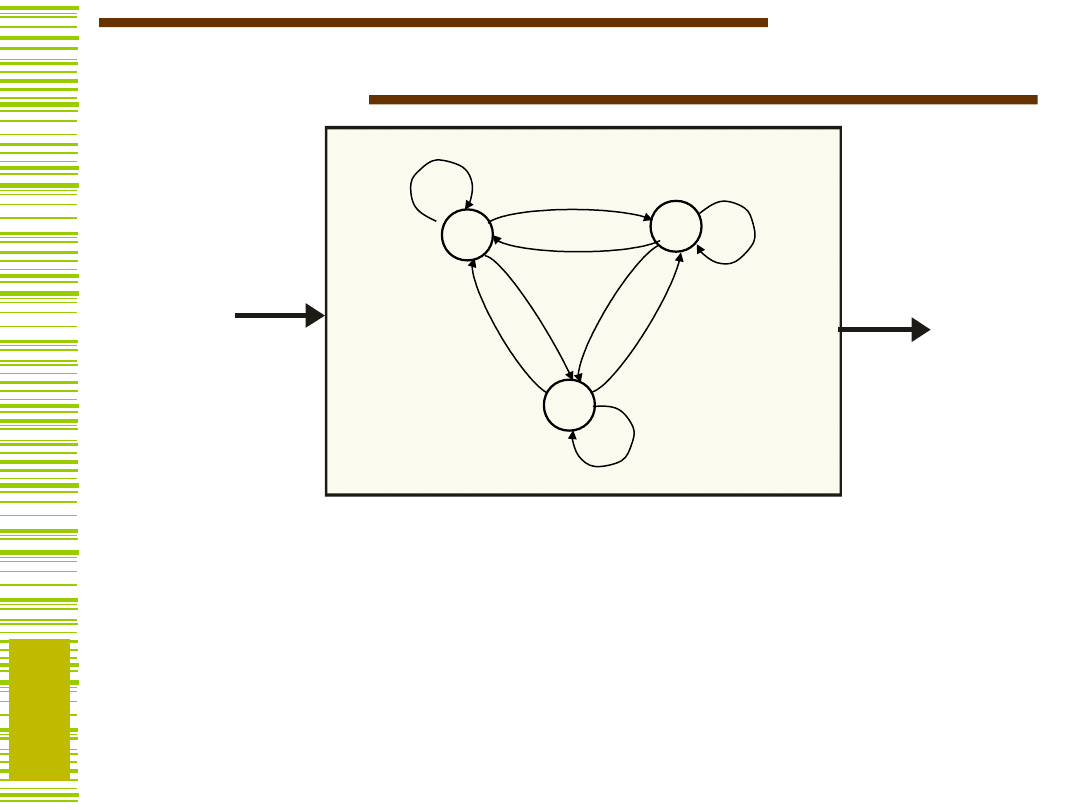
Układy sekwencyjne - pojęcie

automatu

 Automat

a) zbioru liter wejściowych V (X)

b) zbioru stanów wewnętrznych S,

c) funkcji przejść (ozn. ),

d) funkcji wyjść (ozn. ).

i wyjściowych Y,

v  V

y  Y

jest definiowany przez określenie: 

S

1

S

1

S

2

S

2

S

3

S

3

v

1

v

1

v

2

v

2

v

2

v

2

v

2

v

2

v

1

v

1

v

1

v

1

v

3

v

3

v

3

v

3

v

3

v

3

v

2

v

2

Y

2

Y

2

v

1

v

1

Y

1

Y

1

Y

3

Y

3

v

3

v

3

v

1

v

1

/Y

2

/Y

2

/

Y

1

/

Y

1

/Y

3

/Y

3

2

I

T
P

W

ZPT

Funkcja przejść i wyjść

Funkcja wyjść:

: S  Y (tzw. automat

Moore’a)

Funkcja przejść: : S  X  S

: S  X  Y (tzw. automat Mealy’ego)

Automat może być zupełny lub niezupełny

3

I

T
P

W

ZPT

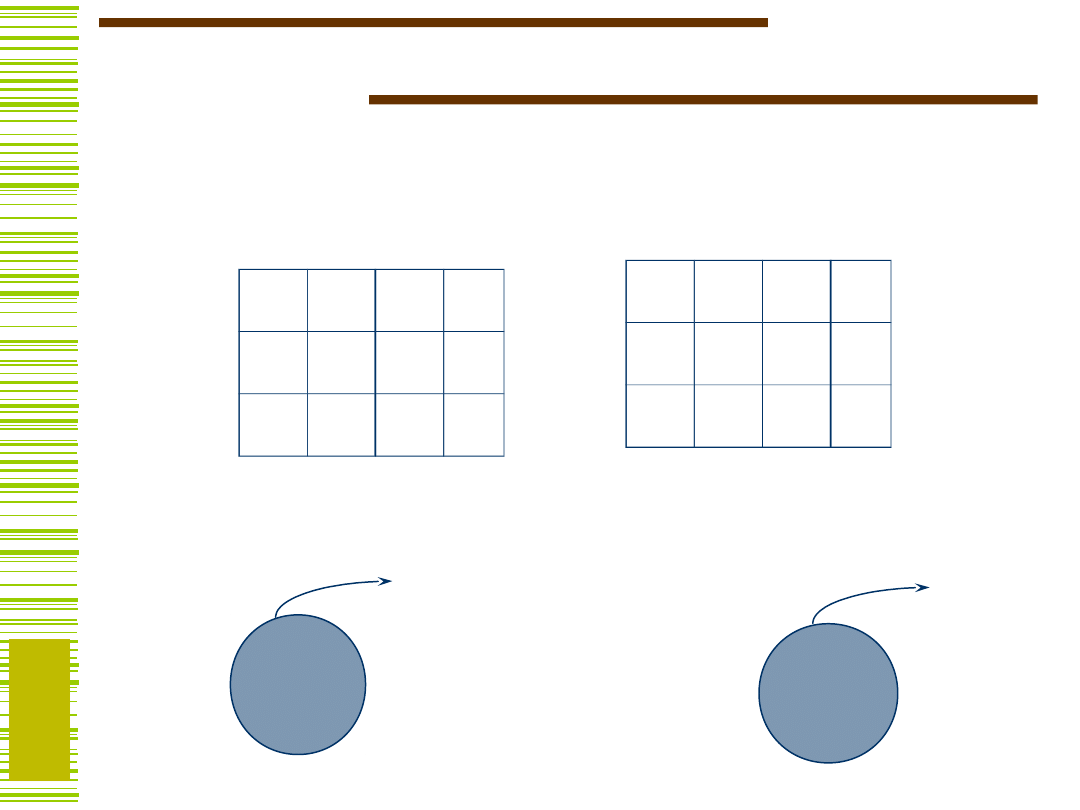
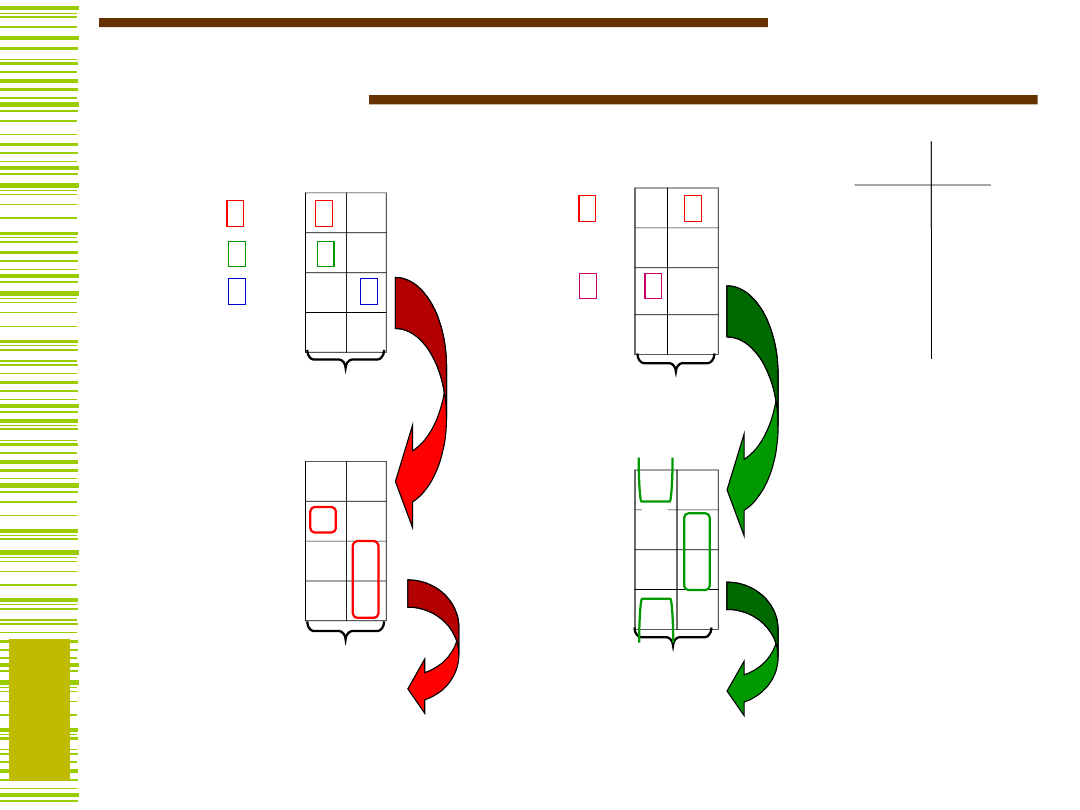
Specyfikacja automatu

Mealy’ego

Tablica przejść-wyjść automatu:

Moore’a

v

1

v

2

v

1

v

2

S

1

S

2

S

1

y

1

y

2

S

2

S

3

S

2

y

3

y

1

S

3

S

2

S

1

y

2

y

3

v

1

v

2

v

3

y

S

1

S

2

S

1

S

3

y

2

S

2

S

3

S

1

S

2

y

1

S

3

S

1

S

3

S

2

y

3

... i graf

Mealy’ego:

Moore’a:

stan/

wyjści

e

wejści
e

sta

n

wejście/wyjś
cie

4

I

T
P

W

ZPT

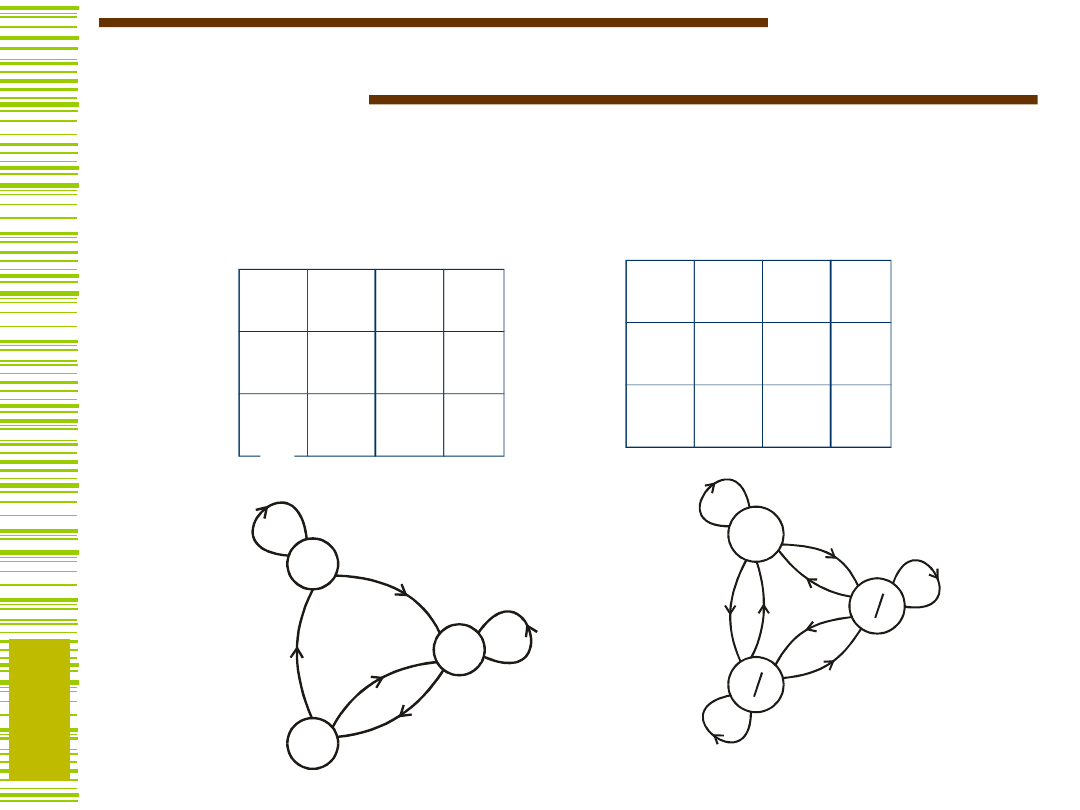
Specyfikacja automatu

Mealy’ego

Tablica przejść-wyjść automatu:

Moore’a

v

1

v

2

v

1

v

2

S

1

S

2

S

1

y

1

y

2

S

2

S

3

S

2

y

3

y

1

S

3

S

2

S

1

y

2

y

3

v

1

v

2

v

3

y

S

1

S

2

S

1

S

3

y

2

S

2

S

3

S

1

S

2

y

1

S

3

S

1

S

3

S

2

y

3

... i graf

Mealy’ego

Moore’a

v

v

v

v

v

v

v

v

v

1

1

1

2

2

3

3

2

3

y

y

1

3

2

S

S

S

3

1

/y

2

v / y

v / y

v / y

v / y

v / y

v / y

1

1

1

1

2

2

2

1

2

3

3

2

1

S

3

S

2

S

5

I

T
P

W

ZPT

x

1

x

n

y

1

y

m

Q

1

Q

k

q

1

q

k

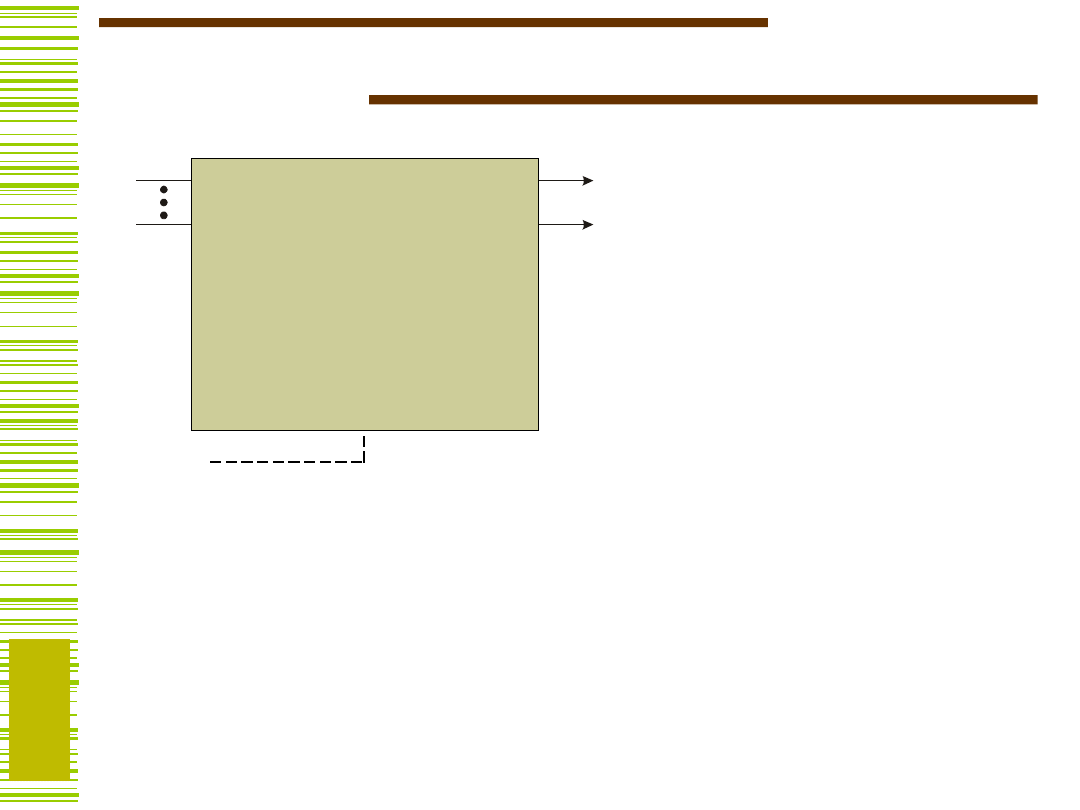
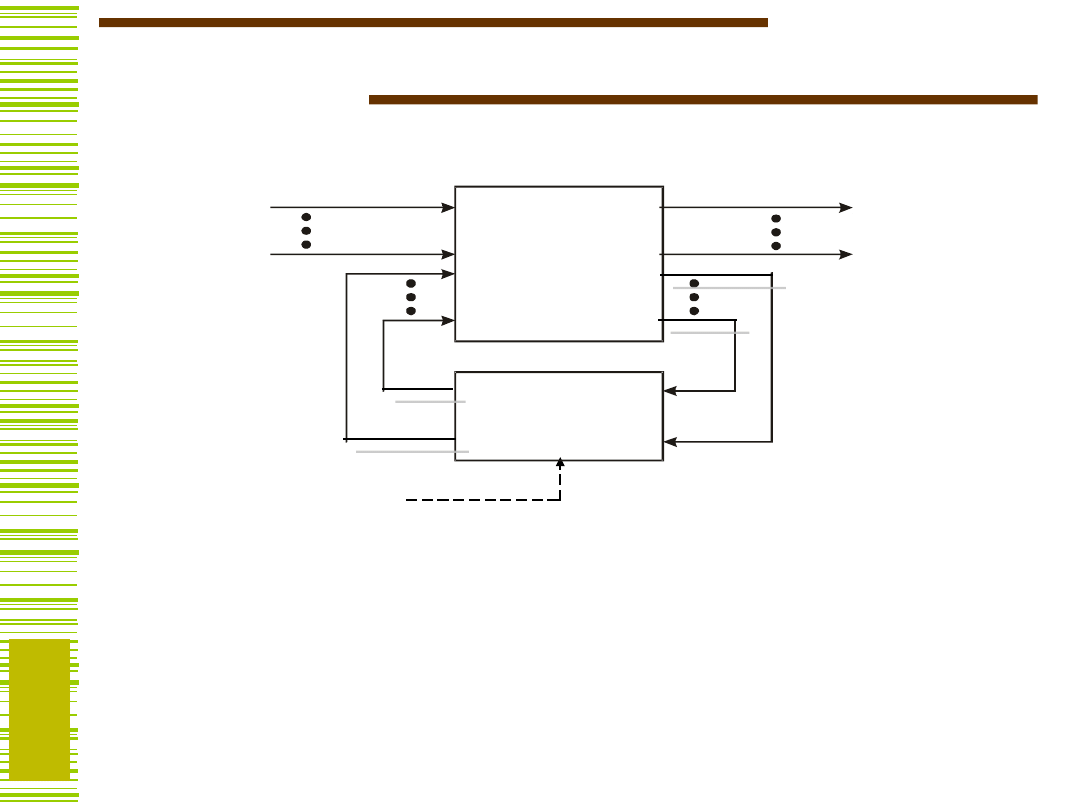
Układ sekwencyjny

układ kombinacyjny

Układy sekwencyjne:

Synchroniczne

(BP zbudowany z przerzutników

synchronicznych)

wejście synchronizujące

Asynchroniczne

(BP realizują opóźnienia lub

przerzutniki asynchroniczne)

blok pamięci

UK

BP

CLK

US

Zakodowane litery wejściowe

Zakodowane litery wyjściowe

Zakodowane stany automatu

6

I

T
P

W

ZPT

x

1

x

n

y

1

y

m

Q

1

Q

k

q

1

q

k

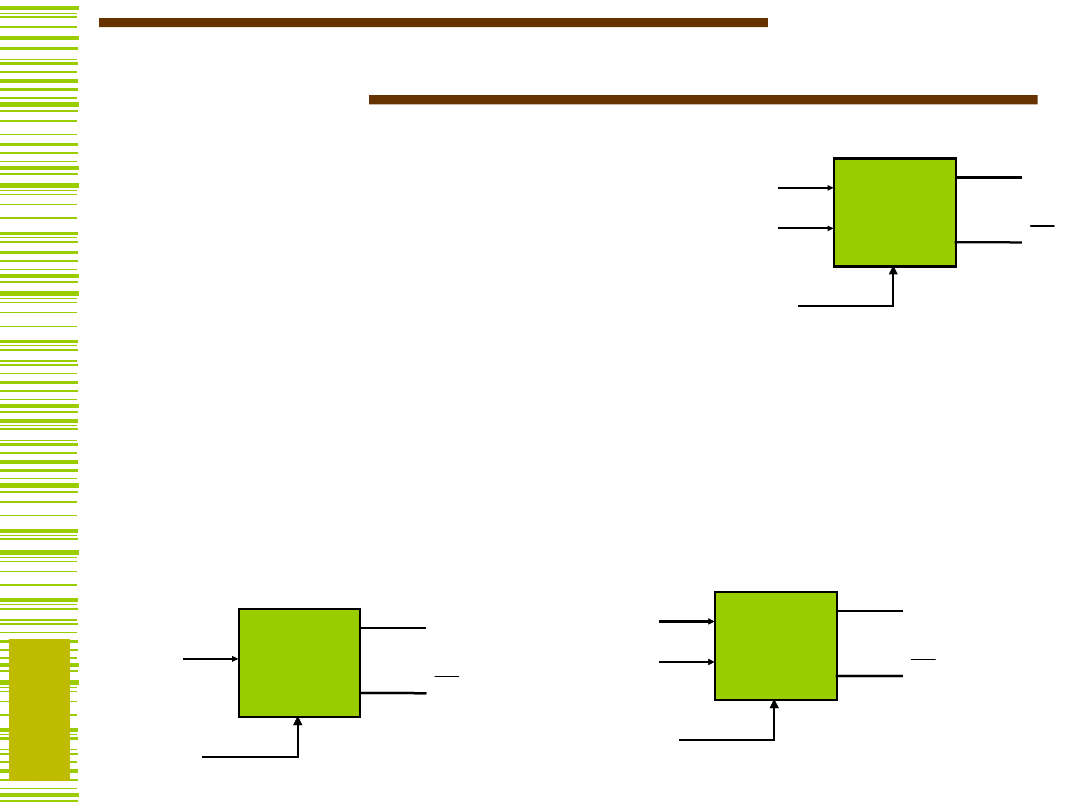
Synchroniczne układy

sekwencyjne

UK

Przerzutniki

CLK

BP

7

I

T
P

W

ZPT

Przerzutniki

Przerzutnik

– to automat typu Moore’a
o dwóch stanach wewnętrznych,
jednym lub dwóch wejściach informacyjnych,
dwóch wyjściach (prostym i zanegowanym)
oraz wejściu synchronizującym (zegarowym).

W zależności od rodzaju wejść
informacyjnych wyróżniamy przerzutniki
typu: D, T, SR oraz JK.

FF

I

1

I

2

Q

Q

CLK

FF

D

Q

Q

CLK

FF

T

Q

Q

CLK

FF

S

R

Q

Q

CLK

FF

J

K

Q

Q

CLK

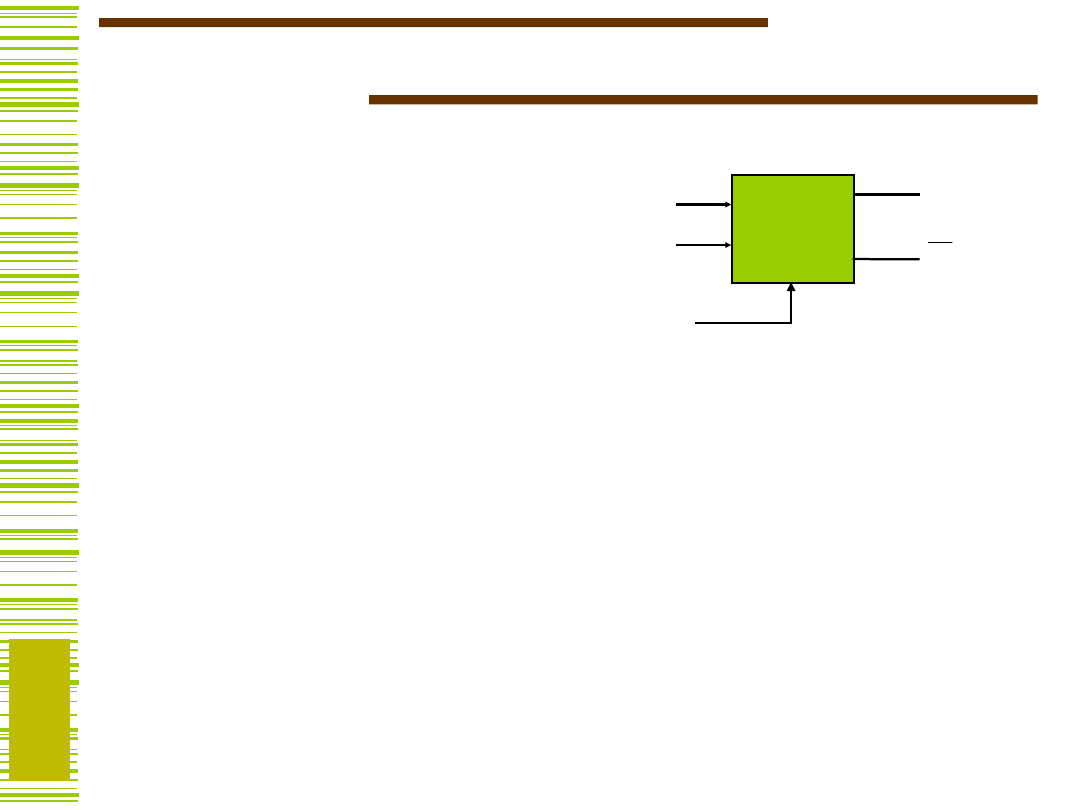
8

I

T
P

W

ZPT

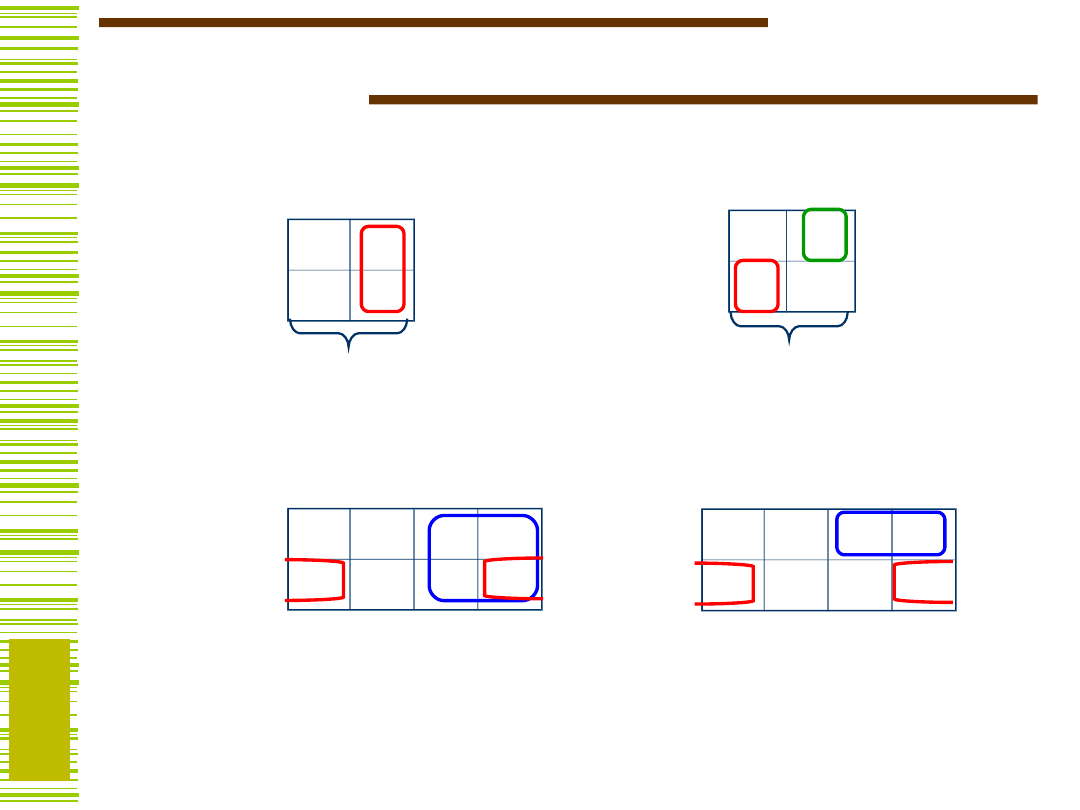
Przerzutniki

Przerzutnik jest określony:

 tablicą przejść,

 równaniem charakterystycznym,

 tablicą wzbudzeń.

FF

I

1

I

2

Q

Q

CLK

9

I

T
P

W

ZPT

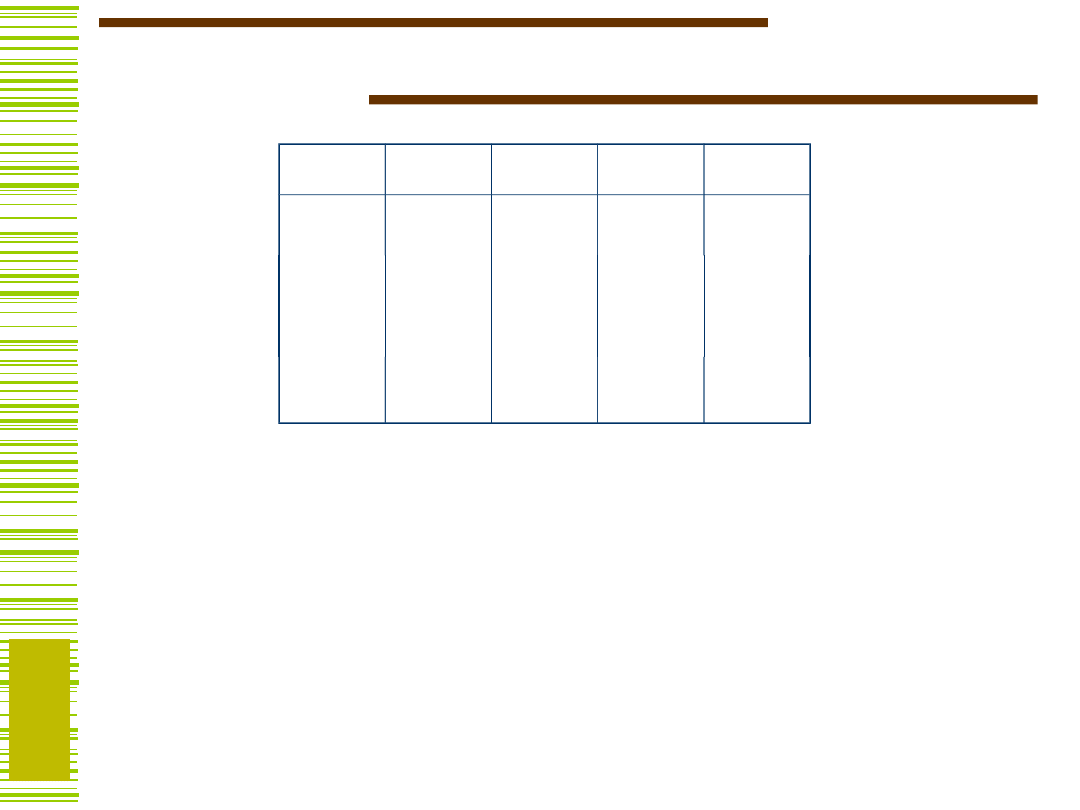
Przerzutniki – tablice przejść

D

Q

0

1

0

0

1

1

0

1

Q’ = D

T

Q

0

1

0

0

1

1

1

0

Q

T

Q

T

Q'





SR

Q

0

0 01 11 10

0

0

0

–

1

1

1

0

–

1

JK

Q

0
0

01 11 10

0

0

0

1

1

1

1

0

0

1

Równanie charakterystyczne: Q’ = f(I

1

,I

2

,Q)

10

I

T
P

W

ZPT

Przerzutniki – tablice wzbudzeń

Q Q’

D

T

S R

J K

00

0

0

0 –

0 –

01

1

1

1 0

1 –

10

0

1

0 1

– 1

11

1

0

– 0

– 0

D – delay T – trigger

S – Set (wejście włączające)

R – Reset (wejście

wyłączające)

J – wejście włączające

K – wejście wyłączające

11

I

T
P

W

ZPT

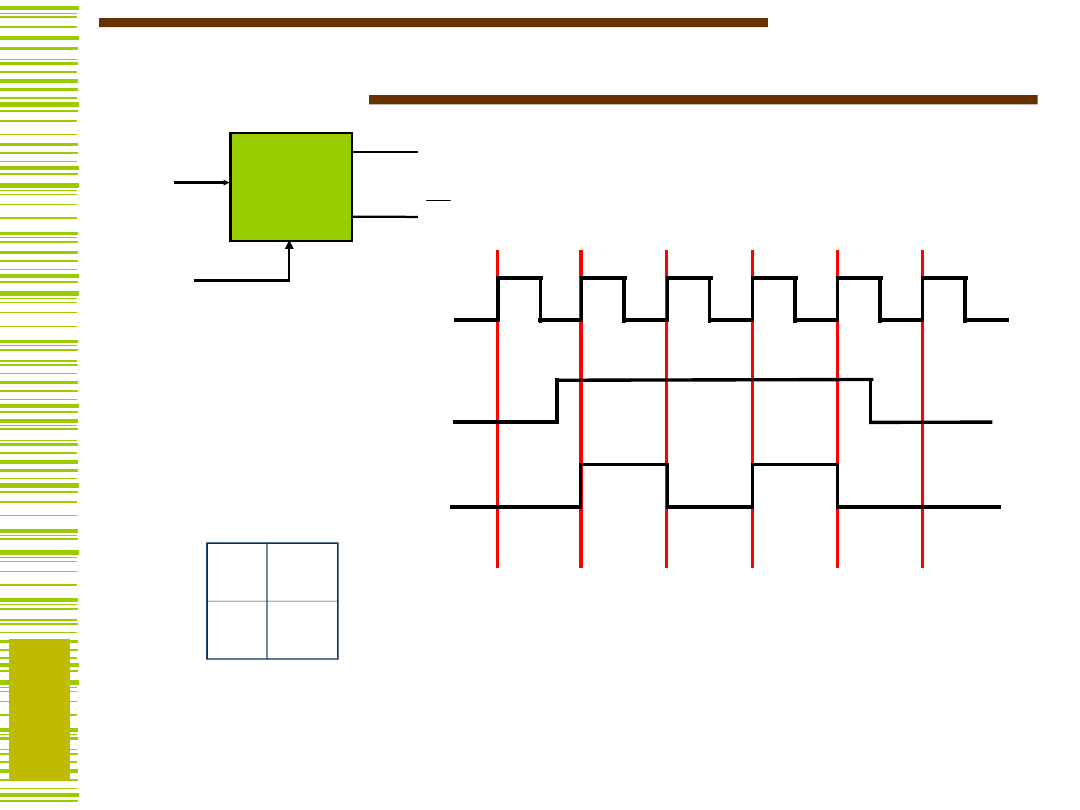
Przebiegi czasowe – przerzutnik

typu D

D

Q

CLK

FF

D

Q

Q

CLK

D

Q

0 1

0 0 1
1 0 1

12

I

T
P

W

ZPT

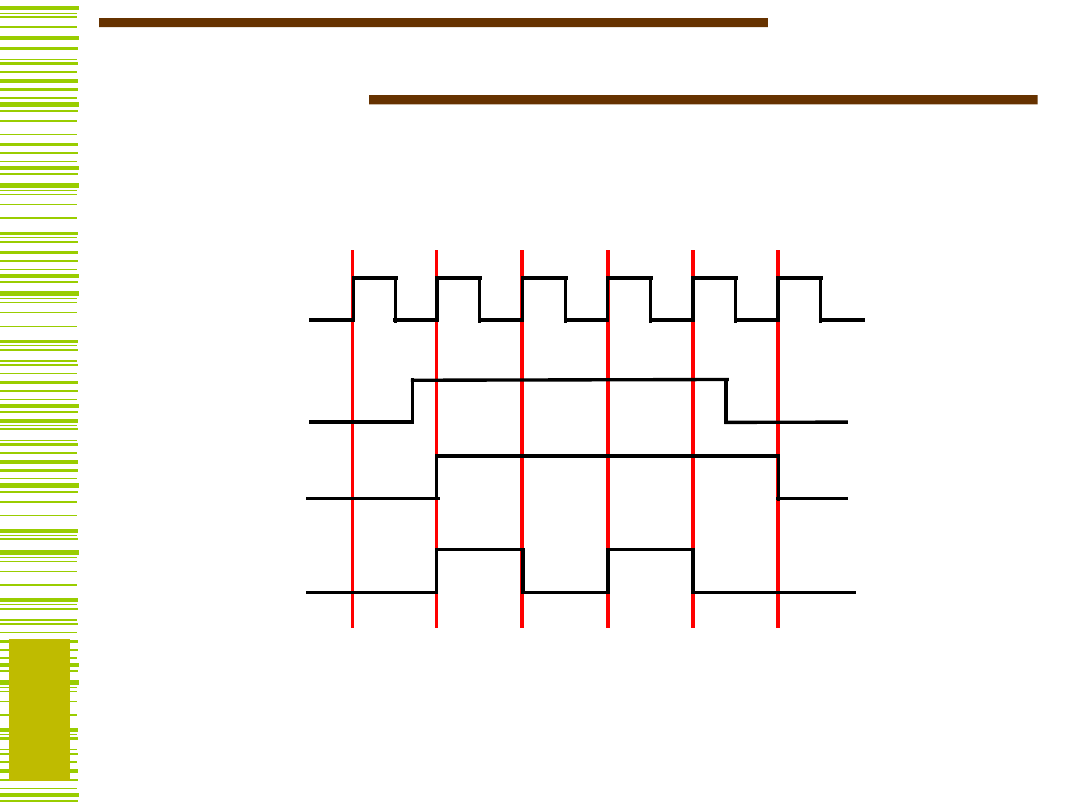
Przebiegi czasowe – przerzutnik

typu T

T

Q

CLK

FF

T

Q

Q

CLK

T

Q

0

1

0

0

1

1

1

0

13

I

T
P

W

ZPT

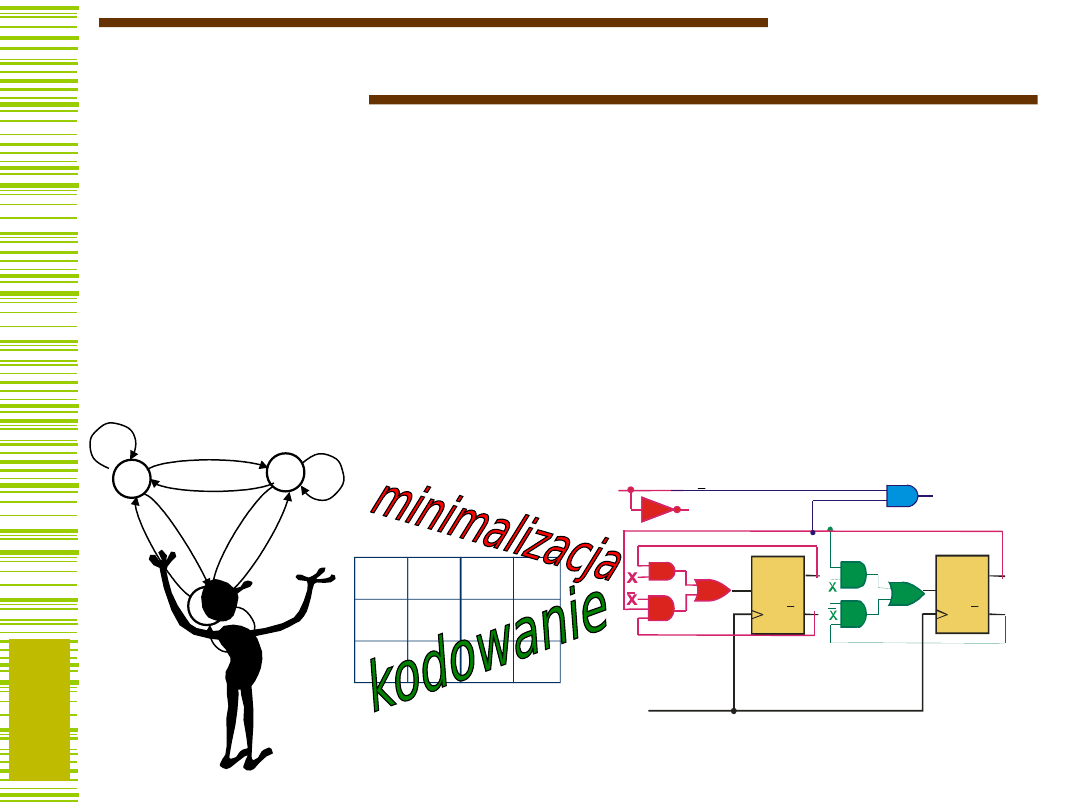
Przebiegi czasowe - porównanie

D (T)

Q (D)

Q (T)

CLK

14

I

T
P

W

ZPT

Synteza układów sekwencyjnych

Etapy syntezy:



synteza abstrakcyjna (utworzenie tablicy

przejść-wyjść)



redukcja (minimalizacja) liczby stanów



kodowanie stanów, liter wejściowych i

wyjściowych



synteza kombinacyjna (obliczanie funkcji

wzbudzeń
przerzutników i funkcji wyjściowych)

S

1

S

1

S

2

S

2

S

3

S

3

v

1

v

1

v

2

v

2

v

2

v

2

v

2

v

2

v

1

v

1

v

1

v

1

v

3

v

3

v

3

v

3

v

3

v

3

/Y

2

/Y

2

/

Y

1

/

Y

1

/Y

3

/Y

3

v

1

v

2

v

1

v

2

S

1

S

2

S

1

y

1

y

2

S

2

S

3

S

2

y

3

y

1

S

3

S

2

S

1

y

2

y

3

T1

Q1

Q1

Q1

Q1

T0

Q0

Q 0

CLK

x

x

Y

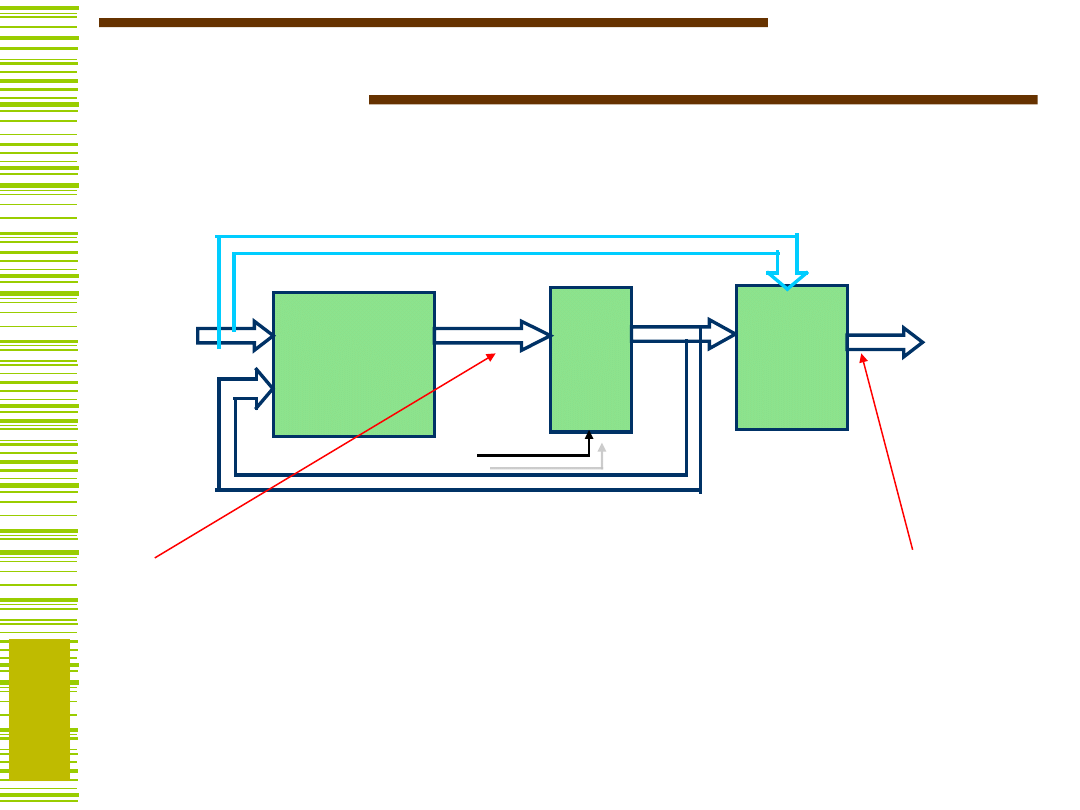
15

I

T
P

W

ZPT

Synteza kombinacyjna…

UK we

Prz

erz

u

tnik

i

UK wy

X

X

Y

Y

Obliczanie funkcji sterujących
wejściami przerzutników (funkcje
wzbudzeń)

Obliczanie funkcji wyjściowych

CLK

Q

Q

Q’

Q’

Q’ = f(X,Q)

Y = f(Q) (Moore)

Y = f(X,Q) (Mealy)

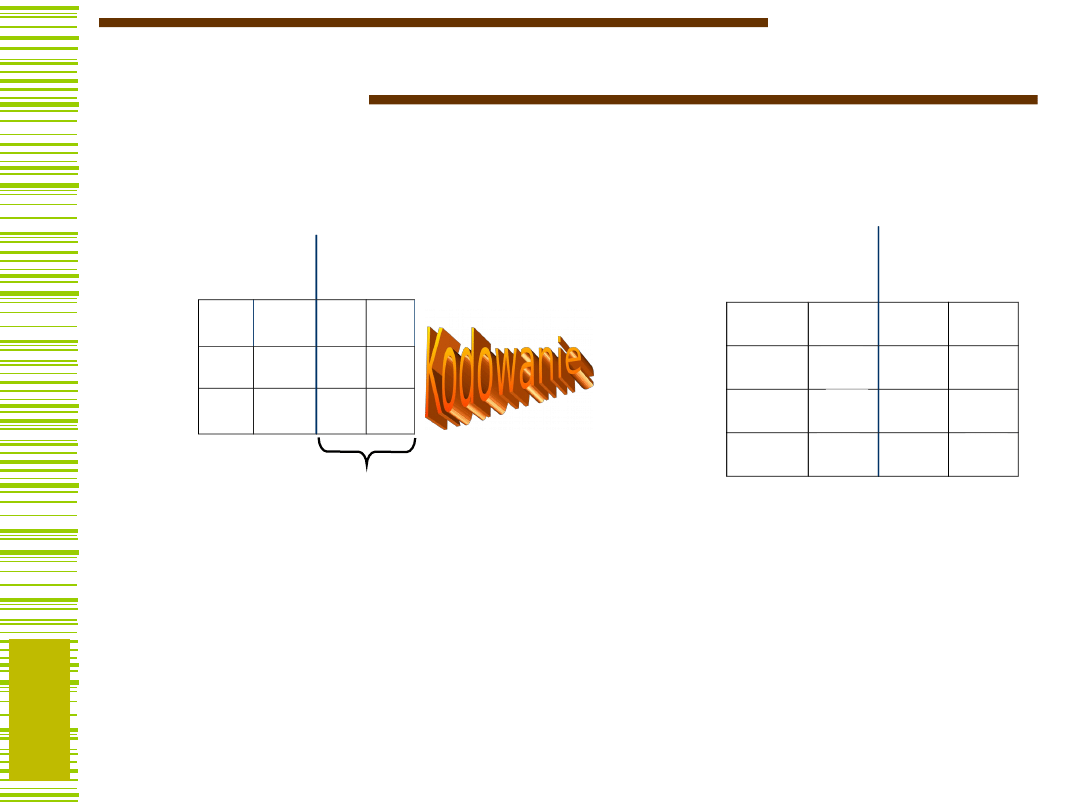
16

I

T
P

W

ZPT

Przykład syntezy (detektor

sekwencji)

X

S

0

1

0

1

A

B

A

0

0

B

C

A

0

0

C

C

A

0

1

X

S Q1Q0

0

1

0

1

A 00

01

00

0

0

B 01

11

00

0

0

C 11

11

00

0

1

(–) 10

– –

– –

–

–

Y

Wystarczą dwa

przerzutniki

Na razie staramy się spełnić wyłącznie

warunek jednoznaczności kodowania

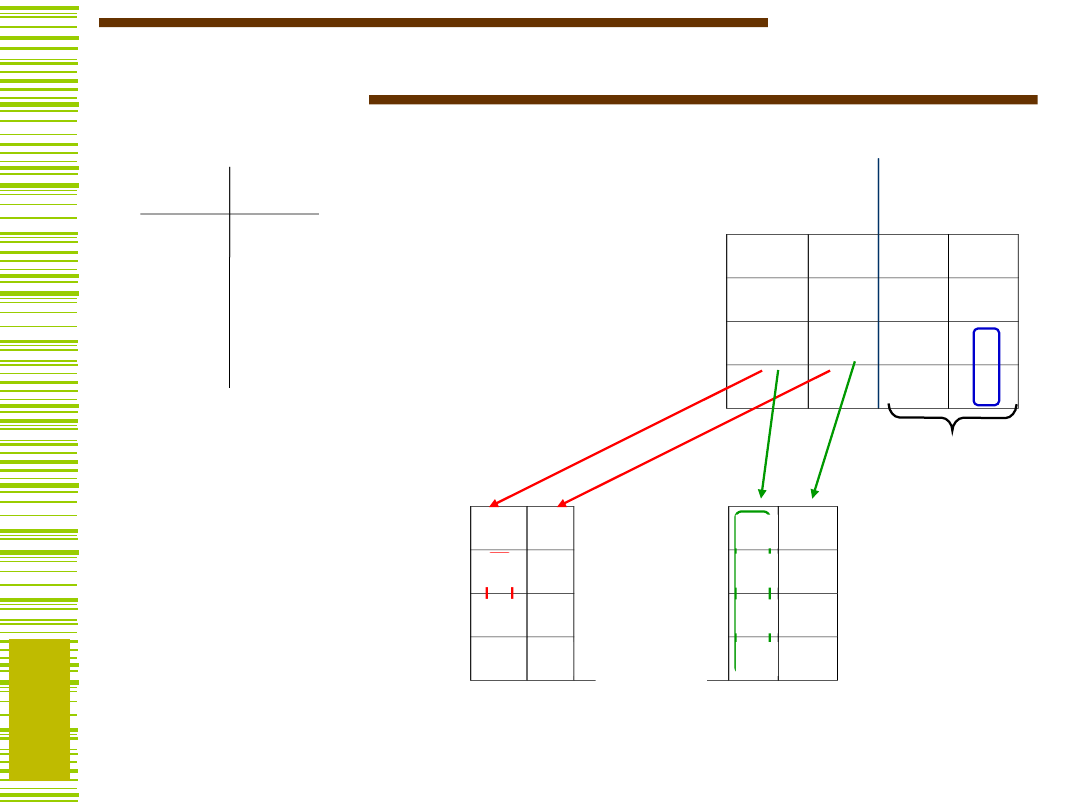
17

I

T
P

W

ZPT

Obliczanie funkcji wzbudzeń i

wyjściowych

X

S Q1Q0

0

1

0

1

A 00

01

00

0

0

B 01

11

00

0

0

C 11

11

00

0

1

(–) 10

– –

– –

–

–

X

Q1Q0

0

1

X

Q1Q0

0

1

00

0

0

00

1

0

01

1

0

01

1

0

11

1

0

11

1

0

10

–

–

10

–

–

D1=Q1

’

D0=Q0’

Y

xQ1

Y 

Q0

x

D1

Q1'





x

D0

Q0'





QQ’

D

00

0

01

1

10

0

11

1

18

I

T
P

W

ZPT

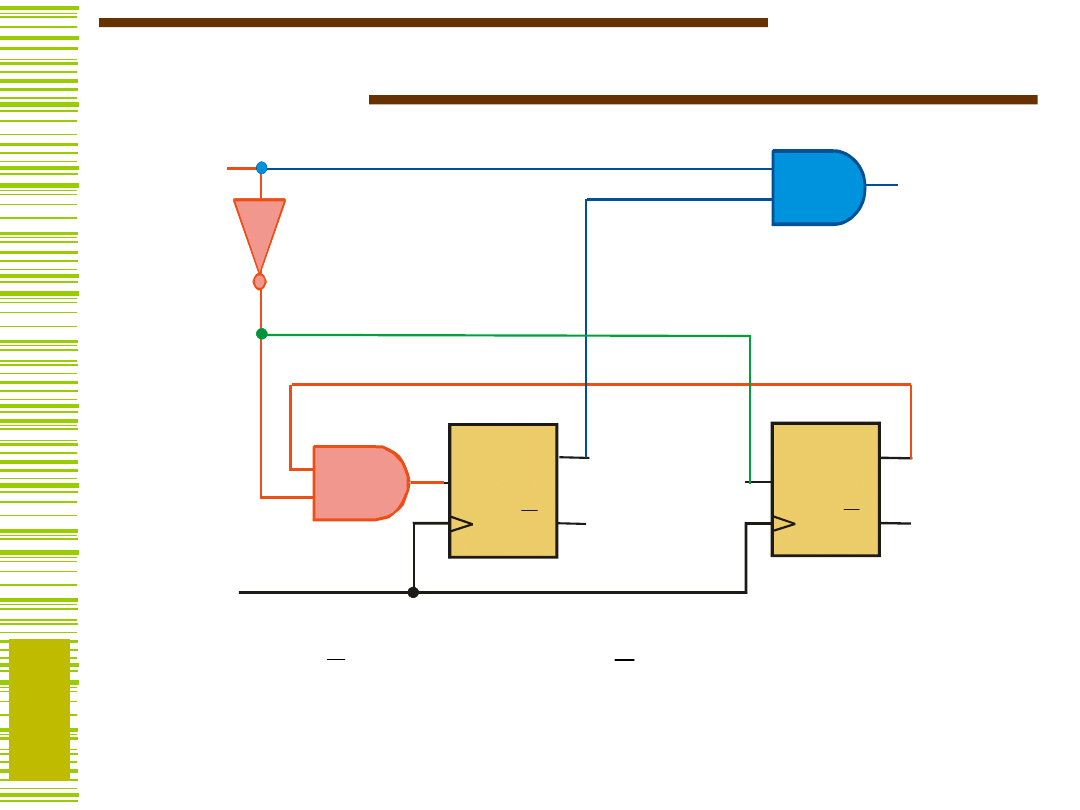
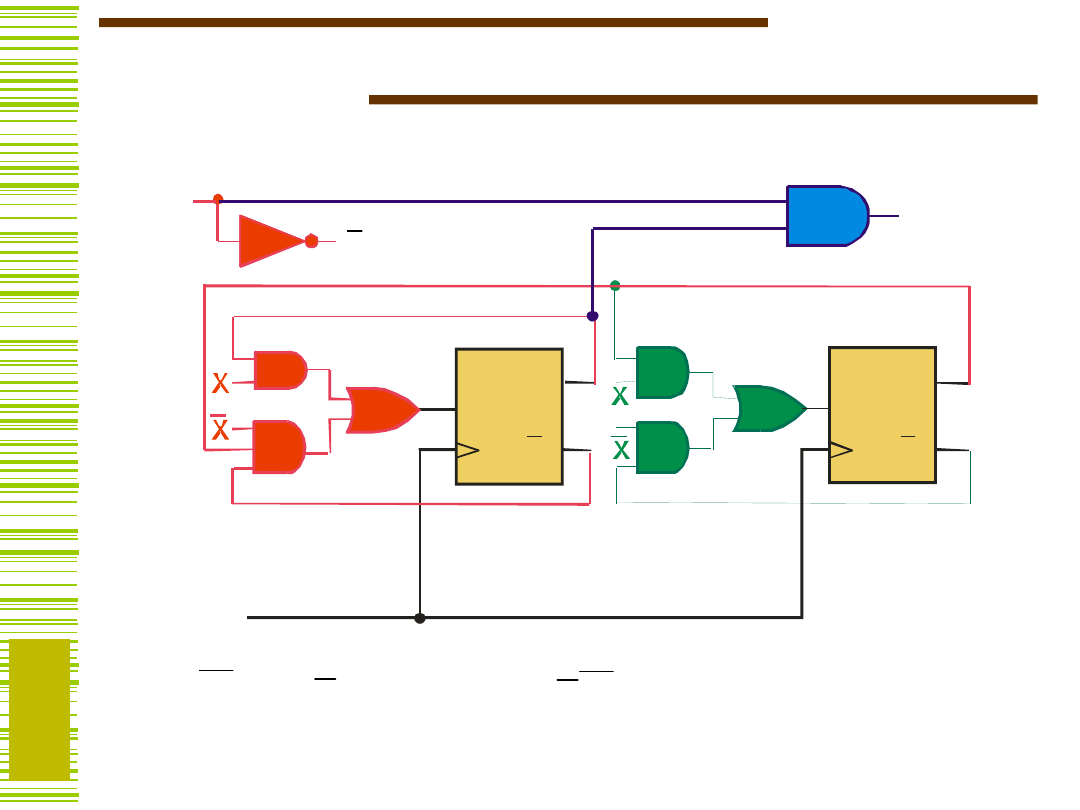
Schemat logiczny detektora

sekwencji

xQ1

Y 

Q0

x

D1

x

D0

D 1

Q 1

Q 1

D 1

Q 1

Q 1

D 0

Q 0

Q 0

x

Y

19

I

T
P

W

ZPT

Przykład... Realizacja T

X

Q1Q0

0 1

00

0 0

01

1 0

11

1 0

10

–

–

X

Q1Q0

0 1

00

1 0

01

1 0

11

1 0

10

–

–

QQ’

T

00

0

01

1

10

1

11

0

X

Q1Q0

0 1

00
01
11
10

–

–

X

Q1Q0

0 1

00
01
11
10

–

–

Q1’

Q0’

T1

T0

xQ1

x

1Q0

Q

T1





xQ0

0

Q

x

T0





Y – jak poprzednio

0 0

0

0

1

1

0

0

0 1

1

1

20

I

T
P

W

ZPT

Schemat logiczny detektora (T)

xQ1

x

1Q0

Q

T1





xQ0

0

Q

x

T0





Y – jak poprzednio

T1

Q1

Q 1

Q1

Q 1

T0

Q0

Q 0

CLK

x

x

Y

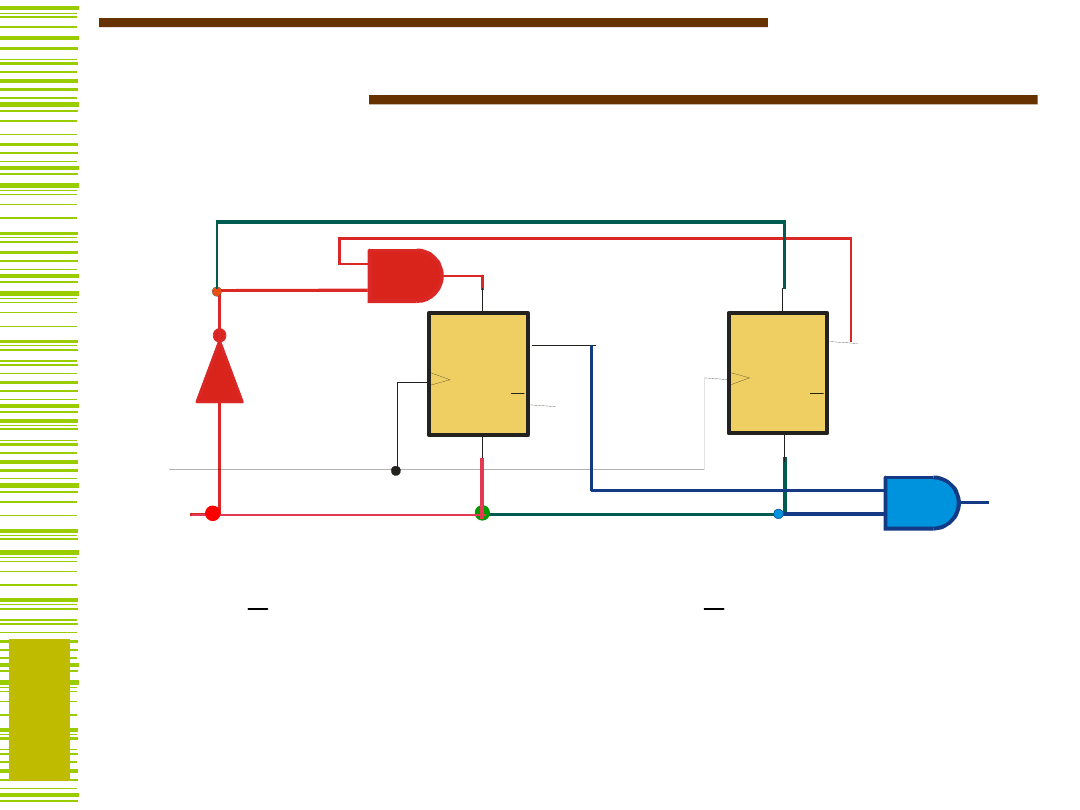
21

I

T
P

W

ZPT

Schemat logiczny detektora (JK)

Q0

x

J1 

x

J0 

x

K1

x

K0 

1

Q

J

K Q

0

K

J Q

Q

CLK

Y

Y – jak poprzednio

x

22

I

T
P

W

ZPT

Nie martwmy się ...

trzeba przetwarzać ogromne

tablice wypełnione

zerami i jedynkami.

Ale nie martwmy się!
Proces ten – w systemach
komputerowego projektowania
– jest całkowicie
zautomatyzowany.

Synteza kombinacyjna układów

sekwencyjnych może być

(i zazwyczaj jest) procesem żmudnym,

011

001

00

100

1 11

10

010

010

00

010

101

01

010

100

1 11

23

I

T
P

W

ZPT

Nie martwmy się ...

AHDL lub VHDL

…dalej automatycznie

…aż do zaprogramowania

jedyną czynnością użytkownika

jest ...

24

I

T
P

W

ZPT

Specyfikacja automatu

Nie wnikając w szczegóły takiego zapisu (będą
one omawiane na innych wykładach) trzeba
podkreślić, że jest to wierne odwzorowanie
tablicy przejść wyjść automatu.

AHDL
VHDL

AHDL
VHDL

25

I

T
P

W

ZPT

Na przykład licznik ze

sterowaniem...

TABLE

% current current

next next

%

% state

input

state output

%

s, v[] =>

s,

y;

s0,

B"00„ =>

s1,

0;

s0,

B"01„ =>

s4,

0;

s0,

B"1X„ =>

s0,

0;

s1,

B"00„ =>

s2,

0;

s1,

B"01„ =>

s0,

0;

s1,

B"1X„ =>

s0,

0;

s2,

B"00„ =>

s3,

0;

s2,

B"01„ =>

s1,

0;

s2,

B"1X„ =>

s0,

0;

s3,

B"00„ =>

s4,

0;

s3,

B"01„ =>

s2,

0;

s3,

B"1X„ =>

s0,

0;

s4,

B"00„ =>

s0,

1;

s4,

B"01„ =>

s3,

1;

s4,

B"1X„ =>

s0,

1;
END TABLE;

X

S

00

01

10

Y

S0

S1

S4

S0

0

S1

S2

S0

S0

0

S2

S3

S1

S0

0

S3

S4

S2

S0

0

S4

S0

S3

S0

1

zapisany w języku

AHDL,

po

wprowadzeniu...

26

I

T
P

W

ZPT

…specyfikacji do edytora tekstowego

TABLE

%

current

current

next next %

%

state

input

state output %

s,

v[] => s, y;

s0,

B"00„ =>

s1, 0;

s0,

B"01„ =>

s4, 0;

s0,

B"1X„ =>

s0, 0;

s1,

B"00„ =>

s2, 0;

s1,

B"01„ =>

s0, 0;

s1,

B"1X„ =>

s0, 0;

s2,

B"00„ =>

s3, 0;

s2,

B"01„ =>

s1, 0;

s2,

B"1X„ =>

s0, 0;

s3,

B"00„ =>

s4, 0;

s3,

B"01„ =>

s2, 0;

s3,

B"1X„ =>

s0, 0;

s4,

B"00„ =>

s0, 1;

s4,

B"01„ =>

s3, 1;

s4,

B"1X„ =>

s0, 1;

END TABLE;

27

I

T
P

W

ZPT

i uruchomieniu kompilatora…

q0 _EQ001 = !q0 & q1 & !X1 & X2
# q2 & !X1 & X2
# !q0 & !q2 & !X1 & !X2;

q1 _EQ002 = q2 & !X1 & X2
# q0 & q1 & !X1 & X2
# !q0 & q1 & !q2 & !X1 & !X2
# q0 & !q1 & !q2 & !X1 & !X2;

q2 _EQ003 = !q0 & !q1 & !q2 & !X1 & X2
# q0 & q1 & !q2 & !X1 & !X2;

EPM7032

...zostanie automatycznie zrealizowany bez udziału

projektanta.

28

I

T
P

W

ZPT

Wniosek

Skoro kompilator oblicza funkcje wzbudzeń
automatycznie, to umiejętność ta nie jest
w dzisiejszych czasach sprawą
najważniejszą.

Lepiej skoncentrować się na tych
metodach
i procedurach syntezy logicznej, które
nie są jeszcze wbudowane do systemów
komercyjnych.