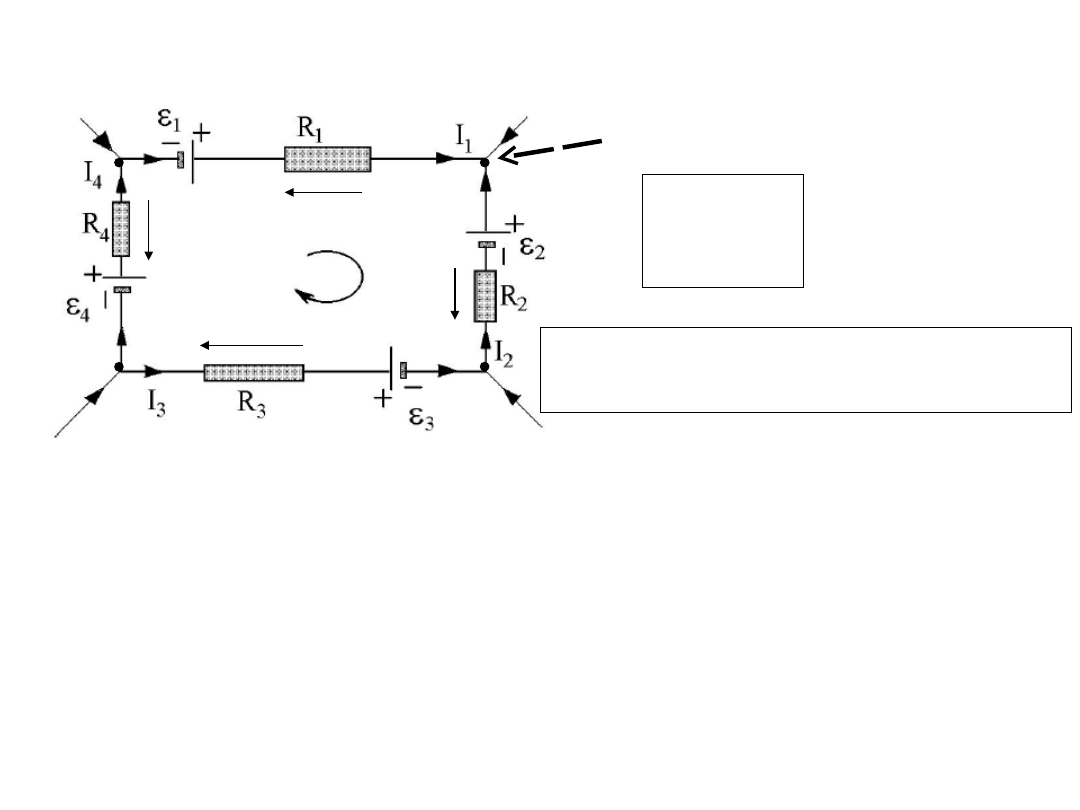
Pierwsze prawo Kirchhoffa.
Suma natężeń prądów wchodzących do węzła sieci elektrycznej
jest równa sumie natężeń prądów wychodzących z punktu
węzłowego.

Drugie prawo Kirchhoffa.
Suma sił elektromotorycznych w oczku jest równa sumie spadków
napięć na wszystkich rezystorach w tym oczku:













n

i

m

j

j

j

i

R

I

E

1

1

)

(

Obwody rozgałęzione. Prawa
Kirchhoffa

Węzeł

Oczko

I

5

I

1

+I

2

+I

5

=

0

E

1

- I

1

*R

1

- E

2

+ I

2

*R

2

+E

3

+ I

3

*R

3

+E

4

-

I

4

*R

4

=0

Metoda praw
Kirchhoffa

W ogólnym przypadku w każdej gałęzi obwodu płynie inny prąd, z

czego wynika że liczba prądów jest równa liczbie gałęzi obwodu. Do
obliczenia tych prądów należy ułożyć tyle niezależnych równań, ile
dany obwód ma gałęzi. Korzysta się tu z zależności, jaka zachodzi
między liczbą gałęzi g, liczbą węzłów w oraz liczbą oczek o obwodu w
postaci g=(w-1)+o

Tok obliczeń jest następujący:
1. Strzałkuje się dowolnie prądy we wszystkich gałęziach obwodu.
2. Strzałkuje się napięcia (przeciwnie do strzałki prądu) na wszystkich

elementach rezystancyjnych oraz źródła napięcia.

3. Układa się (w-1) równań gałęziowych według pierwszego prawa

Kirchhoffa
opuszczając jeden dowolny węzeł.

4. Układa się tyle równań według drugiego prawa Kirchhoffa ile dany

obwód zawiera oczek.

5. Rozwiązuje się powyższy układ ze względu na nieznane prądy

gałęziowe.

Zaletą metody równań Kirchhoffa jest duża prostota w trakcie układania

równań, natomiast wadą jest duża pracochłonność przy ich
rozwiązywaniu.

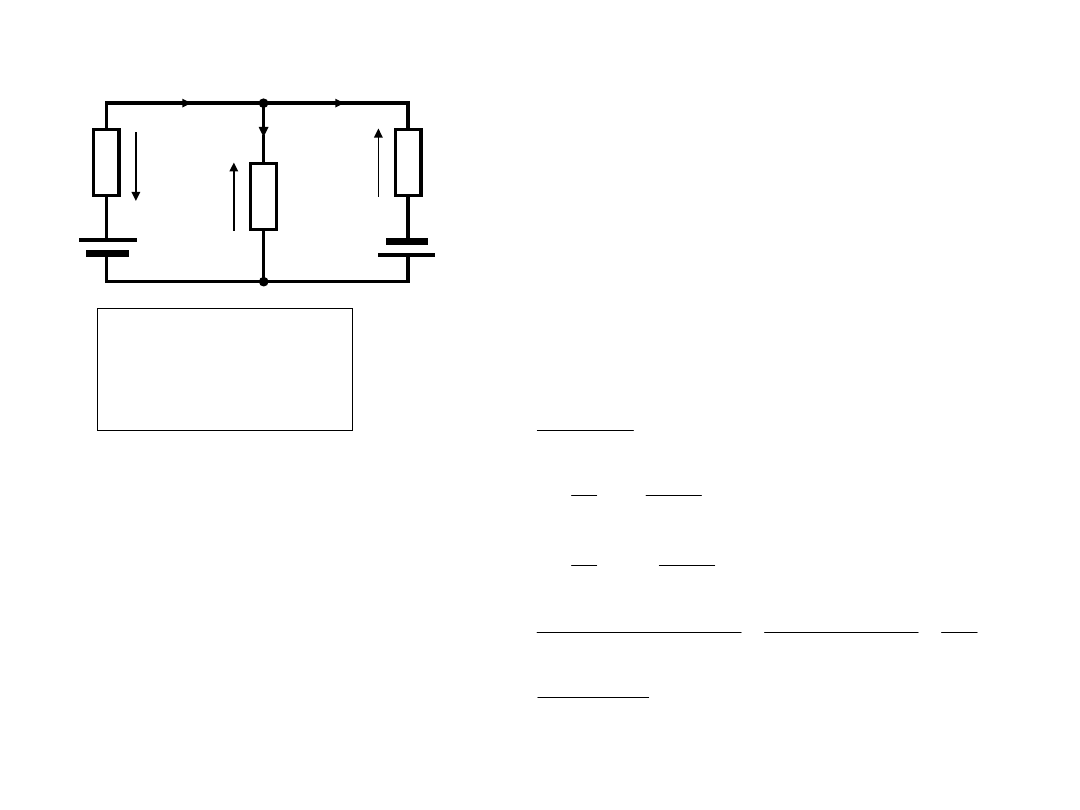
Rozwiązywanie obwodu metodą praw
Kirchhoffa

I

1

I

2

I

3

R

1

=5

Ω

R

3

=10

Ω

R

2

=10

Ω

E

1

=10

V

E

2

=5V

I

1

=I

2

+I

3

E

1

-I

1

*R

1

-I

3

*R

3

=0

I

3

*R

3

-I

2

*R

2

+E

2

=0

E

1

-(I

2

+I

3

)*R

1

-I

3

*R

3

=0

E

2

+I

3

*R

3

-I

2

*R

2

=0

E

1

-I

2

*R

1

-I

3

*R

1

-I

3

*R

3

=0

E

2

-I

2

*R

2

+I

3

*R

3

=0

E

1

-I

2

*R

1

-I

3

*(R

1

-R

3

)=0

E

2

-I

2

*R

2

+I

3

*R

3

=0



I

2

=(E

2

+I

3

*R

3

)/R

2









A

I

A

I

A

R

R

R

R

R

R

R

E

R

E

I

R

R

R

R

R

I

R

R

E

E

R

R

I

R

R

R

I

R

R

E

E

R

R

I

R

R

R

I

E

E

25

,

1

875

,

0

375

,

0

875

,

0

10

10

375

,

0

5

375

,

0

200

75

5

5

10

5

10

5

5

5

10

10

0

0

1

2

3

2

2

1

3

1

1

2

2

1

3

3

1

2

3

1

3

2

1

2

1

3

1

3

2

1

3

3

2

1

2

1

3

1

3

1

2

3

3

2

1



















































































































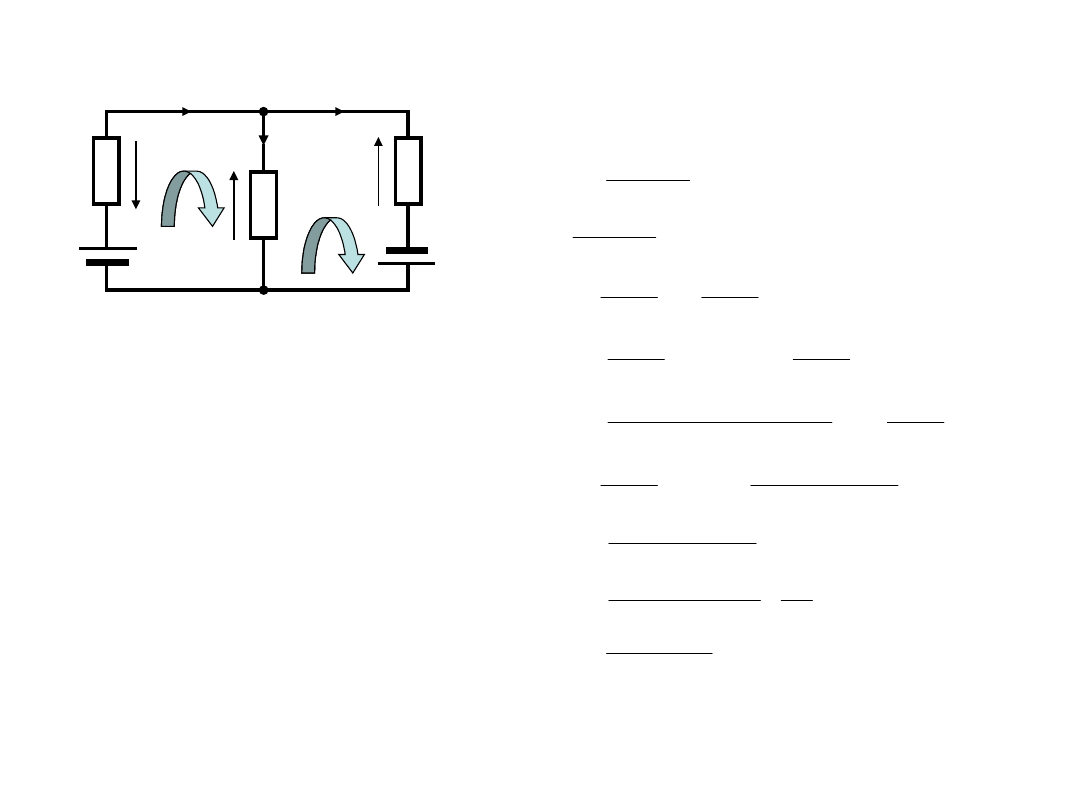
Metoda
oczkowa

I

1

I

2

I

3

R

1

=5

Ω

R

3

=10

Ω

R

2

=10

Ω

E

1

=10

V

E

2

=5V

I’

1

I’

2









0

0

2

2

3

2

3

1

3

2

3

1

1

1

































E

R

R

I

R

I

R

I

R

R

I

E













A

I

I

I

A

I

I

A

I

I

A

I

A

I

R

R

R

R

R

R

R

R

E

R

E

I

R

R

R

R

R

R

R

R

I

E

R

R

R

E

E

R

R

R

E

R

R

R

R

R

R

R

R

R

R

I

E

R

R

R

E

R

R

R

R

R

I

E

R

R

I

R

R

R

I

R

R

R

E

E

R

R

I

R

R

R

R

I

E

R

R

R

I

E

I

375

,

0

875

,

0

25

,

1

25

,

1

10

5

10

875

,

0

10

875

,

0

200

175

10

10

10

5

10

5

)

10

5

(

5

10

10

0

0

0

0

2

1

3

2

2

1

1

1

2

3

2

3

1

2

1

3

1

2

3

1

2

3

1

3

2

3

1

2

1

2

2

3

1

3

1

2

3

1

3

1

3

1

2

3

3

2

3

1

2

1

2

3

2

2

3

1

3

1

3

2

3

1

2

3

2

2

3

2

2

3

1

2

3

2

3

1

3

1

2

2

3

2

3

3

1

3

2

1

3

1

3

2

1

1





































































































































































































































W

rozpatrywanym

obwodzie

wprowadzamy prądy oczkowe, krążące
jak gdyby wzdłuż poszczególnych
oczek obwodu.

Najwygodniej jest przyjąć, że zwroty
prądów oczkowych są takie same we
wszystkich oczkach, na przykład są
zgodne z ruchem wskazówek zegara.
Prądy w gałęziach zewnętrznych
obwodu, tj. w gałęziach nie będących
wspólnymi dla dwóch oczek, są równe
odpowiednim

prądom

oczkowym.

Prądy w gałęziach wspólnych dla
dwóch oczek równają się różnicy
odpowiednich prądów oczkowych.

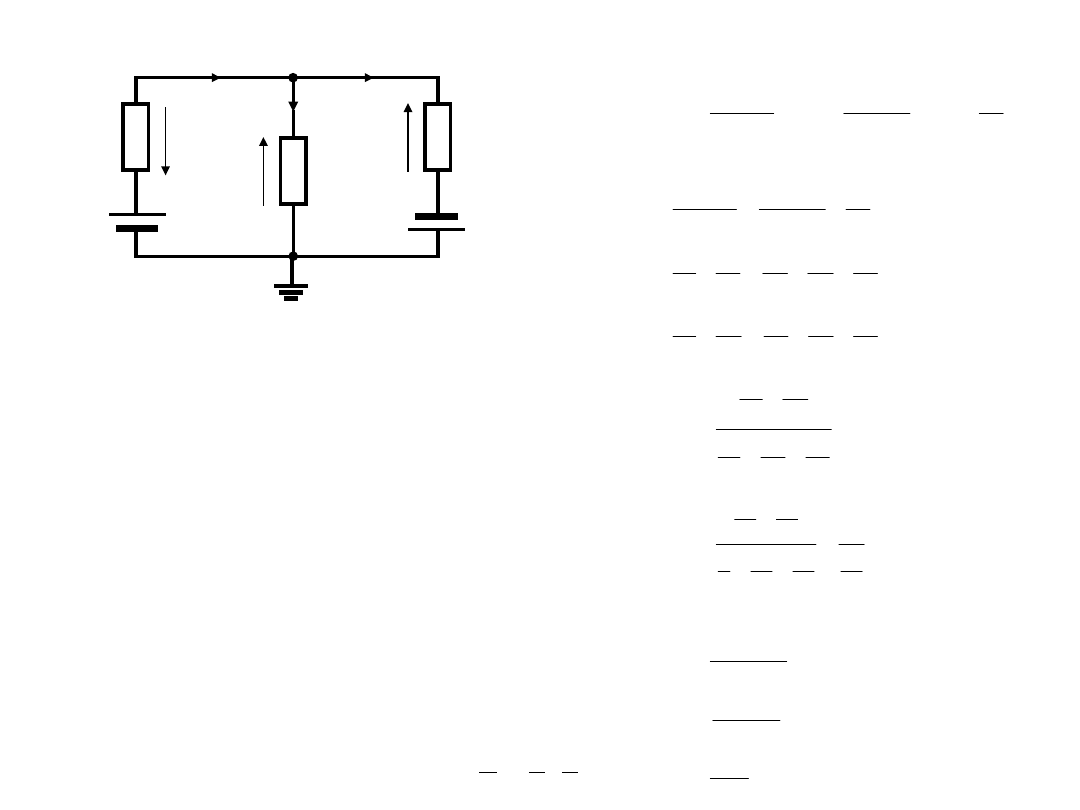
Rozwiązywanie obwodów metodą potencjałów
węzłowych

I

1

I

2

I

3

R

1

=5

Ω

R

3

=10

Ω

R

2

=10

Ω

E

1

=10

V

E

2

=5V

A

B

A

I

A

I

A

I

V

V

R

R

R

R

E

R

E

V

R

V

R

V

R

V

R

E

R

E

R

V

R

E

R

V

R

V

R

E

R

V

R

V

E

R

V

E

R

V

I

R

V

E

I

R

V

E

I

I

I

I

A

A

A

A

A

A

A

A

A

A

A

A

A

A

375

,

0

10

75

,

3

875

,

0

10

5

75

,

3

25

,

1

5

75

,

3

10

75

,

3

10

4

5

,

1

10

1

10

1

5

1

10

5

5

10

1

1

1

1

2

1

3

2

1

2

2

1

1

3

2

1

2

2

1

1

3

2

2

2

1

1

1

3

2

2

1

1

3

3

2

2

2

1

1

1

3

2

1











































































Tok obliczeń prądów gałęziowych jest

następujący:

1. Strzałkuje się dowolnie prądy we wszystkich

gałęziach obwodu.

2. Strzałkuje się napięcia (przeciwnie do strzałki

prądu) na wszystkich elementach
rezystancyjnych obwodu.

3. Oznacza się potencjały węzłów, przyjmując

potencjał jednego dowolnego węzła równy
zeru (węzeł odniesienia).

4. Układa się równania węzłowe dla (w-1) węzłów

obwodu, opuszczając węzeł odniesienia.

5. Rozwiązuje się powyższy układ równań ze

względu na potencjały węzłowe.

6. Oblicza się napięcia występujące na

poszczególnych gałęziach wzorem U

kl

=V

k

-V

l

.

7. Prądy gałęziowe wyznacza się z prawa Ohma.

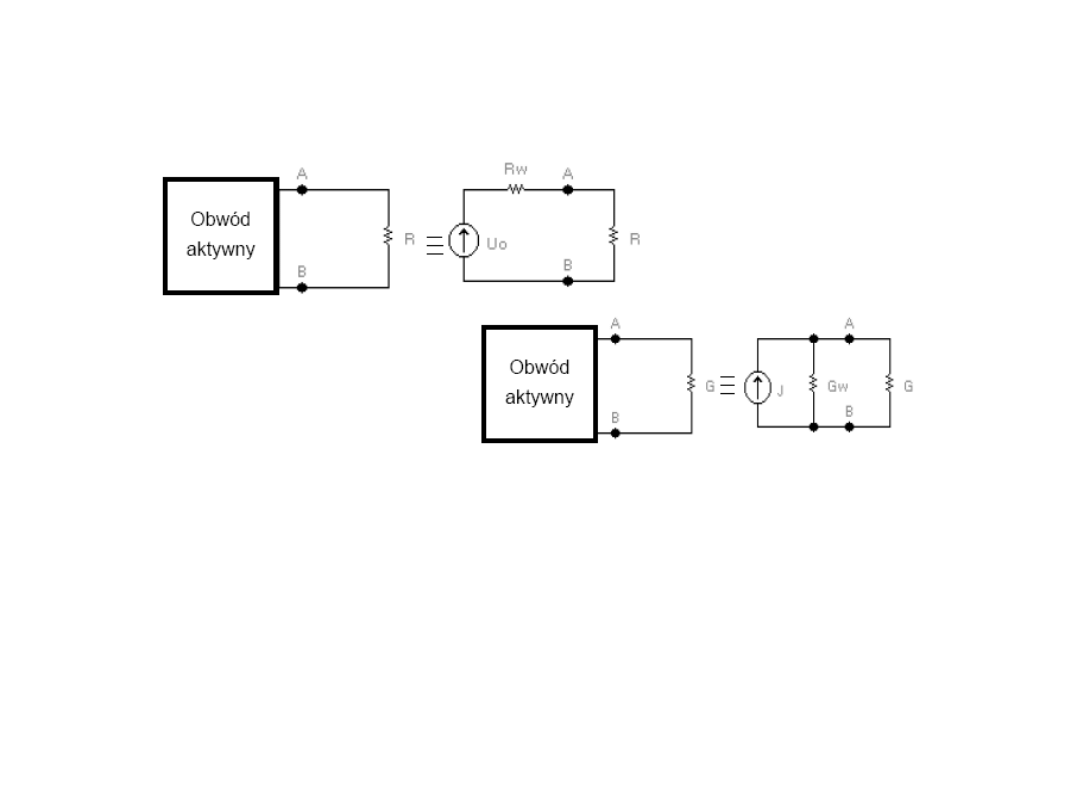
Metoda źródła zastępczego. Twierdzenie Thevenina i
Nortona

Rozwiązywanie obwodu metodą Thevenina

Każdy liniowy dwójnik aktywny można przedstawić w postaci źródła
napięcia o sile elektromotorycznej równej napięciu między
rozwartymi zaciskami wyjściowymi dwójnika aktywnego.
Rezystancja wewnętrzna tego źródła jest równa rezystancji tego
dwójnika po usunięciu wszystkich źródeł energii.

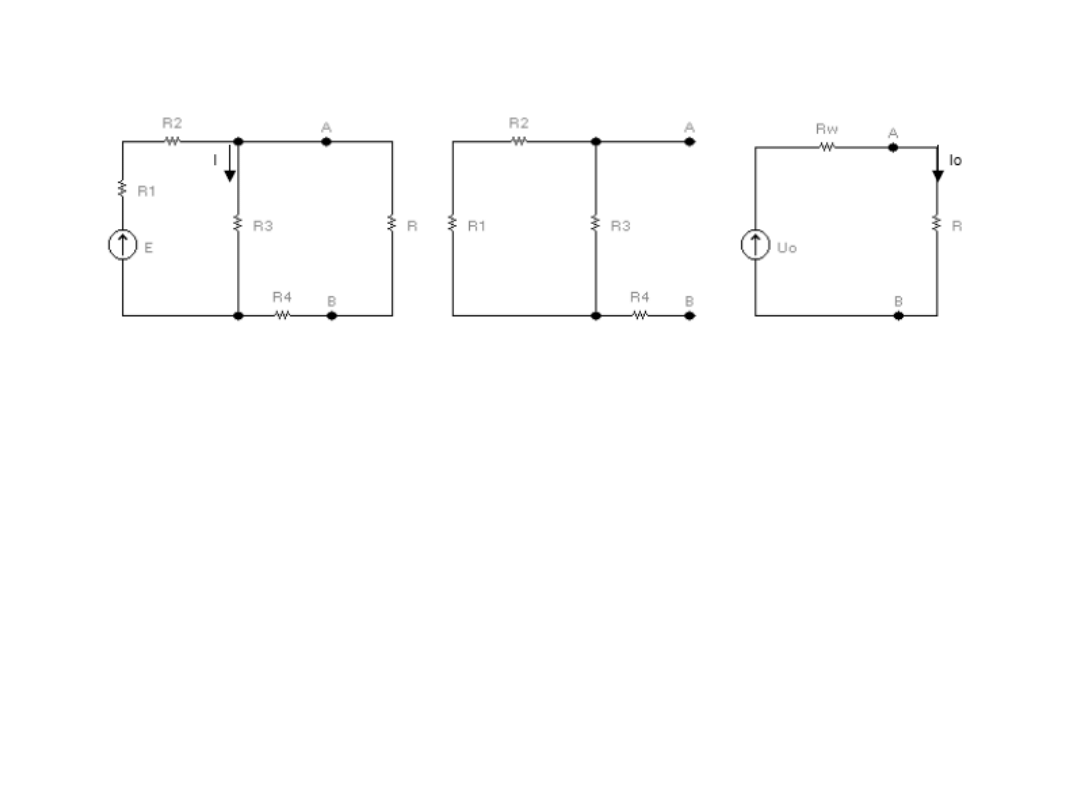
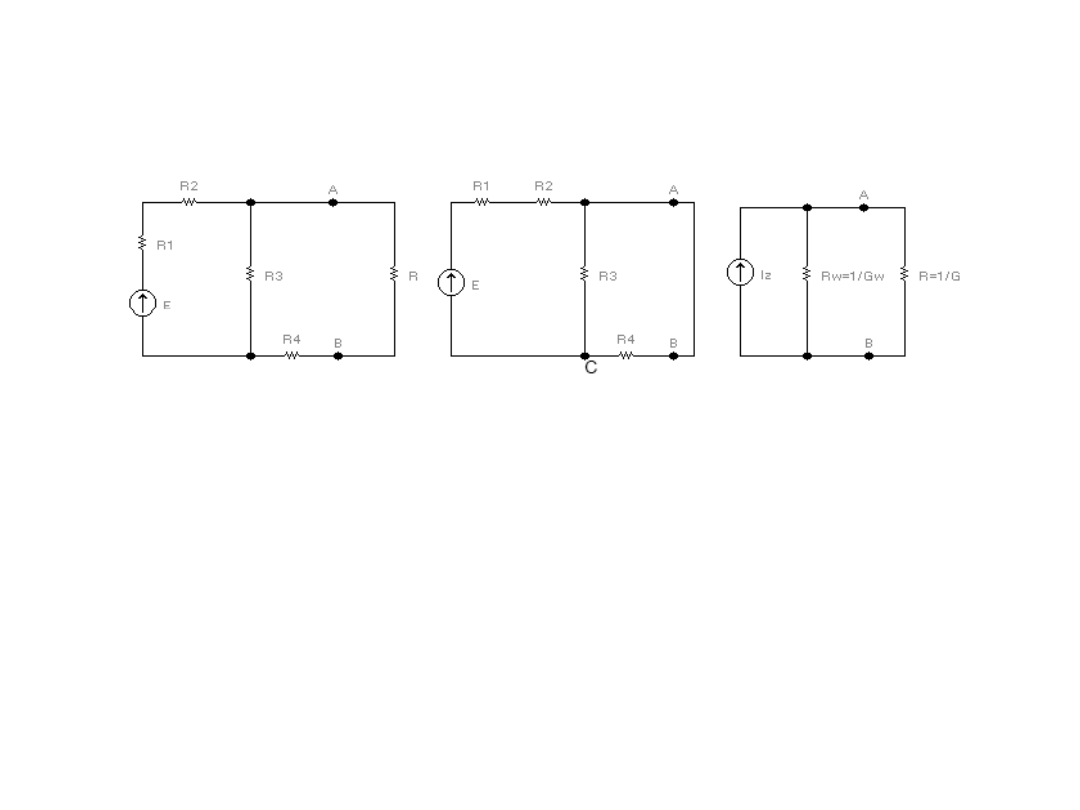
Rozwiązywanie obwodu metodą Thevenina

I

1

I

2

I

3

R

1

=5

Ω

R

3

=10

Ω

R

2

=10

Ω

E

1

=10

V

E

2

=5V

A

B

R

w

R

3

U

3

U

AB

A

B

A

R

R

U

I

R

R

R

R

R

napięa

źródła

y

Likwidujem

V

U

R

R

R

E

E

E

R

I

E

U

B

i

A

zaciski

Rozwieramy

w

AB

w

AB

AB

375

,

0

40

15

10

3

1

3

5

3

1

3

10

5

10

5

5

5

10

5

5

10

10

3

3

2

1

2

1

1

2

1

2

1

1

1

1

1

























































Rozwiązywanie obwodu metodą Nortona

Twierdzenie Nortona
Każdy liniowy dwójnik aktywny można przedstawić w postaci źródła
prądu. Prąd źródłowy tego źródła równy jest prądowi płynącemu w
bezoporowym przewodzie zwierającym zaciski dwójnika
aktywnego, zaś rezystancja wewnętrzna tego źródła jest równa
rezystancji tego dwójnika po usunięciu wszystkich źródeł energii.

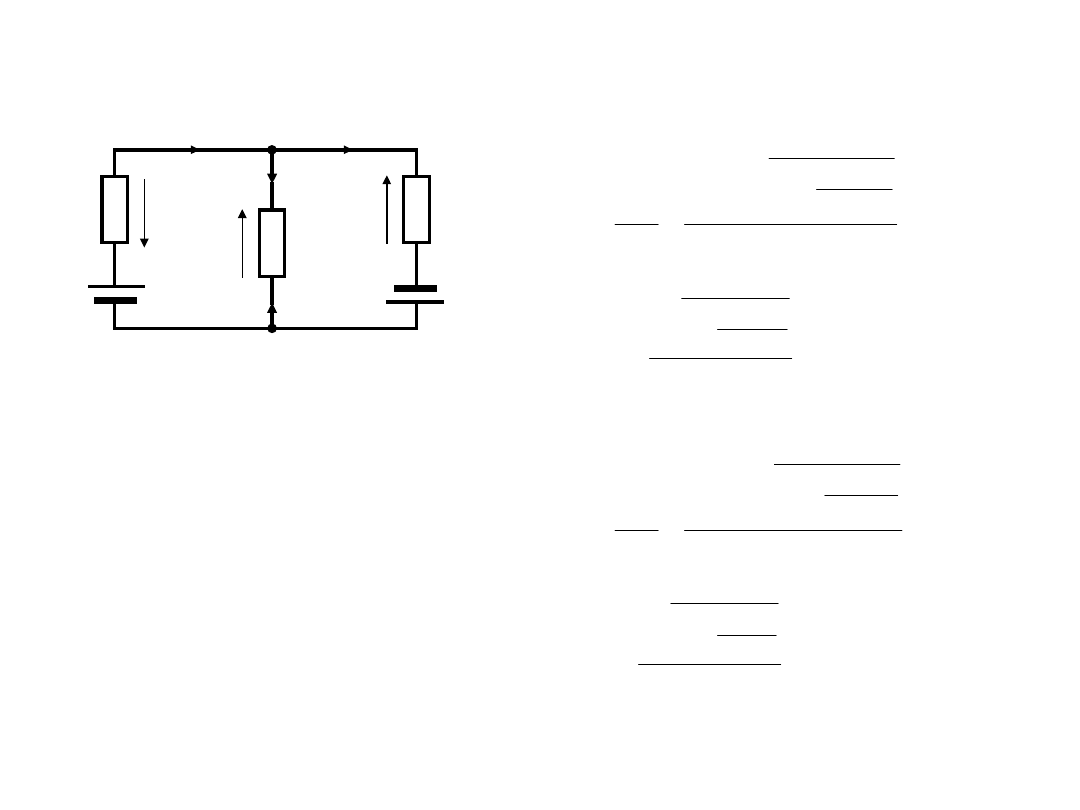
Zasada
superpozycji

I

1

I

2

I’

3

R

1

=5

Ω

R

3

=10

Ω

R

2

=10

Ω

E

1

=10

V

E

2

=5V

I”

3

A

I

A

I

R

R

R

R

R

R

R

E

E

R

U

I

E

Zakladamy

A

I

R

R

R

R

R

R

R

E

E

R

U

I

E

Zakladamy

I

I

I

AB

AB

375

,

0

125

,

0

5

,

0

125

,

0

10

10

5

10

5

10

10

1

5

0

5

,

0

10

10

10

10

10

5

5

1

10

0

3

3

3

3

1

3

1

2

2

2

2

3

3

1

3

3

3

2

3

2

1

1

1

1

3

3

2

3

3

3





















































































Odpowiedź liniowego układu
fizycznego, obwodu
elektrycznego lub jego gałęzi
na kilka wymuszeń, równa się
sumie odpowiedzi na każde
wymuszenie z osobna.