Optyka

Zasada Fermata

Światło przebiegając miedzy dwoma punktami wybiera zawsze taką drogę, by
czas na to zużyty był ekstremalny (zwykle najkrótszy).

Prawa odbicia i załamania są konsekwencją tez zasady.

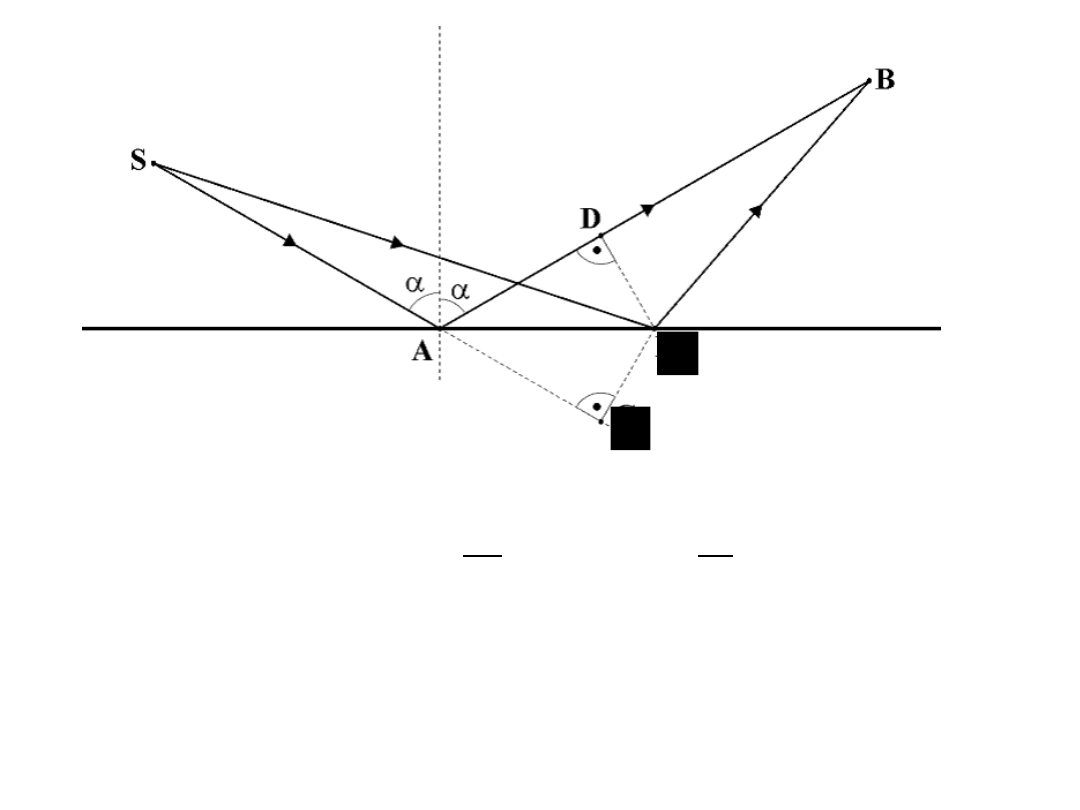
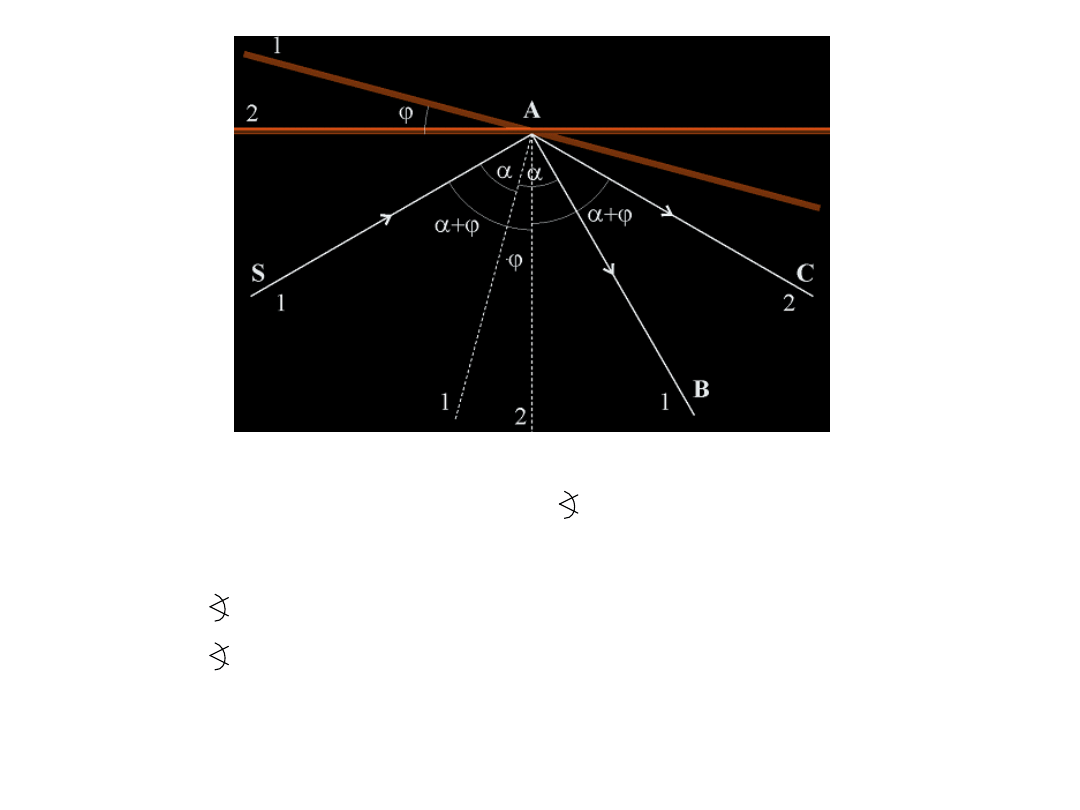
ACE i ADC są przystające, stąd AD = AE. Droga przebyta przez promień SAB

może być zapisana: SA + AD + DB = SA + AE + DB = SE + AB

Czy możliwa jest droga SCB ?

Droga SC + CB jest dłuższa od SA + AB, ponieważ SE i DB są to
przyprostokątne w trójkątach: SEC i BCD, zaś S.C. i CB są to przeciw
prostokątne w tych trójkątach. Zatem SE + DB < SC +CB.
Każda inna droga niż SAB będzie dłuższa i dłuższy czas na jej przebycie.
Zatem zgodnie z zasadą Fermata możliwa jest tylko droga SAB.

Prawo odbicia

E

C

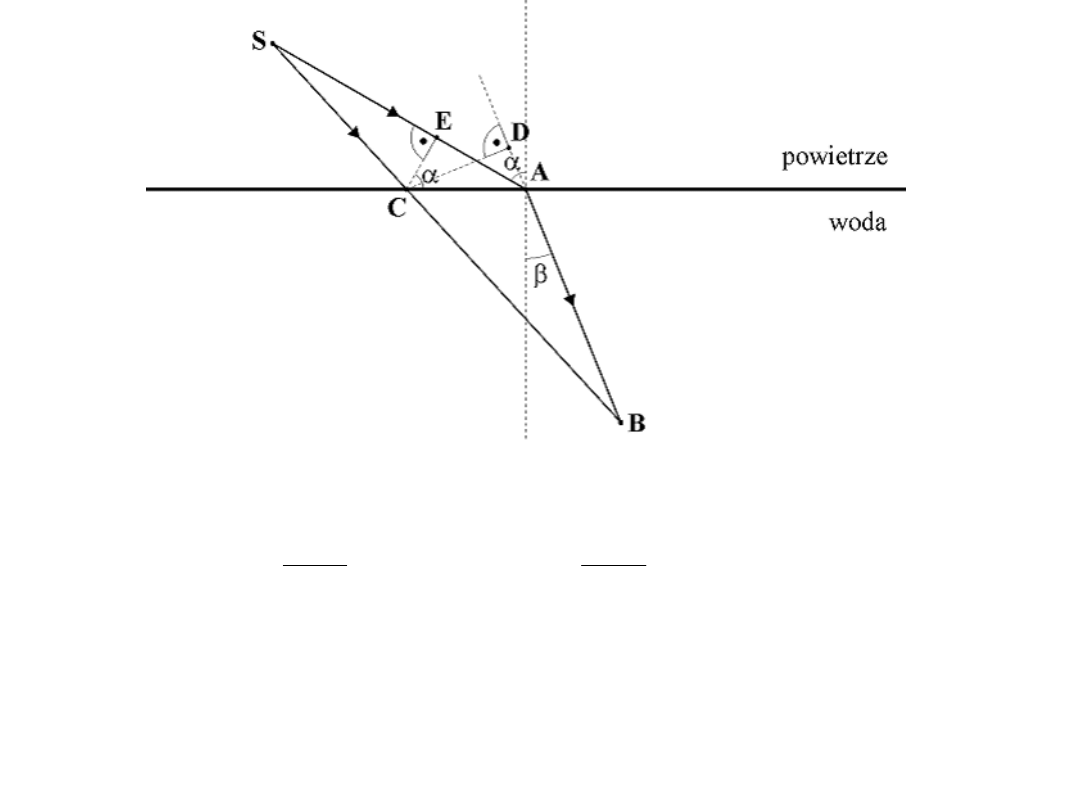
Należy wykazać, że na przebycie drogi SCB światło musi zużyć więcej czasu,
niż na przebycie drogi SAB. Z trójkątów ADC i AEC możemy napisać:

sin

AE AC

a

=

sin

AD

AC

b

=

sin

sin

AE AD

AD n

a

b

=

=

�

DB DA AB

=

+

Droga optyczna przebyta przez promień SAB jest równa:

SA AB n SE EA AB n SE AD n AB n SE DB n

+

�=

+

+

�=

+

�+

�=

+

�

Ponieważ SE < SC oraz BD < BC zatem

SE DB n SC CB n

+

�<

+

�

Najkrótsza

droga optyczna

jest dla promienia przechodzącego z S do B

prowadzi przez A, zgodnie z prawem załamania. Światło przebędzie drogę
SAB w najkrótszym czasie.

, stąd

Prawo załamania

v

1

v

2

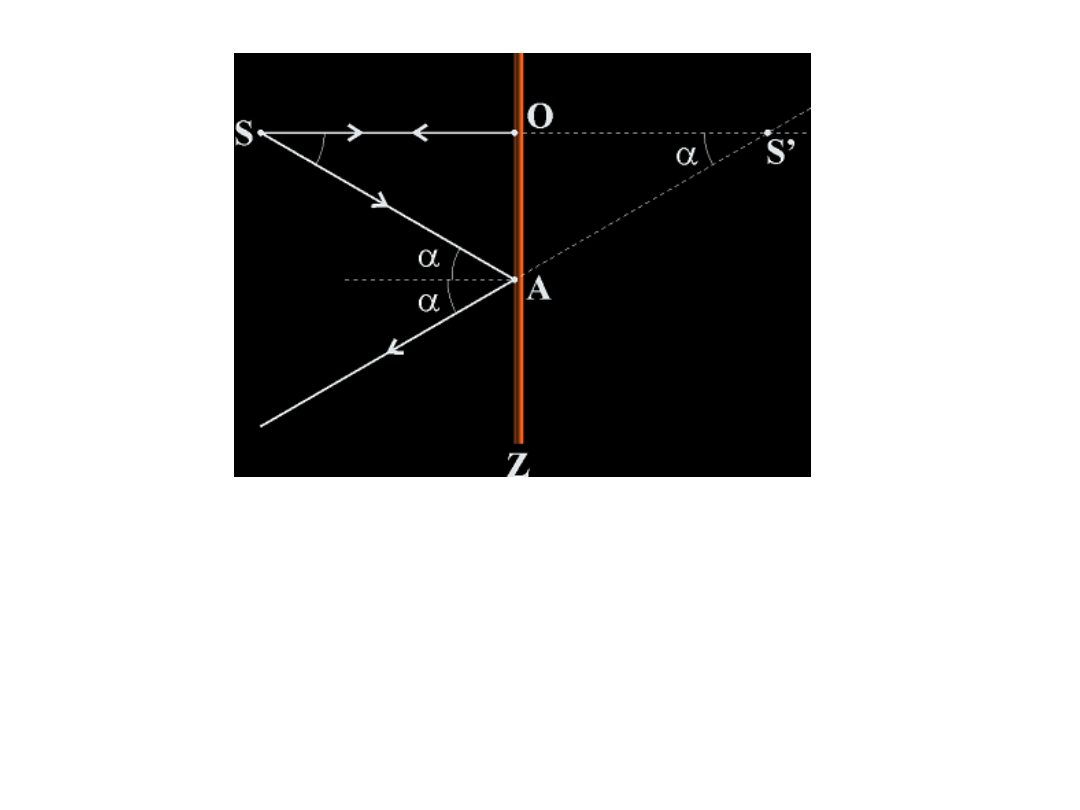
Zwierciadła płaskie

SOA

=



S’OA, zatem SO = S’O

Odległość przedmiotu i obrazu od zwierciadła są sobie równe.

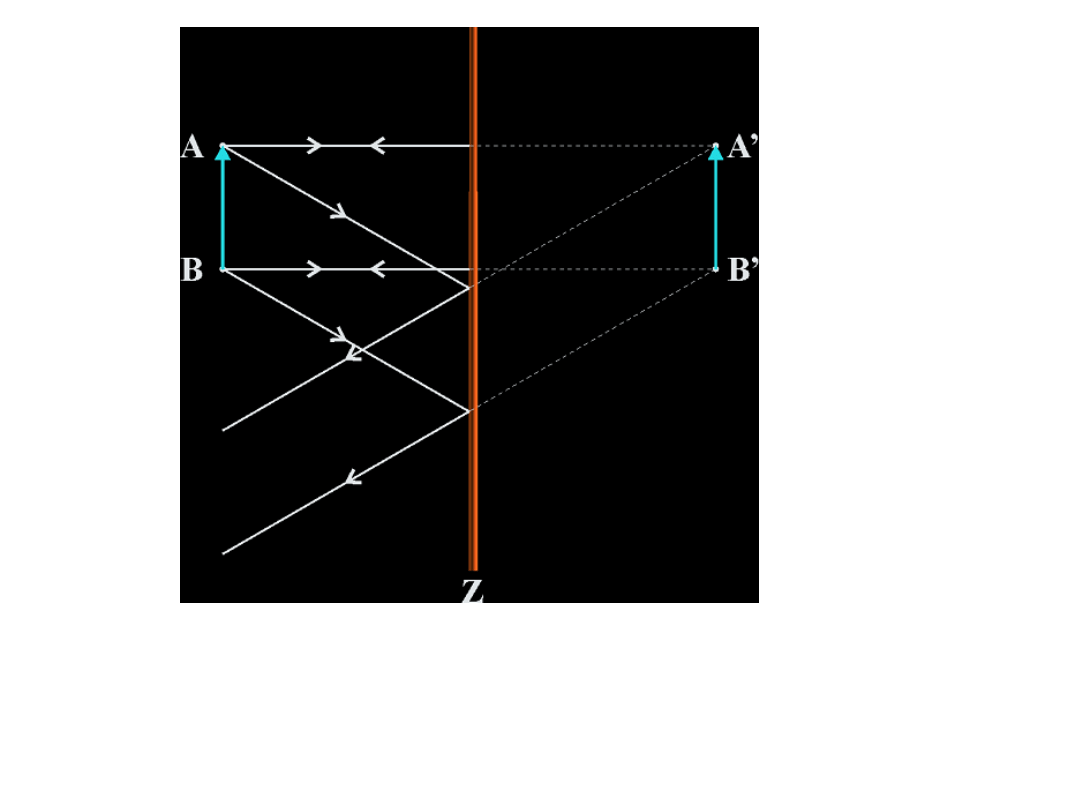
AB = A’B’ Powstaje obraz pozorny tej samej
wielkości co przedmiot, prosty (nieodwrócony)

Kąt między promieniem padającym i odbitym

2

SAB

a

=

R

Po obrocie zwierciadła o kąt  wzrasta kąt zawarty między promieniem

padającym i odbitym o 2.

2

2

2

SAB
SAB

a a

a

a j

a j

a

j

= + =
= + + + =

+

R
R

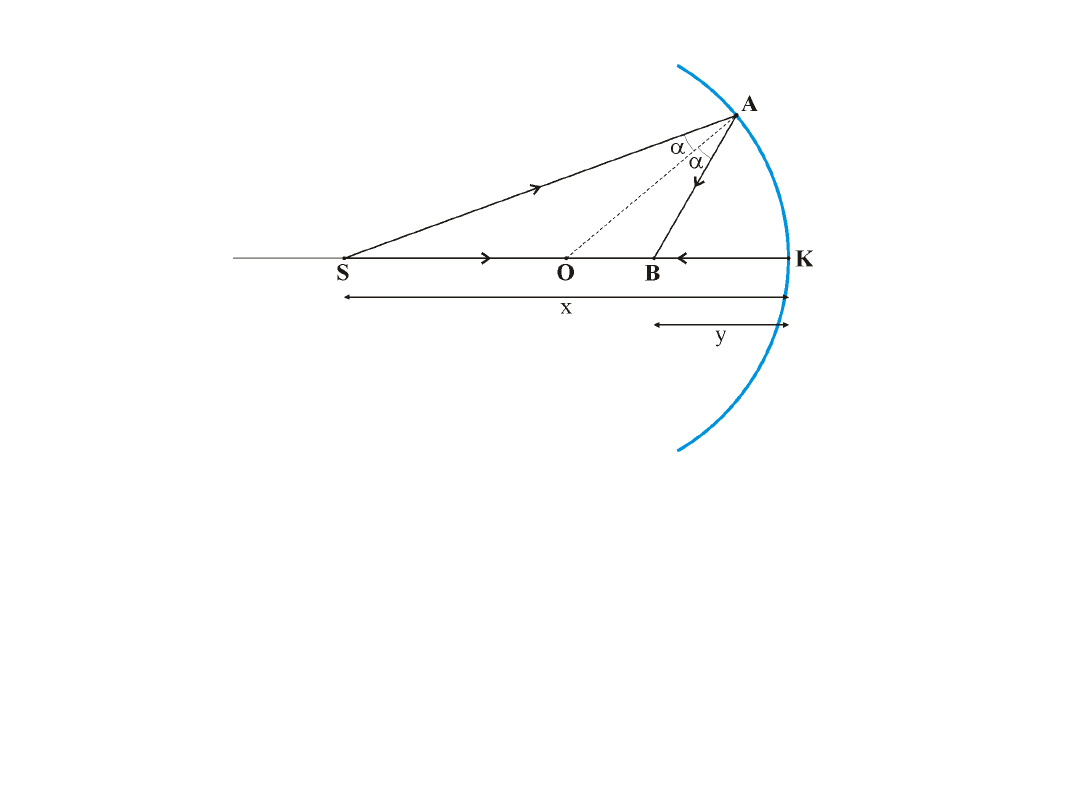
Zwierciadła kuliste

gdzie:

OK – promień krzywizny (R)
SK – odległość przedmiotu od zwierciadła (x)
BK – odległość obrazu od zwierciadła (y)

Z SAB

OB BA

OS SA

=

Jeśli BA i SA tworzą małe kąty z osią główną ( ok. 5

o

)

to można przyjąć, że SA = SK oraz AB = BK.

SO = x – R; OB = R - y

Zatem

(

)

(

)

2

1 1 2

R y y

x R x

x R y

y x R

xR xy xy yR

xR yR

xy

y x R

-

=

-

-

=

-

-

= -

+

=

+ =

oznaczamy 2 1

R

f

=

1 1 1

x y

f

+ =

gdzie f - ogniskowa

RÓWNANIE ZWIERCIADŁA

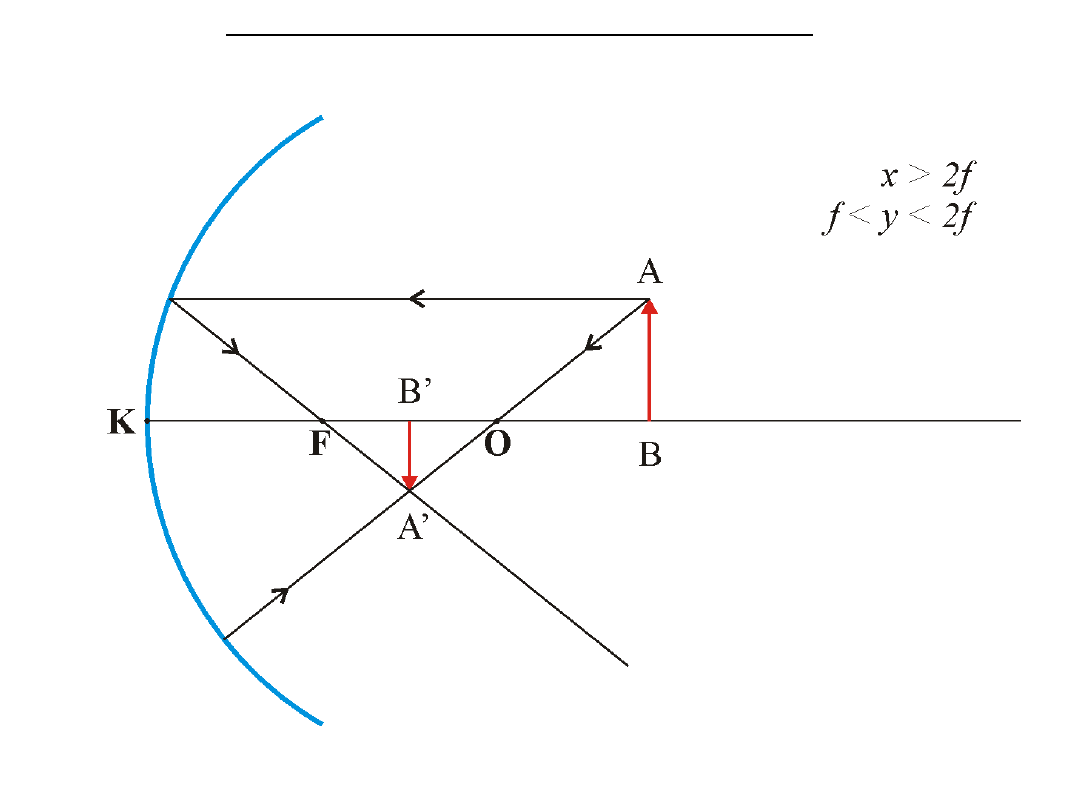
Obrazy w zwierciadłach kulistych wklęsłych

Powstaje obraz rzeczywisty, odwrócony, zmniejszony.

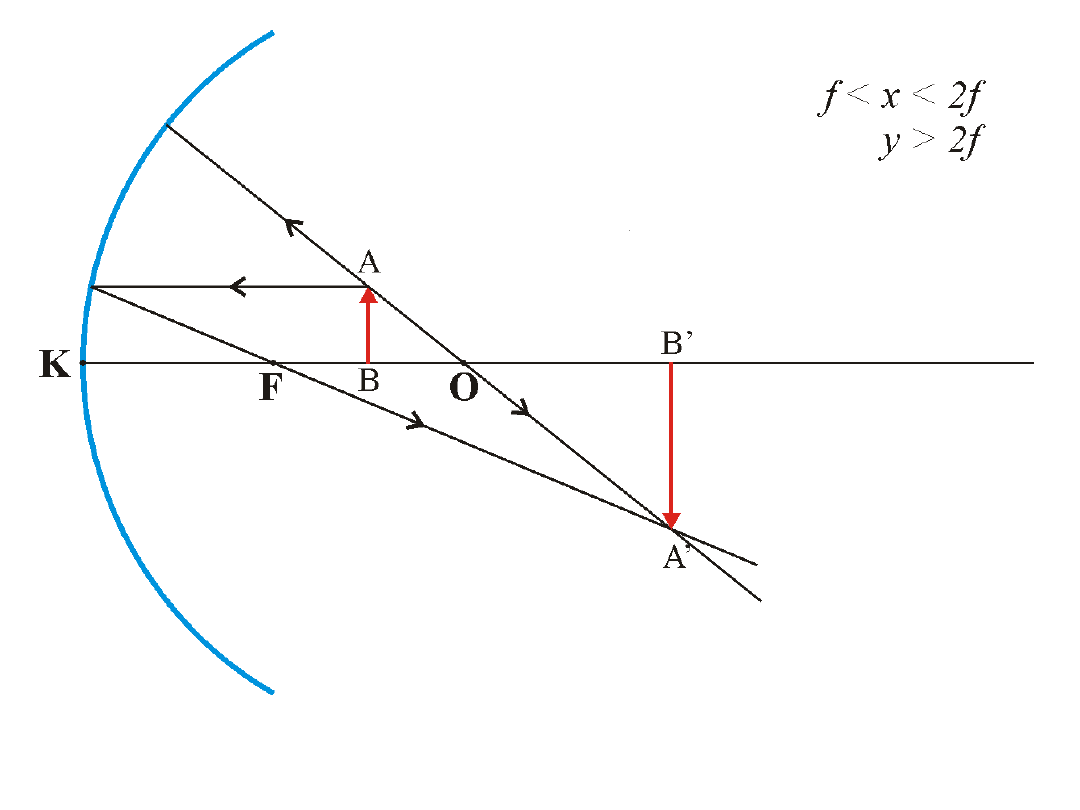
Powstaje obraz rzeczywisty, odwrócony, powiększony.

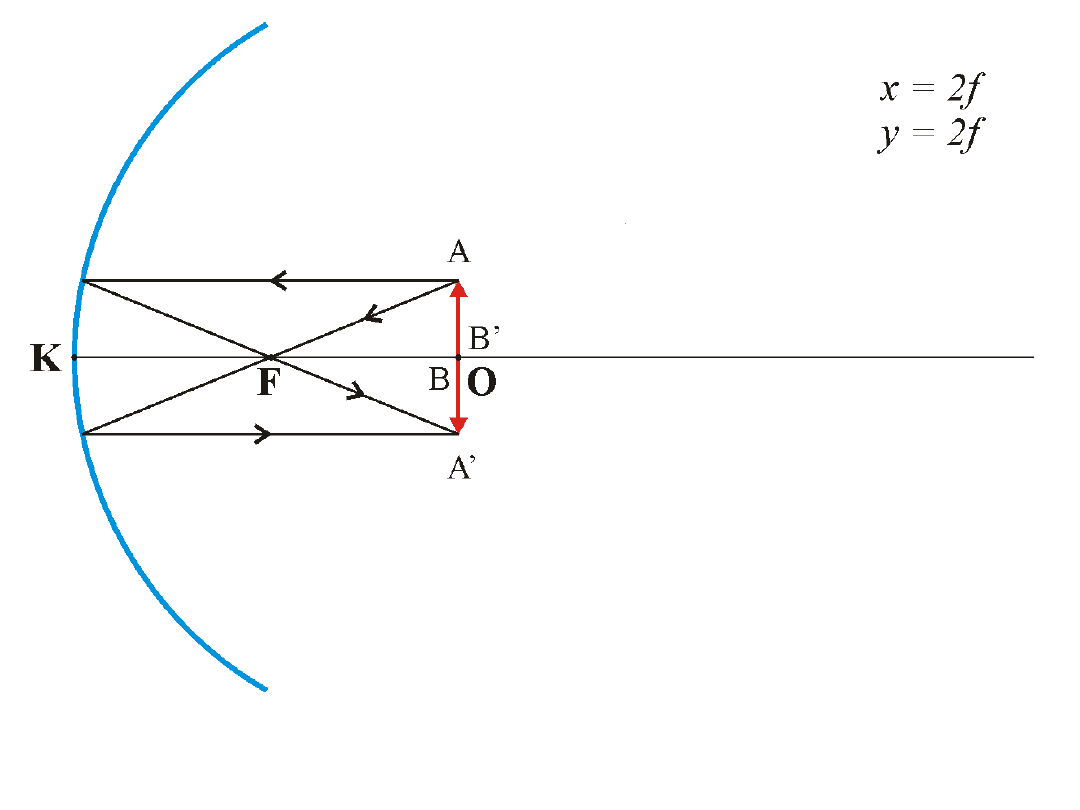
Powstaje obraz rzeczywisty, odwrócony, tej samej wielkości co przedmiot.

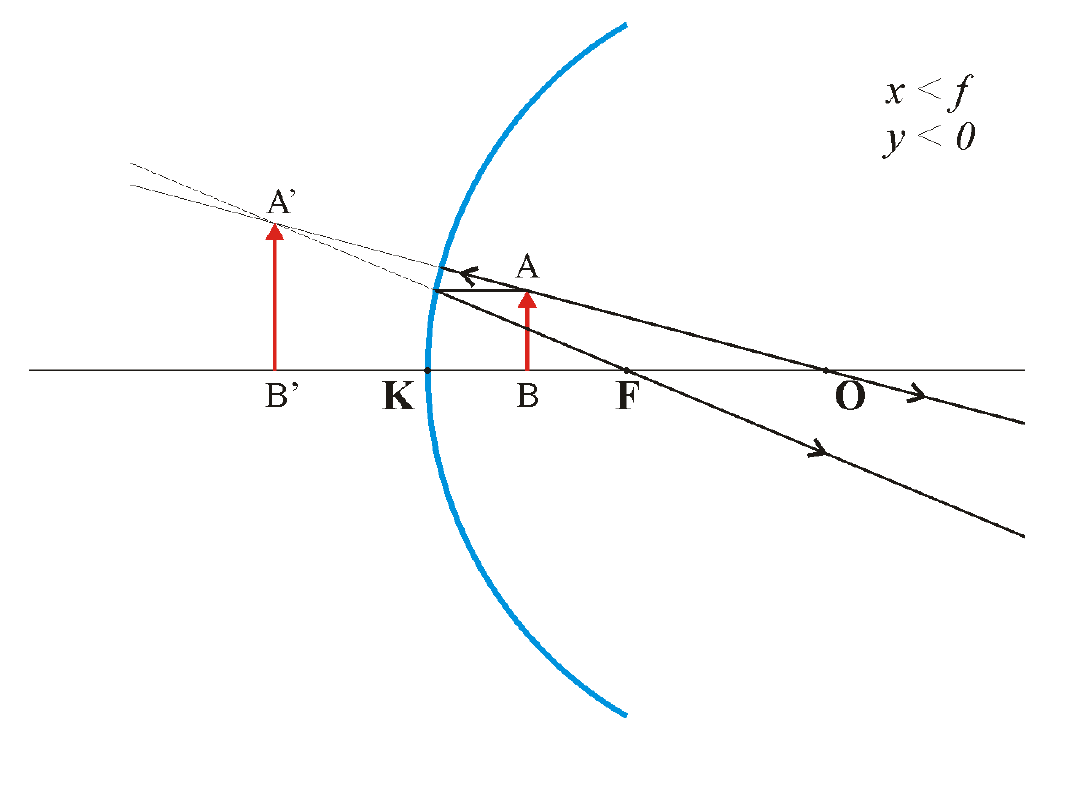
Powstaje obraz pozorny, prosty, powiększony.

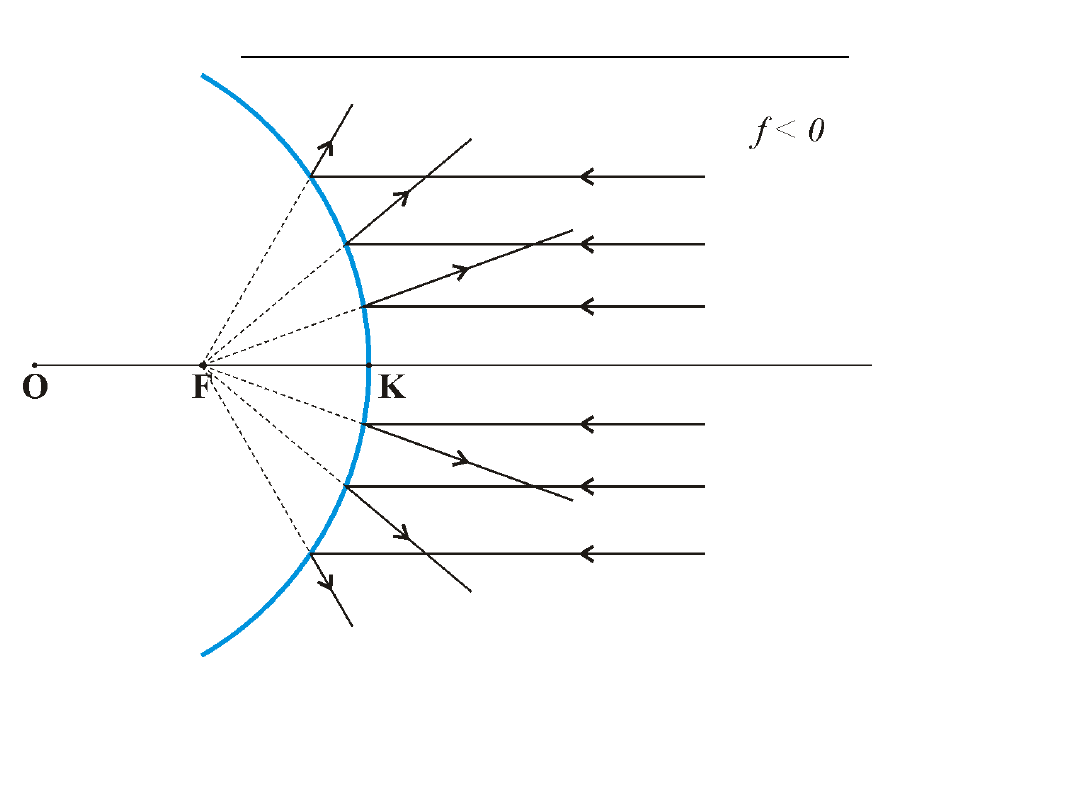
Obrazy w zwierciadłach kulistych wypukłych.

gdzie:

F – ognisko pozorne

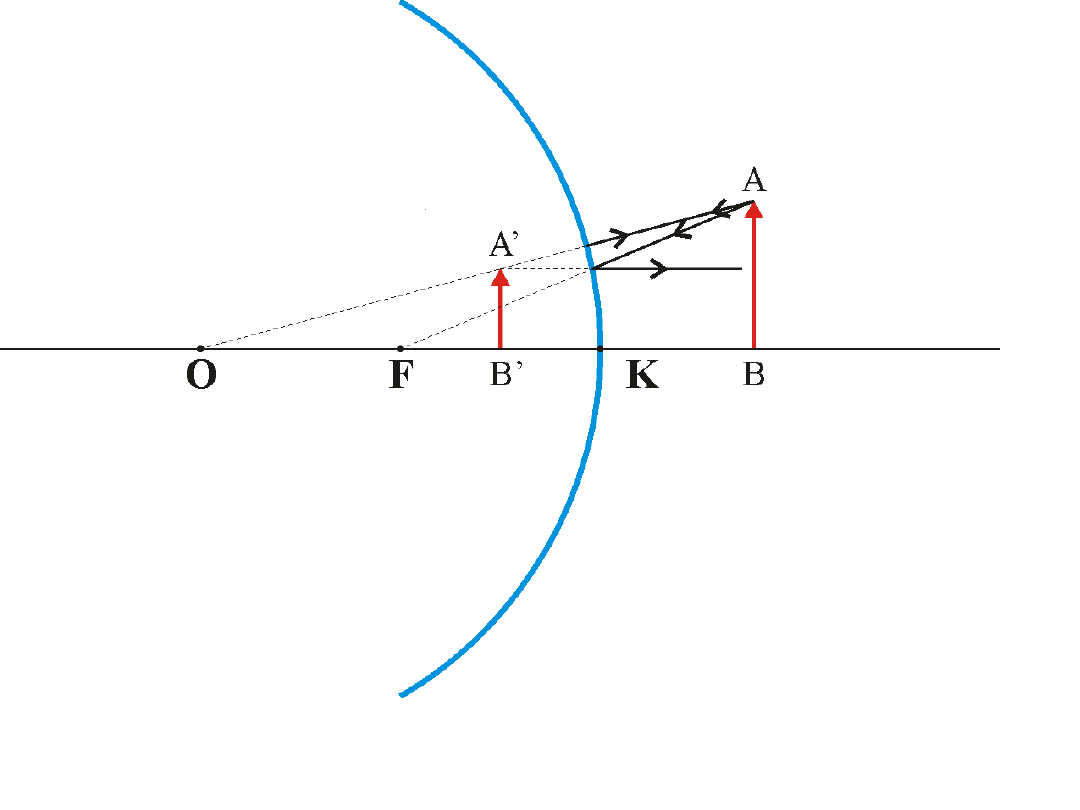
Powstaje obraz zmniejszony, pozorny, prosty.

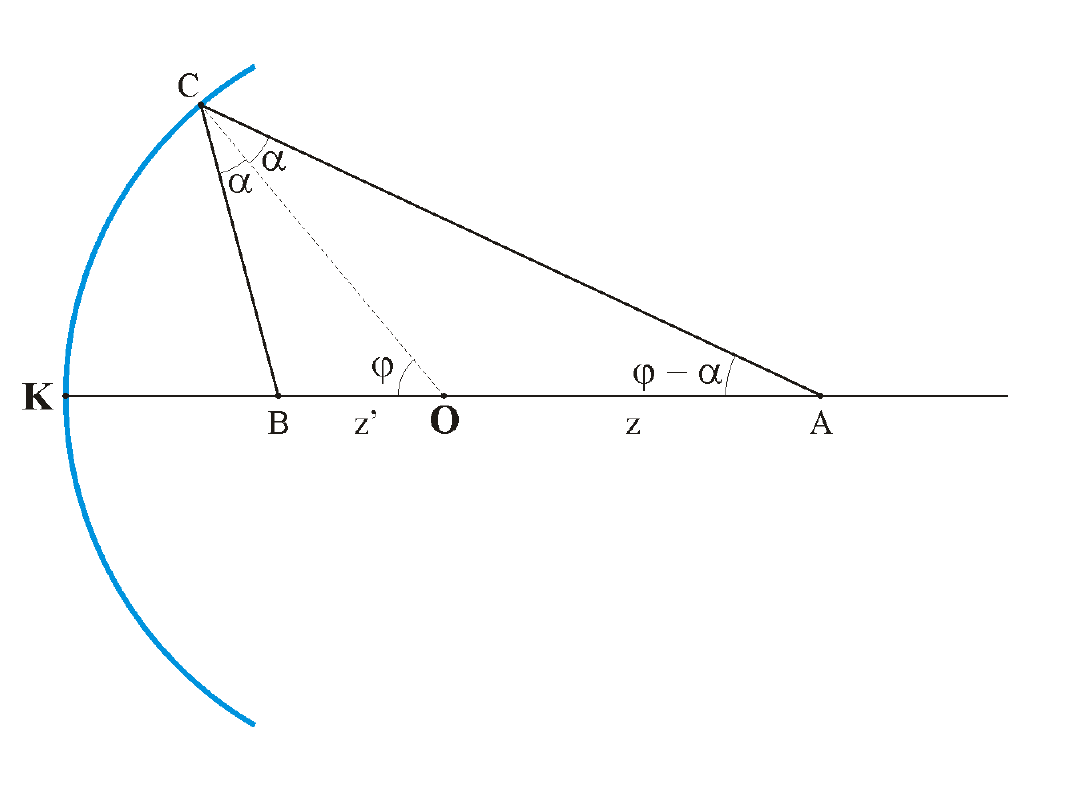
Aberracja sferyczna zwierciadeł

sin

' sin

AC

z

CBA

CB z

CAB

= =

R

R

Ale

180 (

)

CBA
CAB

a j

j

a

=

-

+

= -

R
R

Stąd

sin(

)

' sin(

)

AC

z

CB z

j

a

j

a

+

= =

-

Ponieważ odcinek z’ znajduje się w lewo od O liczymy ujemnie.

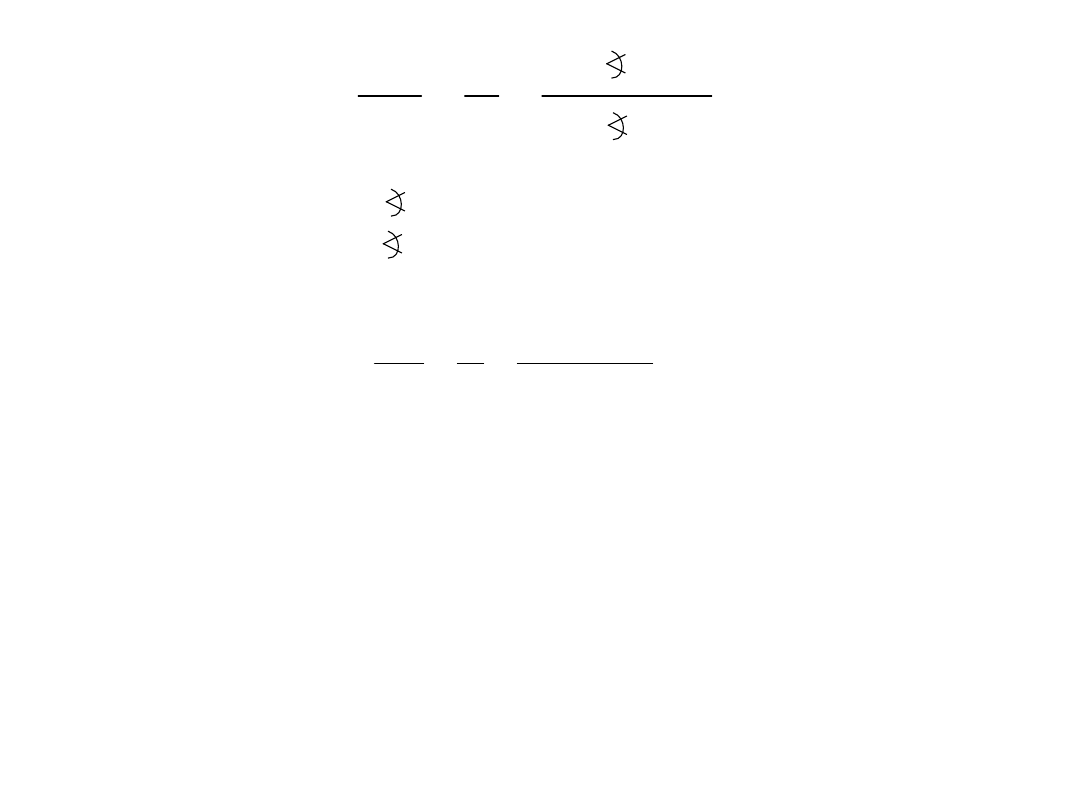
sin(

)

' sin(

)

sin(

)

'

sin(

)

sin(

)

1

1

'

sin(

)

' sin(

) sin(

)

'

sin(

)

z

z

z

z

z

z

z z

z

j

a

j

a

j

a

j

a

j

a

j

a

j

a

j

a

j

a

+

-

=

-

+

=-

-

+

+ = -

-

+

-

-

+

=

-

'

2cos sin

'

sin(

)

z z

z

j

a

j

a

+

-

=

-

Z AOC

sin

sin(

)

OA

z

OC

r

a

j

a

-

=

=

-

Zatem

' 2 cos

:

'

' 2cos

'

1 1 2cos

'

z z

z

z

z

r

z z

zz

r

z z

r

j

j

j

+

=

+

=

+ =

Jeśli

z� �

1 2cos

'

z

r

j

=

'

2cos

r

z

j

=

(*)

Gdy

0

j �

to

'

2

r

z �

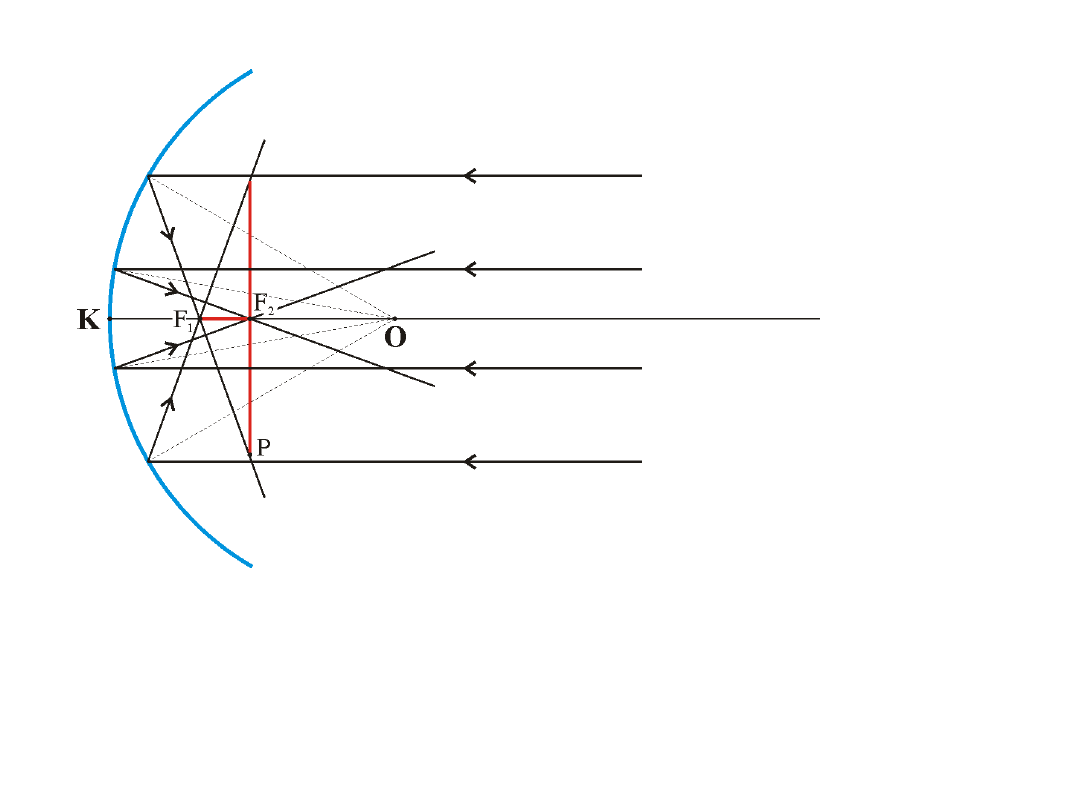
Ze wzoru (*) wynika, że im większe

 tym większa jest wartość z’. Promienie

biegnące dalej od osi zwierciadła przecinają się bliżej wierzchołka zwierciadła.

Promienie skrajne wiązki przecinają się w punkcie F

1

leżącym bliżej

wierzchołka zwierciadła.

Odległość F

1

F

2

nazywamy aberracją podłużną zwierciadła.

Na ekranie ustawionym w punkcie F

2

powstaje jasny krążek o promieniu F

2

P –

koło rozproszenia. F

2

P – aberracja poprzeczna.

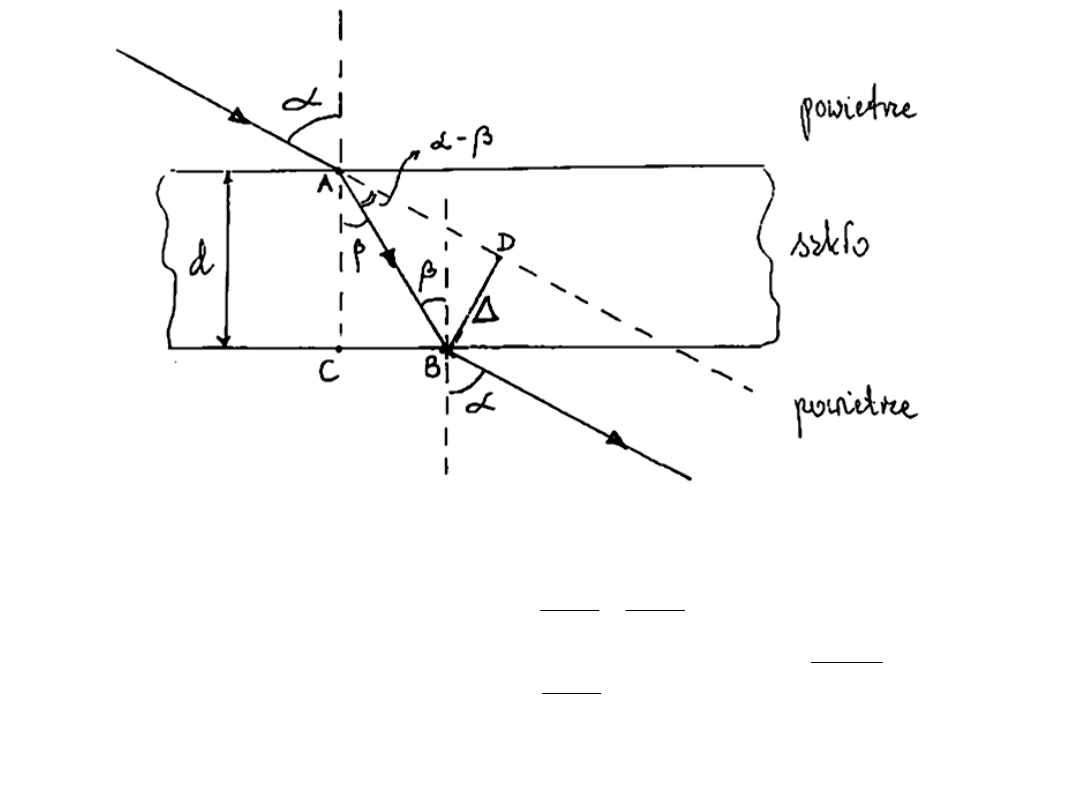
Kierunek promienia nie ulega zmianie przy przejściu przez płytkę. Następuje
przesunięcie promienia

BD =D

sin(

)

cos

cos

sin(

)

cos

BD AB

AC

d

AB

d

BD

a b

b

b

a b

b

=

-

=

=

=

-

sin(

)

cos

d

a b

b

D=

-

Wielkość przesunięcia jest wprost proporcjonalna do grubości płytki d oraz
zależy od wartości kąta padania promienia i współczynnika załamania.

Przejście promienia przez płytkę równoległościenna

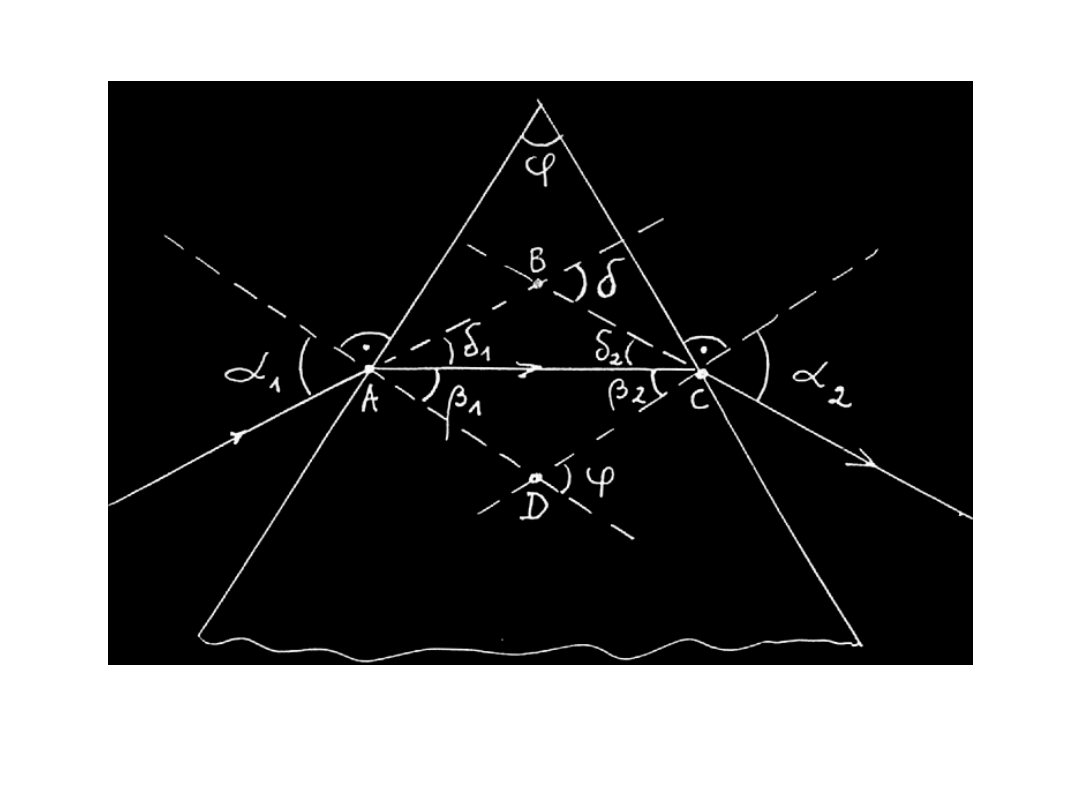
Przejście promienia przez pryzmat

gdzie:

 - kąt łamiący pryzmatu

 - kąt odchylenia

1

2

1

2

1

2

(

)

d d d

d a

a

b

b

= +

= + -

+

1

1

1

2

2

2

1

2

d a

b

d

a

b

j

b

b

= -

= -

= +

1

2

d a a

j

= + -

Minimum kata odchylenia otrzymujemy, gdy

1

2

a

a

=

oraz

1

2

2

j

b

b

b

= = =

min

2

d

a j

=

-

Stąd

min

2

d

j

a

+

=

sin

sin

n

a

b

=

min

2

sin

2

n

d

j

j

+

=

Jeśli

min

d

i

 jest małe, to

min

2

2

n

d

j

j

+

=

Stąd

min

min

(

1)

n

n

j

d

j

d

j

=

+

=

-

Dla pryzmatu o bardzo małym kącie łamiącym, małych katach padania,
odchylenie promienia nie zależy od kąta padania.

sin

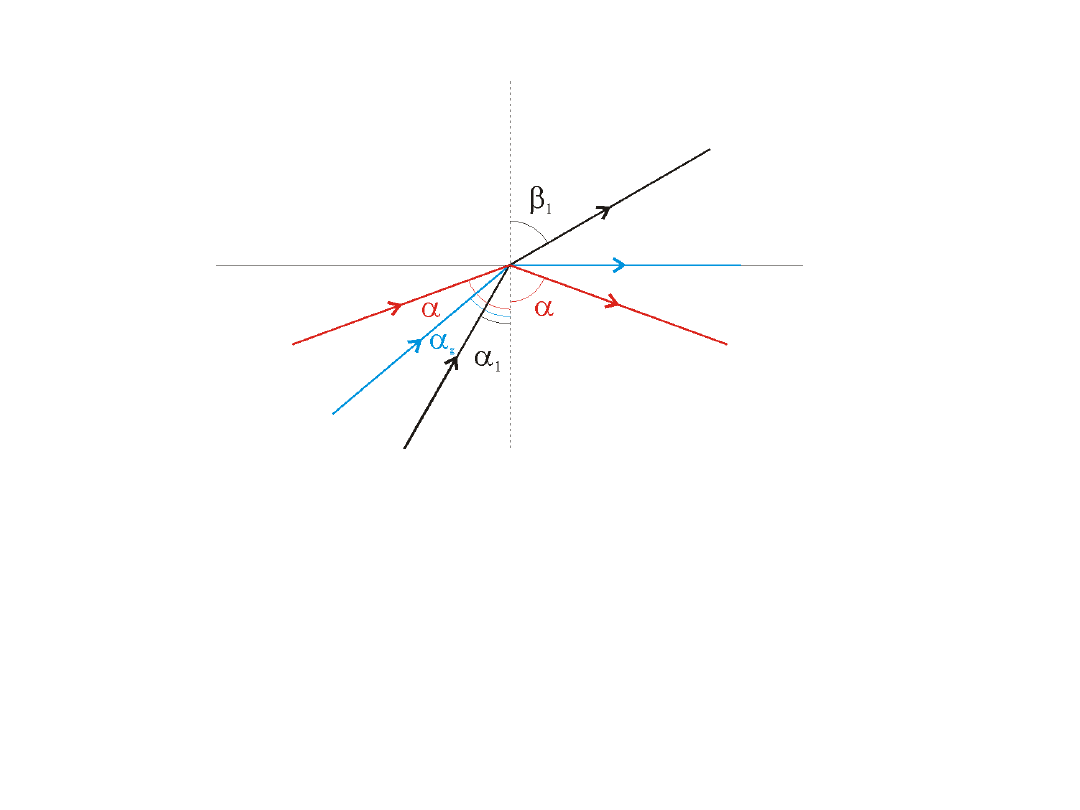
Zjawisko całkowitego wewnętrznego odbicia

Warunki:

•Światło przechodzi z ośrodka optycznie gęstszego do ośrodka optycznie rzadszego.

•Kąt padania większy od

g

a

zwanego kątem granicznym

.

g

a

jest to kąt padania, któremu w drugim ośrodku odpowiada kąt załamania 90

o

v

1

v

2

v

1

>

v

2

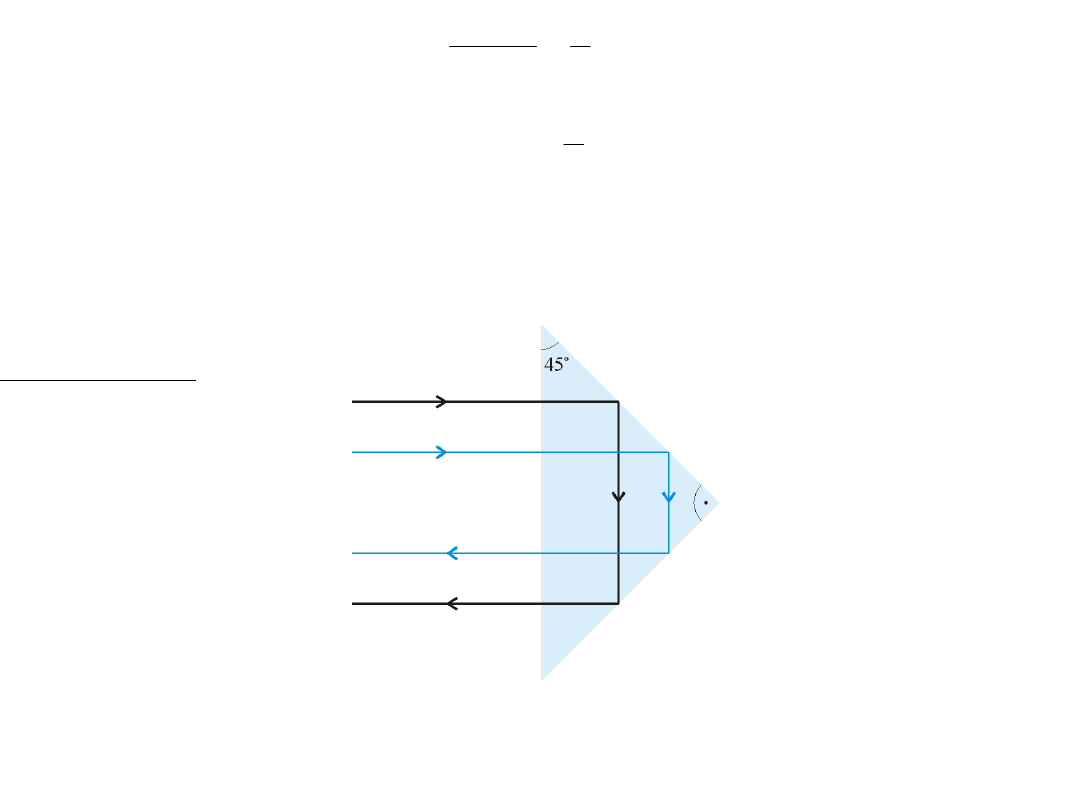
sin

1

sin90

1

sin

g

g

n

n

a

a

=

=

o

Dla szkła: n=1,5 to


g

=41

o

Dla diamentu: n=2,4 to 

g

=24

o

Zastosowanie:

Pryzmat Porro

Następuje odwrócenie wiązki, przy czym kierunek wiązki nie ulega
zmianie. Zastosowanie w lornetkach w celu otrzymania obrazu
prostego.

Dlatego odpowiednio oszlifowany diament,
czyli brylant błyszczy!

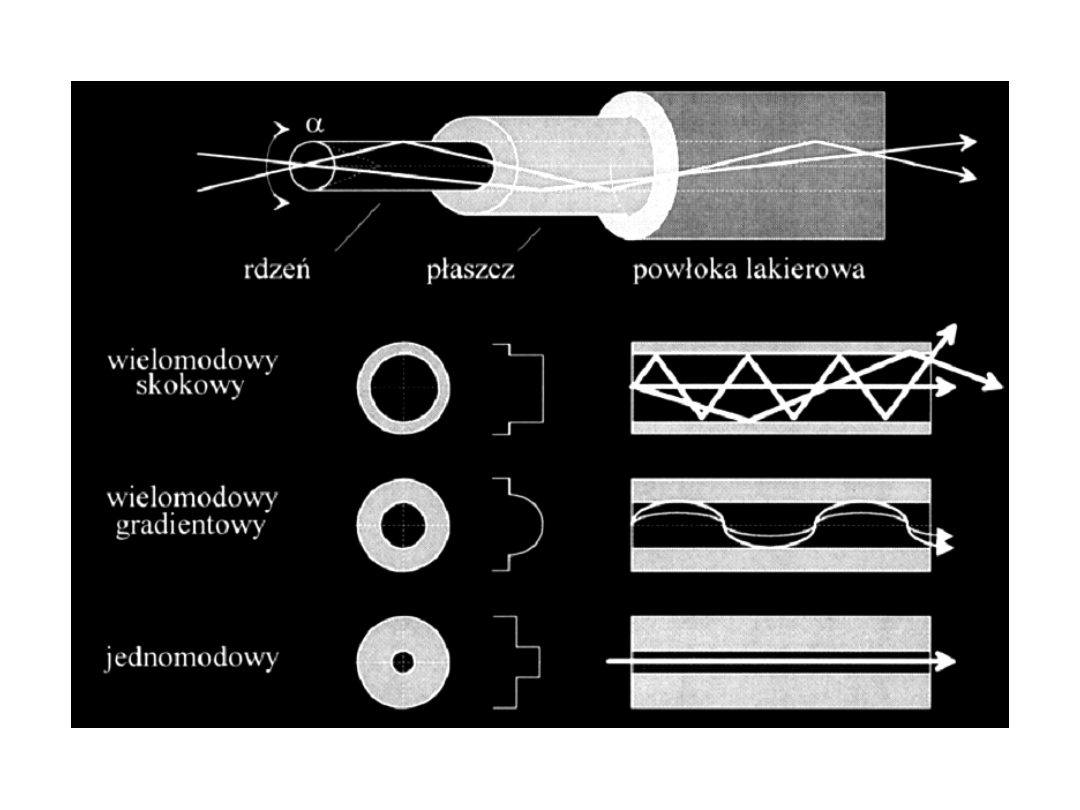
Światłowody

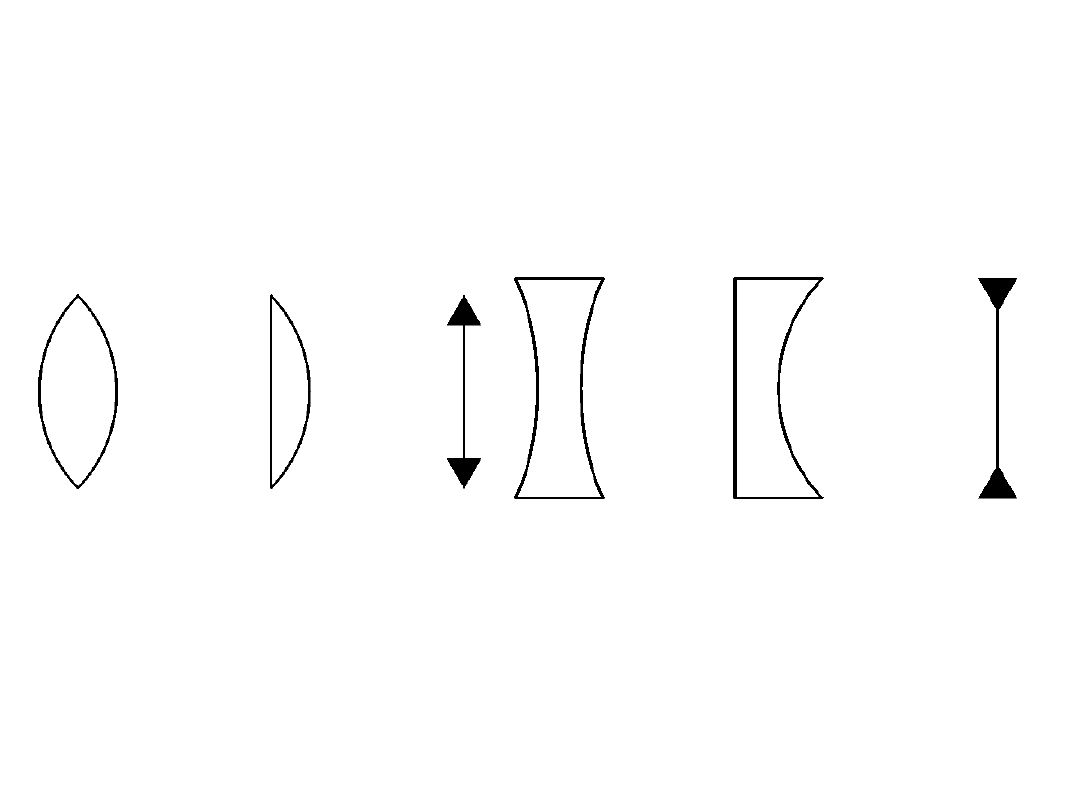
Soczewki

Soczewką nazywamy warstwę ośrodka ograniczoną powierzchniami
kulistymi (cylindrycznymi) lub jedną powierzchnią kulistą (cylindryczną)
i drugą płaską.

soczewki wypukłe

soczewki wklęsłe

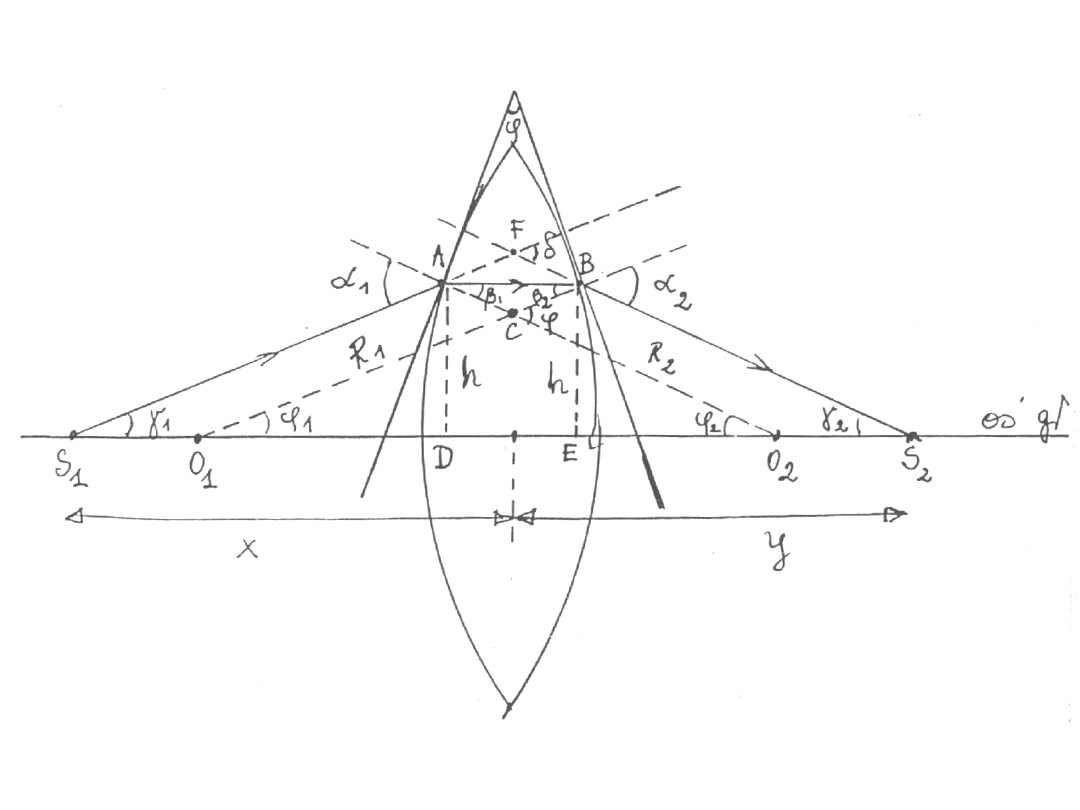
Założenia:

, 

1

,



2

–

małe

  kąt zewnętrzny w

1

2

SFS

V

1

2

d g g

= +

  kąt zewnętrzny w

1

2

OCO

V

1

2

j

j

j

= +

(

1)

n

d

j

= -

Mamy więc:

ponieważ



1

,



2

,



1

,



2

są małe, możemy zapisać:

1

1

1

1

1

1

tg

sin

AD

SD

BE

OB

g g

j

j

=

B

B B

2

2

2

2

2

2

tg

sin

BE

S E

AD

O A

g

g

j

j

=

B

B

B









=

=

1

2

1

2

(

1)(

)

n

g g

j

j

+ = +

+

-

1

2

1

1

2

2

;

;

;

;

AD BE h

SD x

S E y

OB R

O A R

=

=

B

B

B

B

1

2

(

1)

h h

h

h

n

x y

R

R

�

�

+ = -

+

�

�

�

�

:h

1

2

1 1

1

1

(

1)

n

x y

R

R

�

�

+ = -

+

�

�

�

�

równanie

soczewki cienkiej

Gdy

x� �

y

f

�

to

,

1

2

1

1

1

(

1)

n

f

R

R

�

�

= -

+

�

�

�

�









wzór soczewkowy

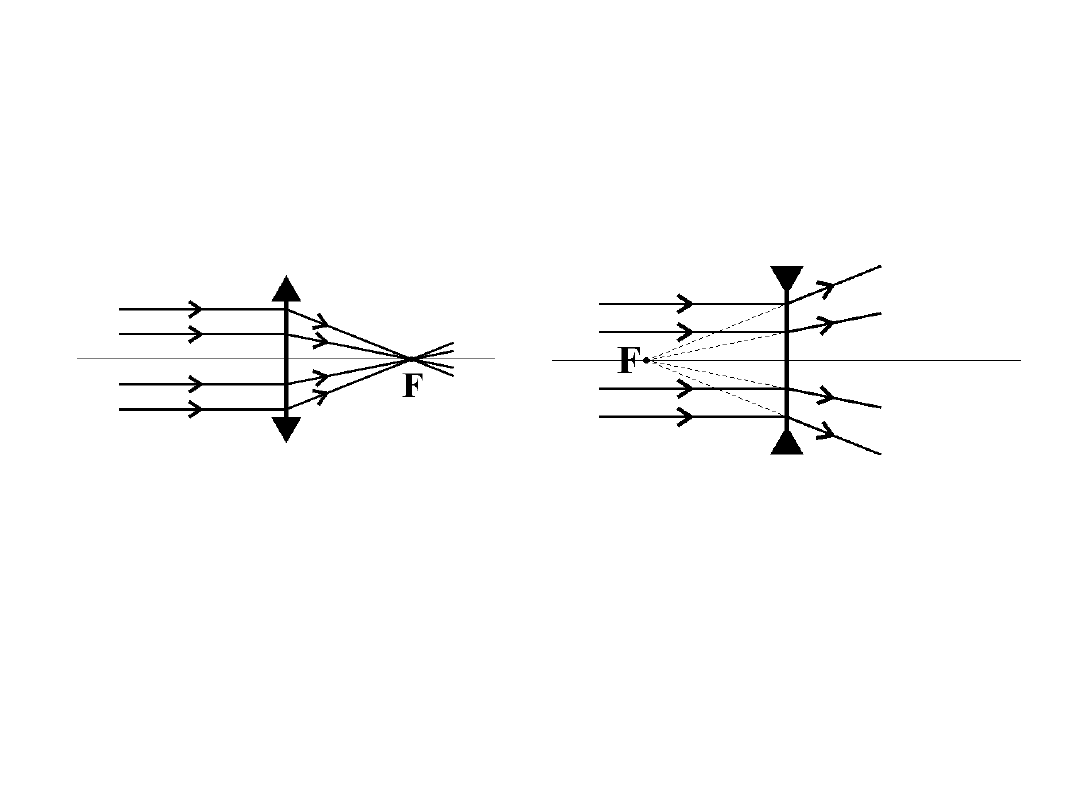
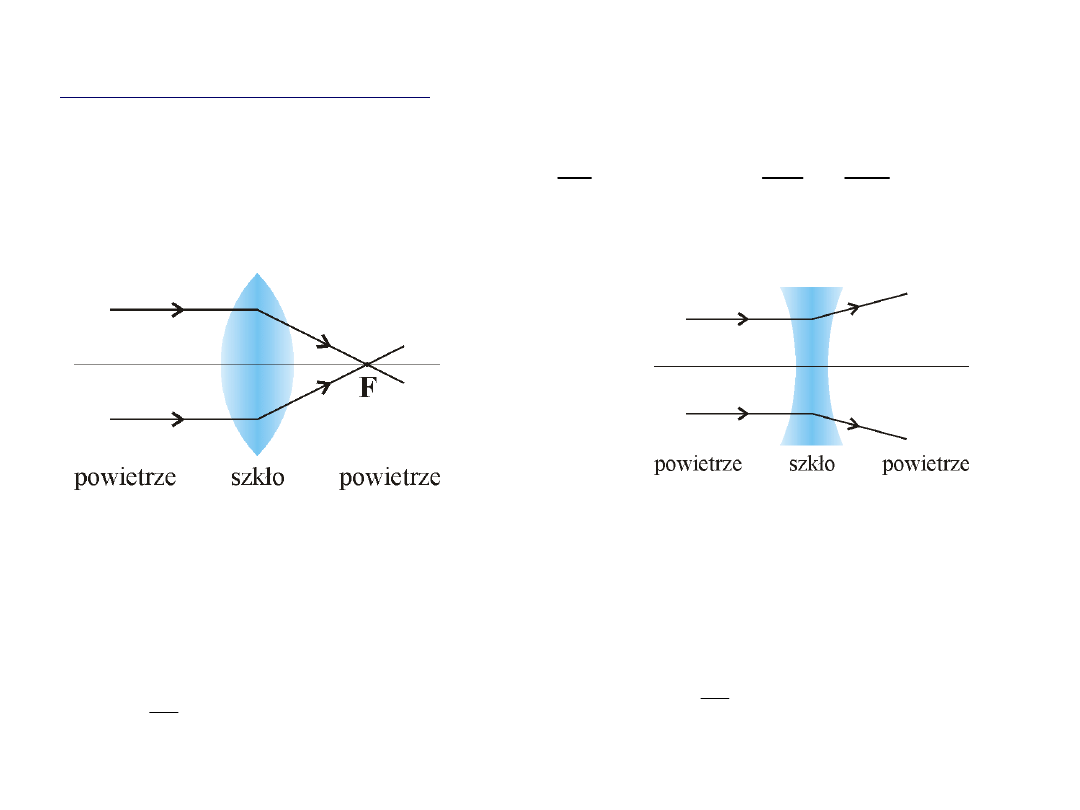
Soczewka wypukła

Soczewka wklęsła

f > 0

(soczewka skupiająca)

f < 0

(soczewka rozpraszająca)

Analiza równania soczewek

1

2

1

1

1

(

1)

n

f

R

R

�

�

= -

+

�

�

�

�

1

2

1

0;

0

1

0;

0

n

R

R

f

f

>

>

>

>

>

1

2

1

0;

0

1

0;

0

n

R

R

f

f

>

<

<

<

<

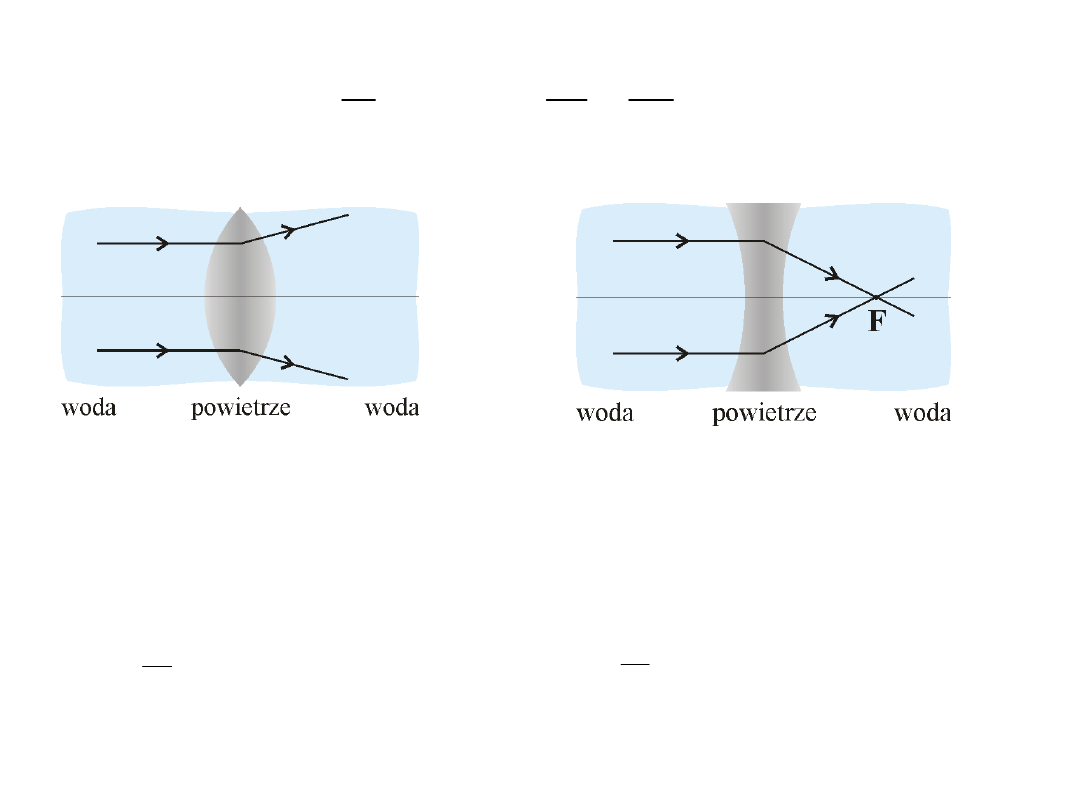
1

2

1

0;

0

1

0;

0

n

R

R

f

f

<

>

>

<

<

1

2

1

0;

0

1

0;

0

n

R

R

f

f

<

<

<

>

>

1

2

1

1

1

(

1)

n

f

R

R

�

�

= -

+

�

�

�

�

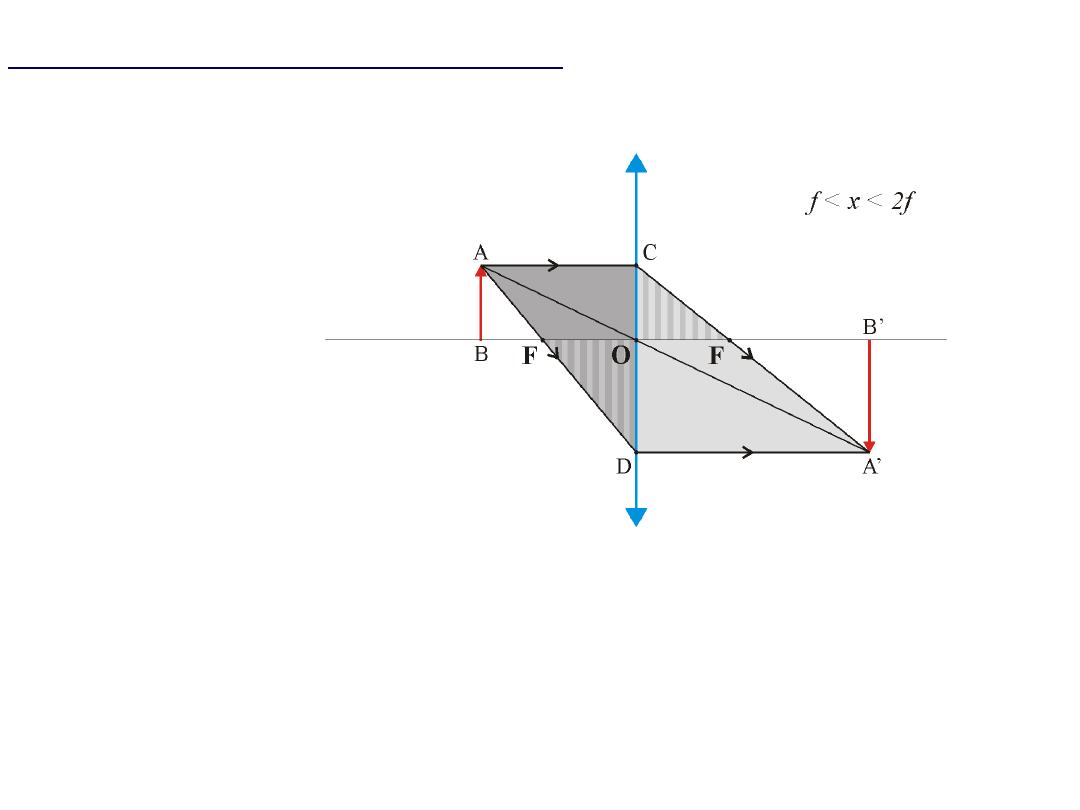
Obrazy uzyskiwane przy użyciu soczewki

Obraz rzeczywisty, powiększony, odwrócony

'

'

f OF

AC BO x
A D B O y

=

=

=

=

=

'

;

' '

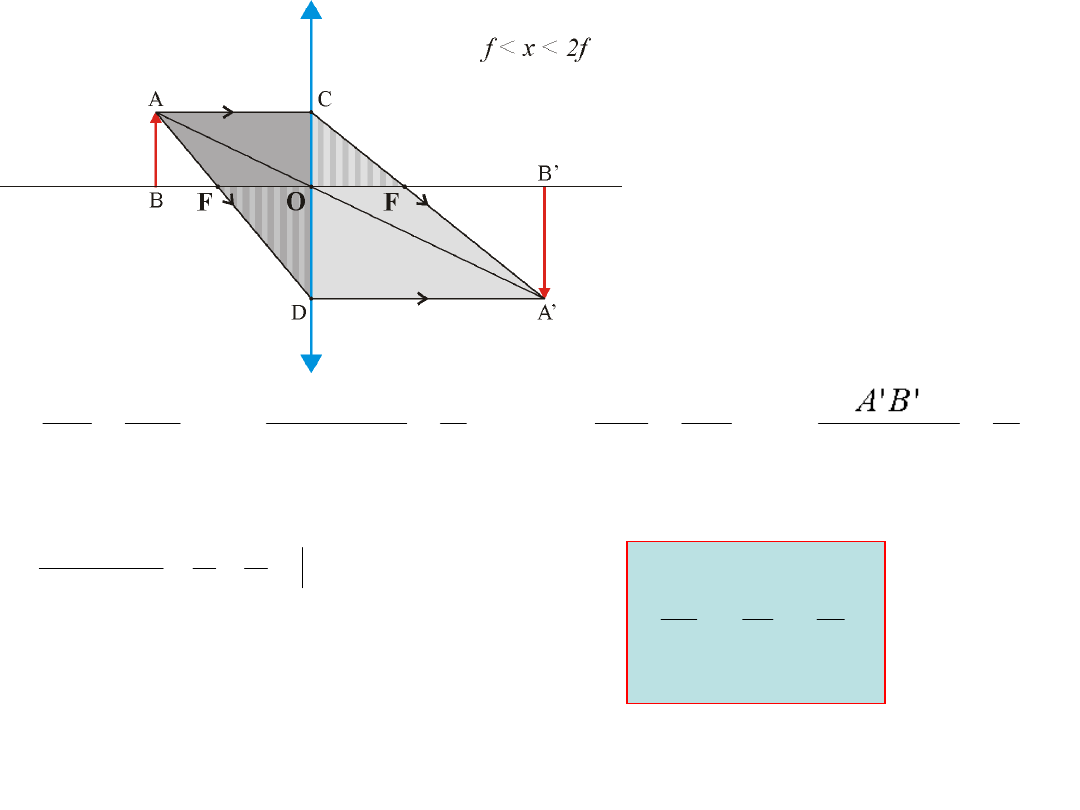
DO OF

AB

f

DC

AC

AB A B

x

=

=

+

' '
' '

AB A B

f

AB A B

y

x

+

= +

+

: f

1 1 1

f

y x

= +

wzór soczewkowy

;

'

' '

CO OF

AB

f

CD DA

AB A B

y

=

=

+

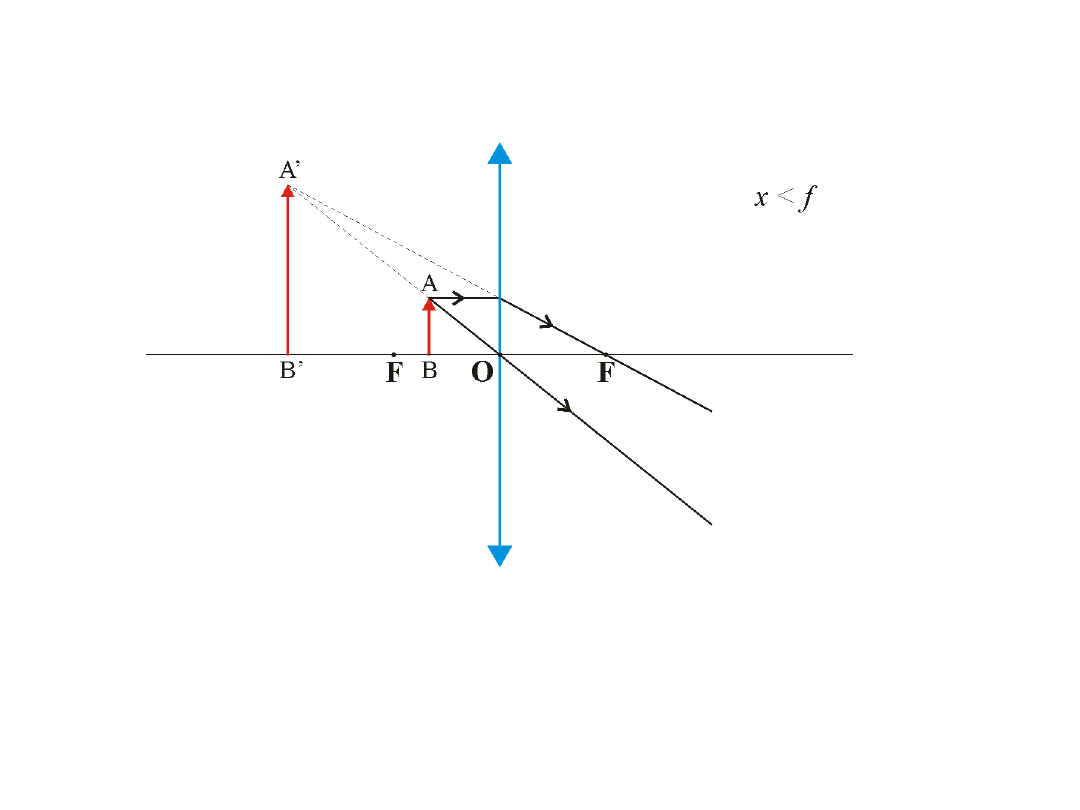
Obraz pozorny, powiększony, prosty

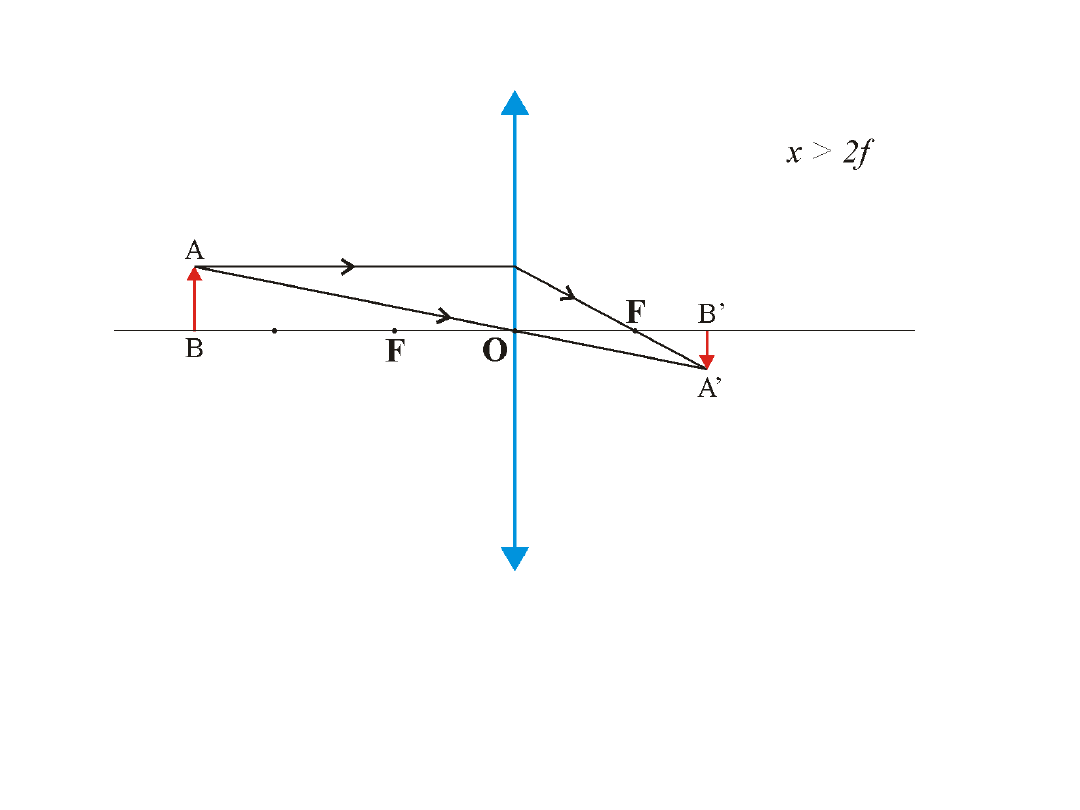
Obraz rzeczywisty, odwrócony,
zmniejszony

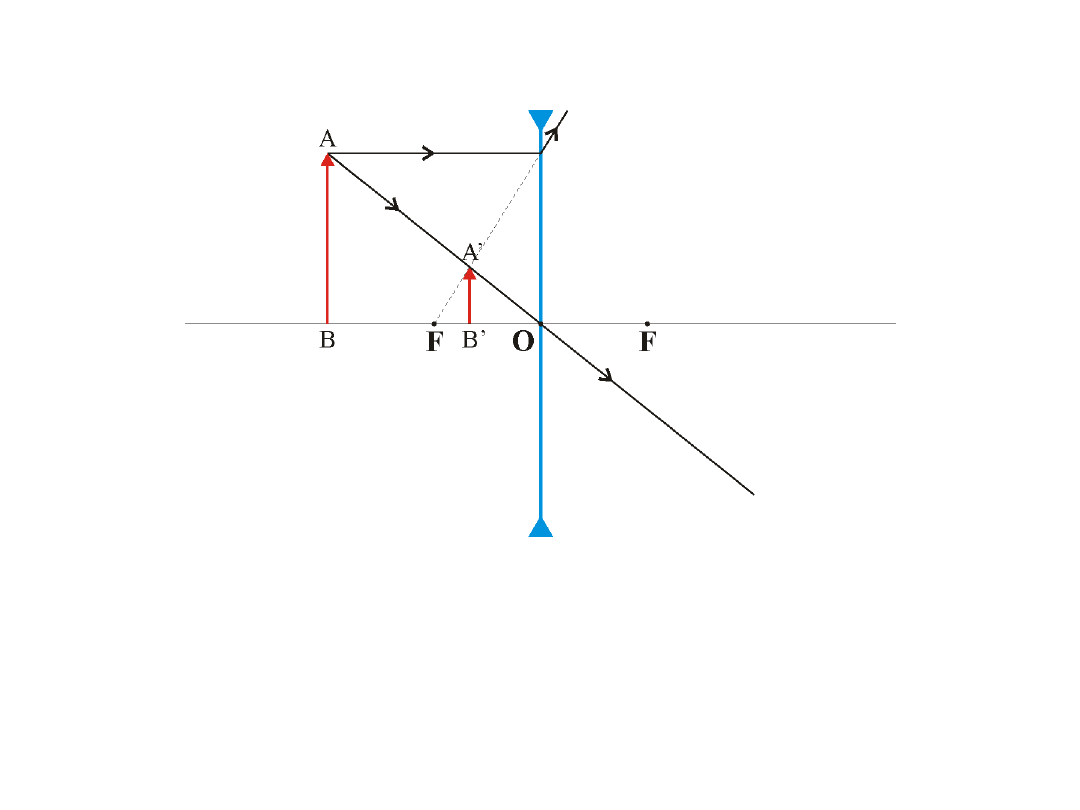
Soczewka rozpraszająca

Obraz pozorny, zmniejszony, prosty

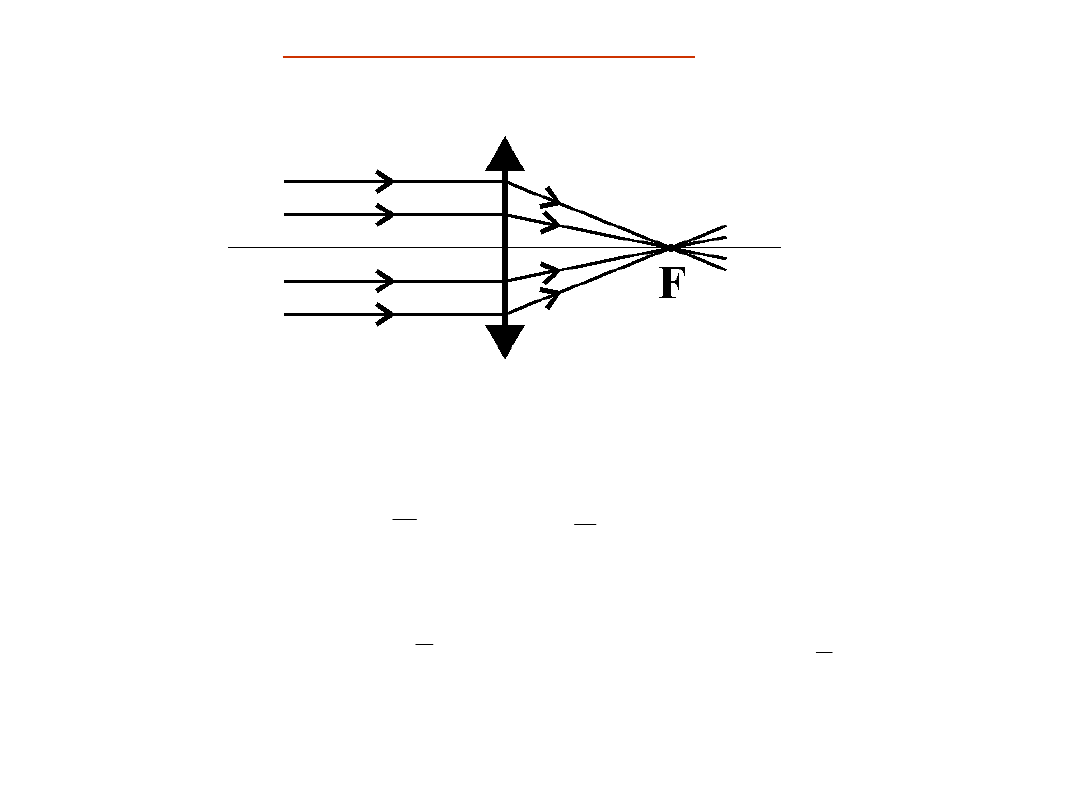
Zdolność skupiająca soczewek

D – zdolność skupiająca

1

D

f

=

1

[ ]

[1 dioptria]

D

m

� �

=

=

� �

� �

np.

1

50 cm

m

2

2 dioptrie

f

D

=

=

=

1

20 cm

m

5

5 dioptrii

f

D

=

=

=

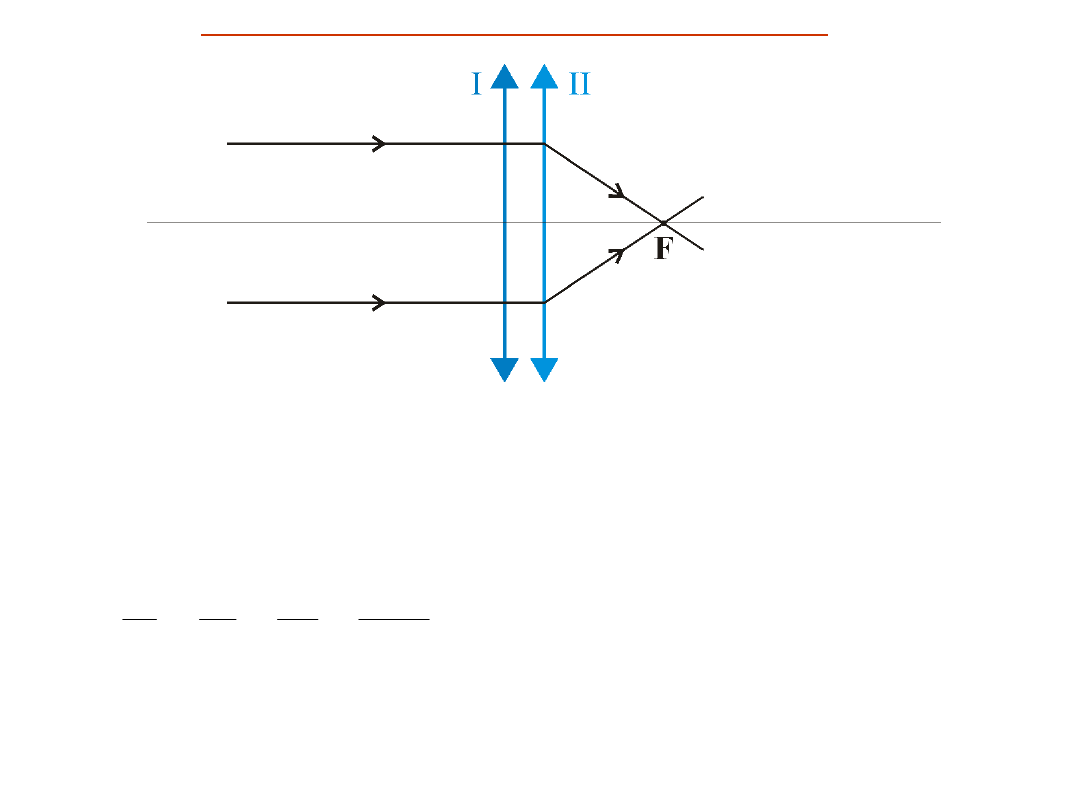
Układy soczewek. Zdolność zbierająca układu.

1

2

D D D

= +

Zdolność skupiająca układu soczewek = sumie zdolności

skupiających poszczególnych soczewek.

1

2

1 2

1

1

1

d

f

f

f

= + -

d – odległość między

soczewkami

Soczewki rozpraszające mają ujemną ogniskową (f
< 0)
oraz ujemna zdolność skupiającą (np. D = -5
dioptrii).

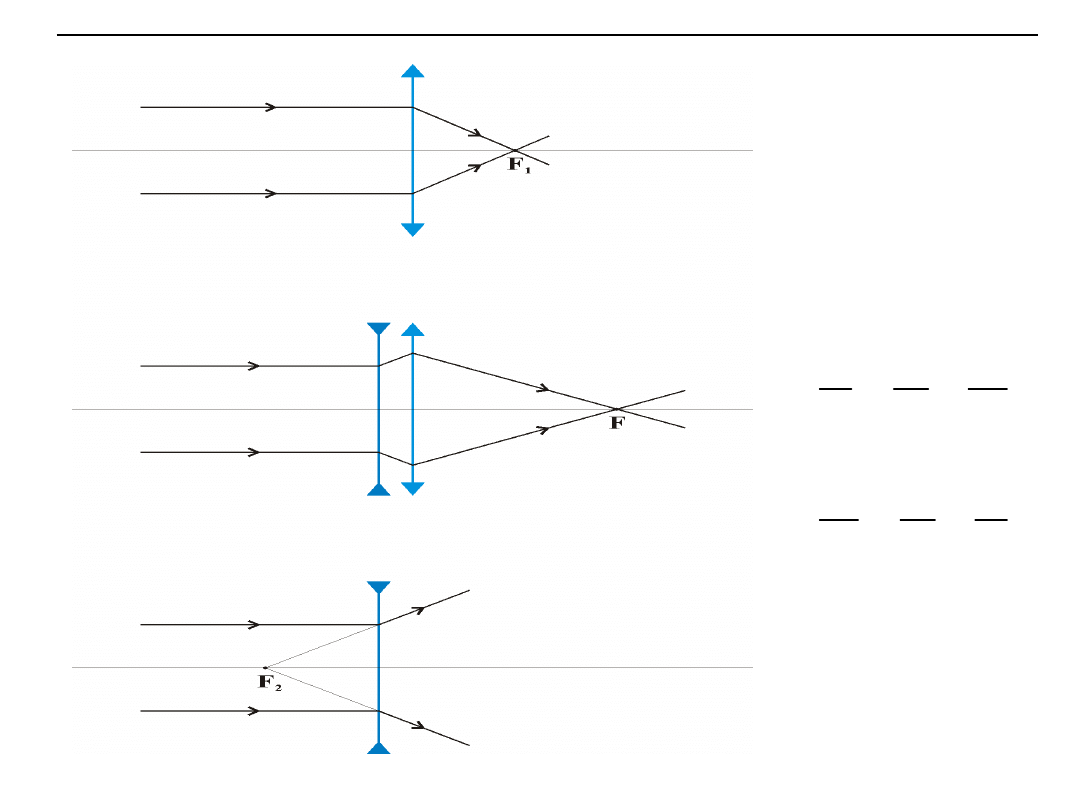
Wyznaczanie zdolności skupiającej (ogniskowej) soczewki rozpraszającej

1

2

2

1

1

1

1

1

1

1

f

f

f

f

= -

= -

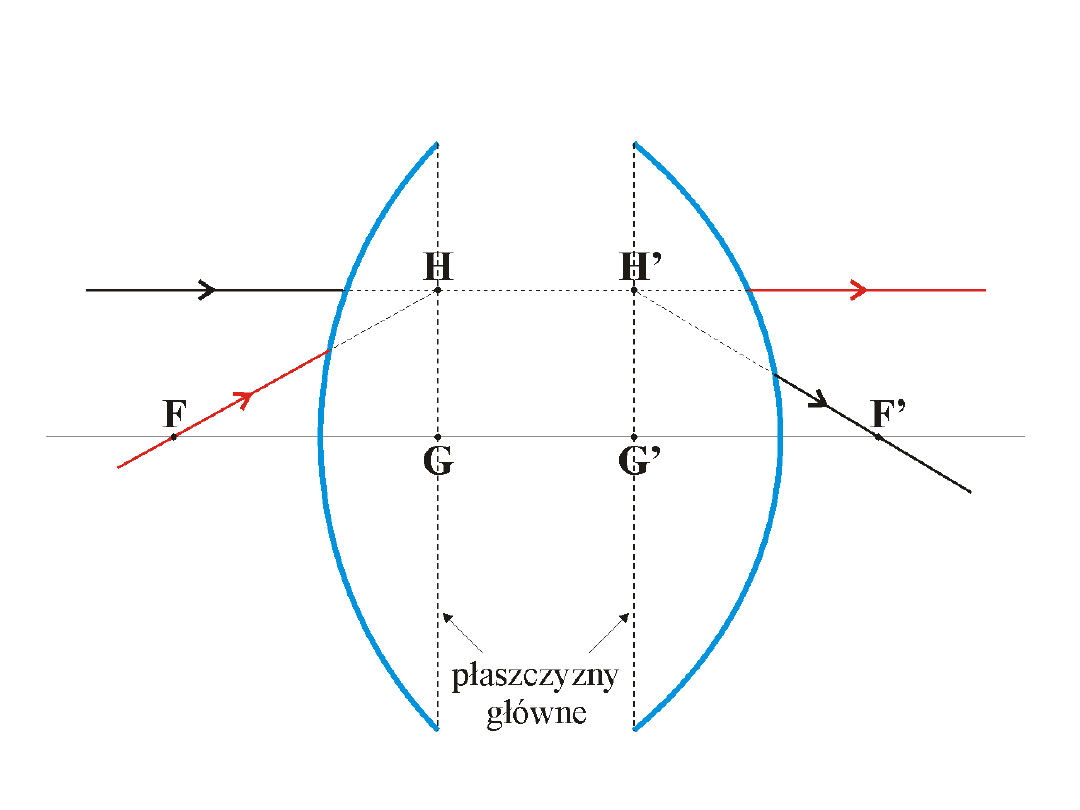
Soczewki grube

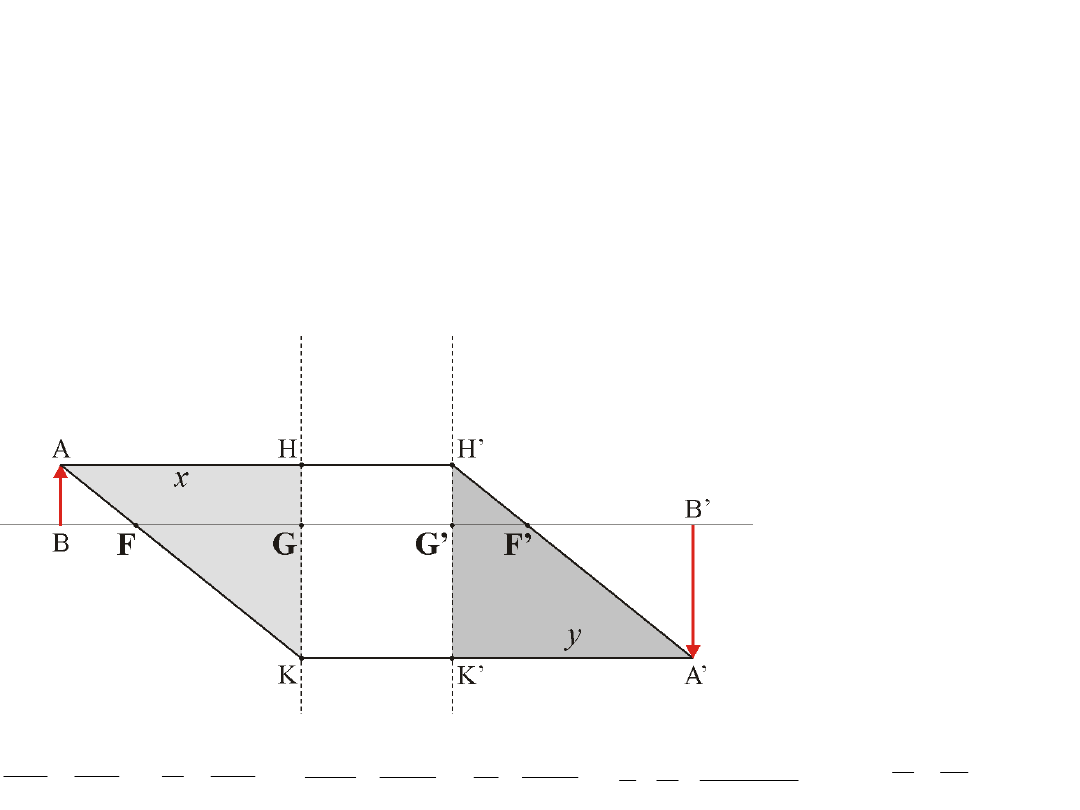
G,G’

punkty główne

f FG

=

- pierwsza ogniskowa

'

' '

f

F G

=

- druga ogniskowa

Konstrukcja obrazu

' ' '

' ' '

KGF

KHA

H G F

K H A

V

: V

V

: V

' '

' '

' '

GH G H
GK G K

KH K H

=

=

=

;

FG

KG

f

KG

AH KH

x KH

=

=

' '

' '

'

' '

;

' '

' '

' '

F G

H G

f

H G

A K

K H

y

K H

=

=

'

' '

1

f

KG H G

x

y

KH

+

+

=

=

'

1

f

x

y

+

=

Przyrządy optyczne

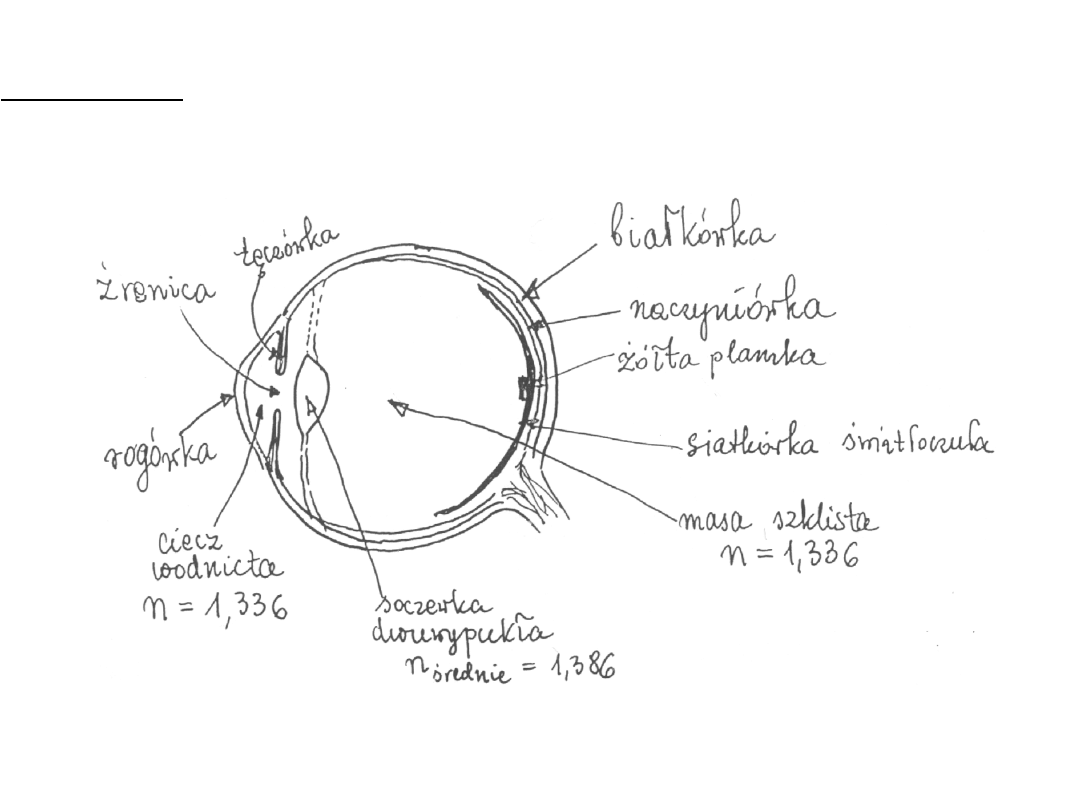
1.Oko ludzkie

Promień krzywizny przedniej powierzchni soczewki wynosi ok. 10 mm,

a tylnej powierzchni ok. 6 mm.

Obrazy powstające na siatkówce są rzeczywiste, zmniejszone, odwrócone.

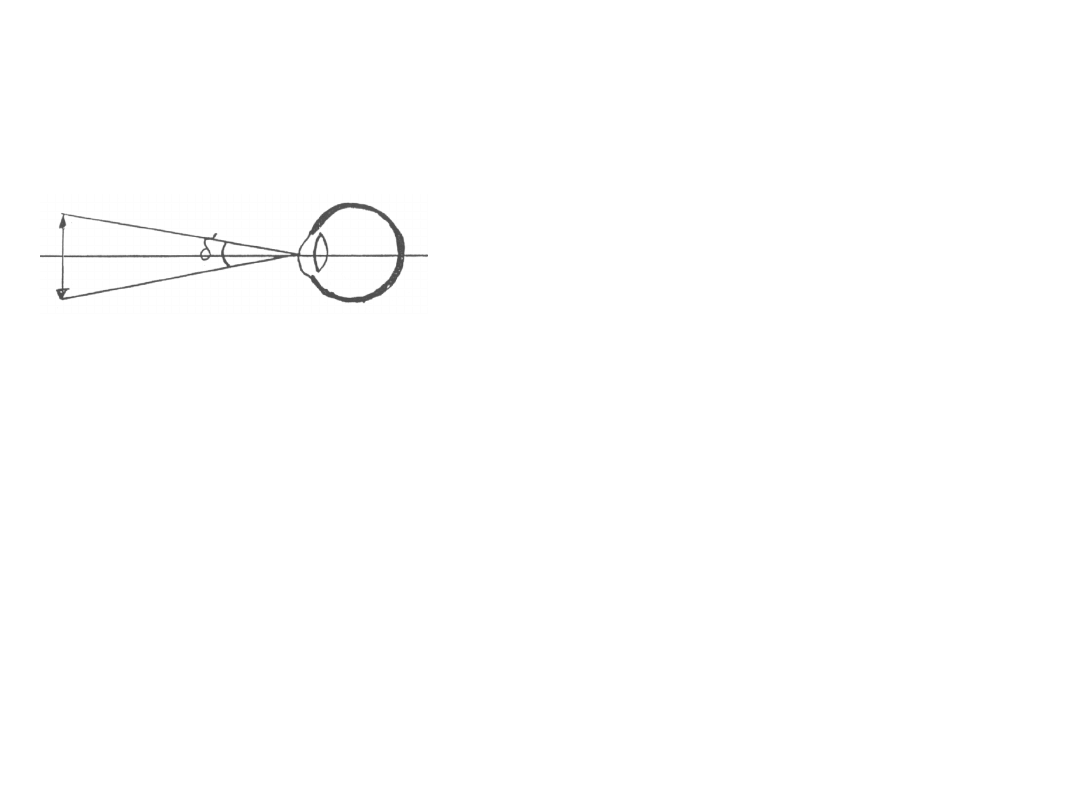
 – kąt widzenia

Najmniejszy kąt widzenia, pod jakim rozróżniamy jeszcze dwa punkty wynosi ok. 1’.

Najmniejsza energia, na którą reaguje oko wypoczęte wynosi ok. 10

-17

J.

Akomodacja polega na zmianie kształtu soczewki oka.
Zakres akomodacji: od

�

do 10 cm.

Odległość dobrego widzenia – 25 cm.

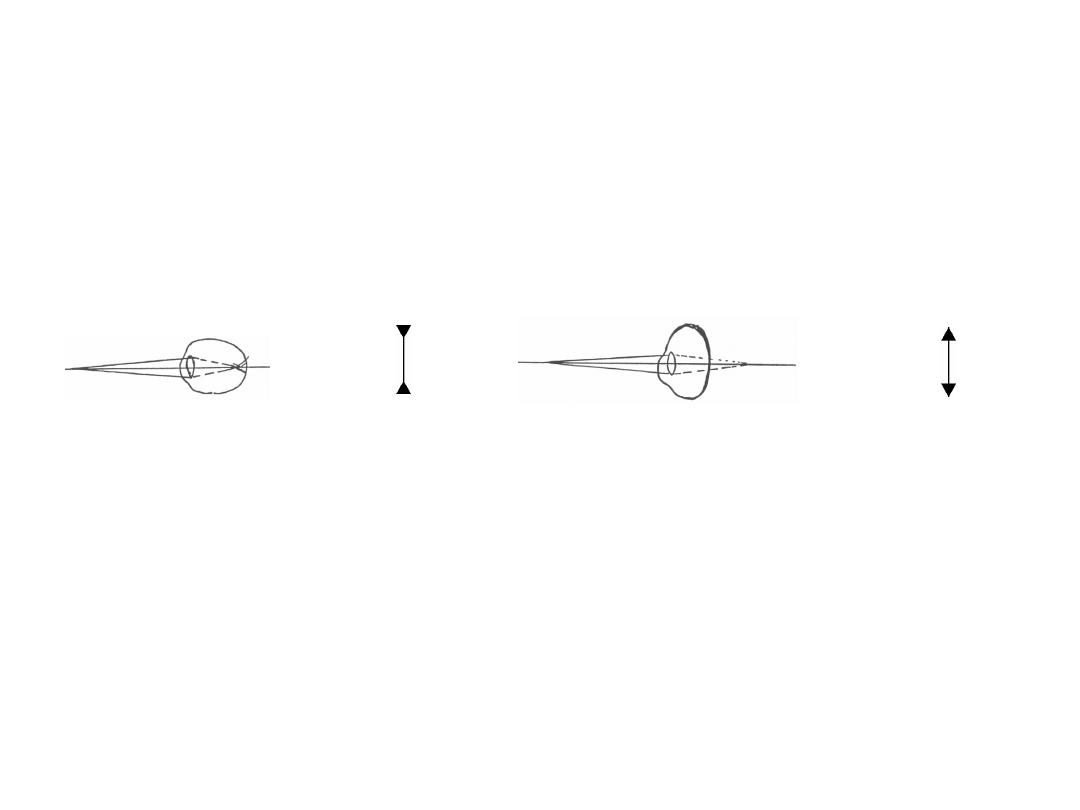
Oko krótkowzroczne

korekcja

korekcja

Wady wzroku:

Oko dalekowzroczne

okulary, lub szkła kontaktowe
„plusy”, a więc o D>0

okulary, lub szkła kontaktowe
„minusy”, a więc o D<0

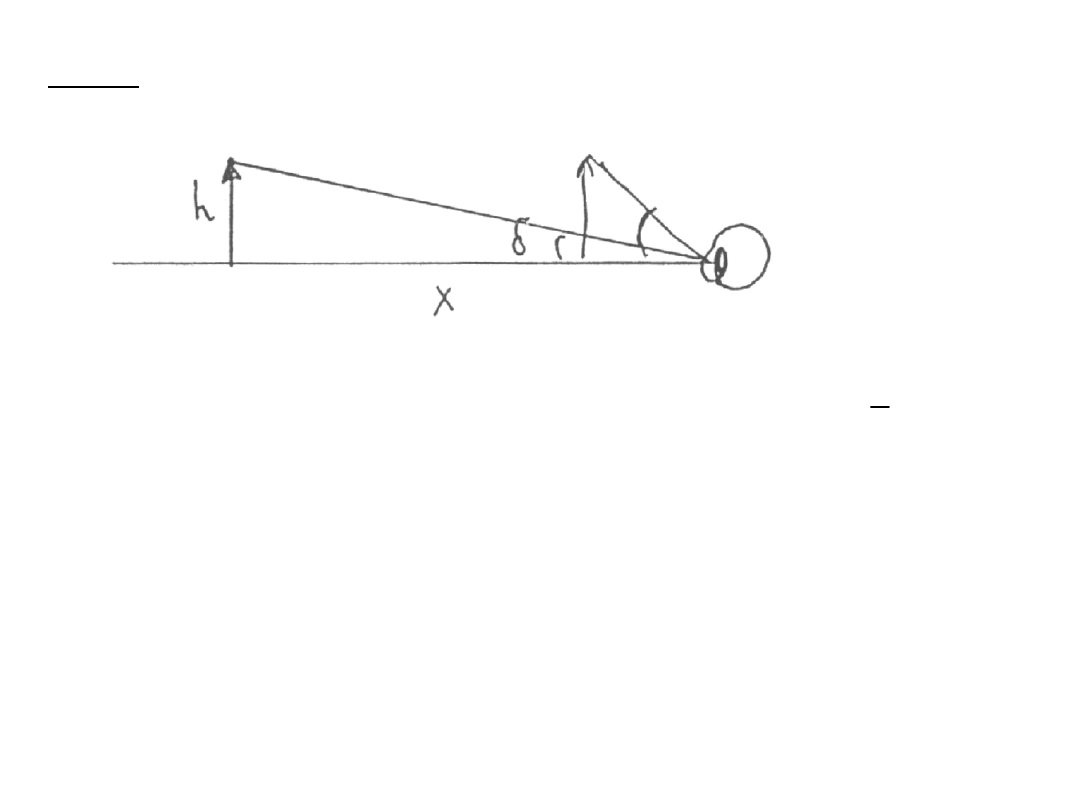
2.Lupa

tg

h

x

d =

Powiększeniem kątowym lupy nazywamy
stosunek kąta, pod jakim widzimy dany
przedmiot przez lupę, do kata, pod jakim
widzimy go gołym okiem.

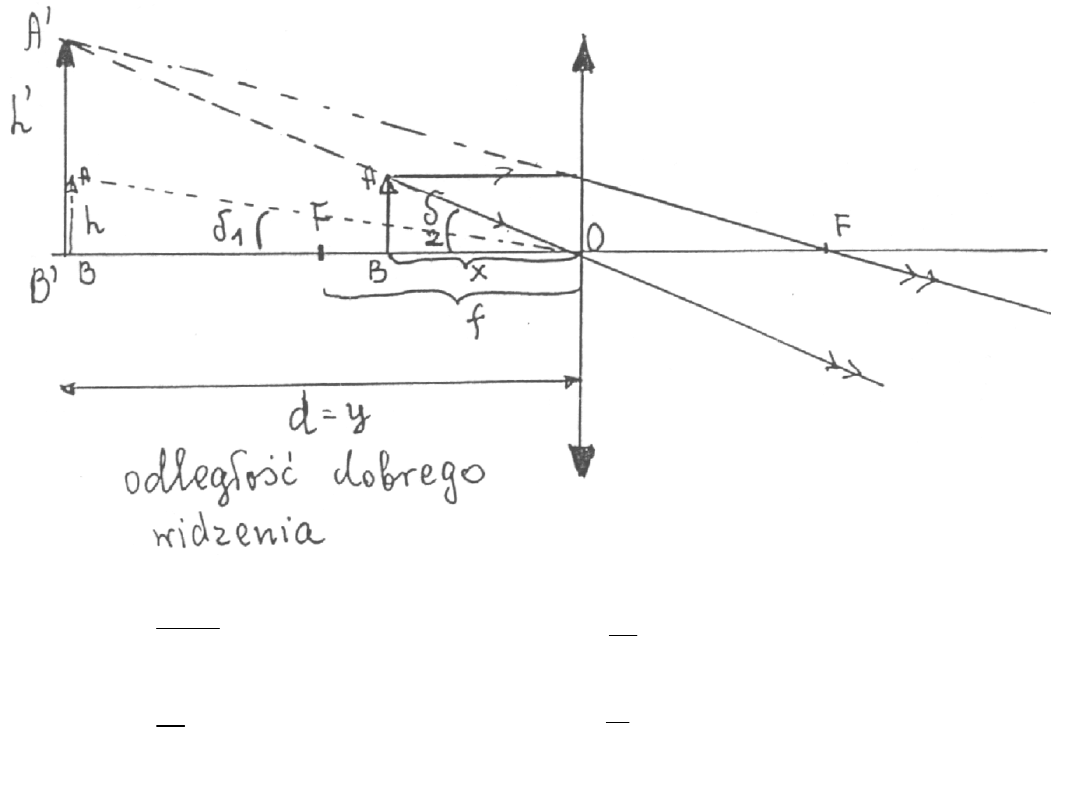
2

1

tg

tg

'

p

h

p

h

d

d

=

=

2

1

'

tg

tg

h

d

h

d

d

d

=

=

' '

A B O

ABO

V

: V

'

h

d

h

x

d

p

x

=

=

1 1 1 1 1

x y x d

f

fd

x

f d

-

= -

=

=

+

1

f

p

d

= +

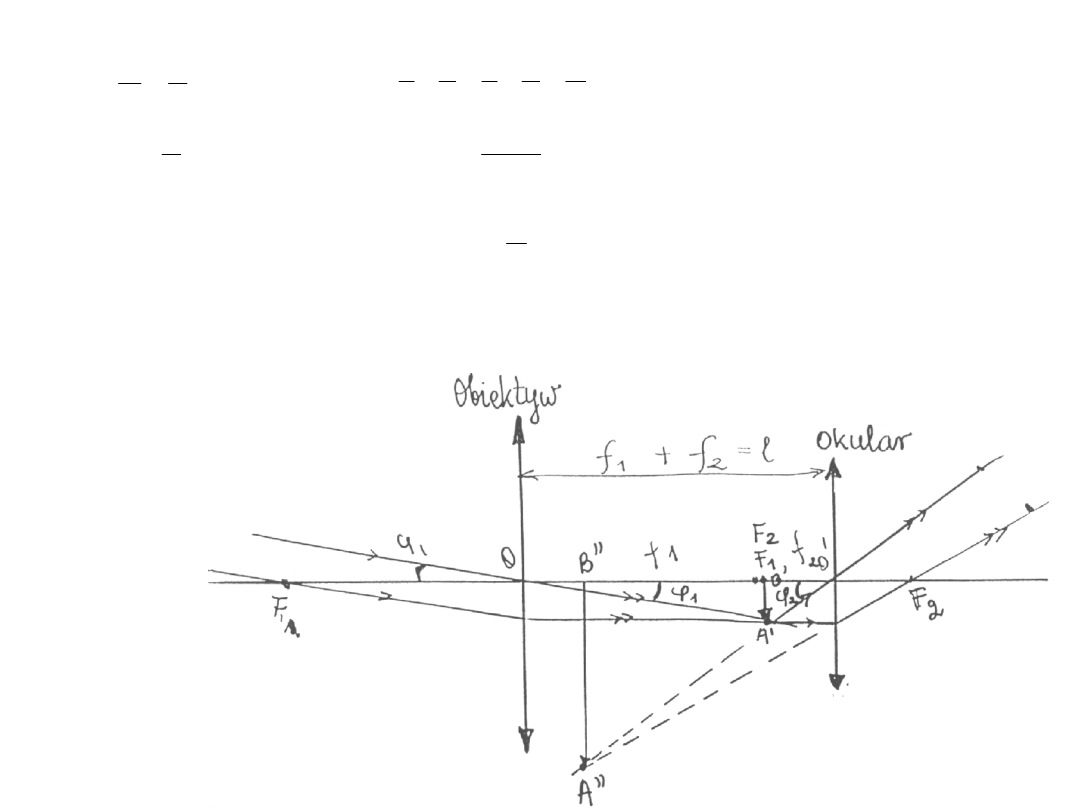
3.Luneta astronomiczna

gdzie:

f

1

– ogniskowa obiektywu

f

2

– ogniskowa okularu

1

1

' '

tg

A B

f

j =

2

2

' '

tg

A B

f

j =

2

2

1

1

' '

tg

tg

A B

f

p

AB

f

j

j

=

=

1

2

f

p

f

=

A”B” – obraz pozorny, odwrócony

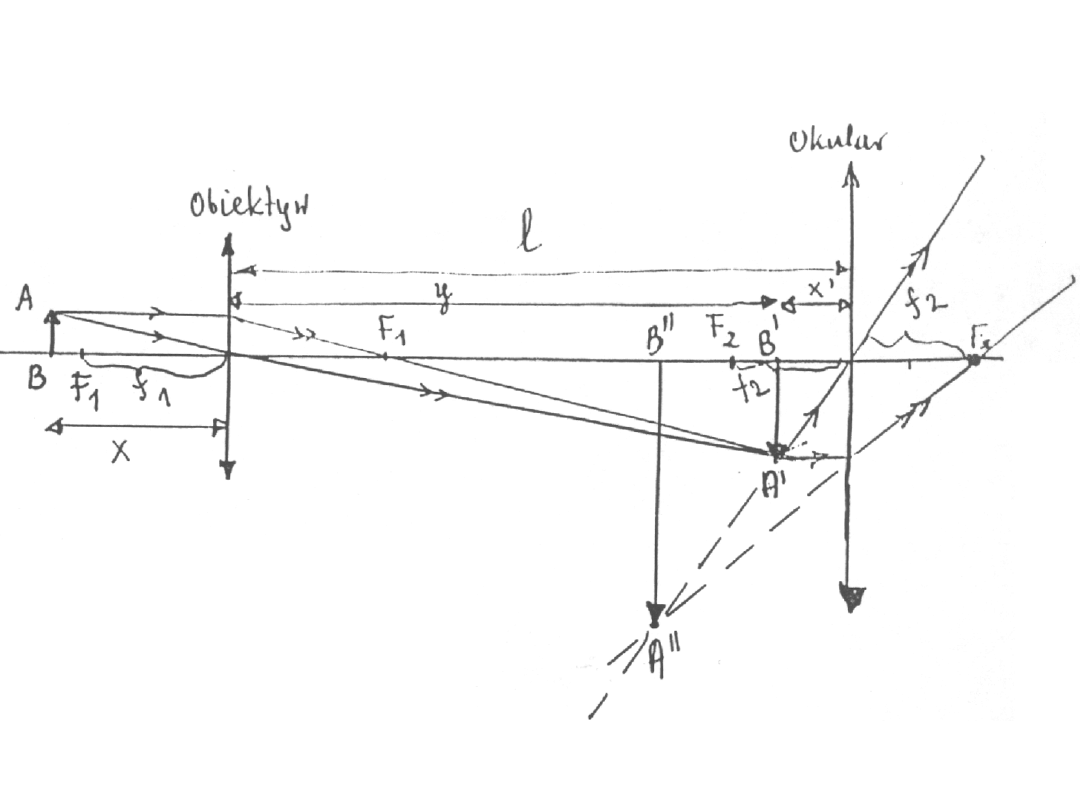
4.Mikroskop

gdzie:

f

1

– ogniskowa obiektywu

f

2

– ogniskowa okularu

d –

odległość

dobrego

widzenia

l

–

długość

mikroskopu

(tubusa)

2

;

;

1

ob

ok

ob

ok

y

d

p p p

p

p

x

f

=

�

=

= +

2

2

1

y d

yd

p

x f

xf

�

�

=

+ �

�

�

�

�

Ponieważ f

2

jest małe, a x’ <

f

2

, to

l y

�

.

Przedmiot ustawiany jest tuż za ogniskiem F

2

, zatem

2

x f

�

.

W przybliżeniu powiększenie uzyskane za pomoc mikroskopu wynosi:

1 2

ld

p

f

=

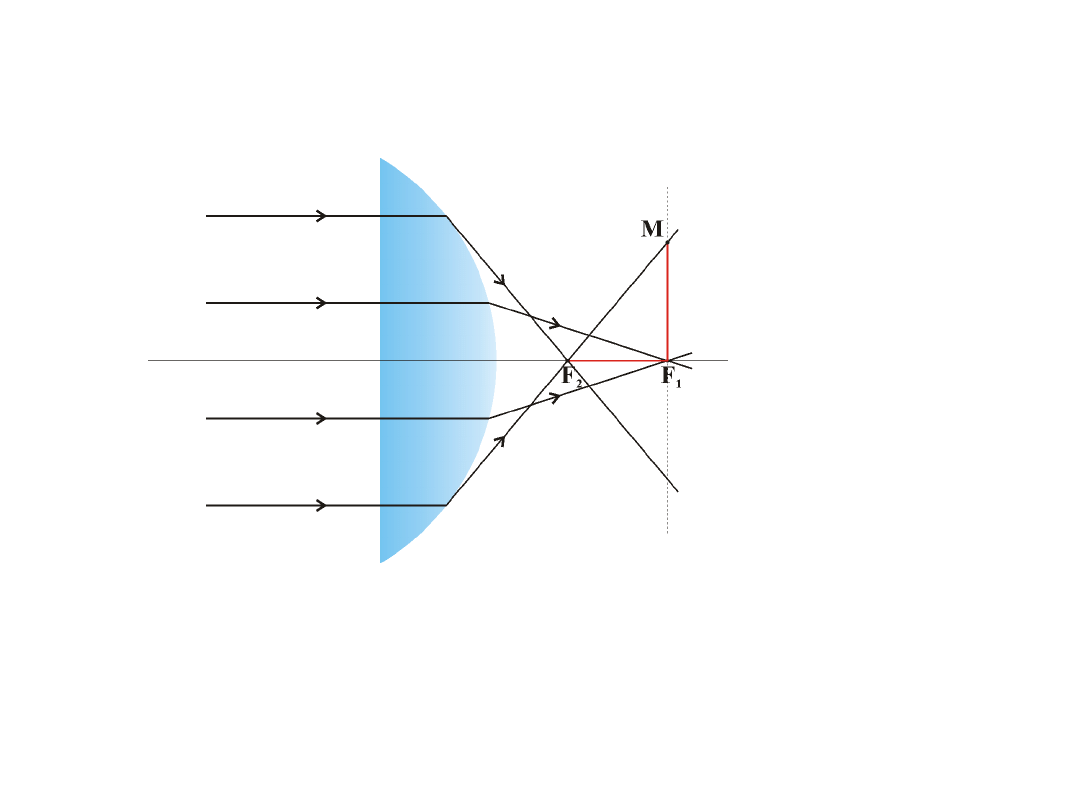
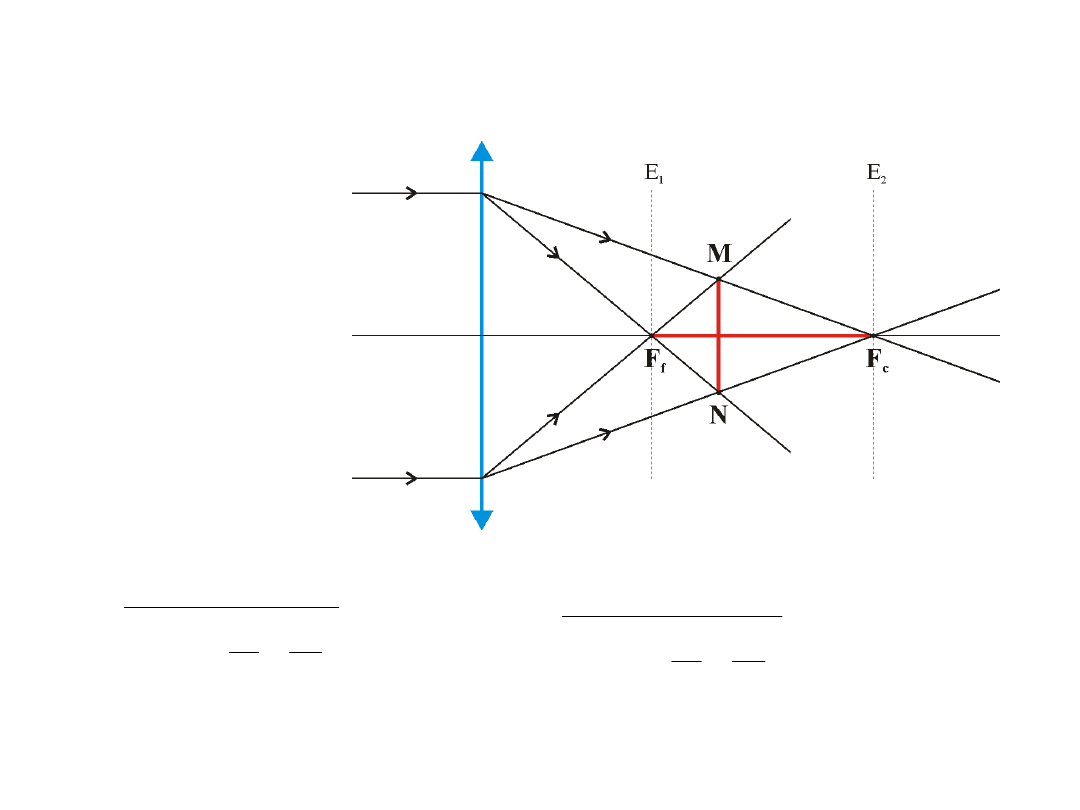
Aberracja sferyczna

gdzie:

F

1

F

2

–

aberracja

podłużna

soczewki

F

1

M –

aberracja

poprzeczna

soczewki

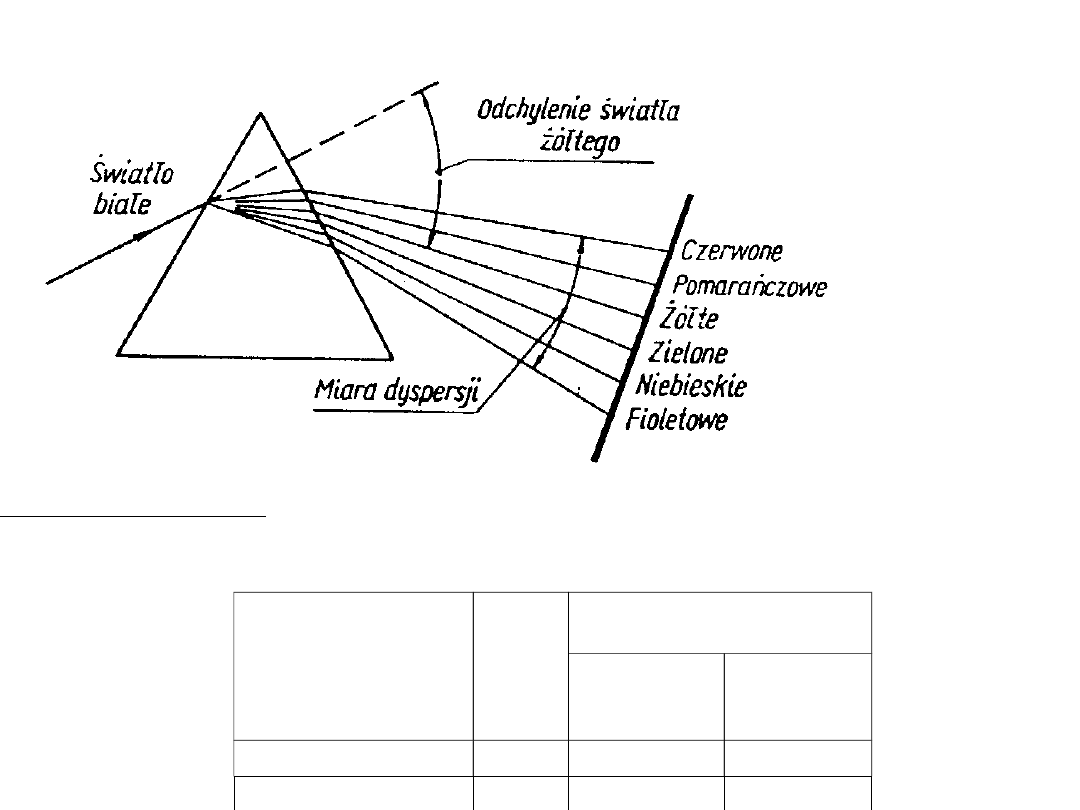
Zjawisko dyspersji światła

Dyspersja normalna

Rodzaj

promieniowania

Długoś

ć

fali 

Współczynnik załamania

(n)

szkło

kronowe

szkło

flintowe

F fioletowe

486,1

1,52225

1,71748

D żółte

589,6

1,51666

1,70100

C czerwone

656,3

1,51418

1,69427

Dyspersja
średnia:

F

C

n

n

-

Dyspersja względna:

1

F

C

D

n

n

n

-

D=

-

Szkło kronowe

1

0,02

50

D=

=

(mała dyspersja)

Szkło flintowe

1

0,03

30

D=

=

(wysoka dyspersja)

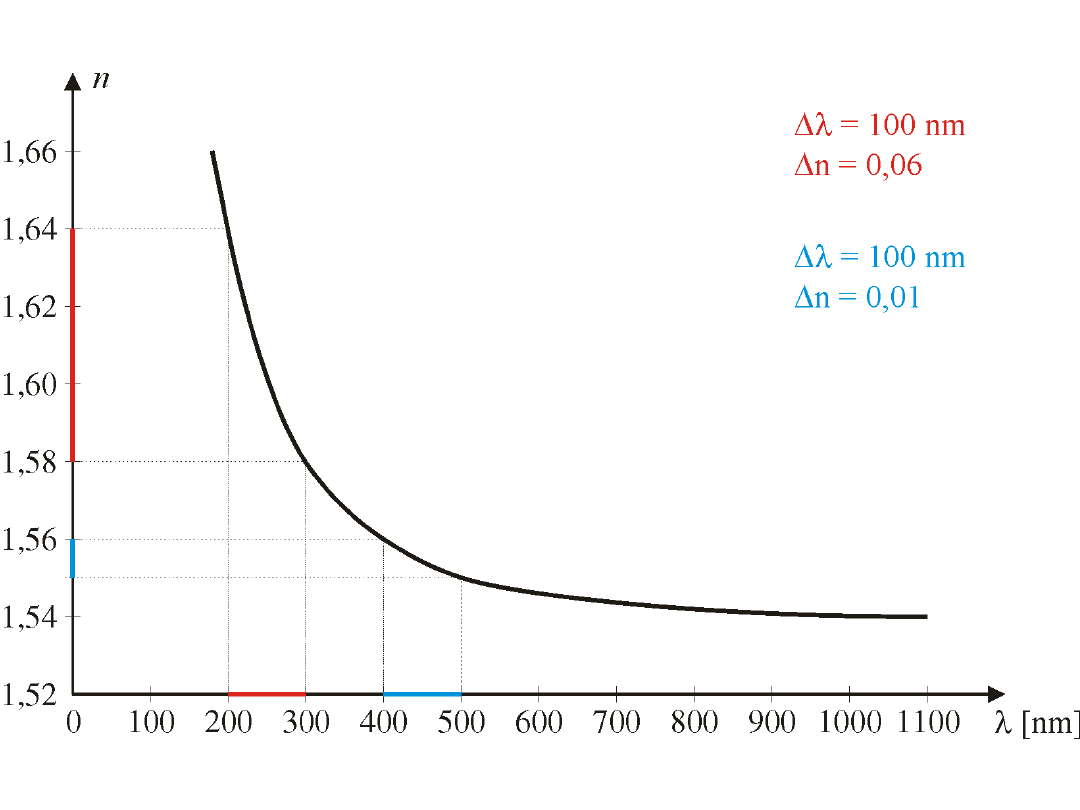
Wykres zależności współczynnika załamania kwarcu od długości

Zależność współczynnika n od długości fali

 opisuje równanie Cauchy’ego.

2

4

...

B

C

n A

l

l

= +

+

+

gdzie:
A,B,C – stałe charakterystyczne dla danej substancji

Skrócone równanie Cauchy’ego:

2

B

n A

l

= +

Różniczkując to równanie

 względem otrzymujemy:

3

2

dn

B

dl

l

=-

Dyspersja jest odwrotnie proporcjonalna do trzeciej potęgi

. Np. przy długości fali

400

l =

nm dyspersja jest około 8 razy większa niż przy długości fali

800

l =

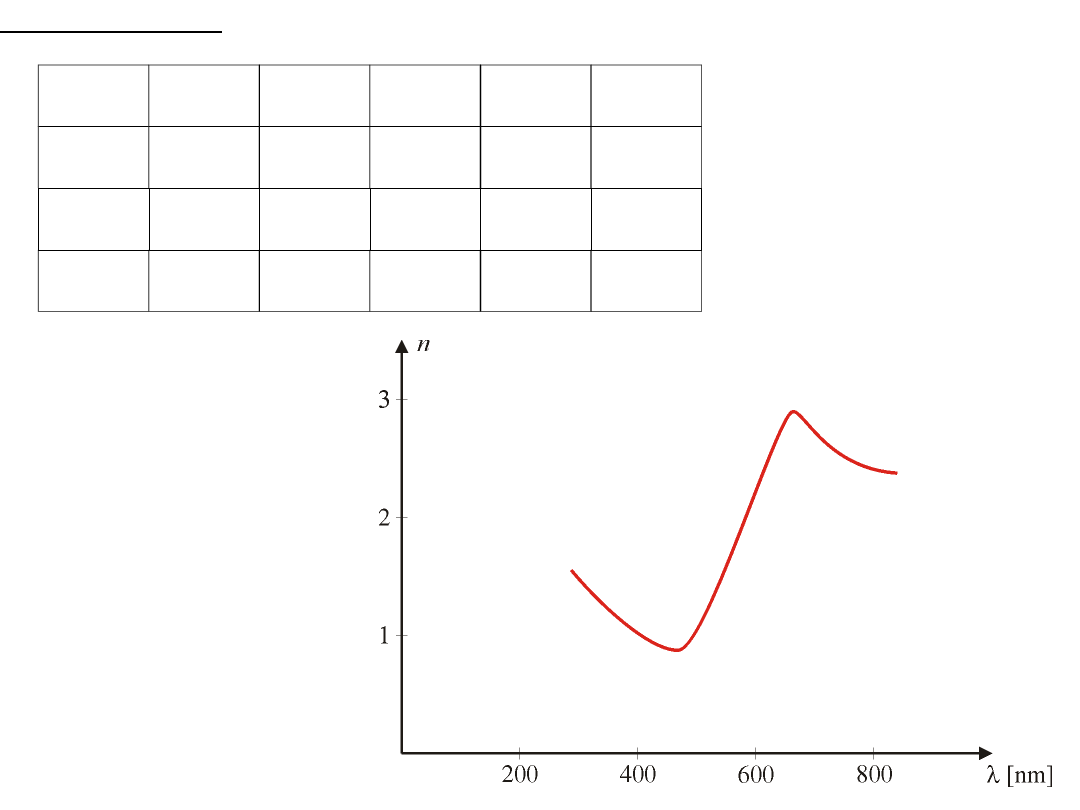
Dyspersja anormalna

 [nm]

n

 [nm]

n

 [nm]

n

703

2,30

535

1,95

434

1,04

671

2,34

486

1,05

410

1,17

589

2,64

461

0,83

405

1,38

Wykres dyspersji fuksyny

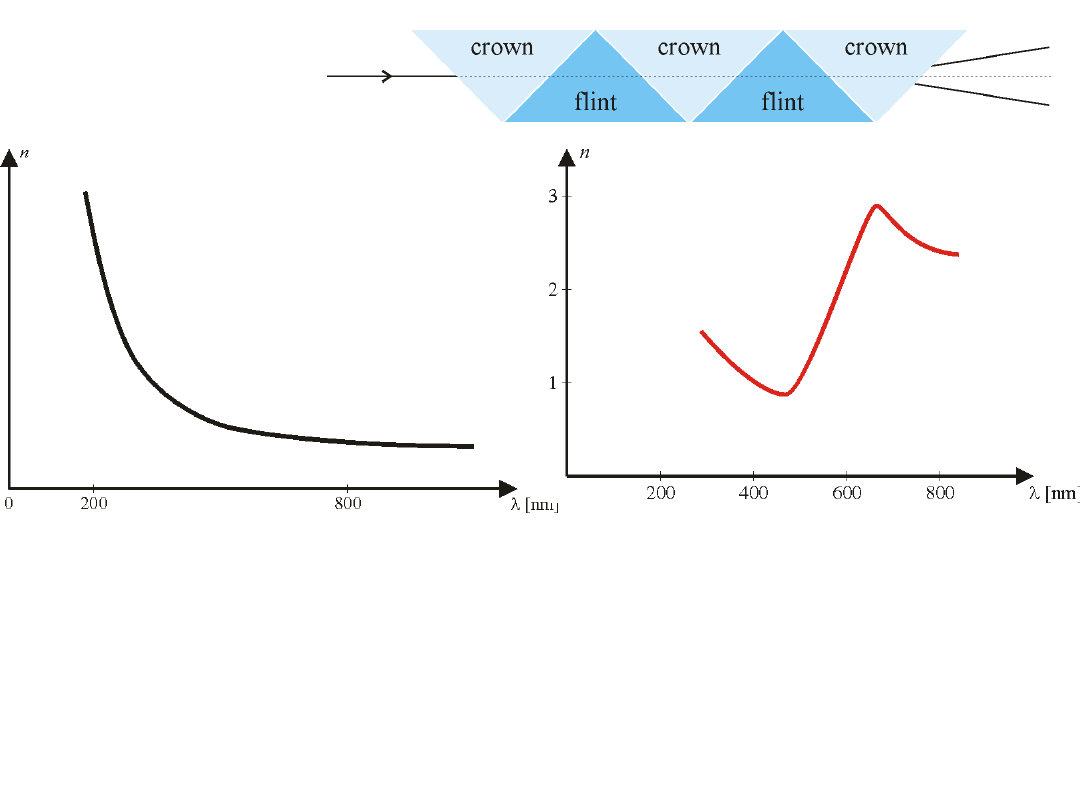
Pryzmat á vision directe

Dyspersja anormalna

Dyspersja normalna

Współczynnik załamania n jest funkcją długości fali

.

W zjawisku dyspersji normalnej współczynnik załamania n maleje ze
wzrostem długości fali

 zgodnie z równaniem Cauchy’ego. Tak jest w

przypadku, gdy substancja jest dla przeźroczysta.

W obszarze pochłaniania (np. fuksyna) pojawia się dyspersja anormalna.
Przechodząc od fali dłuższych do krótszych początkowo n rośnie, następnie
gwałtowanie maleje i znowu rośnie.

Aberracja chromatyczna

1

2

1

1

1

(

1)

c

c

f

n

R

R

=

�

�

-

+

�

�

�

�

1

2

1

1

1

(

1)

f

f

f

n

R

R

=

�

�

-

+

�

�

�

�

1

2

1

2

(

1) (

1)

1

1

1

1

(

1)(

1)

(

1)(

1)

f

c

f

c

c

f

c

f

c

f

n

n

n

n

f

n

n

n

n

R

R

R

R

-

-

-

-

-

=

=

�

�

�

�

-

-

+

-

-

+

�

�

�

�

�

�

�

�

(

) (

)

c

f

c

f

n

n

-

-

:

- aberracja podłużna

MN

– aberracja poprzeczna

1

2

1

2

0

f

D

D

+

=

Układ nie ma aberracji chromatycznej

1

2

1

2

1

1

2

2

f

f

f

D

D

=-

D

-

=

D