Tarcie

Wszystkie ciała poruszające się w naszym
otoczeniu napotykają w swoim ruchu na opory.
Siły oporu są skierowane przeciwnie do wektora
prędkości ciał i starają się powstrzymać ruch.
Opory ruchu występują zawsze gdy ciała się
poruszają, czyli ślizgają się, toczą.

Przyczyną tego rodzaju
tarcia są mikroskopijne
zadziory zaczepiające
o siebie na trących
powierzchniach.

Dlatego nawet pozornie gładkie
powierzchnie nie ślizgają się swobodnie.

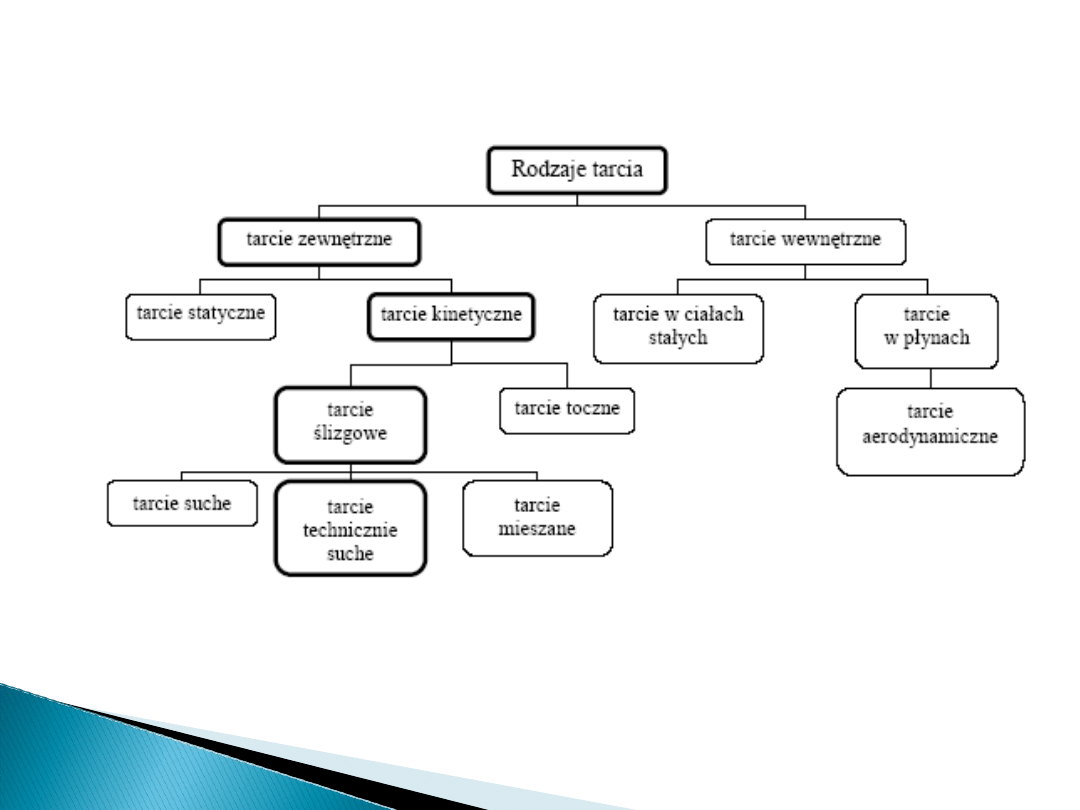
Tarcie poślizgowe - powstające podczas ruchu
postępowego jednego ciała po powierzchni drugiego

Tarcie poślizgowe dzielimy z kolei na tarcie spoczynkowe i tarcie
kinematyczne .
Tarcie spoczynkowe czyli statyczne występuje pomiędzy
wzajemnie nieruchomymi ciałami. Z powodu występowania tego
tarcia, aby poruszyć z miejsca spoczywające ciało, należy użyć
pewnej siły. Najmniejszą wartość tej siły, która wprawi to ciało w
ruch nazywa się siłą tarcia statycznego
Tarcie kinematyczne występuje pomiędzy ciałami, które już są w
ruchu. Jako siłę tarcia kinematycznego przyjmuje się minimalną
wartość siły, która niezbędna jest do podtrzymania ruchu.

Tarcie poślizgowe może być:
1)  suche, gdy nie ma czynnika oddzielającego
powierzchnie ślizgające się po sobie,
2) półsuche, półpłynne lub płynne, gdy taki czynnik
oddzielający: na to, który z tych rodzajów tarcia wystąpi,
mają wpływ różne czynniki, jak wielkości powierzchni
stykających się, prędkości poślizgu, rodzaju smaru,
rodzaju materiałów stykających się itp.

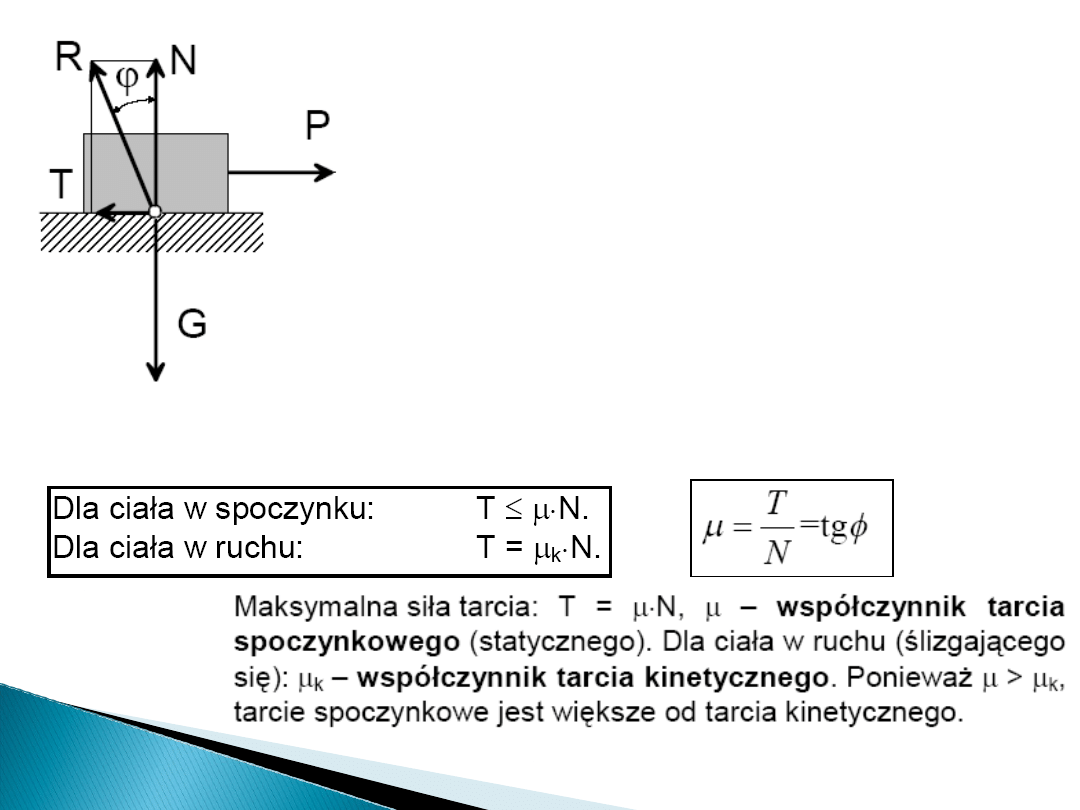
P – siła zewnętrzna czynna
(obciążenie),
G – siła zewnętrzna czynna (ciężar),
R – reakcja,
N – składowa normalna reakcji,
T – siła tarcia.

CIAŁO ZNAJDUJE SIĘ W RÓWNOWADZE
GDY SIŁA P < T LUB P = T.
Gdy P > T – ciało zacznie się porusza
(ślizgać).
Wartość siły tarcia jest ograniczona i nie
może przekroczyć pewnej maksymalnej
wartości.

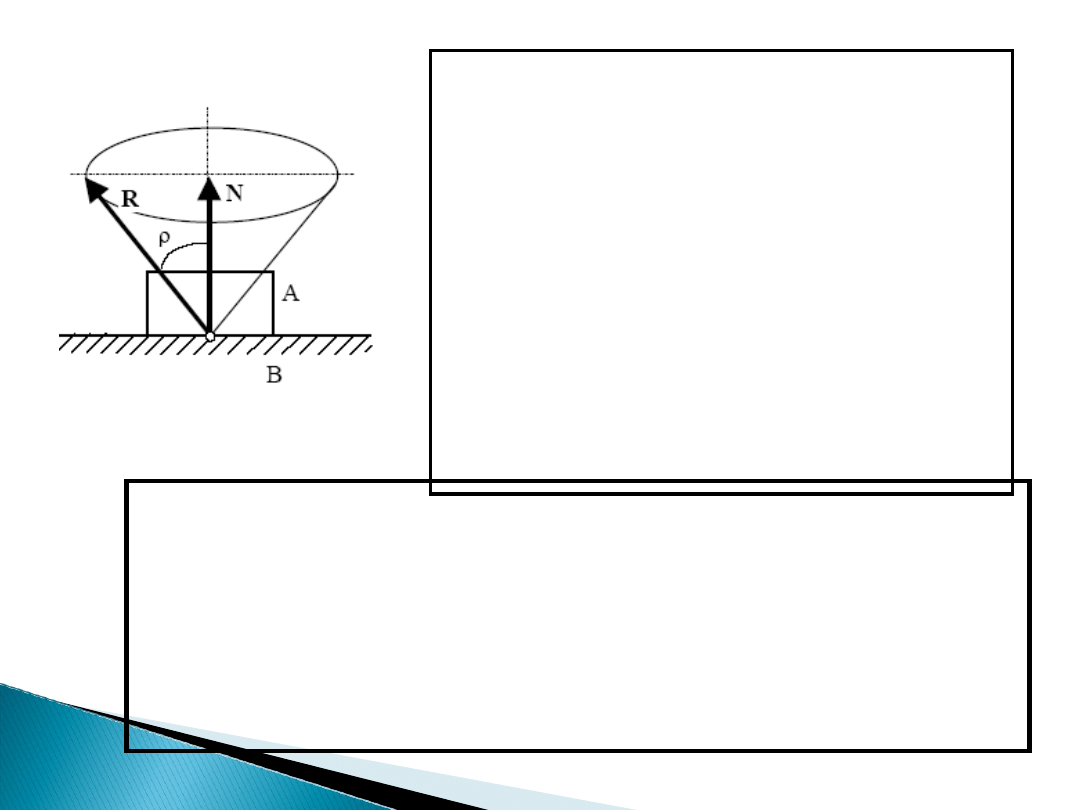
Wypadkowa R zataczająca
względem kierunku działania
siły N stożek o kącie
wierzchołkowym  tworzy stożek

tarcia. Zatem graniczną siłą
tarcia spoczynkowego
(statycznego) nazwano taką
maksymalną wartość siły, którą
należy przyłożyć do ciała
będącego w spoczynku, aby
spowodować jego ruch (a ściślej
równowagę chwiejną).

Stożek tarcia – określa kierunek siły przyłożonej
do ciała,
która może spowodować ruch ciała.
Jeżeli siły zewnętrzne będą mniejsze od zakresu
obejmowanego przez stożek tarcia, to ciało
pozostanie w spoczynku.

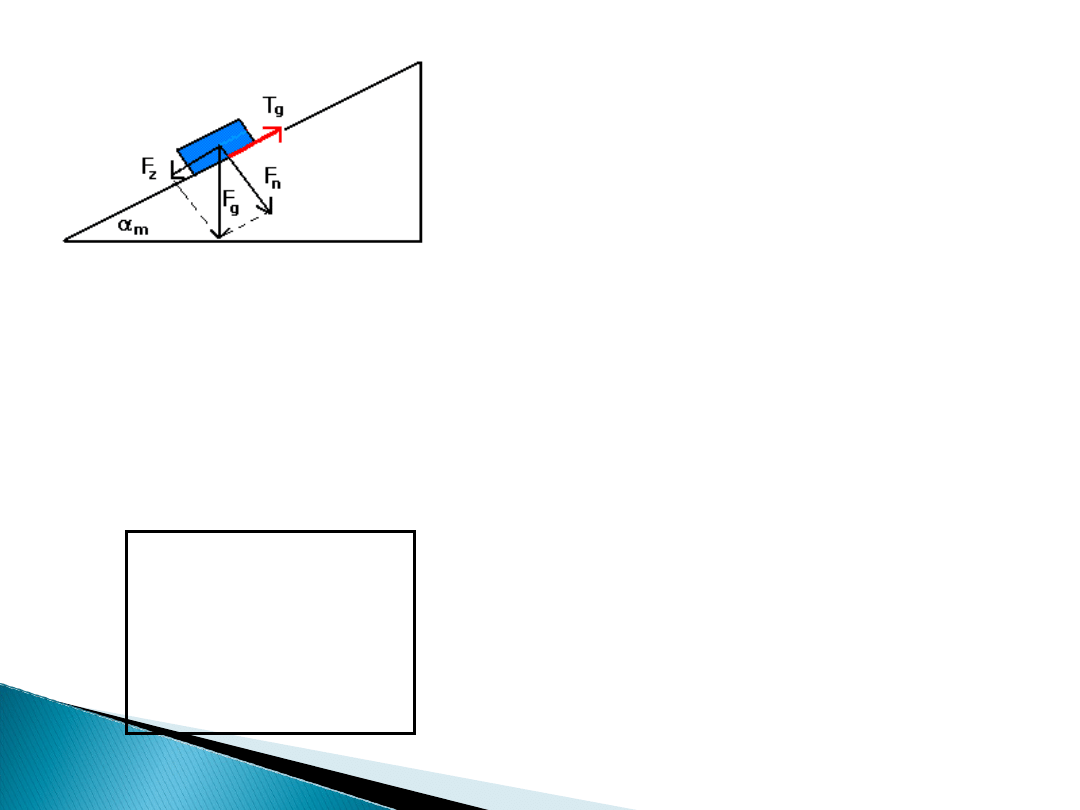
Na ciało umieszczone na równi działa siła
grawitacji F

g

, która rozkłada się na siłę

zsuwającą F

z

i na siłę nacisku F

n

= N

Z zależności geometrycznych, możemy
wyznaczyć kąt pomiędzy F

n

a F

g

. Okazuje

się, że jest on zawsze równy kątowi
nachylenia równi. W naszym przypadku
będzie to: α

m

.

Dzięki temu, możemy ze wzorów
trygonometrycznych wyznaczyć zależności:
F

z

= F

g

sinα

m

F

n

= F

g

cosα

m

= N

w przypadku granicznej siły tarcia statycznego: T

g

= μ

s

N =

μ

s

F

g

cosα

m

.

Skoro ciało się jeszcze nie zsuwa, to siła zsuwająca musi być równoważona
przez siłę tarcia granicznego. A więc:

T

g

= F

z

μ

s

F

g

cosα

m

=

F

g

sinα

m

μ

s

cosα

m

= sinα

m

μ

s

= tgα

m

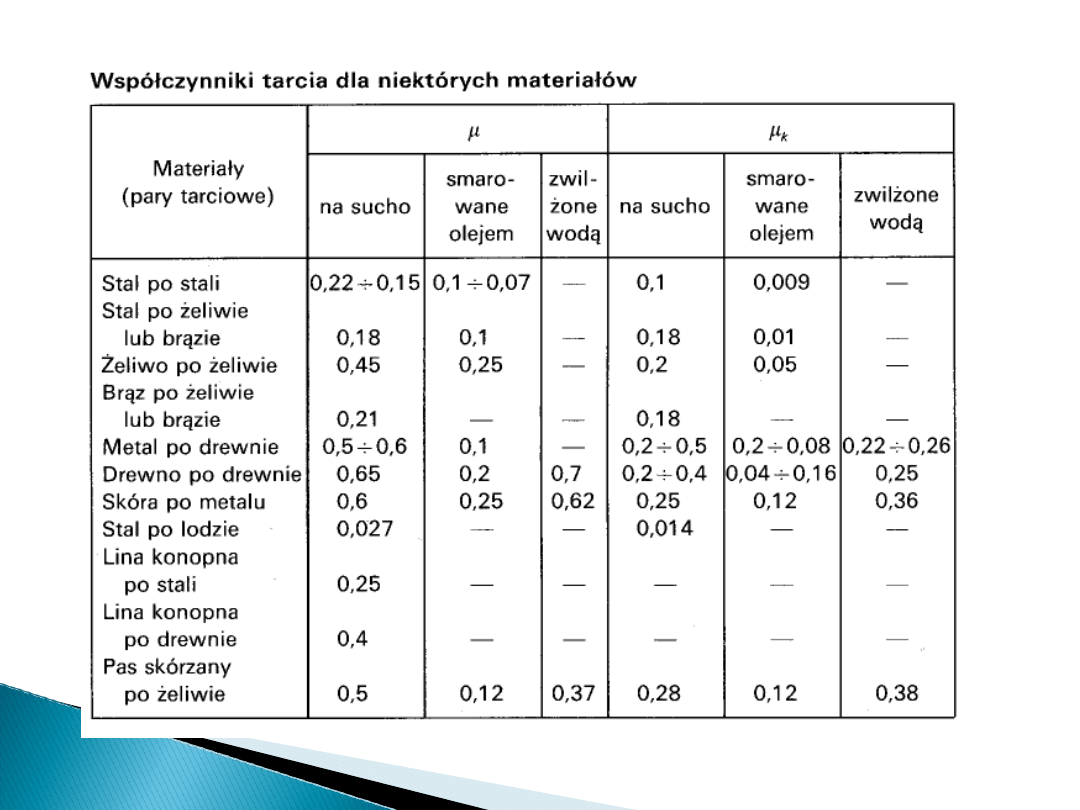
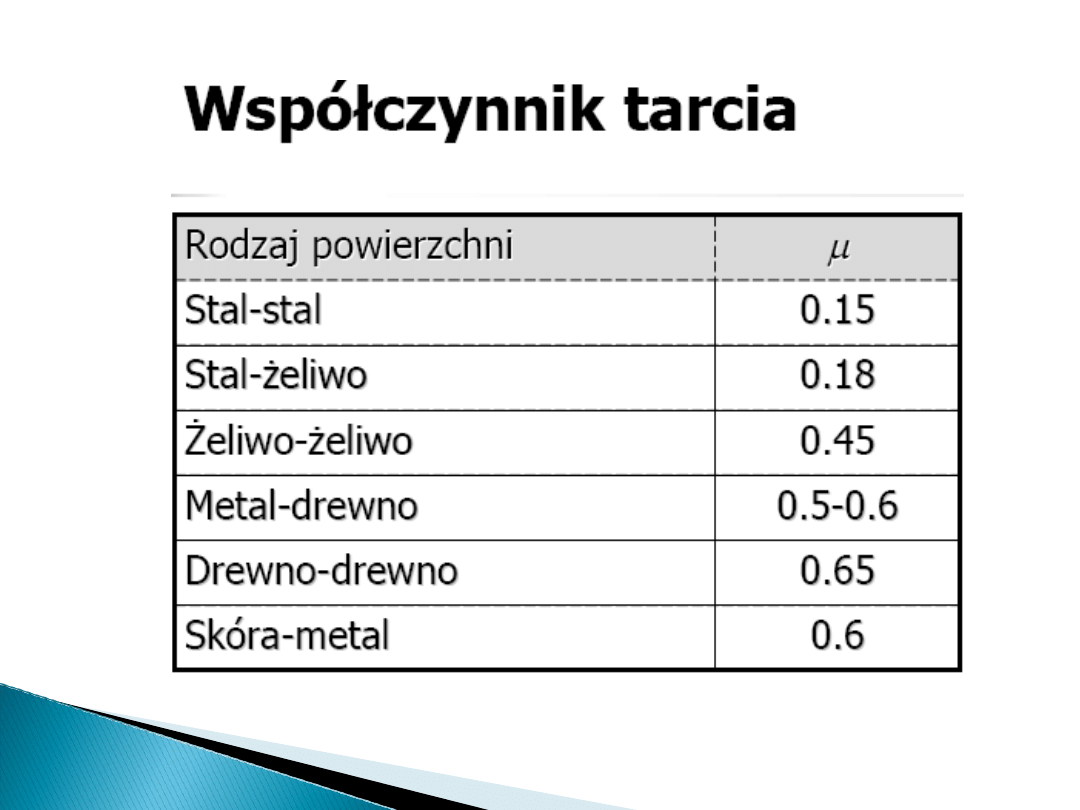
współczynnik tarcia statycznego równy jest po
prostu tangensowi maksymalnego kąta
nachylenia równi, przy którym ciało się jeszcze z
niej nie zsuwa. Współczynnik ten będzie różny, w
zależności od materiałów, z jakich zrobione są
ciało i równia oraz od stanu ich powierzchni.

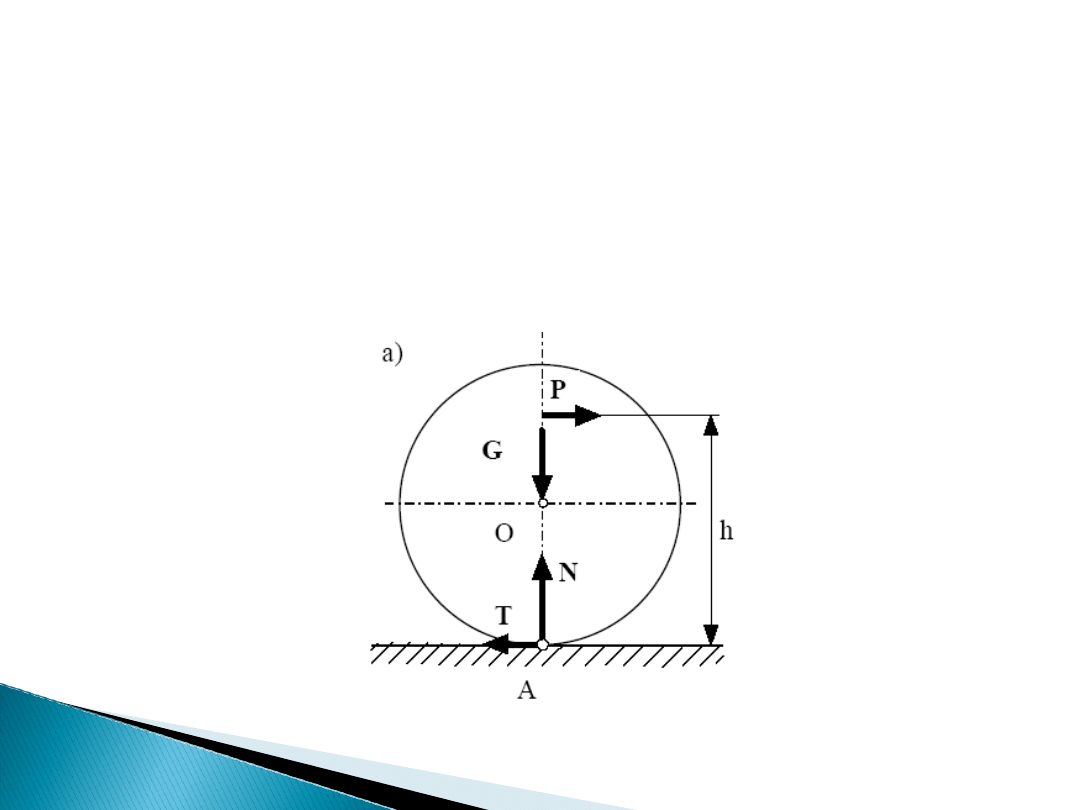
Toczeniu walca po odkształcalnej powierzchni
towarzyszą skomplikowane zjawiska tarcia. Tarcie
toczenia lub

opór toczenia

powstaje przy

usiłowaniu przetoczenia walca o ciężarze

G

po

poziomej płaszczyźnie. Gdyby walec toczący się po
podłożu i podłoże były idealnie sztywne, to styk
występowałby tylko wzdłuż tworzącej walca,
przechodzącej przez punkt A

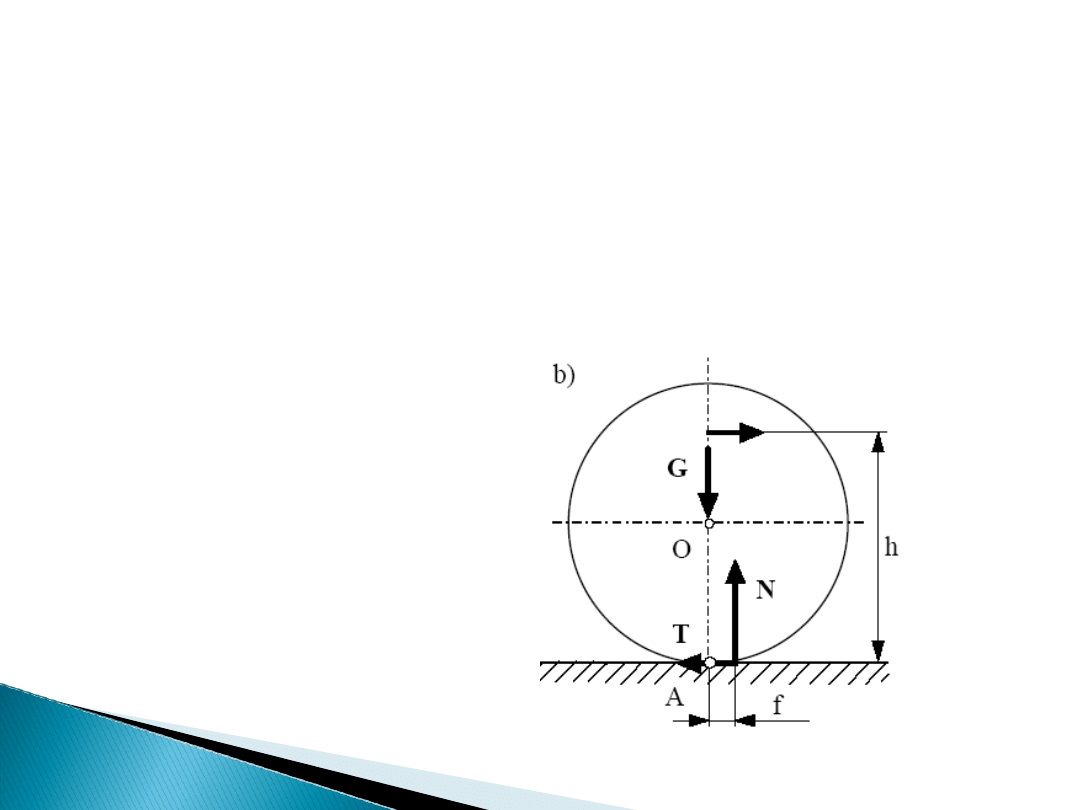
Zjawisko oporu toczenia jest spowodowane odkształcaniem
się zarówno walca, jak i płaszczyzny, na której on spoczywa.
Wtedy styk walca i płaszczyzny nie odbywa się wzdłuż
tworzącej przechodzącej przez punkt A, lecz na ograniczonej
powierzchni wynikającej ze wzajemnych odkształceń w
miejscu styku walca i powierzchni. Reakcja normalna N jest
wtedy wypadkową nacisków normalnych występujących na
płaszczyźnie styku i działających na walec i jest przesunięta
o pewną odległość w stosunku do punktu A w kierunku
możliwego toczenia się

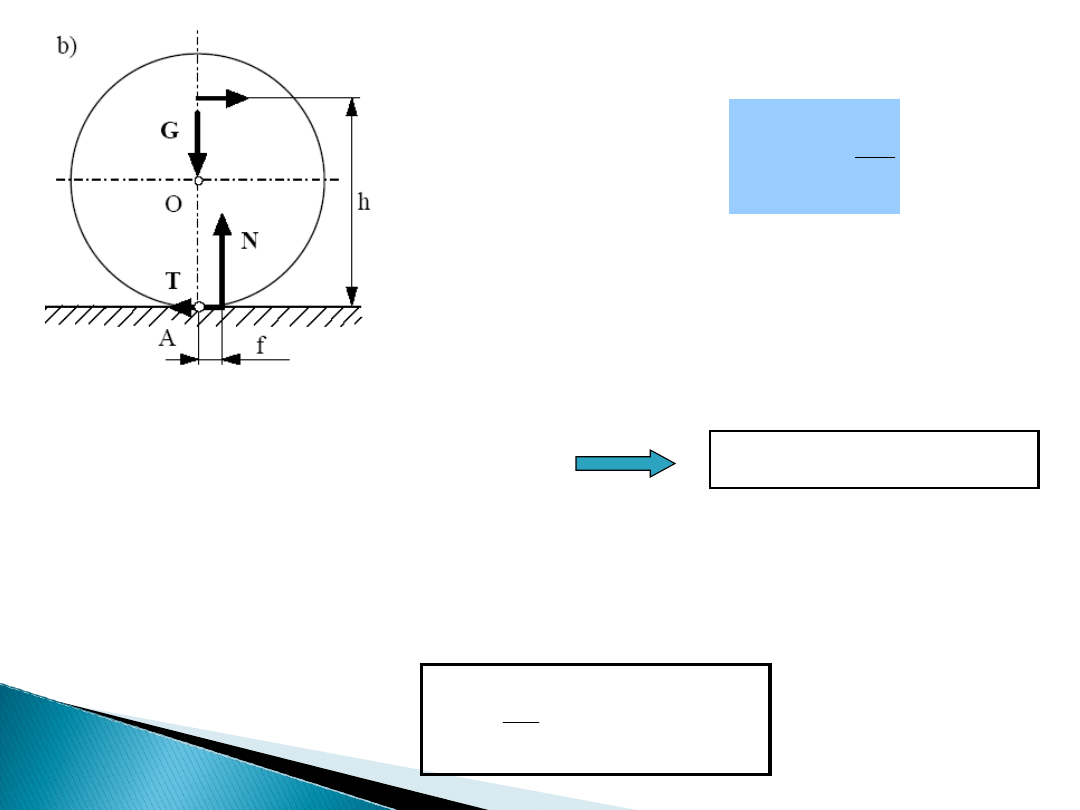
Siła tarcia tocznego musi spełniać warunki
(przy równowadze walca)

gdzie f  współczynnik tarcia tocznego,

r  promień walca

r

f

G

T 

Aby nie mógł wystąpić poślizg
walca po podłożu, musi być
spełniony warunek, wynikający
z praw tarcia

G

N

P

T











Toczenie walca wystąpi, gdy wartość
siły tarcia tocznego

T

będzie mniejsza

od wartości siły tarcia ślizgowego



N

rozwiniętego, co wyraża się
nierównością

G

N

G

r

f

T











p

r

f

G

T 

Współczynnik tarcia toczonego- współczynnik o
wymiarach długości występujący we wzorze na siłę tarcia
toczonego. Współczynnik ten zależy od rodzaju materiału
ciała toczącego się i podłoża, stanu ich powierzchni.

Łożysko ślizgowe poprzeczne

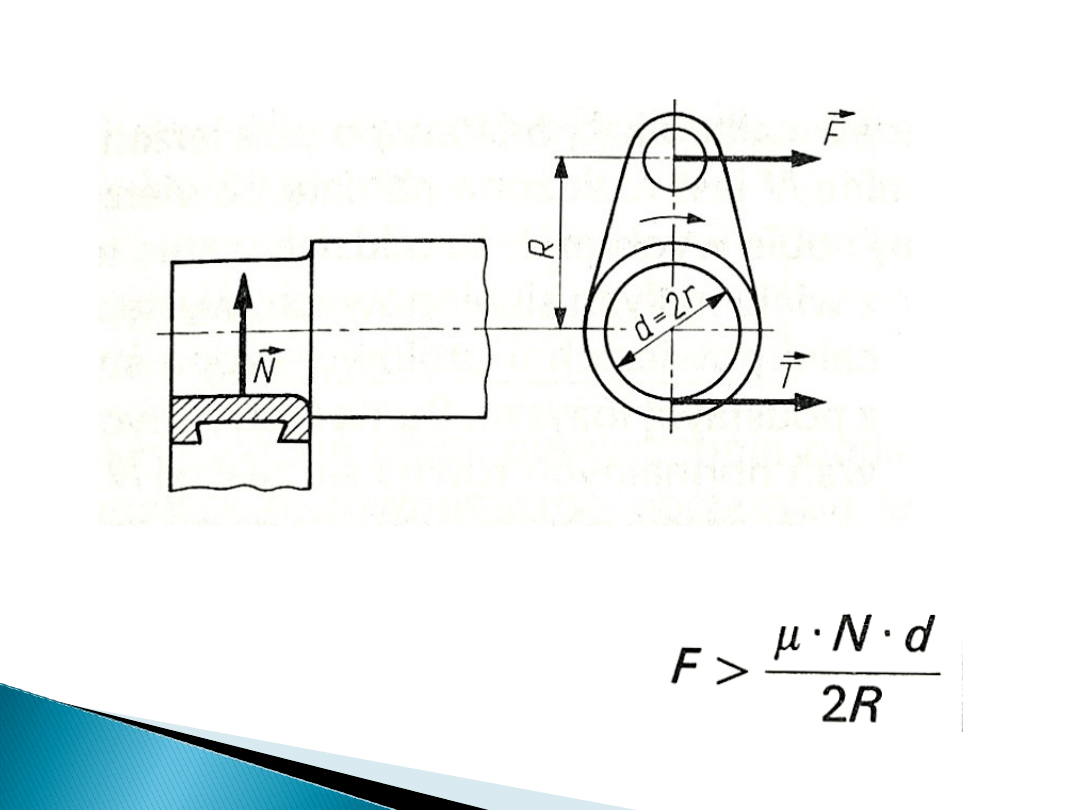
Tarcie w łożyskach ślizgowych

Ruch obrotowy wału nastąpi, gdy na korbie
będzie działać siła czynna:

Łożysko ślizgowe wzdłużne

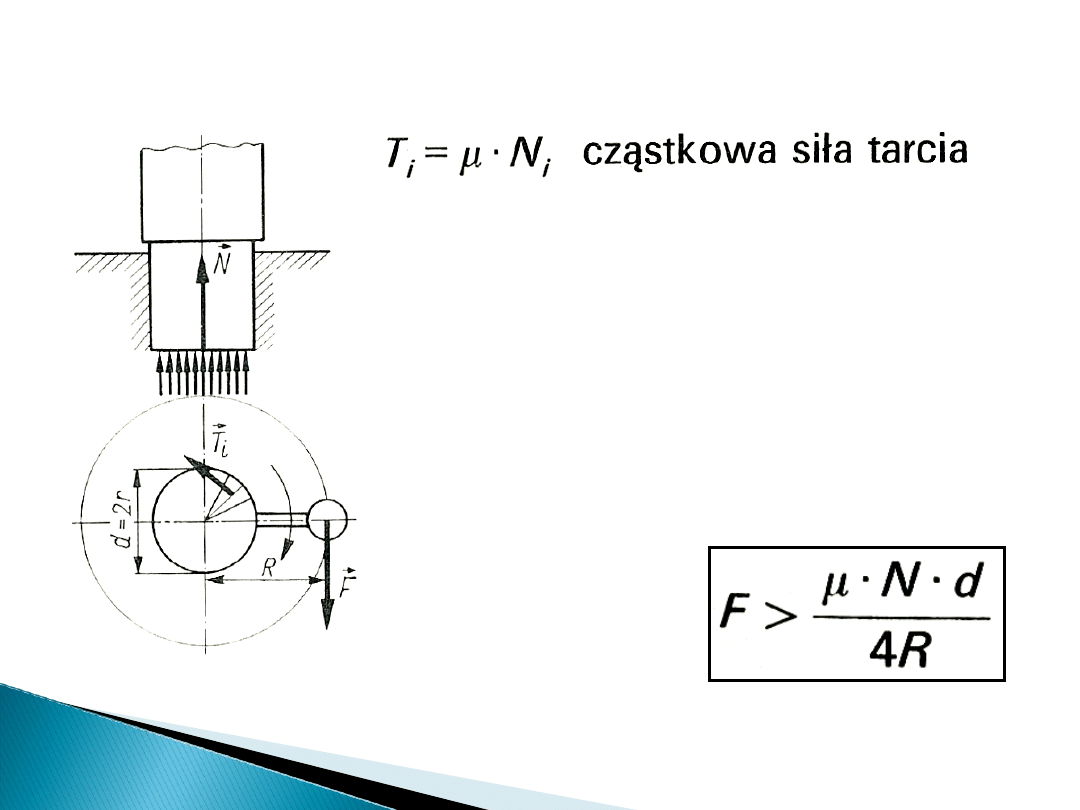
Tarcie w łożyskach ślizgowych wzdłużnych

Ruch obrotowy wału nastąpi,
gdy na korbie będzie działać siła czynna:

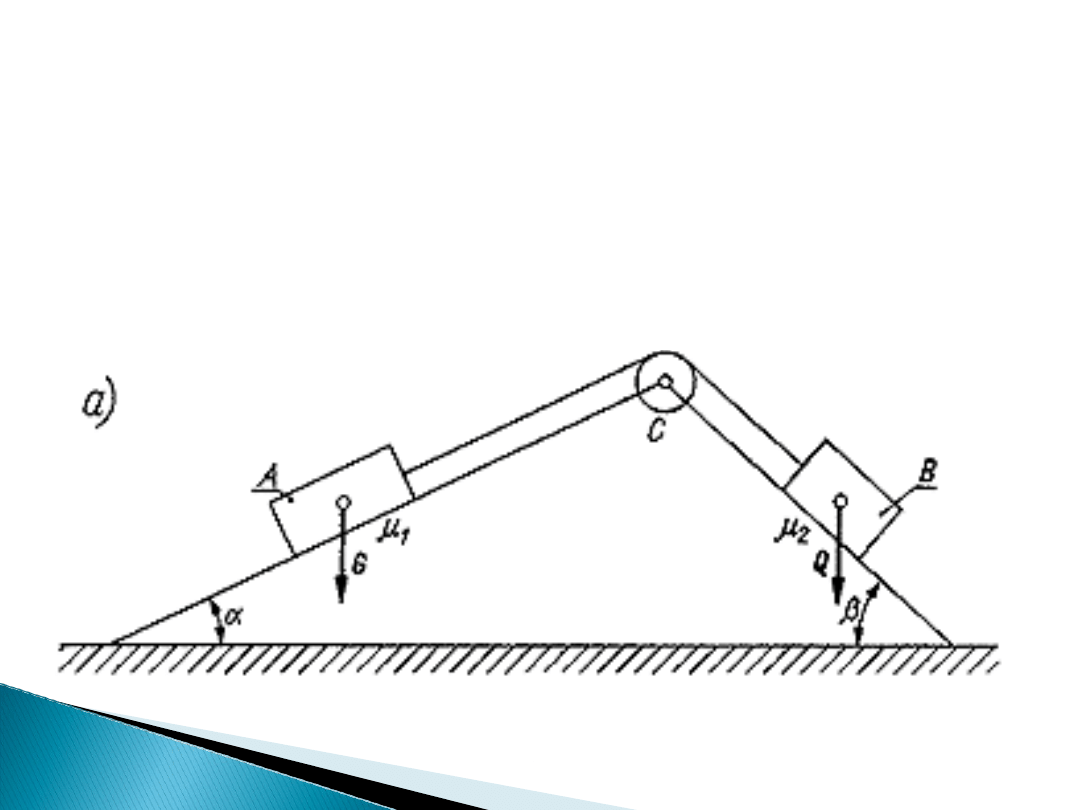
Przykład1
Na dwóch równiach pochyłych, tworzących z poziomem kąty
i , ustawiono dwa ciała A i B o ciężarach G i Q połączone

nieważkim cięgnem wiotkim przerzuconym przez krążek C.
Współczynniki tarcia obu ciał o równie są równe  



i 

2

.

Określić, w jakich granicach może się zmieniać wartość ciężaru
Q ciała B ( przy założeniu, że ciężar G ciała A jest stały), aby
układ ciał A i B pozostawał w równowadze.

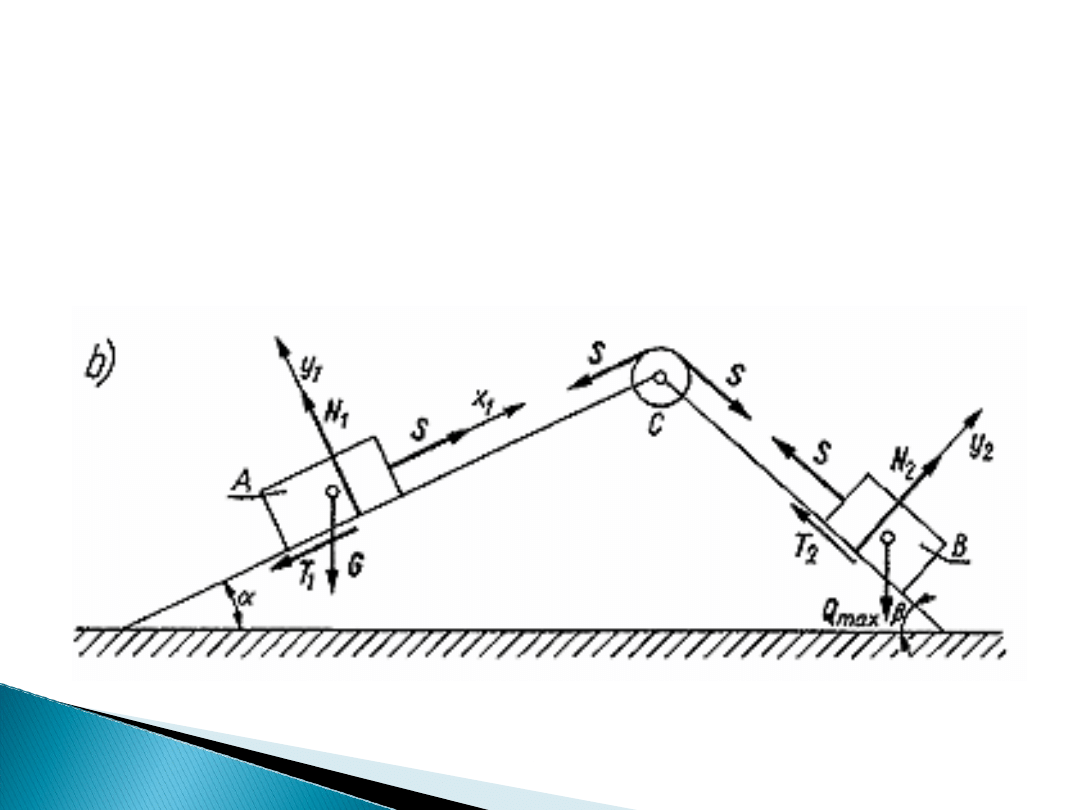
Zacznijmy od przypadku, gdy ciężar Q ciała B ma wartość
maksymalną, przy której możliwa jest jeszcze równowaga. Po
przekroczeniu tej wartości ciało B zacznie zjeżdżać z równi
pochyłej o kącie , a ciało A zacznie się poruszać do góry po

równi pochyłej o kącie . W rozważanym granicznym przypadku

(rys. b) siły tarcia T

1

i T

2

osiągną maksymalne wartości i

skierowane są przeciwnie do możliwego ruchu.

Przyjmując prostokątne układy współrzędnych Oxy, związane z
obydwoma ciałami, w których oś Oy jest prostopadła do równi, a oś 
Ox równoległa do równi, otrzymujemy następujące równania
równowagi dla:
ciała A

ciała B

Ponadto na podstawie praw tarcia możemy
napisać

Po rozwiązaniu otrzymanego układu równań znajdujemy
maksymalną wartość ciężaru ciała B

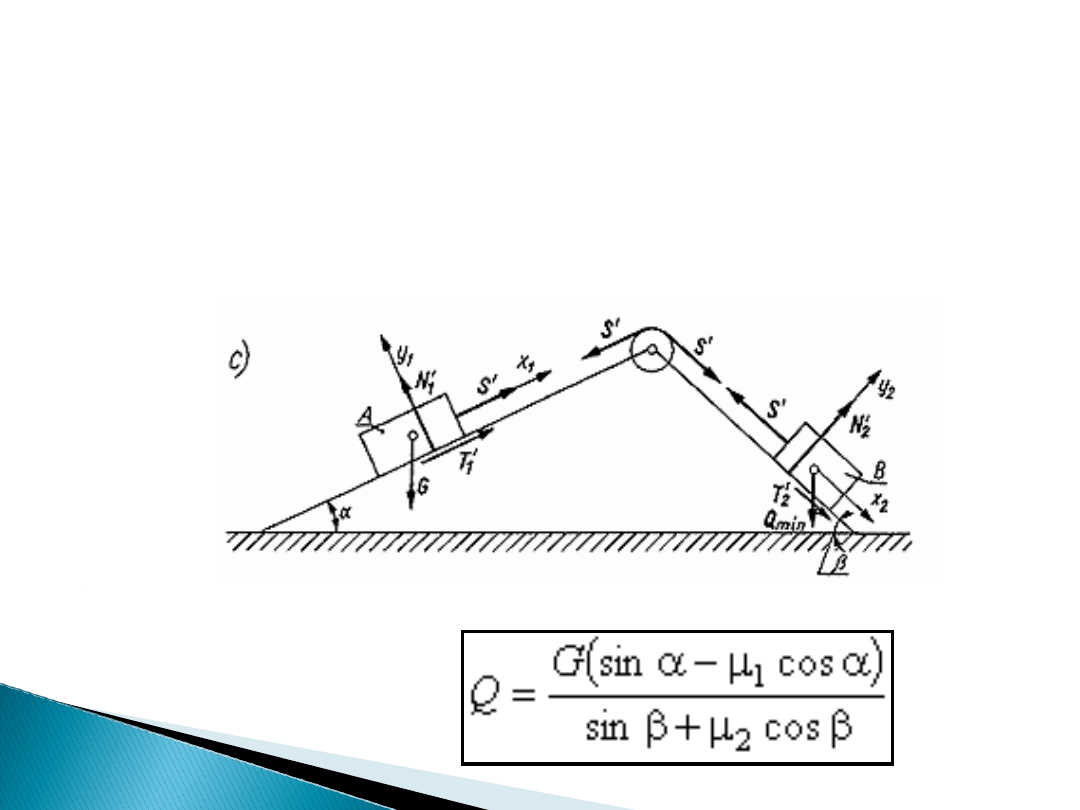
Postępując podobnie jak poprzednio, przy założeniu, że wartość ciężaru Q
będzie minimalna, tzn. układ będzie miał tendencję ruchu w przeciwną stronę
 ciało A będzie miało tendencję do zjeżdżania z równi kącie , a ciało B

zacznie poruszać się do góry po równi pochyłej o kącie . W tym granicznym

przypadku (rys. c), siły tarcia T

1

i T

2

są skierowane przeciwnie do możliwego

ruchu. Pisząc odpowiednie równania równowagi i zależności między siłami
tarcia a siłami normalnymi (korzystając z praw tarcia), otrzymamy również
układ równań. Po rozwiązaniu równań otrzymamy minimalną wartość ciężaru
ciała B

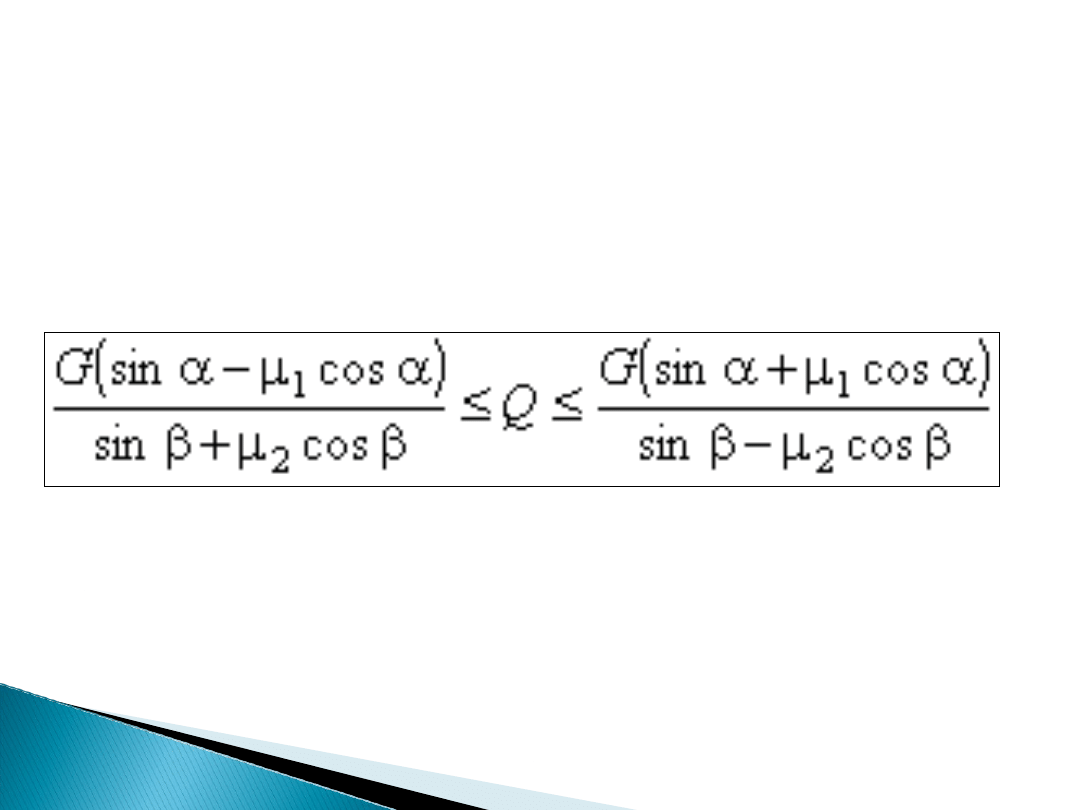
Na podstawie otrzymanych wyników możemy stwierdzić,
że wartość ciężaru ciała B powinna pozostawać w
następujących granicach

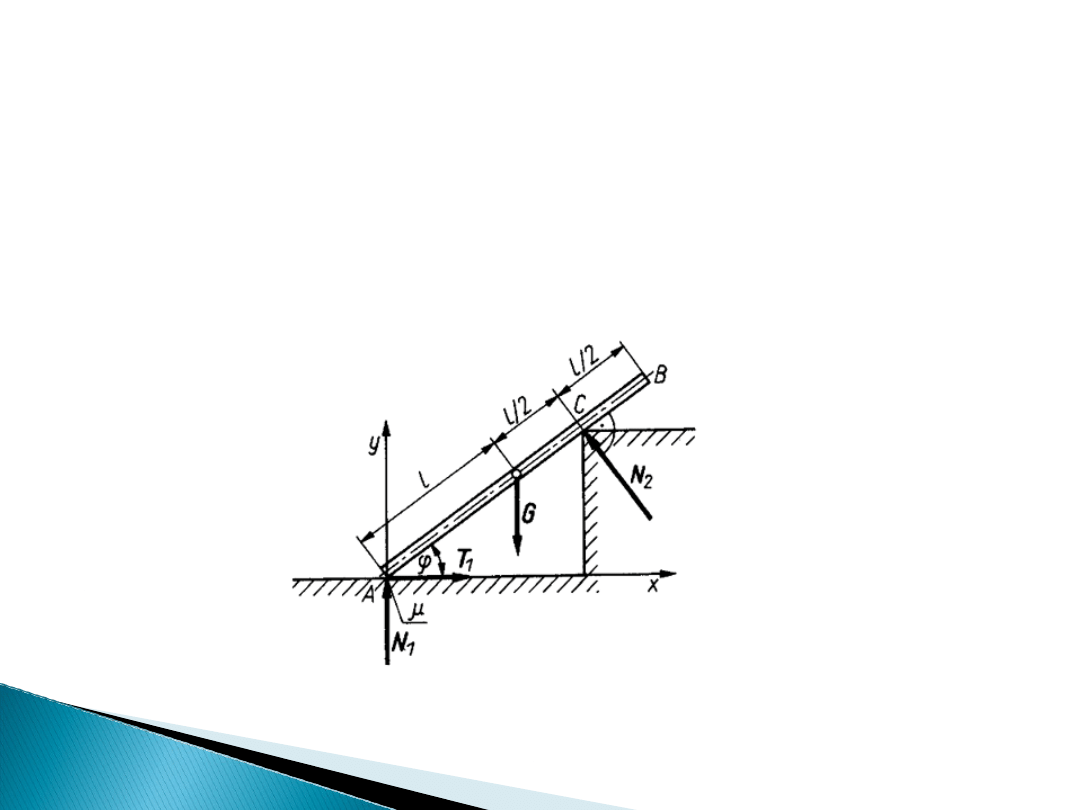
Przykład 2
Jednorodna belka o długości 2l i ciężarze G jest oparta
dolnym końcem A o chropowatą poziomą płaszczyznę, a w
punkcie C o gładki występ. W położeniu równowagi belka
tworzy z płaszczyzną poziomą kąt , a odcinek AC = 1,5l.

Znaleźć współczynnik tarcia ślizgowego statycznego  w

punkcie A.

W położeniu równowagi belki jej koniec A ma tendencję do przesuwania
się w lewo. Siła tarcia T

1

jest skierowana przeciwnie do możliwego ruchu,

a więc w prawo. Po przyjęciu prostokątnego układu współrzędnych
otrzymuje się następujące równania równowagi belki

W przypadku poszukiwania współczynnika tarcia ślizgowego 

statycznego w położeniu granicznym równowagi belki (tarcie
całkowicie rozwinięte) otrzymuje się

Po rozwiązaniu powyższego układu równań
współczynnik tarcia wynosi