14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

1

Wykład 7

Wykład 7

Rachunek predykatów

Rachunek predykatów

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

2

Funkcje zdaniowe

Funkcje zdaniowe

Niech X.Funkcją zdaniową jednej zmiennej x, której

zakresem zmienności jest przestrzeń X, nazywamy
wyrażenie f(x), w którym występuje zmienna x i które
staje się zdaniem prawdziwym lub fałszywym, gdy w
miejsce zmiennej x wstawimy dowolny obiekt ze zbioru
X.

Uwaga Funkcja zdaniowa f(x),jednej zmiennej x, jest
po prostu funkcją f : X --> {0,1} taką, że dla
dowolnego xX, f(x) jest zdaniem w sensie rachunku

zdań.

Przykład
x+x

2

>0 , x Z

n+1 < 2, n

 N

|x| 3 , x R

x

2

+ y

2

>0, (x,y)

R

2

Przestrzeń X może sama być
produktem kartezjańskim X1...

Xn. Wtedy zmienna x przyjmuje
jako wartości elementy tego
produktu. Mówimy wówczas, że
mamy do czynienia z funkcją
zdaniową n argumentową.

Każda funkcja

zdaniowa wyznacza

pewien podzbiór

(pewna własność)

przestrzeni, w której

została określona.

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

3

Predykaty złożone

Predykaty złożone

Funkcje zdaniowe (inaczej predykaty) można
łączyć spójnikami logicznymi. Powstają w ten
sposób nowe, złożone funkcje zdaniowe.

Przykłady złożonych predykatów:

xx , (xx ,

(xxx
x  

3 0

x+y  

4

y 

1

Jeśli po wstawieniu w miejsce zmiennej x elementu a
X w predykacie (x) określonym w pewnym zbiorze X

otrzymujemy zdanie prawdziwe, to mówimy, że a spełnia
funkcję zdaniową (x). Ogół tych wartości x X dla

których funkcja zdaniowa (x) jest spełniona

oznaczamy przez {xX: (x) }.

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

4

Spełnianie

Spełnianie

Element a X spełnia funkcję zdaniową

xx wttw a spełnia x lub a spełnia x

Fakt 1 {x X : xx} = {x X : x}  {x X
:x}

Element a X spełnia funkcję zdaniową

xx wttw a spełnia x i a spełnia x

Fakt 2 {x X : xx} = {x X : x}  {x
X :x}

Element a X spełnia

funkcję zdaniową 

x wttw a nie

spełnia x

Fakt 3

{x X : x} = X \{x X :

x}

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

5

Kwantyfikatory

Kwantyfikatory

(x)x

(x)x

Kwantyfikator

egzystencjalny (szczegółowy)

istnieje x takie, że

x

Kwantyfikator

uniwersalny (ogólny)

dla każdego x,

x

xjest zakresem kwantyfikatora

szczegółowego lub ogólnego.

Zmienna x będąca w zakresie
kwantyfikatora wiążącego tę
zmienną jest zmienną związaną

Kwantyfikato
r wiąże
wymienioną
zmienną

Przykład

(x)( x+y<6 

x*y>0)

(x) (y)(x 

y
(x) x,y (y)

y

Wolne wystapienie y

związane
wystapienie y

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

6

Spełnianie

Spełnianie

Niech x będzie predykatem określonym w pewnym

zbiorze X.

Zdanie (x)x jest prawdziwe w X wttw istnieje element

a X , który spełnia funkcję zdaniową x
Zdanie (x)xjest prawdziwe w X wttw każdy

element a spełnia funkcje zdaniową x

Zdanie (x)x

jest prawdziwe w
X wttw {xX :

x

Zdanie ( x)x

jest prawdziwe w X
wttw {xX :

x}= X.

(x)x jest

zdaniem
fałszywym wttw
{xX : x

( x)x jest

zdaniem fałszywym
wttw
{xX : x}  X.

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

7

Przykład

Przykład

Przykład Rozważmy funkcję zdaniową (x+2)*(x-
3)<0 w zbiorze liczb rzeczywistych R. Ponieważ 2
spełnia tę funkcję a liczba 3 nie spełnia tej funkcji,
to

(x) ((x+2)*(x-3)<0) jest zdaniem

prawdziwym, a

( x) ( (x+2)*(x-3)<0) jest zdaniem

fałszywym.

Uogólnienie Niech (x)x,y będzie funkcją zdaniową

o zmiennych wolnych x X, yY. Wtedy (x)x,y

oraz (x)x,y są funkcjami zdaniowymi zmiennych

wolnych yY.
Element y Y spełnia

funkcję zdaniową
(x)x,ywttw istnieje

takie a X, że a,yjest

zdaniem prawdziwym.

Element y Y spełnia

funkcję zdaniową (

x)x,ywttw dla

dowolnego a X,

a,yjest zdaniem

prawdziwym.

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

8

Operacje logiczne a

Operacje logiczne a

kwantyfikatory

kwantyfikatory

Kwantyfikator ogólny
można uważać za
uogólnienie koniunkcji.

Jeśli X ={a

1

a

2

a

n

}, a

xpredykatem określonym w

zbiorze X, to prawdziwa jest
następująca równoważność
(x)x

(a

1

a

2

a

n



Jeśli X jest zb. skończonym o
elementach a

1

a

2

a

n

 a

xpredykatem określonym

w zbiorze X, to prawdziwa
jest następująca
równoważność
( x)x

(a

1

a

2

a

n



Kwantyfikator
szczegółowy można
uważać za uogólnienie
alternatywy.

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

9

Działania uogólnione a

Działania uogólnione a

kwantyfikatory

kwantyfikatory

Niech A={ A

i

}

iI

będzie indeksowaną

rodziną podzbiorów pewnej przestrzeni X.



iI

A

i

= {x: x A

j

dla pewnego j  I}



iI

A

i

= {x: x  A

j

dla każdego j  I}

Suma

uogólniona

Iloczyn

uogólniony

Rozważmy funkcję zdaniową 2 zmiennych (x,y), x  X,

y  Y.



yY

{

x  X : (x,y)

}

= {x  X : (y)

(x,y)}



yY

{x  X : (x,y)}

= {x  X : (y)

(x,y)}

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

10

Kwantyfikatory

Kwantyfikatory

ograniczone

ograniczone

Notacja : (x) x(

x) x

Przykład Warunek Cauchy’ego

ciąg (a

n

) jest zbieżny do liczby a

wttw dla każdego >0 istnieje

liczba naturalna n

0

taka, że dla

każdego n>n

0

|a

n

-a | < 

Kwantyfikator

o zakresie ograniczonym

przez funkcję

zdaniową

(x) xjestprawdziwe wttw (x)(x  xjest

prawdziwe.

( x) xjestprawdziwe wttw ( x)(x  xjest

prawdziwe.

ciąg (a

n

) jest zbieżny do a wttw ( >0 ) ( n

0

) ( n>n

0



|a

n

-a | < 

ciąg (a

n

) jest zbieżny do a wttw

()(>0  ( n

0

)(n

0

 (nn>n

0

 |a

n

-a | <

))

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

11

Język rachunku

Język rachunku

predykatów

predykatów

Niech V

0

będzie zbiorem zmiennych zdaniowych, V-

zbiorem zmiennych indywiduowych, P-zbiorem nazw
relacji F-zbiorem nazw funkcji.

Zbiór termów jest
to najmniejszy zbiór
zawierający V i taki,
że jeśli f jest nazwą
funkcji n
argumentowej a
t1,...,tn termami, to
f(t1,...,tn) jest
termem.

Zbiór formuł jest to najmniejszy
zbiór wyrażeń zawierających V

0

i

taki, że
- jeśli r jest nazwą relacji n
argum., a t1,...,tn są termami, to
r(t1,...,tn) jest formułą,
- jeśli  i  są formułami, to ,

(), (), (), (), są

formułami,
- jeśli x jest formułą ze

zmienną wolną x, to (x)x i

(x)x są formułami.

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

12

Semantyka

Semantyka

Aby określić sens formuły rachunku
funkcyjnego potrzeba:

Ustalić interpretację symboli funkcyjnych i
predykatywnych
oraz wybrać wartości dla zmiennych.

STR, v |= xxwttw STR, v |= x lub STR, v |=

x
STR, v |= xxwttw STR, v |= x i STR, v |=

x
STR, v |= (x)xwttwSTR, v(x/a) |= xdla

wszystkich a STR
STR, v |= ( x)xwttwSTR, v(x/a) |= xdla

pewnego a STR

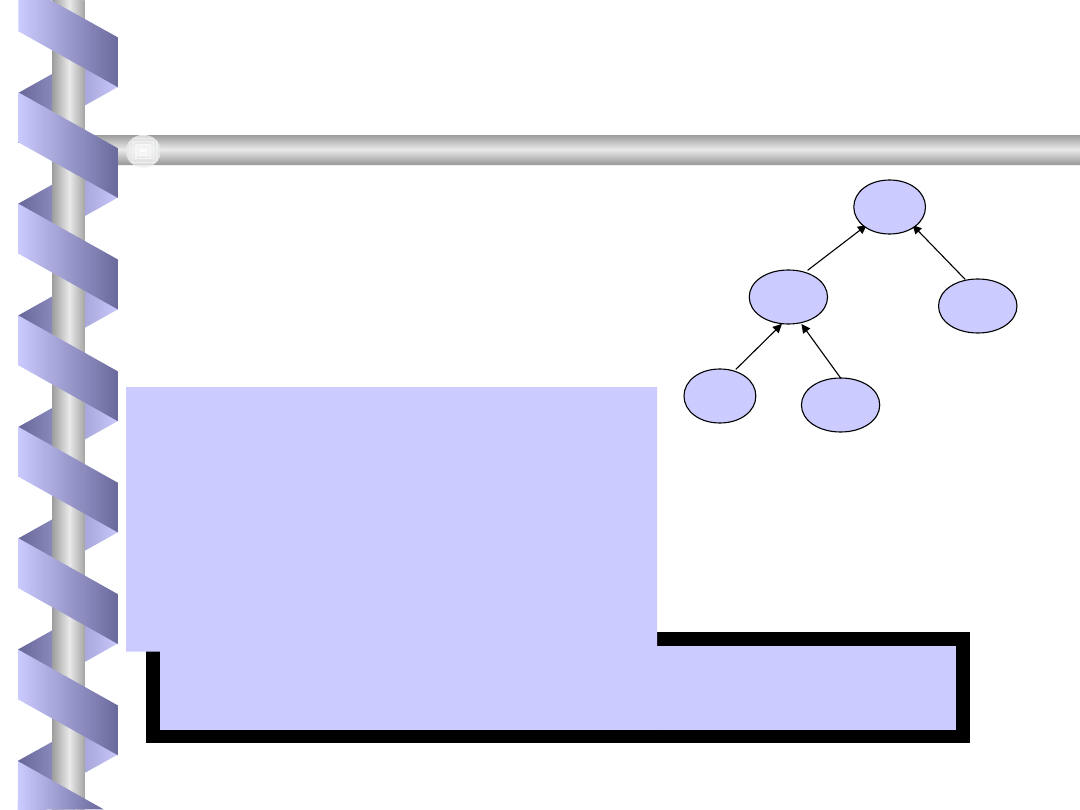
x + y = (x,y)

Jak policzyć

wartość

tego wyrażenia?

Czyli ustalić

strukturę

danych STR i

wartościowanie v

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

13

Przykład

Przykład

(2) Stosy |= (e) (s)

top(pop(push(e, s))) =

top(s)

(1) N, (x/1,y/3) |= (x + y >2 )

Zatem mamy też
N |= ( x) ( y) (x + y

>2 )

oraz N |= (z) ( x) ( y) (x +

y >z )

(x+y) * z

x/ 3

y/5

z/ 3

+

*

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

14

Tautologie

Tautologie

Definicja Formułę rachunku funkcyjnego nazywamy
tautologią(lub prawem rachunku funkcyjnego), jeżeli jej
wartością jest prawda, niezależnie od wartości
zmiennych oraz interpretacji symboli relacyjnych i
funkcyjnych w niej występujących

Przykłady.  (x)  (x)

xxyxxy(y)

xxxx

Jeśli  jest prawem rachunku

zdań,
to podstawiając za zmienne
zdaniowe występujące w ,

dowolne formuły rachunku
funkcyjnego otrzymujemy
tautologię rachunku
predykatów.

Dowód (*) Gdyby ta
implikacja była fałszywa
przy pewnej interpretacji
formuły xw niepustym

uniwersum X, wtedy byłoby
{xX: x}=Xoraz {xX:

x}= . Czyli X=  ,

sprzeczność.

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

15

Przykłady tautologii

Przykłady tautologii

Następujące formuły są prawami rachunku predykatów (są
tautologiami)

(1)x xx xprawa de Morgana

(2) x x xx

(3) x(x)(x))x xx(x))

(4)x(x)(x))x xx(x))

(5) x(x))x(x)o ile zmienna x nie

występuje w 

prawo włączania i

wyłączania kwantyfikatorów


Oznaczenie Zamiast „ jest tautologią rachunku

funkcyjnego” piszemy krótko |= .

Np.:x x

2

>x+1x x

2

>x+1

jest zdaniem prawdziwym w R

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

16

Reguły wnioskowania

Reguły wnioskowania

Reguły dowodzenia (reguły wnioskowania) są to
przekształcenia postaci



1



2



n



które pewnemu skończonemu zbiorowi formuł (formuł)


1

,..., 

n

, przyporządkowują formułę , w taki sposób, że

dla dowolnej struktury danych STR takiej, że STR |=


1

...  

n

, to STR |=  (tzn. wniosek też jest zdaniem

prawdziwym w strukturze STR).

przesłanki

wniosek

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

17

Przykłady reguł

Przykłady reguł

, 

 





x

x x



x





 x x

x nie występuje w 

Reguła odrywania

Reguła uogólniania

Reguła dołączania kwantyfikatora

egzystencjalnego

Ad (*) Przypuśćmy, że

(1) STR |=
x



oraz (2) nie

zachodzi
STR |=  x

xWtedy z (2)

dla pewnego
wartościowania v mamy
STR,v |=  x x

STR,v |=  Czyli dla

pewnego a STR,
STR,v(x/a) |= x

STR,v(x/a) |=  
Tzn. STR,v(x/a) |=
x



Sprzeczność

z (1).

Wniosek

To są poprawne

reguły wnioskowania

w rachunku predykatów

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

18

Zastosowanie

Zastosowanie

Rozważmy program

{
z:= x; y :=1;m :=
n;

while (m  0)

{ if odd(m)
{ y := y

*

z; }

m := m div 2;
z := z

*

z;

}
}

z

m

*

y = x

n

/*Gdy m
nieparzyste*/

z

m

*

y = x

n

oraz m=0

z

m

*

y = x

n

Odd(m)  (z

*

z)

mdiv 2

*

y

*

z =x

n

lub

Odd(m)  (z

*

z)

mdiv 2

*

y =x

n

z

m

*

y = x

n

14 listopada 2001

Matematyka Dyskretna Rachu
nek funkcyjny, G.Mirkowska,
PJWSTK

19

Zastosowanie

Zastosowanie

Niech będzie rodzina podzbiorów zbioru
X, ( A

i

) i I oraz funkcja f : X -> Y.

Udowodnimy, że

f(



A

i

) 



f(A

i

)