Rachunek

prawdopodobieństwa

w SKJ

Czym jest teoria

prawdopodobieństwa, rachunek

prawdopodobieństwa oraz

probablistyka?

- zdarzenie losowe,

- prawdopodobieństwo.

- zmienna losowa,

Elementy rachunku

prawdopodobieństwa:

1. Zdarzenie losowe:

Dany podzbiór zbioru zdarzeń elementarnych.

• U – zdarzenie pewne,
• V – zdarzenie niemożliwe,
• A – zdarzenie losowe (A  Ω)

Jeżeli w procesie losowania zmienna losowa x

przyjęła wartość ze zbioru A to mówimy, że zaszło
zdarzenie A.

S= {A} – zbiór wszystkich zdarzeń

2. Prawdopodobieństwo:

Miara możliwości zajścia zdarzenia losowego.
Jeżeli w warunkach losowania zmienna
losowa X przyjmuje wartość to dane
zdarzenie A może zajść lub nie.
P(A) – prawdopodobieństwo zajścia zdarzenia
A
0 ≤ P(A) ≤ 1
P(V) = 0
P(U) = 1

Własności

prawdopodobieństwa:

a) 0 ≤ P(A) ≤ 1
Jeżeli P(A)=0, to A jest niemożliwe (V)
Jeżeli P(A)=1, to A jest pewne (U)
b) A,B  R,

Jeżeli A∩B=V to A,B wykluczają się wzajemnie
P(A∩B)= P(A) + P(B)
c) A,B  Ω

Jeżeli zajście zdarzenia A nie wpływa na prawdopodobieństwo

zajścia zdarzenia B, to A,B są niezależne.

Jeżeli A,B są niezależne to P(A∩B)= P(A)*P(B)
Własności A i B można rozszerzyć na większą liczbę zdarzeń.

3. Zmienna losowa:

Funkcja odwzorowująca zbiór zdarzeń, zbiór

wartości.

x - liczba
x єΩ - liczba losowa jako wynik losowania
Ω - zbiór wartości zmiennej losowej
Liczba losowa x jest wartością zmiennej losowej

X.

Zmienna losowa jest zmienną, która przyjmuje

wartości liczbowe ze zbioru Ω w sposób
losowy.

4. Rodzaje zmiennych

losowych:

a) skokowa:

b) ciągła:

a) skokowa:

Rozkład zmiennej losowej skokowej:
P(X=xi)=pi
∑pi=1
Wartość oczekiwana : E(X)= ∑ xipi
Wariancja: D2(X)= ∑ (xi – E(X))2 * pi
Odchylenie standardowe: D(X)=√
D2(X)

b) ciągła:

Funkcja f(x) gęstości prawdopodobieństwa określa

rozkład zmiennej losowej ciągłej.
Własności:
- f(x)0 funkcja nieujemna
- -∞∫+∞ f(x)dx=1
P(x1<x<x2)= x1∫x2 f(x)dx
P(X=x)= x∫x f(x)dx=0
P(x<X<x+dx)=f(x)dx
Wartość oczekiwana: E(X)= -∞∫+∞ xf(x)dx
Wariancja: D2(X)= -∞∫+∞ [x- E(X)]2 f(x)dx
Odchylenie standardowe: D(X)=√ D2(X)

5. Trzy ważne rozkłady

zmiennych losowych:

1) Rozkład dwumianowy
2) Rozkład Poissona
3) Rozkład normalny

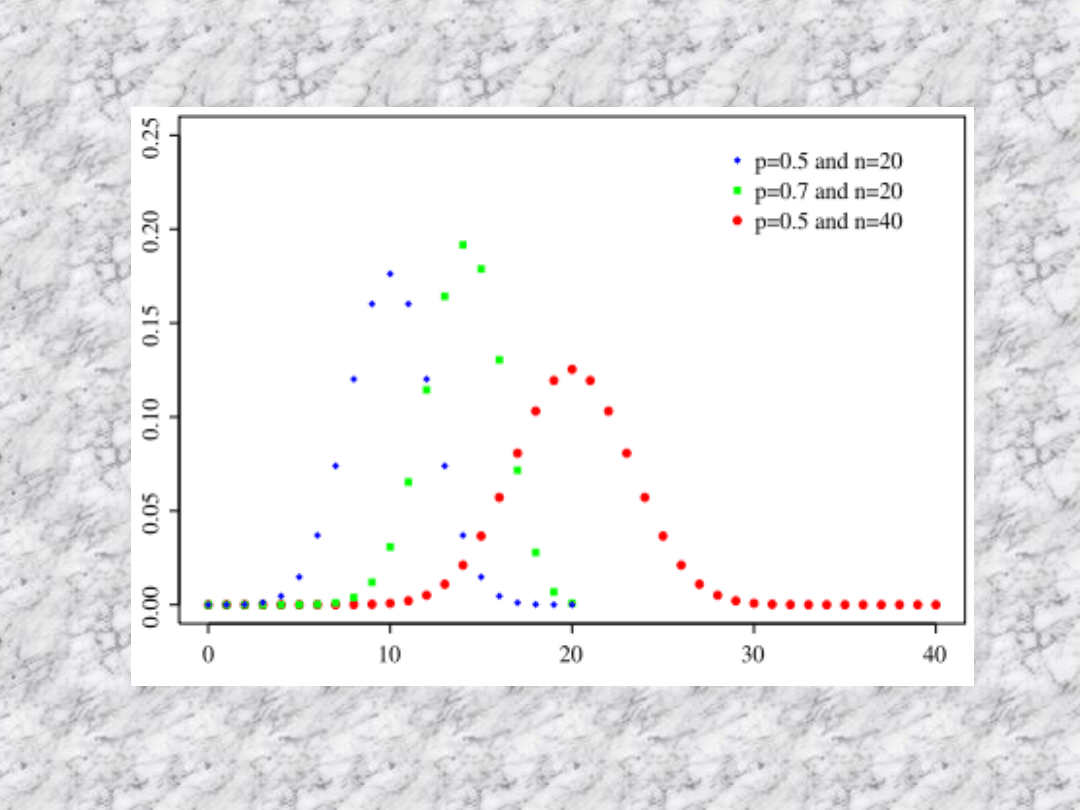
Rozkład dwumianowy

(Bernullego)

p- prawdopodobieństwo sukcesu,

1 – p- prawdopodobieństwo porażki,
n- liczba doświadczeń,
k- liczba sukcesów w „n” doświadczeniach.

P(X=k)= (nk)*pk (1-p)n-k - rozkład

dwumianowy
Wartość oczekiwana: E(X)= np
Wariancja: D2(X)= np(1-p)

Przykład:

Wadliwość żarówek wynosi 10%.

Bierzemy 10 żarówek. Jakie jest

prawdopodobieństwo, że maksymalnie

2 żarówki będą wadliwe?
p= 0,1 ; n= 10
P(X≤2)=P(X=0)+P(X=1)+P(X=2)=

(100)*0,10*0,910+(101)*0,11*0,99+(1

02)*0,12*0,98 = 0,93

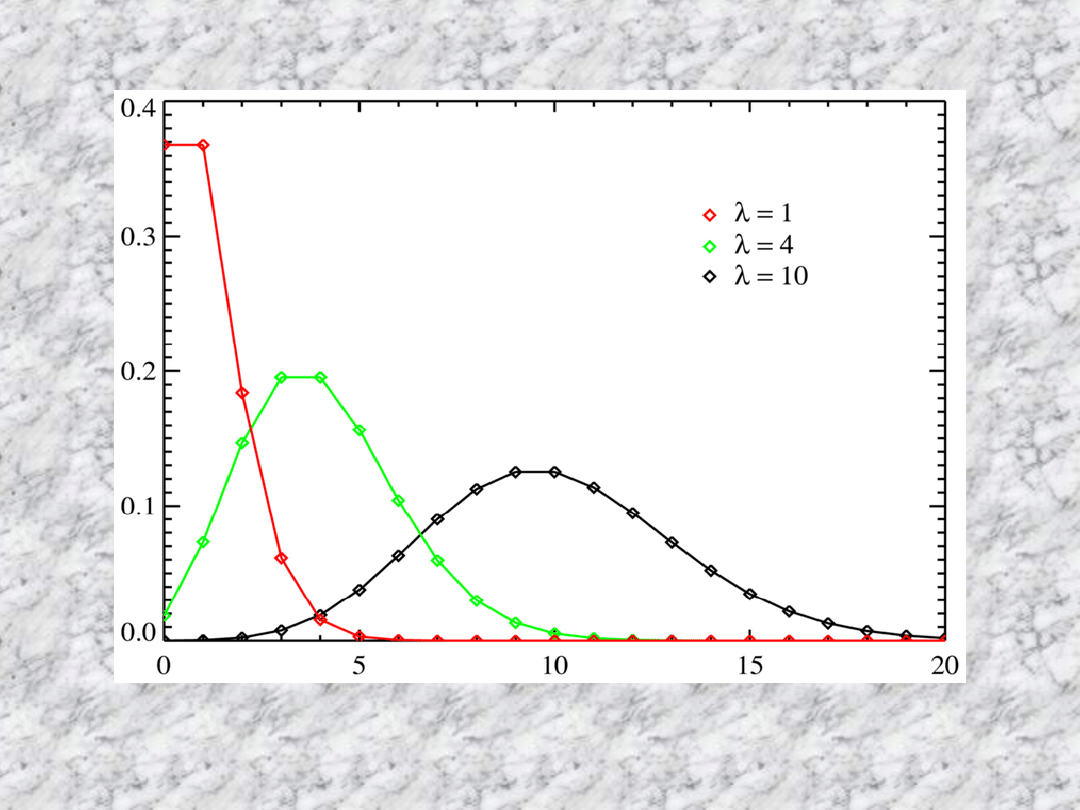
Rozkład Poissona (rozkład

zdarzeń rzadkich)

λ (parametr rozkładu) – spodziewana
liczba zdarzeń rzadkich
E(X)= λ
x- zmienna losowa skokowa
określająca liczbę zdarzeń rzadkich
P(X=k)= (λk/k!)*e- λ
E(X)=D2(X)=x

Przykład:
Nie świecące piksele.
E(X)= λ = 1
Prawdopodobieństwo, że wszystkie
świecą: P(X=0)= (10/0!)*e- 1= 0,37
Prawdopodobieństwo, że 5 pikseli nie
świeci: P(X=5)= (15/5!)*e- 1= 0,0031

Rozkład Poissona jest rozkładem granicznym rozkładu

dwumianowego.

Przykład:
Jakie jest prawdopodobieństwo, że liczba sztuk niezgodnych

w tej próbie będzie ≤2.
p= 0,1 ; n= 30
Rozkład dwumianowy:
P(X≤2)= P(X=0)+P(X=1)+P(X=2)=

(300)*0,10*0,930+(301)*0,11*0,9229 +(302)*0,12*0,928=

0,411
Rozkład Poissona:
λ= np= 30*0,1= 3
P(X≤2)= P(X=0)+P(X=1)+P(X=2)= (30/0!)*e- 3+(31/1!)*e-

3+(32/2!)*e- 3= 0,422

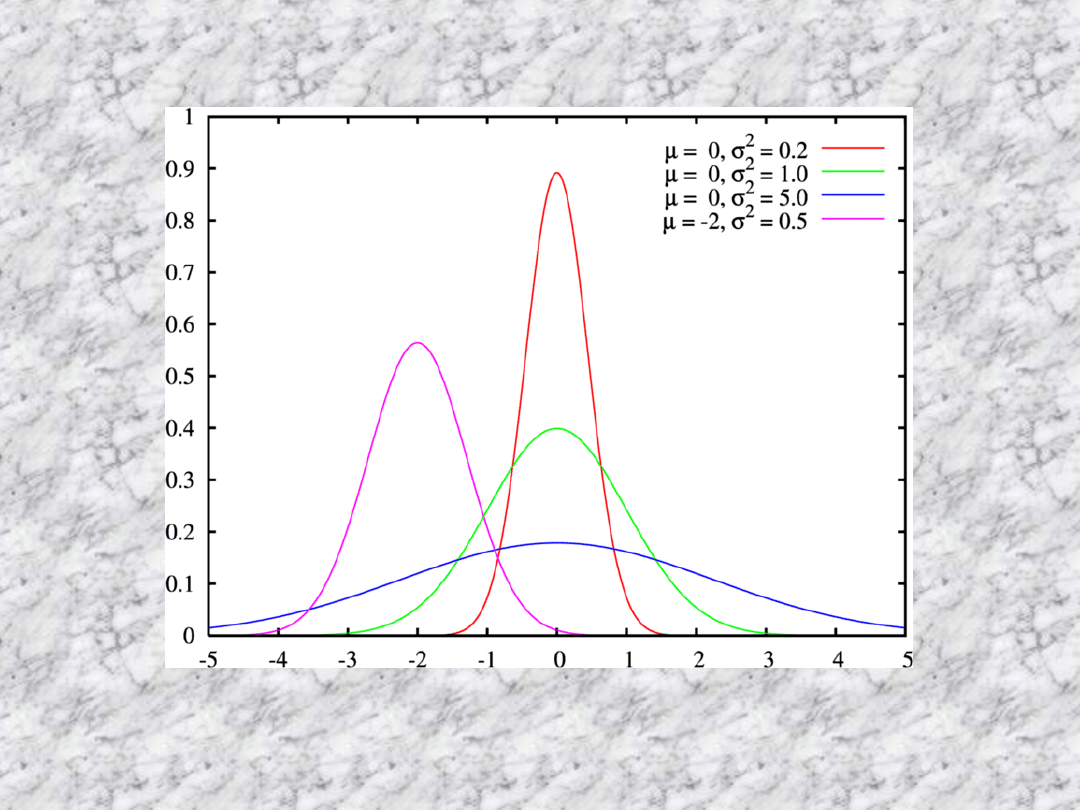
Rozkład normalny

Zwany też rozkładem Gaussa, lub
krzywą dzwonową, jest jednym z
najważniejszych rozkładów
prawdopodobieństwa. Odgrywa
ważną rolę w statystycznym opisie
zagadnień przyrodniczych,
przemysłowych, medycznych,
socjalnych itp.

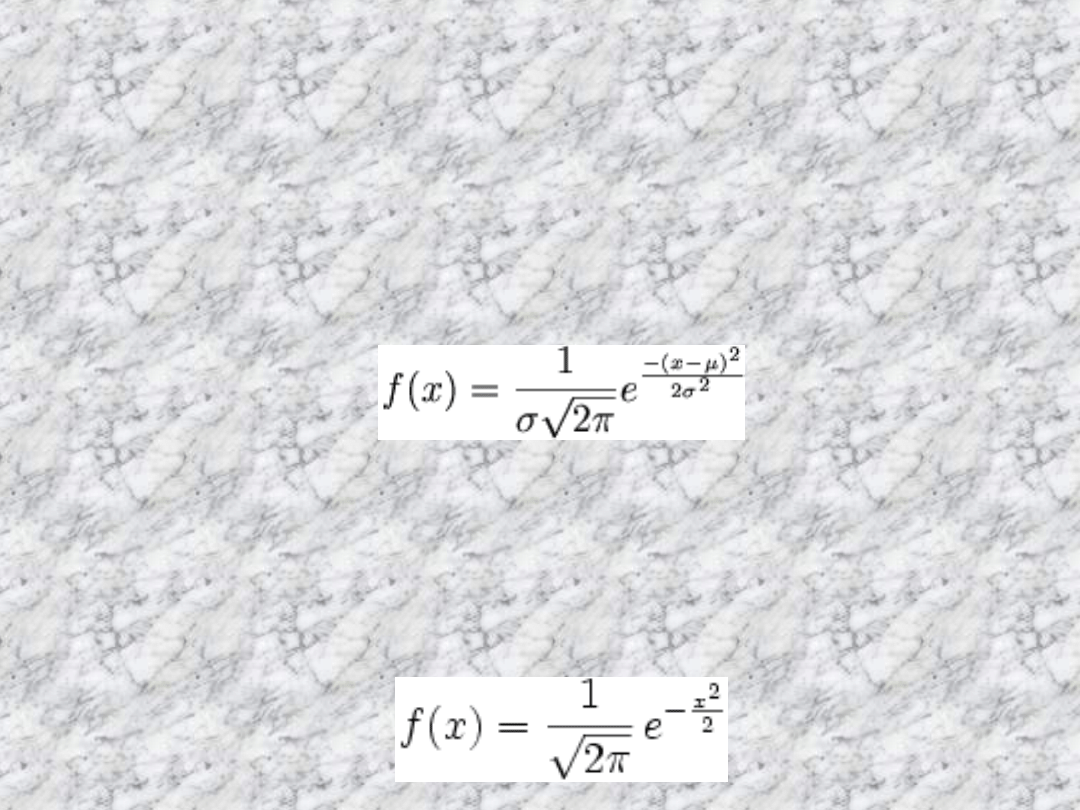
Funkcja gęstości dla rozkładu normalnego

ze średnią μ i odchyleniem standardowym σ

jest przykładem funkcji Gaussa.

Jeśli zmienna losowa X ma ten rozkład,

piszemy X ~ N(μ, σ²). Jeśli μ = 0 i σ = 1,

rozkład nazywamy standardowym

rozkładem normalnym, którego funkcja

gęstości opisana jest wzorem:

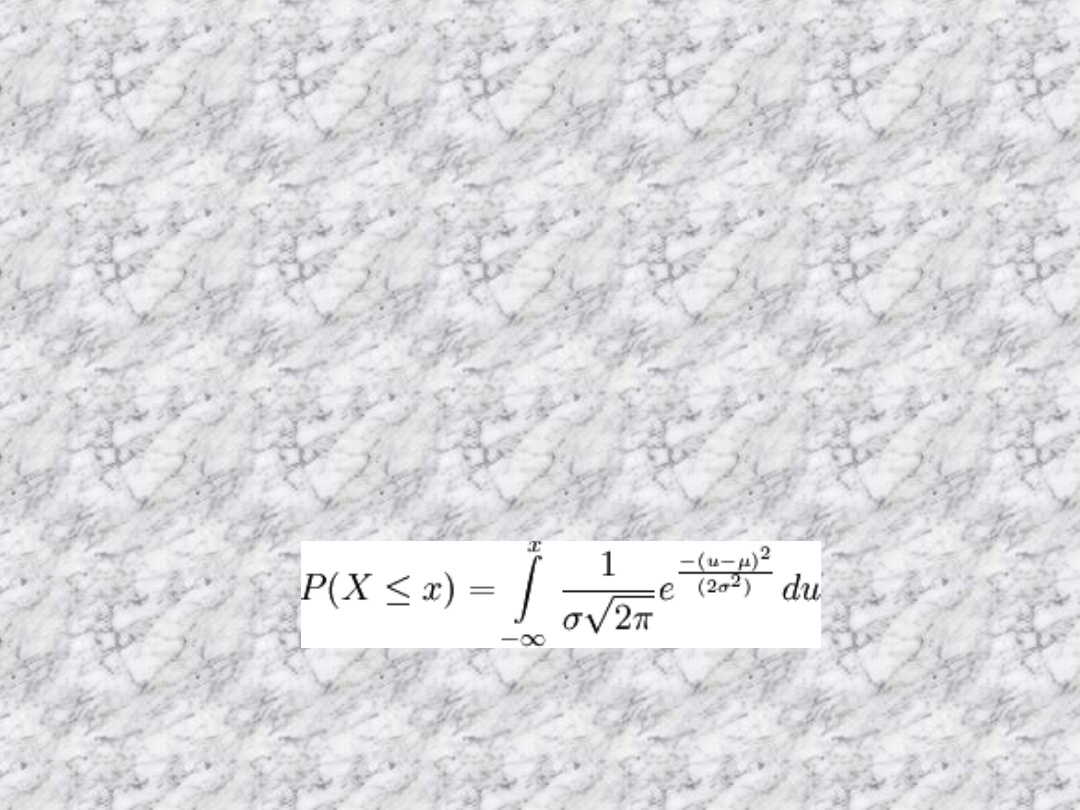
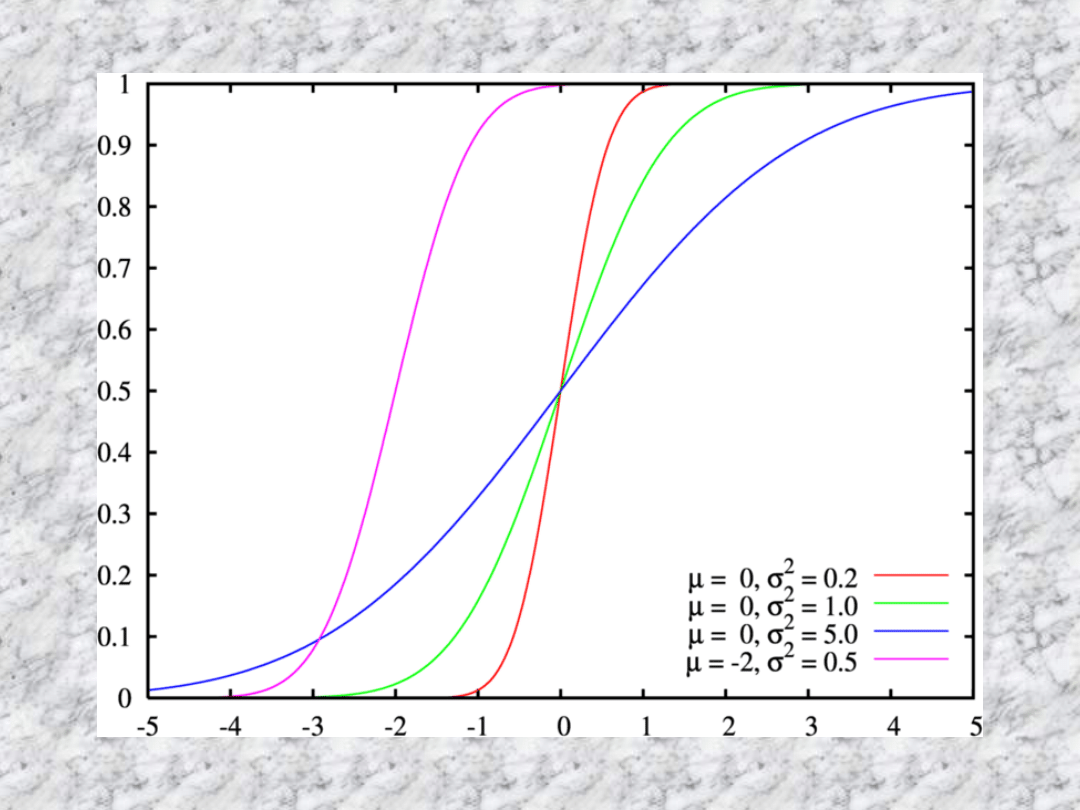
Dystrybuanta

Jest definiowana jako

prawdopodobieństwo tego, że
zmienna X ma wartości mniejsze
bądź równe x i w kategoriach funkcji
gęstości wyrażana jest (dla rozkładu
normalnego) wzorem:

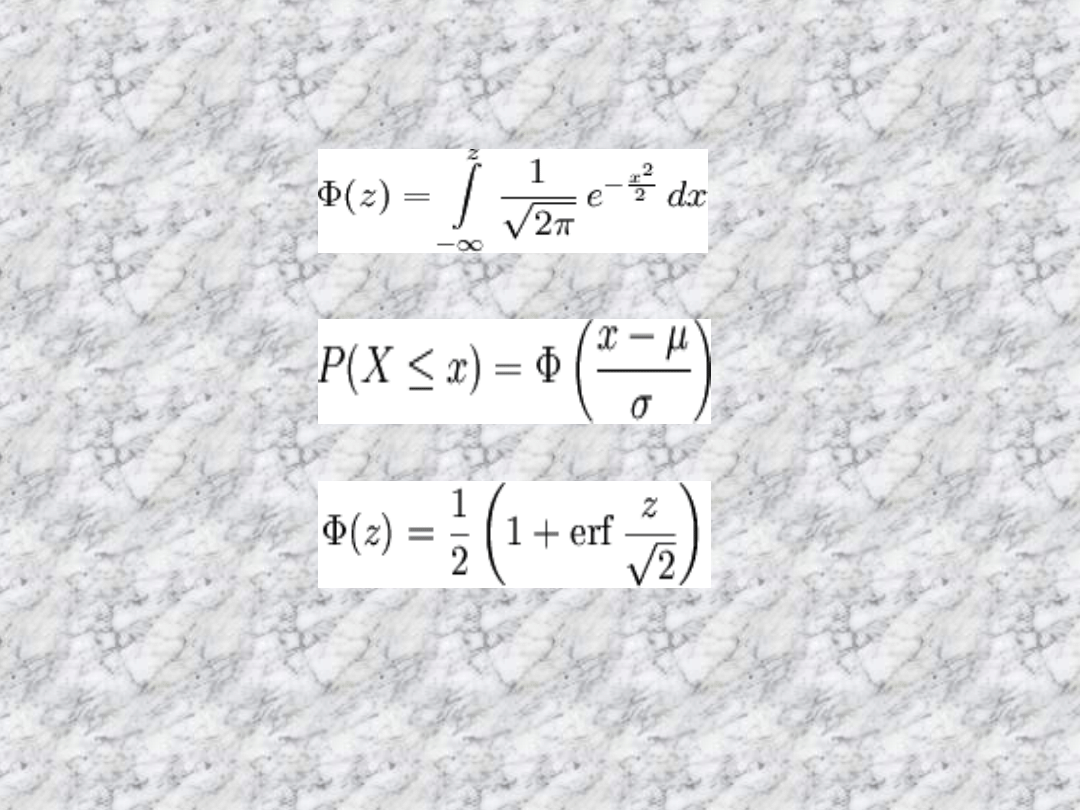
Rozkład Studenta

(rozkład t lub rozkład t-Studenta)
ciągły rozkład prawdopodobieństwa
stosowany często w statystyce w
procedurach testowania hipotez
statystycznych i przy ocenie błędów
pomiaru.

Rozkład Studenta z v stopniami swobody
jest rozkładem zmiennej losowej

gdzie U jest zmienną losową
zestandaryzowaną, czyli mającą
standardowy rozkład normalny ~ N(0,1), a Z
- zmienną losową o rozkładzie chi kwadrat i
v stopniach swobody oraz U i Z są
zmiennymi losowymi niezależnymi.

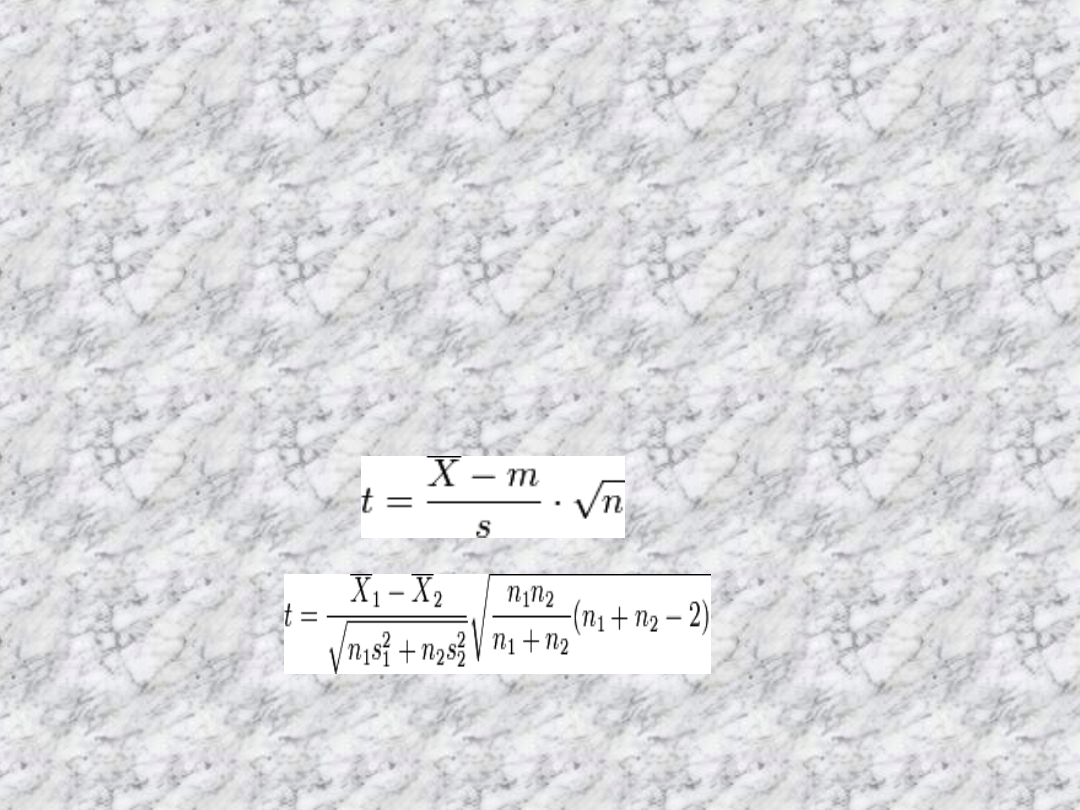
Zastosowania rozkładu Studenta w
metrologii i statystyce opierają się w
większości na następujących dwóch
twierdzeniach:
a)

b)

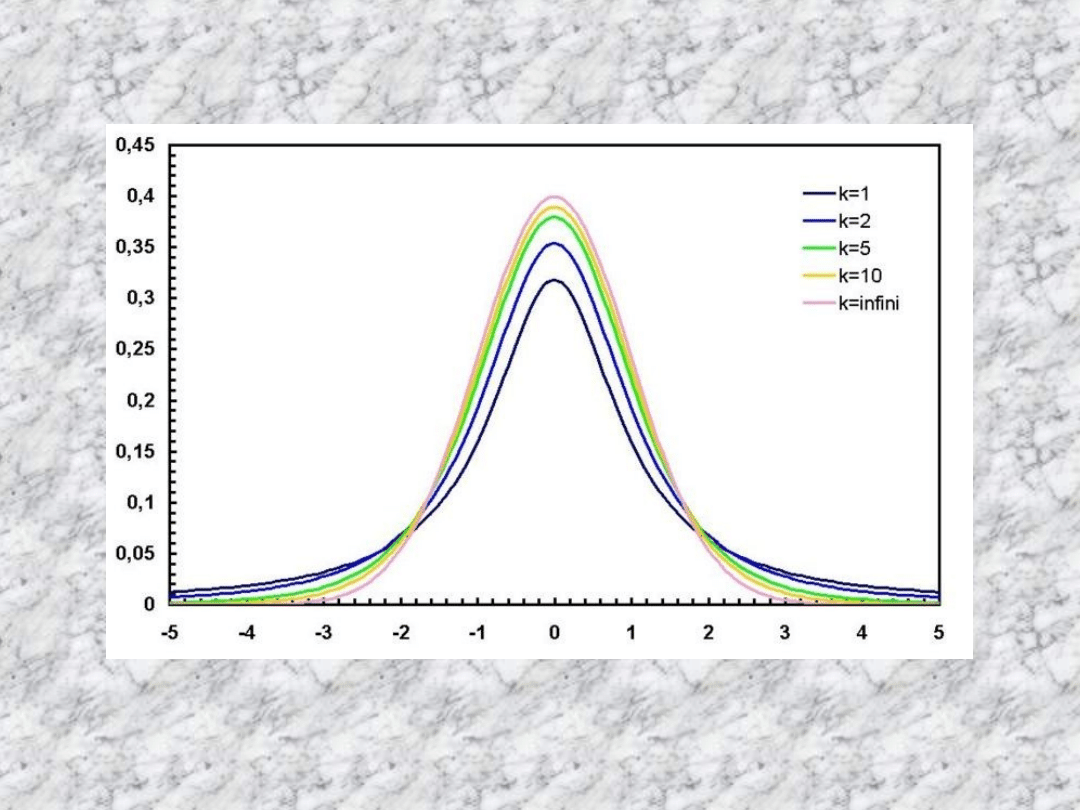
Rozkład chi kwadrat

(zapisywany także jako χ²) to rozkład
zmiennej losowej, która jest sumą k
kwadratów niezależnych zmiennych
losowych o standardowym rozkładzie
normalnym. Liczbę naturalną k
nazywa się liczbą stopni swobody
rozkładu zmiennej losowej.

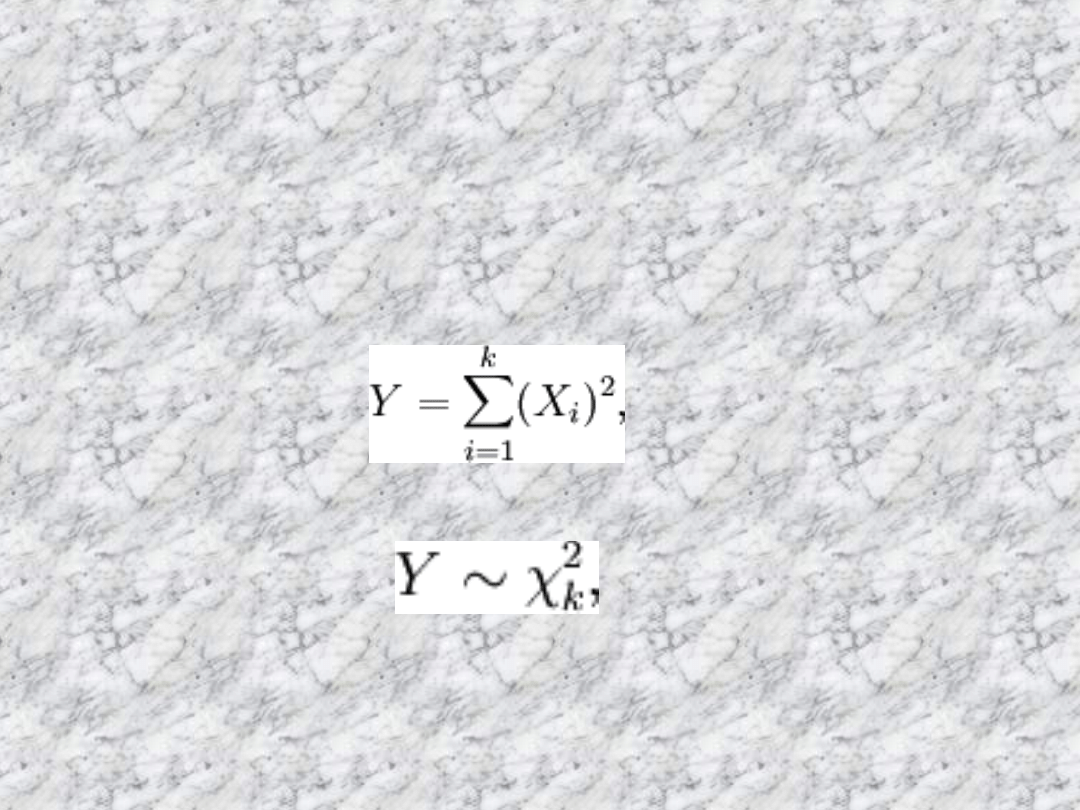
Jeżeli ciąg niezależnych zmiennych
losowych oraz:

To:

Koniec

Dziekujemy za uwage