1

Krystalizacja polimerów

POLITECHNIKA ŁÓDZKA

POLITECHNIKA ŁÓDZKA

WYDZIAŁ INŻYNIERII PROCESOWEJ I OCHRONY ŚRODOWISKA

WYDZIAŁ INŻYNIERII PROCESOWEJ I OCHRONY ŚRODOWISKA

Prof. dr hab. Maria Mucha

POLIMERY

8

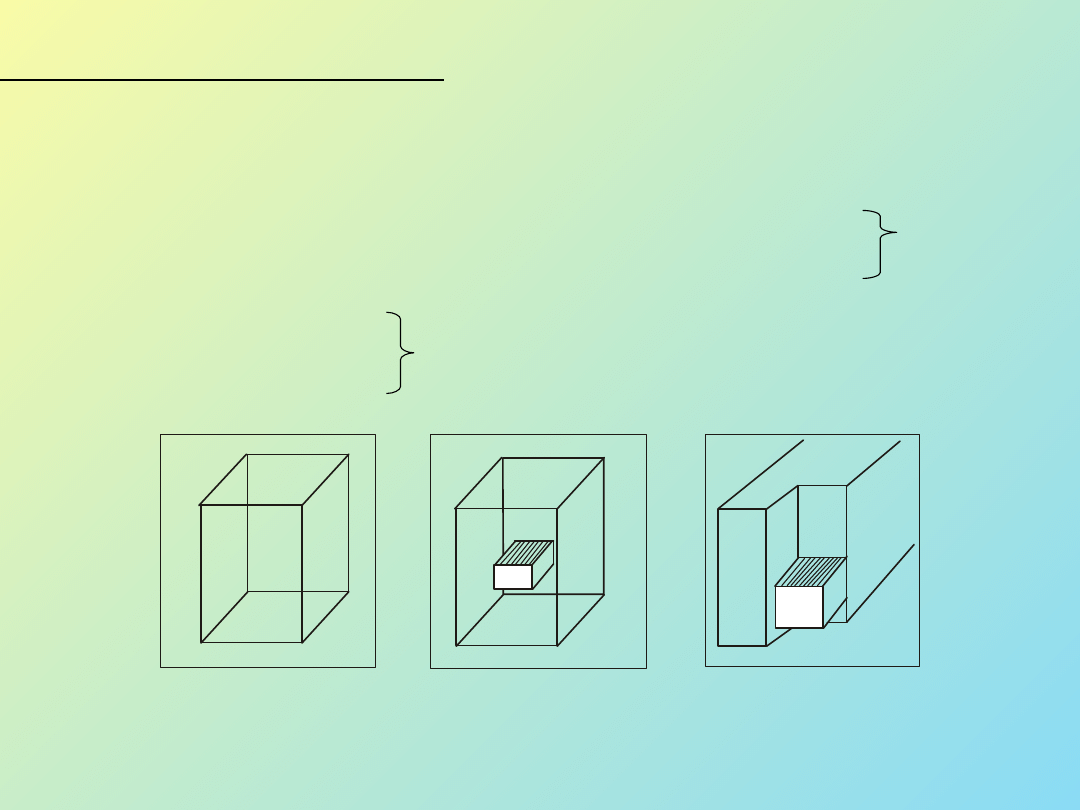
2

Krystalizacja polimerów:

1.Proces nukleacji - powstanie termodynamicznie stabilnych zarodków,
2.Proces wzrostu fazy krystalicznej.

Nukleacja homogeniczna (jednorodna);

I podział.

Nukleacja heterogeniczna (niejednorodna), (na domieszkach, granicach);

a) nukleacja pierwotna,
b) nukleacja wtórna,

II podział.

c) nukleacja trzeciorzędowa.

a )

b )

c )

a

b

l

a

b

l

a

b

l

Rys. 1 Graficzna prezentacja nukleacji

3

nukleacja termiczna, (zachodzi w czasie)

III podział.

nukleacja atermiczna, (wszystkie zarodki powstają natychmiast)

Krystalizacja to proces termodynamiczny:

w procesie krystalizacji następuje zmiana entalpii swobodnej G;

Entalpia swobodna:

 – właściwa energia

powierzchniowa,
A – powierzchnia kryształu,
G

v

– objętościowa entalpia swobodna,

G = G

kr

– G

st

G = H - TS

G

kr

=G

v

+ A

w temperaturze topnienia Tm G =0

Proces krystalizacji zachodzi poniżej Tm G <0

G = G

v

+ A

zmiana entalpii w

zmiana entalpii związana

zmiana entalpii związana
procesie krystalizacji

z różnicą objętości

z powstaniem

zarodka

(tzw. objętościowa)

po wszystkich

powierzchniach

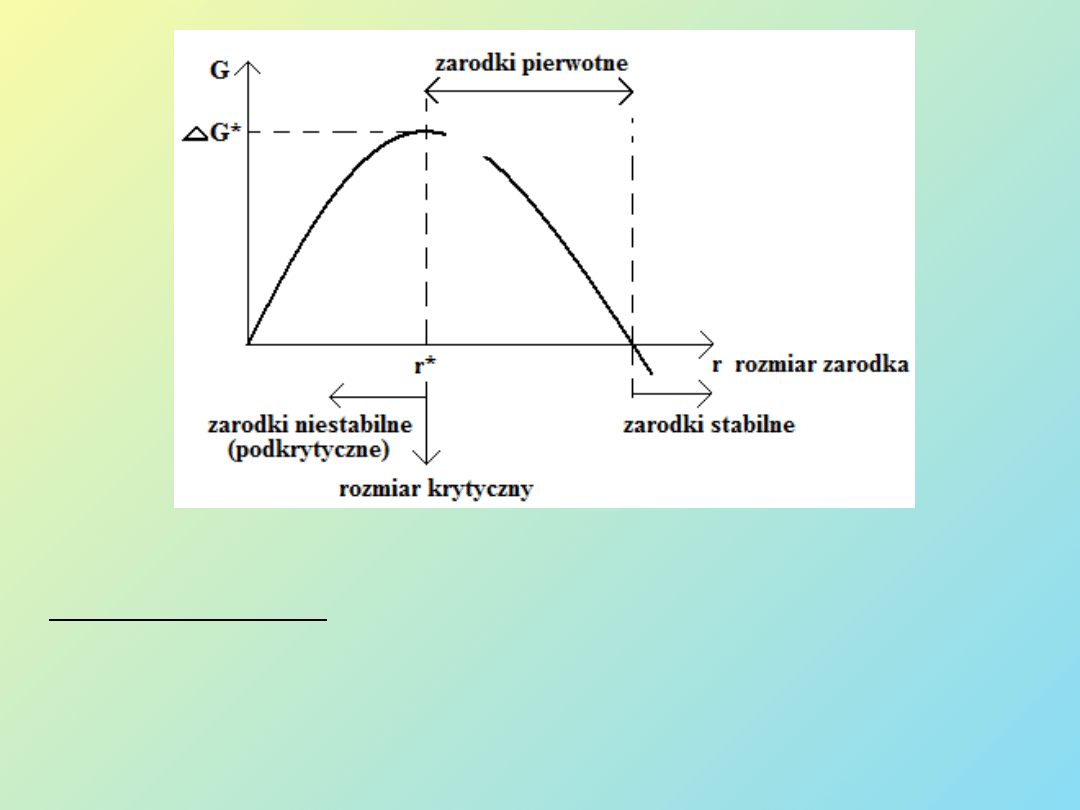
4

Rys. 2 Zależność

G od rozmiaru zarodka.

Proces nukleacji

Przyczyna powstania zarodków - termiczne fluktuacje konformacyjne
łańcuchów w stopie lub roztworze prowadzące do ciągłego tworzenia
się i rozpadania uporządkowanych ugrupowań cząsteczek.

(nadkrytycz

ne)

5

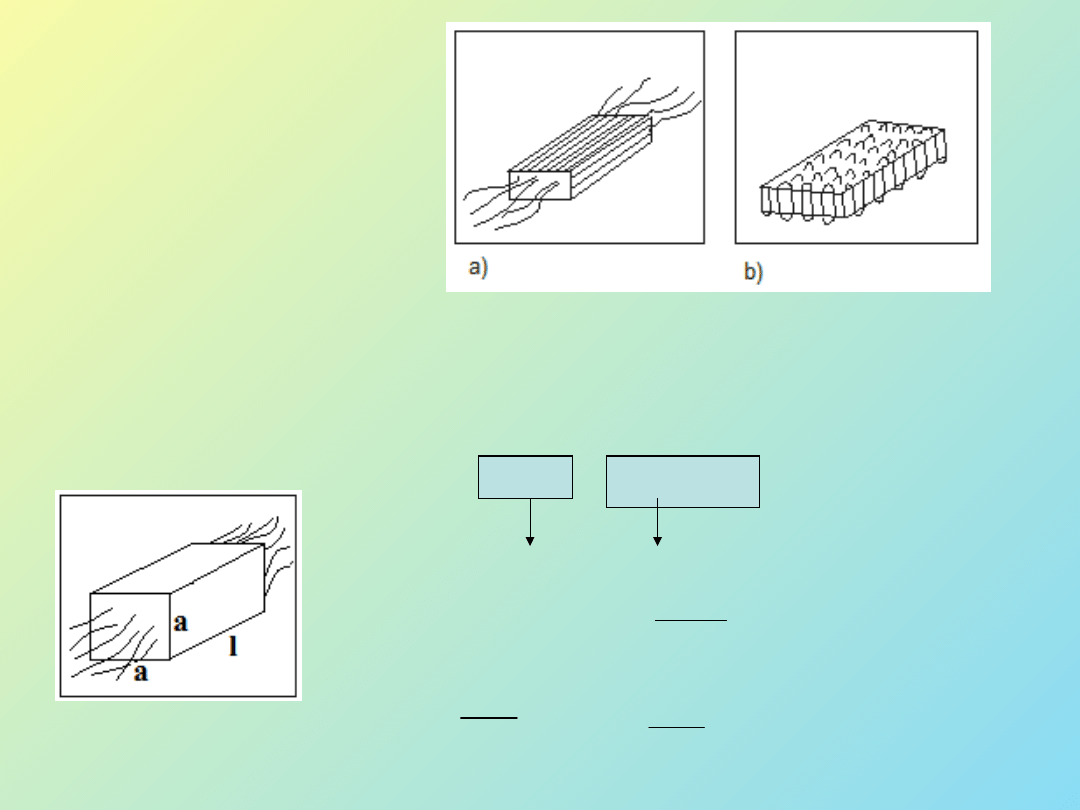
Kształty zarodków:
• kulisty (teoria
Gibbsa),
• prostopadłościenny,
• cylindryczny.

Rys. 3 Kształty zarodków w
polimerach:
a) micelarny (frędzlowaty), b)
lamelarny.

Pierwotna nukleacja, homogeniczna (prostopadłościenny zarodek micelarny);

G = -a

2

lg

f

+ 4al + 2a

2



e

G

v

A

dla rozmiaru krytycznego:

0

di

)

G

(

d





l

a

i

G

G

,

,

*









f

g

b

a









4

*

*

i

f

e

g

l







4

*

rozmiar krytyczny

6

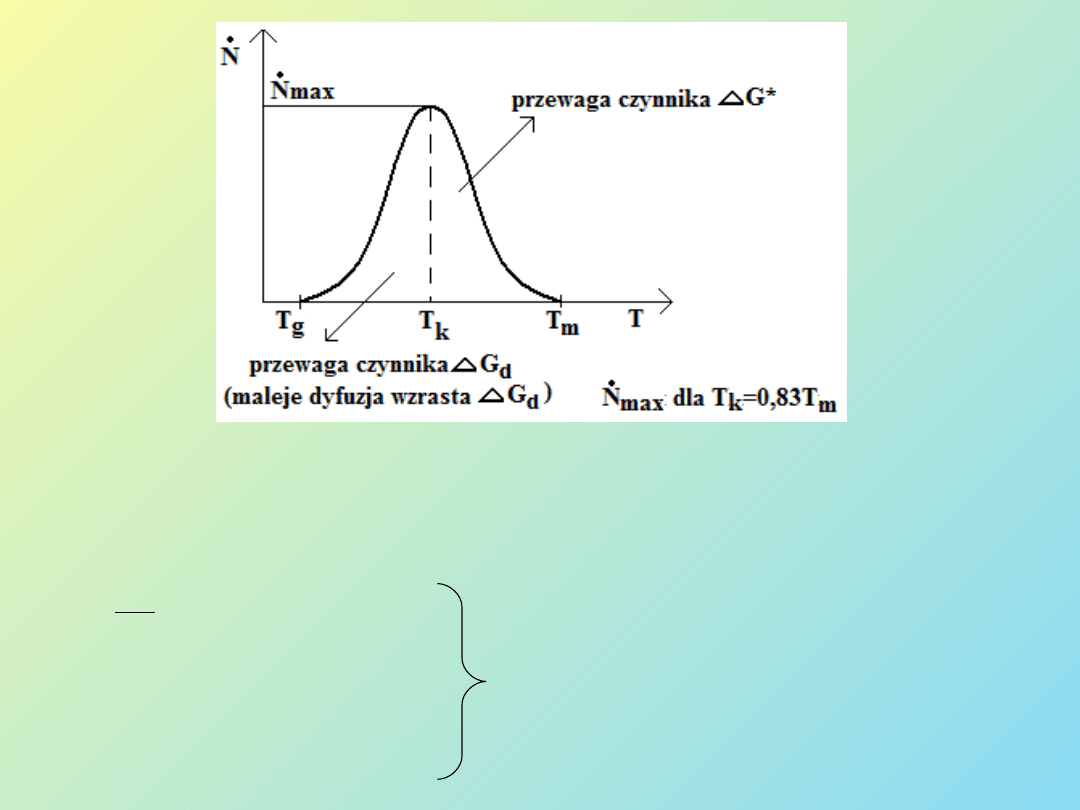
– równowagowa (termodynamiczna) temperatura topnienia,
T – przechłodzenie, różnica pomiędzy temperaturą topnienia, a

temperaturą np. krystalizacji,
h

v

– zmiana entalpii równa ciepłu topnienia (pod stałym ciśnieniem).

podstawiając

*

*

l

i

a

do

G



otrzymujemy

:

2

2

)

(

32

*

v

e

g

G











g

v

= h

v

–

TS

v

O

m

v

v

T

h

S







T

T

T

m







przechłodzenie

Wtedy:

O

O

O

O

m

v

m

m

v

m

v

v

v

T

T

h

T

T

T

h

T

h

T

h

g























gdzie:

o

m

T

7

Prawdopodobieństwo powstania zarodka w danym rozmiarze w stałej

objętości i energii

jest zgodne z prawem Boltzmanna

– liczba zarodków powstających w jednostce objętości i czasu,
– liczba segmentów (merów) biorących udział w nukleacji,
– temperatura krystalizacji,
– stałe Boltzmana i Plancka,
– temperatura zredukowana,
– molekularne ciepło parowania
– zmiana entalpii swobodnej dla powstania krytycznych
rozmiarów zarodka,
– zmiana entalpii związana ze swobodną energią aktywacji w
procesie dyfuzji
krystalizującego elementu przez powierzchnię granic
fazowych ciecz –
kryształ.





W

k

S

ln





)

kT

G

exp(

)

k

S

exp(

P











Szybkość nukleacji:

































kT

)

G

*

G

(

exp

h

N

d

kT

n



N













h

kT

*

G



d

G



h

k

T

n

,

v

h

















































2

v

2

m

e

2

d

)

T

(

h

kT

T

32

kT

G

exp

h

n

kT

N

8

Rys. 4 Zależność szybkości nukleacji od temperatury

Proces wzrostu fazy krystalicznej. Kinetyka krystalizacji – równanie Avramiego

Szybkość przemiany fazy ciekłej w stałą.

V

V

V

k

dt

dV

o

)

( 







o

V

objętość fazy ciekłej w t=0



V

objętość fazy ciekłej w t



 V

V

o

k – stała szybkości

objętość fazy krystalicznej

9

3

t

N

a

V

V

o







wzrost trójwymiarowy

2

t

N

a

V

V

o







wzrost dwuwymiarowy

a – czynnik kształtu,
n – wykładnik czasowy,
– szybkość nukleacji.

1









n

o

t

N

a

V

V

ogólnie:



N

Po scałkowaniu:



o

V

V

n

Kt

e

X







1

równanie Avramiego

X – stopień krystaliczności,
1-X – udział fazy ciekłej,
K – stała krystalizacji;

n

N

a

k

K









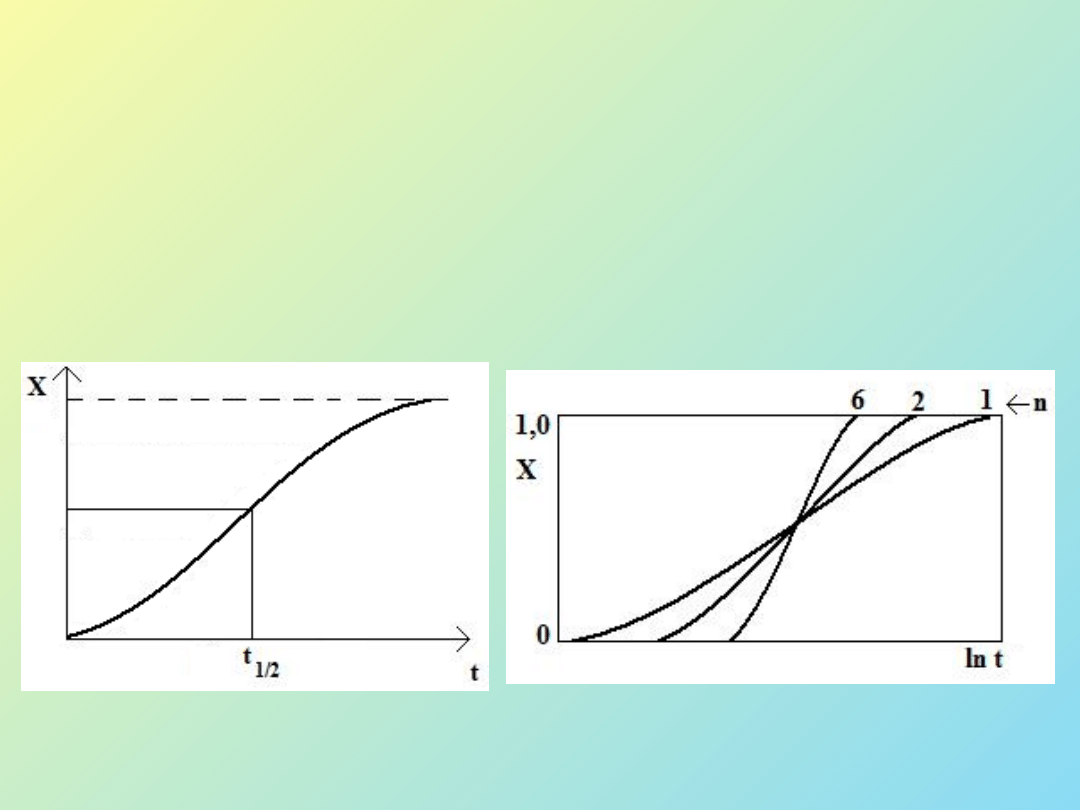
10

Rys. 5 Zależność stopnia krystaliczności od czasu

Równanie jest spełnione dla następujących założeń:
1. proces nukleacji jest I-go rzędu,
2. szybkość wzrostu jest stała,
3. gęstość krystalitów jest stała,
4. zarodki są rozmieszczone statystycznie,
5. brak nukleacji wtórnej.

Krzywe procesu krystalizacji:

2

/

1

t

- połówkowy czas krystalizacji

Rys. 6 Stopień krystaliczności X od ln t,
wpływ n na przebieg krzywej.

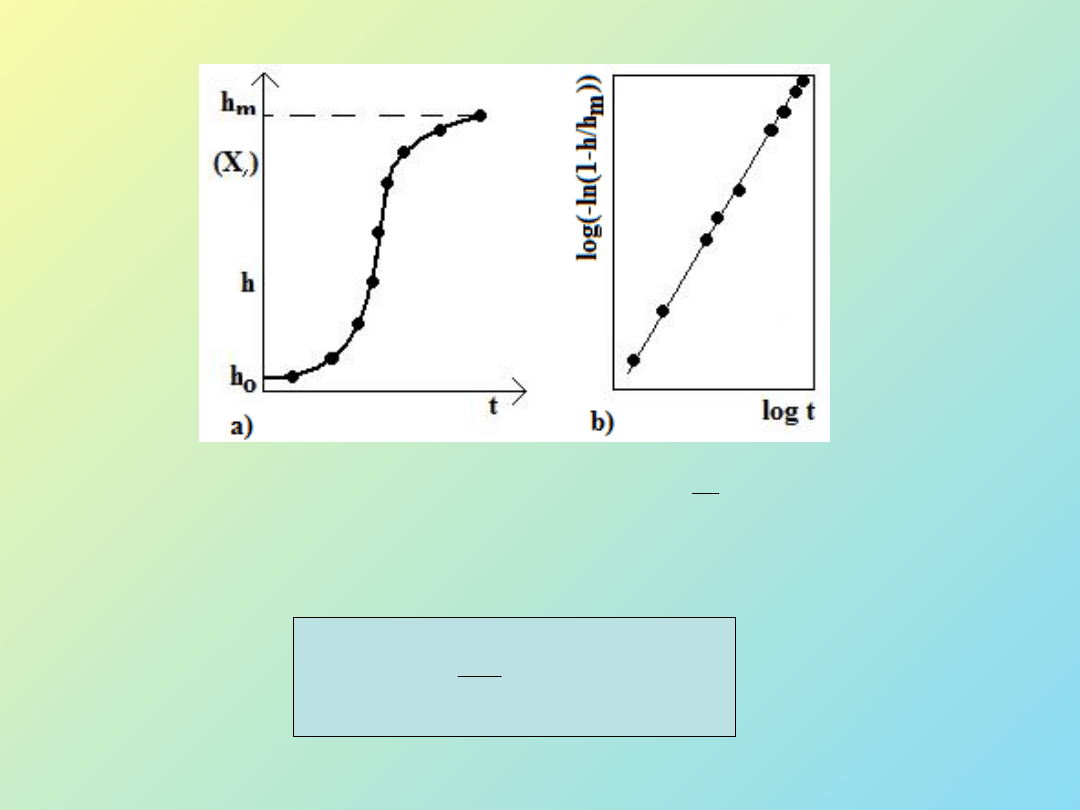
11

Experyment:

Rys. 7 a) Wykres h

m

od czasu t oraz b)































m

h

h

1

ln

log

od log t.

Eksperymentalne wyznaczanie k,n z zalezności:

logt

n

logK

h

h

1

ln

log

m

































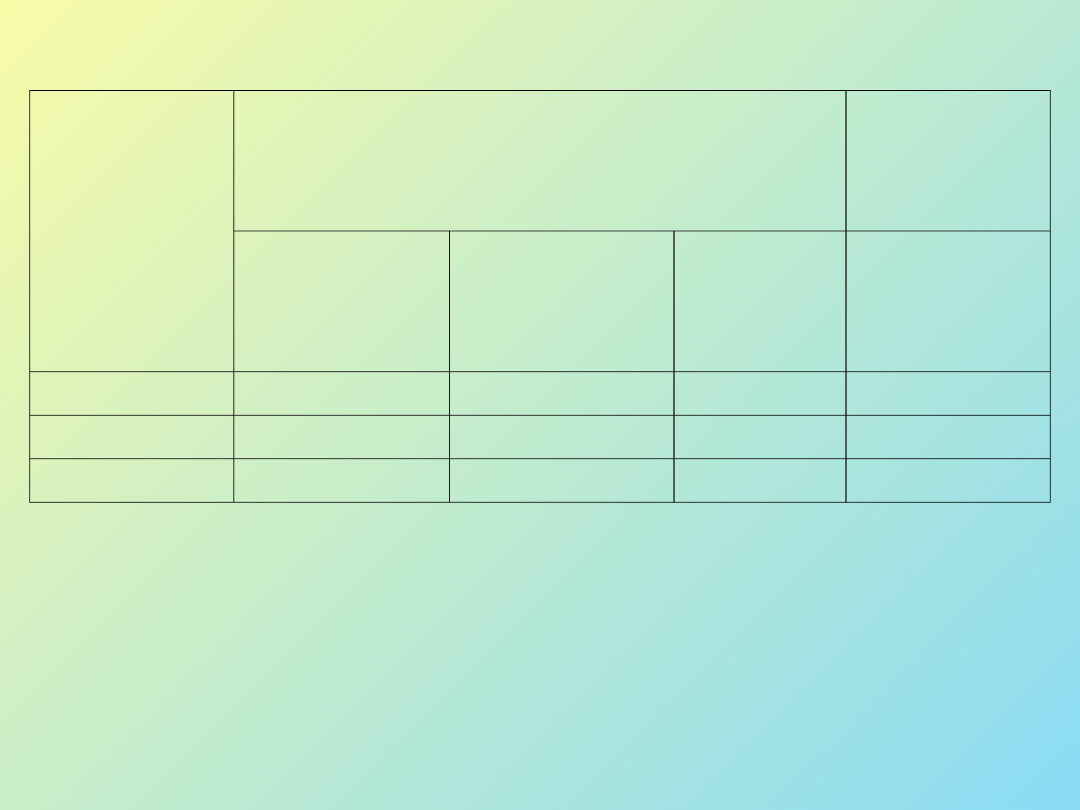
12

Wartości współczynnika n:

Wymiarowo

ść

wzrostu

kryształów

Nukleacja

Wzrost

kontrolowa

ny

dyfuzją

homogenicz

na

termiczna

heterogenicz

na

atermicz

na

3

4

3 < n < 4

3

5/2

2

3

2 < n < 3

2

2

1

2

1 < n < 2

1

3/2