Geometria wykreślna
i grafika komputerowa

Wykład 2

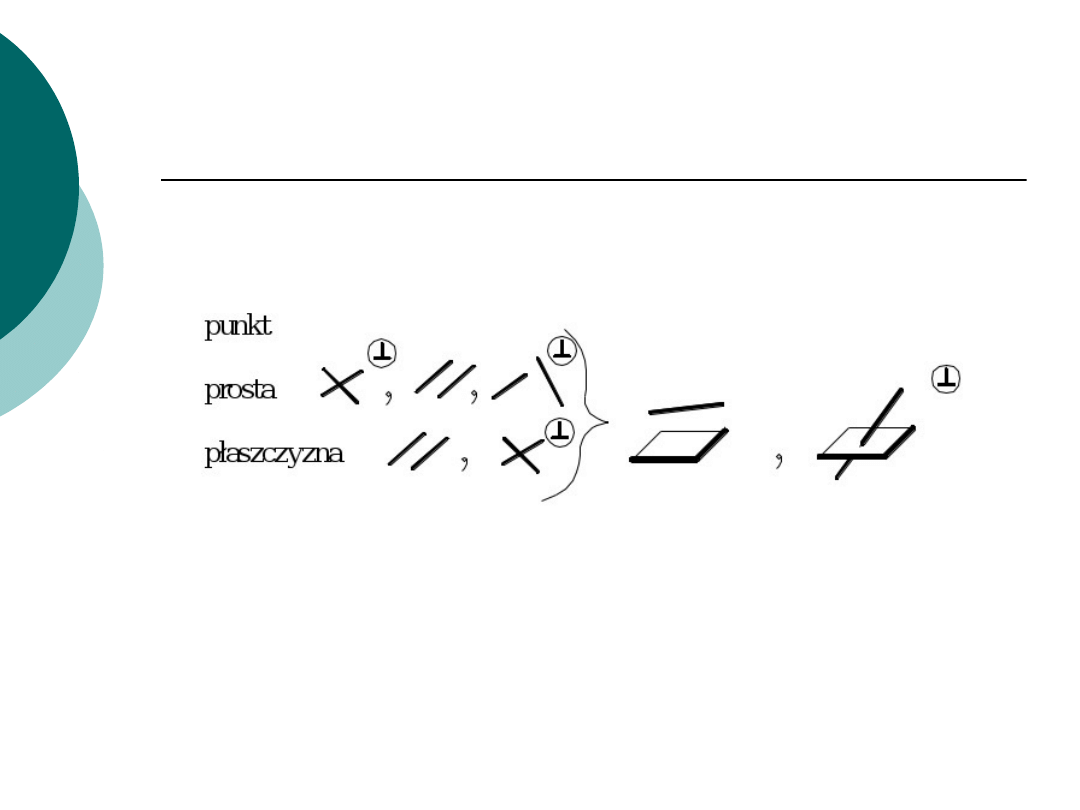
Wzajemne położenie

Proste przecinające się

Twierdzenie.

Warunkiem koniecznym

i wystarczającym

na to by dwie proste

a

i

b

przecinały się, z których żadna nie jest ani
równoległa, ani prostopadła do rzutni jest,
aby proste

a’

i

b’

przecinały się w punkcie,

mającym tę samą cechę na obu prostych,
oraz aby proste łączące punkty prostych

a’

i

b’

o tych samych cechach były równoległe.

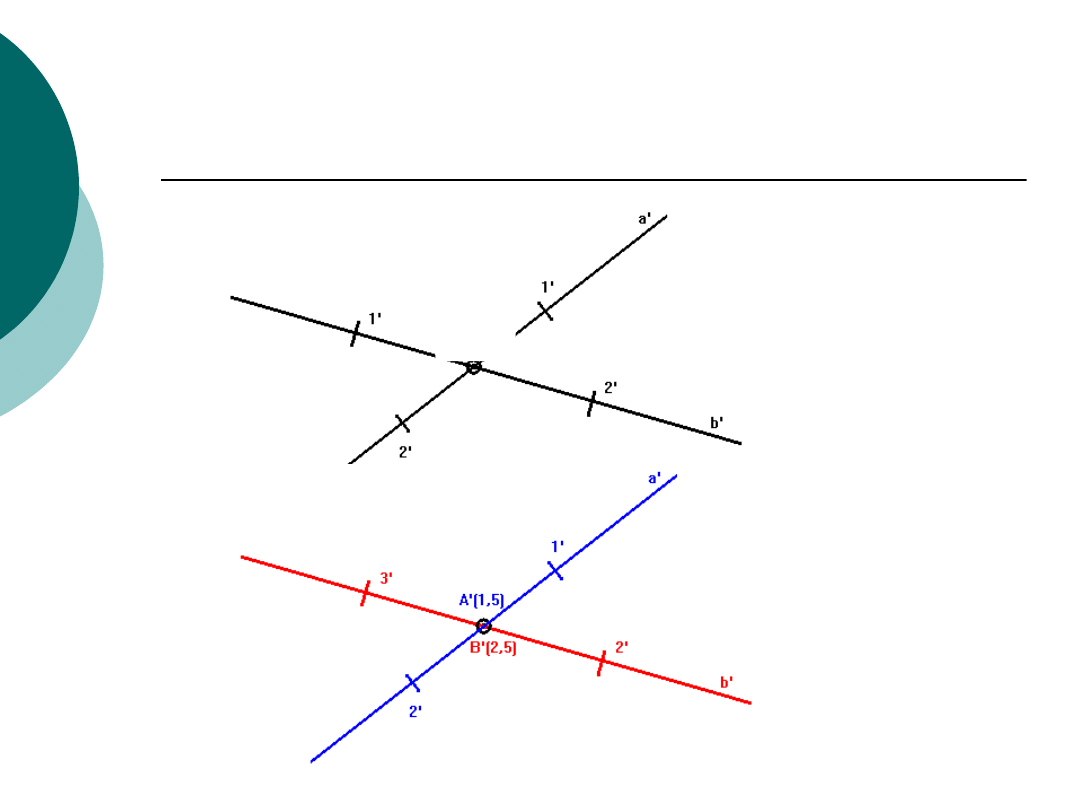
Proste przecinające się i
skośne

A’(2,5)

Równoległość prostych

Twierdzenie.

Wkw

równoległości dwóch

prostych

a

i

b

, z których żadna nie jest

ani równoległa, ani prostopadła do rzutni
jest, aby:

•

proste

a’

i

b’

miały ten sam kierunek





a

=



b

•

zwroty prostych

a’

i

b’,

określone

cechami punktów leżących na nich, były
zgodne

•

rzuty punktów głównych o tych samych

cechach były różnymi punktami

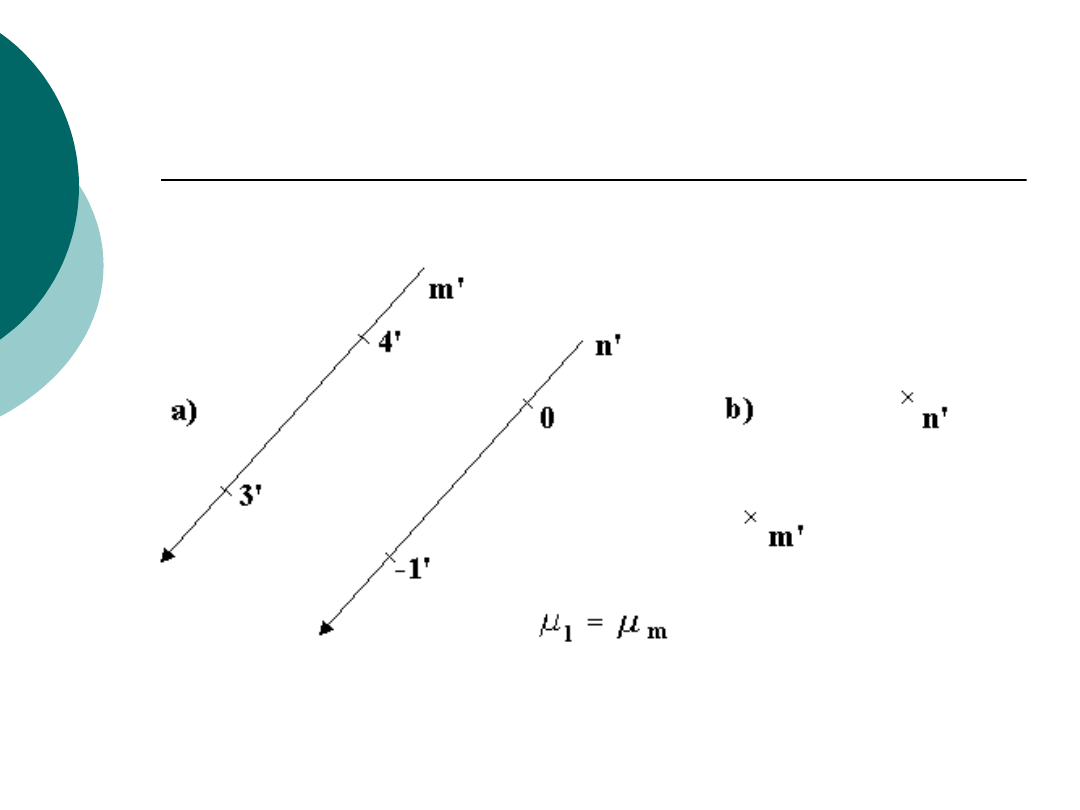
Równoległość prostych

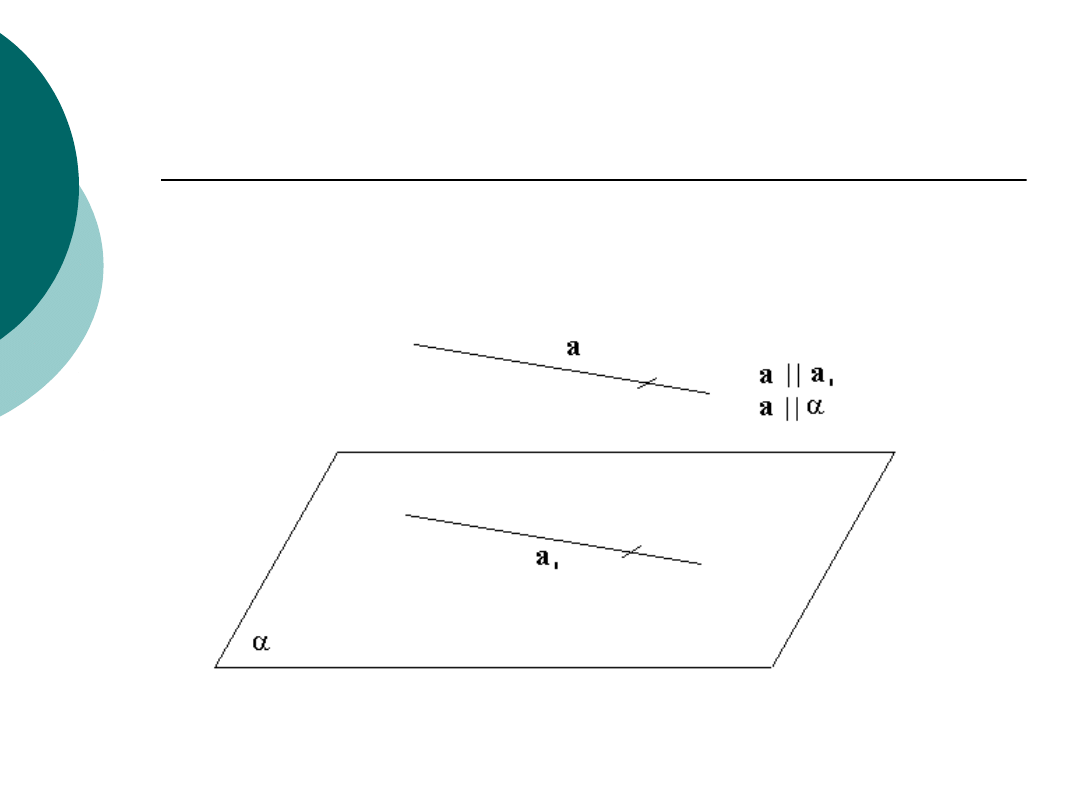
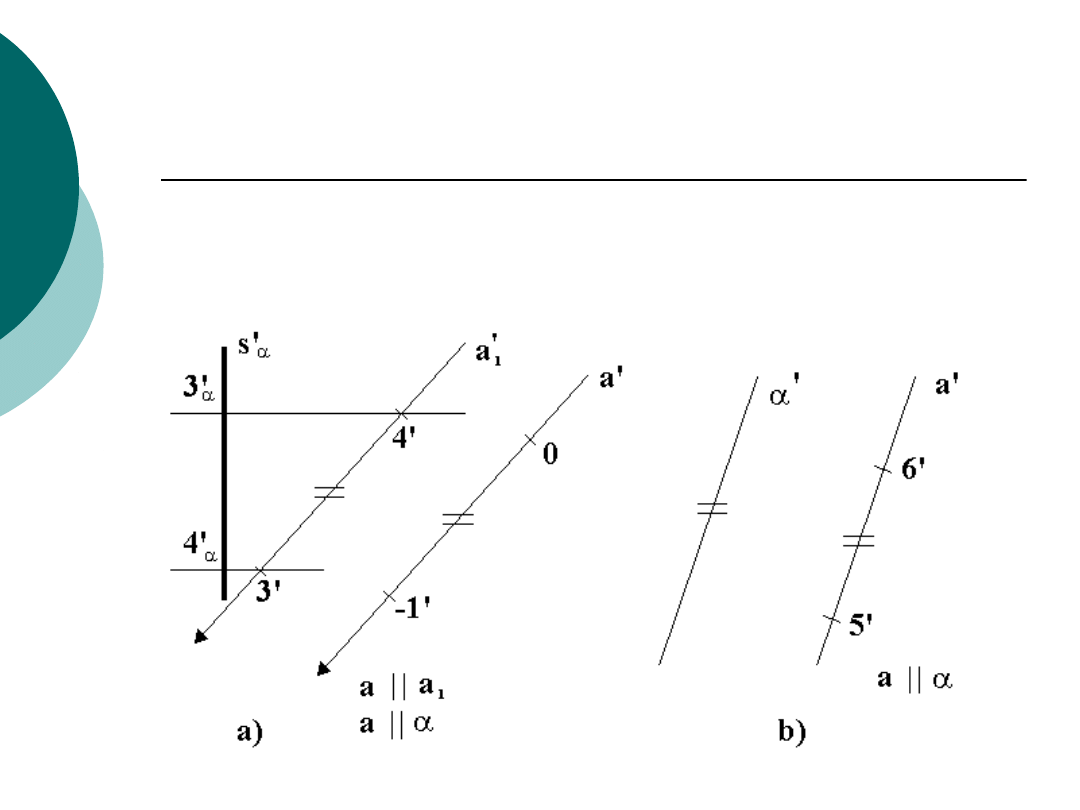
Równoległość płaszczyzny i prostej

Prosta a jest równoległa do płaszczyzny



, jeśli

istnieje prosta

b

taka, że

b||a

.

Równoległość płaszczyzny i prostej

Prosta

a

jest równoległa do płaszczyzny



, jeśli

istnieje prosta

b

taka, że

b||a

.

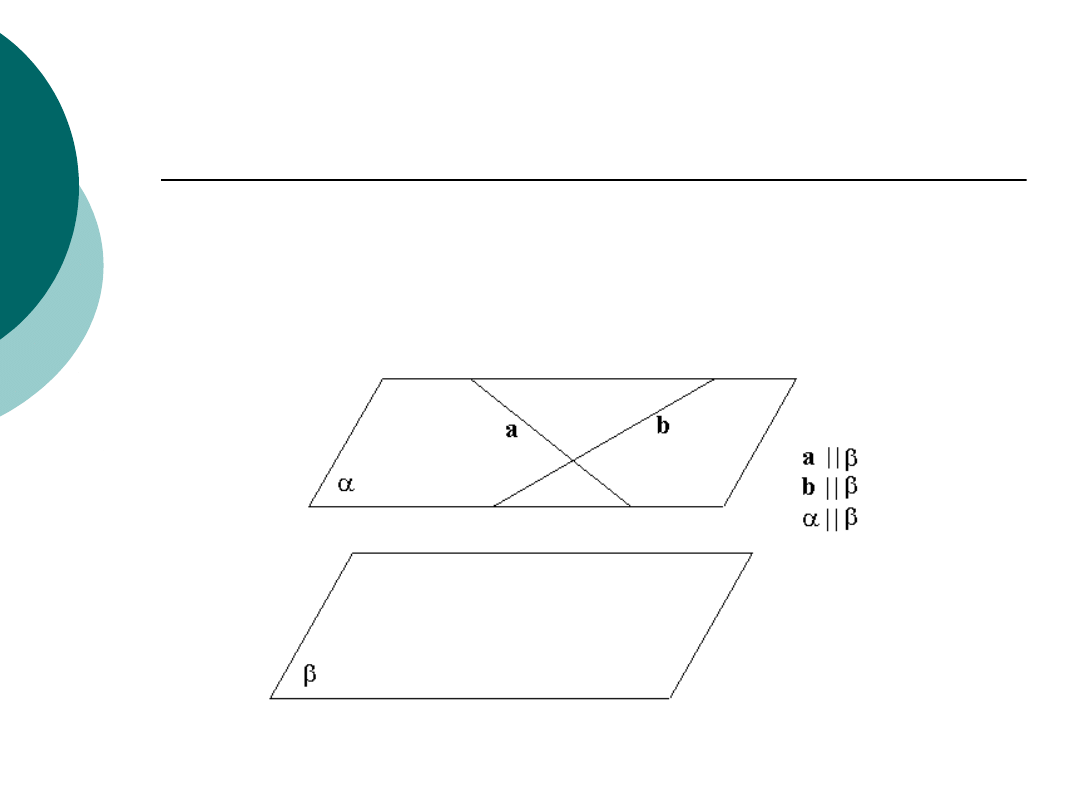
Równoległość płaszczyzn

Jeżeli w płaszczyźnie



istnieją dwie różne

proste

a

i

b

równoległe do płaszczyzny



, to

płaszczyzny



i



są równoległe

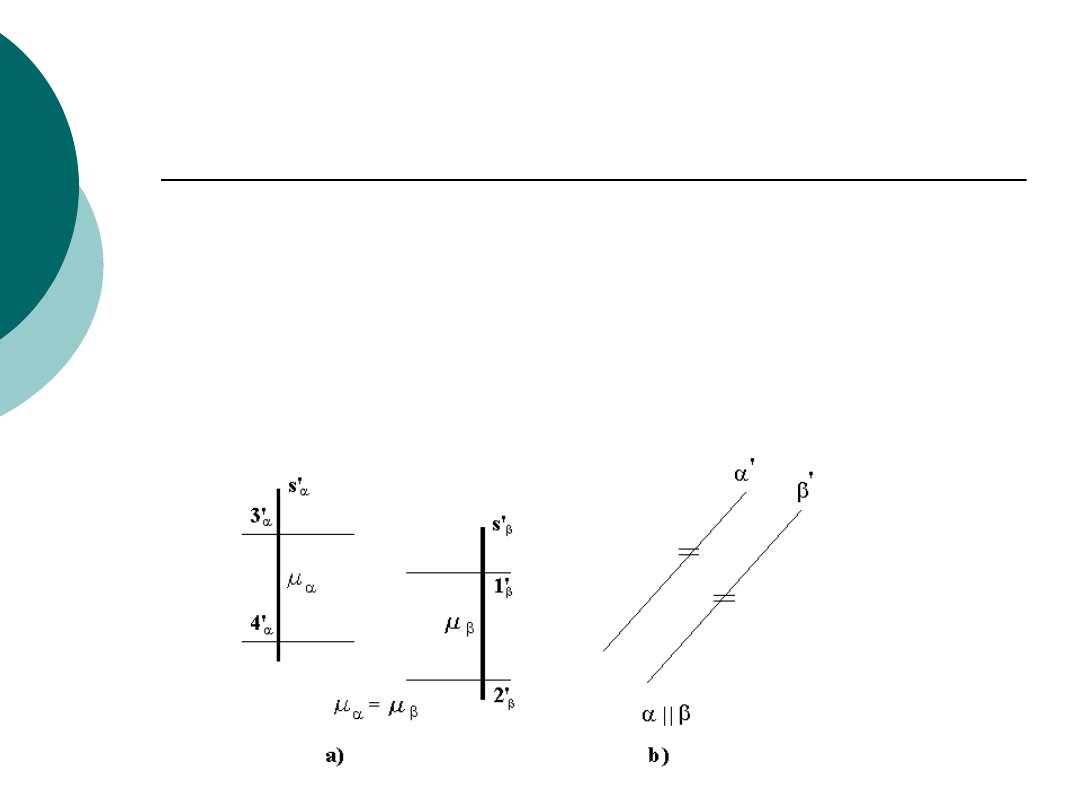
Równoległość płaszczyzn

Twierdzenie . Dwie płaszczyzny są równoległe,
jeżeli posiadają:

•

  równoległe rzuty linii największego spadu

•

  zgodne zwroty na rzutach tych linii

•

  równe moduły

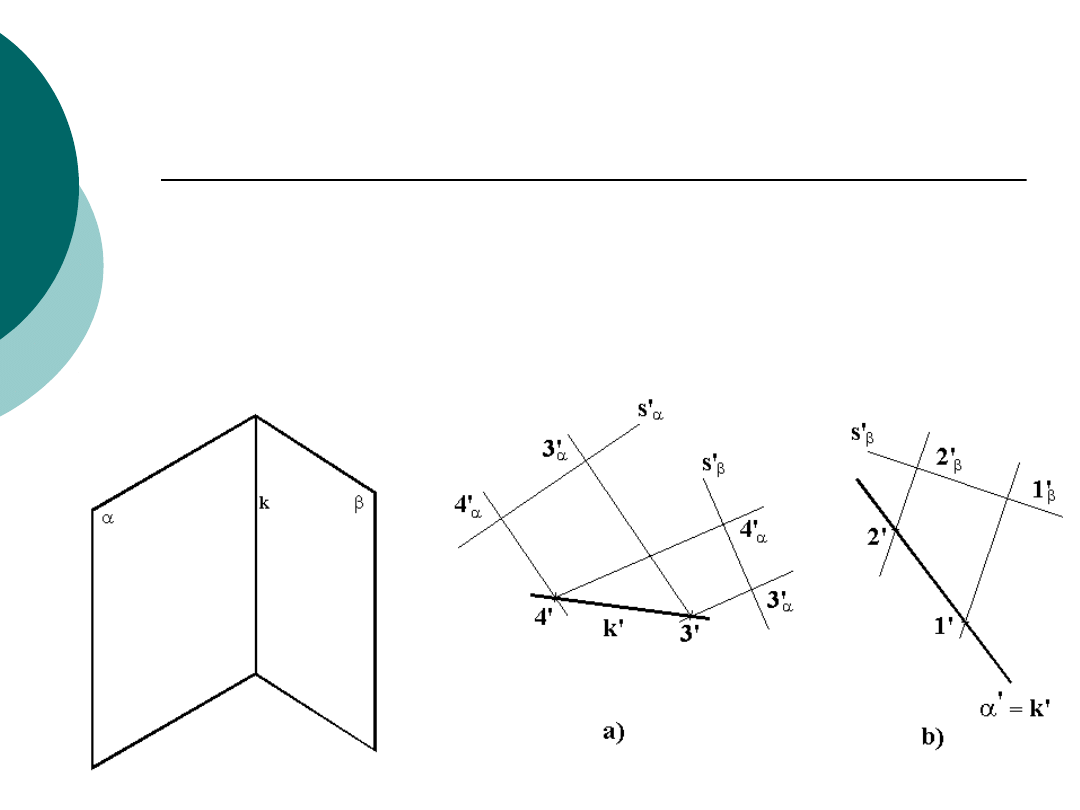
Krawędź dwóch płaszczyzn

Krawędź dwóch płaszczyzn

Elementem wspólnym dwóch płaszczyzn jest
prosta nazywana

krawędzią

. Wystarczy określić

dwa dowolne punkty tej krawędzi, aby była ona
jednoznacznie określona. Weźmy pod uwagę
warstwice obu płaszczyzn o tej samej cesze.
Punkt przecięcia warstwic jednoimiennych jest
punktem należącym do obu płaszczyzn
jednocześnie. Wszystkie jednoimienne warstwice
przecinają się w punktach krawędzi , a więc
wystarczy określić dwa punkty i opisać prostą w
sposób typowy dla rzutu cechowanego.

Krawędź płaszczyzn

Trzy krawędzie

k, a, b

płaszczyzn

, , 

przecinają się w jednym punkcie

P

.

Zadanie

Dane są rzuty cechowane płaszczyzn

α i β i punktu A. Przez punkt A
poprowadzić prostą i równoległą do
obu płaszczyzn .

Punkt przebicia płaszczyzny
prostą

Jeżeli prosta

a

i płaszczyzna  nie są do

siebie równoległe, posiadają wówczas
wspólny punkt

P

, zwany

punktem

przebicia płaszczyzny prostą

lub

punktem przecięcia prostej
płaszczyzną

.

Aby wyznaczyć ten punkt należy:

•

przez prostą

a

przeprowadzić dowolną

płaszczyznę 

•

wyznaczyć krawędź płaszczyzn  i 

•

znaleźć punkt przecięcia się krawędzi

k

i prostej

a

, który jest szukanym punktem

P

przebicia.

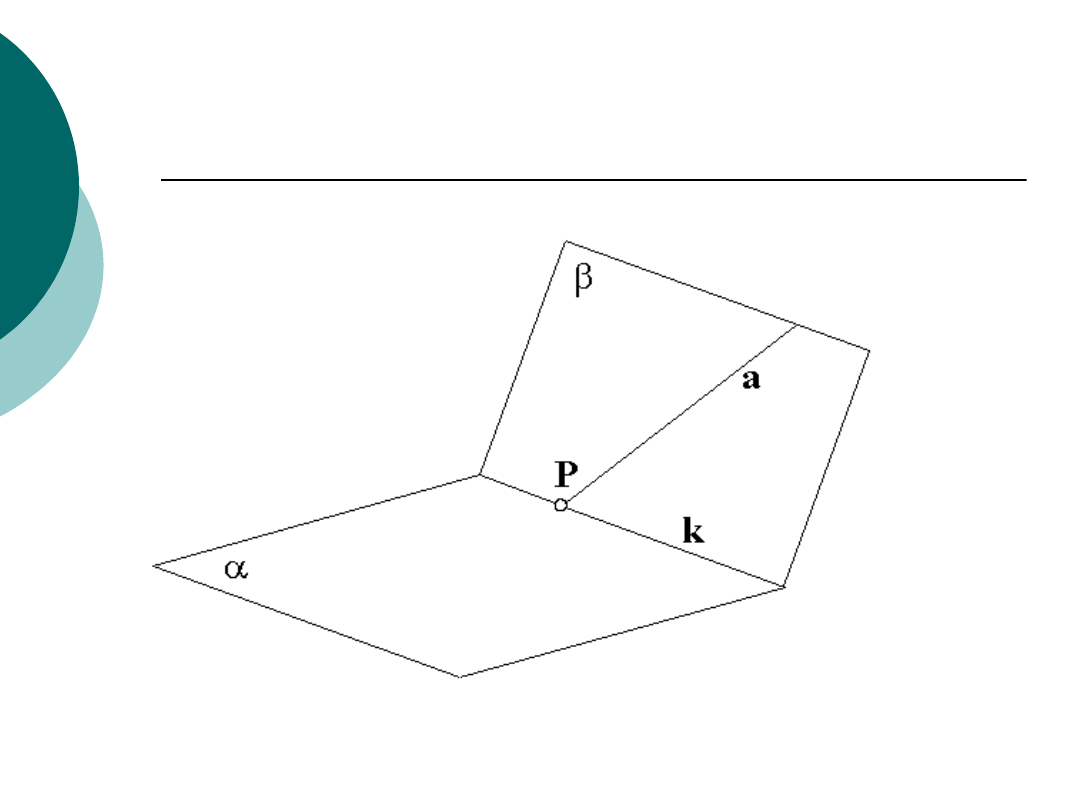
Punkt przebicia płaszczyzny
prostą

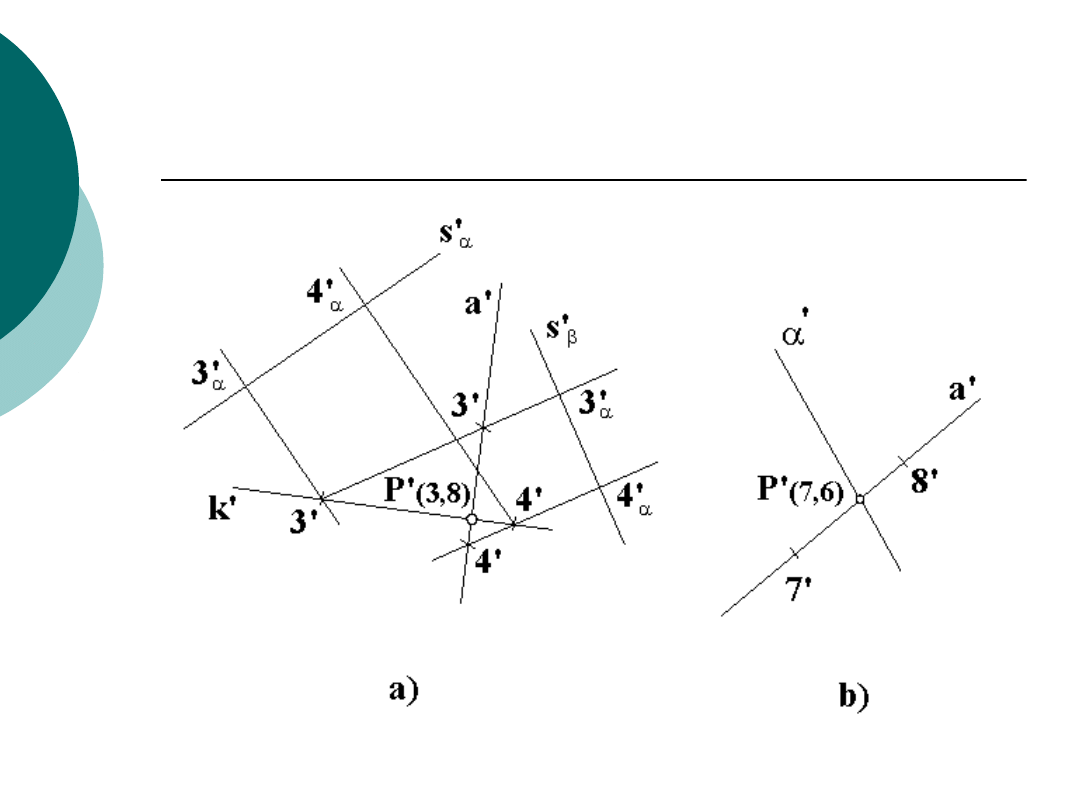
Punkt przebicia płaszczyzny
prostą