Regulacja cyfrowa

Wykład przygotowany przez pracownika

Instytutu Technik Wytwarzania PW

Wojciecha Kramarka

Regulacja cyfrowa

Regulacja cyfrowa (digital control) jest to (najkrócej) –

zastosowanie komputerów w systemach sterowania.

Rozwój i powszechność zastosowań regulacji cyfrowej

można podzielić na okresy:
- okres pionierski ok.1955r.,
- okres bezpośredniego sterowania cyfrowego ok. 1962r.,
- okres minikomputerów ok. 1972r.,
- okres mikrokomputerów oraz powszechne zastosowanie

sterowania cyfrowego ok. 1980r.,
- sterowanie rozproszone ok. 1990r. (distributed control).

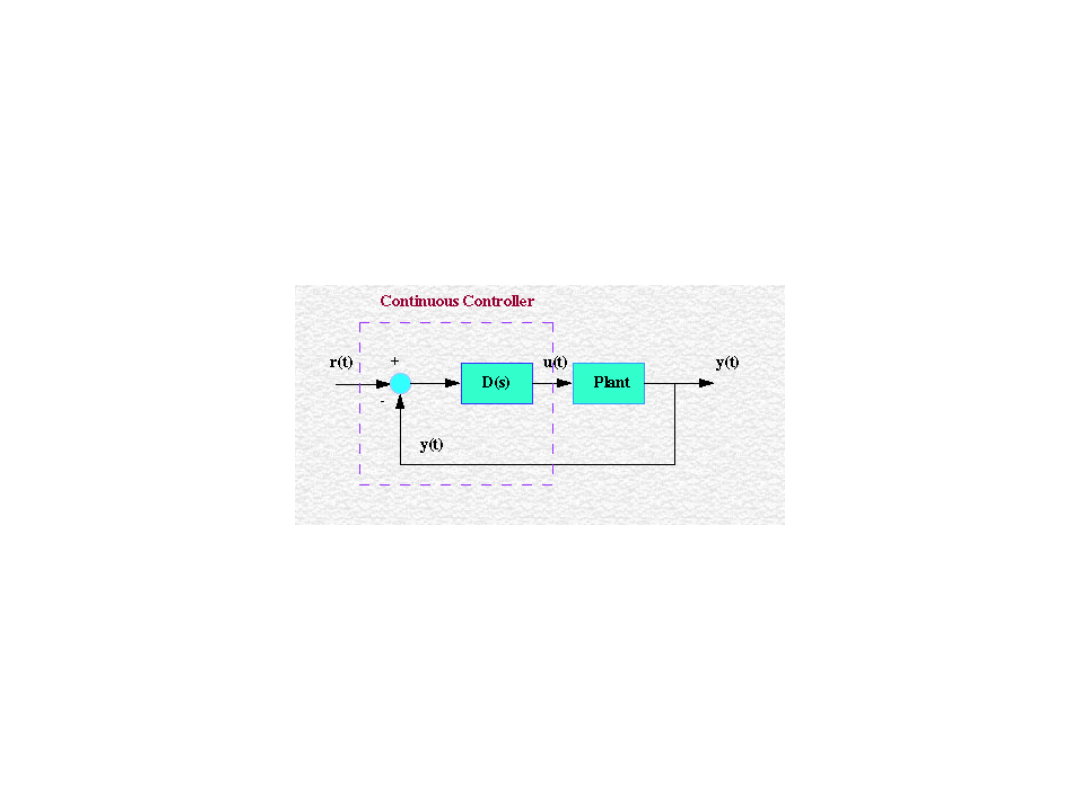
Analogowy układ regulacji

automatycznej

Układ z regulatorem analogowym, ciągłym

Zadania regulatorów

1. Porównanie wartości mierzonej wielkości regulowanej z

wartością
zadaną (określenie wartości sygnału uchybu regulacji).
2. Wytwarzanie wyjściowego sygnału sterującego o wartości

zależnej od uchybu regulacji, czasu występowania uchybu i

szybkości jego zmian.
3. Zapewnienie sygnałowi sterującemu postaci i mocy

potrzebnej do
uruchomienia urządzeń wykonawczych.
Regulatory przemysłowe często zawierają również urządzenia,

które umożliwiają:
a) nastawianie wartości zadanej (tzw. zadajniki),
b) przełączniki rodzaju pracy (ręczna, automatyczna),
c) urządzenia do sterownia ręcznego,
d) mierniki do pomiaru wielkości istotnych dla procesu regulacji

Rodzaje regulatorów

Podział regulatorów ze względu na rodzaj wykorzystywanej

energii:
-regulatory bezpośredniego działania (najstarsze);
-regulatory korzystające z energii pomocniczej: elektryczne,
pneumatyczne, hydrauliczne.
Podział regulatorów ze względu na postać sygnału

wyjściowego:
-regulatory z sygnałem wyjściowym nieciągłym: dwustawne,
trojstawne (inaczej dwupołożeniowe, trojpołożeniowe),

-regulatory dwustawne i trojstawne z korekcją;

-regulatory z sygnałem wyjściowym ciągłym typu P, PI, PD,

PID,
( elektryczne (analogowe lub cyfrowe), pneumatyczne i

hydrauliczne).
-regulatory uniwersalne bądź specjalizowane.

Sterowanie binarne

Sterowanie binarne- wykorzystuje się w nim sygnały

dwuwartościowe.

Sygnały te są reprezentowane przez dwie różne

wartości

lub

stany

, np: włączony i wyłączony, czarny i biały,

stan zwarty i rozwarty lub po prostu 0 i 1. Większość

układów sterowania

wykorzystuje sygnały dwuwartościowe,

a zatem są to układy sterowania

binarnego

.

Do ważniejszych elementów składowych układów

sterowania binarnego, należą:
-p

rzekaźniki

,

-zawory przełączające,
-

diody

,

-binarne elektroniczne obwody przełączające

Przykład regulatora analogowego

Przykład regulatora cyfrowego

Przykład elektronicznego dwustawnego

regulatora

Regulatory bezpośredniego działania

Regulatory bezpośredniego działania pobierają energię

potrzebną do przestawiania zaworu nastawczego z procesu

regulowanego za pośrednictwem czujnika pomiarowego.
Zalety: prosta i zwarta budowa, niska cena i duża

niezawodność.
Wady: ograniczenie do regulacji stałowartościowej o małej
dokładności.
Typowe elementy regulatora: czujnik, nastawnik (zawór

regulacyjny)
i element wykonawczy (siłownik).
Typowe zastosowania: regulacja temperatury, ciśnienia,

strumienia,
poziomu.

Regulatory dwustawne i trójstawne

Istota regulacji polega na tym, że na wyjściu regulatora

sygnał może przyjmować tylko dwa stany: załączony lub

wyłączony (dla regulatora trojpołożeniowego trzy stany).

Regulatory nadają się do obiektów o dużych stałych

czasowych, gdzie nie jest istotna duża dokładność regulacji,

np. sterowanie temperaturą w obiektach cieplnych.

Zalety: prostota budowy i sterowania, wady: oscylacje (o

dużej amplitudzie) wartości wielkości regulowanej wokół

wartości zadanej.

Regulacja dwustawna

Regulatory dwustawne (dwupołożeniowe)

charakteryzują się dwoma, jednoznacznie określonymi
wartościami sygnału wyjściowego. Element wykonawczy ma
tylko dwa ustalone położenia, które zazwyczaj polega na
załączeniu lub wyłączeniu urządzenia.

Sterowanie dwupołożeniowe jest stosunkowo proste i

niedrogie i dlatego jest szeroko stosowane w przemyśle i w
urządzeniach gospodarstwa domowego.

Zastosowanie regulatora dwustawnego

Sygnał wyjściowy z regulatora oznaczany jest zazwyczaj jako

U(t), natomiast wejściem do regulatora jest wykonawczy

sygnał uchybu E. W sterowaniu dwupołożeniowym sygnał

wyjściowy U(t) przyjmuje jedną z dwóch wartości:

maksymalną i minimalną: w zależności od tego czy sygnał

wykonawczy uchybu jest dodatni lub ujemny.
Wielkości U1 i U2 są stałymi.
Przykładem zastosowania regulatora dwupołożeniowego jest

układ regulacji temperatury. Bimetaliczny sensor, element

porównujący wartość zadaną z wartością rzeczywistą oraz

przełącznik wykonawczy stanowią jedną, konstrukcyjną

całość. Jeżeli temperatura wzrasta ponad wartość zadaną, to

ogrzewana płytka bimetaliczna wygina się (pomiar wartości

rzeczywistej temperatury) i rozłącza obwód grzejny (działanie

wykonawcze). Jeżeli temperatura jest mniejsza od wartości

zadanej, to bimetal załącza obwód grzejny

.

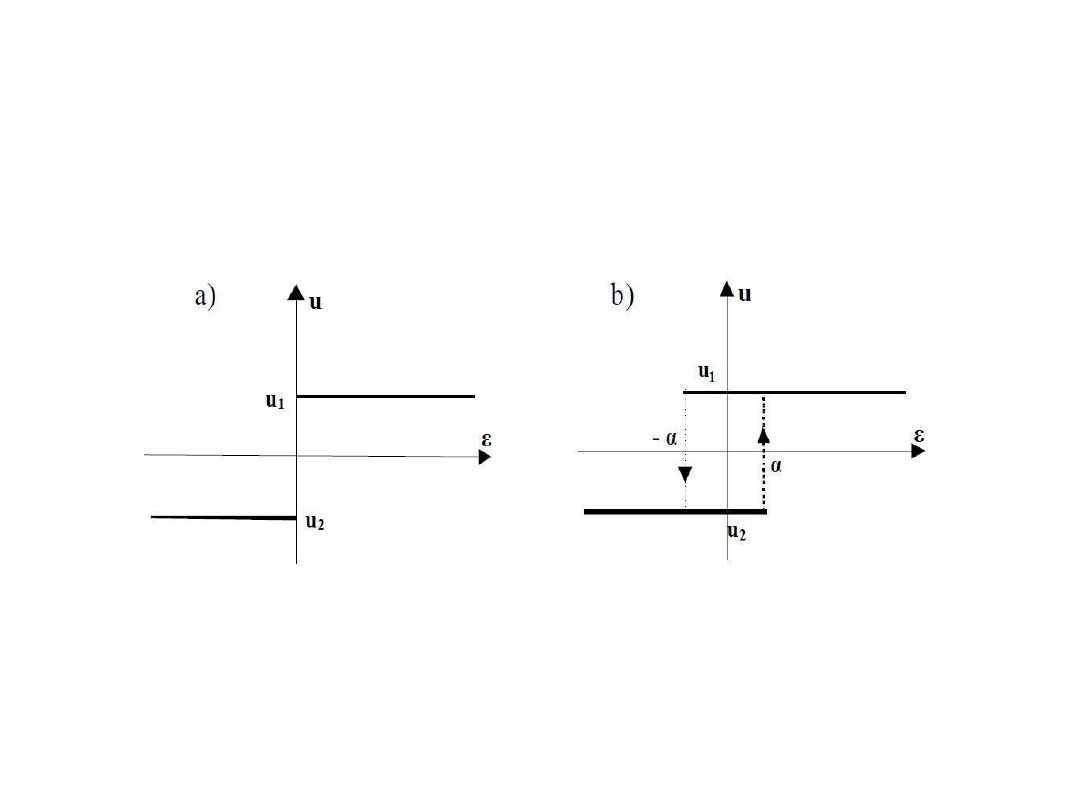
Charakterystyki regulatora dwustawnego :

a) idealnego, b) rzeczywistego

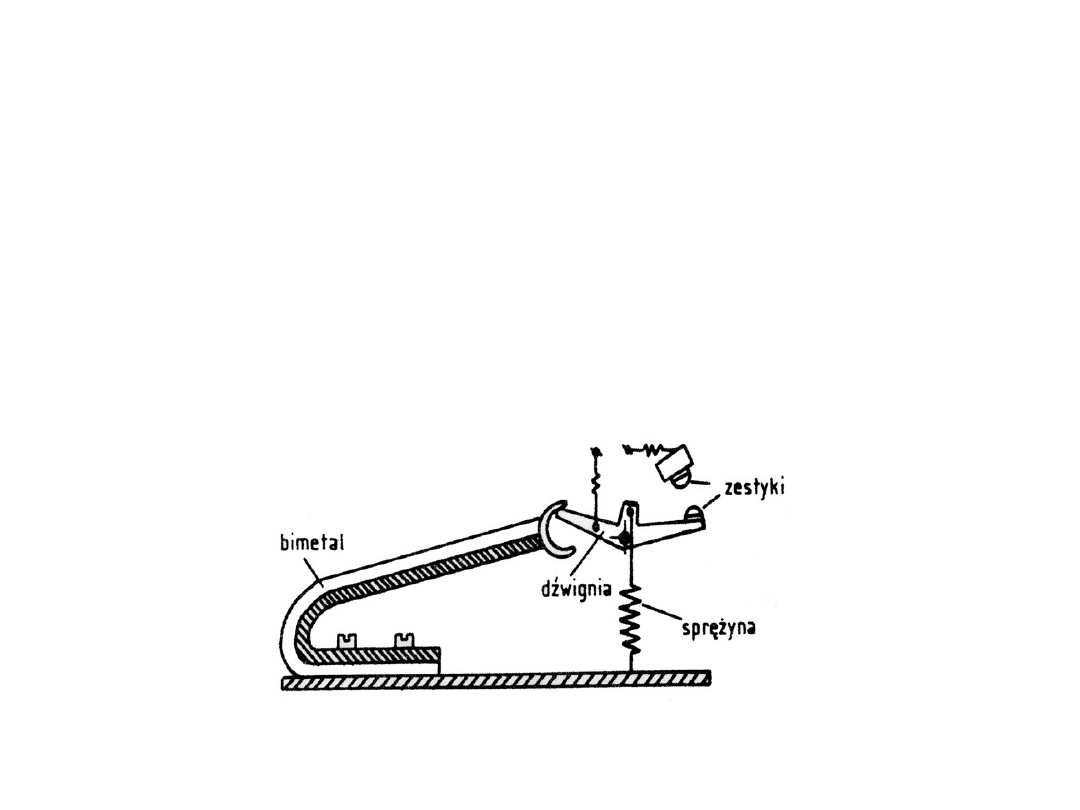
Przykład regulatora dwustawnego

Przykładem regulatora z zestykiem bezpośrednio

przełączanym przez czujnik jest wyłącznik bimetaliczny.
Działa on w taki sposób, że pod wpływem temperatury
zewnętrznej bimetal ulega odkształceniu i powoduje
przełączenie zestyku elektrycznego. Regulatory tego typu
są powszechnie używane w domowych urządzeniach
grzewczych (żelazkach, suszarkach itp.).

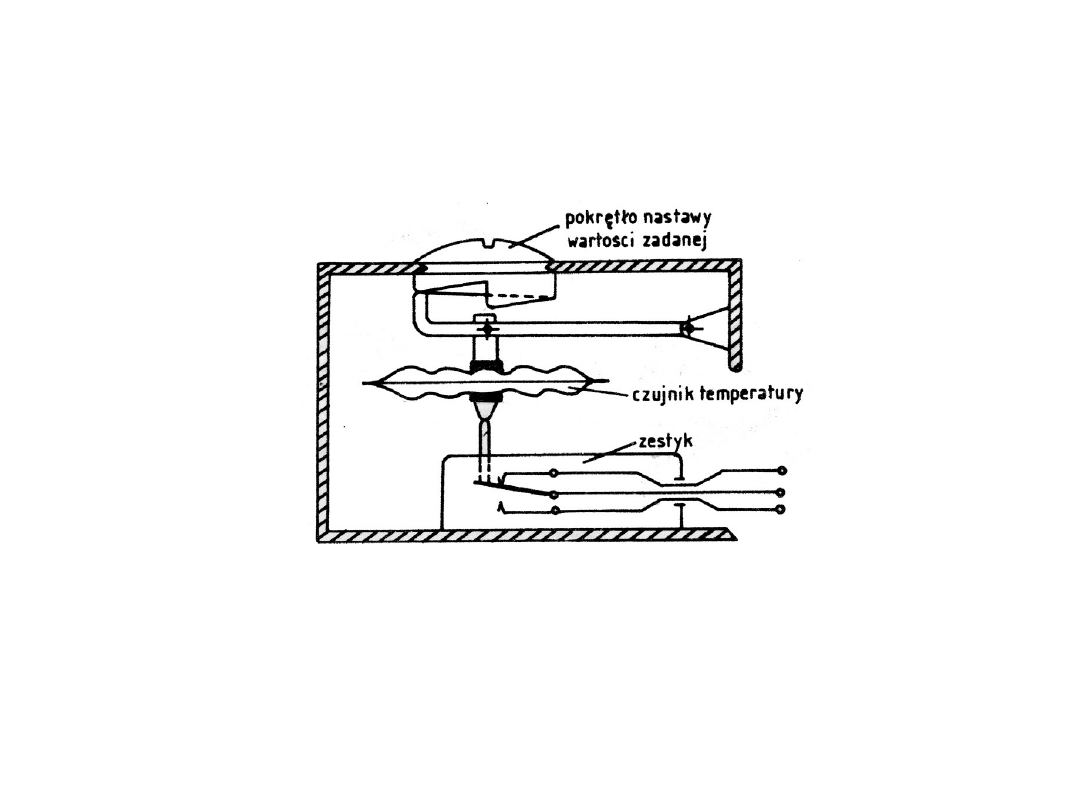
Układ regulacyjny dwustawny

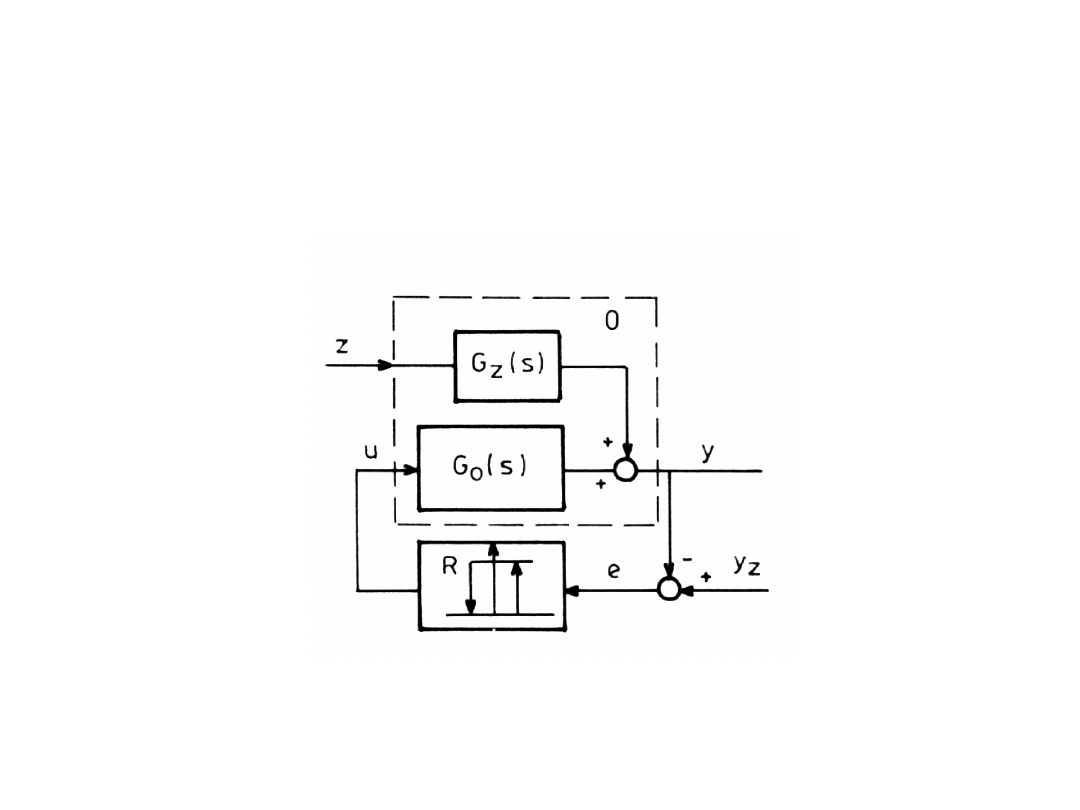
UAR z regulatorem dwustawnym

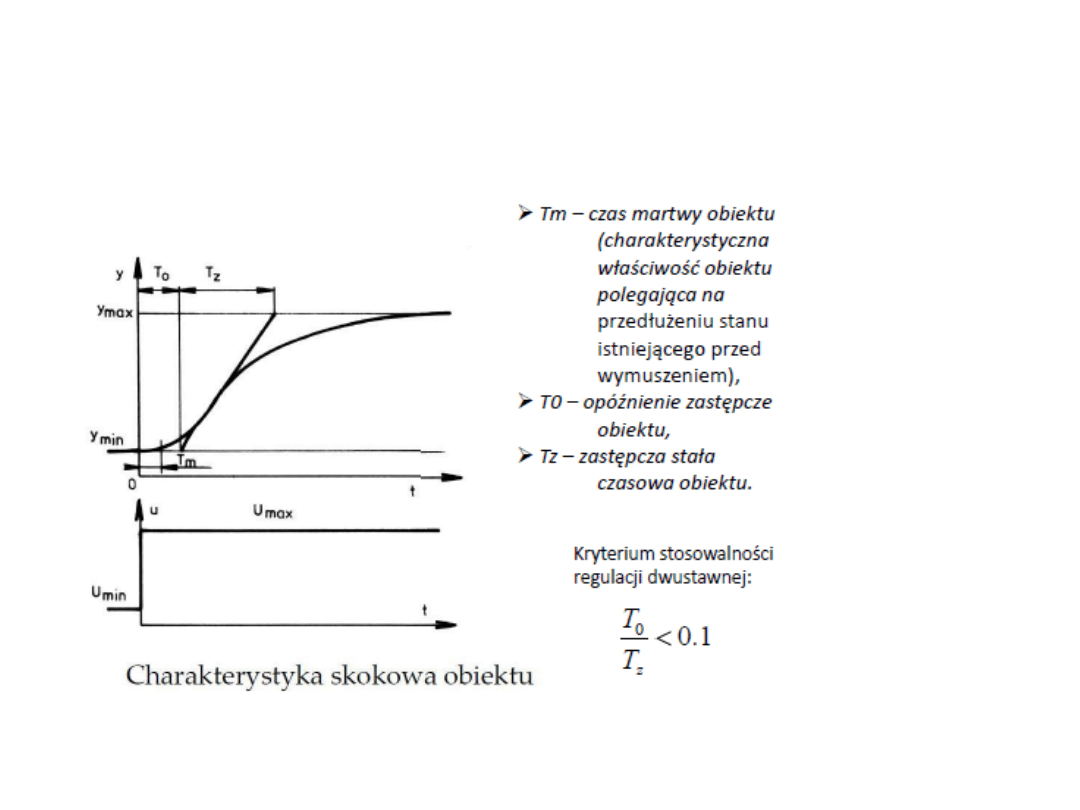
Obiekt statyczny z opóźnieniem

Odpowiedź obiektu

Jeżeli na wejście obiektu ( rysunek poprzedni)

załączymy Umax, to w czasie t → ∞ sygnał wyjściowy
osiągnie wartość ymax.
Odpowiednio dla u = Umin otrzymamy wartość ymin.

Z charakterystyki skokowej obiektu wyznaczono:

-Tm – czas martwy obiektu (charakterystyczna właściwość
obiektu polegająca na przedłużeniu stanu istniejącego
przed wymuszeniem),
-T0 – opóźnienie zastępcze obiektu,

-Tz – zastępcza stała czasowa obiektu

.

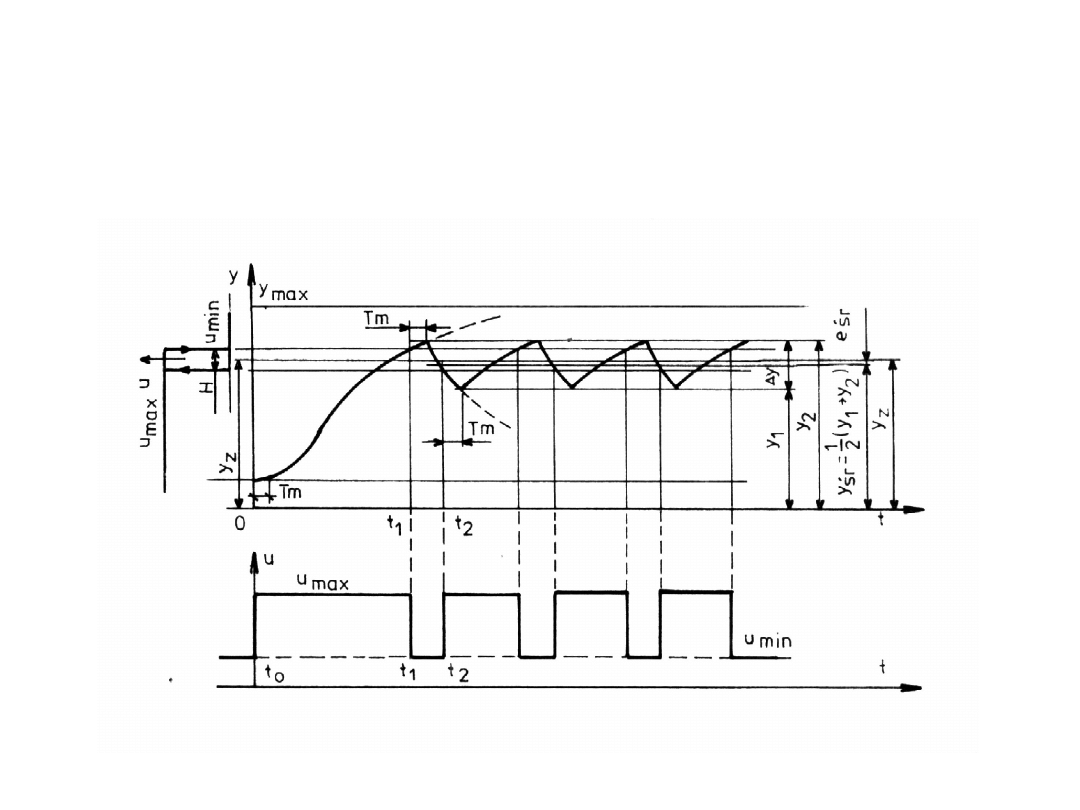
Przebieg temperatury w obiekcie

Przebieg temperatury

Wykres przebiegu temperatury w układzie regulacji

dwustawnej pokazano na poprzednim rysunku. W chwili t0
na wejście obiektu jest załączone napięcie Umax,
temperatura y w obiekcie narasta. W chwili t1 temperatura
obiektu osiągnęła wartość yz + H/2. W tym
momencie regulator wyłączy grzanie (u = Umin). Pomimo to
temperatura obiektu nadal narasta przez czas Tm, po czym
zaczyna maleć. W chwili t2 temperatura zmalała do
wartości yz – H/2. Regulator załączył grzanie (Umax).
Jednak temperatura nadal maleje i dopiero po czasie Tm
nastąpi w obiekcie ponowny jej wzrost. Omówiony cykl
powtarza się.

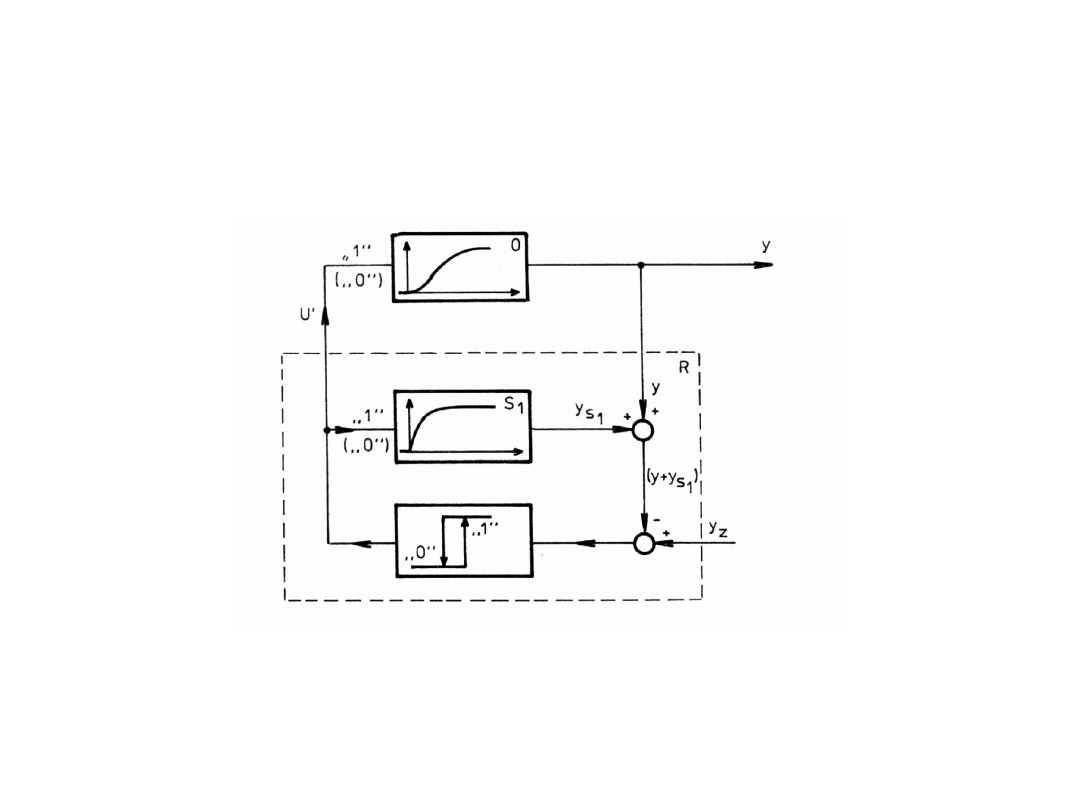
Regulatory dwustawne z korekcją

Przebiegi sygnału regulowanego

Zmniejszenie amplitudy oscylacji wielkości

regulowanej, w układzie regulacji dwustawnej, można

uzyskać dzięki zastosowaniu regulatora z korekcyjnym

sprzężeniem zwrotnym. Schemat blokowy układu regulacji

dwustawnej z inercyjnym sprzężeniem zwrotnym pokazano

na poprzednim rysunku.

Stała czasowa T członu w sprzężeniu zwrotnym

powinna być znacznie mniejsza od zastępczej stałej

czasowej Tz obiektu regulacji.. Jak widać, po zastosowaniu

pojedynczego sprzężenia zwrotnego wzrosła częstotliwość

oscylacji, zmalała amplituda wahań, wystąpiła natomiast

różnica między wartością średnią yśr
a zadaną yz

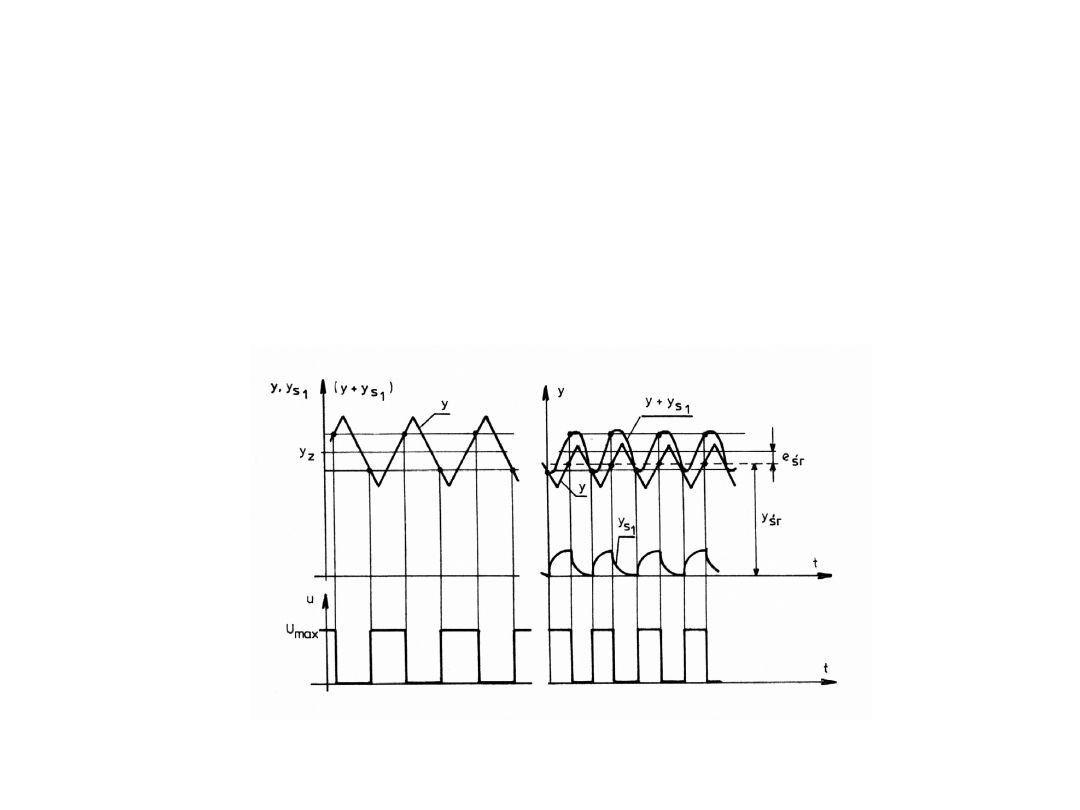
Porównanie przebiegów

Porównanie przebiegu regulacji w układzie regulacji

dwustawnej bez sprzężenia zwrotnego z przebiegami w
układzie z pojedynczym sprzężeniem zwrotnym.

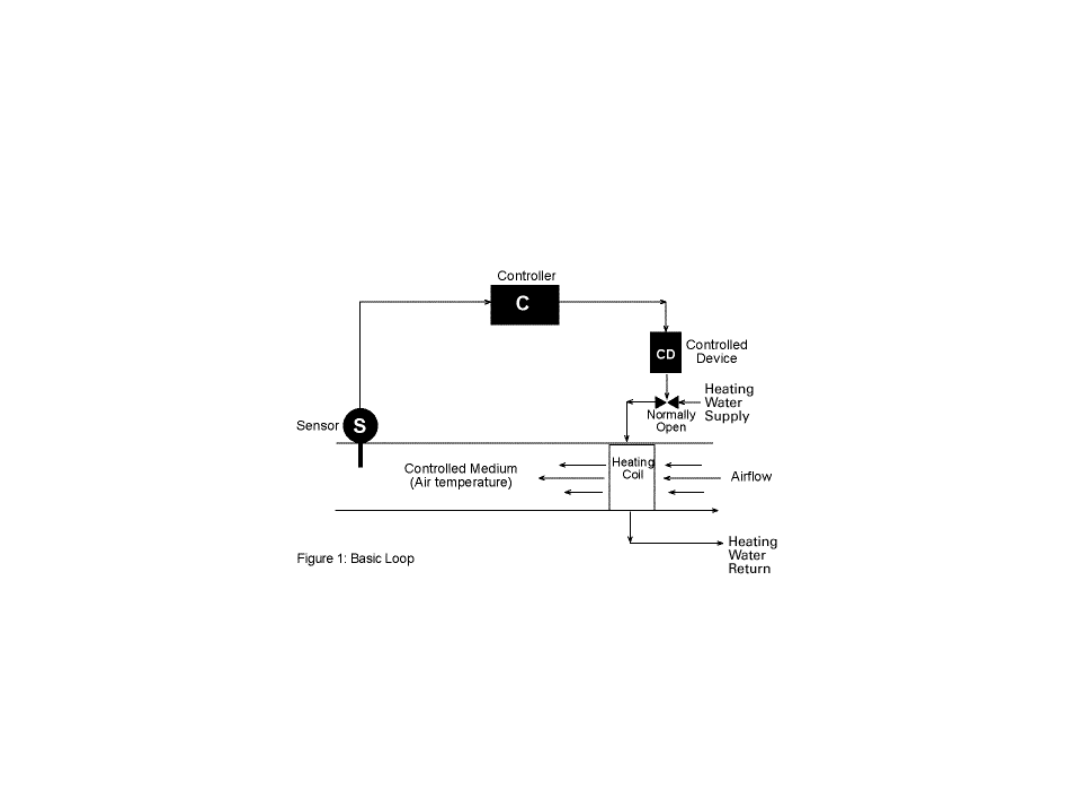
Analogowy UAR

Elementy układu regulacyjnego

Układ regulacyjny pokazany powyżej składa się z trzech

głównych komponentów: sensory, regulator oraz nastawnik

oddziałujący na obiekt (proces). Wielkością kontrolowaną w

omawianym układzie jest temperatura.

Układ pomiarowy (sensor) określa stan wielkości

kontrolowanej, regulator przetwarza dane natomiast nastawnik

wykonuje polecenia płynące z regulatora. W układzie jako

regulator może występować regulator płynowy, mechaniczny,

elektryczny lub elektroniczny. W rozważanym przypadku regulator

jest urządzeniem hardwerowym o określonych wymiarach, masie i

mocy.

Regulacja cyfrowa

W układzie regulacji analogowej, przedstawionym na

wcześniejszym schemacie, można zastąpić regulator
analogowy regulatorem cyfrowym. Regulator ten będzie
spełniał te same zadania jak regulator analogowy.
Podstawowa różnica pomiędzy tymi regulatorami polega na
tym, że regulator cyfrowy do działania potrzebuje sygnałów
dyskretnych zamiast sygnałów ciągłych.

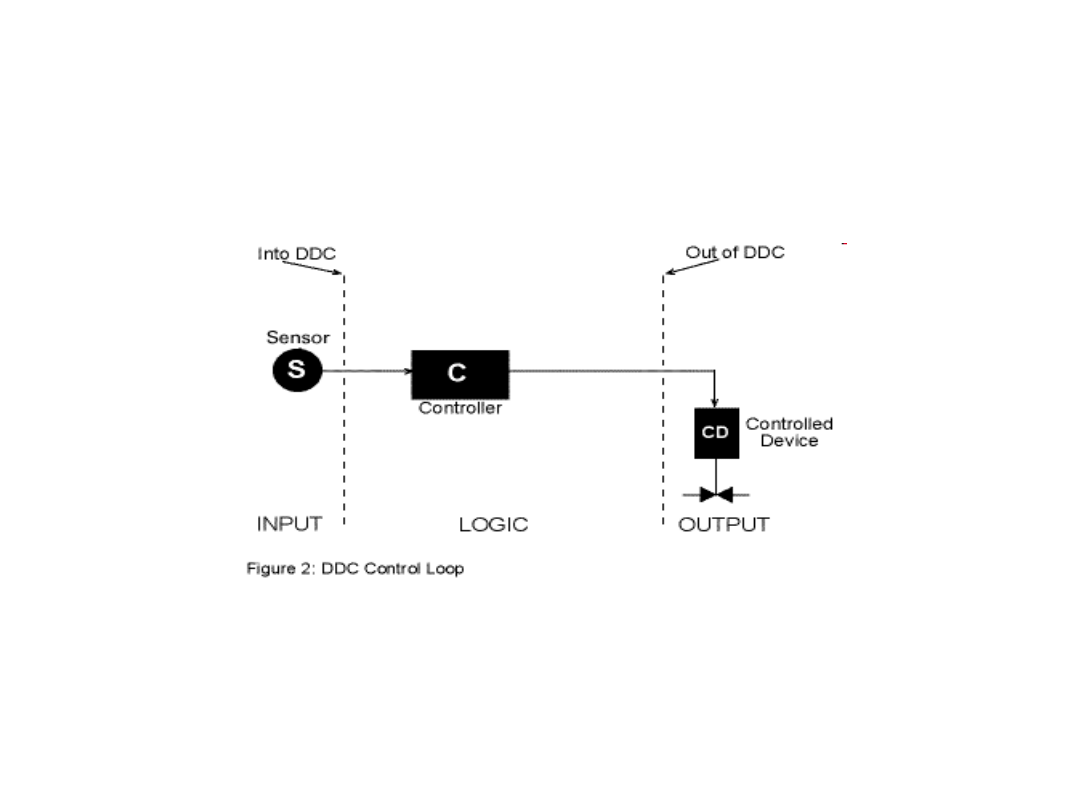
Direct Digital Control Systems

Systemy regulacji cyfrowej

Różnice pomiędzy regulatorami

analogowymi i cyfrowymi

Podstawowa różnica pomiędzy regulatorami

analogowymi i cyfrowymi polega na tym, że w :
-regulatorach analogowych sygnały analogowe ulegają
ciągłej obróbce a w regulatorach cyfrowych następuje
zamiana sygnału analogowego na cyfrowy, następnie
obróbka sygnału i ponowna zamiana na sygnał analogowy.

Ponadto sygnały w regulatorach cyfrowych są

próbkowane co ustalony odstęp czasu (cykliczny charakter
pracy).

Obliczenia cyfrowe wykonywane są tylko dla

dyskretnego czasu zamiast w sposób ciągły; potrzebny jest
więc impulsator po stronie wejściowej i ekstrapolator po
stronie wyjściowej.

Sensory

Sensory mają za zadanie mierzyć wielkość kontrolowaną
albo inne wielkości wejściowe dokładnie i powtarzalnie.
Sensory (czujniki) są stosowane do pomiaru napięcia, prądu,
temperatury, ciśnienia, przepływu, stężenia gazów, itp..
Oprócz pomiaru wielkości kontrolowanych przez regulator
czujniki dostarczają informacji o innych stanach maszyny
lub procesu, które mogą być istotne przy wyznaczaniu
sygnałów wyjściowych regulatora. Dodatkowe informacje
które mogą w pewnych sytuacjach wpływać na logikę
decyzji regulatora mogą dotyczyć pewnych parametrów jak
przepływ wody, zadymienie , pożar , graniczne wielkości
pewnych parametrów. Itp…
Sensory są bardzo ważną częścią układu regulacji, będąc
zarazem słabym ogniwem tego układu.

Regulatory

Regulator odczytuje sygnały płynące z czujników,

przetwarza te informacje zgodnie z pewnym algorytmem
sterowania wbudowanym w niego i powoduje wytworzenie
pewnych działań sterujących. Wytworzony sygnał sterujący
może być wysłany bezpośrednio do nastawnika lub może
być wysłany po przejściu przez dodatkowe układy logiczne.

Rodzaje regulatorów zależą od wbudowanych w nie

algorytmów. Najczęściej są wykorzystywane następujące
rodzaje regulatorów :

• -dwupozycyjne (dwustawne),

• -proporcjonalne,

• -proporcjonalno-całkujące,

• -proporcjonalno-całkująco-różniczkujące.

Nastawniki

Nastawniki (urządzenia wykonawcze) są urządzeniami

wykonującymi polecenia regulatora albo układów
logicznych. Nastawniki zmieniają stan wielkości
regulowanych przez zmianę sygnałów sterujących
urządzeniami końcowymi. Przykładami tych urządzeń mogą
być zawory dwupozycyjne lub analogowe, przekaźniki
elektryczne, pompy, wentylatory, grzałki lub silniki o
regulowanej prędkości obrotowej służące do napędu tych
elementów.

Definicja Direct Digital Control DDC

(regulacja cyfrowa)

Regulacja cyfrowa DDC składa się z

mikroprocesorowych regulatorów w których logika regulacji

jest wykonywana przez software. Przetworniki analogowo-

cyfrowe przekształcają analogowe wartości sygnałów na

sygnały cyfrowe zrozumiałe dla mikroprocesora

W większości złożonych systemów regulacji programy

softwarowe są przekazane do rozproszonych regulatorów

aby wyeliminować konieczność ciągłej wymiany informacji

pomiędzy nimi. Nadrzędny komputer jest stosowany

głównie do monitorowania systemu, przechowywania kopii

programów oraz do zapisu alarmowych sygnałów.

Kalibracja czujników może być prowadzona

matematycznie, przez co zmniejszamy ilość roboczogodzin

na jej prowadzenie. Programy oraz sposób programowania

są systematycznie doskonalone stając się bardziej

przyjacielskie dla użytkownika.

Zalety DDC

Cyfrowe układy scalają regulację, sterowanie i

optymalizację.
Do istotnych zalet układów DDC należy możliwość:
- realizacji dowolnie złożonych algorytmów sterowania,
włącznie ze sterowaniem optymalnym i adaptacyjnym,
- ciągłego pomiaru i rejestracji wartości dowolnych
parametrów procesu,
- przetwarzania danych pomiarowych,
- wykrywania i sygnalizacji stanów awaryjnych,
- zwiększenia dokładności sterowania na skutek
dokładniejszej identyfikacji obiektu regulacji.

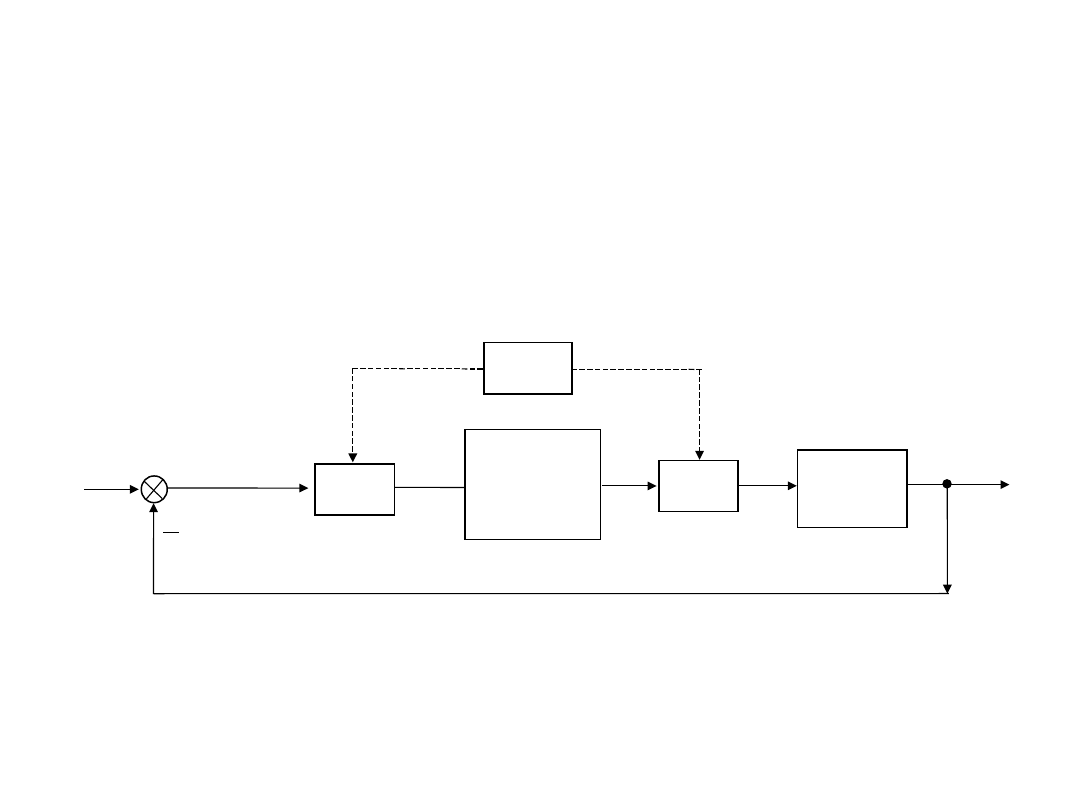
Schemat blokowy cyfrowego układu regulacji

Schemat blokowy

A/D

sygnał
analogowy

Zegar

Cyfrowy
algorytm
regulacji

Obiekt
(proces)

D/A

y

y

0

e

e

d

u

d

u

a

y

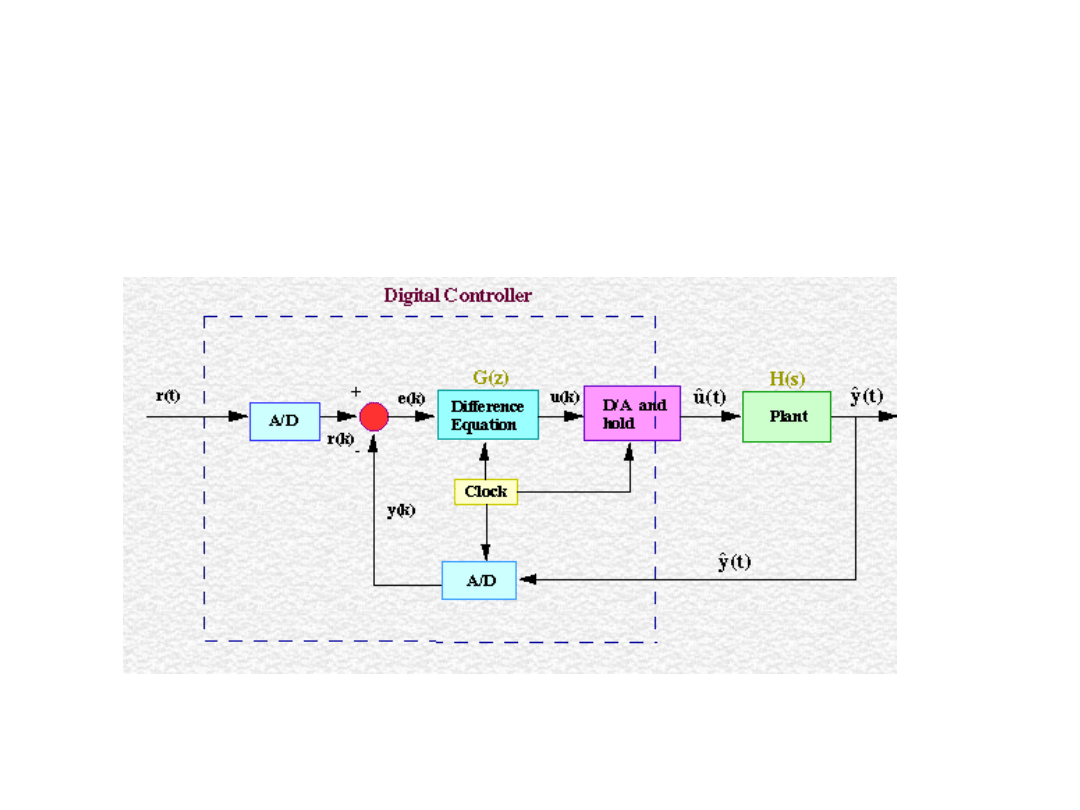
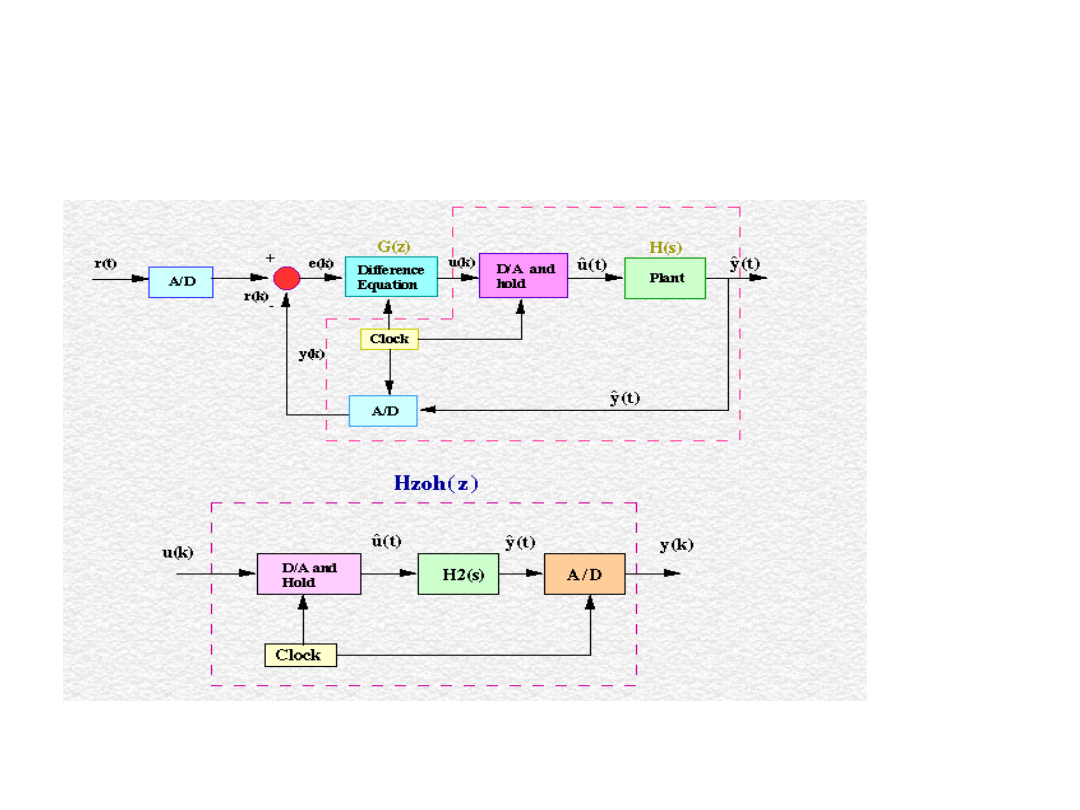
Schemat blokowy cyfrowego układu

regulacji

Przepływ sygnałów w układzie

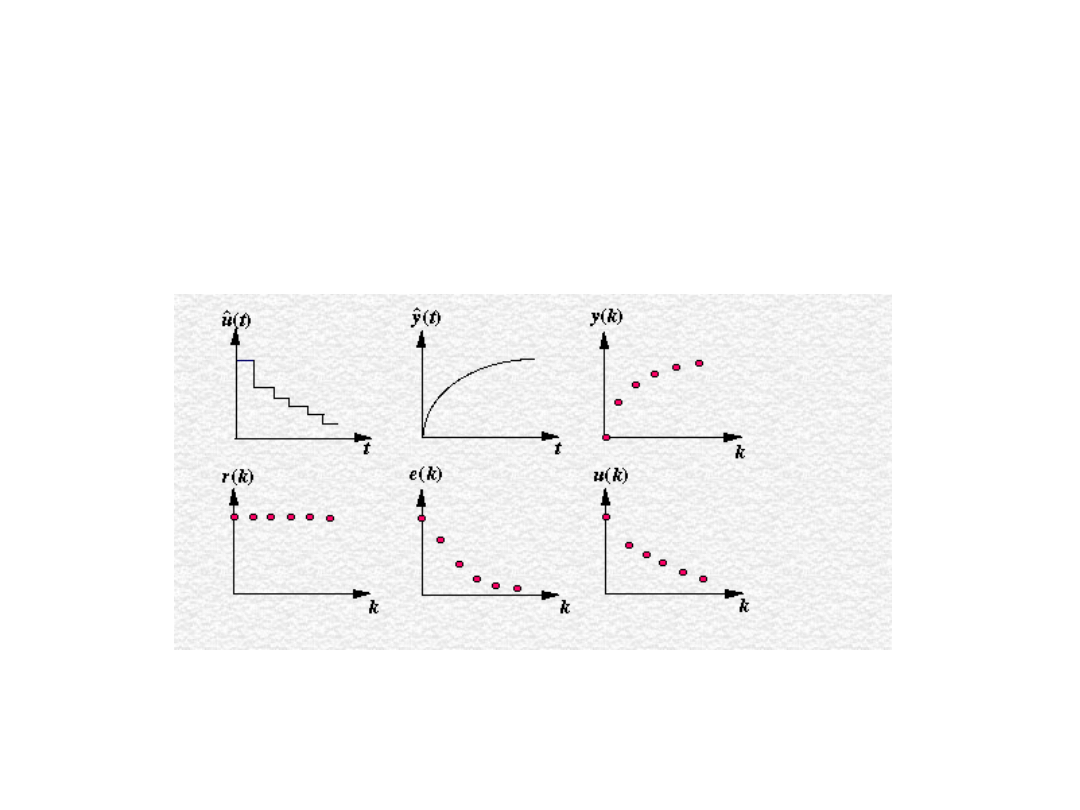
Przebiegi sygnałów

Przebiegi sygnałów ciągłych i dyskretnych

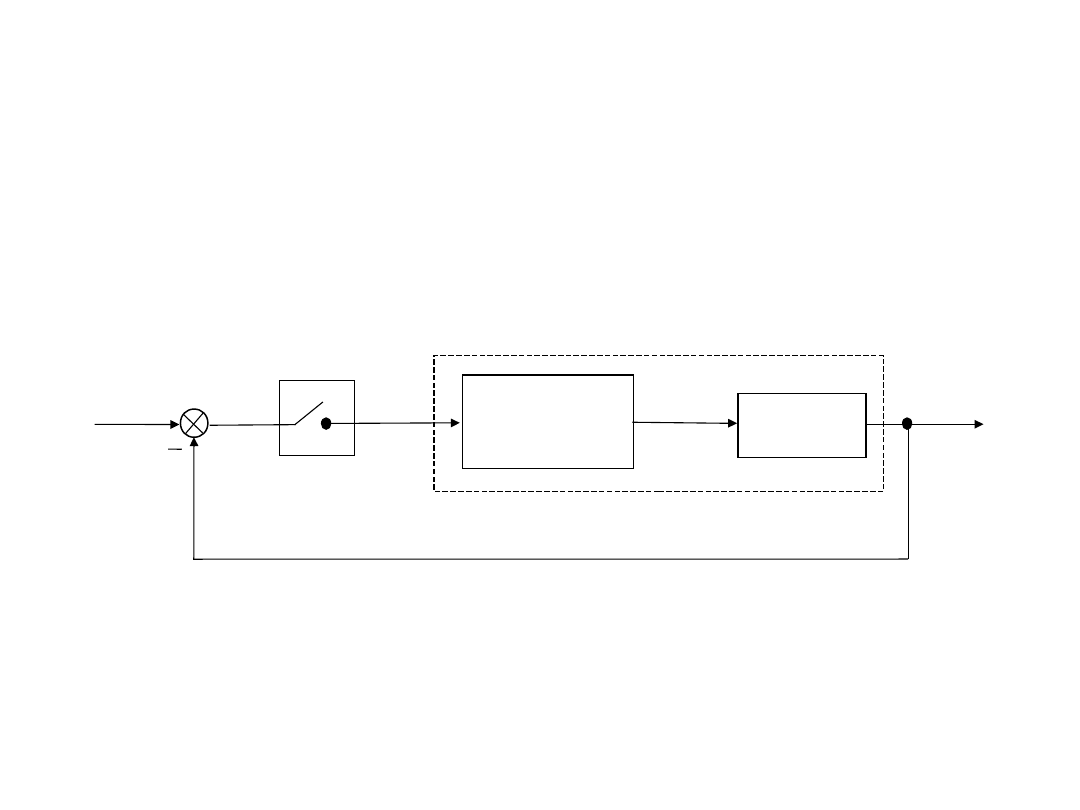
Układ regulacji dyskretnej z ekstrapolatorem

Układy dyskretne

Układami dyskretnymi regulacji automatycznej nazywa

się układy, w których strumień informacji jest przekazywany
za pomocą sygnałów dyskretnych (nieciągłych). Mogą one
być dyskretne w poziomie (realizuje to tzw. quantizer –
rzadko stosowane) lub dyskretne w pionie – w czasie (tutaj
bardziej precyzyjne jest określenie system z czasem
dyskretnym – najczęściej stosowane).

Układy dyskretne

Sygnały dyskretne w czasie nazywa się sygnałami

impulsowymi, a układ automatycznej regulacji operujący

takimi sygnałami nazywa się impulsowym układem

automatycznej regulacji. Impulsowe układy regulacji to

takie, w jakich informacja jest przekazywana tylko w

chwilach impulsowania.

Klasycznym układem regulacji impulsowej są układy

sterowane mikroprocesorowo, w których mikroprocesor

oblicza wartości sygnałów sterujących lub sygnałów

regulacji, generując wynik w postaci ciągu impulsów.

Przetworniki analogowo-cyfrowe

W procesach przemysłowych dominują sygnały

analogowe
( przemieszczenie, prędkość, temperatura, przepływ,
ciśnienie ) i aby mogły być wykorzystane w systemie
cyfrowym ( z komputerem jako regulatorem cyfrowym),
powinny być przetworzone na sygnały cyfrowe.

Sygnały cyfrowe otrzymuje się przez operacje

próbkowania oraz kwantowania sygnałów analogowych,
które następnie są kodowane.

Układ impulsowy

Schemat blokowy jednowymiarowego (SISO) układu
impulsowego

Element formujący

Proces

Impulsator idealny

część ciągła

e(t)

y

0

(t)

e

*

(t)

e

1

(t)

y(t)

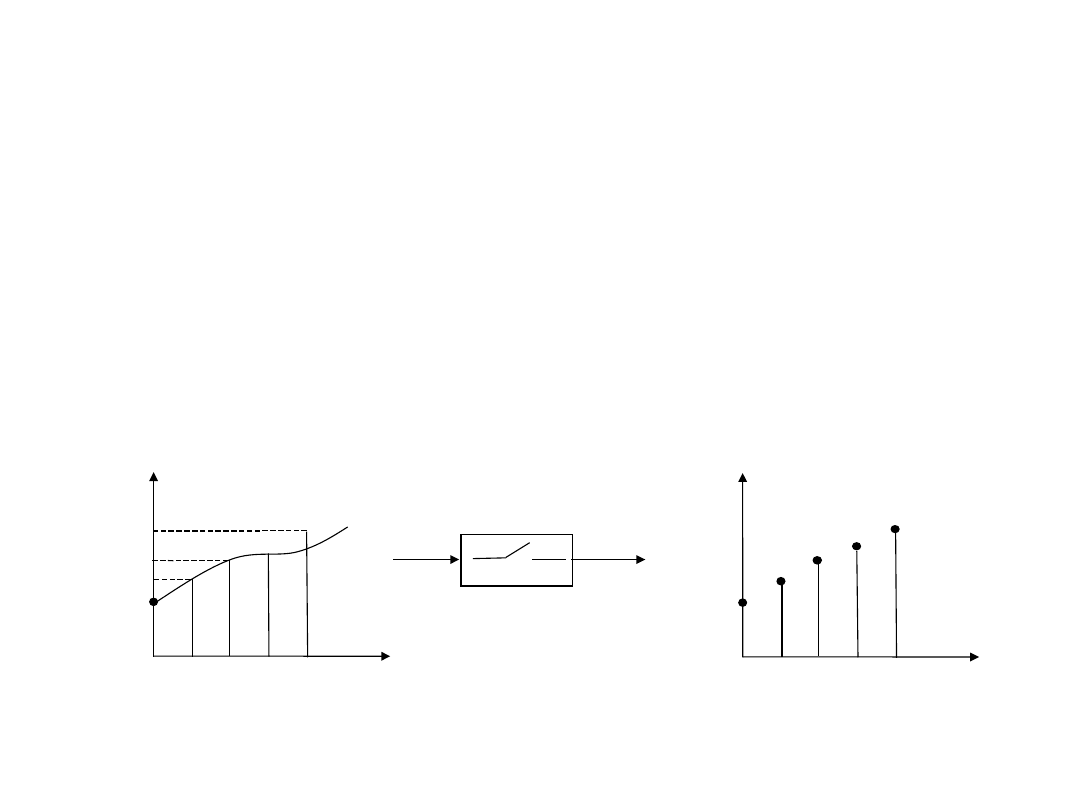
Działanie impulsatora

Impulsator idealny przekształca ciągłą funkcję czasu

e(t) w ciąg impulsów Diraca e* (t) , przesuniętych względem
siebie o okres impulsowania Ts , o polach impulsów równych
wartościom funkcji e(t) w chwilach impulsowania t=nTs
(n=0,1,2,…). Działanie idealnego impulsatora pokazuje
rysunek.

e(2T

s

)

e(t)

e(4T

s

)

e(T

s

)

e(0)

0

T

s

2T

s

3T

s

4T

s

t

e(t)

e

*

(t)

e

*

(t) (impulsy Diraca)

0

T

s

2T

s

3T

s

4T

s

n

e

(0

)

δ

(t

) e(

T

s

)

δ

(t

-

T

s

)

e

(2

T

s

)δ

(t

-

2

T

s

)

e

(3

T

s

)δ

(t

-

3

T

s

)

e

(4

T

s

)δ

(t

-

4

T

s

)

Ekstrapolator

Sygnał czasu przekształcony przez impulsator na ciąg

impulsów jest podawany na ekstrapolator czyli element
formujący. Ekstrapolatorem (elementem podtrzymującym)
jest najczęściej układ o transmitancji:

-gdzie Ts oznacza okres impulsowania.
Odpowiedzią elementu o transmitancji K1(s) na ciąg

impulsów Diraca e*(t) jest funkcja schodkowa e1(t).

s

e

s

K

s

sT







1

)

(

1

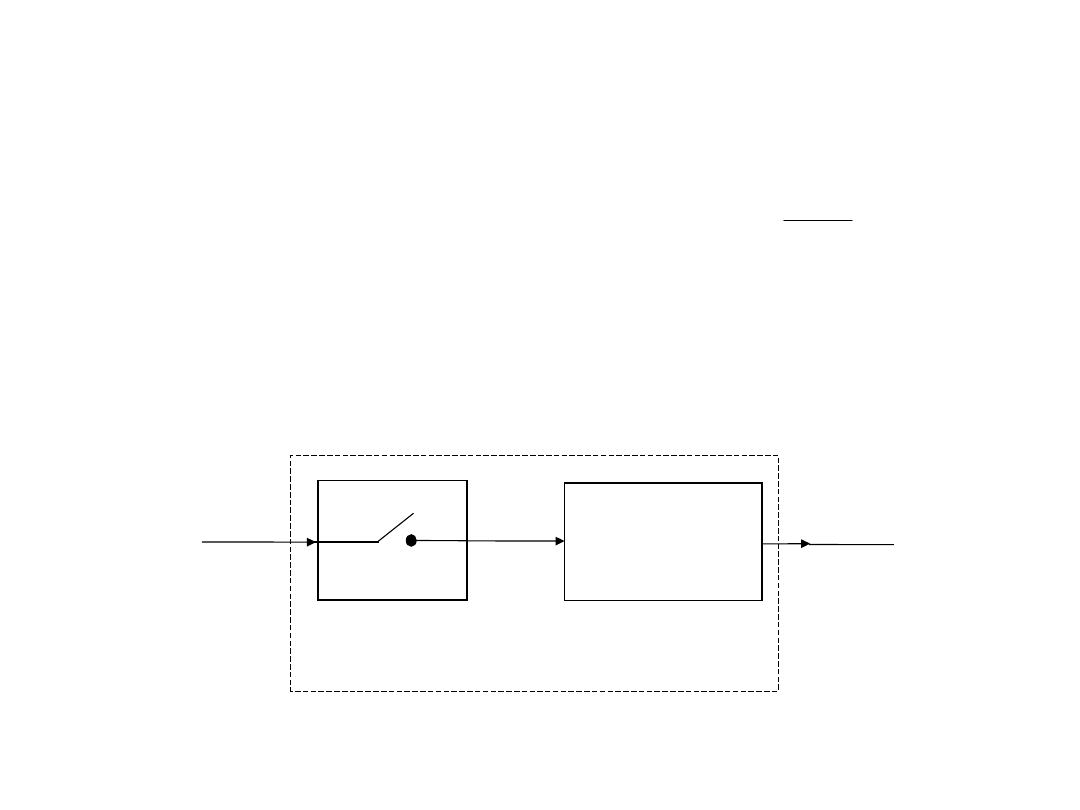
Ekstrapolator zerowego rzędu

• Impulsator idealny i element o transmitancji

nazywa

się ekstrapolatorem zerowego rzędu - Zero Order Hold
(ZOH) Taki blok dokonuje rekonstrukcji sygnału e*(t), która
polega na aproksymacji wielomianem zerowego rzędu
(aproksymacja prostokątna).

e(t)

e

*

(t)

K

1

(s)

element
formujący

e

1

(t)

impulsator idealny

s

e

s

K

s

sT







1

)

(

1

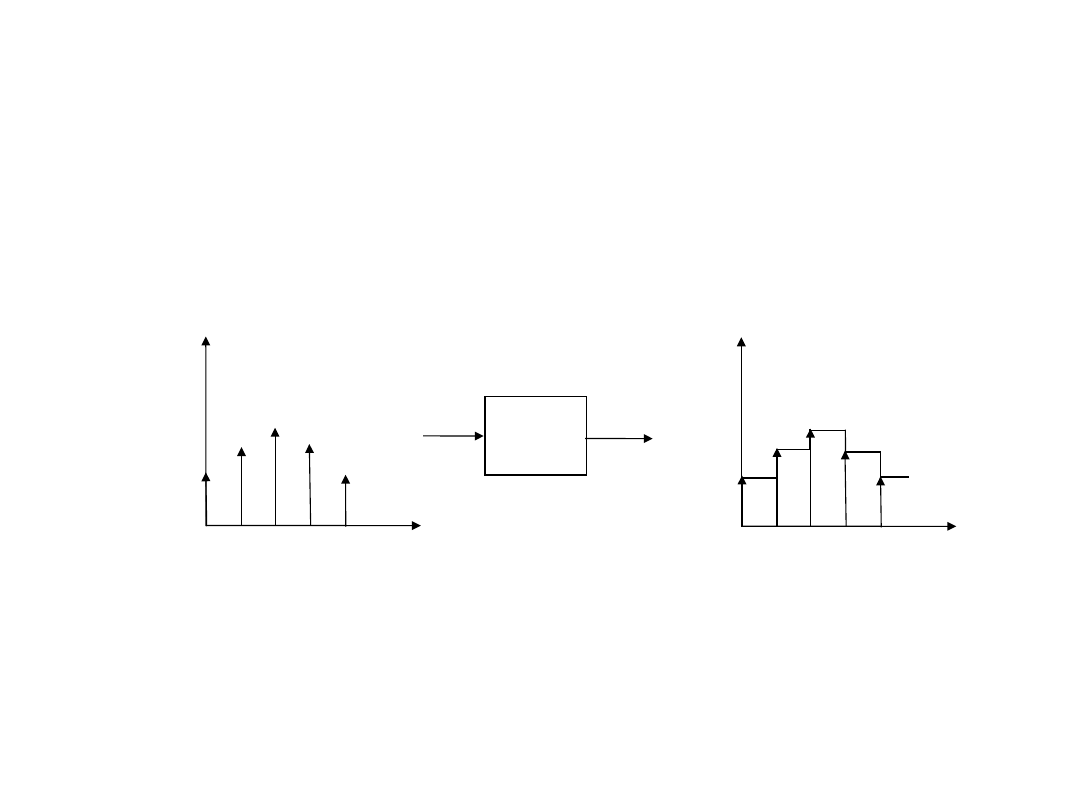
Działanie ekstrapolatora

Przebieg w dziedzinie czasu sygnału wychodzącego z

ekstrapolatora

e

*

(t)

0

T

s

2T

s

3T

s

4T

s

t

e

*

(t)

e

1

(t)

e

1

(t)

t

Próbkowanie i kwantowanie

Próbkowanie to przetworzenie sygnału analogowego

ciągłego na sygnał dyskretny, o wartościach równych
sygnałowi ciągłemu w chwilach próbkowania. Pobrany ciąg
próbek powinien umożliwiać jak najwierniejsze odtworzenie
całego przebiegu sygnału analogowego. Odstępy między
kolejnymi chwilami próbkowania są jednakowe i noszą
nazwę okresu próbkowania T .

Kwantowanie polega na przyporządkowaniu

jednakowych wartości sygnału między dwiema różnymi
wartościami sygnałów impulsowych.

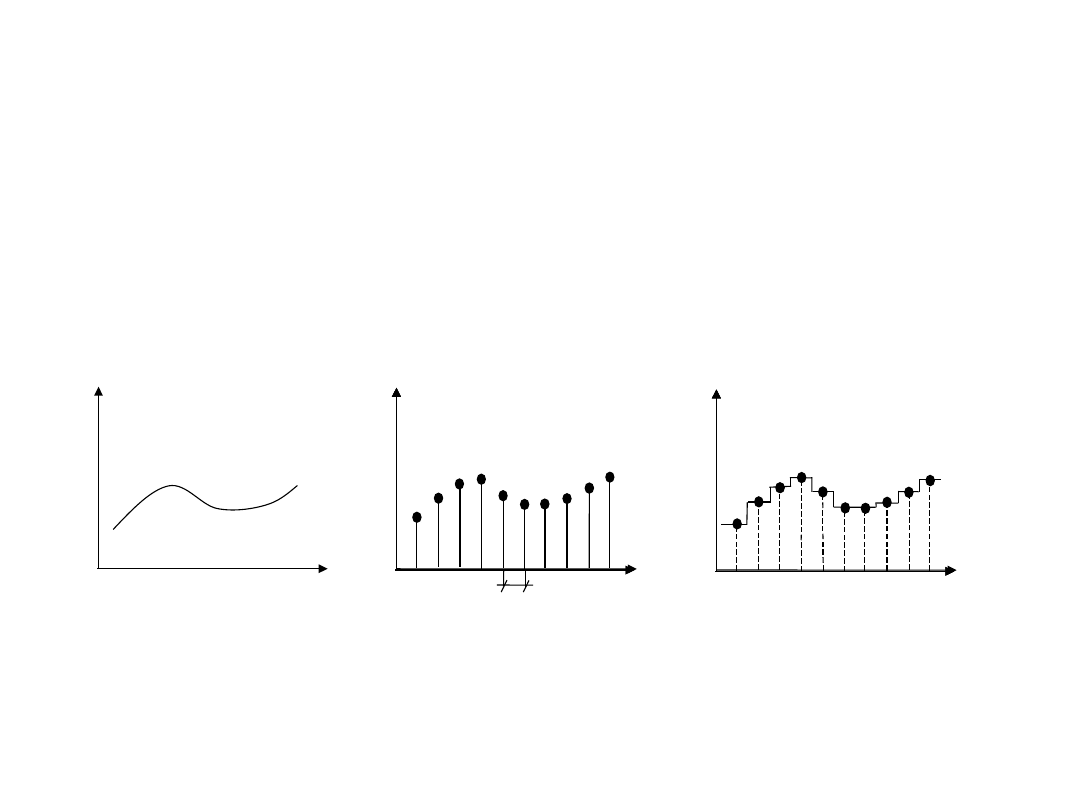
Sygnał przed i po próbkowaniu

Wykresy: sygnał analogowy e(t), oraz sygnał e(i) po

wykonaniu próbkowania i operacji kwantowania.

e(t)

e(i)

e(i)

n

T

s

n

t

Kodowanie

Sygnał wyjściowy przetwornika A/D jest kodowany.

Najczęściej jest to kod dwójkowy prosty ( nazywany też

kodem B lub kodem naturalnym). Innym podstawowym

kodem jest kod BCD (Binary Coded Decimal – kod

dwójkowo-dziesiętny, kod 8421).

W kodzie tym każda cyfra liczby zapisanej w układzie

dziesiętnym jest przedstawiona w kodzie dwójkowym.

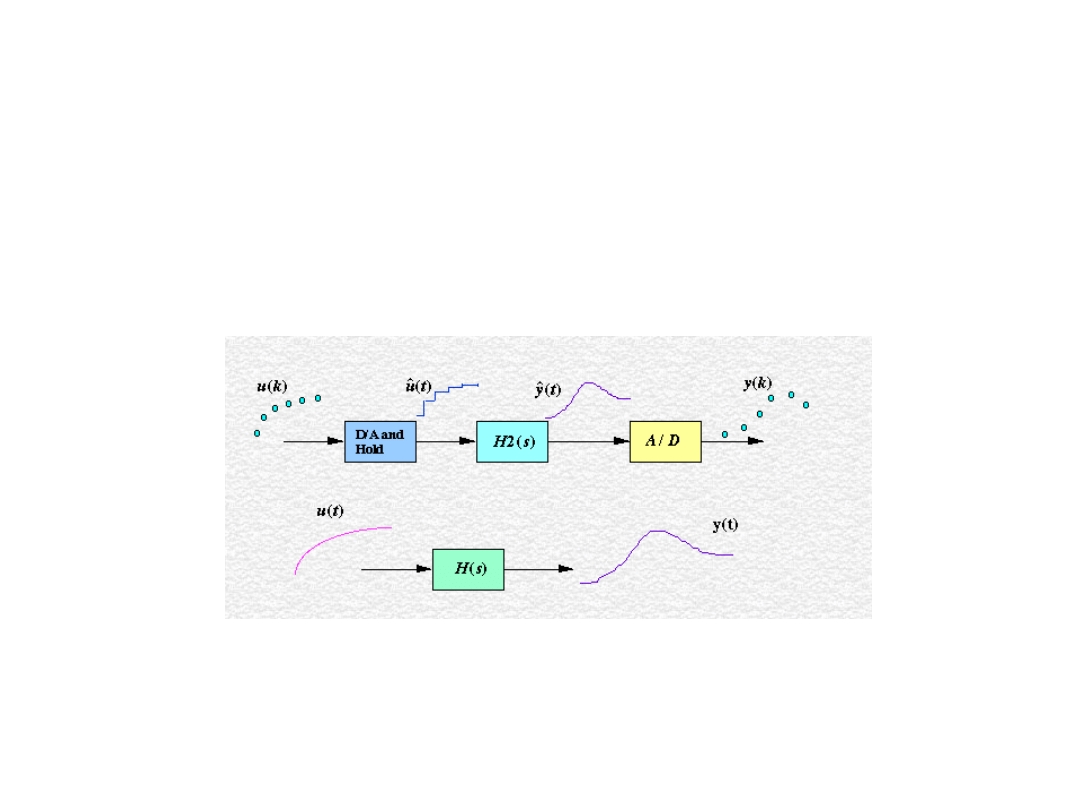
Przebiegi sygnałów

• Przebiegi sygnałów ciągłych i dyskretnych

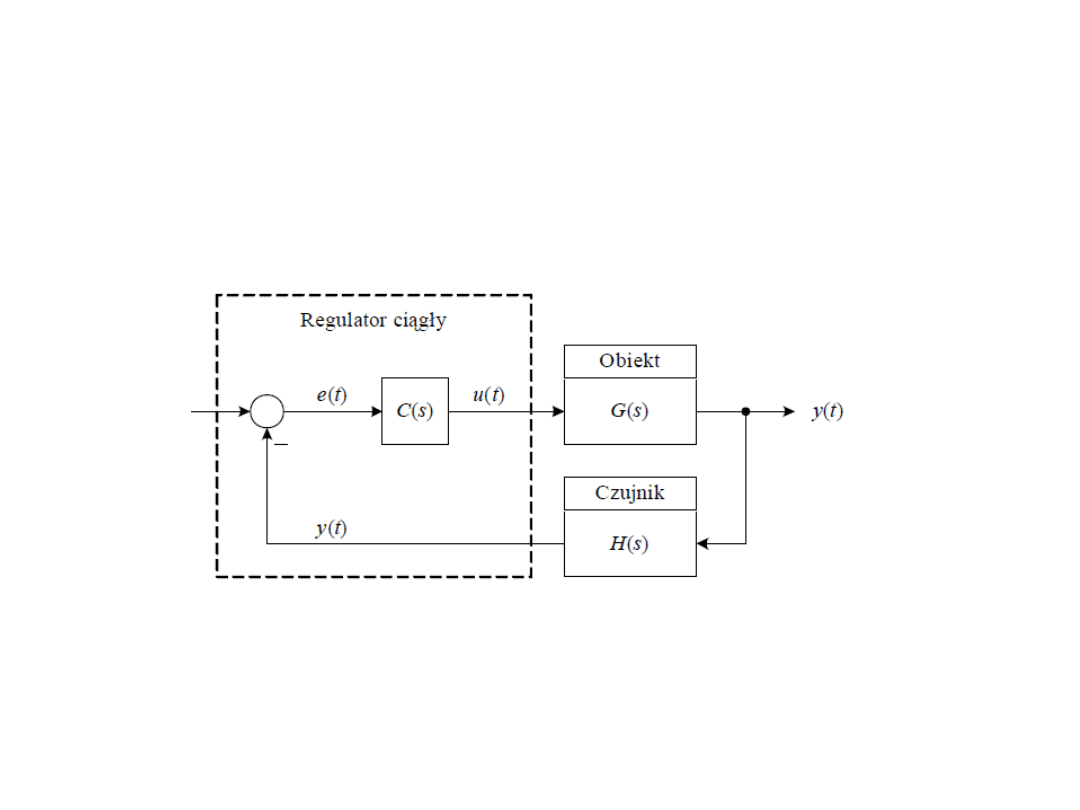
Układ cyfrowy

• Podstawowy schemat blokowy układu sterowania, układ

ciągły

Funkcje dyskretne

Z dowolnej funkcji ciągłej e(t) można

otrzymać funkcję dyskretną e(nT ) lub e(n) dla
Ts=1, gdy wezmie się pod uwagę tylko ciąg
wartości tej funkcji e(0), e(Ts), e(2Ts),… w
chwilach impulsowania t=0,Ts,2Ts,3Ts,…

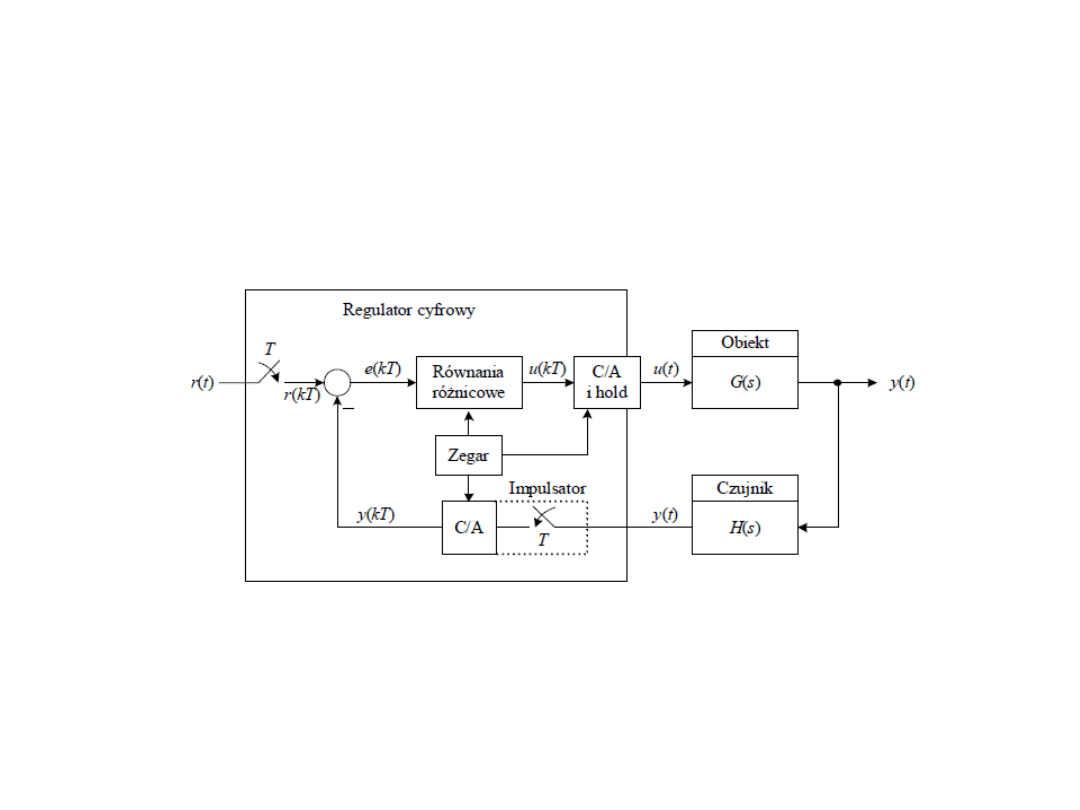
Układ cyfrowy

• Podstawowy schemat blokowy układu sterowania, układ

cyfrowy

Równania różniczkowe i różnicowe

W układach sterowania coraz częściej stosowane są

regulatory cyfrowe i stąd konieczność określania równań,

które opisują sygnały cyfrowe i dyskretne. Tak jak równania

różniczkowe stosowane są do opisu układów z sygnałami

analogowymi, tak równania różnicowe stosowane są dla

układów z sygnałami dyskretnymi lub cyfrowymi. Równania

różnicowe używane są również do aproksymacji równań

różniczkowych w celu zapisania ich w programach

komputerowych wykorzystywanych w różnego rodzaju

symulacjach.

Rachunek operatorowy Laplace’a może być stosowany

do rozwiązywania liniowych równań różniczkowych

zwyczajnych, natomiast transformata Z jest metodą

wykorzystywaną do
rozwiązywania liniowych równań różnicowych i układów

liniowych z danymi dyskretnymi lub cyfrowymi. Zmienna z

jest liczbą zespoloną.

Algorytm PID

• Uniwersalnym algorytmem regulatorów o działaniu ciągłym jest

algorytm PID, określany jako działanie

• proporcjonalno – całkująco – różniczkujące opisywany równaniem.

Algorytm różnicowy regulatora

PRZEKSZTAŁCENIE RÓWNANIA RÓŻNICOWEGO DO

POSTACI TRANSFORMATY Z

Podobnie jak w przypadku transformaty Laplace'a,

wprowadzenie transformaty Z ma na celu umożliwienie
wykonywania matematycznych operacji algebraicznych co
może być wykonywane w dziedzinie zmiennej zespolonej z,
ostateczna odpowiedź czasowa wyznaczana jest przez
zastosowanie odwrotnej transformaty Z. Odwrotna
transformata Z funkcji Y(z) daje informacje tylko o y(kT), a
nie o y(t). Innymi słowy transformata Z zachowuje

informacje tylko w chwilach próbkowania

.

Przekształcenie równań

różnicowych

Sygnały występujące w dyskretnych chwilach czasu

opisywane są przez równania różnicowe. Na tym wykładzie
pokazane zostanie w jaki sposób dokonuje się zastąpienia
równania różnicowego odpowiadającą mu transformatą Z.
W tabeli poniżej znajdują się podstawowe twierdzenia w
oparciu o które dokonuje się przekształcenia równania
różnicowego do postaci transformaty Z. Na podstawie
równania różnicowego w sposób sekwencyjny można
dokonać wyznaczenia dyskretnego sygnału czasowego.
Takie same wartości próbek sygnału dyskretnego można
uzyskać rozwiązując równanie różnicowe metodą
transformaty Z.

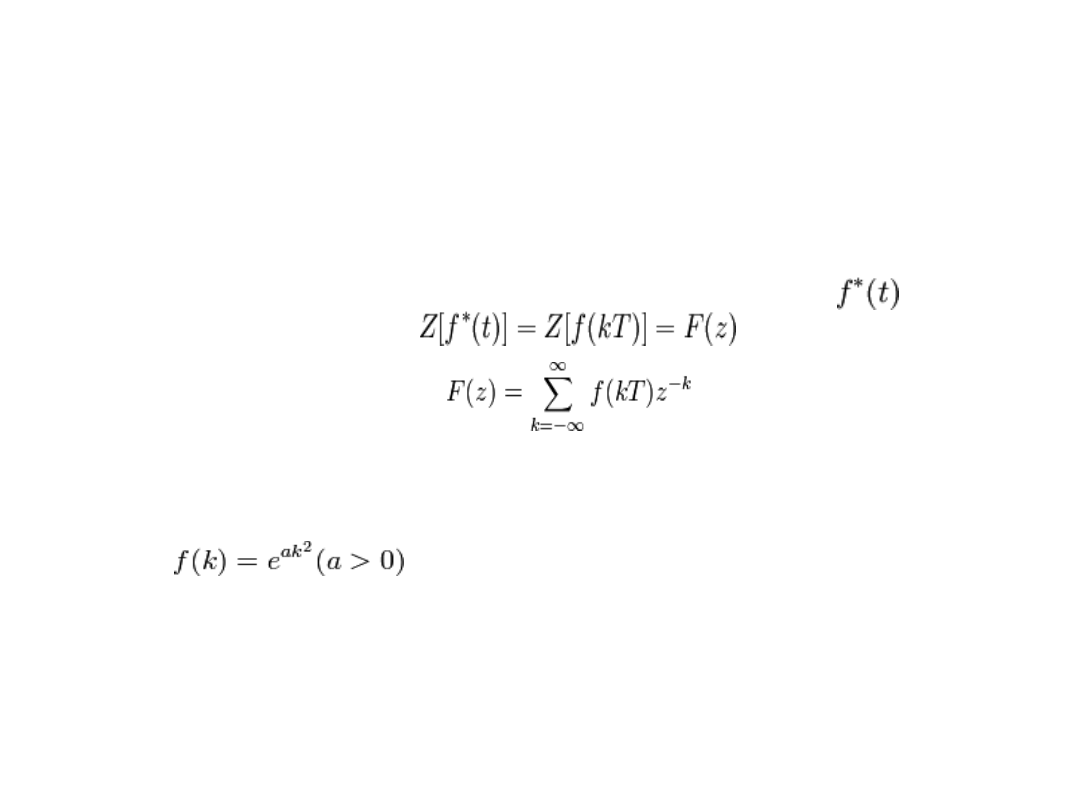
Transformata Z

Transformata Z (transformata Laurenta) jest

odpowiednikiem

transformaty Laplace'a

stosowanym do

opisu i analizy układów dyskretnych.

Transformatą Z dyskretnej (impulsowej) funkcji czasu

jest nazywana funkcja

określona wzorem

gdzie: F(z) – transformata oryginału; f(kT) – oryginał

dyskretny; Transformaty Z istnieją dla funkcji dyskretnych,

które nie rosną szybciej niż

funkcja wykładnicza

.

Przykładowo, dla funkcji f(k) = k! lub

nie istnieją transformaty Z, ponieważ nie spełniają one

powyższego warunku

.

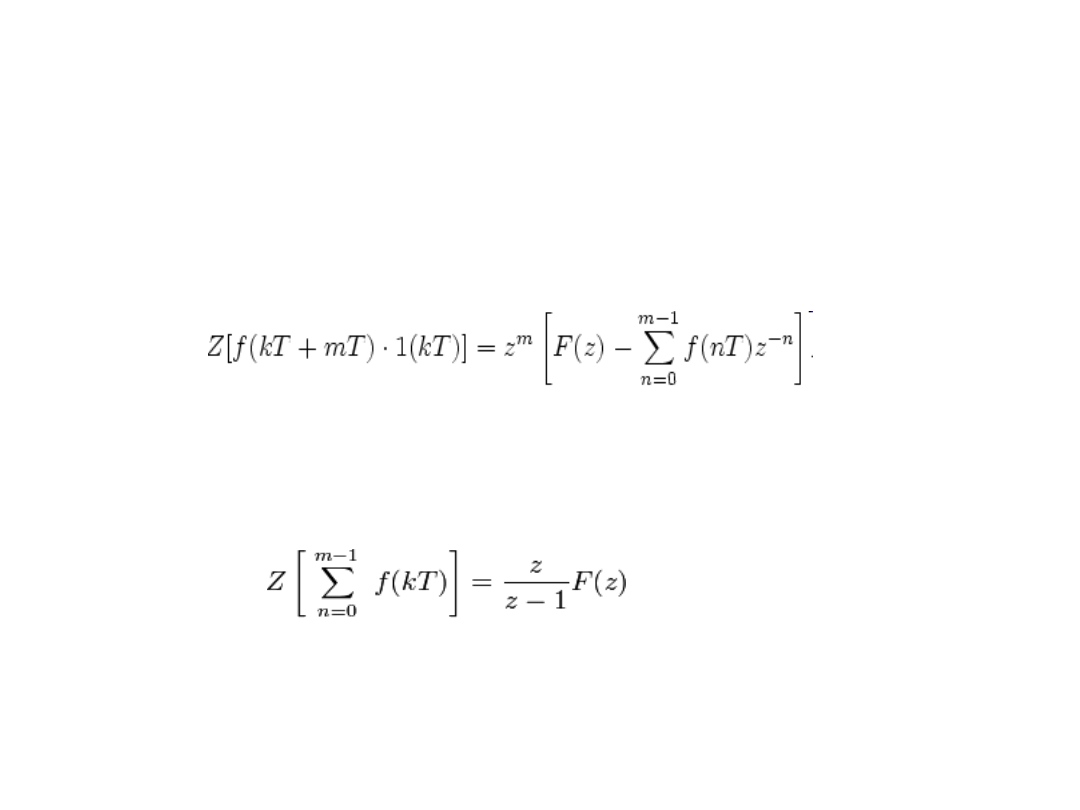
Właściwości transformaty Z

• Liniowość:
• Z[af1(kT) + bf2(kT)] = aF1(z) + bF2(z)
• Przesunięcie w dziedzinie czasu:

• gdzie m – dowolna dodatnia

liczba całkowita

; 1(kT) –

funkcja skokowa

.

• Transformata sumy:

• Transformata różnicy
• Z[f((k + 1)T) − f(kT)] = (z − 1)F(z) − zf(0)

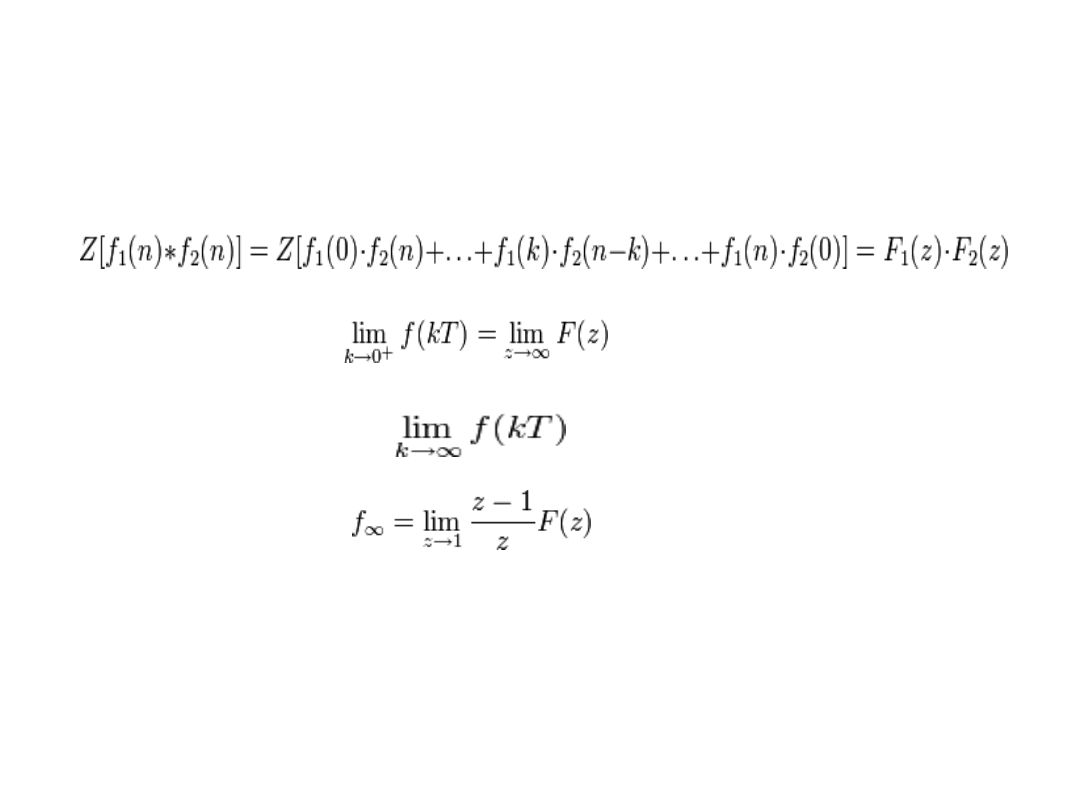
Właściwości transformaty Z

• Splot

• Twierdzenie o wartości początkowej:

• Jeśli istnieje granica,

, to ma ona wartość

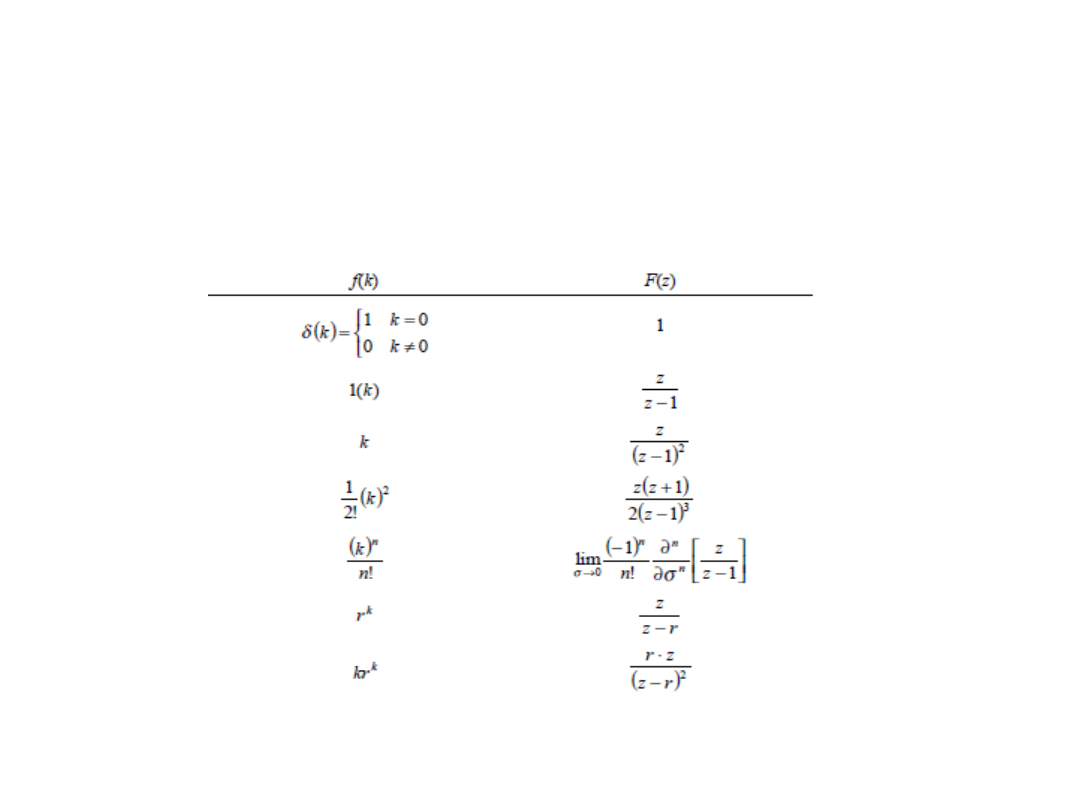
Wybrane transformaty Z

Transformaty Z funkcji podstawowych

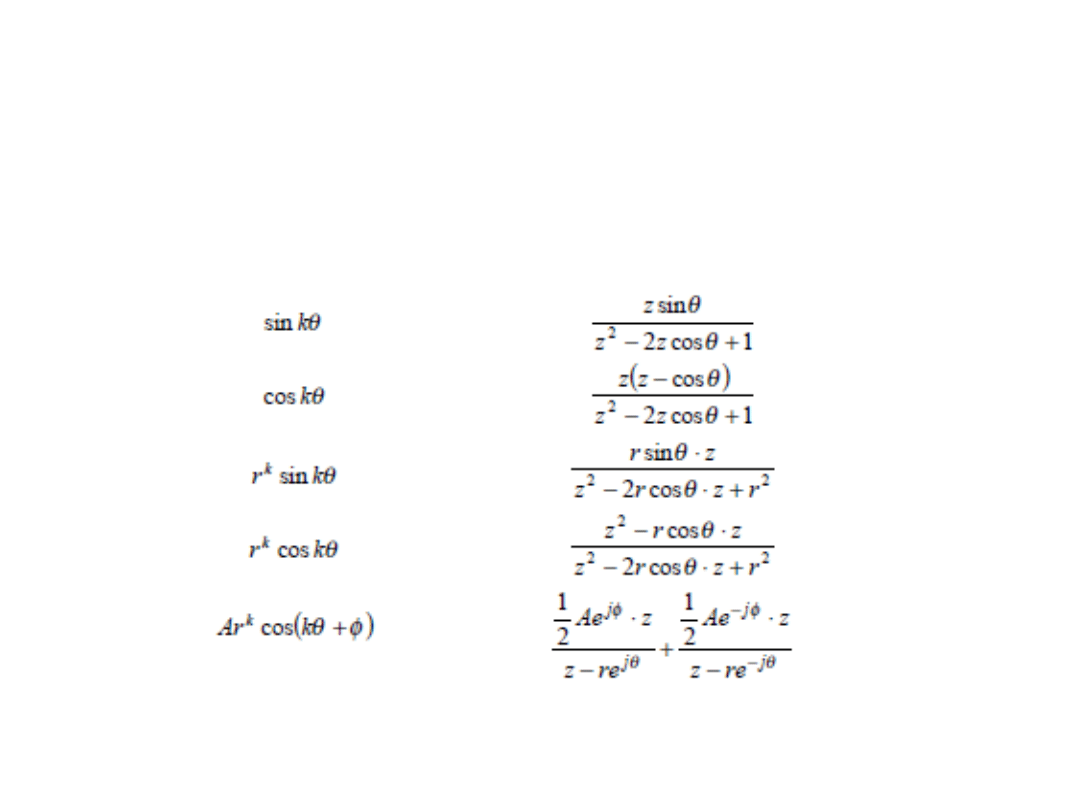
Wybrane transformaty Z

Transformaty Z funkcji okresowych

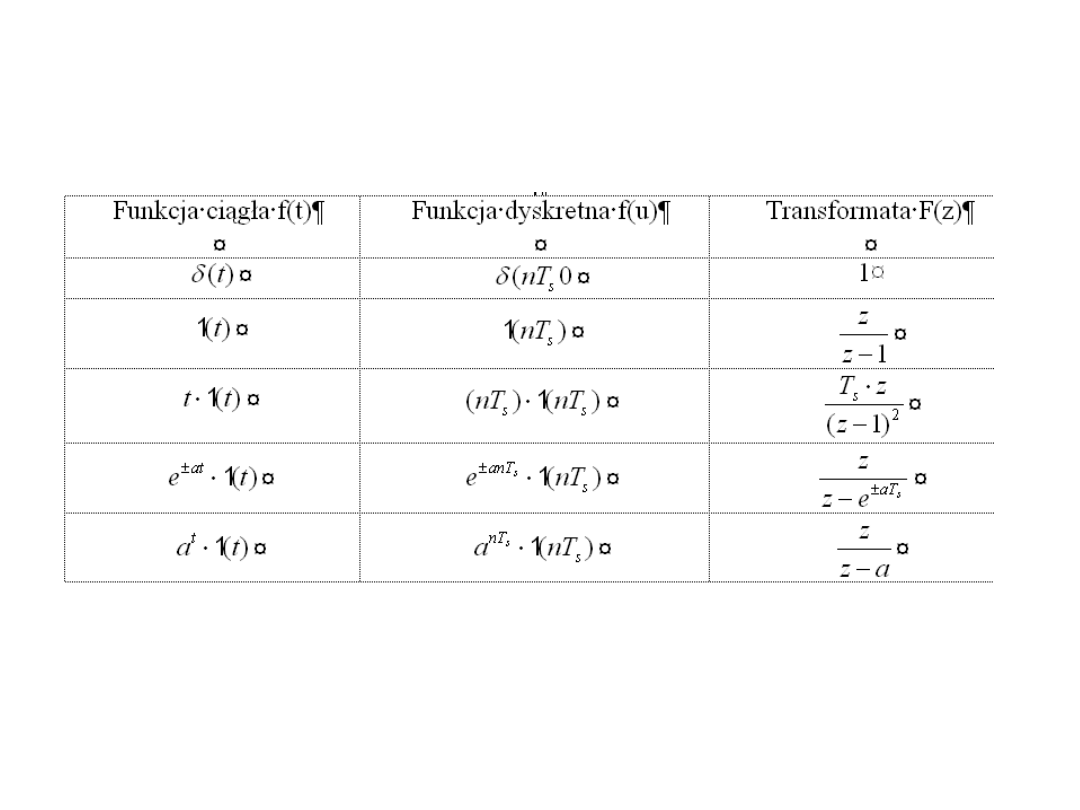
Porównanie funkcji