Plan wykładu

1.  Wymagania do aparatury pomiarowej
2. Ograniczenia występujące podczas

pomiarów wielkości elektrycznych.

3. Klasyfikacja przyrządów pomiarowych

według ich funkcji i właściwości.

4. Przykładowy schemat strukturalny

multimetru elektronicznego
cyfrowego (DMM - ang. Digital Multi-
Meter).

1. Wymagania do aparatury

pomiarowej

Podstawowymi wymaganiami są:

•Możliwość pomiaru wartości wielkości w zadanym

zakresie

(tak małych jak i dużych wartości), jest

to wymagania amplitudowe;

•Możliwość pomiarów wielokanałowych – kilka

wielkości

jednego lub różnego rodzaju

•Brak obciążenia obiektu badanego

–

odpowiednia wartość rezystancji wejściowej

•Zadana dokładność pomiarów

, zapewnia się

odpowiednią klasą dokładności woltomierza oraz

innymi wartościami jego parametrów: stabilnością

temperaturową oraz czasową, odpornością na inne

wielkości wpływające

1. Wymagania do aparatury

pomiarowej

•Odporność na oddziaływania zakłóceń

tak

regularnych jak i losowych wpływu zakłóceń to

wymaganie jest ważne przy pomiarach wielkości

niskiego poziomu, w warunkach przemysłowych

•Szybkość pomiaru

– to wymaganie jest ważne

przy pomiarach wielkości szybko zmiennych

(dynamicznych),.

•Możliwość współpracy z PC

– jest to ważne przy

automatyzacji pomiarów

•Możliwość opracowania wyników

wg zadanego

algorytmu

•Łatwość obsługi

•Niska cena oraz niski koszty pomiarów

2. Ograniczenia występujące podczas

pomiarów wielkości elektrycznych

.

Fundamentalnym czynnikiem ograniczającym jest szum

cieplny lub szum Jonson’a.

Na dowolnej rezystancji

R

energia cieplna powoduje ruch

nośników ładunków elektrycznych, który z kolei

powodują szum elektryczny.

Moc tego szumu opisuje się wzorem

P=4kTB

,

gdzie:

k=1.38·10

-23

J/K-

stała Boltsmana;

T

–temperatura (K);

B

– pasmo częstotliwościowe szumu (Hz).

Wartość skuteczna szumu Jonsona

U

sz

na rezystancji (

R

)

równa się:

a wartość prądu szumu Jonsona

I

sz

:

kBTR

PR

U

sz

4





R

kBT

R

P

I

sz

4





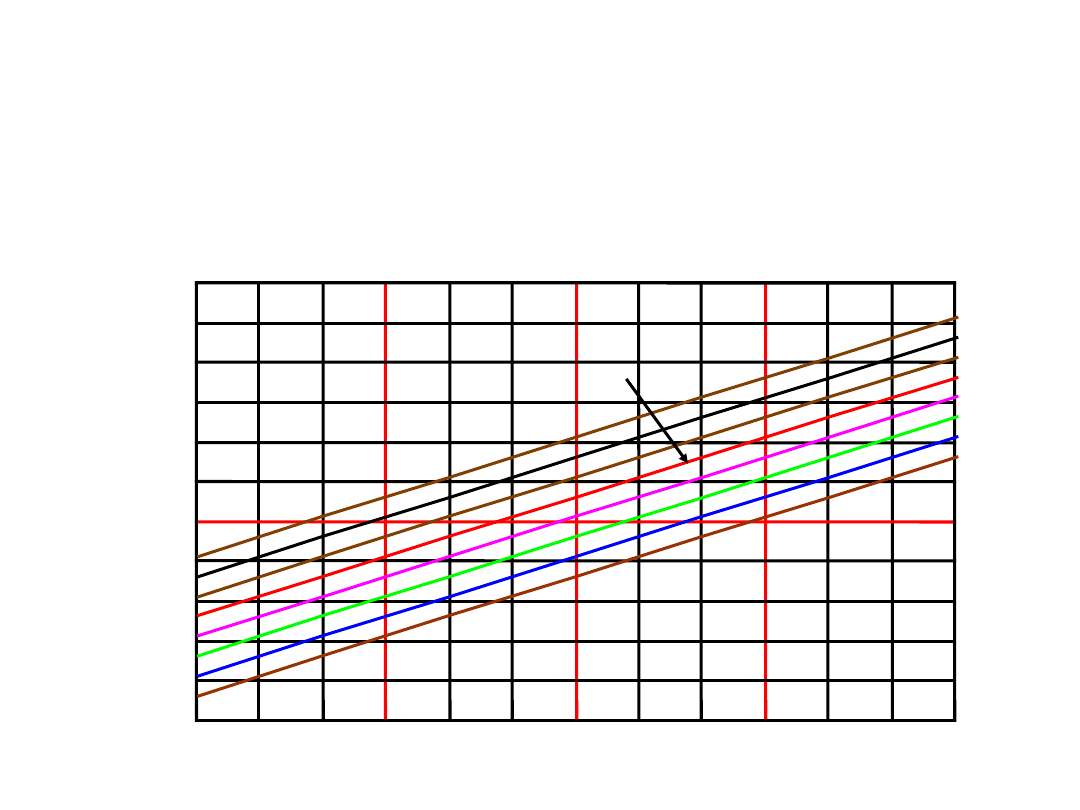
2. Ograniczenia występujące podczas

pomiarów wielkości elektrycznych

.

Zależności wartości napięcia oraz prądu szumu cieplnego

przy

T=295 K

(

22

o

C

) jako funkcje rezystancji oraz

szerokości pasma pokazane niżej

1 

Ω

1 k

Ω

0.01

0.1

10

100

10

100

B=0,1 Hz

B=1 MHz

1 µV

B=1 kHz

1 mV

1 V

1 nV

0.01

0.1

1 M

Ω

1 G

Ω

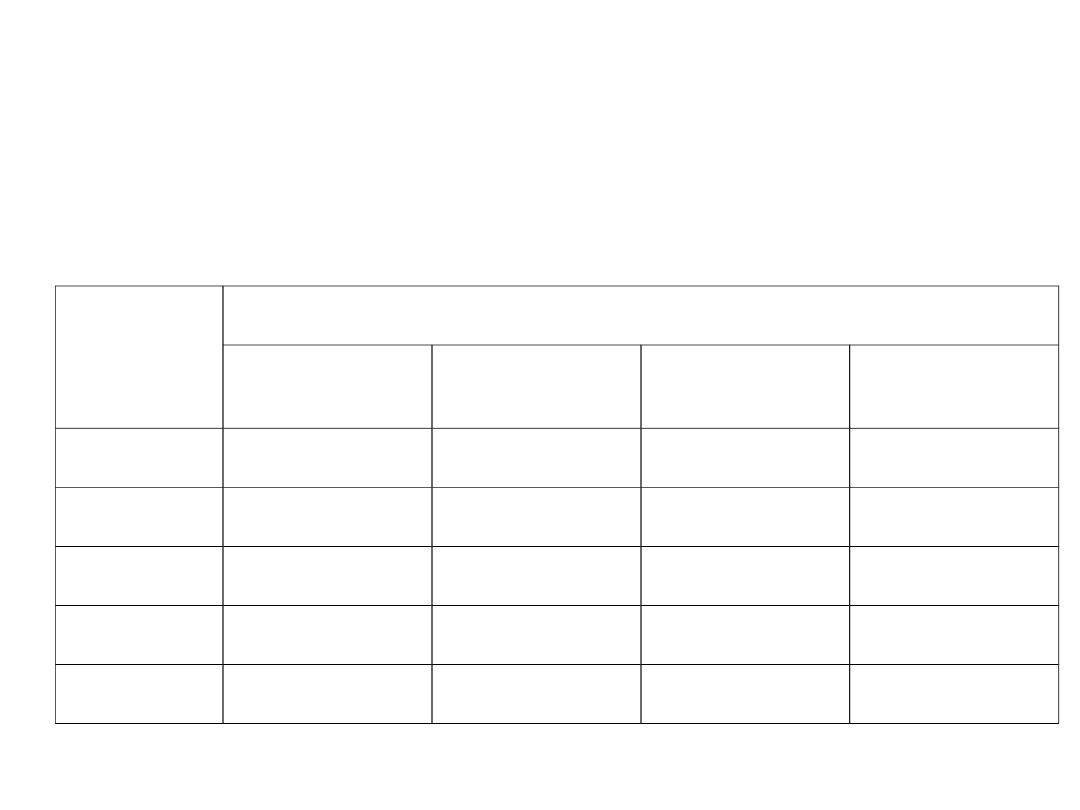
2. Ograniczenia występujące podczas

pomiarów wielkości elektrycznych

.

Teoretyczna granica czułości pomiaru napięcia

Rezystan

cja

Pasmo częstotliwości

0,1 Hz

1 Hz

1 kHz

1 MHz

1 

Ω

0,03 nV

0,1 nV

3 nV

0,1  µV

1 k

Ω

1 nV

3 nV

0,1 µV

3  µV

1 M

Ω

30 nV

0,1  µV

3  µV

100  µV

1 G

Ω

1  µV

3  µV

100  µV

3 mV

1 T

Ω

30  µV

100  µV

3 mV

100 mV

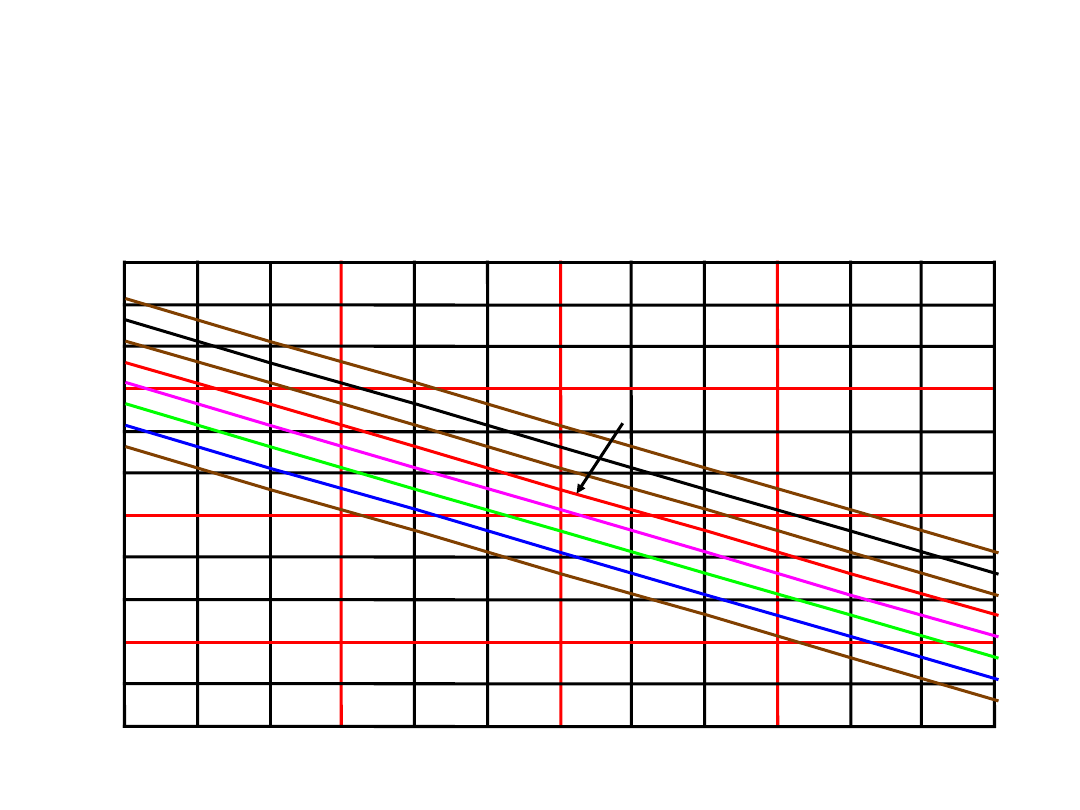
2. Ograniczenia występujące podczas

pomiarów wielkości elektrycznych

.

Zależności wartości skutecznej prądu szumu cieplnego

przy T=295 K (22

o

C) jako funkcje rezystancji oraz

szerokości pasma

1 

Ω

1 k

Ω

0.01

0.1

10

100

10

100

0,1 Hz

1 MHz

1 kHz

1 pA

1 nA

1 µA

1 fA

0.01

0.1

1 M

Ω

1 G

Ω

T

Ω

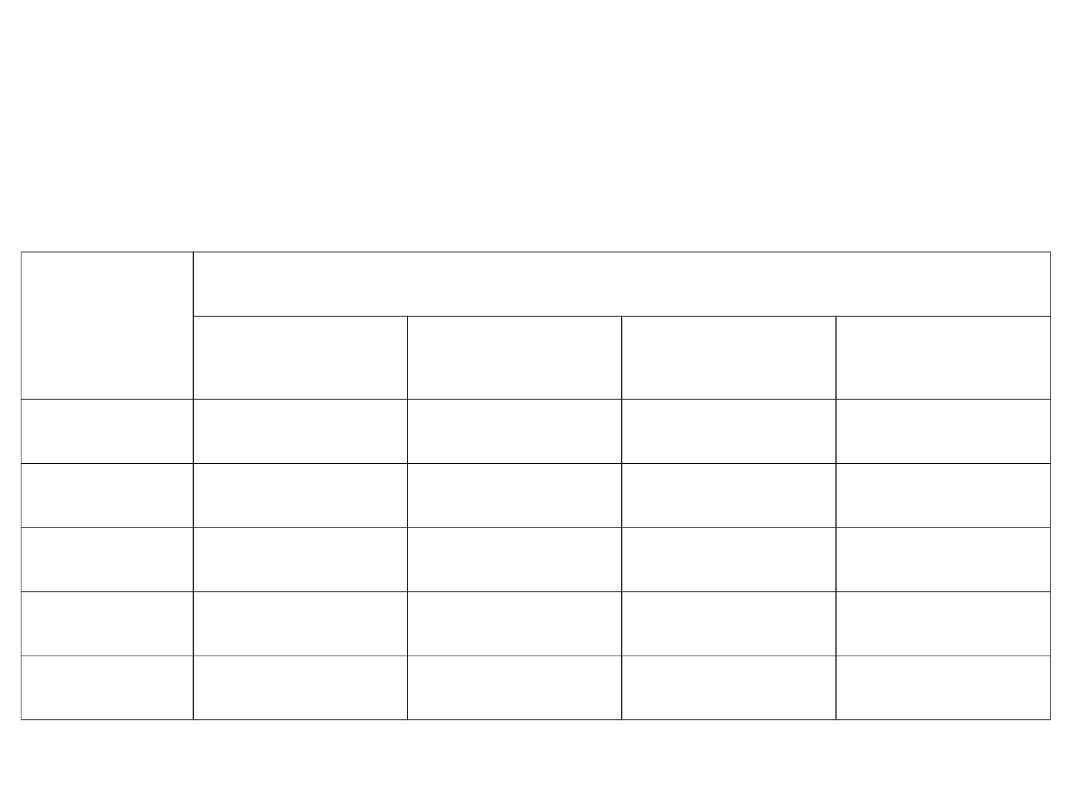
2. Wymagania do woltomierzy DC.

Zakresy

Teoretyczna granica czułości pomiaru prądu

Rezystan

cja

Pasmo częstotliwości

0,1 Hz

1 Hz

1 kHz

1 MHz

1 Ohm

30 pA

100 pA

3 nA

100 nA

1 kOhm

1 pA

3 pA

100 pA

3 nA

1 MOhm

0,03 pA

0,1 pA

3 pA

100 pA

1 GOhm

1 fA

3 fA

0,1 pA

3 pA

1 TOhm

0,03 fA

0,1 fA

3 fA

0,1 pA

3. Klasyfikacja przyrządów

pomiarowych według ich funkcji i

właściwości

W zależności od zakresów i warunków pomiaru (właściwości

obiektu – rezystancja, pasmo częstotliwości) rozróżnia się:

•

multimetry;

• elektrometry,

• nanowoltomierzy,

• pikoamperomierzy,

• mikro-omomierzy,

• przyrządy źródła – mierniki,

• oraz inne.

3. Klasyfikacja przyrządów

pomiarowych według ich funkcji i

właściwości

Multimetry

są to przyrządy dla pomiarów:
-

napięć powyżej 1 mkV ;

- prądów powyżej 1 mkA, oraz
- rezystancji poniżej 1 GOhm

.

Rezystancja wejściowa woltomierza (Rv) DMM stanowi od

około (

1-10-100

) MOhm do maksymalnie (1-10) GOhm

Rozdzielczość DMM wynosi od

3½

cyfr dziesiątkowych

(bardzo tanie) aż do drogich

6½-7½

cyfr

dziesiątkowych.

Maksymalna czułość DMM stanowi do (

0,1-0,01

) mkV (do

10 nV

).

3. Klasyfikacja przyrządów

pomiarowych według ich funkcji i

właściwości

Elektrometry.

Są to przyrządy pomiarowe dla pomiarów napięć, prądów,

ładunku i rezystancji przy następnych warunkach:

–

prądów

poniżej

1  µA do 100 pA

, napięcie źródła przy

pomiarach

prądu

jest

poniżej kilku set

mV

;

–

napięcia

poniżej

1 µV

, źródło napięcia ma rezystancją

wyjściową rzędu

1 MΩ

i wyżej do

10 TΩ

;

–

rezystancji

powyżej

1 GΩ

;

–

pomiar

ładunku

;

–

pomiary przy

porównywalnych wartościach szumów

cieplnych

oraz innych.

Rezystancja wejściowa

woltomierza elektrometru stanowi

typowo od około

100 T

Ω

nawet do około

100 P

Ω

.

3. Klasyfikacja przyrządów

pomiarowych według ich funkcji i

właściwości

Pikoamperomierze.

Są to bardzo czułe, pracujący w

pobliżu teoretycznej

granicy czułości

oraz przy

mniejszych wartościach

spadku napięcia

(tzw. votage burden) w porównaniu

do elektrometrów.

Pikoamperomierze zapewniają też inne właściwości,

np. lepszą szybkość pomiaru lub możliwość
logarytmicznej charakterystyki.

3. Klasyfikacja przyrządów

pomiarowych według ich funkcji i

właściwości

Mikro-omomierzy.

Mikro-omomierz jest to specjalny omomierz przeznaczony

do pomiaru

bardzo niskich wartości rezystancji

.

Typowy mikro-omomierz ma czułość do około

10 µΩ

.

Pomiar małych rezystancji odbywa się

przez 4-przewodowe

podłączenie

obiektu badanego (w celu eliminacji wpływu

rezystancji przewodów) oraz charakteryzują się

dodatkowymi (w porównaniu do DMM) funkcjami.

Z pośród nich jest to możliwość kompensacji napięcia

przesunięcia (offset), spowodowanego przykładowo

termoelektryczną SEM, możliwość ograniczenia napięcia

wzdłuż badanej rezystancji do

bardzo niskiego poziomu

(typowo poniżej 20 mV)

, co jest bardzo ważne przy

testowaniu takich elementów jak kontakty

przełączników, kluczy oraz (rele) kontaktronów.

3. Klasyfikacja przyrządów

pomiarowych według ich funkcji i

właściwości

Przyrządy źródła – mierniki
Sourse-Measure Unit - SMU

są to przyrządy, funkcjami których są:
-

pomiar napięcia;

- pomiar prądu;
- źródło napięcia;
- źródło prądu.

SMU pozwalają na jednoczesne dokładne (o zadanej

wartości):

-

wymuszanie obiektu napięciowe i pomiar prądu

odpowiedzi oraz

- wymuszanie obiektu prądowe i pomiar napięcia

odpowiedzi.

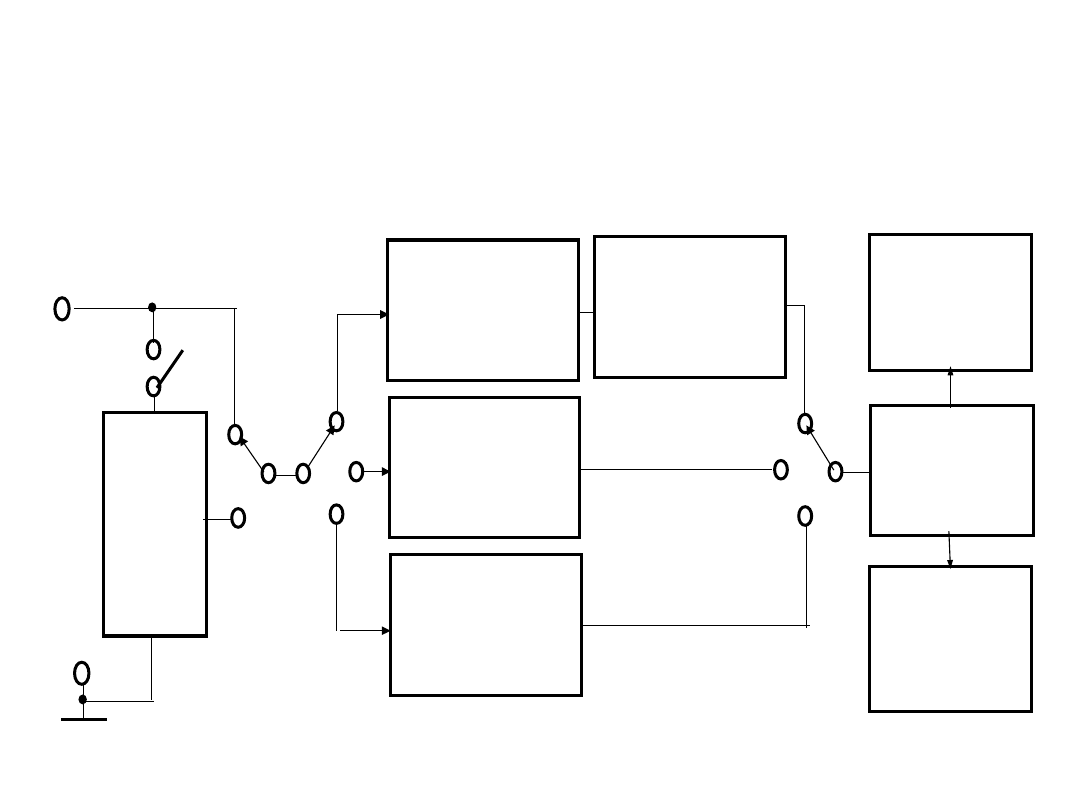
4. Przykładowy schemat strukturalny

multimetru elektronicznego cyfrowego

(DMM - ang. Digital Multi-Meter)

AC

Wzmacniacz/

dzielnik

AC

przetwornik

DC

Wzmacniacz/

dzielnik

Ohms

przetwornik

AC

DC

Ohms

I

U

p

rz

e

tw

o

rn

ik

HI

LO

W

e

jś

c

ie

AC

DC

Ohms

V

A

A

A/C

przetwornik

(+procesor

)

Odczyt

Cyfrowy

(display)

Wyjście

Cyfrowe

(RS 232,

GPIB,

USB)

Problemy pomiaru

małych napięć w

obwodach

elektronicznych

Plan wykładu

1. Wymagania do woltomierzy DC.

2.Korekcja wpływu rezystancji

wejściowej woltomierza

3. Układy wejściowe woltomierza.

4. Układ wejściowy woltomierza ze

wzmacniaczem instrumentalnym.

1. Wymagania do woltomierzy

DC.

Ogólnymi wymaganiami do woltomierze przy pomiarach wartości

napięcia DC są

:

1.

Możliwość pomiaru wartości napięcia w zadanym
zakresie

(małych jak i dużych wartości napięcia),

jest to wymagania amplitudowe;

2.

Brak obciążenia obiektu badanego

– odpowiednia

wartość rezystancji wejściowej;

1. Wymagania do woltomierzy

DC.

Ogólnymi wymaganiami do woltomierze przy pomiarach wartości

napięcia DC są

:

3.

Zadana dokładność pomiaru

, zapewnia się odpowiednią

klasą dokładności woltomierza oraz innymi wartościami jego
parametrów: stabilnością temperaturową oraz czasową,
odpornością na inne wielkości wpływające min. Zakłócenia;

4.

Szybkość pomiaru

– ten problem jest ważny przy

pomiarach wielkości szybko zmiennych (dynamicznych),
jest związany z odpornością do wpływu zakłóceń;

5.

Możliwość przesyłania danych pomiarowych do PC

–

jest to ważne przy automatyzacji pomiarów oraz
opracowania wyników.

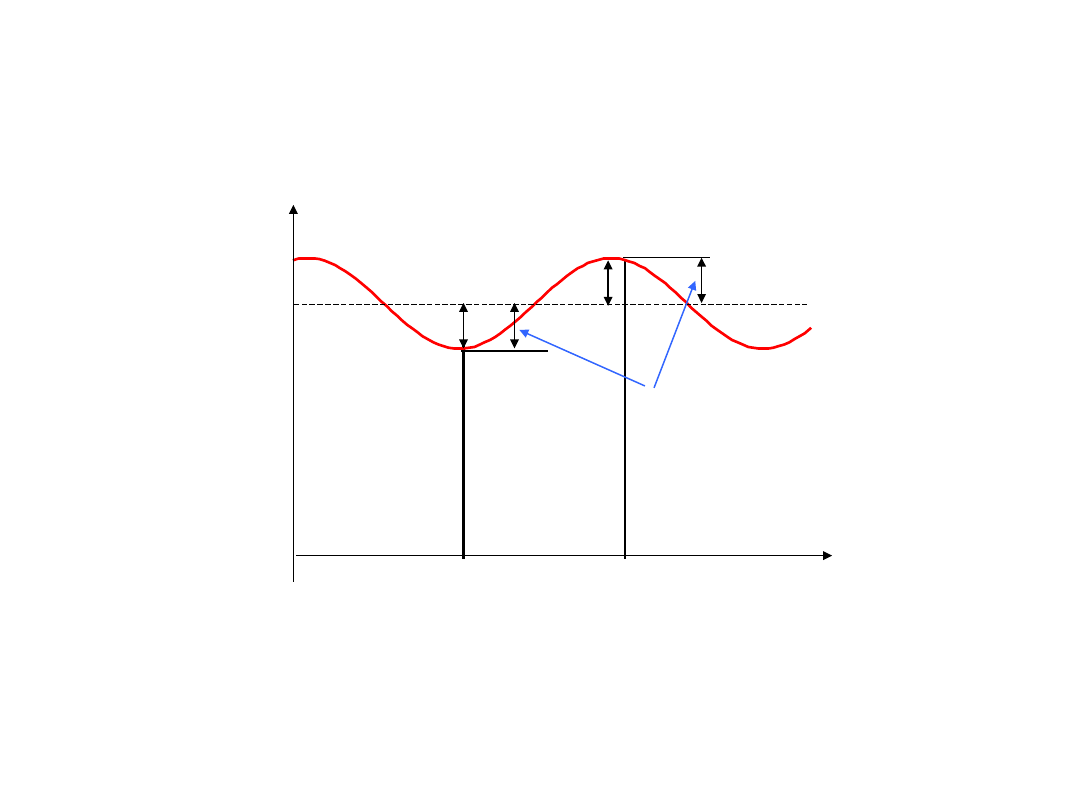
Wpływ zakłócenia

-U

m

ΔU

x.max

=U

m

U

x

Zakłócenie

ΔU

x2

ΔU

x1

Czas

Maksymalne błędy

pomiaru napięcia DC

(U

x

)

U

m

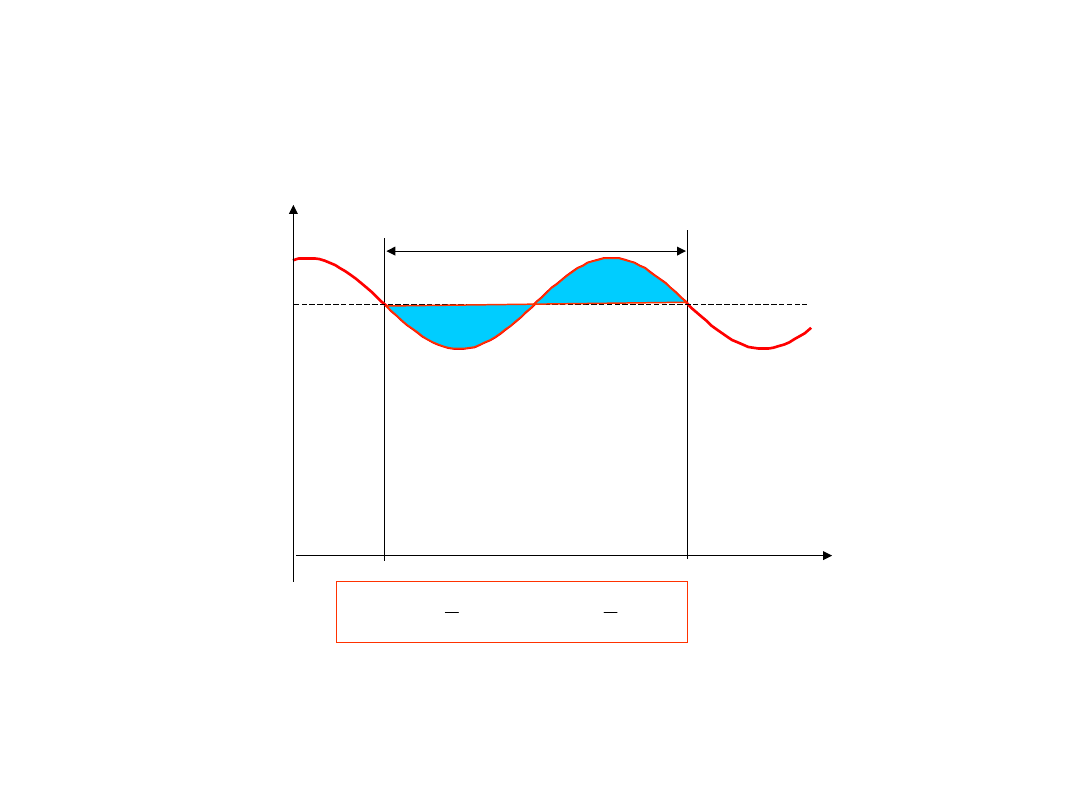
Wartość średnia zakłócenia w czasi

okresu

U

x

Zakłócenie

Czas

Wartość średnia od zakłócenia

harmonicznego w czasie jego

okresu T równa się zeru!

+S

Uz

-S

Uz

-S

Uz

+S

Uz

=0

T

!

!

!

0

2

sin

2

cos

1

1

1

1









































dt

T

t

U

dt

T

t

U

T

t

t

m

T

t

t

m





t

1

+T

t

1

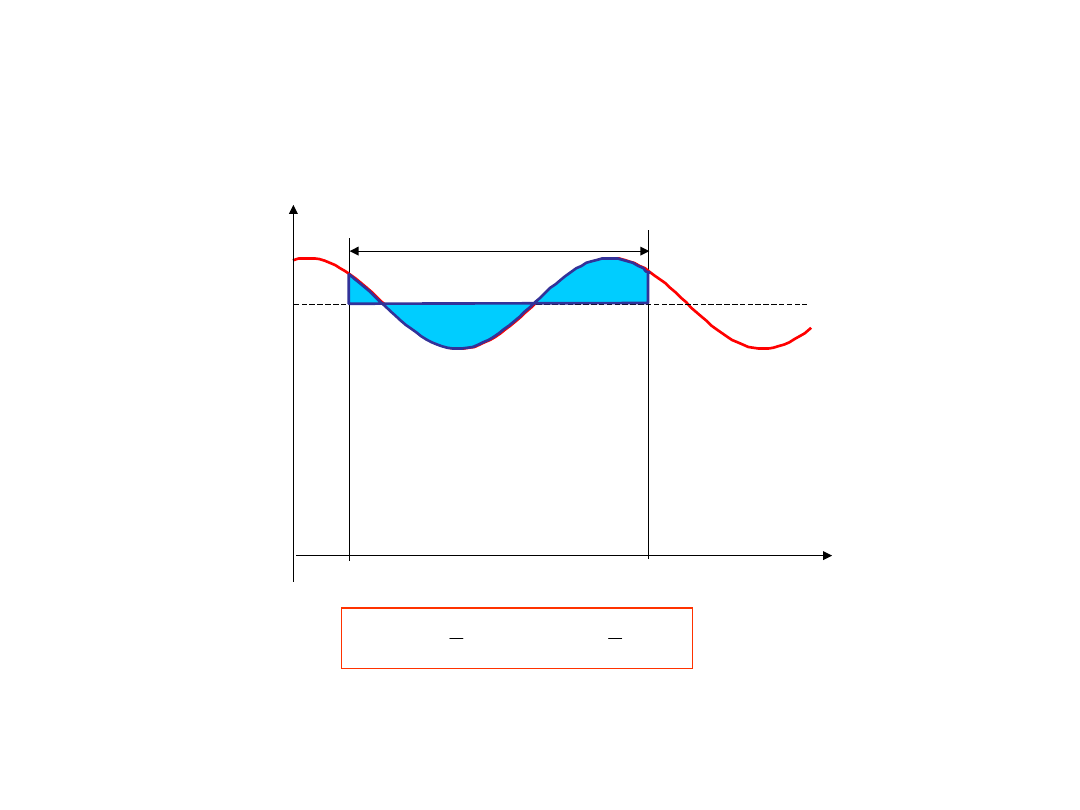
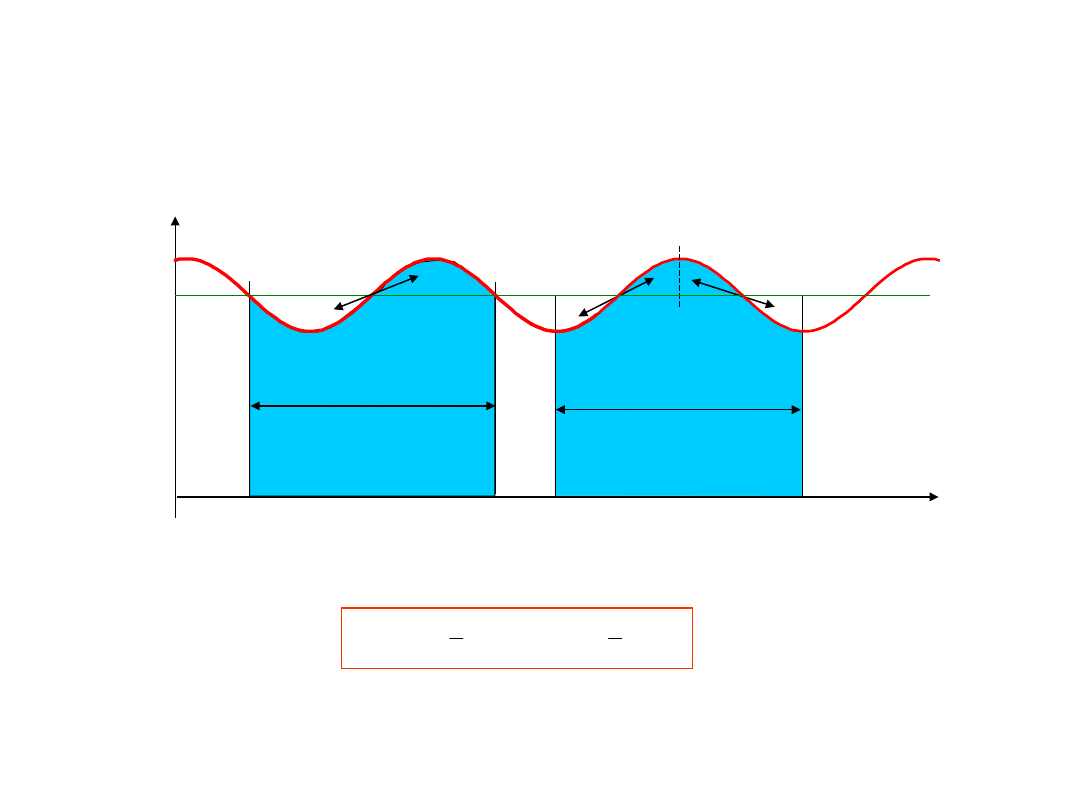
Wartość średnia zakłócenia w czasi

okresu

t

1

+T

U

x

Zakłócenie

Czas

Wartość średnia od zakłócenia

harmonicznego w czasie jego okresu T

równa się zeru niezależnie od początku

całkowania!

+S

Uz

-S

Uz

+

S

Uz1

-S

Uz

+S

Uz2

=0

T

+SU

z1

-SU

z

+SU

z2

!

!

!

0

2

sin

2

cos

1

1

1

1









































dt

T

t

U

dt

T

t

U

T

t

t

m

T

t

t

m





t

1

Wartość średnia zakłócenia w czasi

okresu

Wartość średnia od zakłócenia

harmonicznego w czasie jego okresu T

równa się zeru niezależnie od początku

całkowania!

!

!

!

0

2

sin

2

cos

1

1

1

1









































dt

T

t

U

dt

T

t

U

T

t

t

m

T

t

t

m





U

x

Zakłócenie

T

1

=T

-

+

-

-

+

Czas

+

T

1

=T

 

Metoda tłumienia zakłóceń okresowych

w woltomierze z dwukrotnym całkowaniem

Metoda ta charakteryzuje się bardzo dobrymi

parametrami metrologicznymi, zwłaszcza w stosunku

dokładności przetwarzania oraz odporności na

zakłócenia.

Zasada przetwarzania

polega na:

całkowaniu sygnału

(napięcia, prądu) wejściowego U

x

(t)

w

ciągu interwału czasowego zadanej trwałości T

1

(pierwsza faza) i

zgromadzeniu ładunku Q

1

proporcjonalnego wartości średniej sygnału

wejściowego

z

następną kompensacją tego ładunku przez całkowanie

sygnału

(napięcia, prądu) referencyjnego U

ref

odwrotnej

polaryzacji i wyznaczaniu interwału czasowego T

x

tej

kompensacji (druga faza).

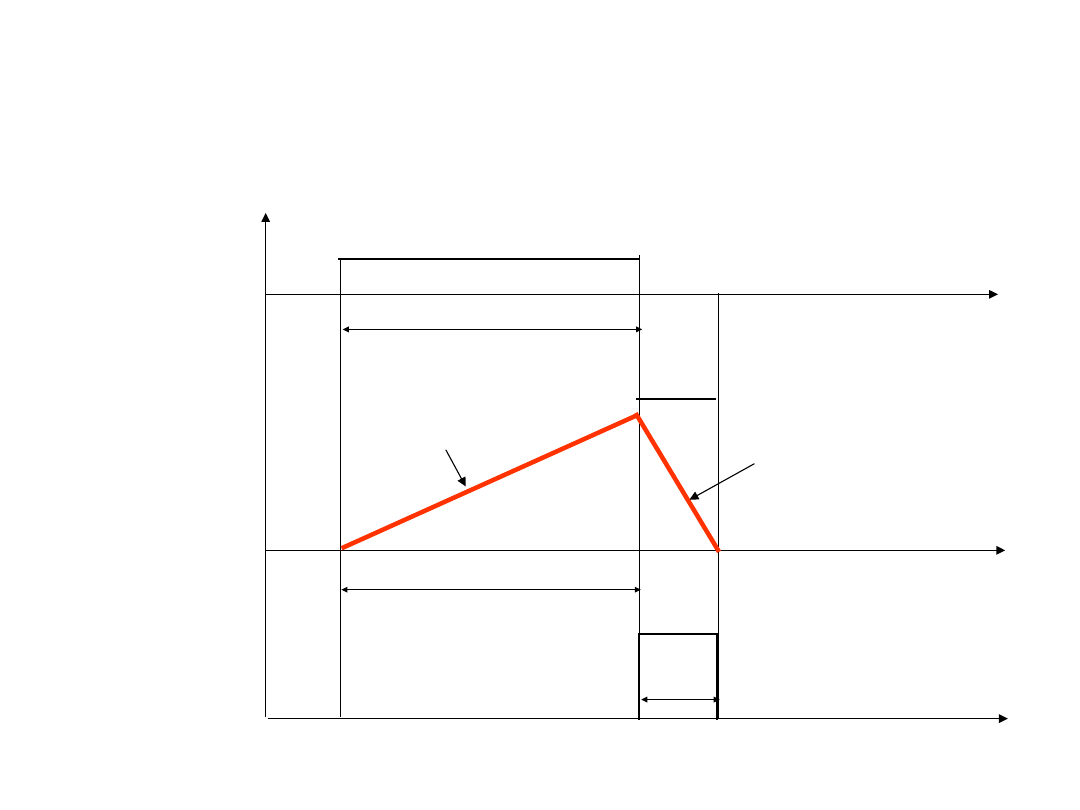
Metoda tłumienia zakłóceń okresowych

w woltomierze z dwukrotnym

całkowaniem

U

int

Całkowanie -U

ref

(2 faza)

t

1

t

2

T

x

U

x

(t)

-U

ref

T

1

Całkowanie U

x

(t)

(1 faza)

t

1

t

2

U

we

Czas

Wyjście

Czas

Czas

T

1

t

2

+T

x

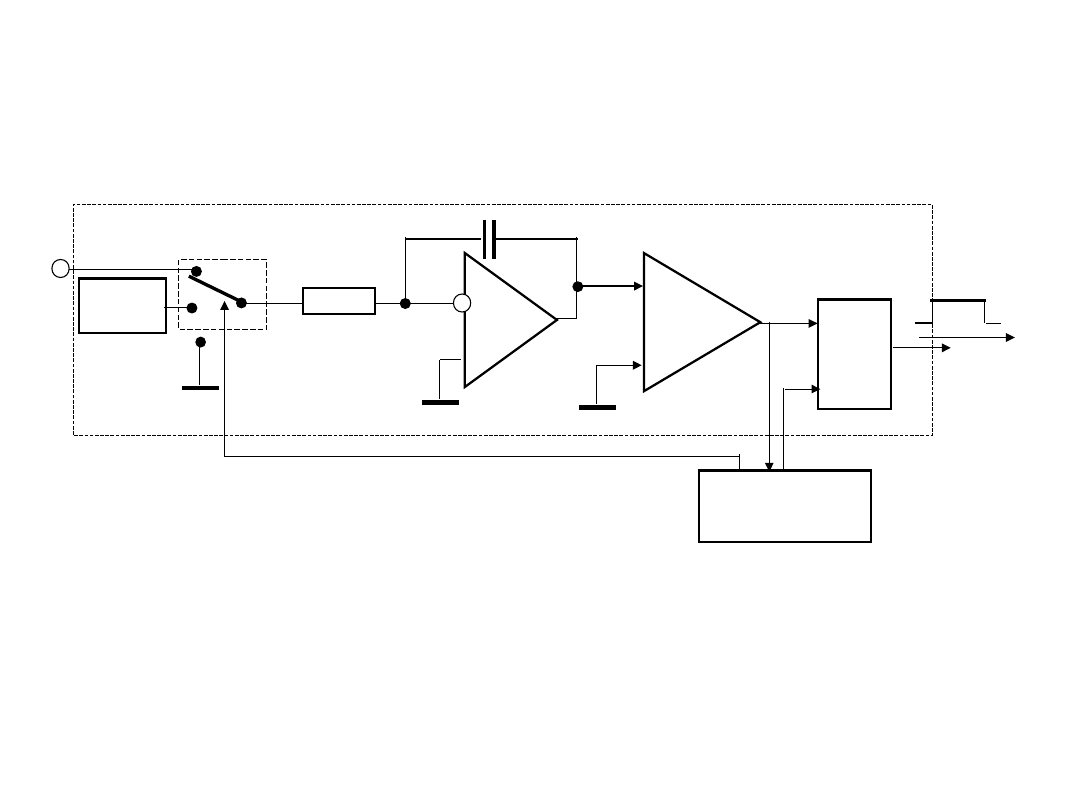
Uproszczony schemat przetwornika

napięcie – interwał czasowy z

dwukrotnym całowaniem

P

U

we

=U

x

(t)

U

int

(t)

-U

ref

Układ

sterowani

a

WO

Komp

.

C

R

1

T

x

Stop

RS

Start

t

0i

Wyjście

1

2

3

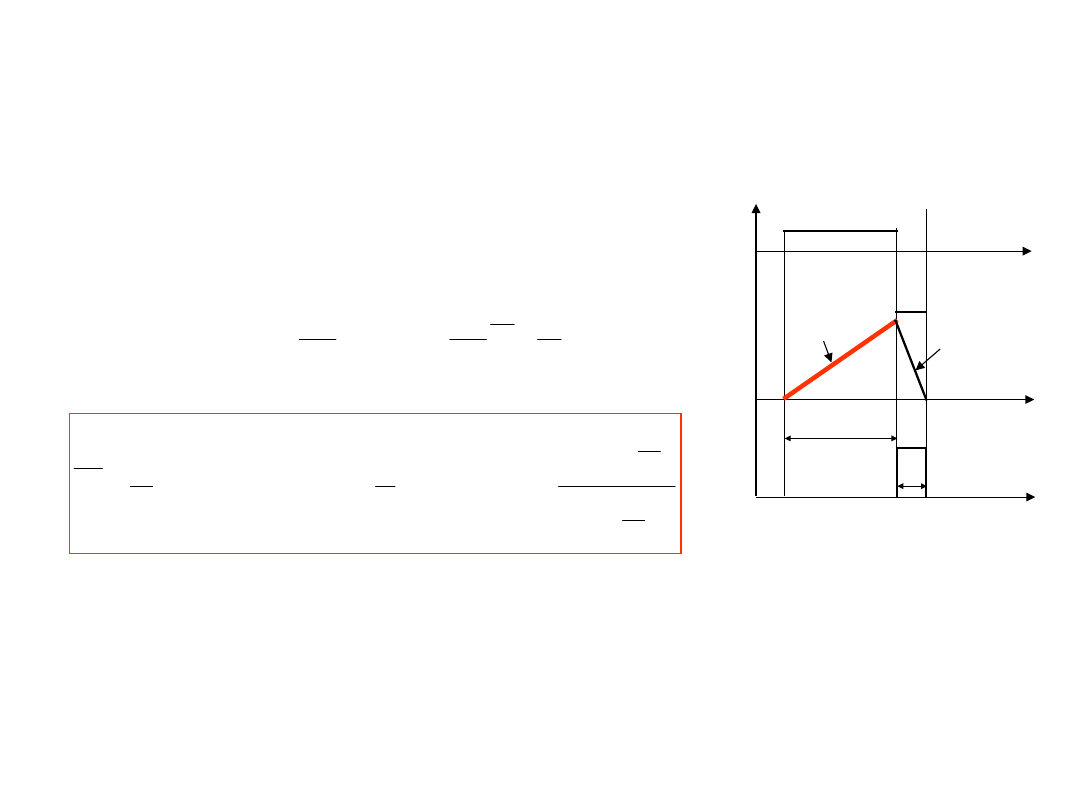
Metoda przetwarzania

w woltomierze z dwukrotnym

całkowaniem

Podczas całkowania napięcie wejściowego U

x

(t) w

interwale czasowym od t

1,i

do t

2,i

=t

1,i

+T

1

(w

ciągu zadanego i stałego interwału czasowego

T

1

) napięcie na wyjściu integratora osiąga

wartość

gdzie

jest wartością średnią napięcia wejściowego

(przetwarzanego) w czasie pierwszego

całkowania T

1

(pierwsza faza całkowania)

C

Q

U

C

R

T

dt

t

U

C

R

T

U

x

T

t

t

x

1

1

1

1

1

int

1

1

1

)

(

1

)

(











T

T

T

T

U

U

dt

T

t

U

U

T

U

m

x

T

t

t

m

x

x

1

1

1

2

2

sin

2

cos

1

1

1

1























































Całkowanie -U

ref

(2 faza)

t

0

t

1

T

x

U

x

(t)

-U

ref

T

1

Całkowanie

U

x

(t) (1

faza)

t

1

t

2

=t

1

+T

1

U

we

U

int

Czas

Wyjście

Czas

Czas

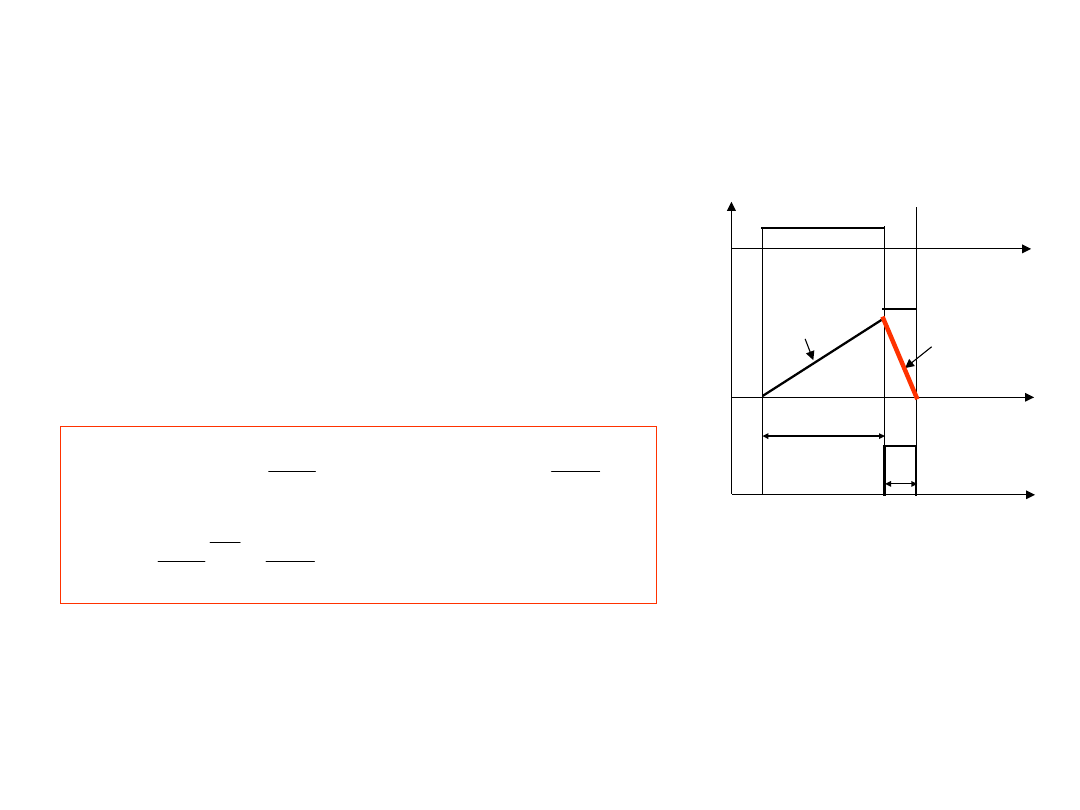
Metoda przetwarzania

w woltomierze z dwukrotnym

całkowaniem

Następnie do wejścia integratora zostaje

podłączone napięcie referencyjne

U

ref

odwrotnej

polaryzacji

i na jego wyjściu wartość napięcia

będzie się obniżać (2 faza całkowania) aż do

zera w moment czasowy

t

3

= t

2

+T

x

Całkowanie

-U

ref

(2 faza)

t

1

t

2

T

x

U

x

(t)

-U

ref

T

1

Całkowanie

U

x

(t) (1 faza)

t

1

t

3

=t

2

+T

x

U

we

U

int

Czas

Wyjście

Czas

Czas

x

ref

x

x

ref

T

t

t

ref

T

C

R

U

U

C

R

T

T

C

R

U

T

U

dt

U

C

R

T

U

t

U

x

1

1

1

1

1

int

1

1

int

int

)

(

1

)

(

)

(

2

2



















t

2

t

3

=t

2

+T

x

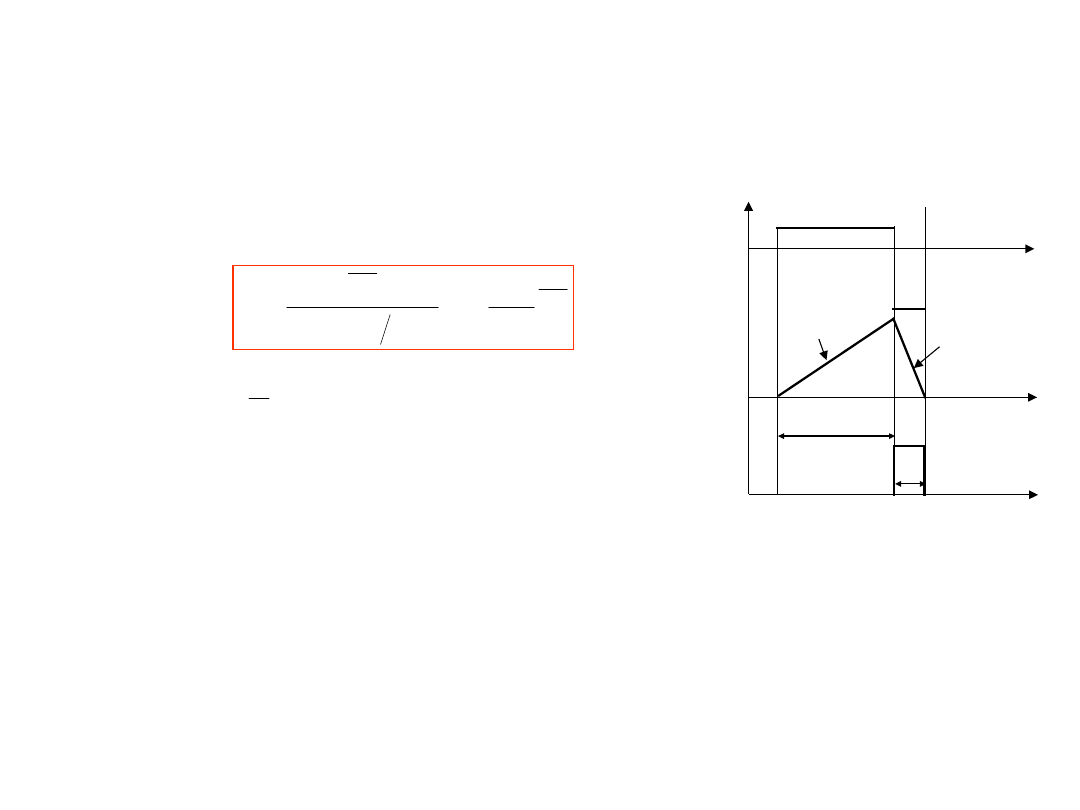
Metoda przetwarzania

w woltomierze z dwukrotnym

całkowaniem

Interwał czasowy podczas którego został

rozładowany kondensator równa się

I jest proporcjonalny do wartości średniej

napięcia wejściowego

I jest to

funkcja przetwarzania przetwornika

.

x

ref

ref

x

x

U

U

T

T

C

R

U

C

R

U

T

1

1

1

`

1

`





Całkowanie

-U

ref

(2 faza)

t

1

t

2

T

x

U

x

(t)

-U

ref

T

1

Całkowanie

U

x

(t) (1 faza)

t

1

t

2

U

we

U

int

Czas

Wyjście

Czas

Czas

t

3

t

3

x

U

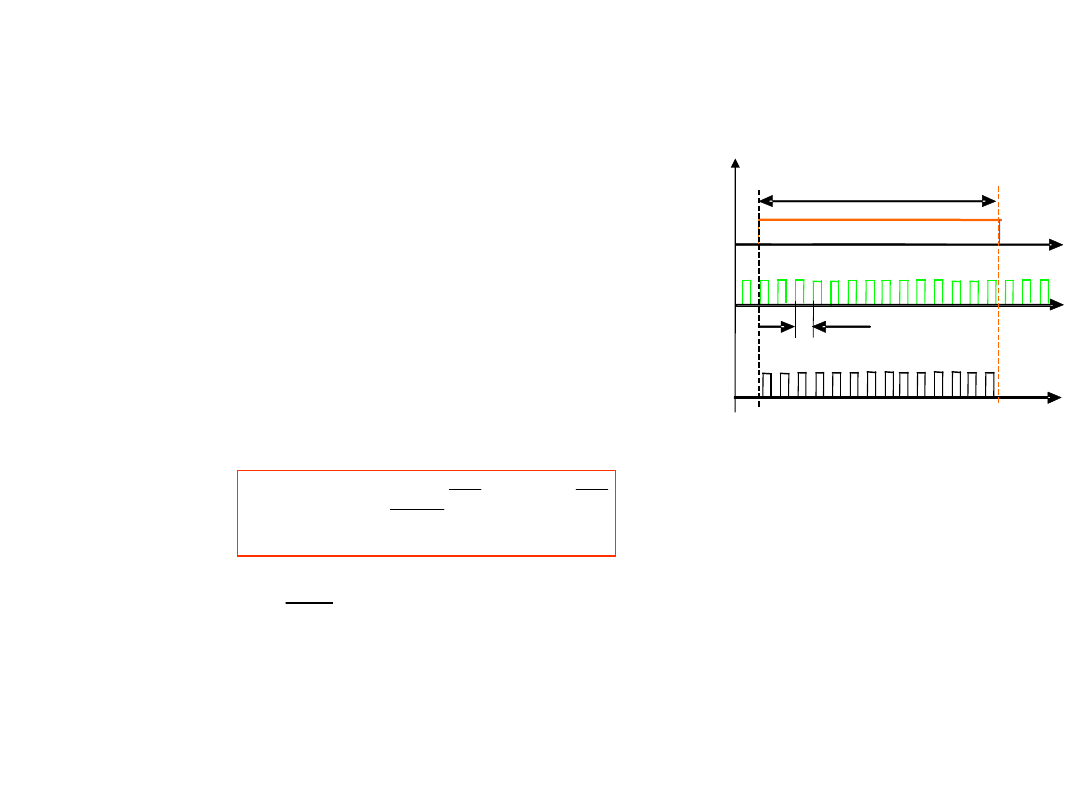
Metoda przetwarzania

w woltomierze z dwukrotnym

całkowaniem

W interwale czasowym

T

x

będą

zliczany impulsy o częstotliwości

wzorcowej

f

w

, dlatego wynik

przetwarzania A/C w zależności

od wartości średniej napięcia

wejściowego

(

funkcja przetwarzania

) opisuje się

wzorem

Gdzie
jest

współczynnikiem

przetwarzania

przetwornika A/C z

dwukrotnym całkowaniem

x

C

A

x

ref

w

w

x

x

U

k

U

U

f

T

f

T

N









/

1

ref

w

C

A

U

f

T

k

1

/



Czas

Czas

Impulsy o częstotliwości f

w

Impulsy zliczany przez licznik

T

x

T

w

=1/f

w

Czas

N

x

=T

x

f

w

t

1

t

x

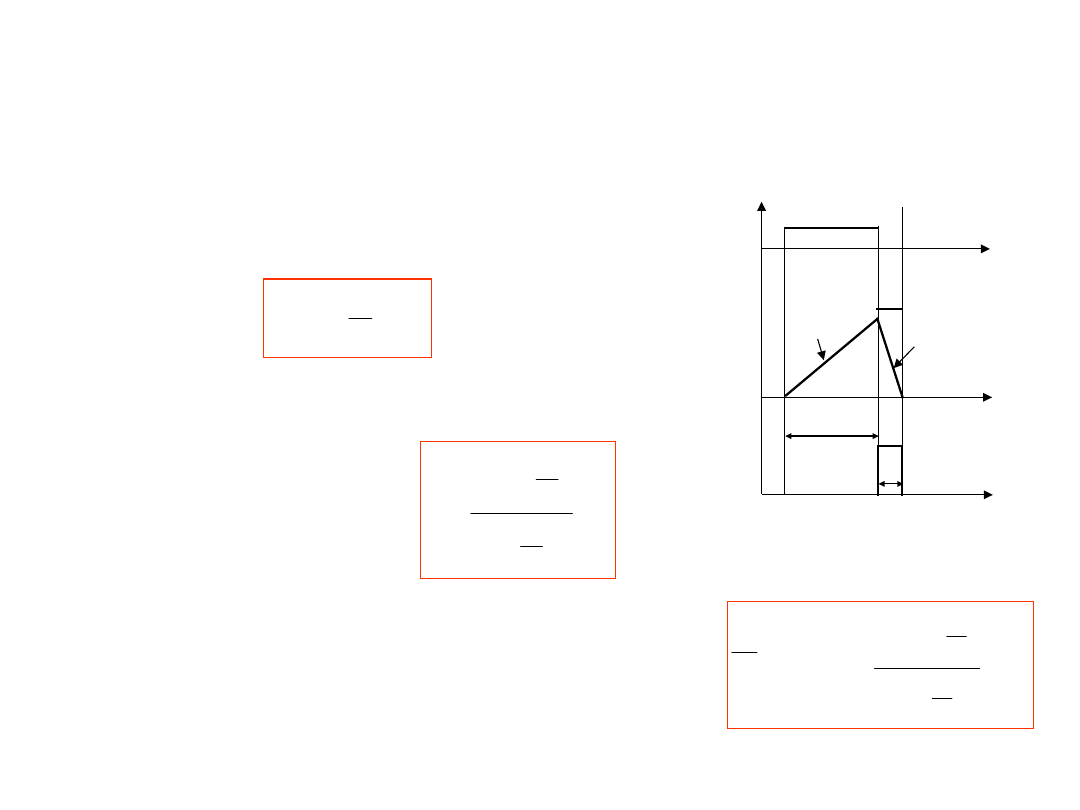
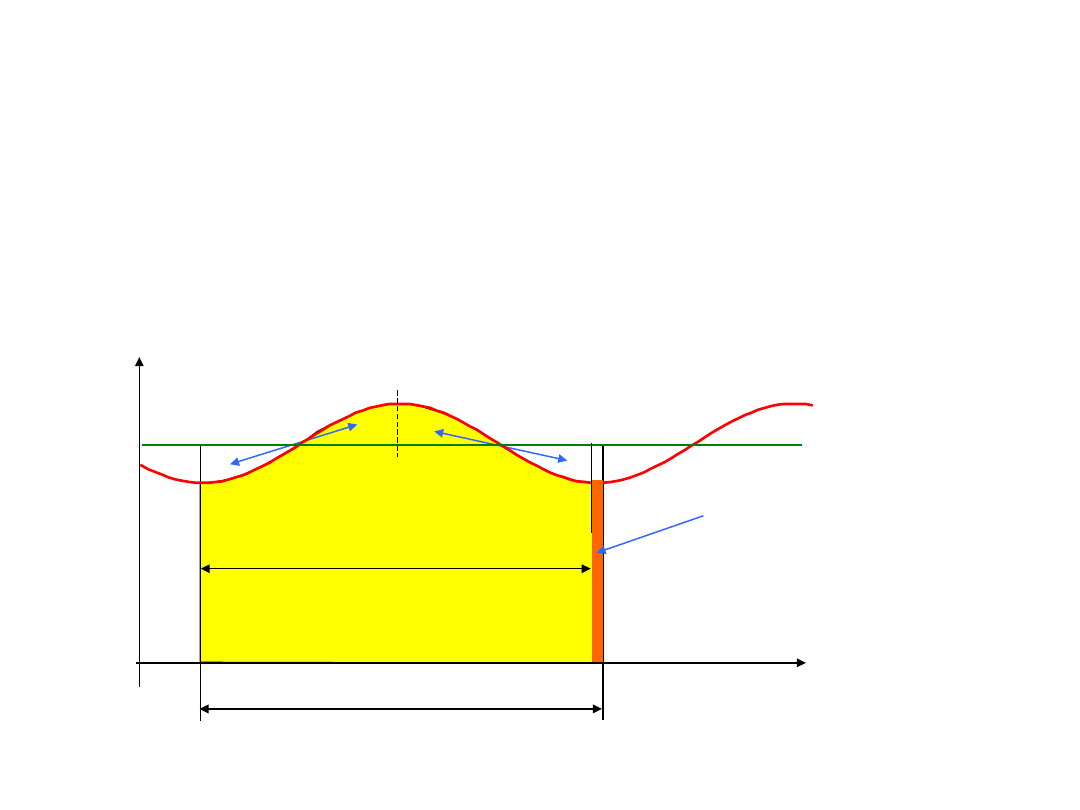
Współczynnik tłumienia zakłócenia okresowego w

woltomierzu z dwukrotnym całkowaniu

Jeśli czas

całkowania w pierwszej fazie jest równy

okresu zakłócenia okresowego

T

1

=T

Wtedy wartość składowej od zakłócenia

To jest we wzorze dla wartości średniej

składowa

od zakłócenia też równa się zeru

:

To jest

wynik przetwarzania nie zależy od

wartości zakłócenia a tylko od wartości

napięcia korzystnego U

x

Całkowani

e

-U

ref

(2

faza)

t

0

t

1

T

x

U

x

(t)

-U

ref

T

1

Całkowanie

U

x

(t) (1

faza)

t

0

t

1

U

we

U

int

Czas

Wyjście

Czas

Czas

t

x

t

x

0

2

sin

1















T

T



0

sin

1

1

















T

T

T

T

U

m





x

m

x

x

U

T

T

T

T

U

U

U





















1

1

2

2

sin





Współczynnik tłumienia zakłócenia okresowego w

woltomierzu z dwukrotnym całkowaniu

U

x

Zakłócenie

T

1

T

+

-

-

+

Czas

Błąd

T

Jeśli jednak

czas całkowania w pierwszej fazie nie jest równy okresu

zakłócenia okresowego

T

1

≠T

,

na przykład w wyniku odchylenia częstotliwości

f

od wartości

nominalnej

f

n

wtedy wartość składowej od zakłócenia w wyniku całkowania
zakłócenia nie równa się zeru i przy :

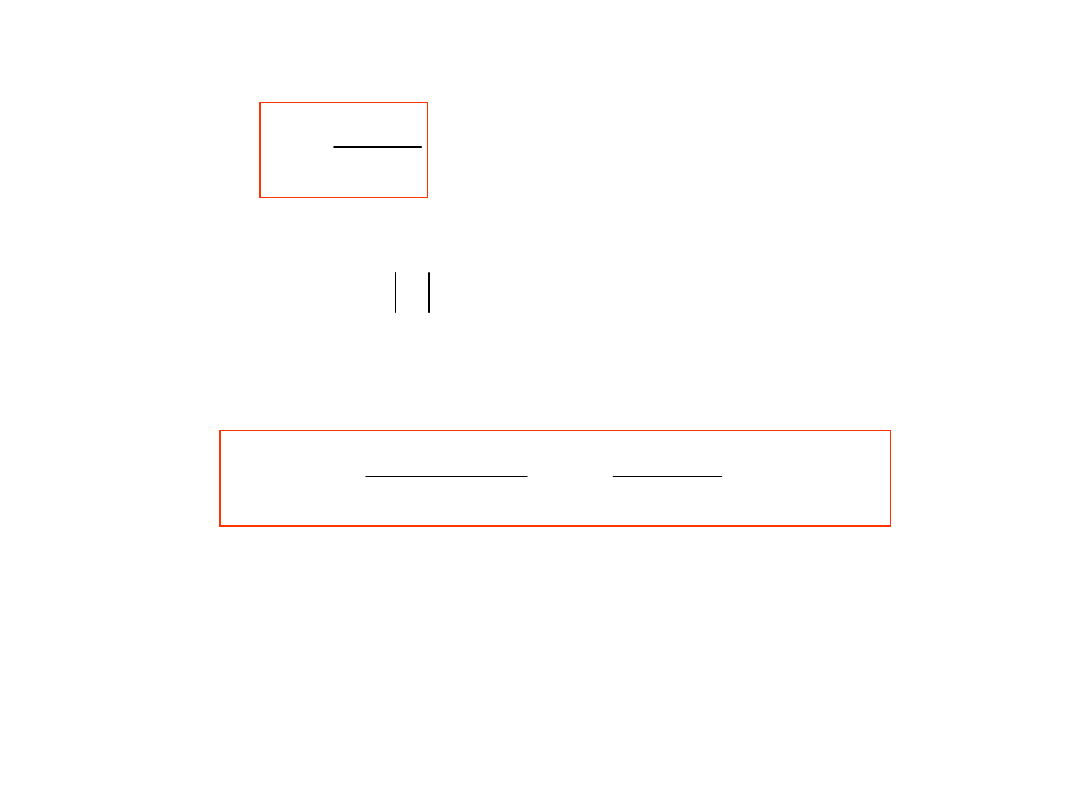
Współczynnik tłumienia zakłócenia okresowego w

woltomierzu z dwukrotnym całkowaniu

Jeśli

względnym odchyleniem częstotliwości od nominalnej i jest małym

wtedy wartość składowej od zakłócenia (wartość błędu) w wyniku

całkowania zakłócenia nie równa się zeru i równa się :

Wynik przetwarzania nie zależy od wartości zakłócenia a tylko od

wartości napięcia korzystnego U

x

n

n

f

f

f

f 

















 





0

1

sin

1

1

sin























f

m

f

f

m

f

f

m

z

U

U

U

U

















1



f



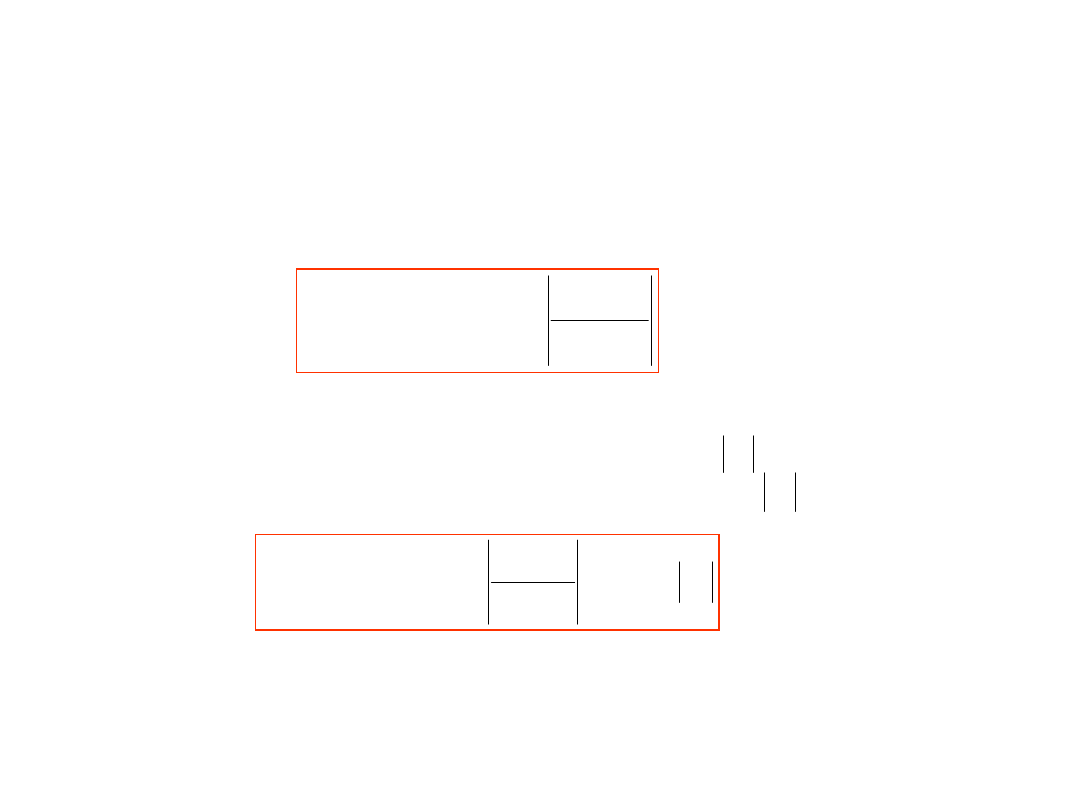
Współczynnik tłumienia zakłócenia okresowego

w woltomierzu z dwukrotnym całkowaniu

Współczynnikiem tłumienia zakłóceń szeregowych (K

tł

, NMRR

– normal mode rejection ratio) jest wyrażony decybeli stosunek
amplitudy U

m

zakłócenia sinusoidalnego do wartości

maksymalnego błędu ΔU

z,max

spowodowanego oddziaływaniem

tego zakłócenia

Dla małych odchyleń częstotliwości zakłócenia od nominalnej (jak

na przykład w przypadku zakłócenia sieciowego)
wartość współczynnika tłumienia zakłóceń zależy tylko od

max

,

lg

20

z

m

tl

U

U

NMRR

K







1



f



f



f

f

m

m

tl

U

U

NMRR

K





lg

20

lg

20











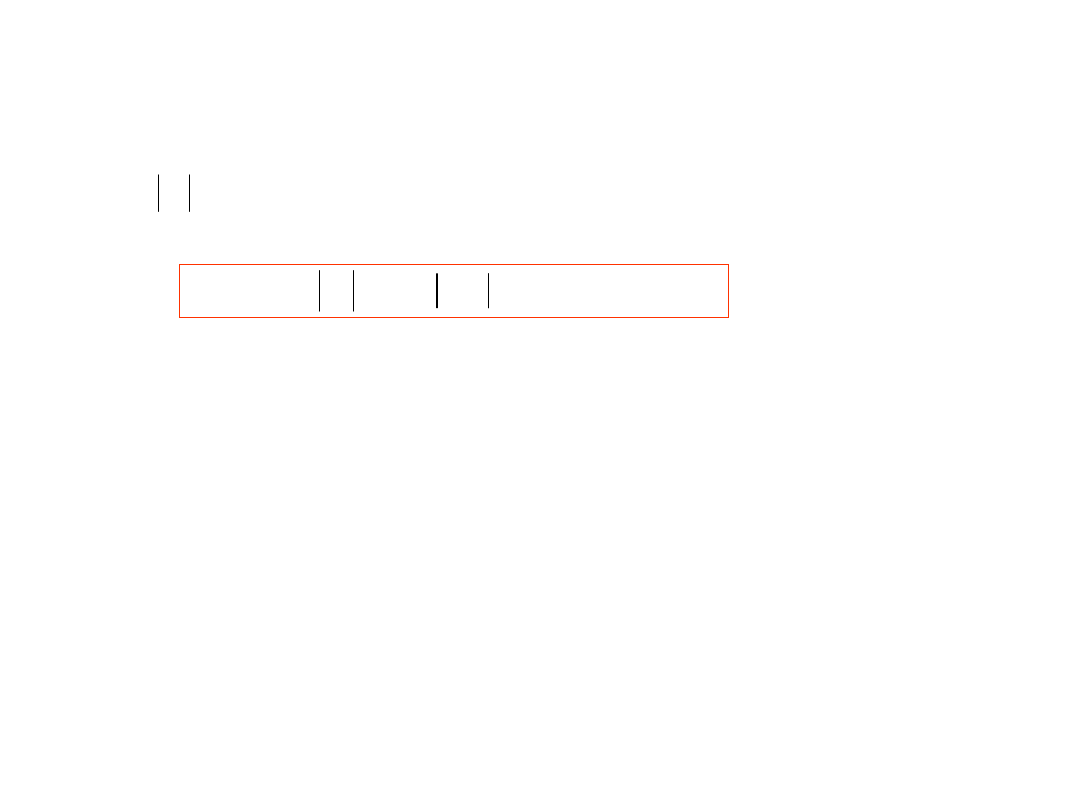
Współczynnik tłumienia zakłócenia okresowego

w woltomierzu z dwukrotnym całkowaniu

Dla

%)

1

(

01

,

0



f



)

100

(

40

01

,

0

lg

20

lg

20

razy

dB

K

f

tl











Współczynnik tłumienia zakłócenia okresowego

w woltomierzu z dwukrotnym całkowaniu

Jeśli odchylenia częstotliwości zakłócenia od nominalnej jest duże

wtedy teoretyczna wartość współczynnika tłumienia zakłóceń
wyznaczana jest wzorem

Gdzie

Jest względną częstotliwością (według czasu całkowania w pierwszej

fazie)





 

v

v

T

f

v

K

z

teor

tl





sin

lg

20

1

,









1

T

f

v

z





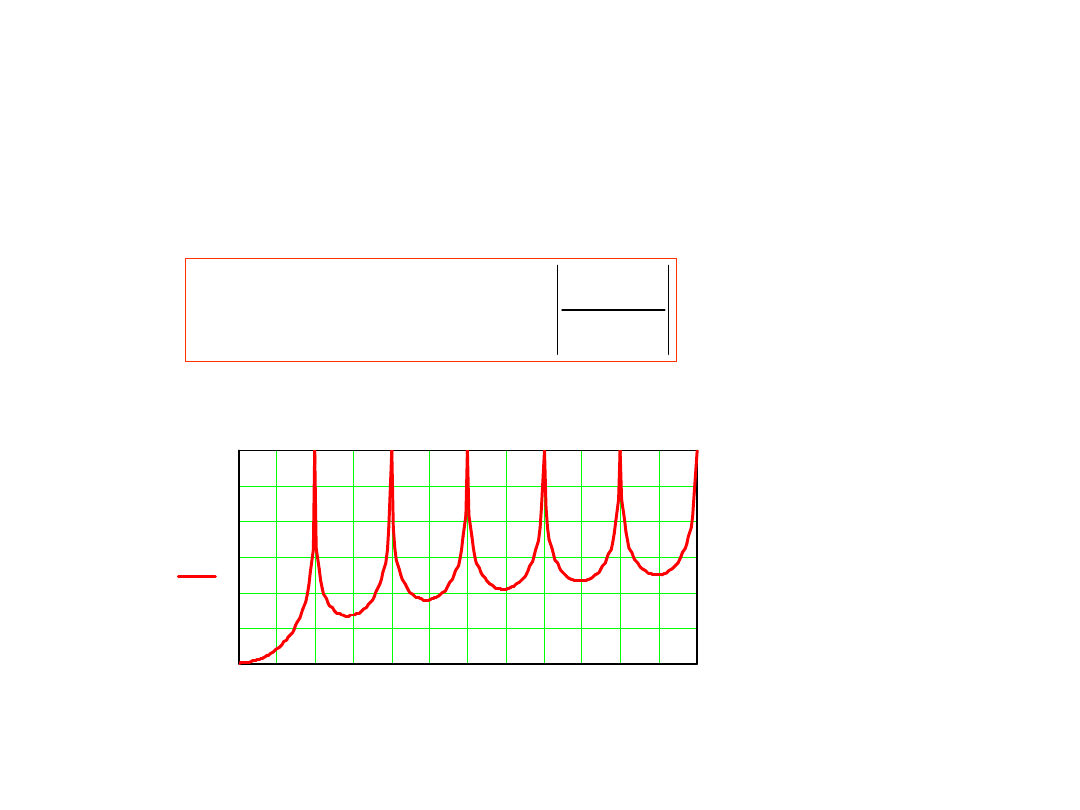
Współczynnik tłumienia zakłócenia okresowego

w woltomierzu z dwukrotnym całkowaniu

Jeśli odchylenia częstotliwości zakłócenia od nominalnej jest duże

wtedy teoretyczna wartość współczynnika tłumienia zakłóceń
wyznaczana jest wzorem





 

v

v

T

f

v

K

z

teor

tl





sin

lg

20

1

,









0 0.5 1

1.5 2 2.5 3

3.5 4 4.5 5

5.5 6

0

10

20

30

40

50

60

Ktl

i

v

i

Współczynnik tłumienia zakłócenia okresowego

w woltomierzu z dwukrotnym całkowaniu

Wnioski:
1.

Dla pełnego tłumienia zakłócenia harmonicznego należy
całkować sygnał wejściowy w czasie jednego lub kilku okresów
zakłócenia

T

1

=m×T

z

=m/f

z

.

1.

Oprócz pierwszej składowej harmonicznej bęą tłumione
wszystkie wyższe składowe: wielokrotności podstawowej

f

k

=k×f

z

2.

Jeśli częstotliwość zakłócenia zmienia się tak, że w czasie
całkowania

nie umieszcza się całkowita liczba okresów

zakłócenia

, to zakłócenia nie będzie tłumione całkowicie i

pozostawanie

niezerowy błąd od zakłócenia

.

3.

Współczynnikiem tłumienia zakłócenia szeregowego (

K

tł

) jest

wyrażony decybeli stosunek amplitudy

U

m

zakłócenia

sinusoidalnego do wartości maksymalnego błędu

ΔU

z,max

4.

Dla małych odchyleń częstotliwości zakłócenia od nominalnej
wartość współczynnika tłumienia zakłóceń zależy tylko od
względnej niestabilności częstotliwości

f

tl

K



lg

20





max

,

lg

20

z

m

tl

U

U

K





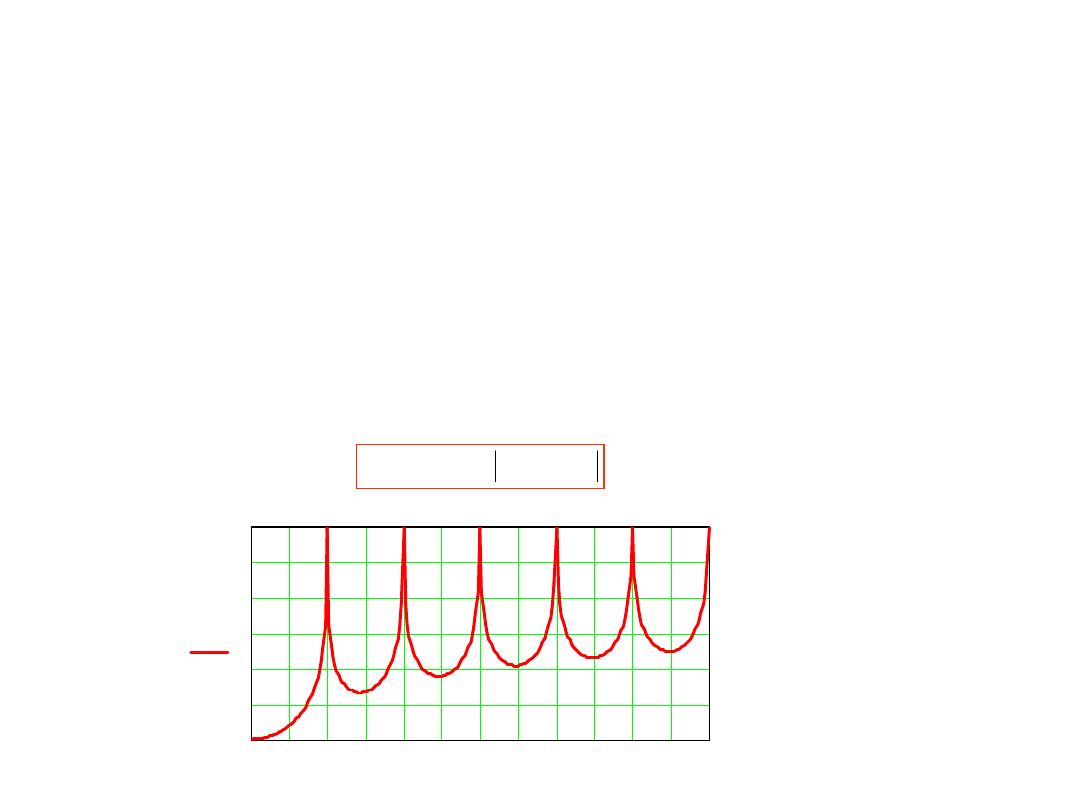
Współczynnik tłumienia zakłócenia okresowego

w woltomierzu z dwukrotnym całkowaniu

7. Dla dużych odchyleń częstotliwości zakłócenia od nominalnej

wartość współczynnika tłumienia zakłóceń osiąga teoretycznie
nieskończone wartości na częstotliwościach krotnych
odwrotności interwału czasowego całkowania w pierwszej fazie

f

k

=k×1/T

1

a dla częstotliwości pomiędzy tymi częstotliwościami osiąga

minimalne wartości

0 0.5 1

1.5 2 2.5 3

3.5 4 4.5 5

5.5 6

0

10

20

30

40

50

60

Ktl

i

v

i





5

,

0

lg

20

,





k

K

teor

tl



2. Wymagania do woltomierzy DC.

Zakresy

Możliwość pomiaru wartości napięcia w różnych zakresach

zapewnia się wykorzystaniem na wejściu woltomierza

-

wzmacniacza

- dla małych wartości napięć;

-

dzielnika

– dla dużych wartości napięć.

8.937m

V

0,1 mV 1 mV 10 mV

100mV

1 V 10 V 100 V
1000 V

2. Wymagania do woltomierzy DC.

Zakresy

Typowe zakresy woltomierzy są krotne:
wartościom

10

n

, gdzie

n

– liczba całkowita, ujemna i

dodatnia, na przykład

0,001 V (1 mV) 0,01 V (10 mV); 0,1 V (100 mV); 1 V,

10 V, 100 V; 1000 V

,

lub krotne wartościom

2·10

n

, na przykład :

0,002 V (2 mV) 0,02 V (20 mV); 0,2 V (200 mV); 2 V,

20 V, 200 V

.

2. Wymagania do woltomierzy DC.

Zakresy

Z zakresami pomiarowymi są powiązane

liczba cyfr

(miejsc znaczących) wskazania oraz

wartość cyfry

najmniej znaczącej

.

W woltomierze cyfrowym z liczbą cyfr dziesiątkowych

n

z zakresem

10

n

krotnym istnieje różnych

wskazań

od do ,

przy tym wartości cyfry najmniej znaczącej – CNZ

(ang. LSB) równa się:







n

0

...

00







n

9

...

99

n

z

U

LSB

CNZ

10





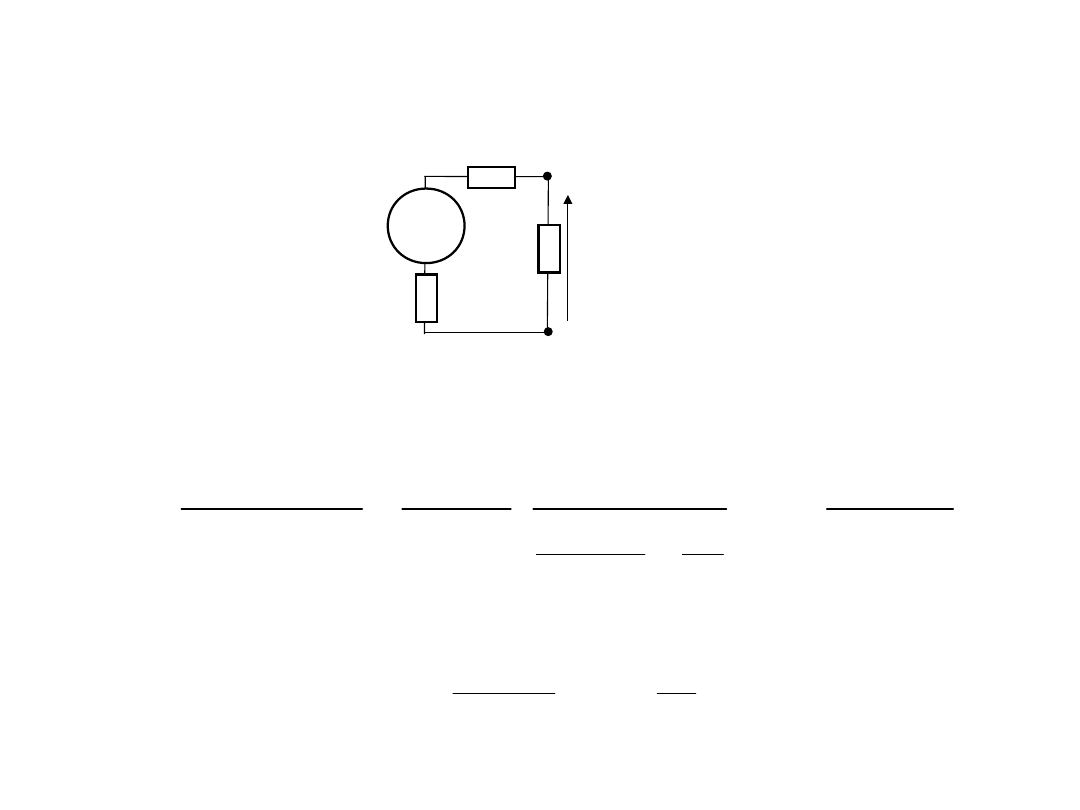
2. Wymagania do woltomierzy DC.

Rezystancja wejściowa

Do podłączenia

woltomierza wartość tego napięcia

wynosi

Po podłączeniu

woltomierza wynik pomiaru tego

napięcia wynosi

R

0

U

x

U

0

R

1

R

2

V

V

V

V

R

R

R

R

R

R

U

R

R

R

R

R

R

U

U

1

1

1

1

2

1

0

1

0

0

2

1

0

2

0



















2

01

01

0

2

1

0

1

0

0

2

1

0

2

0

1

1

1

G

G

G

U

R

R

R

R

R

U

R

R

R

R

U

U

x























2

2

1

0

01

1

,

1

R

G

R

R

G







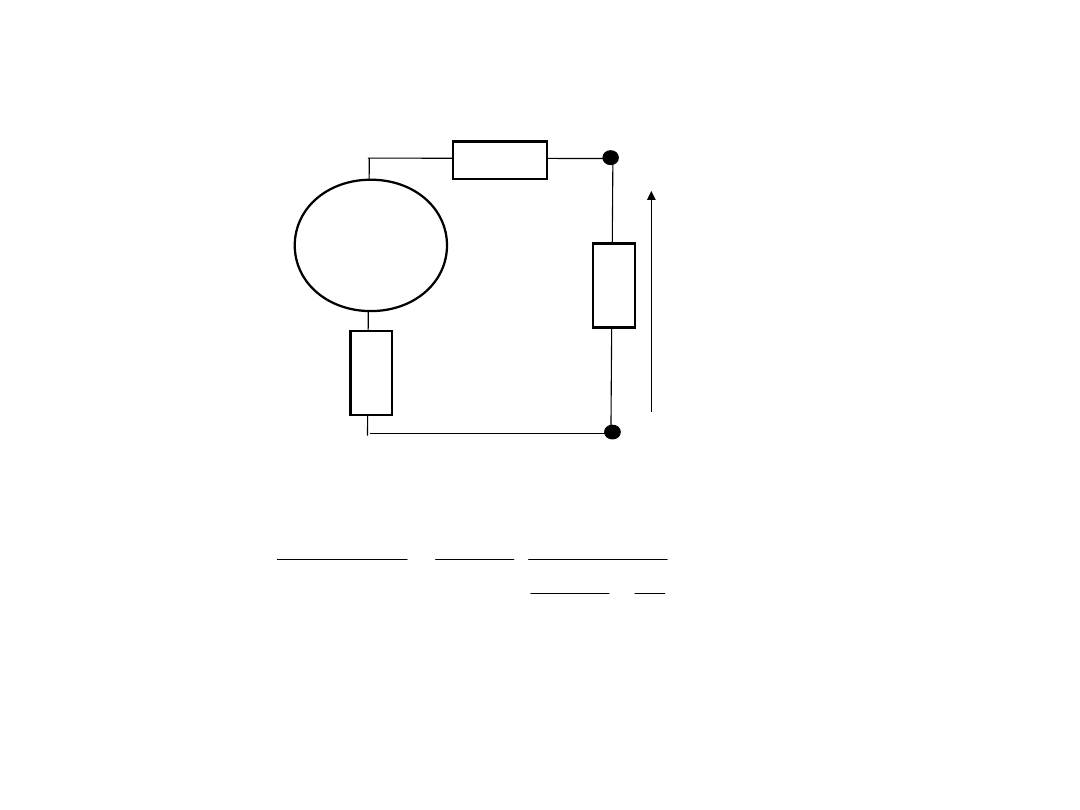
2. Wymagania do woltomierzy DC.

Rezystancja wejściowa

Do podłączenia

woltomierza wartość tego napięcia wynosi

V

R

R

R

R

R

U

R

R

R

R

U

U

x

9975

.

4

1

1

1

2

1

0

1

0

0

2

1

0

2

0



















100Ω

10V

100k

Ω

100kΩ

4.9975
V

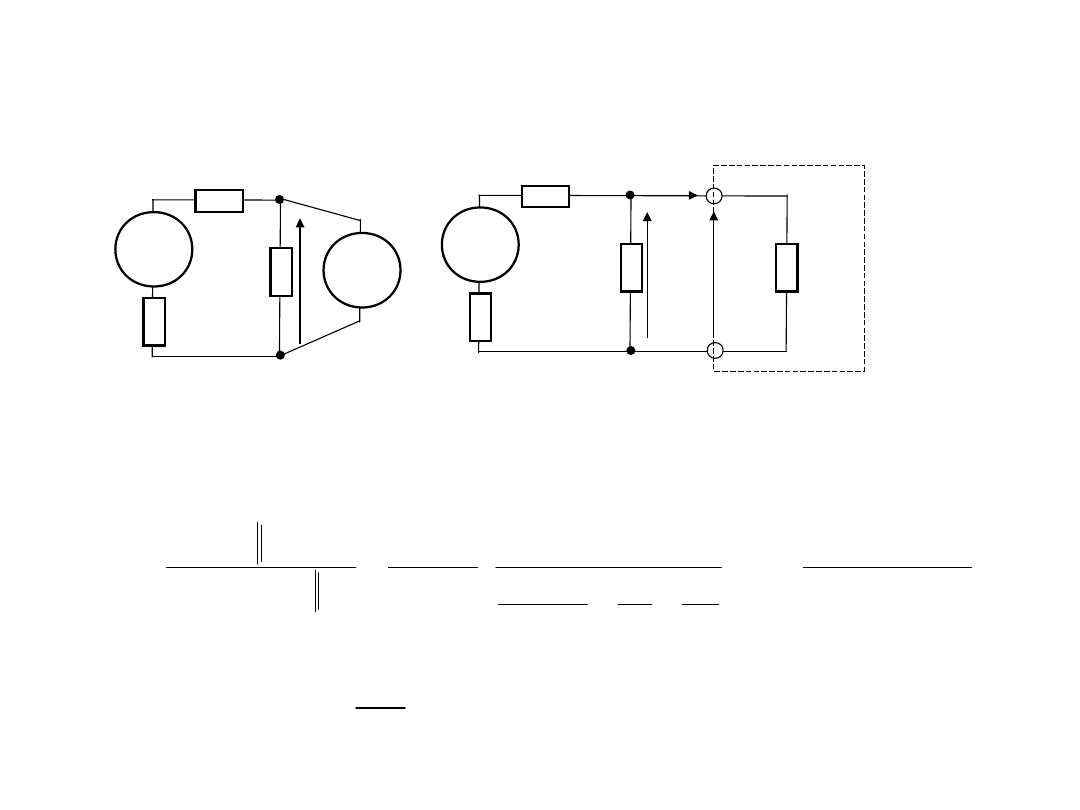
2. Wymagania do woltomierzy

DC.

Rezystancja wejściowa

Po podłączeniu

woltomierza wynik pomiaru tego

napięcia wynosi

I

V

R

0

U

V

U

0

R

1

R

2

R

V

V

U

x’

R

0

U

x

U

0

R

1

R

2

V

V

V

V

V

V

G

G

G

G

U

R

R

R

R

R

R

U

R

R

R

R

R

R

U

U



























2

01

01

0

2

1

0

1

0

0

2

1

0

2

0

1

1

1

1

V

V

R

G

1



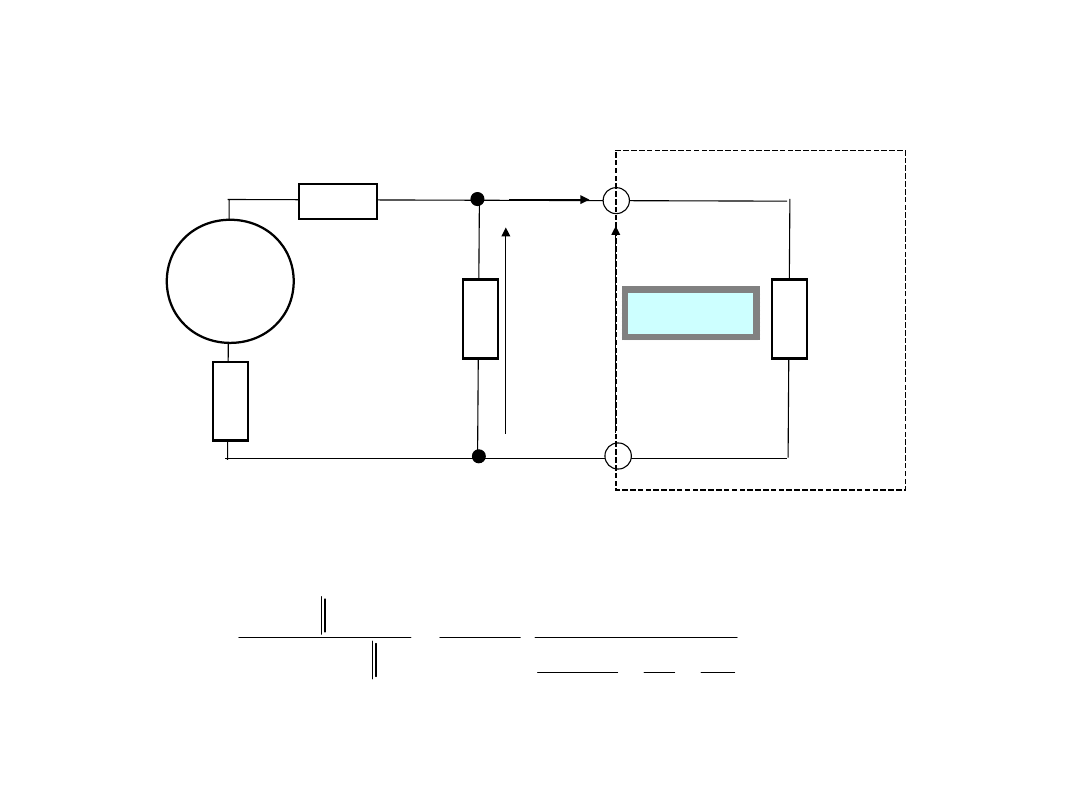
2. Wymagania do woltomierzy

DC.

Rezystancja wejściowa

Po podłączeniu

woltomierza wynik pomiaru tego

napięcia wynosi

V

R

R

R

R

R

R

U

R

R

R

R

R

R

U

U

V

V

V

V

97263

.

4

1

1

1

1

2

1

0

1

0

0

2

1

0

2

0





















I

V

100Ω

4.97263
V

10V

100k

Ω

100k
Ω

10MΩ

V

U’

x

U

V

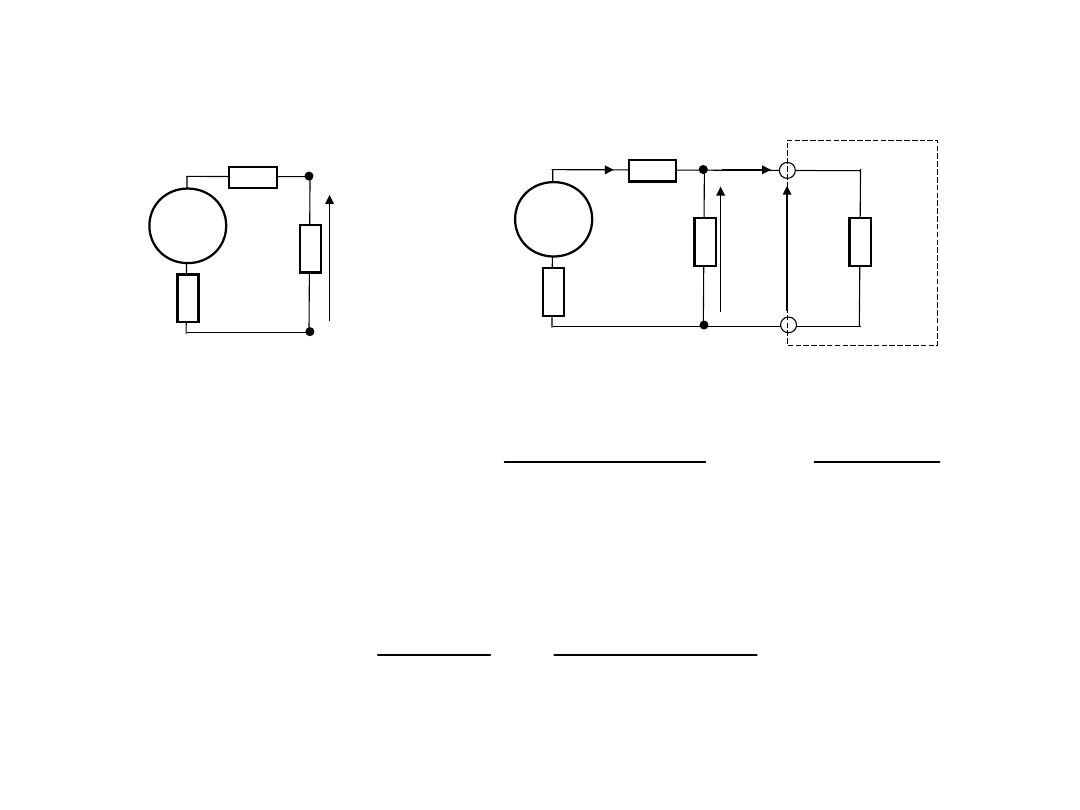
2. Wymagania do woltomierzy

DC. Rezystancja wejściowa

Zmniejszenie napięcia pomiarowego wynosi

Względny błąd

R

0

U

x

U

0

R

1

R

2

I

V

R

0

U

V

U

0

R

1

R

2

R

V

V

U’

x

I

0

2

01

2

01

)

(

G

G

G

U

G

G

G

G

U

U

U

U

V

V

V

V

x

x

V

R

v





















V

V

x

R

R

G

G

G

G

U

U

V

v













2

01

)

(



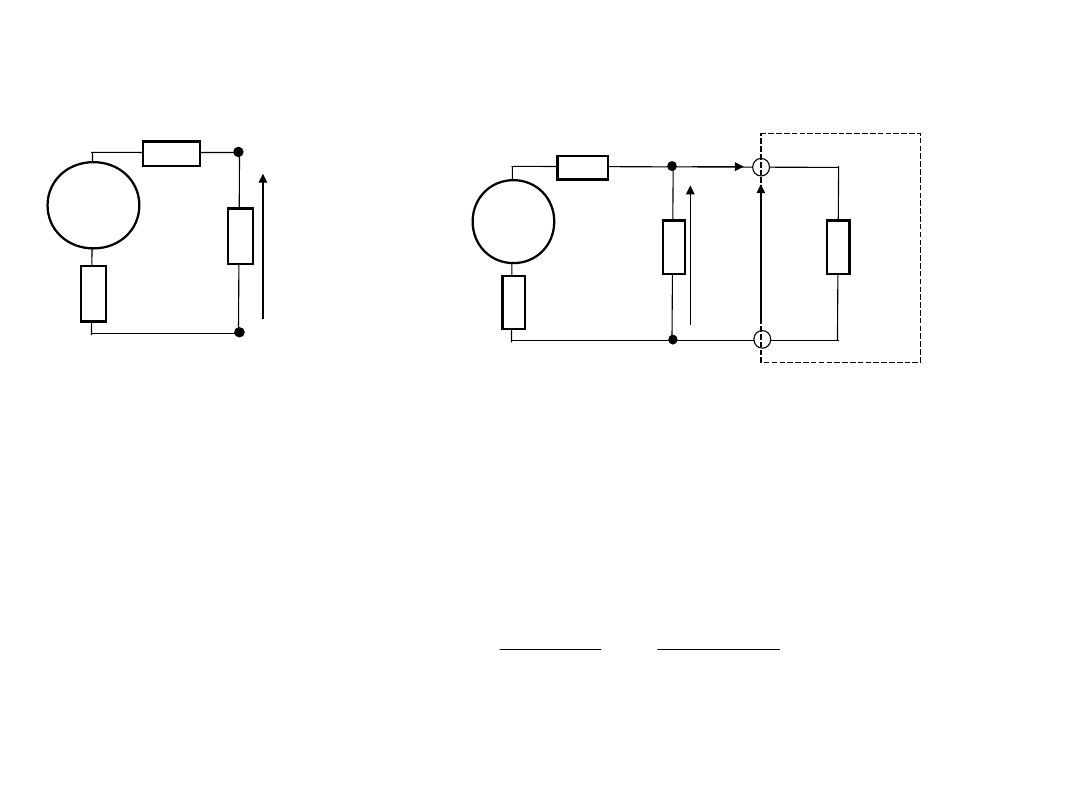
2. Wymagania do woltomierzy

DC. Rezystancja wejściowa

Zmniejszenie napięcia pomiarowego

wynosi

Względny błąd

100Ω

U

x

=

=4.9975V

10V

100kΩ

100kΩ

I

V

100Ω

U

V

=

=4.97263

V

10V

100kΩ

100kΩ

10MΩ

V

U’

x

V

V

V

U

U

U

x

V

R

v

025

.

0

9975

.

4

97263

.

4

)

(















%

5

.

0

%

100

9975

.

4

025

.

0

)

(











V

V

U

U

x

R

R

V

v



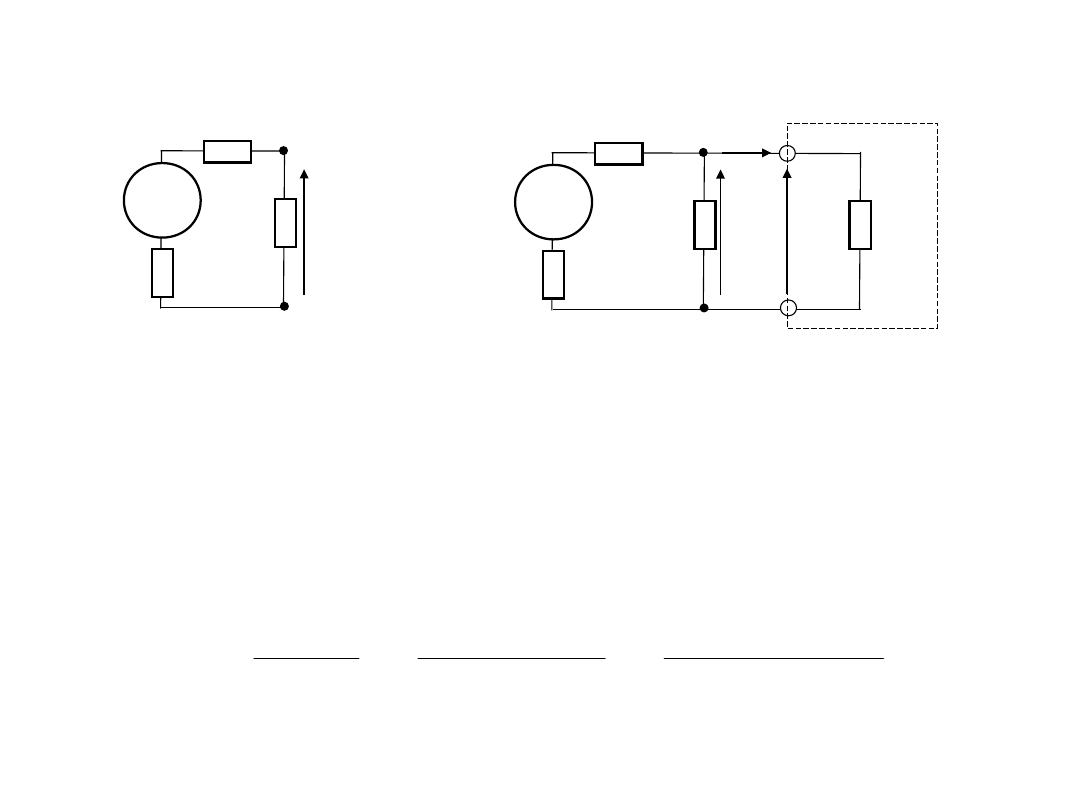
2. Wymagania do woltomierzy

DC. Rezystancja wejściowa

Otóż wartość błędu metodycznego, spowodowanego

ograniczonej wartością rezystancji wejściowej woltomierza
zależy od stosunku ekwiwalentnej rezystancji obwodu ze
strony źródła (R

0

+R

1

) i rezystancji wejściowej woltomierza R

V

.

Zwiększenie rezystancji wejściowej woltomierza R

V

zapewnia

zmniejszenie błędu metodycznego

R

0

U

x

U

0

R

1

R

2

I

V

R

0

U

V

U

0

R

1

R

2

R

V

V

U

x’

1

)

(

1

)

(

2

01

2

01





















G

G

R

G

G

G

G

U

U

V

V

V

x

R

R

V

v



2. Wymagania do woltomierzy DC.

Rezystancja wejściowa

Przykład 2.

Jeżeli wartości rezystancji obiektu badanego będą

o 10 razy

większe

R

1

=1 MOhm , R

2

=1 MOhm otrzymuje się:

- wskazanie woltomierza
- błąd metodyczny bezwzględny:
- błąd metodyczny względny:

Przy wartości rezystancji obiektu badanego porównywalnej do

rezystancji woltomierza R1=10 MOhm, R2=10 MOhm
otrzymuje się błąd metodyczny względny: .

Dla zmniejszenia tego błędu należy wykorzystać elektrometr z

większą rezystancję wejściową, na przykład RV=1 TOhm lub
większej, wtedy w ostatnim przypadku błąd metodyczny
względny:

V

U

x

4,99975



V

U

V

4,761655



V

U

v

R

0,24

)

(







%

8

,

4





v

R



%

33





v

R



%

5

,

0





v

R



2. Wymagania do woltomierzy DC.

Rezystancja wejściowa

Przykład 2.

Jeżeli wartości rezystancji obiektu badanego będą

o 10 razy

większe

R

1

=1 MOhm , R

2

=1 MOhm otrzymuje się:

- wskazanie woltomierza
- błąd metodyczny bezwzględny:
- błąd metodyczny względny:

Przy wartości rezystancji obiektu badanego porównywalnej do

rezystancji woltomierza R

1

=10 MOhm , R

2

=10 MOhm

otrzymuje się błąd metodyczny względny: .

Dla zmniejszenia tego błędu należy wykorzystać elektrometr z

większą rezystancję wejściową, na przykład R

V

=1 TOhm lub

większej, wtedy w ostatnim przypadku błąd metodyczny
względny:

V

U

x

4,99975



V

U

V

4,761655



V

U

v

R

0,24

)

(







%

8

,

4





v

R



%

33





v

R



%

5

,

0





v

R



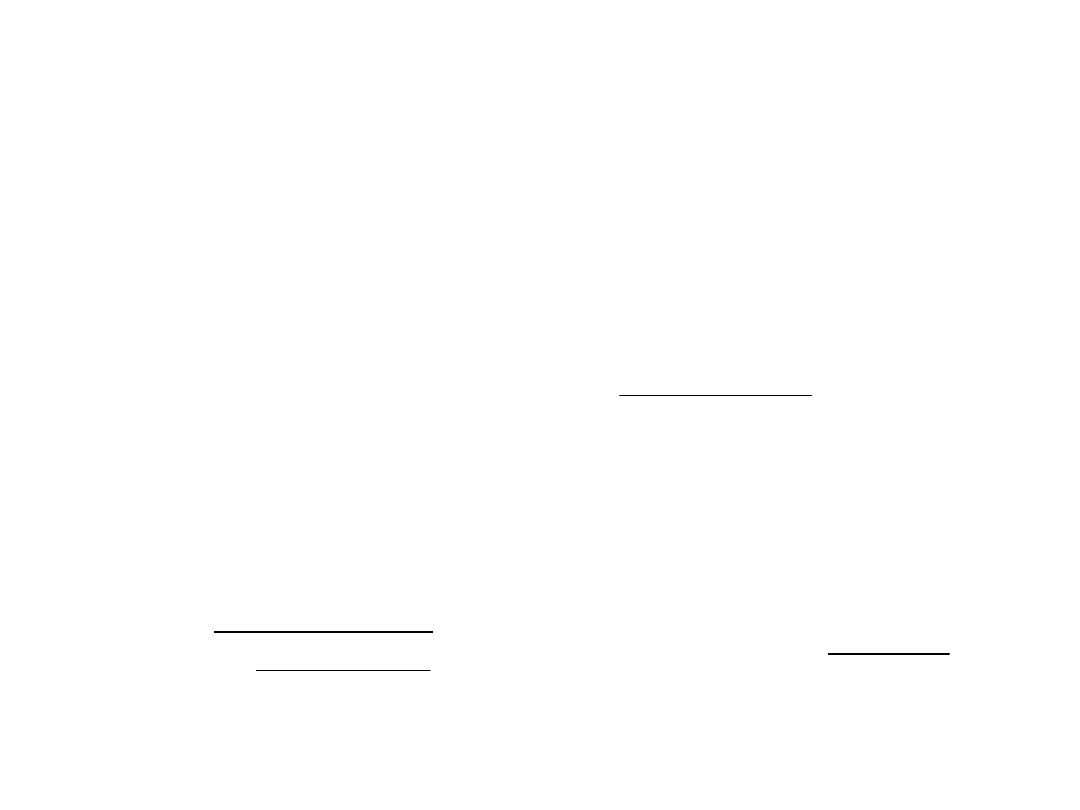
3.Korekcja wpływu rezystancji

wejściowej woltomierza

• Jeżeli wartości parametrów obwodu pomiarowego

nie są znane, wtedy w eksperymentalny sposób

można oszacować wartość błędu metodycznego a

nawet jego skorygować!

• Ze wzoru podstawowego dla błędu

• wynika, że skorygowana wartość napięcia równa się

• lub

V

V

x

x

V

R

G

G

G

G

U

U

U

U

v















2

01

)

(

V

V

V

x

G

G

G

G

U

U









2

01

1





















2

01

1

G

G

G

U

U

V

V

x

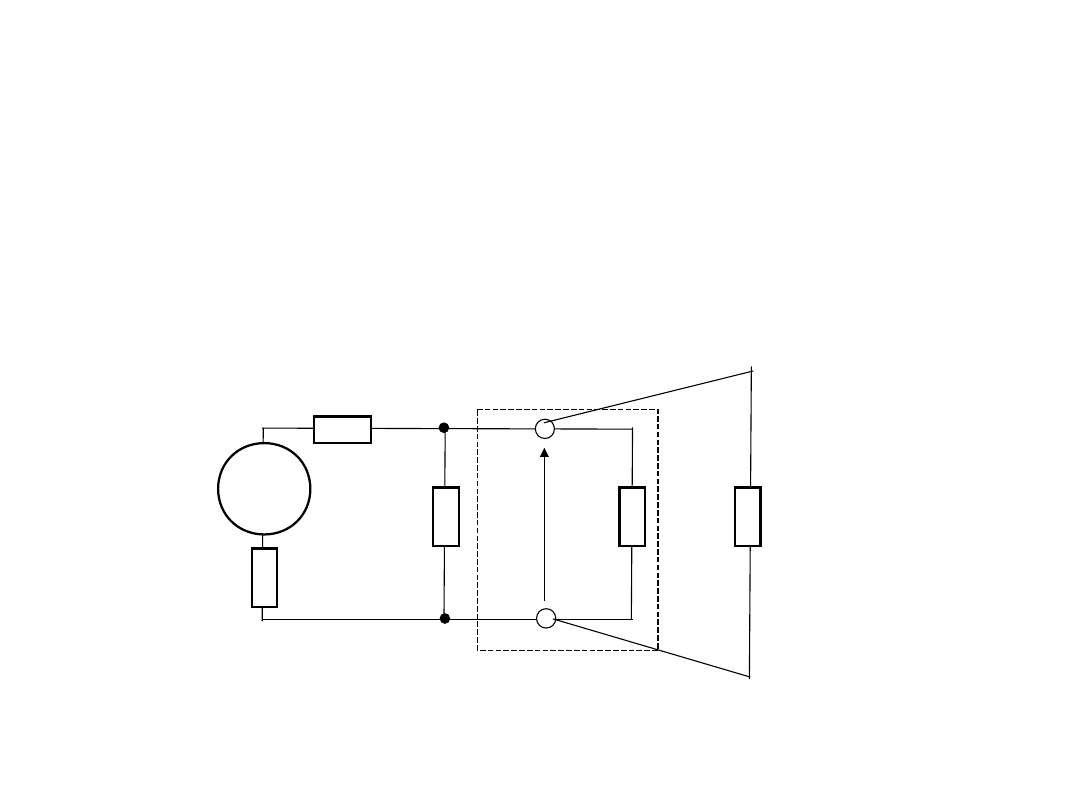
3.Korekcja wpływu rezystancji

wejściowej woltomierza

• W celu jej wyznaczania i dalej dla korekcji wpływ rezystancji

woltomierza RV na wynik pomiaru napięcia należy

przeprowadzić dodatkowy pomiar napięcia z równoległym

włączeniem do woltomierza bocznika Rb o znanej wartości, na
przykład R

b

=R

V

R

0

U

Vb

U

0

R

1

R

2

R

V

V

R

b

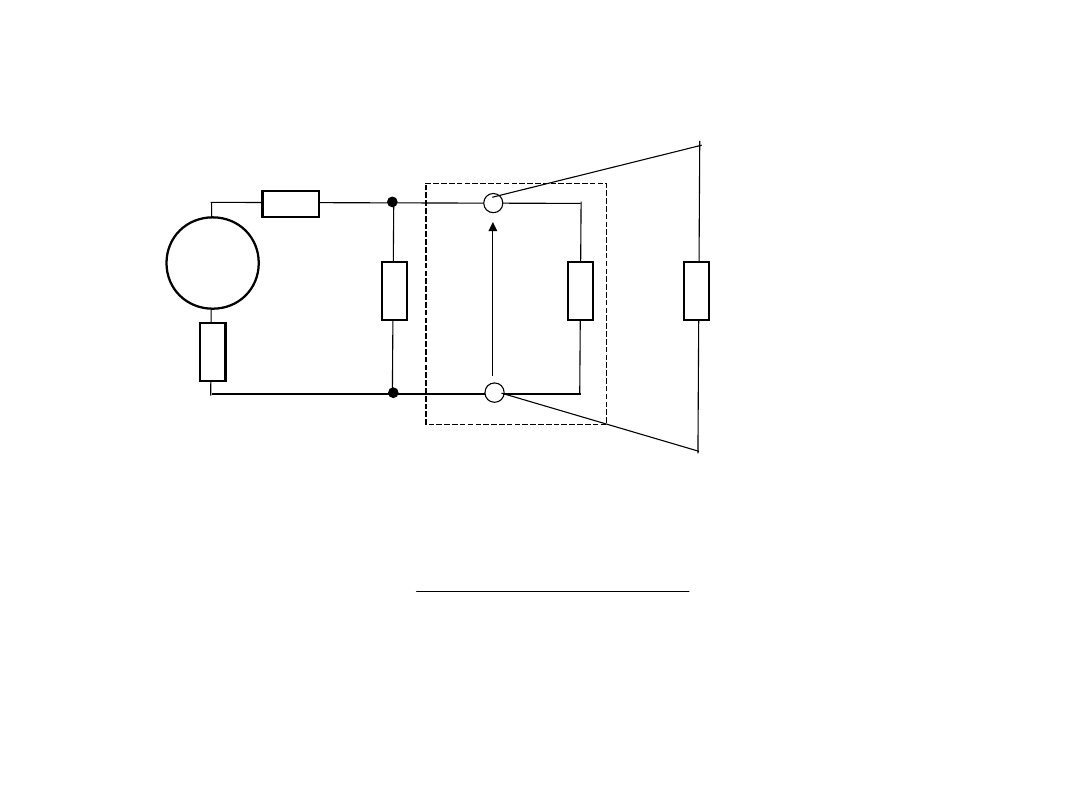
3.Korekcja wpływu rezystancji

wejściowej woltomierza

• Wtedy wynik pomiaru napięcia w drugim pomiarze

R

0

U

Vb

U

0

R

1

R

2

R

V

V

R

b

b

V

Vb

G

G

G

G

G

U

U











2

01

01

0

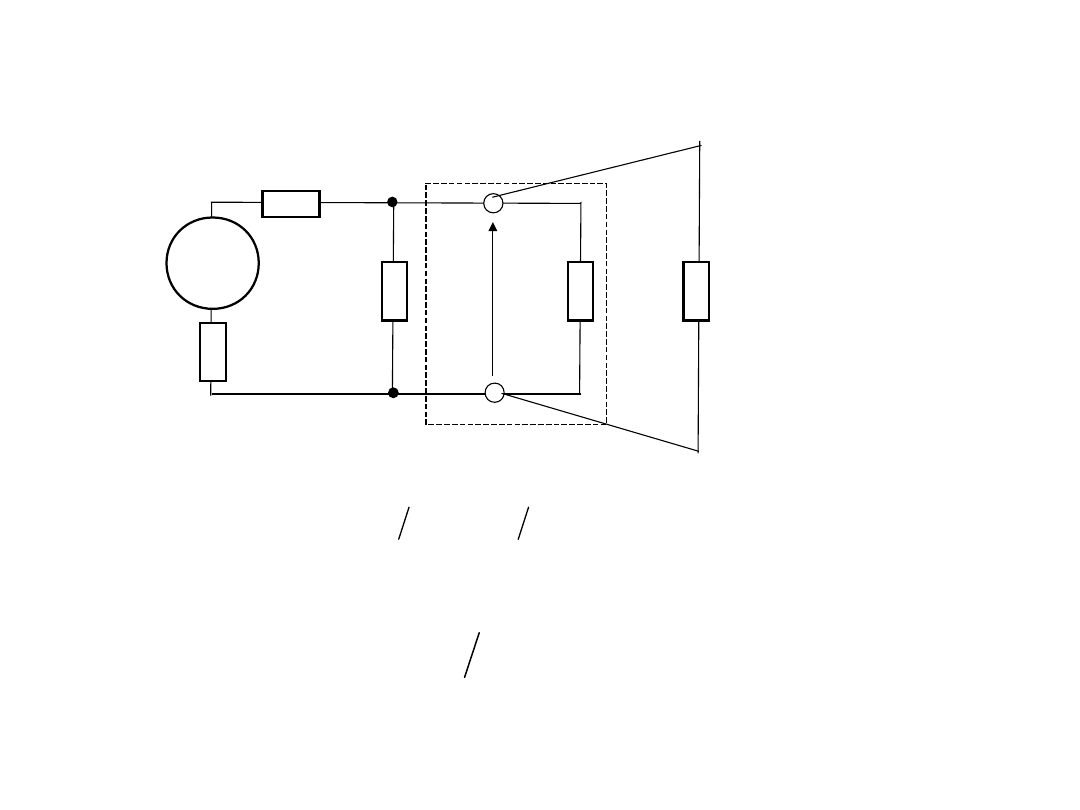
3.Korekcja wpływu rezystancji

wejściowej woltomierza

• Jeśli stosunek rezystancji

• Oraz stosunek wskazań woltomierza

100

U

Vb

10V

100k

100k

R

V

=

=1M

V

R

b

= R

V

=1M

b

V

V

b

R

R

G

G







b

,

V

V

U

U





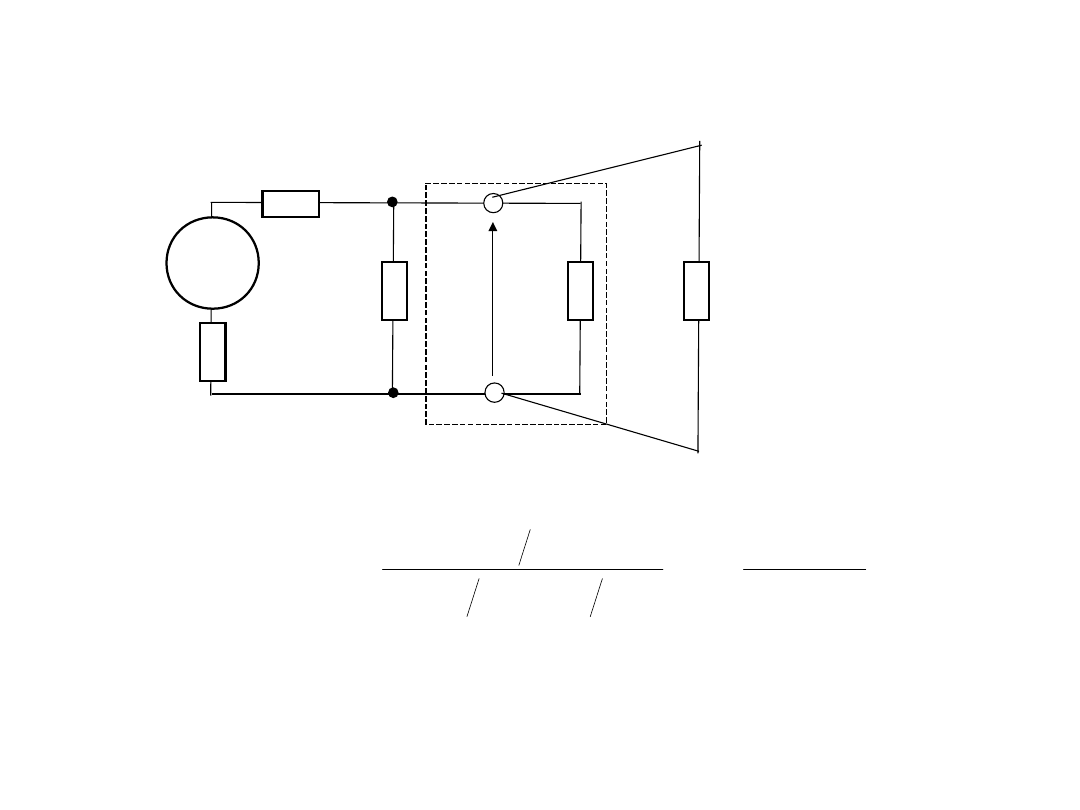
3.Korekcja wpływu rezystancji

wejściowej woltomierza

• Wtedy skorygowana wartość napięcia



















1

1

V

b

,

V

V

b

V

b

V

V

sk

U

U

U

R

R

R

R

U

U

R

0

U

Vb

U

0

R

1

R

2

R

V

V

R

b

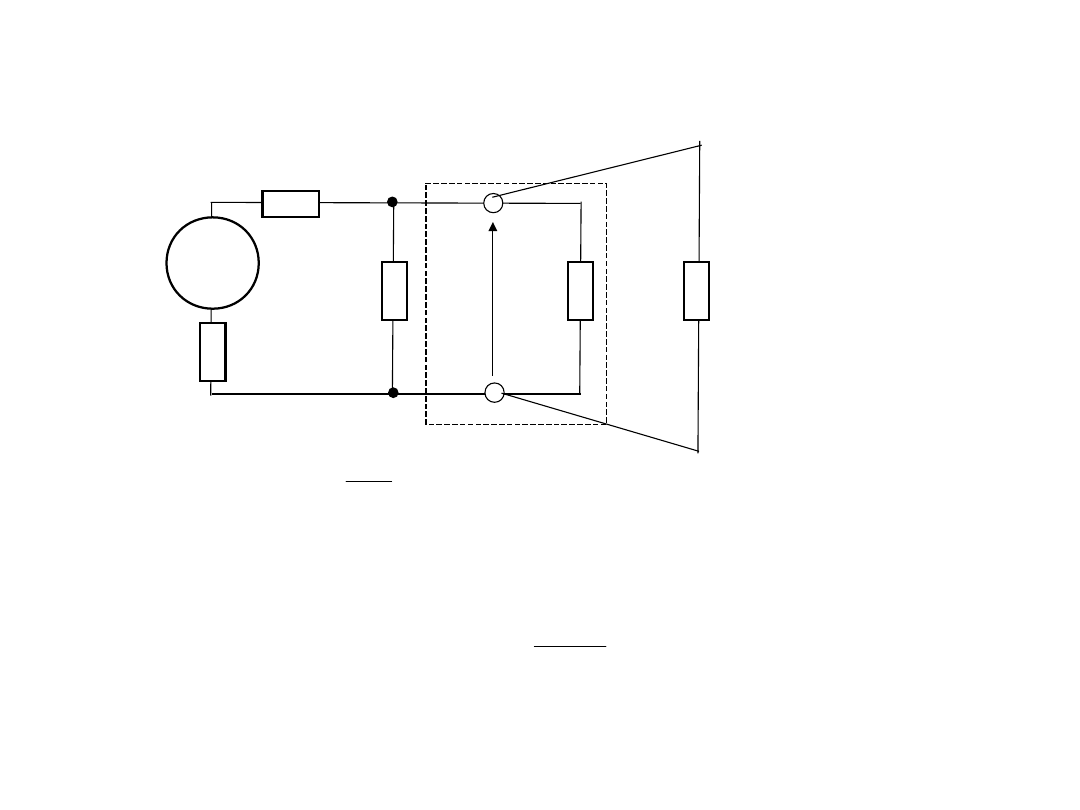
3.Korekcja wpływu rezystancji

wejściowej woltomierza

• Przy R

b

=R

v

• Wtedy skorygowana wartość napięcia







2

1

V

sk

U

U

R

0

U

Vb

U

0

R

1

R

2

R

V

V

R

b

1





b

V

R

R



3.Korekcja wpływu rezystancji

wejściowej woltomierza

• Przykład 1d. U

0

=10 V, R

0

=100 Ohm, R

1

=1 MOhm,

R

2

=1 MOhm, R

V

=10 MOhm

1. Wartość rzeczywista napięcia

2. Wynik pierwszego pomiaru

3. Wynik drugiego pomiaru przy R

b

=R

v

(β=1)

V

4,99975

1

1

1

2

1

0

1

0

0













R

R

R

R

R

U

U

x

V

4,76166

1

1

1

1

2

1

0

1

0

0















V

V

R

R

R

R

R

R

U

U

V

4,54521

1

1

1

1

1

2

1

0

1

0

0

















b

V

Vb

R

R

R

R

R

R

R

U

U

3.Korekcja wpływu rezystancji

wejściowej woltomierza

• Przykład 1d. U

0

=10 V, R

0

=100 Ohm, R

1

=1 MOhm,

R

2

=1 MOhm, R

V

=10 MOhm

4. Wartość współczynnika

5. Skorygowany wynik pomiaru

Co odpowiada rzeczywistej wartości napięcia

1,04762

V

4,54521

V

4,76166







Vb

V

U

U



V

4,99975

1,04762

2

V

4,76166

2













V

x

U

U

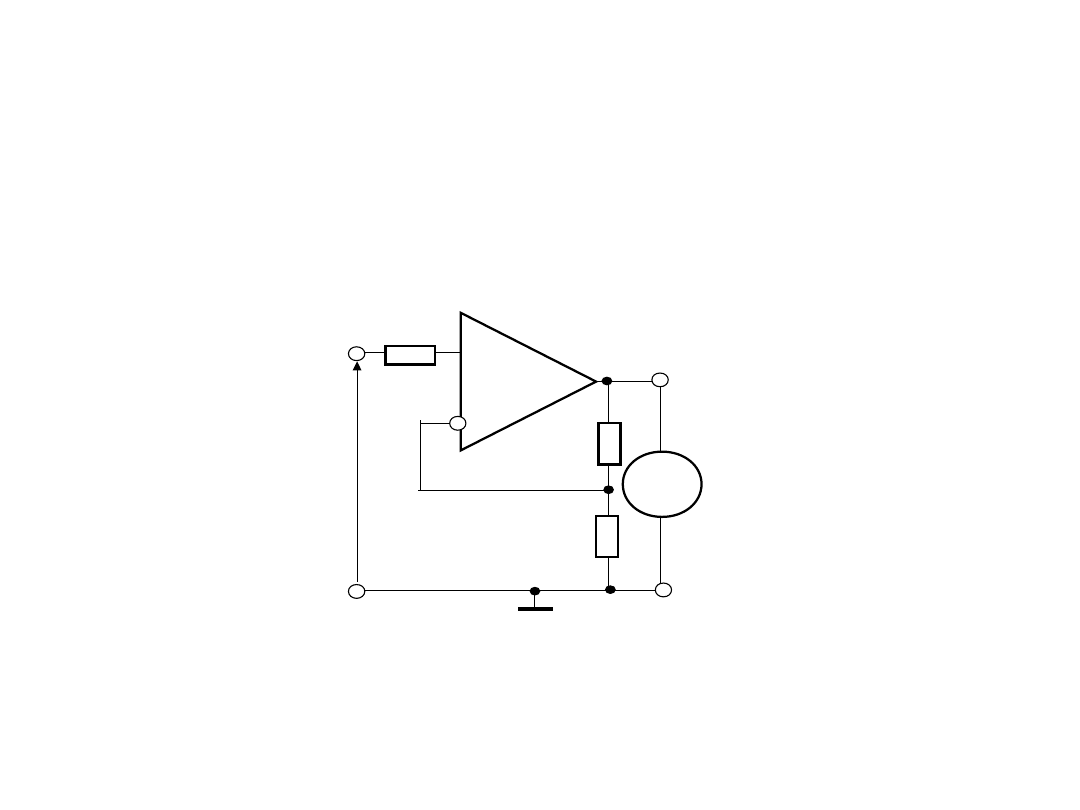
4.Układy wejściowe woltomierza

W celu

zapewnienia dużej rezystancji wejściowej na wejściu

woltomierza wykorzystuje wzmacniacz nieodwracający

,

zbudowany na wzmacniaczu operacyjnym (WO) ze sprężeniem
zwrotnym z dzielnikiem napięcia na rezystorach R

1

oraz R

2

.

Do wyjścia wzmacniacza jest podłączony przetwornik A/C (lub

analogowy woltomierz).

Równanie przetwarzania dla struktury bazowej:

U

v

=U

x



K

wu

,

gdzie K

wu

- współczynnik wzmocnienia napięcia

U

x

WO

U

wy

+

-

R

1

R

2

V

HI

R

3

LO

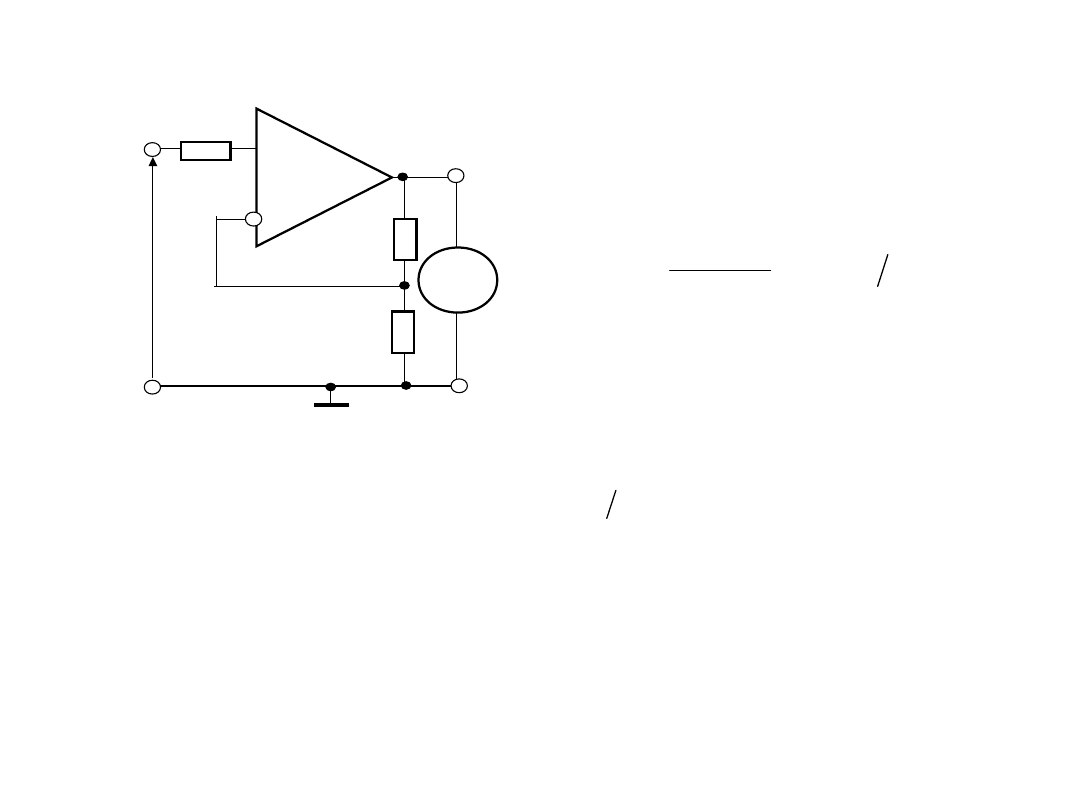
4.Układy wejściowe woltomierza

Rezystancja wejściowa woltomierza równa się rezystancji

wejściowej wzmacniacza:

gdzie R

we,WO

- jest rezystancją wejściową wzmacniacza

operacyjnego, A

0

- współczynnik wzmocnienia rozwartego WO

U

x

WO

U

wy

+

-

R

1

R

2

V

HI

R

3

LO

2

1

2

1

2

1

R

R

R

R

R

K

wu













w

WO

we

we

V

K

A

R

R

R

R

0

,

3

1







4.Układy wejściowe woltomierza

Wpływ zmian wejściowego napięcia przesuwu e

we

:

Wpływ zmian wejściowego prądu przesuwu Δi

we

:

Względny wpływ wartości współczynnika wzmocnienia WO A

0

:

Rezystancja wyjściowa:

Wymagania do WO:
• duża rezystancją wejściową wzmacniacza operacyjnego ,
• małe wartości wejściowego napięcia przesuwu oraz
• wejściowego prądu przesuwu,
• duża wartość współczynnika A

0

wzmocnienia WO

we

we

e

e

U





)

(

3

)

(

R

I

I

U

we

we













wu

I

K

A

A

0

0

1

1

)

(











wu

WO

wy

wy

K

A

R

R

0

,

1



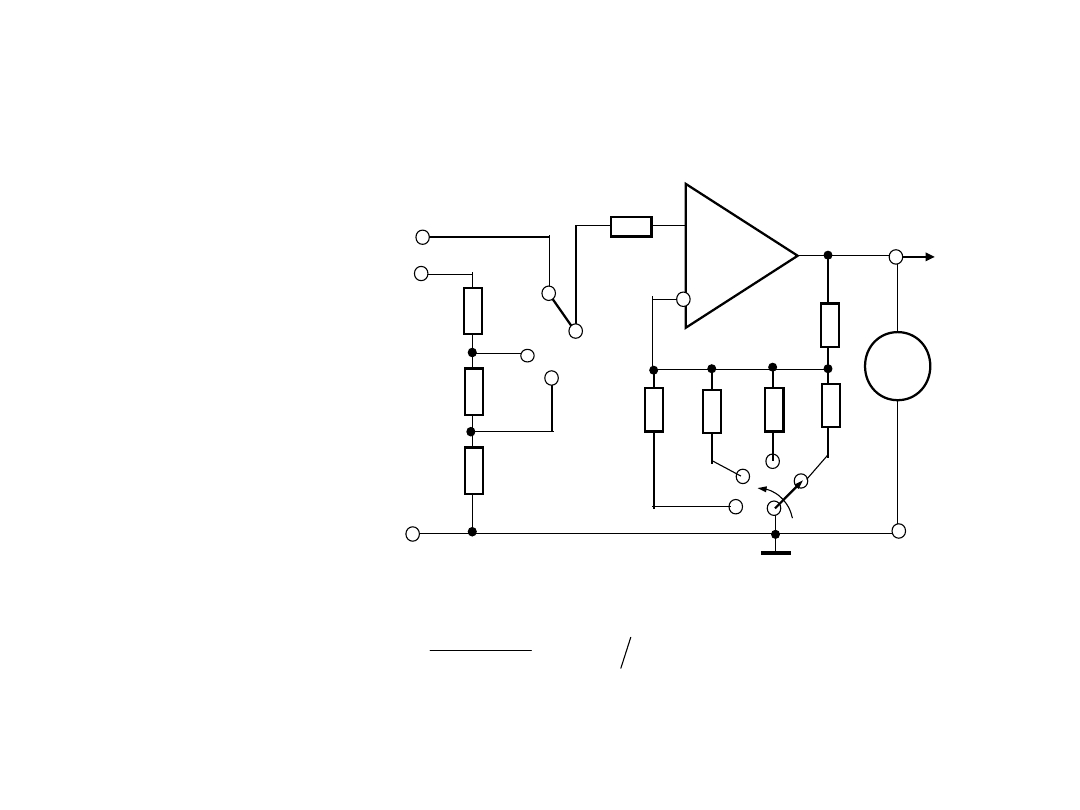
4.Układy wejściowe woltomierza

W celu zapewnienia rozszerzenia zakresów w stronę napięć

mniejszych (poniżej około 1 V) wykorzystuje kilku rezystorów
R

2j

w obwodzie sprężenia zwrotnego WO.

Wtedy współczynnik wzmocnienia równa się:

zwykle maksymalne wzmocnienie stanowi 10

3

-10

4

razy.

WO

U

wy

+

-

R

1

R

2,1

V

R

3

R

2,2

R

2,3

R

4,1

R

4,2

R

5

200V

20V

2V

200mV

20mV

2mV

LO

HI

2mV-2V

20V, 200V

(do A/C)

R

2,4

j

j

j

j

w

R

R

R

R

R

K

,

2

1

,

2

1

,

2

,

1







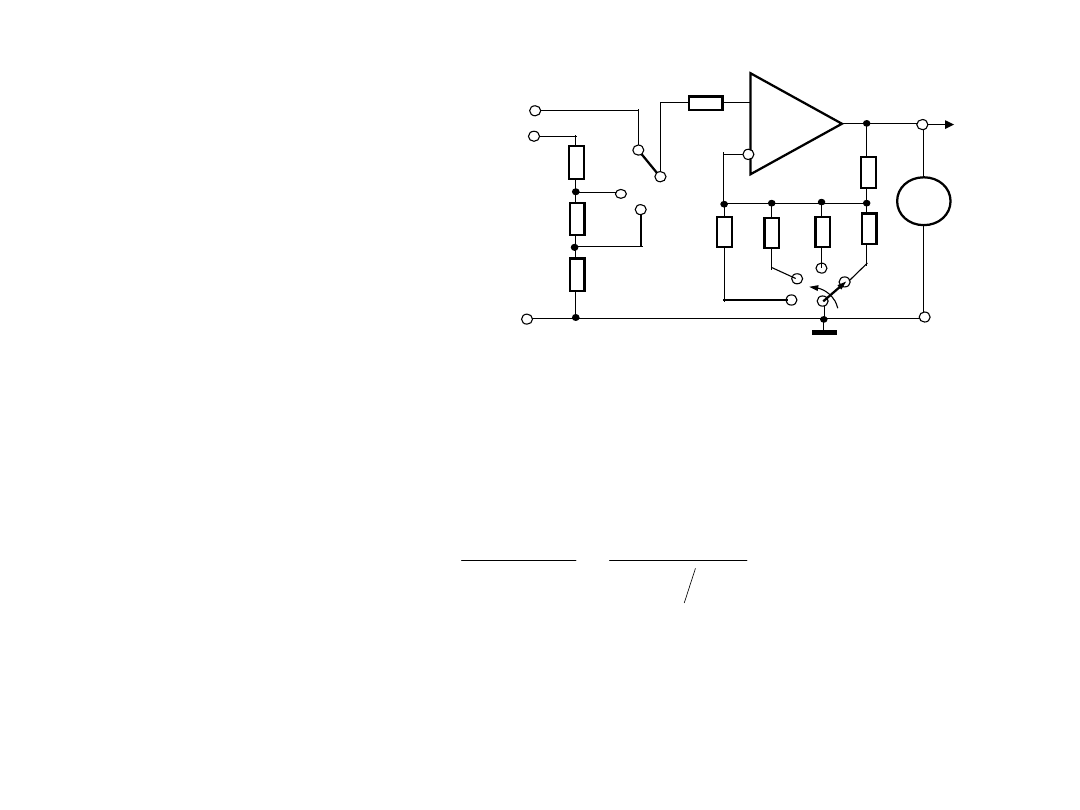
4.Układy wejściowe woltomierza

W celu zapewnienia rozszerzenia zakresów w stronę napięć

większych (ponad około 10 V) jak w DMM wykorzystuje się

dzielnik wejściowy

Równanie przetwarzania dla struktury na rys:

Uv=Ux



K

d,i



K

w,j

,

gdzie K

d,i



- współczynnik podziału napięcia wejściowego dzielnika

Rezystancja wejściowa woltomierza w tym przypadku równa się

rezystancji dzielnika Rd (przyjmując ze rezystancja wejściowa

wzmacniacza W0 jest w dużym stopniu większa od rezystancji

dzielnika):

WO

U

wy

+

-

R

1

R

2,1

V

R

3

R

2,2

R

2,3

R

4,1

R

4,2

R

5

200V

20V

2V

200mV

20mV

2mV

LO

HI

2mV-2V

20V, 200V

(do A/C)

R

2,4

i

i

i

i

d

R

R

R

R

R

K

,

4

5

5

,

4

,

4

,

1

1









d

V

R

R

R

R

R











...

2

,

4

1

,

4

5

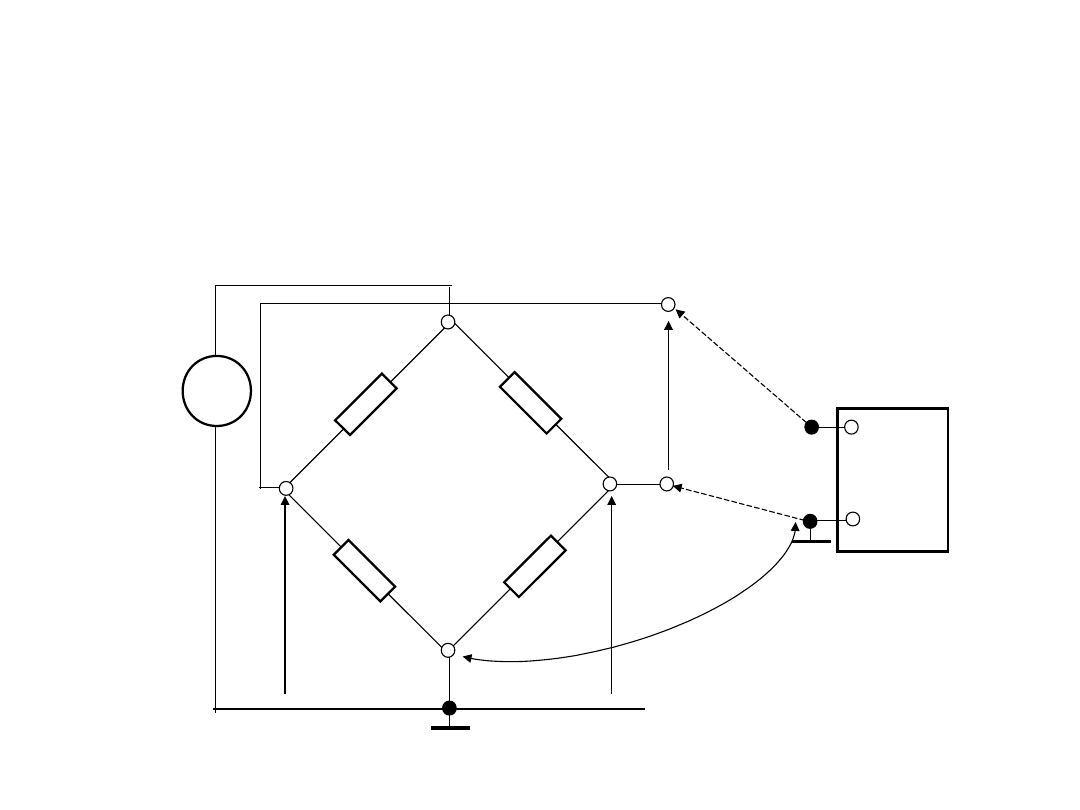
5. Układ wejściowy woltomierza ze

wzmacniaczem instrumentalnym.

Przy pomiarach napięć z obiektów, wyjścia którego są

odseparowani od masy wspólnej (ziemi), podłączenie tych

wyjść do wejść woltomierza z uziemionym wejściem „LO”

może powodować sytuację konfliktową.

E

R

1

R

4

R

3

R

2

U

x

=U

1

-U

2

U

2

U

1

„0(ź)

”

V

HI

LO

?

Konflikt!

„0(

V

)”

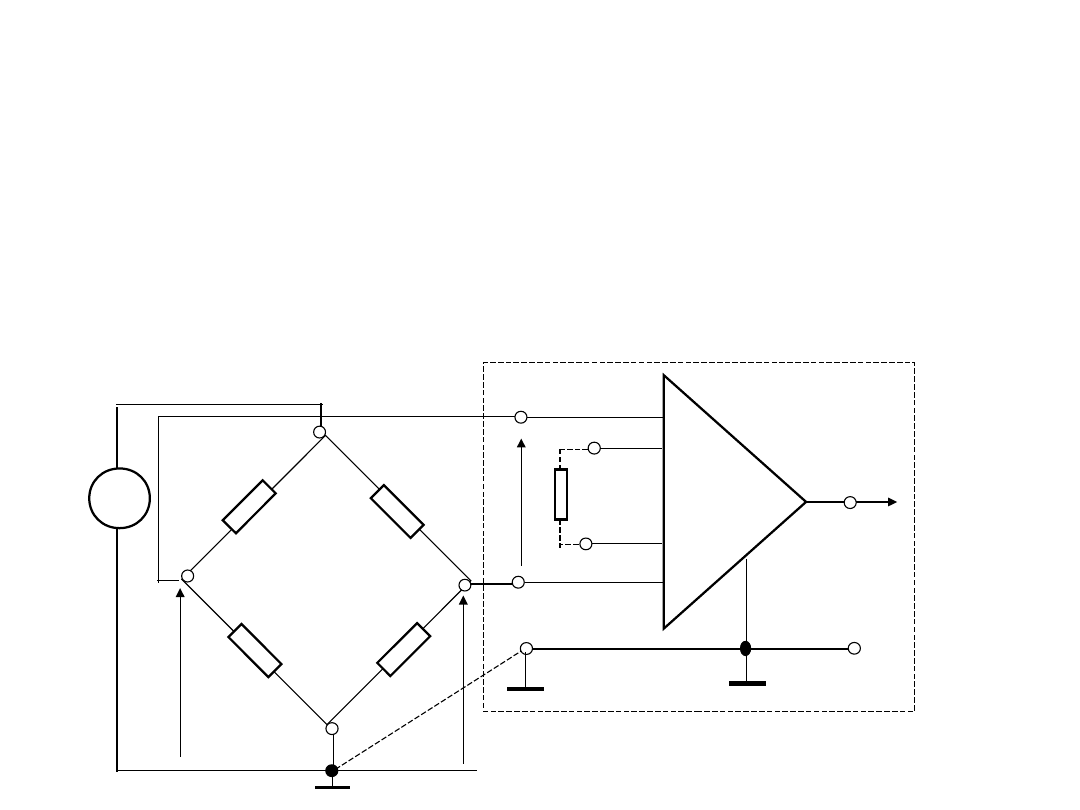
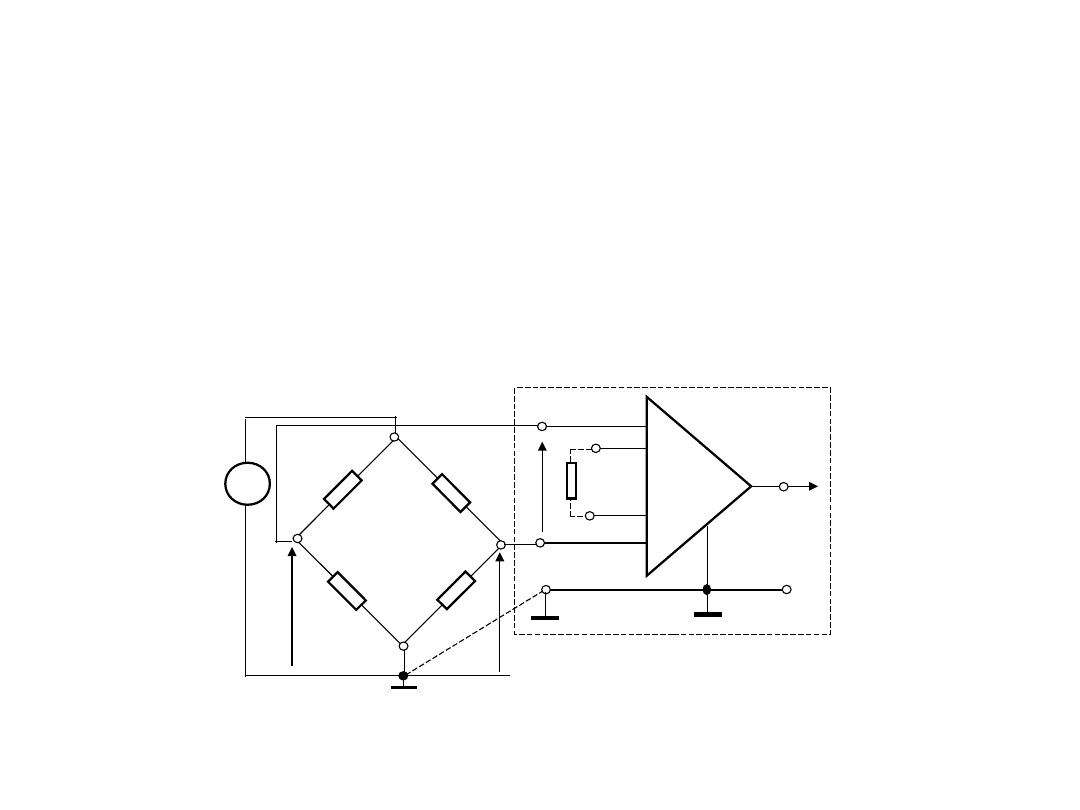
5. Układ wejściowy woltomierza ze

wzmacniaczem instrumentalnym.

W celu uniknięcia takiej sytuacji układ woltomierza powinien

mieć symetryczne (odseparowane od masy) wejścia. Taki

warunki mogą być spełnione przy wykorzystaniu wzmacniacza

instrumentalnego.

W takim układzie woltomierz jest wyposażony w trzy wejścia

(sygnałowe wysokie – „HI” i niskie „LO” oraz masę „0”).

Do sygnałowych wejść są dołączone punkty obwodu obiektu,

różnicę potencjałów należy zmierzyć. Wejście masy mogę być

podłączone do masy obiektu.

R

G

WI

-

+

HI

Do A/C

LO

0

Ref

U

x

=U

1

-

U

2

E

R

1

R

4

R

3

R

2

U

1

„0(ź)

”

U

2

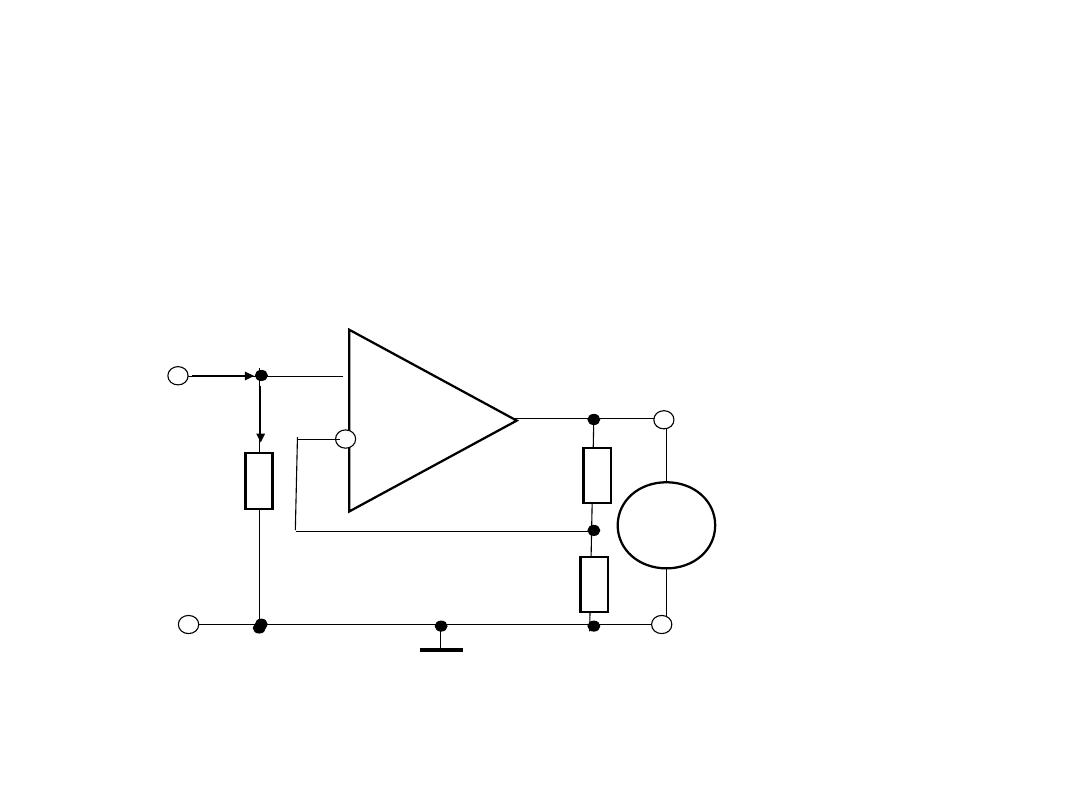
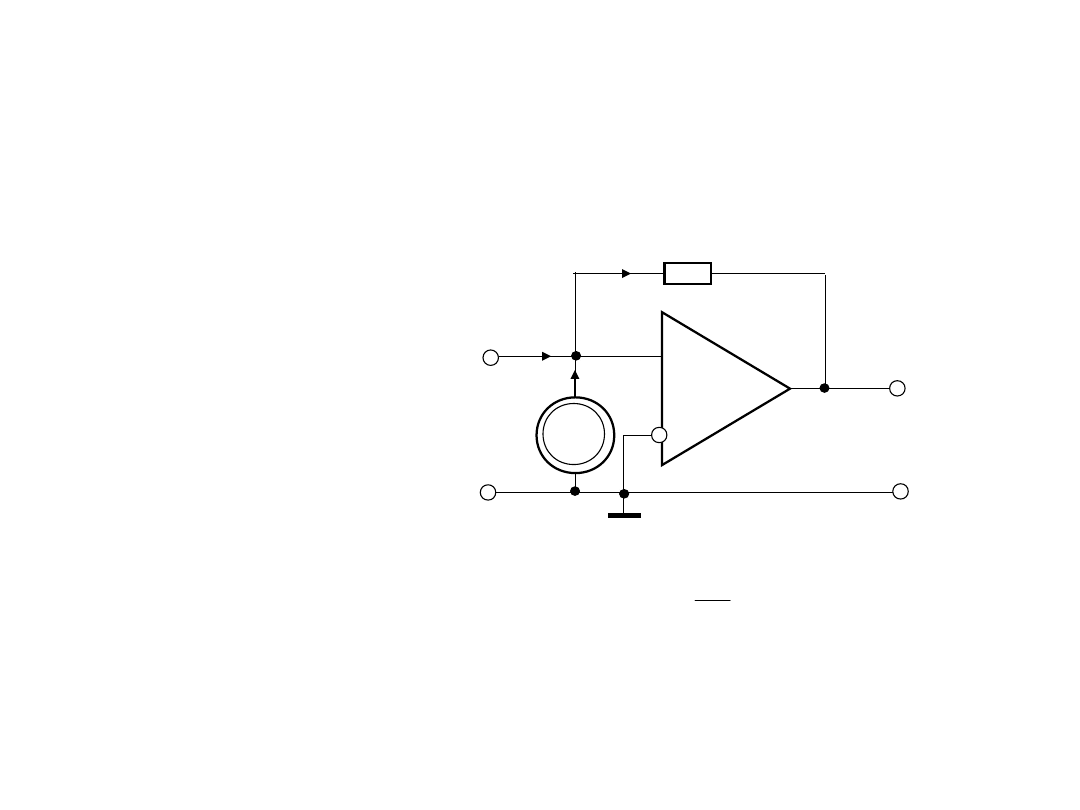
5. Układ wejściowy woltomierza ze

wzmacniaczem instrumentalnym.

Równanie przetwarzania dla struktury woltomierza ze

wzmacniaczem instrumentalnym:

gdzie

K

g

=

K

WI

- współczynnik wzmocnienia wzmacniacza

instrumentalnego.

Rezystancja wejściowa takiego układu równa się rezystancji

wejściowej wzmacniacza instrumentalnego.

R

G

WI

-

+

HI

Do A/C

L

O

0

Ref

U

x

=U

1

-U

2

E

R

1

R

4

R

3

R

2

U

1

„0(ź)

”

U

2

WI

x

V

K

U

U 

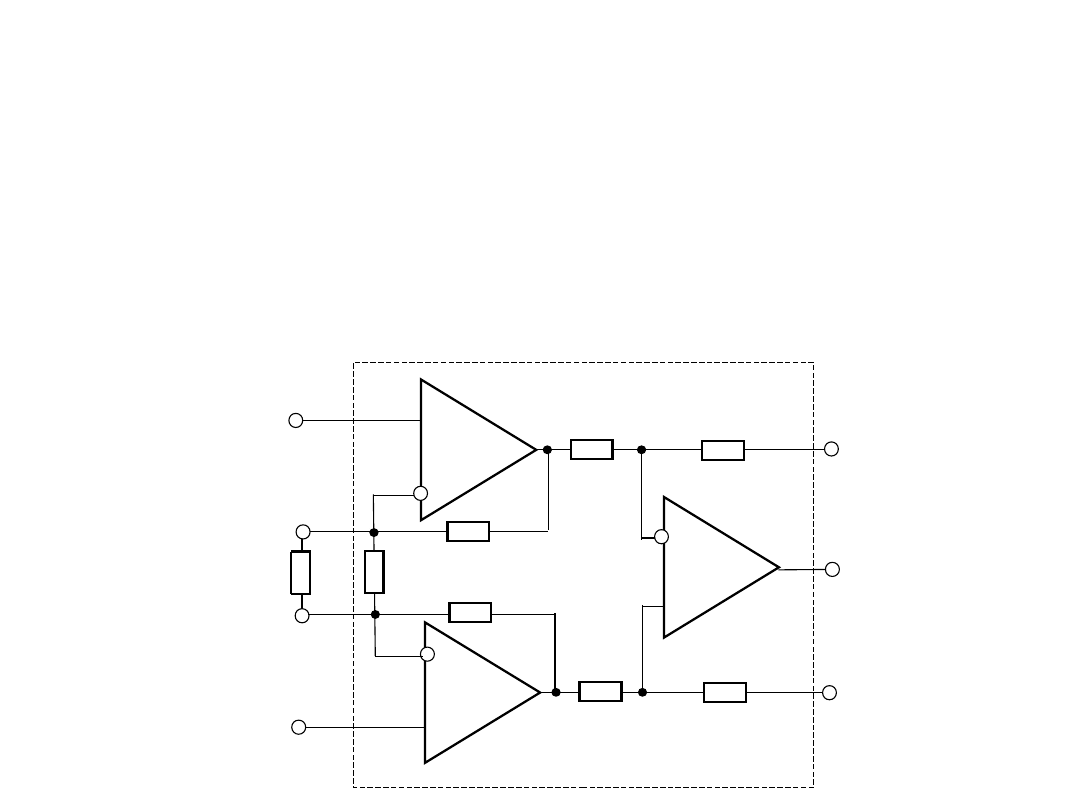
5. Układ wejściowy woltomierza ze

wzmacniaczem instrumentalnym.

Wzmacniacz instrumentalny jest zbudowany na podstawie kilku

wzmacniacze operacyjnych (W0) ze sprężeniem zwrotnym

utworzonych za pomocą rezystorów wewnętrznych, wartości

rezystancji których wyznaczają współczynnik wzmocnienia WI.

W jednym układzie scalonym może być kilku wzmacniacze

instrumentalnych. Typowy układ WI jest zbudowany na trzech

wzmacniaczach operacyjnych W0

1

, W0

2

oraz WO

3

.

V

in1

WO

1

+

-

R

6

V

in2

WO

2

R

5

R

7

R

3

R

4

R

1

R

2

WO

3

U

b

U

a

U

2

U

1

Feedback

V

o

V

ref

R

Go

+

+

-

-

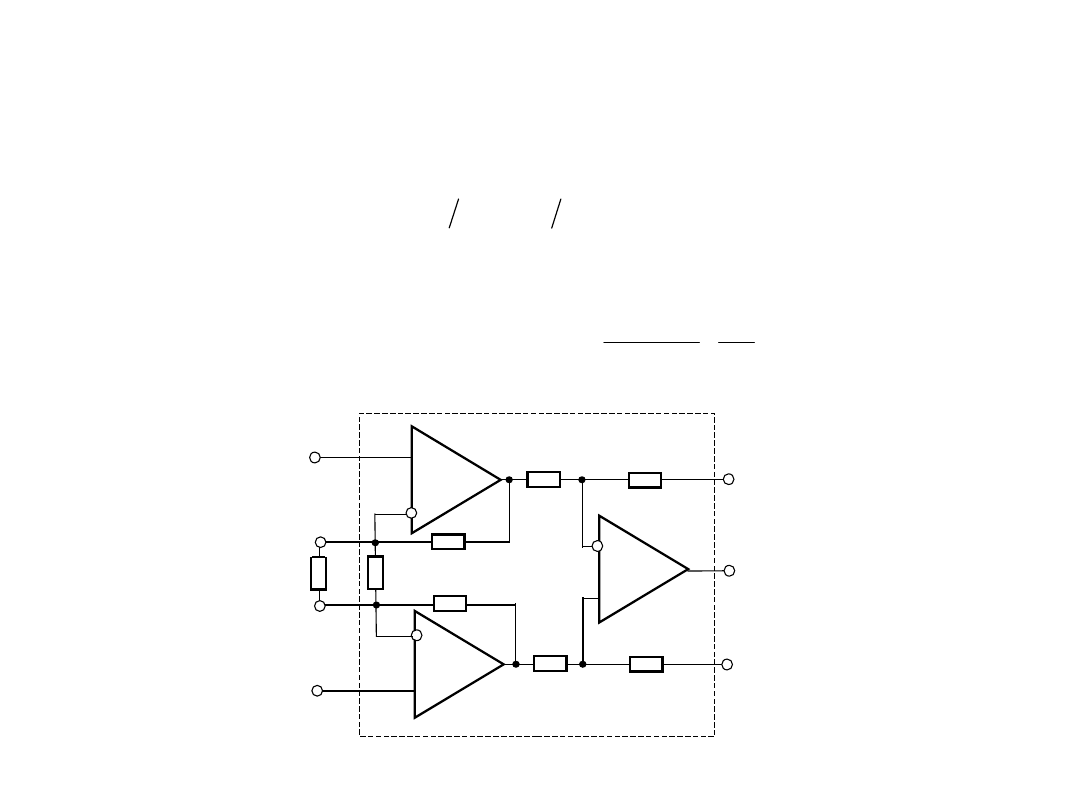
5. Układ wejściowy woltomierza ze

wzmacniaczem instrumentalnym.

W razie spełnienia warunku dla wartości rezystancji rezystorów

napięcie wyjściowe ma wartość

2

3

4

1

2

K

R

R

R

R





V

in1

WO

1

+

-

R

6

V

in2

WO

2

R

5

R

7

R

3

R

4

R

1

R

2

WO

3

U

b

U

a

U

2

U

1

Feedbac
k

V

o

V

ref

R

Go

+

+

-

-

1

2

6

7

5

2

1

1

R

R

R

R

R

K

K

K

g





















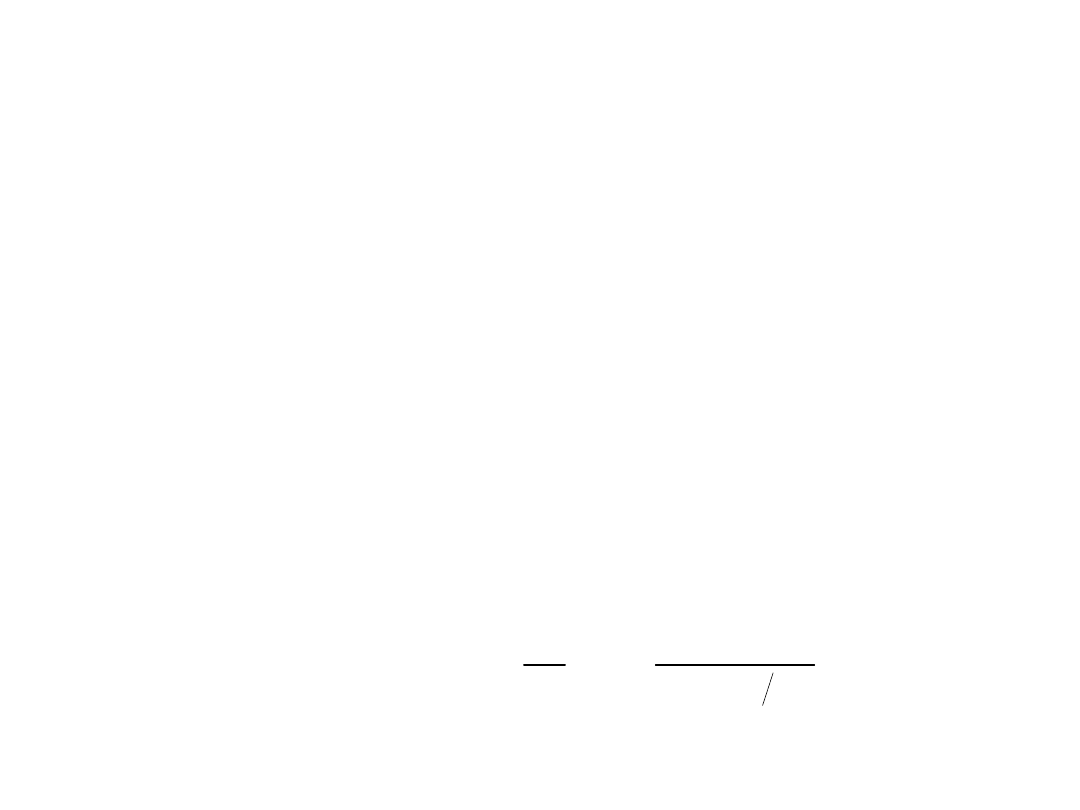
6. Współczynnik tłumienia wejściowego

napięcia wspólnego

Współczynnik tłumienia wejściowego napięcia wspólnego (synfazowego)

– CMMR (ang. Common Mode Rejection Ratio) –

stosunek napięcia wspólnego

U

cm

do wartości różnicowego napięcia

U

dif

,

które należy podać do wejść WI, żeby otrzymać taką sama wartość

napięcia wyjsciowego U

wy

CMMR= U

cm

/U

dif

= U

cm

/(U

wy

/K

g

)=K

g

(U

cm

/U

wy

)=K

g

/K

cm

K

cm

równa się stosunku napięcia wyjściowego

U

wy

do wartości

powodującego jego napięcia wejściowego wspólnego

U

cm

=U

we1

=U

we2

lub

U

cm

=(U

we1

+U

we2

)/2

(jednakowego na obydwu wejściach tzn. przy zerowym napięciu

różnicowym

U

dif

=U

we1

-U

we2

=0

CMMR zwykle jest wyrażany w decybeli

G

we

s

o

s

s

G

K

U

V

U

K

K

CMMR

)

(

lg

20

lg

20

,





6. Współczynnik tłumienia wejściowego

napięcia wspólnego

Przy wartości napięcia wspólnego

Us,we

Ograniczenie wartości współczynnika CMRR powoduje powstanie

błędu

Które odbierane jest jako niekorzystne napięcie różnicowe

wejściowe

Przykładowo, jeżeli CMRR=100 dB, oraz Uwe1=Uwe2=10 V
wtedy odbierane niekorzystne napięcie różnicowe wejściowe (błąd

wejściowy) wynosi

Jak widać, wpływ ograniczenia wartości CMRR przy niezerowej

wartości napięcia wejściowego wspólnego może być dużym.

20

10

CMRR

cm

r

U

U 



mkV

mV

,

V

V

V

V

U

CMRR

cm

r

100

1

0

10

10

10

10

10

10

4

5

20

100

20

















POMIAR PRĄDU.

SCHEMATY UKŁADÓW

WEJŚCIOWYCH

ELEKTRONICZNYCH

AMPEROMIERZE

PRĄDU STAŁEGO

Plan wykładu

1. Wymagania do amperomierze

2. Układy wejściowe

amperomierze.

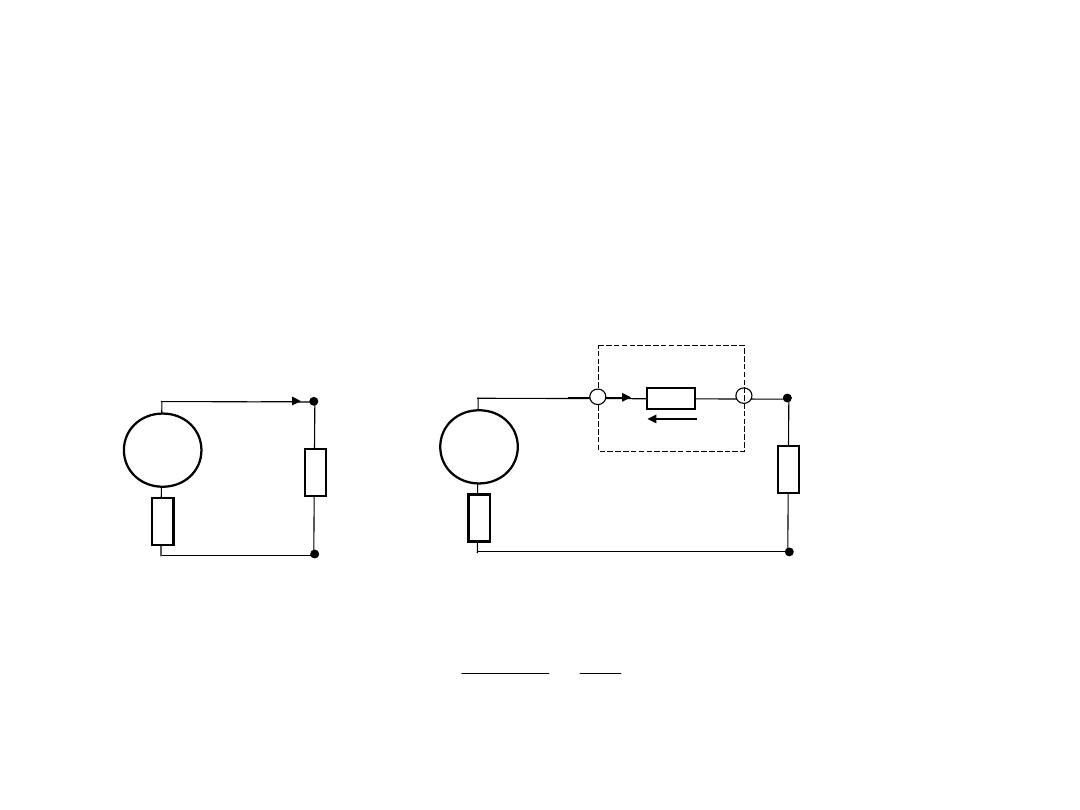
1. Wymagania do

amperomierze

Ogólnym wymaganiem do amperomierze jest zapewnienie małej

rezystancji wejściowej , ponieważ ona decyduje o błędzie
metodycznym pomiaru prądu oraz o spadku napięcia
pomiarowego na wejściu amperomierza (tzw.

Burden

Volage

).

Na rys. pokazano obwód elektryczny, w którym należy zmierzyć

wartość prądu Ix.

Do wprowadzenia amperomierza wartość tego prądu wynosi

R

0

I

x

U

0

R

1

I

A

R

0

U

0

R

A

R

1

A

U

A

01

0

1

0

0

R

U

R

R

U

I

x







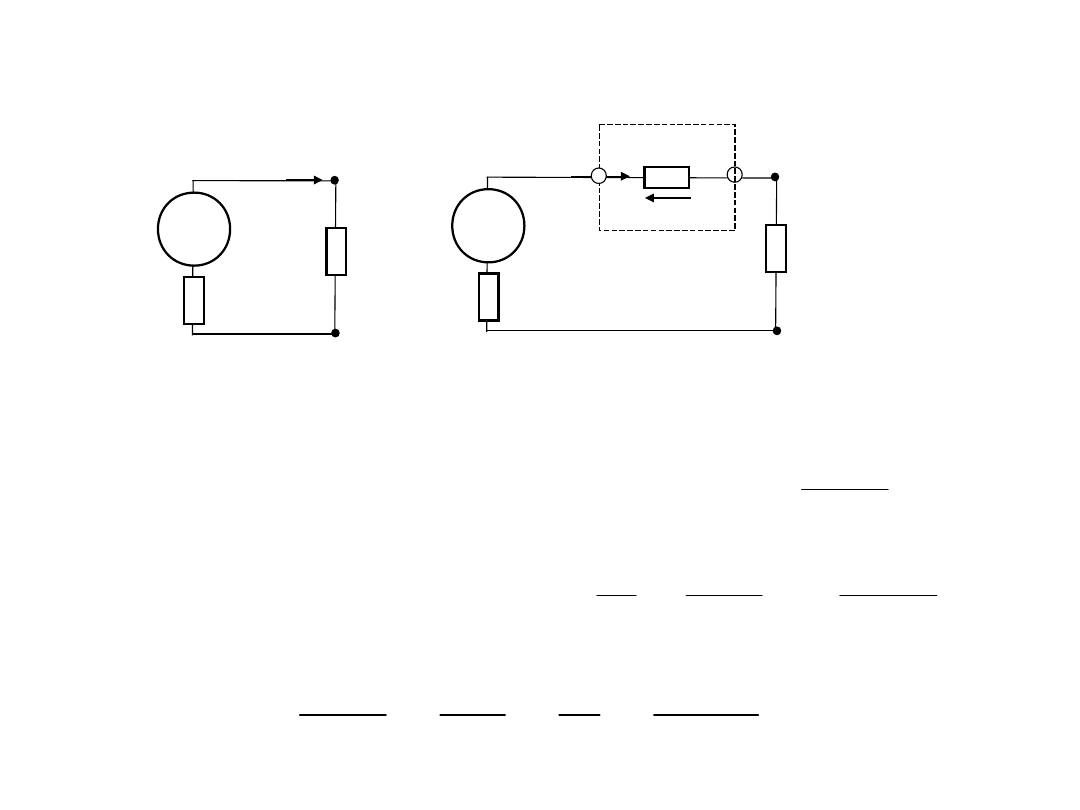
1. Wymagania do

amperomierze

Po szeregowym włączeniu amperomierza z rezystancją

wejściowej RA zmieni się ekwiwalentna rezystancja obwodu,
w wyniku czego zmieni się prąd mierzony (wskazanie
amperomierza)

Zmniejszenie prądu pomiarowego wynosi

Względny błąd

R

0

I

x

U

0

R

1

I

A

R

0

U

0

R

A

R

1

A

U

A

A

x

A

R

R

U

I

I









01

0

 

x

A

A

x

A

A

A

A

x

A

R

I

R

R

R

I

U

R

I

R

R

I

I

I

I

A























01

0

01

A

A

A

A

A

x

R

R

R

R

R

U

U

U

R

I

I

I

A

A



















01

0

0

)

(



1. Wymagania do

amperomierze

Przykład 1a

. Przy R0=100 Ohm, R1=1 kOhm oraz RA=1 Ohm,

U0=1 V otrzymuje się:

Wskazanie mikroamperomierza:

Błąd metodyczny względny:

Przykład 1b

. Jeżeli wartości rezystancji obiektu badanego będą o

10 razy mniejsza R1=100 Ohm , otrzymuje się:

wskazanie amperomierza ;

błąd metodyczny względny:

mA

kOhm

Ohm

V

R

R

U

I

x

90909

,

0

1

100

1

1

0

0











mA

Ohm

kOhm

Ohm

V

R

R

R

U

I

A

A

90827

,

0

1

1

100

1

1

0

0















%

091

,

0

%

100

90909

,

0

90909

,

0

90827

,

0













mA

mA

mA

I

I

I

x

x

A

R

v



mA

I

x

5



mA

I

A

4.97512



%

5

,

0





A

R



1. Wymagania do

amperomierze

Przykład 1c

. Przy R0=10 Ohm, R1=10 Ohm oraz RA=1 Ohm,

U0=1 V otrzymuje się:

Wskazanie miliamperomierza:

Błąd metodyczny względny:

mA

Ohm

Ohm

V

R

R

U

I

x

00

,

50

10

10

1

1

0

0











mA

Ohm

Ohm

Ohm

V

R

R

R

U

I

A

A

47,619

1

10

10

1

1

0

0















%

8

,

4

%

100

00

,

50

00

,

50

47,619













mA

mA

mA

I

I

I

x

x

A

R

v



1. Wymagania do

amperomierze

Dla zmniejszenia tego błędu należy wykorzystać miliamperomierz

z mniejszą rezystancję wejściową, na przykład RA=0,01 Ohm
lub jeszcze mniejszej, wtedy w ostatnim przypadku błąd
metodyczny względny:

%

005

,

0





A

R



1. Wymagania do

amperomierze

Otóż wartość błędu metodycznego, spowodowanego ograniczonej

wartością rezystancji wejściowej amperomierza zależy od

stosunku rezystancji wejściowej amperomierza RA i

ekwiwalentnej rezystancji obwodu ze strony pomiędzy

punktami włączenia amperomierza

Zmniejszenie rezystancji wejściowej amperomierza R

A

zapewnia

zmniejszenie błędu metodycznego.

Z innej strony, wartość błędu metodycznego wyznacza się

stosunkiem spadku napięcia na amperomierze (Burden

Volage) do napięcia obwodu.

Napięcie na amperomierze wynosi
jego wartość powinna być ograniczona.

A

A

A

R

I

U 

A

A

x

R

R

R

R

R

I

I

A

A











01

)

(



0

0

)

(

U

U

U

R

I

I

I

A

A

A

x

R

R

A

A















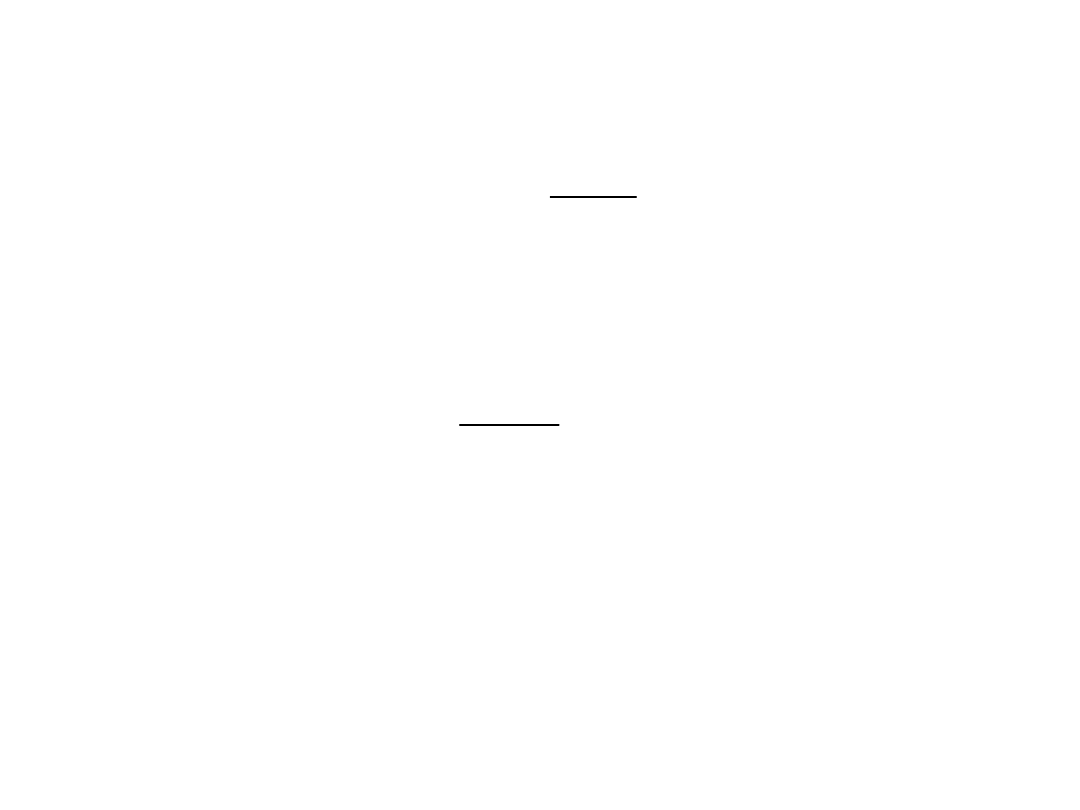
Korekcja błędu od wpływu

rezystancji amperomierza R

A

.

Ze wzoru błędu

wynika, że skorygowana wartość prądu

 

1

0

R

R

R

I

I

I

I

A

A

x

A

R

A































1

0

1

R

R

R

I

I

A

A

x

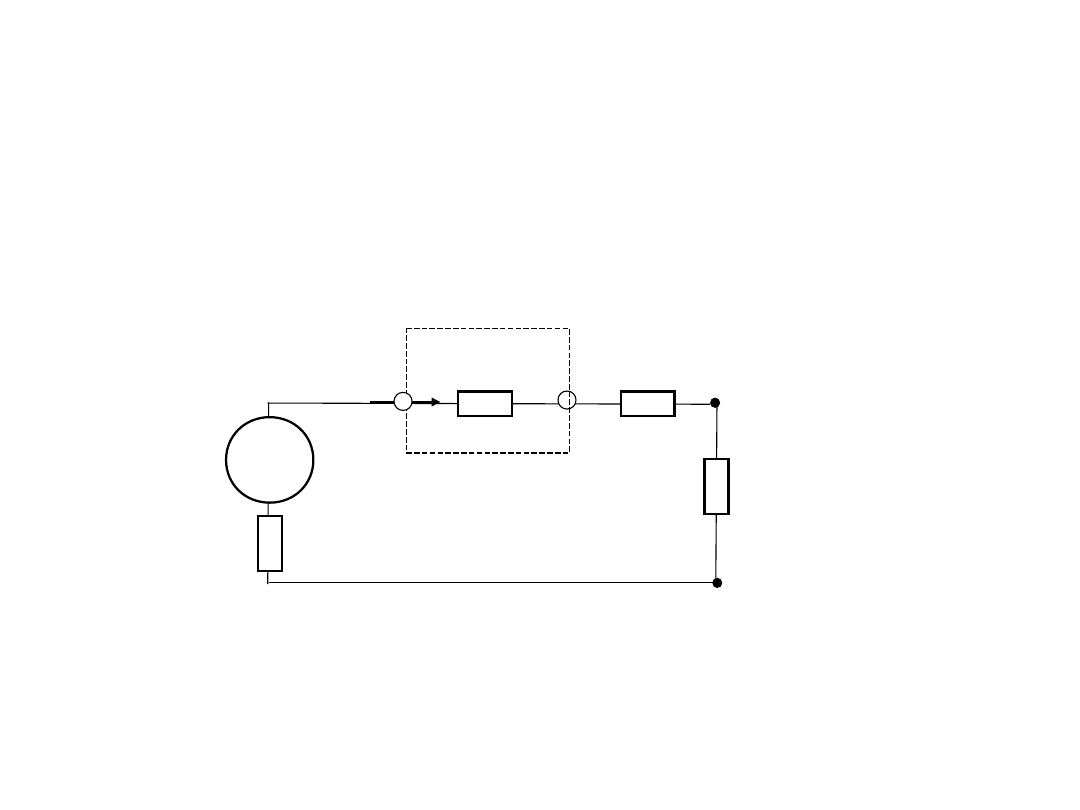
Korekcja błędu od wpływu

rezystancji amperomierza R

A

.

Wpływ rezystancji amperomierza R

A

na wynik pomiaru prądu

może być skorygowany przez dodatkowy pomiar prądu z
włączeniem dodatkowej rezystancji R

d

o znanej wartości,

na

przykład taki samy amperomierz: R

d

=R

A

.

I

A2

R

0

U

0

R

A

R

1

A

R

d

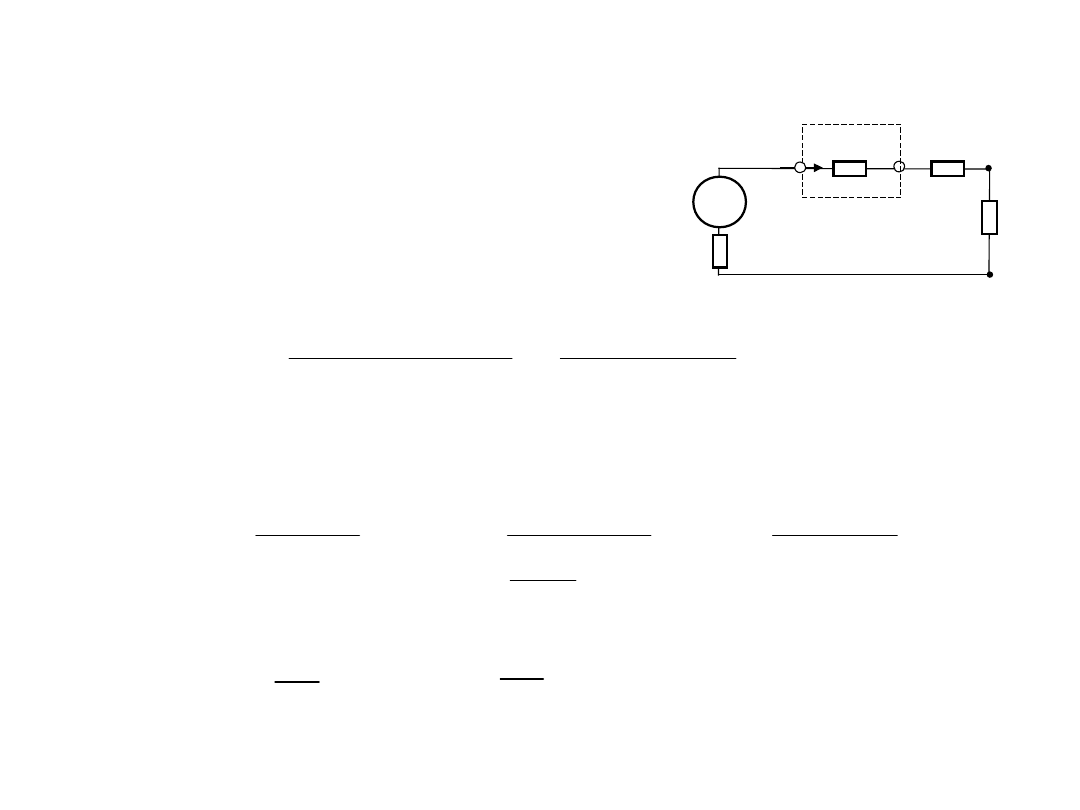
Korekcja błędu od wpływu

rezystancji amperomierza R

A

.

Wtedy wynik pomiaru prądu w drugim pomiarze

Z wartości wyników pomiaru I

A

oraz I

A2

można wyznaczyć wartość

I

x

1

2





A

A

I

I

a

I

A2

R

0

U

0

R

A

R

1

A

R

d



























A

d

A

A

R

R

R

U

R

R

R

R

U

I

2

1

0

0

1

0

0

2



































































a

I

R

a

R

R

I

R

R

R

I

I

A

A

d

A

A

A

A

x





1

1

1

1

1

0

A

d

R

R





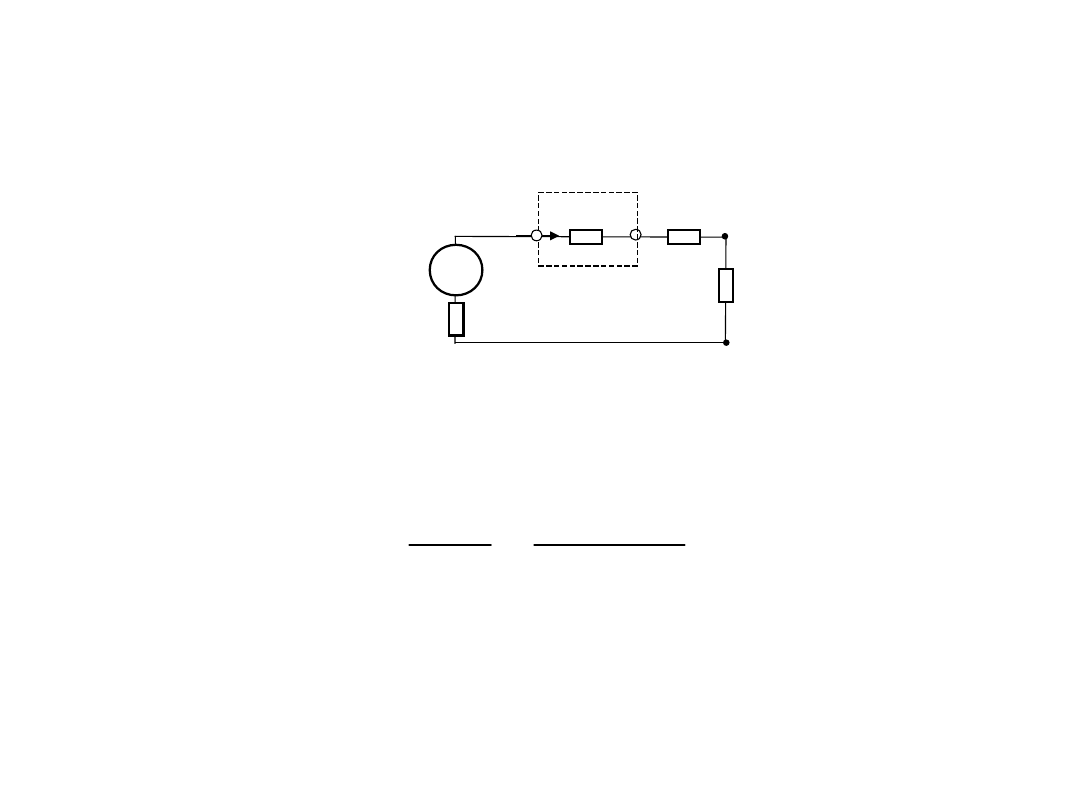
Korekcja błędu od wpływu

rezystancji amperomierza R

A

.

Przy R

d

=R

A

Dlatego skorygowana wartość prądu

A

A

A

A

A

x

I

I

I

I

a

I

I









2

2

2

2

I

A2

R

0

U

0

R

A

R

1

A

R

d

1





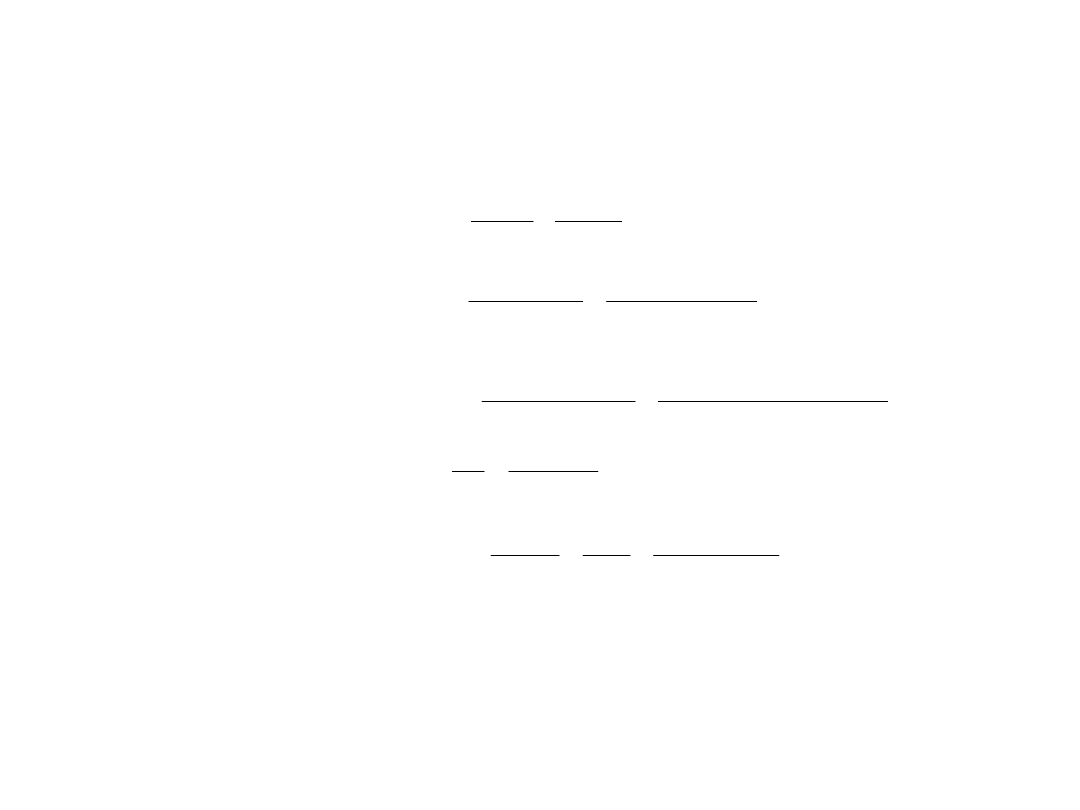
Korekcja błędu od wpływu

rezystancji amperomierza R

A

.

Przykład 1d. U0=10 V, R0+R1=10 Ohm, RA=1 Ohm.

Wartość rzeczywista prądu

Wynik pierwszego pomiaru

Wynik drugiego pomiaru

Wartość współczynnika

Skorygowana wartość prądu

Co odpowiada rzeczywistej wartości prądu.

A

Ohm

V

R

R

U

I

x

000

,

1

10

10

1

0

0









A

Ohm

Ohm

V

R

R

R

U

I

A

A

909091

,

0

1

10

10

1

0

0













A

Ohm

Ohm

Ohm

V

R

R

R

R

U

I

A

A

A

8333333

,

0

1

1

10

10

1

0

0

2



















0909091

,

1

833333

,

0

909091

,

0

2







A

A

I

I

a

A

a

I

R

R

U

I

A

x

000

,

1

0909091

,

1

2

909091

,

0

2

1

0

0















2. Układy wejściowy

amperomierze

2.1. Układy wejściowe amperomierza z bocznikiem

Dla pomiarów prądów o dużej wartości (od kilku miliamperów i

wyżej) wykorzystuje się układ pomiarowy amperomierza z
bocznikiem na wejściu

WO

-

I

x

R

b

I

x

U

v

=Ix

R

b

K

wu

R

1

R

2

V

+

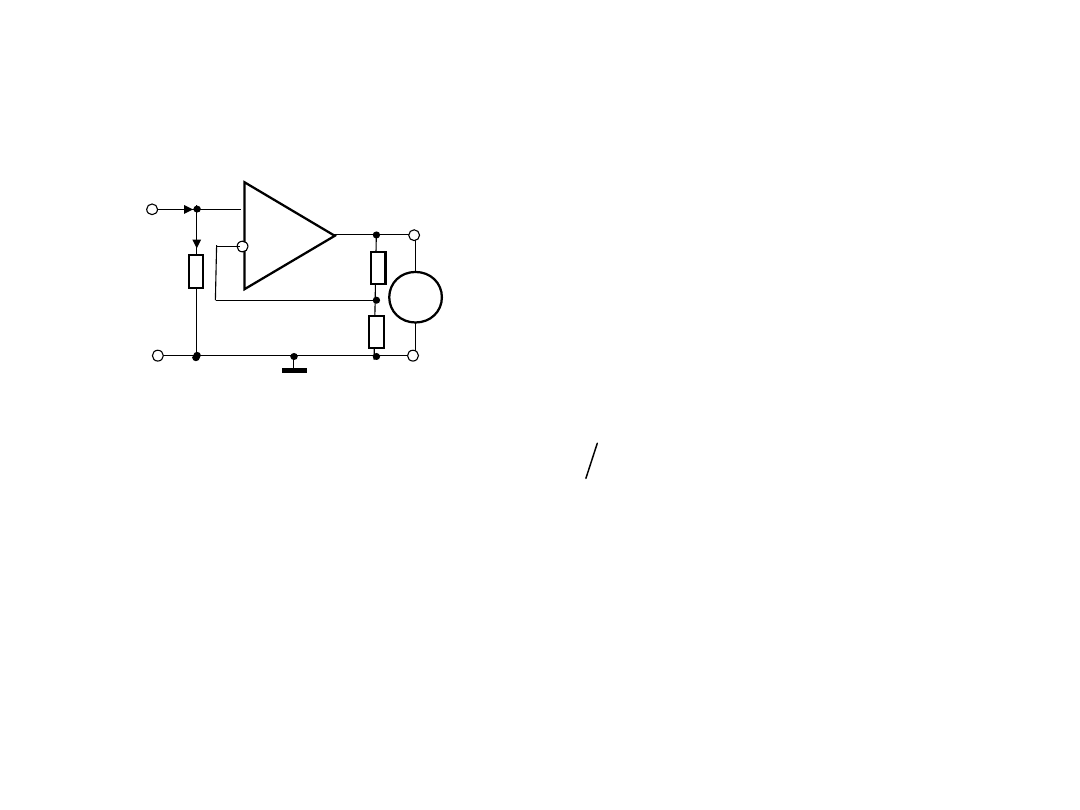
2. Układy wejściowy

amperomierze

2.1. Układy wejściowe amperomierza z bocznikiem

Dla takiego układu napięcie wyjściowe wynosi

R

b

- jest rezystancją bocznika, K

wu

- jest współczynnikiem

wzmocnienia wzmacniacza

WO

-

I

x

R

b

I

x

U

v

=Ix

R

b

K

wu

R

1

R

2

V

+





wu

b

x

b

x

wy

v

K

R

I

R

R

R

I

U

U









2

1

1

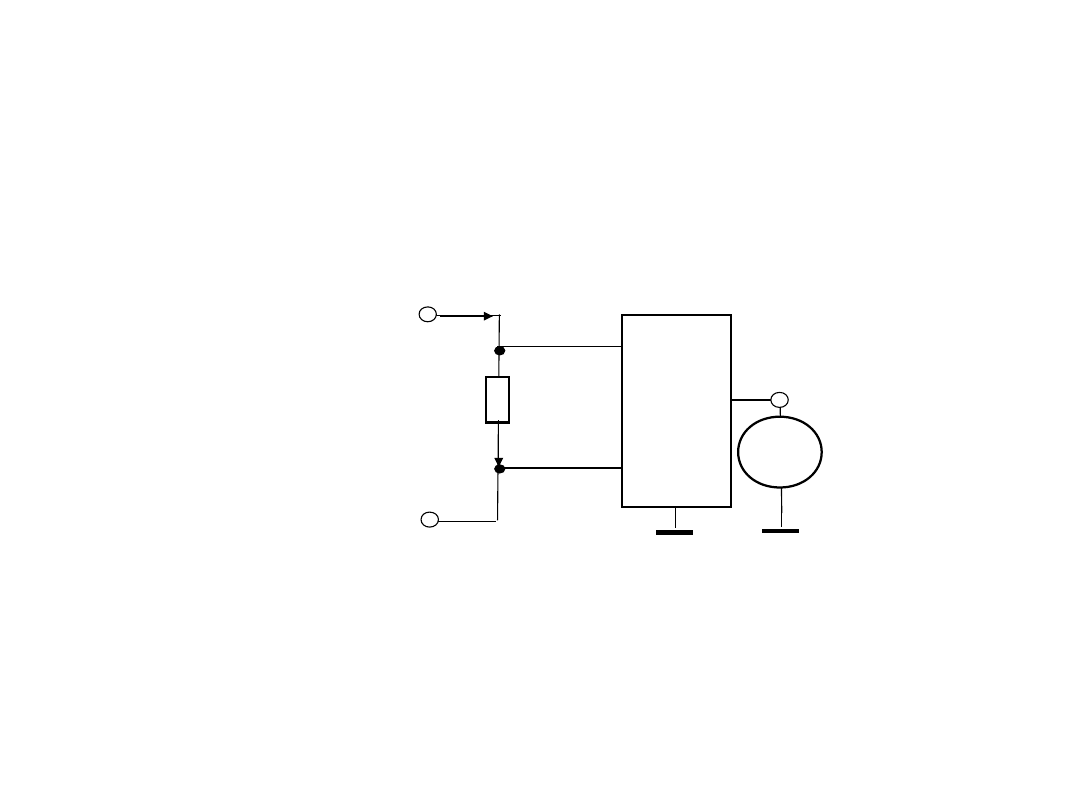
2. Układy wejściowy

amperomierze

2.1. Układ wejściowy amperomierza z bocznikiem

Lepsze charakterystyki można uzyskać stosując wzmacniacz

instrumentalny (WI), zwłaszcza w przypadkach kiedy obiekt

mierzony jest odseparowany od masy wspólnej.

Dla takiego układu napięcie wyjściowe wynosi

Kwi- jest współczynnikiem wzmocnienia WI

I

x

R

b

I

x

U

v

=Ix

R

b

K

wi

V

WI

K

wi

wi

b

x

wy

v

K

R

I

U

U





2. Układy wejściowy

amperomierze

2.1. Układy wejściowe amperomierza z bocznikiem

Dla takich układów wejściowych:

Rezystancja wejściowa amperomierza :

R

A

=Rb

Wartość napięcia na amperomierze: U

A

=I

x

·R

b

Dokładność takiej struktury amperomierza wyznacza się

dokładnością:

•

bocznika - błąd δ

b

;

•

wzmacniacza - błąd δ

w

oraz ;

•

przetwornika analogowo-cyfrowego (na wyjściu) – błąd δ

A/C

:

δ

A

=δ

b

+

δ

W

+

δ

A/C

2. Układy wejściowy

amperomierze

2.1. Układ wejściowy amperomierza z bocznikiem

Przy ograniczeniu wartości współczynnika wzmocnienia na

poziomie K

w

=10

3

-10

4

, oraz napięciu wyjściowym około

U

wy

=1V, wartość spadku napięcia na amperomierze wynosi

około

Wtedy wartość rezystancji bocznika równa się:

Przykład 2

. Przy zakresach prądu mierzonego I

x

od 1mA do 1 A

oraz K

w

=10

4

wartości rezystancji bocznika równają się

mV

V

K

U

U

w

wy

A

)

1

1

,

0

(

10

10

1

4

3











x

x

A

A

b

I

mV

I

U

R

R

)

1

1

,

0

(









Ohm

mOhm

A

mA

mV

R

R

A

b

1

,

0

01

,

0

10

1

1

,

0











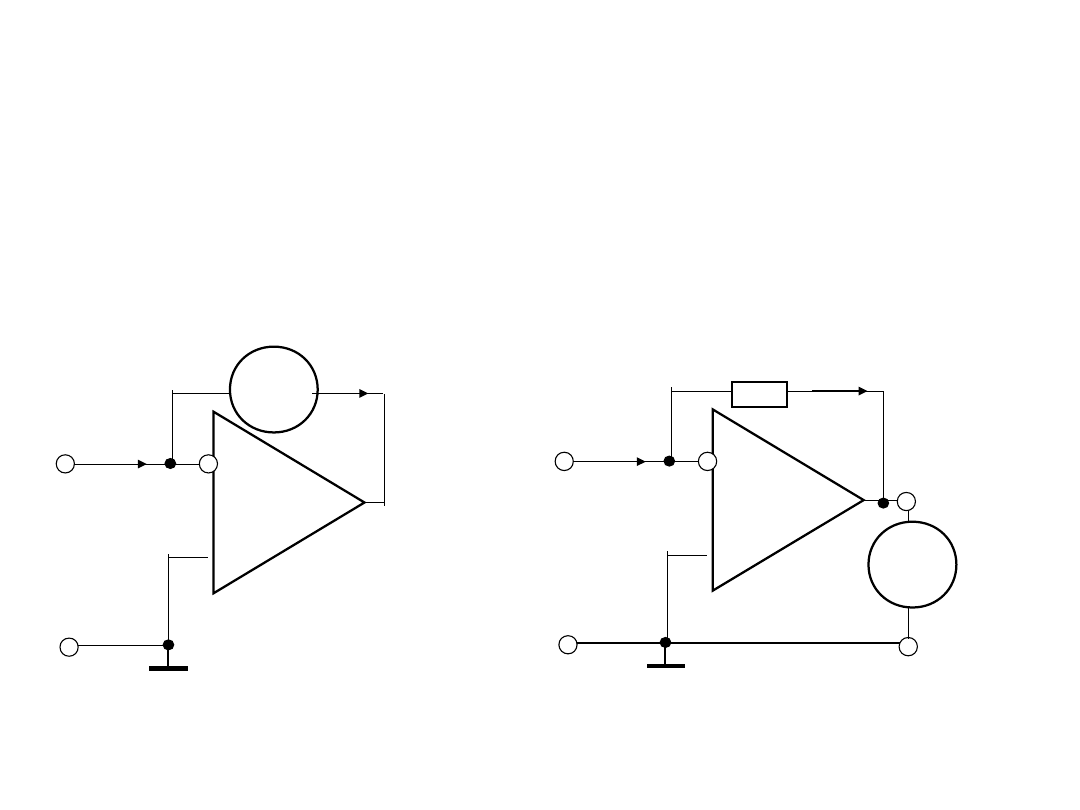
2. Układy wejściowy

amperomierze

2.2. Bazowa konfiguracja układu wejściowego

mikroamperomierze z przetwarzaniem
bezpośrednim

Do pomiarów prądów, których wartości są z zakresie

mikroamperów i niżej, wykorzystują się układy z
bezpośrednim przetwarzaniem prądu.

I

x

WO

-

+

V

R

F

I

x

U

wy

=-Ix

R

F

LO

HI

I

x

WO

-

+

A

HI

I

A

=I

x

LO

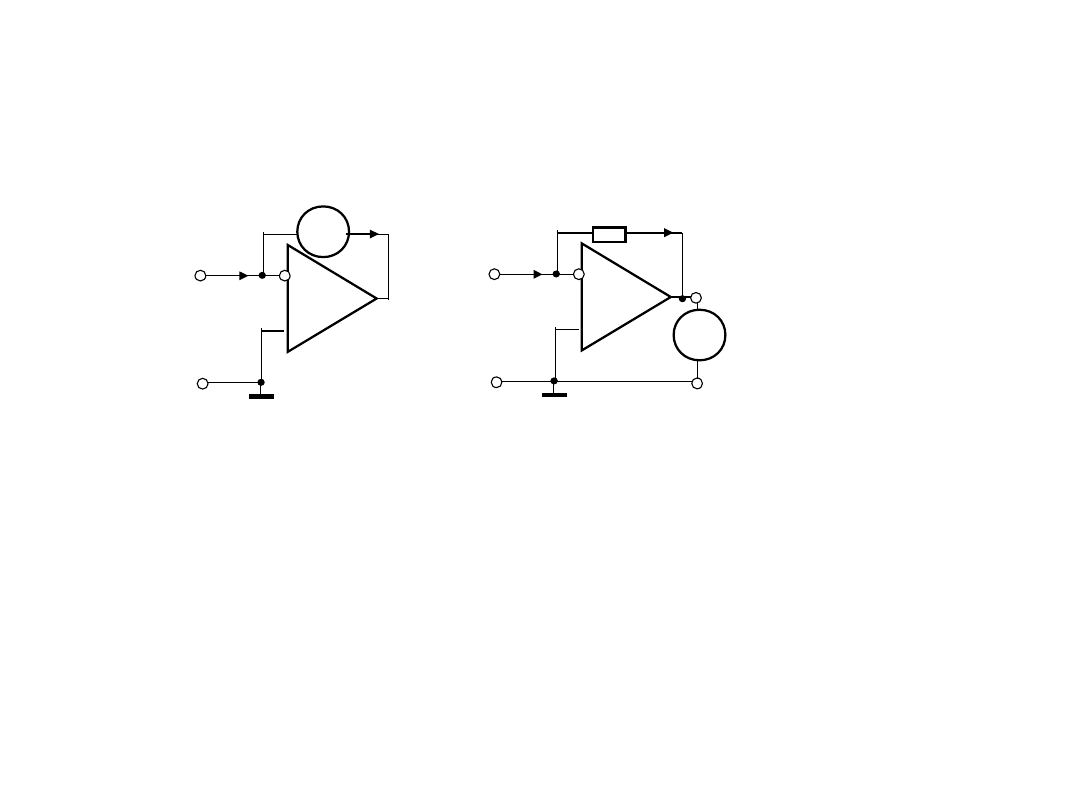
2. Układy wejściowy

amperomierze

2.2. Bazowa konfiguracja układu wejściowego

mikroamperomierze z przetwarzaniem

bezpośrednim

W układzie z przetwarzaniem bezpośrednim prądu napięcie

wyjściowe równa się:

gdzie R

F

- rezystancja sprężenia zwrotnego.

I

x

WO

-

+

V

R

F

I

x

U

wy

=-Ix

R

F

LO

HI

I

x

WO

-

+

A

HI

I

A

=I

x

LO

F

x

wy

v

R

I

U

U







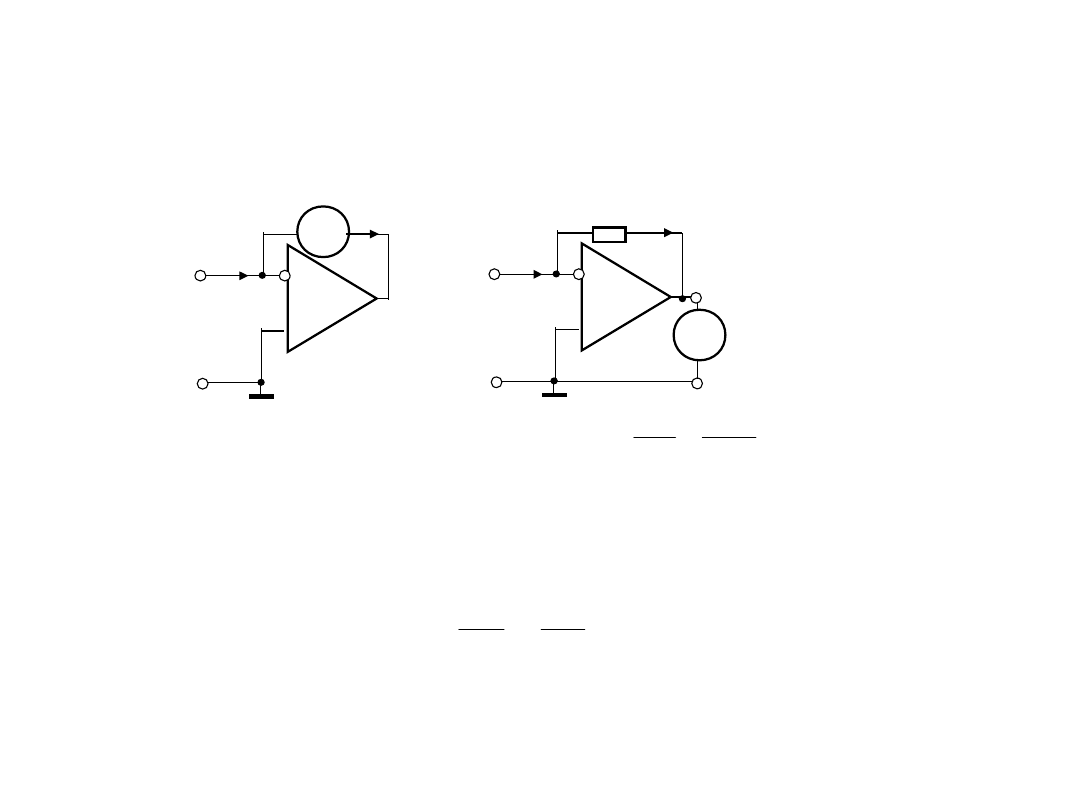
2. Układy wejściowy

amperomierze

2.2. Bazowa konfiguracja układu wejściowego

mikroamperomierze z przetwarzaniem
bezpośrednim

Spadek napięcia na amperomierze

:

Otóż w pierwszym przybliżeniu rezystancja wejściowa

mikroamperomierza:

I

x

WO

-

+

V

R

F

I

x

U

wy

=-Ix

R

F

LO

HI

I

x

WO

-

+

A

HI

I

A

=I

x

LO

WO

F

x

wy

A

A

R

I

A

U

U





0

0

A

R

I

U

R

F

x

A

A







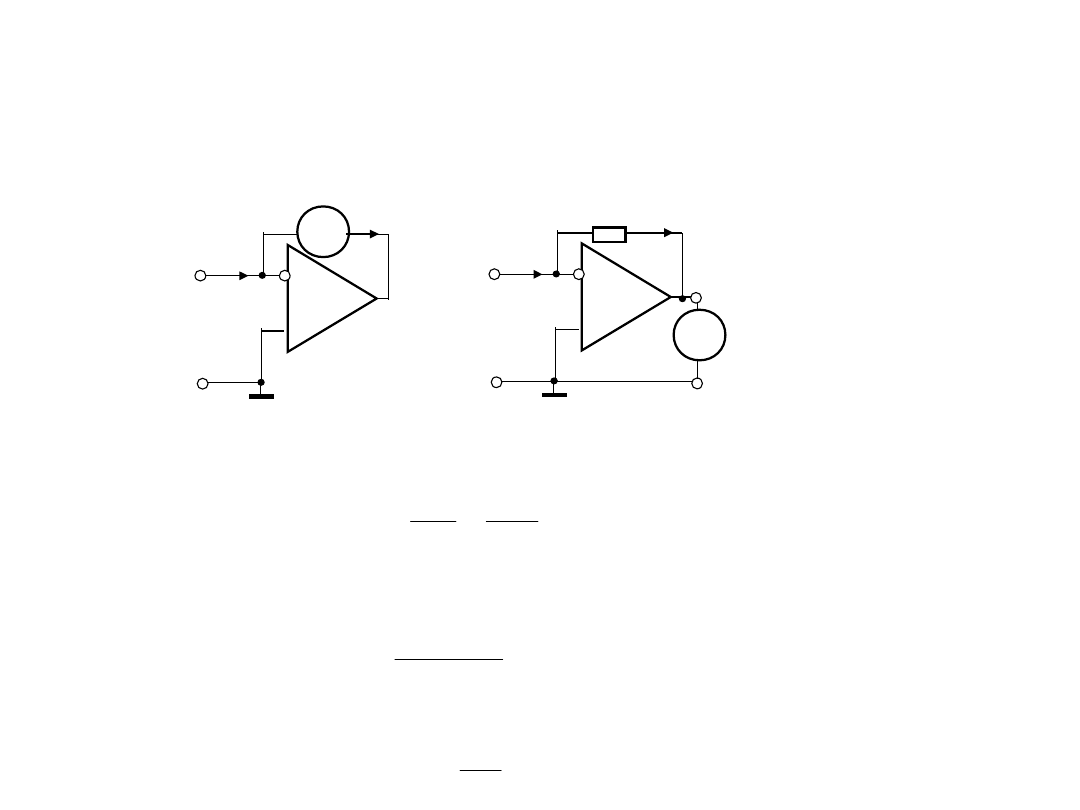
2. Układy wejściowy

amperomierze

2.2. Bazowa konfiguracja układu wejściowego

mikroamperomierze z przetwarzaniem bezpośrednim

Przykład 3

. Jeżeli Ix=1 µA i na wyjściu przetwornika chcemy

otrzymać Uwy=1 V wtedy wartość rezystancji sprężenia
zwrotnego :

Przy wzmocnienie WO A0=10

5

-10

6

wartość rezystancji wejściowej

równa się:

przy tym spadek napięcia na amperomierzu równa się:

I

x

WO

-

+

V

R

F

I

x

U

wy

=-Ix

R

F

LO

HI

I

x

WO

-

+

A

HI

I

A

=I

x

LO

MOhm

A

V

I

U

R

x

wy

F

1

1

1









Ohm

MOhm

R

A

)

10

1

(

10

10

1

6

5











mkV

A

U

I

R

U

wy

x

A

A

)

10

1

(

0











2. Układy wejściowy

amperomierze

2.3. Bazowa konfiguracja układu wejściowego nano – i

pikoamperomierze

Jeżeli zakres pomiaru prądu ma być

1 nA

wtedy wartość

rezystancji sprężenia zwrotnego ma być równą:

a przy zakresie pomiaru prądu 10 pA wartość rezystancji

sprężenia zwrotnego ma być 100 razy większą

Rezystory z takimi wartościami rezystancji nie mogą być

wykorzystywane w precyzyjnych obwodach pomiarowych,
ponieważ te wartości są porównywalne są do wartości
rezystancji izolacji płytek, na których oni są umocowani.

GOhm

nA

V

I

U

R

x

wy

F

1

1

1







GOhm

pA

V

I

U

R

x

wy

F

100

10

1







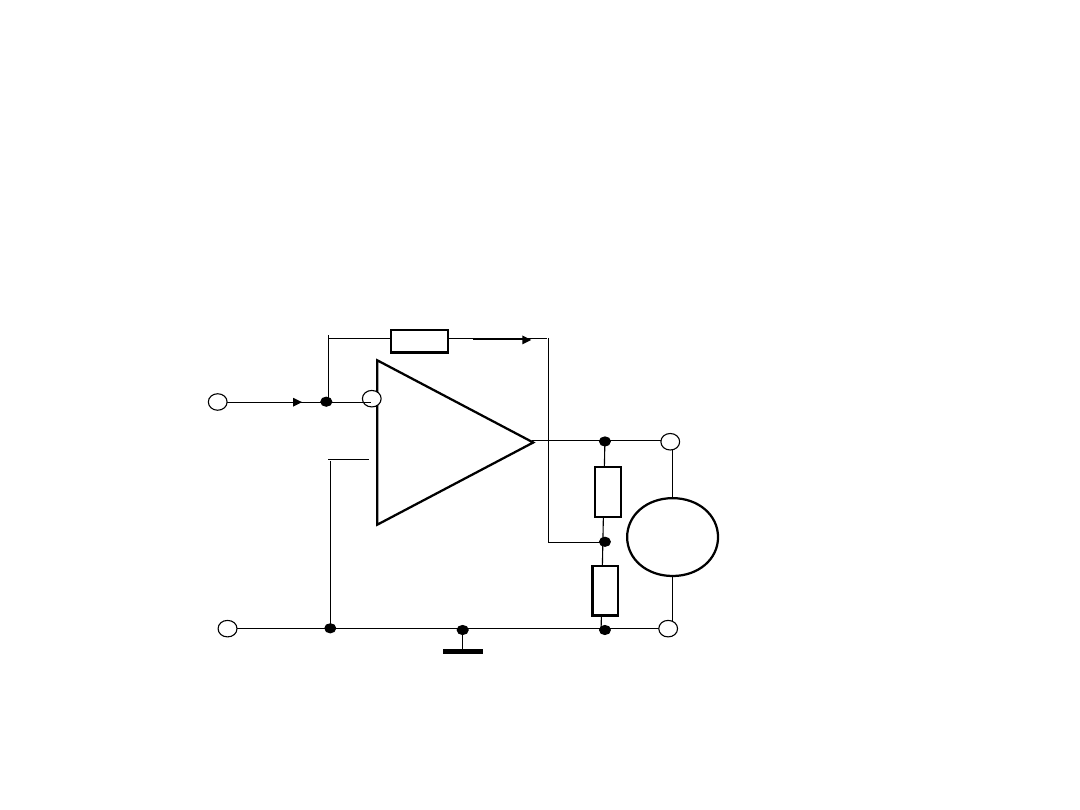
2. Układy wejściowy

amperomierze

2.3. Bazowa konfiguracja układu wejściowego nano – i

pikoamperomierze

Ten problem jest usunięty poprzez wykorzystania właściwości

„wzmacniania” rezystancji obwodu gwiazdowego.

W tym obwodzie odbywa się przetwarzanie prąd-napięcie (R

F

) z

następnym wzmocnieniem napięcia (rezystory R

1

oraz R

2

).

WO

I

x

-

R

F

I

x

U

wy

=-I

x

R

F

K

i

R

1

R

2

V

+

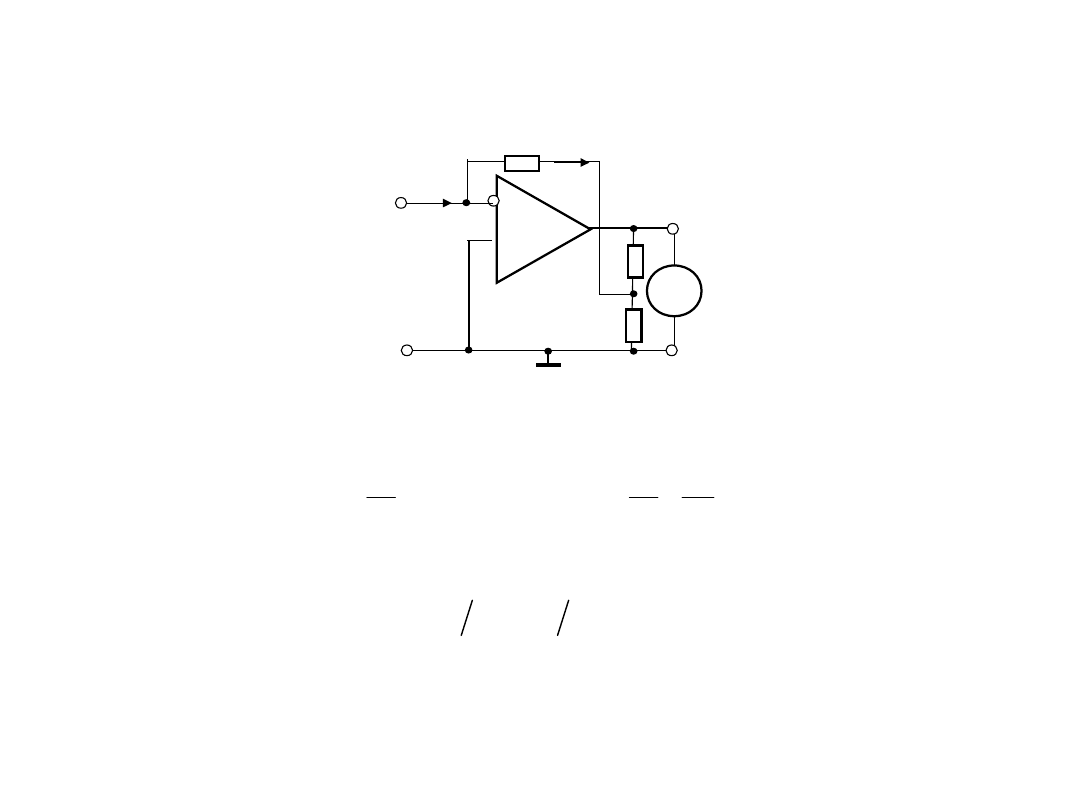
2. Układy wejściowy

amperomierze

2.3. Bazowa konfiguracja układu wejściowego nano – i

pikoamperomierze

W układzie ze wzmocnieniem napięcia wyjściowego (rys.4,b)

napięcie wyjściowe równa się:

Gdzie wzmocnienie prądu wynosi

WO

I

x

-

R

F

I

x

U

wy

=-I

x

R

F

K

wi

R

1

R

2

V

+

I

F

x

F

F

x

F

x

wy

v

K

R

I

R

R

R

R

I

R

R

R

R

I

U

U











































































1

1

1

1

2

1

1

2

1





F

I

R

R

R

K

1

1

1

2

1







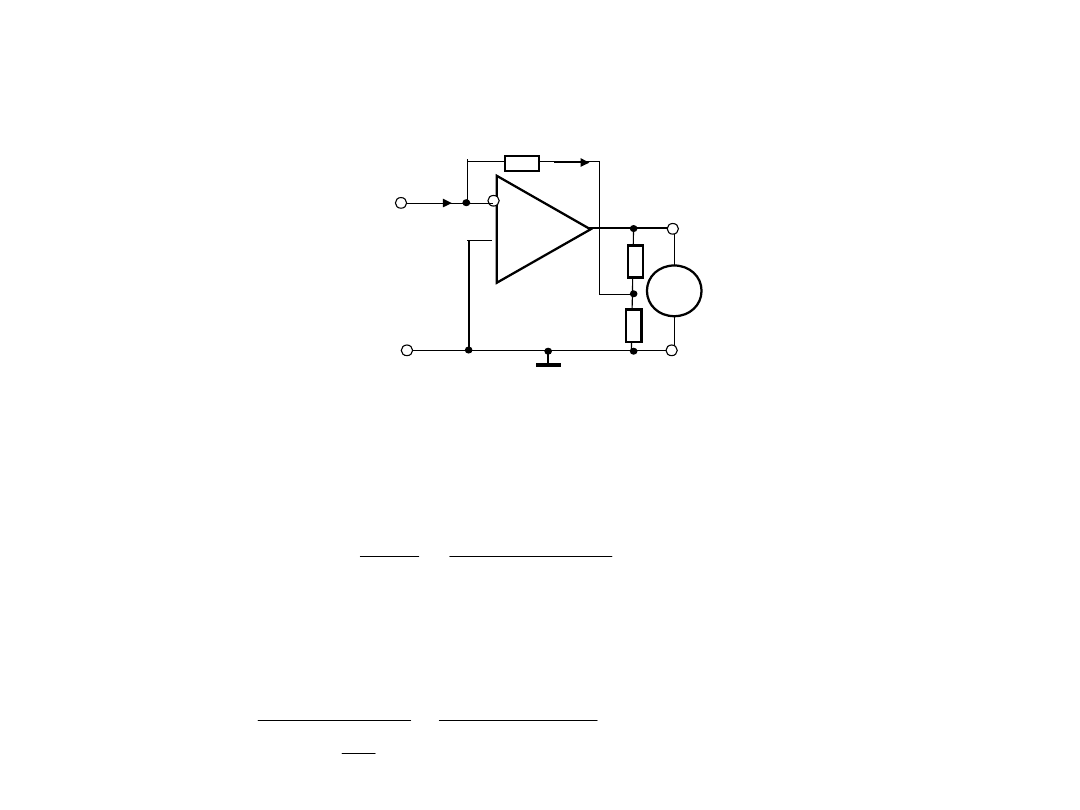
2. Układy wejściowy

amperomierze

2.3. Bazowa konfiguracja układu wejściowego nano – i

pikoamperomierze

Przykład 4a

. Jeżeli

Ix=1 nA

i na wyjściu przetwornika dalej

chcemy otrzymać

Uwy=1 V

przy ograniczonej wartości

rezystancji sprężenia zwrotnego , wtedy wartość
współczynnika wzmocnienia prądu powinna równać się:

Dlatego przy oraz zakładając ograniczoną wartość rezystancji

otrzymuje się wartość rezystancji R2

WO

I

x

-

R

F

I

x

U

wy

=-I

x

R

F

K

wi

R

1

R

2

V

+

1000

1

1

1









MOhm

nA

V

R

I

U

K

F

x

wy

I









kOhm

MOhm

R

R

K

R

R

F

I

F

002

,

1

1

1

1

1000

1

1

1

1

2

















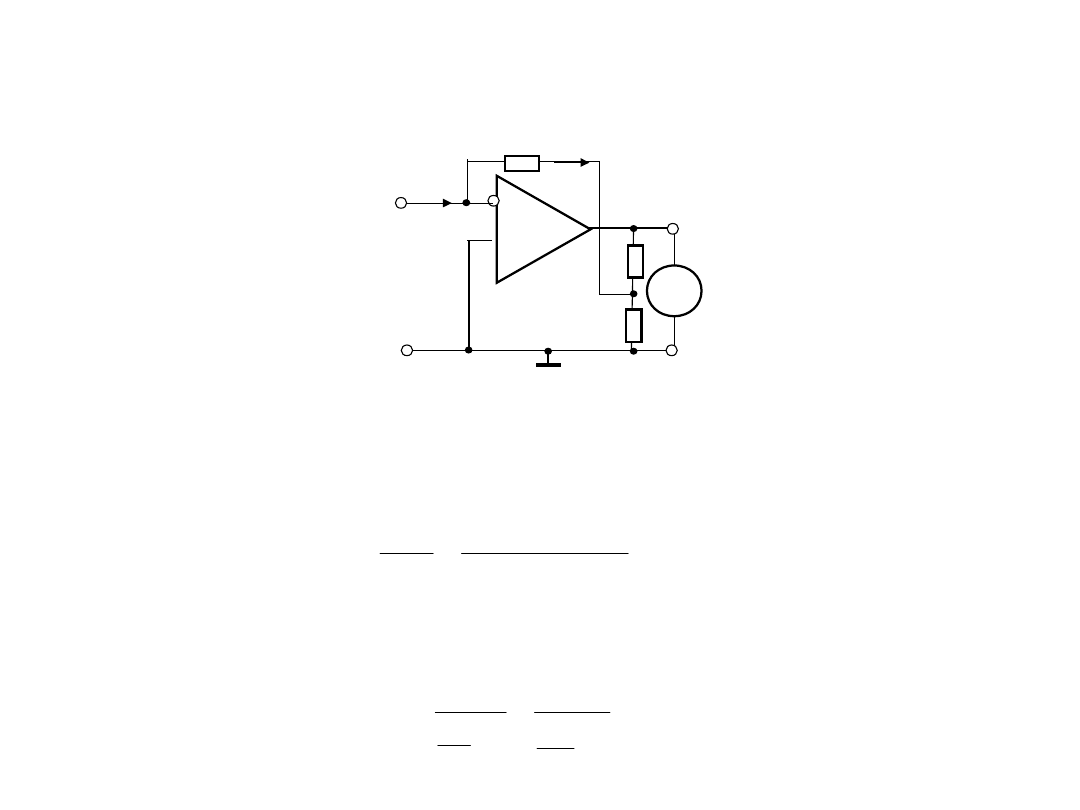
2. Układy wejściowy

amperomierze

2.3. Bazowa konfiguracja układu wejściowego nano – i

pikoamperomierze

Przykład 4b

. Jeżeli

Ix=10 pA

i na wyjściu przetwornika dalej

chcemy otrzymać

Uwy=1 V

przy ograniczonej wartości

rezystancji sprężenia zwrotnego , wtedy wartość
współczynnika wzmocnienia prądu powinna równać się:

Jest to zbyt duża wartość, dlatego ze przy współczynniku

wzmocnienia W0 A

0

=10

6

błąd statyczny będzie równać się:

WO

I

x

-

R

F

I

x

U

wy

=-I

x

R

F

K

wi

R

1

R

2

V

+

100000

1

10

1









MOhm

pA

V

R

I

U

K

F

x

wy

I

%

9

1

10

10

1

1

1

5

6

0

0











I

A

K

A



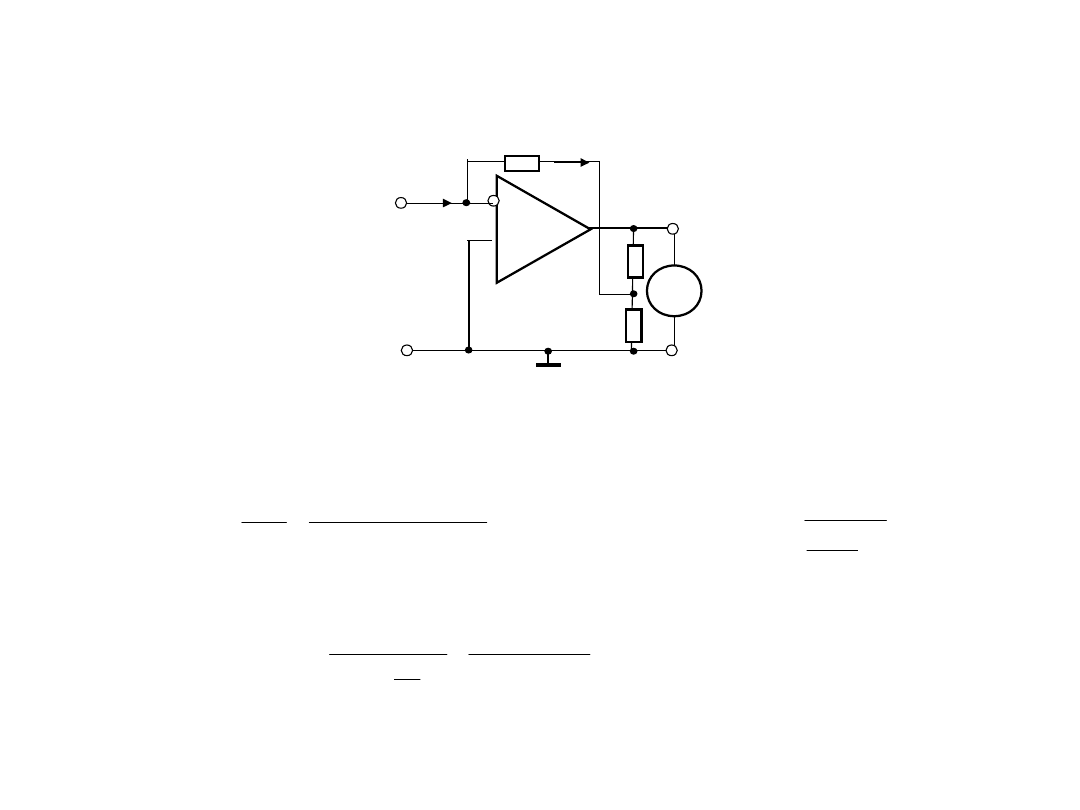
2. Układy wejściowy

amperomierze

2.3. Bazowa konfiguracja układu wejściowego nano – i

pikoamperomierze

Przykład 4b

.

Ix=10 pA

i

Uwy=1 V

:

Dlatego należy zwiększyć wartość rezystancji

R

1

=R

F

=33,333

MOhm

, wtedy wartość współczynnika wzmocnienia prądu

powinna równać się

i wartość rezystancji R2 będzie równać się:

WO

I

x

-

R

F

I

x

U

wy

=-I

x

R

F

K

wi

R

1

R

2

V

+

3000

33

,

33

10

1









MOhm

pA

V

R

I

U

K

F

x

wy

I

%

3

,

0

1

10

3

10

1

3

6

0









A











kOhm

MOhm

R

R

K

R

R

F

I

F

1185

,

11

1

1

1

3000

33

,

33

1

1

1

2

















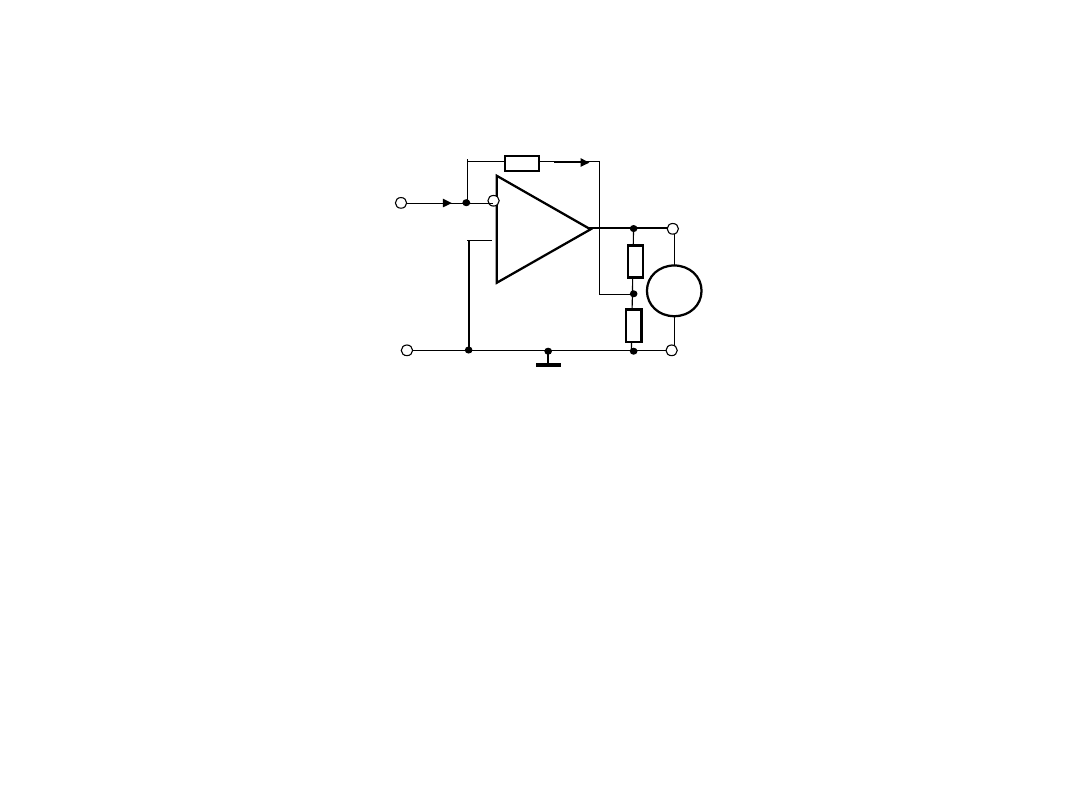
2. Układy wejściowy

amperomierze

2.3. Bazowa konfiguracja układu wejściowego nano – i

pikoamperomierze

Przykład 4b

.

Ix=10 pA

i

Uwy=1 V

:

Są to bardzo dobre wyniki, ponieważ przy ograniczonych

wartościach rezystancji do (1-33) MOhm (zamiast
100 GOhm) otrzymuje się na wyjściu napięcie 1 V przy
prądzie 10 pA.

WO

I

x

-

R

F

I

x

U

wy

=-I

x

R

F

K

wi

R

1

R

2

V

+

2. Układy wejściowy

amperomierze

2.4.

Podstawowym problemem układów nano- i pikoamperomierzy

jest wpływ wejściowego prądu wzmacniacza operacyjnego

(Iwe), który zniekształca prąd mierzony bezpośrednio,

ponieważ prąd przez rezystancję RF równa się sumie prądu

mierzonego Ix oraz prządu wej ościowego WO Iwe:

I

F

=I

x

+I

we

.

Stąd napięcie na wyjściu układu

U

wy

=I

F

·R

F

=(I

x

+I

we

)·R

F

Względny błąd przetwarzania równa się

Dlatego wymagany jest WO o niskim poziomie prądów wejściowych

niezrównoważenia oraz zabezpieczenia przeciw oddziaływań

innych prądów upływu przez rezystancje izolacji płytki

montażowej.

U

wy

WO

-

+

R

F

I

F

=I

x

+I

we

I

x

I

we

x

we

Iwe

I

I





Pomiary małych i

dużych rezystancji

Cel: Zapoznać się z podstawowymi schematami

układów elektronicznych omomierze.

Plan:
1. Wstęp. Problemy przetwarzania

rezystancji w napięcie

2. Pomiary małych rezystancji
3. Pomiary dużych rezystancji

1. Wstęp. Problemy pomiaru małych

rezystancji

Rozróżnia się układy do pomiaru małych, średnich

oraz dużych rezystancji (impedancji).

Przy pomiarach małych rezystancji (poniżej ok.

10 ...100 ) na wynik pomiaru wpływają

rezystancji przewodów (rys. 1,a). Im mniejsza

rezystancja pomiarowa tym większy wpływ

rezystancji przewodów.

Przy pomiarach dużych rezystancji (powyżej ok.

10 M...100 M) na wynik pomiaru wpływają

rezystancji wejściowe przetwornika, izolacja, prądy

upływów i t.p. (rys. 1,b).

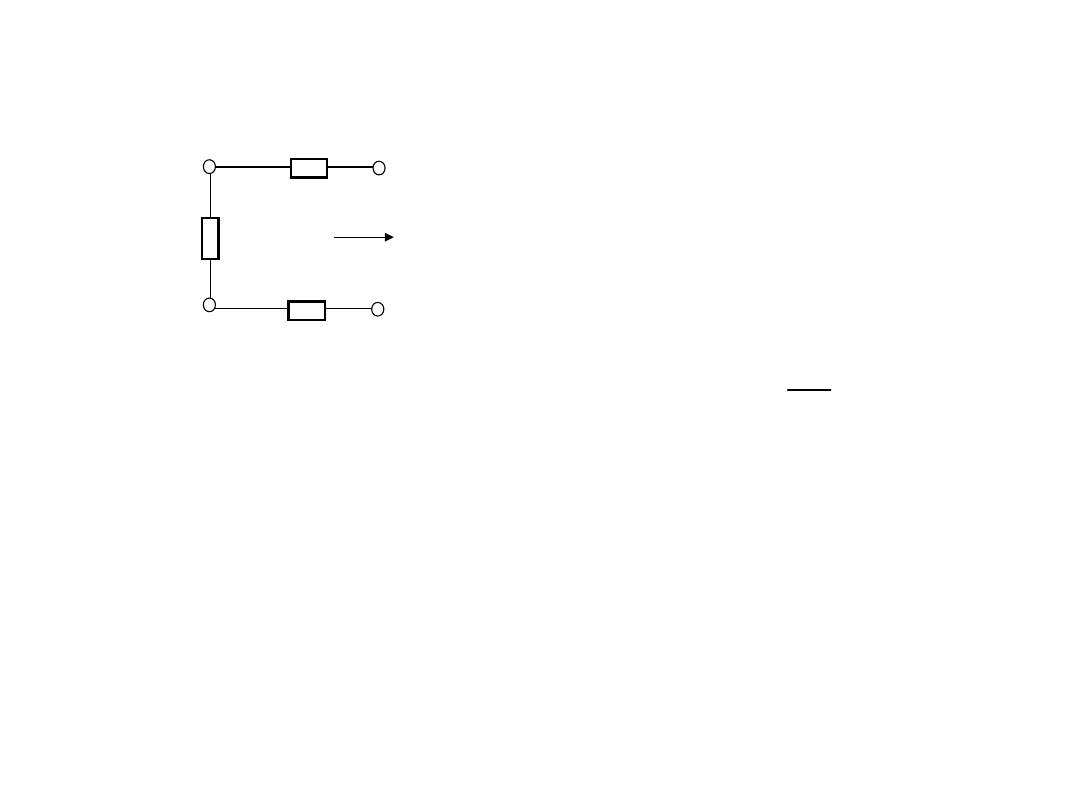
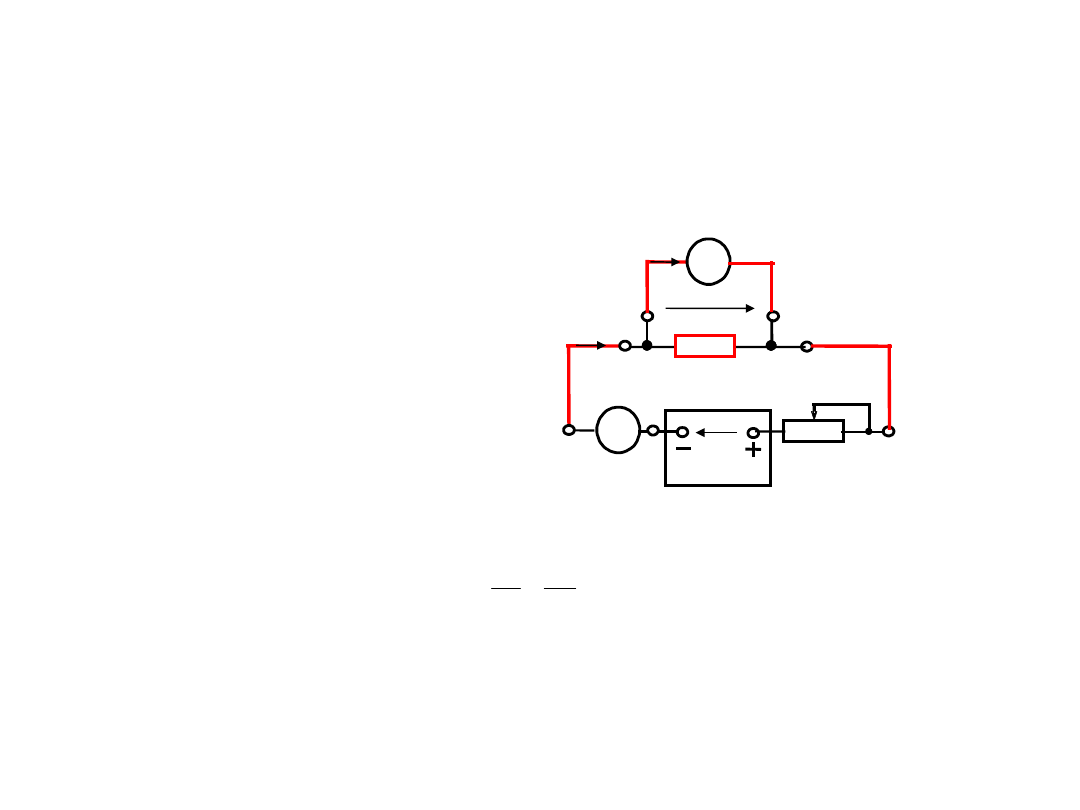
2. Do wpływu rezystancji przewodów linii

• Wpływ rezystancji przewodów

• Dla wartości średnich (od ok. 1 k do ok.

10 M) wpływ przewodów z rezystancją ok.

R

l

=0,1  jest mniejszy od 0,01%

R

x

Do miernika

rezystancji

R

l

R

l

x

l

Rl

R

R

2





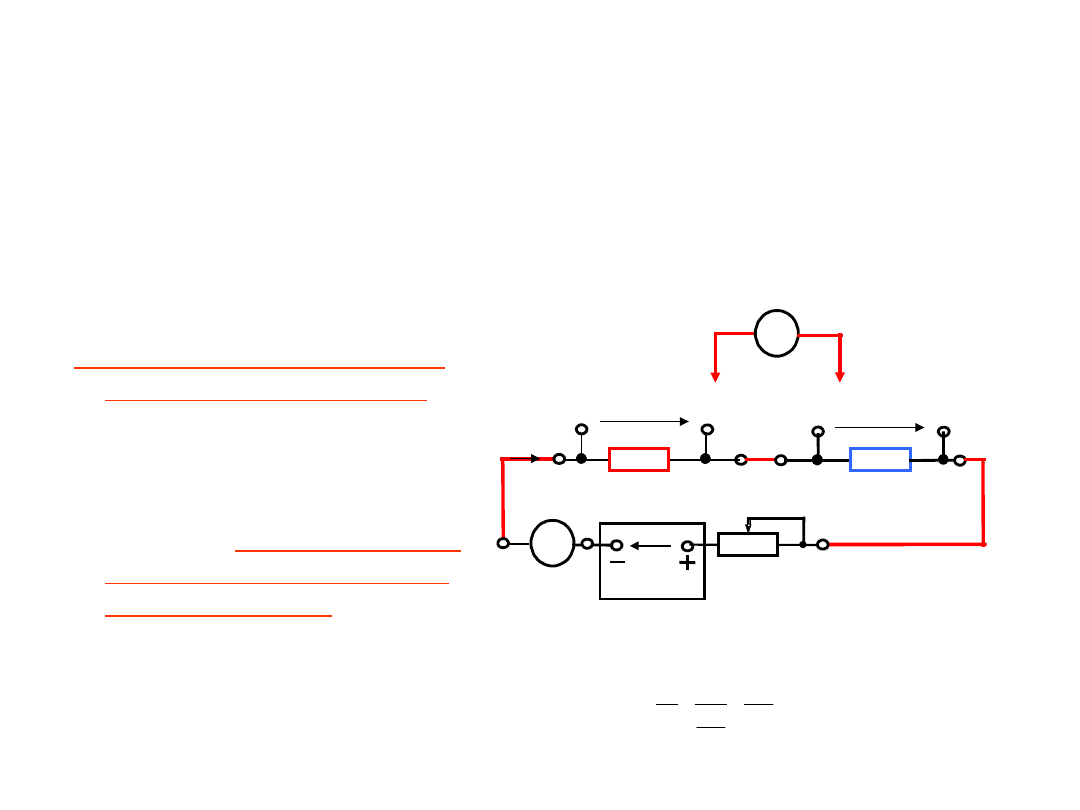
3. Do pomiaru małych rezystancji

4- przewodowe podłączenie

badanego rezystora do
układu pomiarowego:

Rozdzielone obwody:
prądowy (wymuszenie) i

napięciowy (pomiar)

Zas.

R

X

A

R

reg

R

L1

U

0

I

x

V

U

x

I

V

<<I

x

R

L2

R

L3

R

L4

I

V

Jeśli R

V

>> R

x

wtedy I

V

<< R

x

i I

A

= I

x

stąd

praktycznie U

V

=U

x

=I

x

×R

x

A

V

x

x

x

I

U

I

U

R





3. Do pomiaru małych rezystancji

4- przewodowe podłączenie

badanego rezystora do
układu pomiarowego:

Rozdzielone obwody

:

prądowy (wymuszenie) i

napięciowy (pomiar).

Zwiększenie dokładności

:

Pośredni pomiar prądu

poprzez pomiar spadku
napięcia na rezystorze
wzorcowym Rn

Zas.

R

x

A

R

reg

R

L1

U

0

I

x

R

L3

R

L4

U

x

R

L2

R

n

V

U

n

R

L2

1 pomiar

2 pomiar

1 pomiar

: U

V1

=I

x

×R

x

;

2 pomiar

: U

V2

=I

x

×R

n

Wynik

n

V

V

n

V

V

x

x

x

R

U

U

R

U

U

I

U

R

2

1

2

1







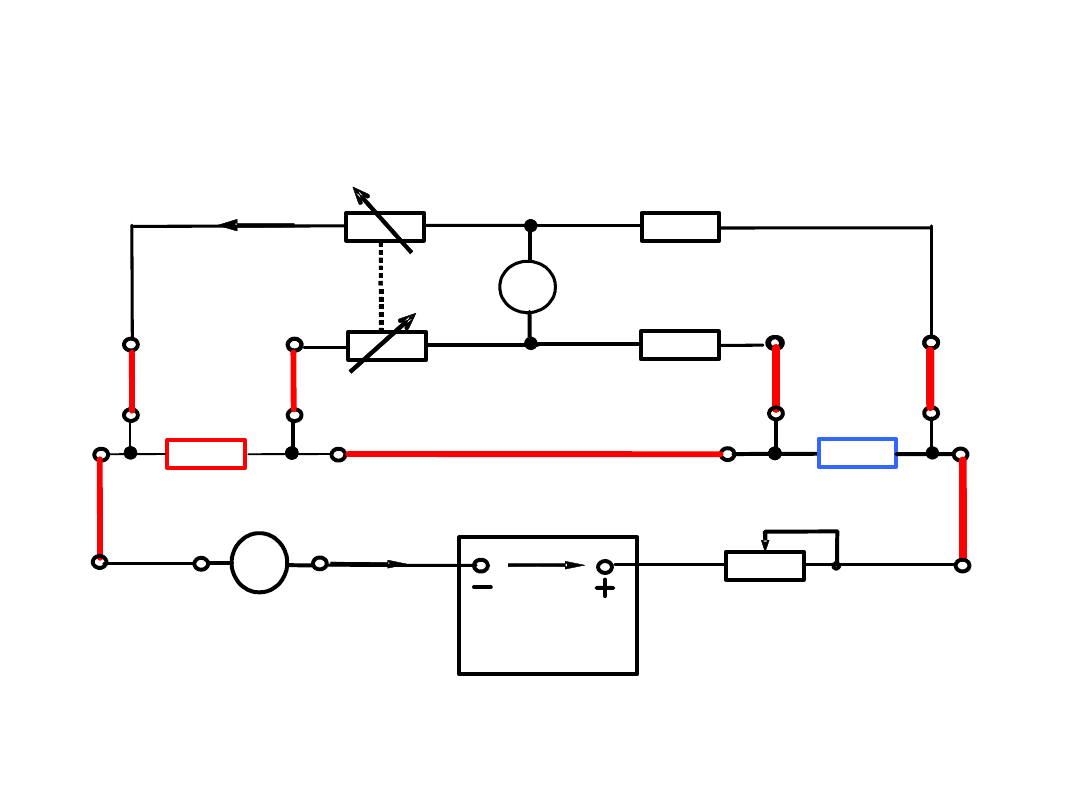
4. Do pomiaru małych rezystancji

Mostek Thomsona

Zas.

r

3

r

r

4

r

1

r

2

R

N

R

B

R

A

R

X

A

R

reg

r

5

R`

zr

R

zr

G

U

0

I

a

c

b

r

6

I

G

=0

g

I

M

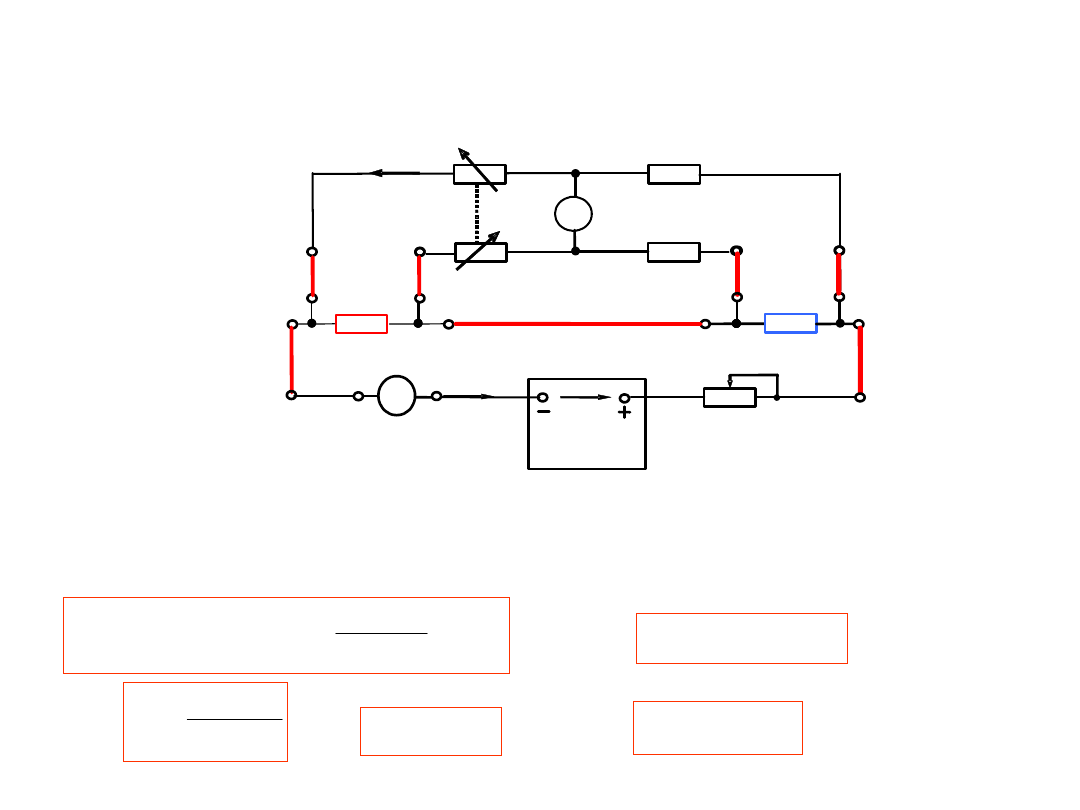
4.

Do pomiaru małych rezystancji:

Mostek

Thomsona

Warunkiem zrównoważenia mostka (przy bardzo małej

rezystancji (r=0) przewodu pomiędzy punktami a-c) – prąd
przez galwanometr równa się zeru (Ig=0) jest równanie

0

















zr

A

zr

N

x

X

zr

M

x

g

R

R

R

U

U

U

R

I

U

U

zr

N

B

x

R

U

R

U





A

zr

N

x

M

R

R

U

U

I







x

x

R

I

U





N

N

R

I

U





Zas.

r

3

r

r

4

r

1

r

2

R

N

R

B

R

A

R

X

A

R

reg

r

5

R`

zr

R

zr

G

U

0

I

a

c

b

r

6

I

G

=0

g

I

M

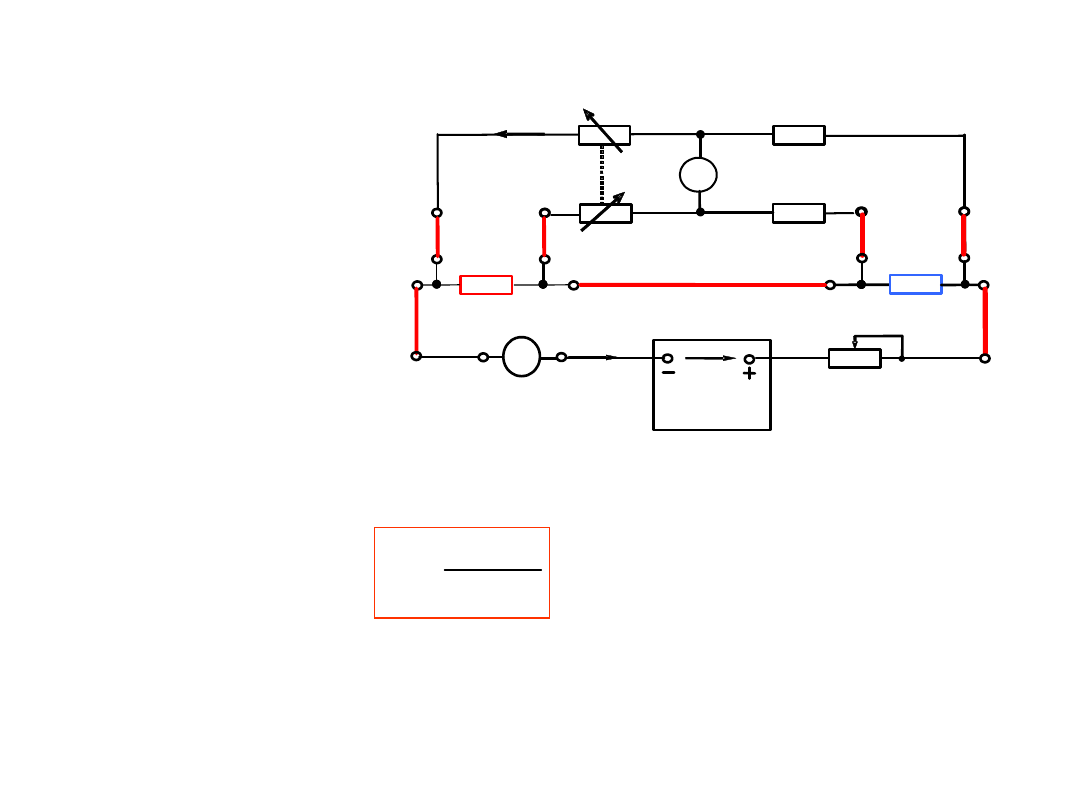
4.

Do pomiaru małych rezystancji:

Mostek

Thomsona

Warunkiem zrównoważenia mostka – równanie pomiaru

A

zr

N

x

R

R

R

R





Zas.

r

3

r

r

4

r

1

r

2

R

N

R

B

R

A

R

X

A

R

reg

r

5

R`

zr

R

zr

G

U

0

I

a

c

b

r

6

I

G

=0

g

I

M

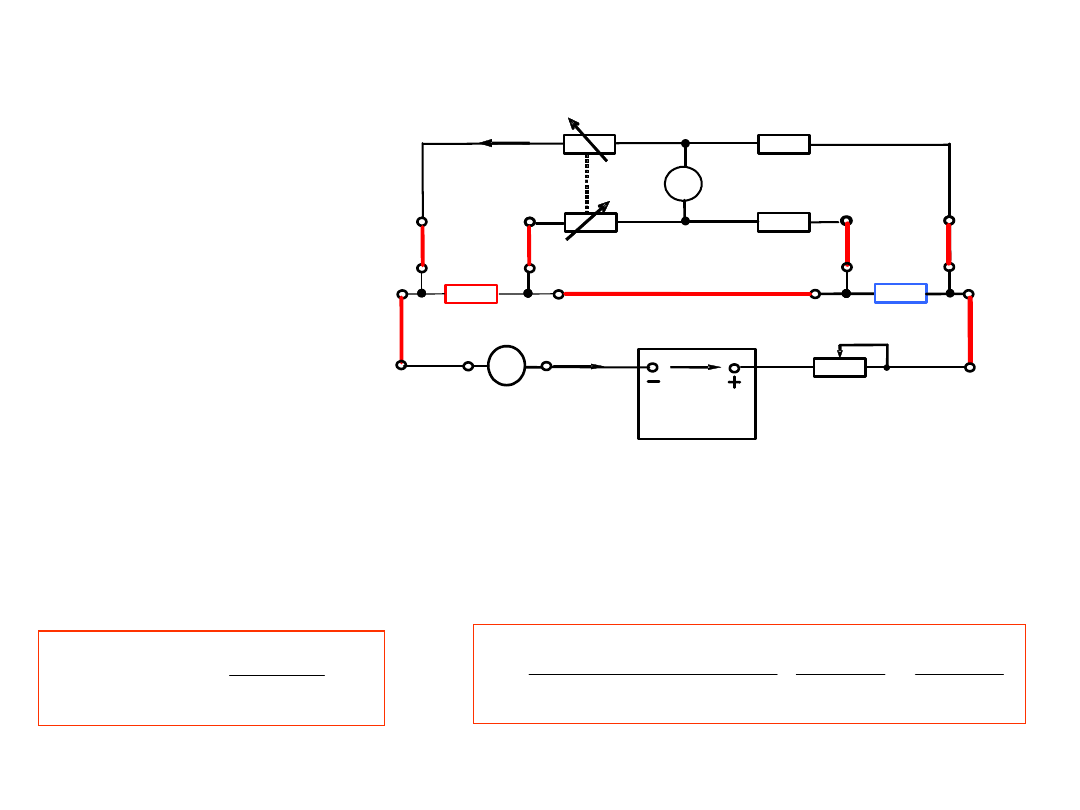
Do pomiaru małych rezystancji

:

Mostek

Thomsona

Start 5.12.2011

Na ogół przy pomiarach bardzo małych wartości rezystancji

należy uwzględniać

niezerowe wartości rezystancji

przewodów

, którymi podłącza się rezystor mierzony

R

x

,

wzorcowy

R

N

oraz elementy mostka. Wtedy równanie mostka

ma postać:

d

r

R

R

r

R

R

B

N

zr

x









2

1

)

(







































4

3

2

1

4

3

/

4

)

(

r

R

r

R

r

R

r

R

r

r

r

R

R

r

r

R

d

А

z

B

zr

zr

A

A

Zas.

r

3

r

r

4

r

1

r

2

R

N

R

B

R

A

R

X

A

R

reg

r

5

R`

zr

R

zr

G

U

0

I

a

c

b

r

6

I

G

=0

g

I

M

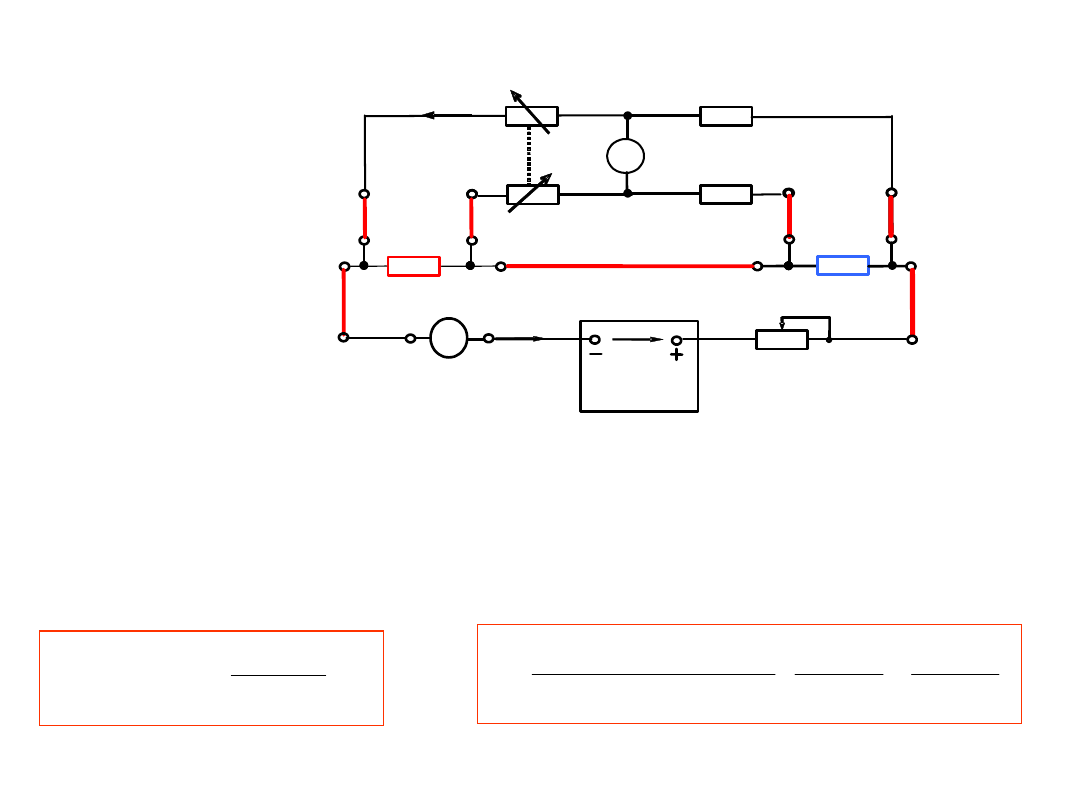
Do pomiaru małych rezystancji:

Mostek

Thomsona

Na ogół przy pomiarach bardzo małych wartości rezystancji

należy uwzględniać

niezerowe wartości rezystancji

przewodów

, którymi podłącza się rezystor mierzony

R

x

,

wzorcowy

R

N

oraz elementy mostka. Wtedy równanie mostka

ma postać:

d

r

R

R

r

R

R

A

N

zr

x









2

1

)

(







































4

3

2

1

4

3

/

4

)

(

r

R

r

R

r

R

r

R

r

r

r

R

R

r

r

R

d

B

z

A

zr

zr

B

B

Zas.

r

3

r

r

4

r

1

r

2

R

N

R

B

R

A

R

X

A

R

reg

r

5

R`

zr

R

zr

G

U

0

I

a

c

b

r

6

I

G

=0

g

I

M

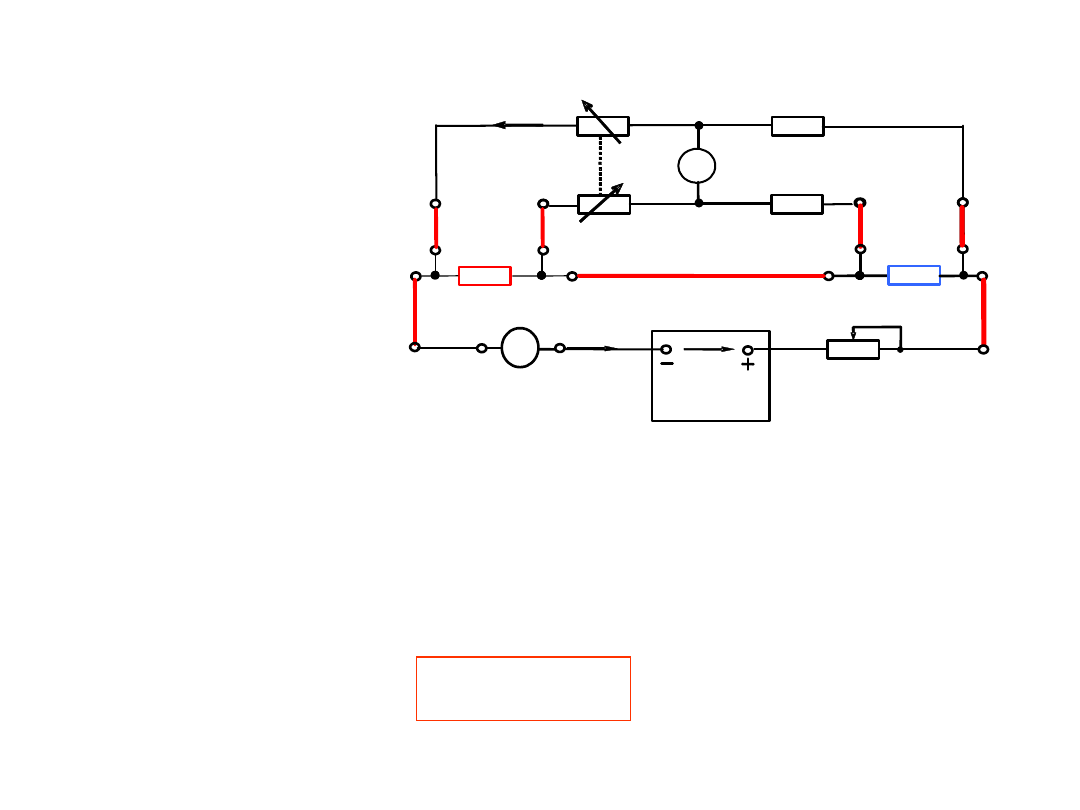
Do pomiaru małych rezystancji:

Mostek

Thomsona

Zwykle rezystancja rezystora wzorcowego

R

N

=10

k

,

gdzie

k

jest liczbą całkowitą ujemną lub dodatnią,

oraz rezystancja rezystora też krotna 10:

R

A

=10

m

,

gdzie

m

jest liczbą dodatnią (R

A

=10; 100; 1000;

10000Ω), dlatego stosunek

R

N

/R

A

=10

n

– jest krotny

10 (n liczba całkowita) i uproszczony wzór na

wartość rezystancji mierzonej ma postać:

Zas.

r

3

r

r

4

r

1

r

2

R

N

R

B

R

A

R

X

A

R

reg

r

5

R`

zr

R

zr

G

U

0

I

a

c

b

r

6

I

G

=0

g

I

M

zr

n

x

R

R



10

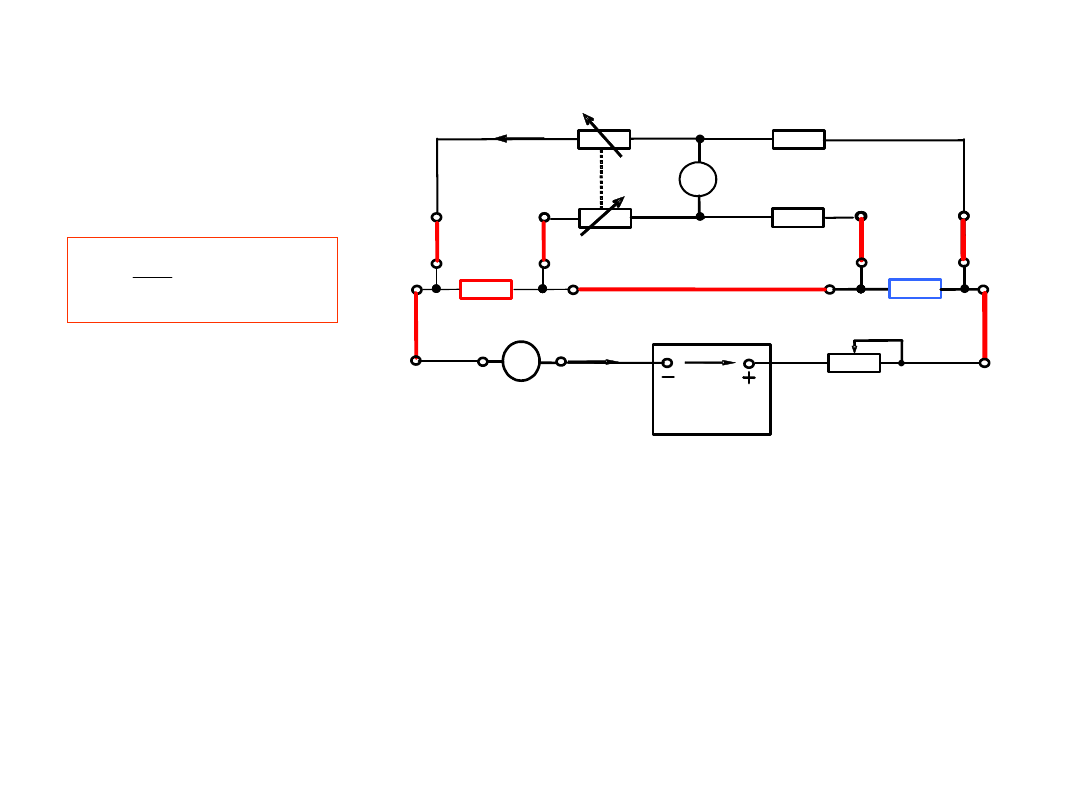
Do pomiaru małych rezystancji:

Mostek

Thomsona

Mostki Thomsona wykorzystują się do pomiaru

małych wartości

rezystancji: w zakresie od

10

-8

do

10

2

Ω

, jest to możliwie dzięki

małym wartościom rezystancji R

N

od

10

-5

…do

10 Ω

.

Zas.

r

3

r

r

4

r

1

r

2

R

N

R

B

R

A

R

X

A

R

reg

r

5

R`

zr

R

zr

G

U

0

I

a

c

b

r

6

I

G

=0

g

I

M

zr

n

zr

A

N

x

R

R

R

R

R







10

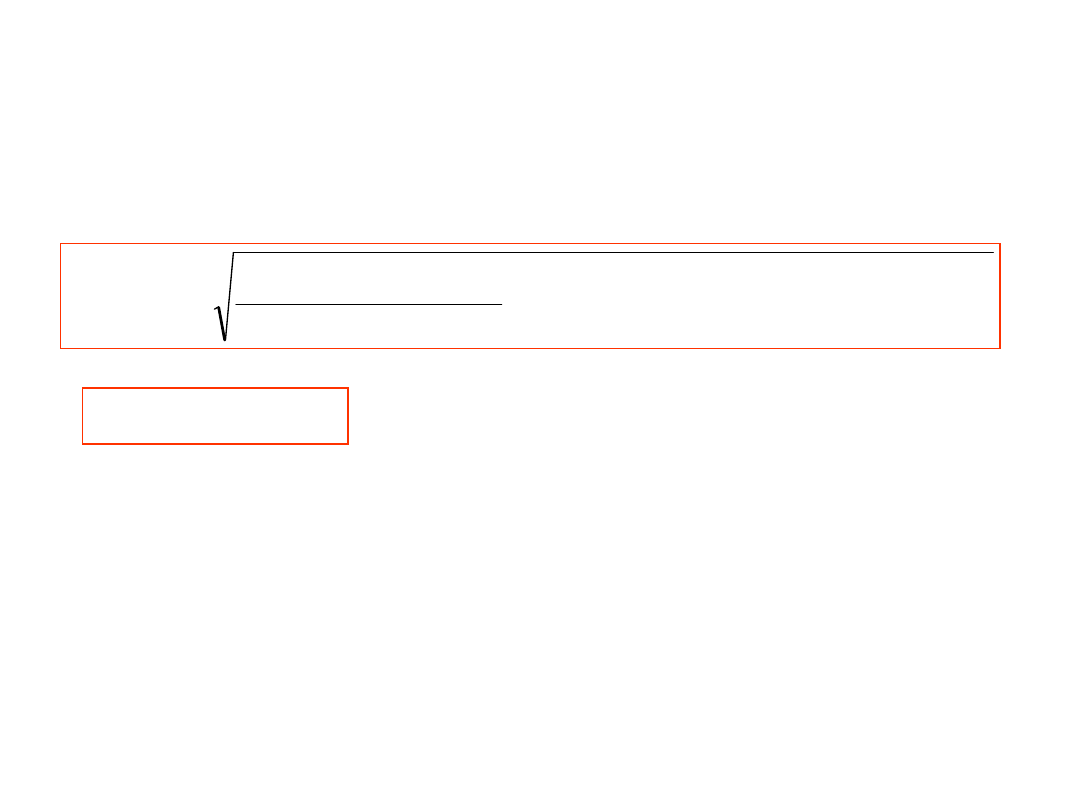
5. Niepewność wyniku pomiaru

mostkiem Thomsona

Względna złożona niepewność standardowa wyniku pomiaru

rezystancji, obliczona metodą typu B:

-

względne graniczne (dopuszczalne)

odchylenia odpowiednich rezystancji mostka od wartości
nominalnych

;

 

(d)

u

)

(R

u

)

(R

u

3

2

rel

B,

nc

x,

2

rel

B,

kw

zr,

2

rel

B,

2

2

2













gr

,

R

gr

,

R

gr

,

R

x

rel

,

B

N

A

zr

R

u







gr

,

R

gr

,

R

gr

,

R

N

A

zr

;

;







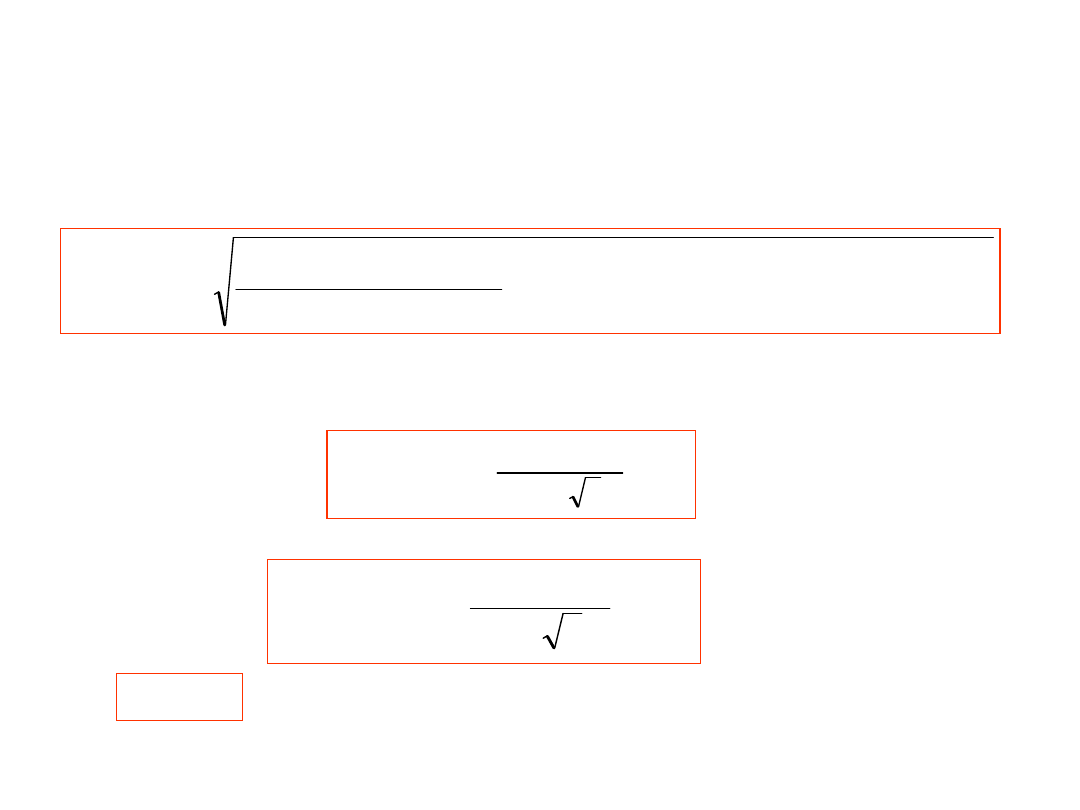
5. Niepewność wyniku pomiaru

mostkiem Thomsona

Względna złożona niepewność standardowa wyniku pomiaru

rezystancji, obliczona metodą typu B:

Względna niepewność od kwantowania

(dyskretności)

rezystancji zrównoważenia R

zr

oblicza się z wzoru

Względna niepewność od nieczułości

oblicza się z wzoru

gdzie

- zmiana rezystancji zrównoważenia wywołująca

odchylenie wskaźnika galwanometru o 0,1 podzialki

 

(d)

u

)

(R

u

)

(R

u

3

2

rel

B,

nc

x,

2

rel

B,

kw

zr,

2

rel

B,

2

2

2













gr

,

R

gr

,

R

gr

,

R

x

rel

,

B

N

A

zr

R

u







%

100

3

)

(

)

(R

u

1

,

0

nc

x,

rel

cB,

zr

dz

zr

R

R





%

100

3

5

,

0

)

(R

u

,

kw

zr,

rel

B,









zr

kw

zr

R

R

dz

zr

R

1

,

0

)

(

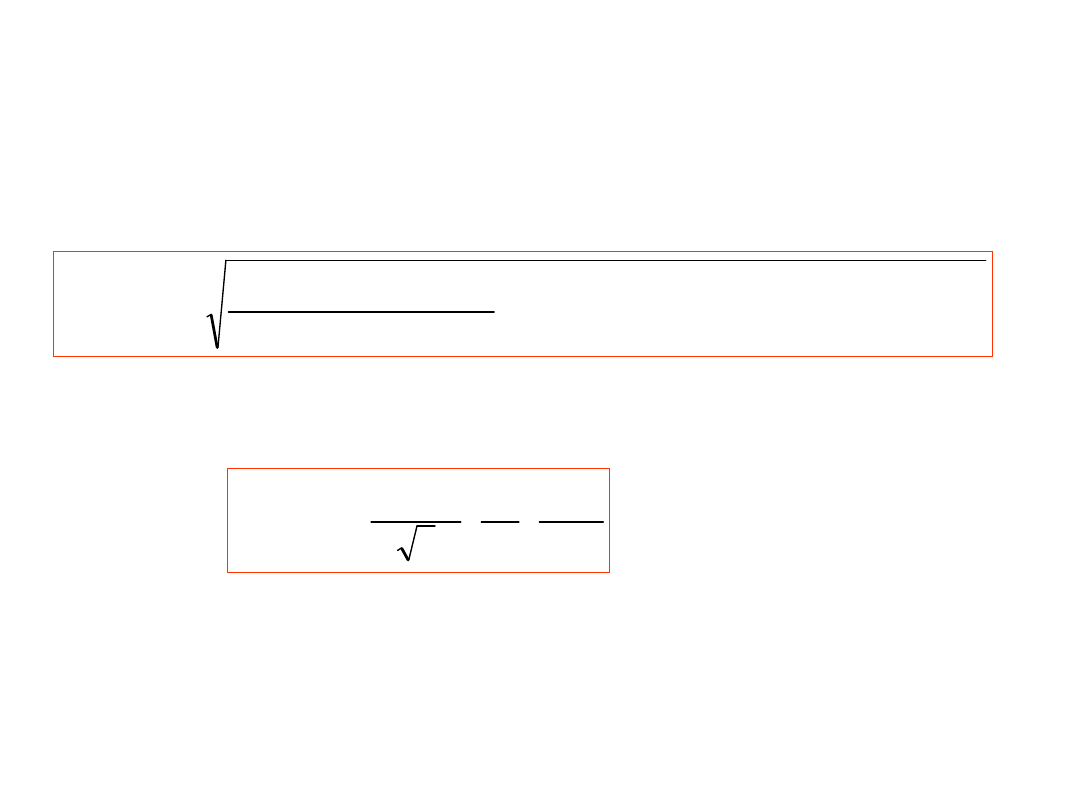
5. Niepewność wyniku pomiaru

mostkiem Thomsona

Względna złożona niepewność standardowa wyniku pomiaru

rezystancji, obliczona metodą typu B:

Względna niepewność od członu

d

(niezerowej wartości rezystancji

r≠0

)

k=R

x

/R

N

 

(d)

u

)

(R

u

)

(R

u

3

2

rel

B,

nc

x,

2

rel

B,

kw

zr,

2

rel

B,

2

2

2













gr

,

R

gr

,

R

gr

,

R

x

rel

,

B

N

A

zr

R

u







 

k

k

R

r

d

u

x

R

rel

,

B

gr

.

zr









1

3

4



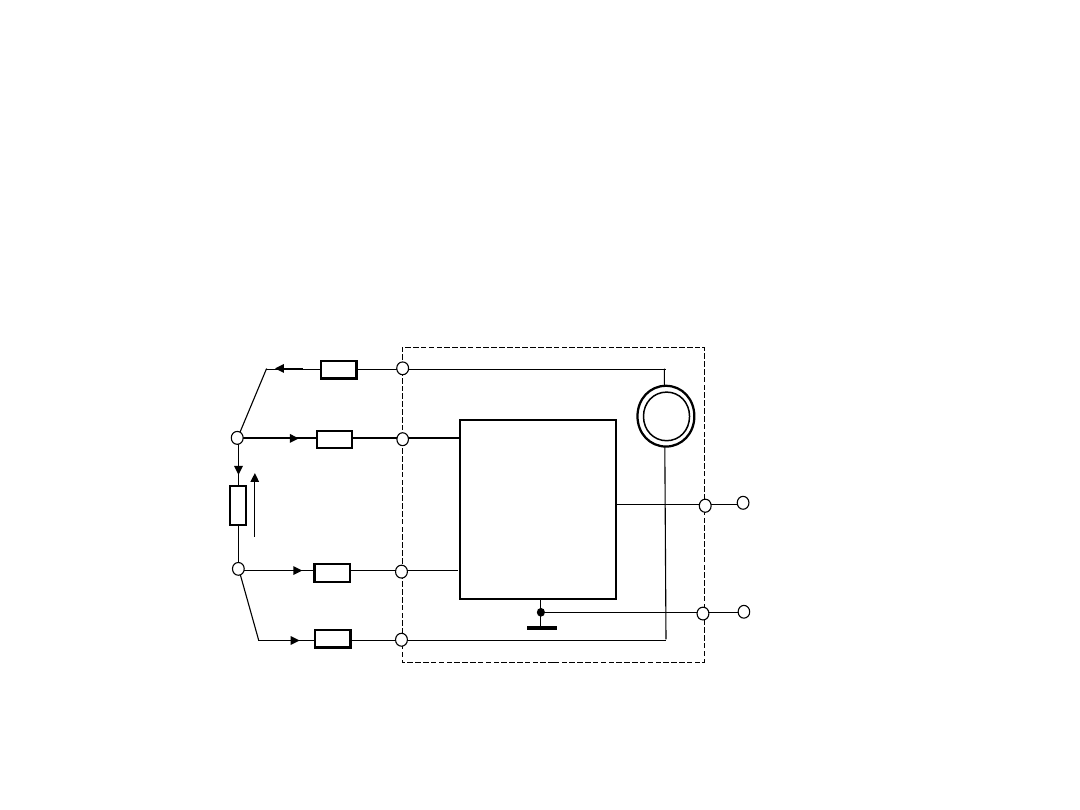
6. Omomierz z 4-przewodowym

podłączeniem rezystora badanego.

- Przetwornik rezystancji ze źródłem prądowym oraz

wzmacniaczem instrumentalnym.

Podstawowy problem polega na eliminacji wpływu rezystancji

przewodów linii. W tym celu wykorzystuje się połączenia

czteroprzewodowe (rys.2).

Do schematu przetwarzania małej wartości rezystancji

Wzmacniacz

instrumentaln

y

K

WI

R

l2

R

l3

R

l1

R

l4

U

wy

=

=K

wi

 I

0



R

x

I

0

WE

WY

1

2

3

4

R

x

U

x

I

0

I

0

I

0

I

we2

=

0

I

we3

=

0

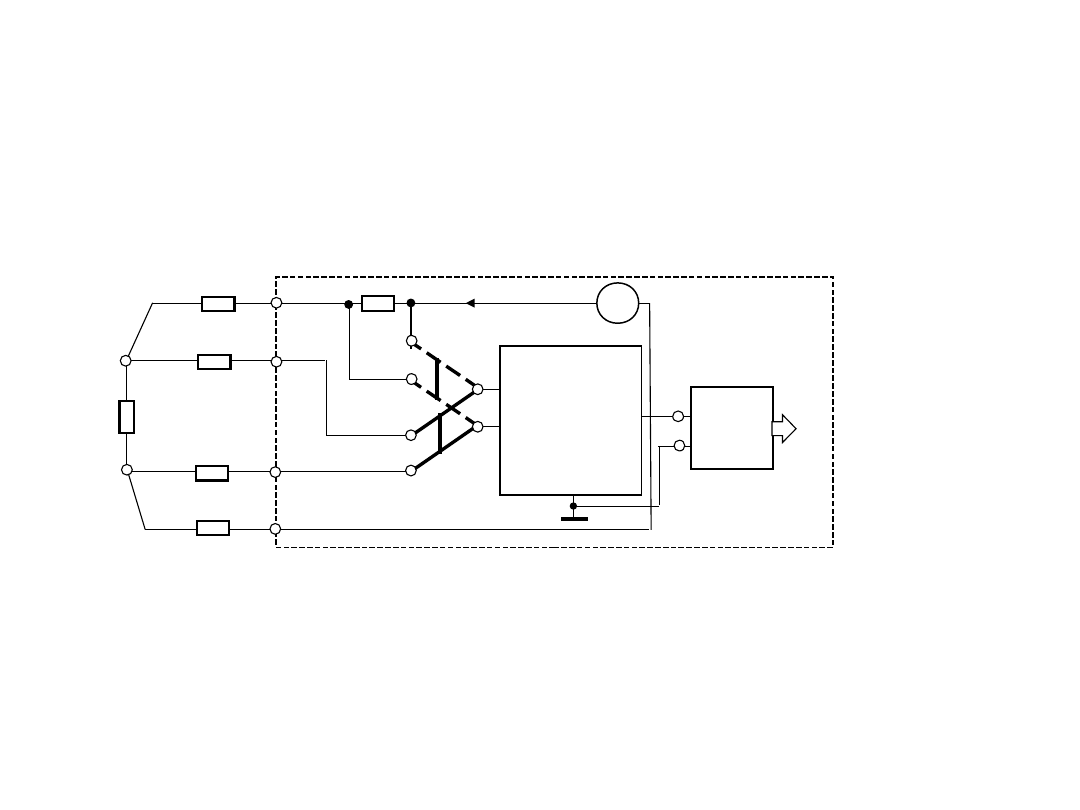
7. Omomierz z 4-przewodowym podłączeniem

rezystora badanego (

ze źródłem napięciowym oraz

rezystorem referencyjnym i wzmacniaczem

instrumentalnym

).

Eliminacja wpływu rezystancji przewodów linii bazuje na pomiarze

prądu wymuszającego, poprzez pomiar spadku napięcia na

rezystorze referencyjnym

Schemat pomiaru małej wartości rezystancji w układzie ze źródłem

napięciowym oraz rezystorem referencyjnym i wzmacniaczem

instrumentalnym

R

x

Wzmacniacz

instrumental

ny

K

WI

R

l2

R

l3

R

l1

R

l4

N

x

=I

pom



R

x

K

wi

k

ADC

WE

WY

1

2

3
3

4

U

0

I

pom

R

ref

U

Rref

U

x

1

2

ADC

k

ADC

N

ref

=I

pom



R

ref

K

wi

k

ADC

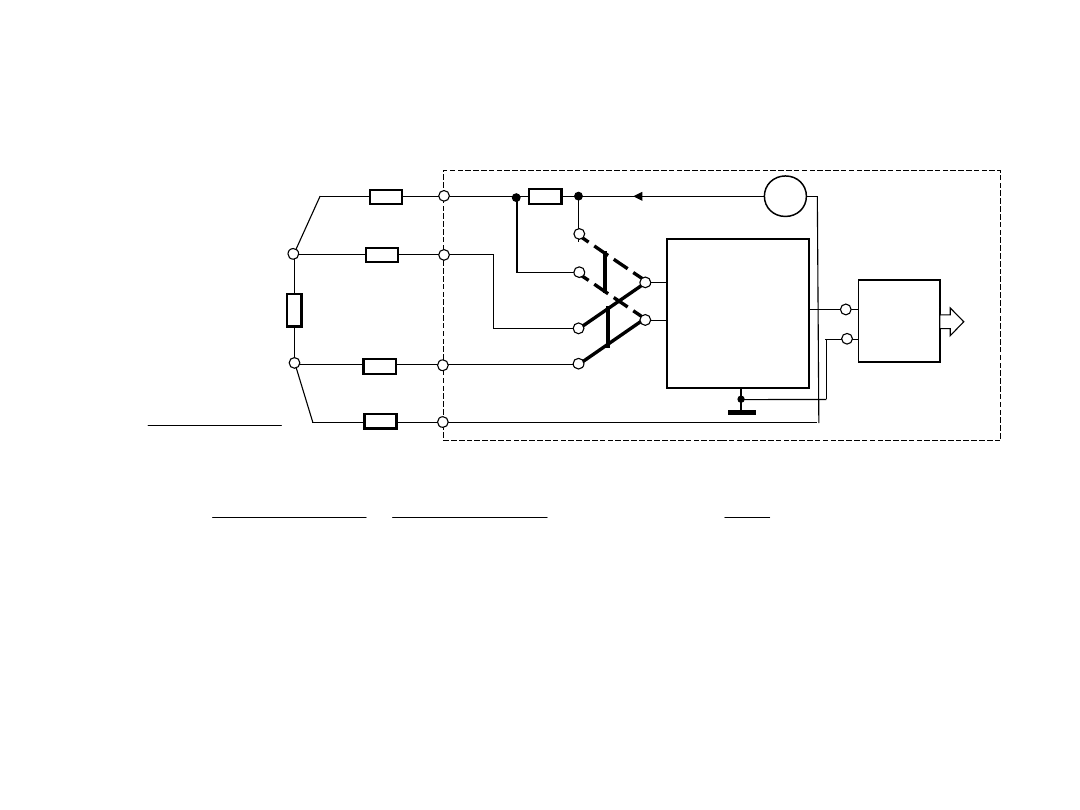
7. Omomierz z 4-przewodowym

podłączeniem rezystora badanego (

ze

źródłem napięciowym oraz rezystorem

referencyjnym i wzmacniaczem

instrumentalnym

).

Otóż wynik pomiaru jest niezależny od wartości napięcia

zasilającego (prądu wymuszającego) oraz rezystancji

przewodów linii. Wymagano jest tylko krótko czasowa stabilność

wszystkich parametrów układu pomiarowego.

R

x

Wzmacniacz

instrumental

ny

K

WI

R

l2

R

l3

R

l1

R

l4

N

x

=I

pom



R

x

K

wi

k

ADC

WE

WY

1

2

3
3

4

U

0

I

pom

R

ref

U

Rref

U

x

1

2

ADC

k

ADC

N

ref

=I

pom



R

ref

K

wi

k

ADC

ADC

wi

ref

ref

pom

k

K

R

N

I



ref

ref

x

ADC

WI

ref

ADC

WI

ref

x

ADC

WI

pom

x

x

R

N

N

k

K

R

k

K

N

N

k

K

I

N

R



















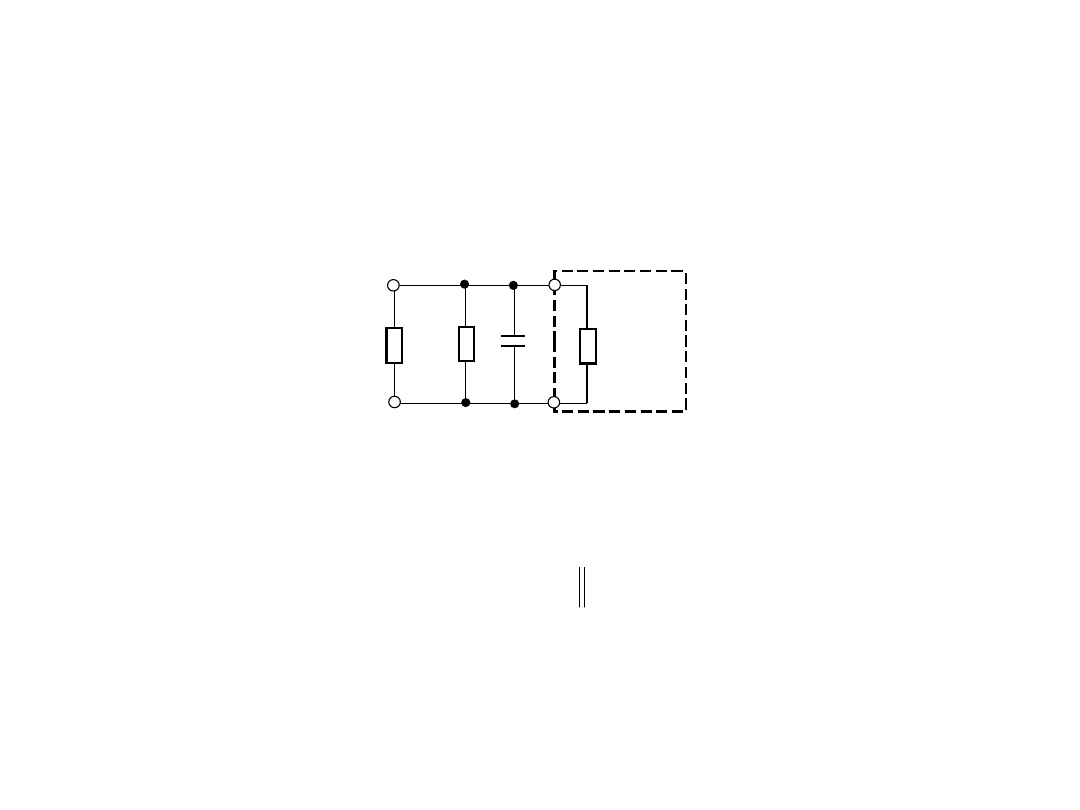
8. Pomiary dużych rezystancji

Problem pomiarów (przetworników) dużych rezystancji

polega we wpływie rezystancji izolacji R

k

i pojemności

C

k

kabla oraz wzmacniacze operacyjnych.

Te parametry bocznikują rezystancją mierzoną, wskutek

czego wynik pomiaru równa się rezystancji

równoległego połączenia mierzonego i kabla

Pojemność kabla powoduje zwiększenie czasu pomiaru

ponieważ wzrasta stała czasowa obwodu

pomiarowego

R

x

R

we

R

k

kabel

Miernik

C

k

k

x

pom

R

R

R



k

x

x

C

R 





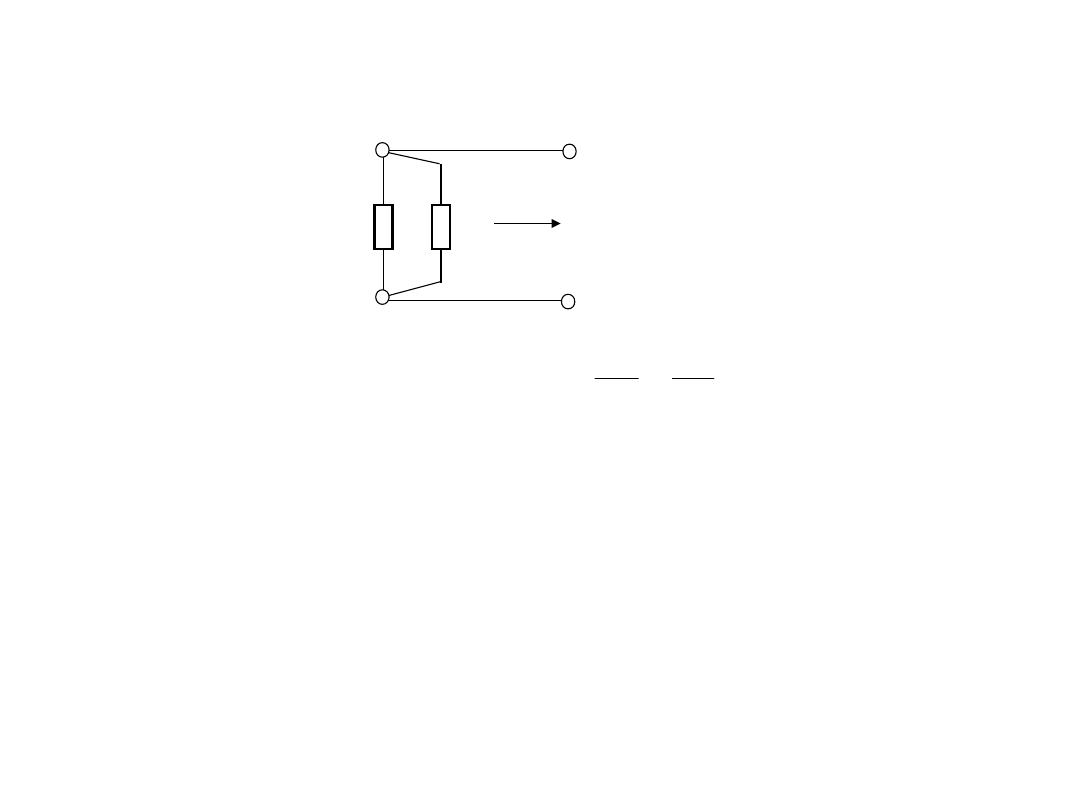
8. Pomiary dużych rezystancji

Wpływ rezystancji izolacji kable

• wpływ izolacji z rezystancją powyżej

R

iz

=100 G przy R

x

<100M

jest mniejszy od 0,1%.

Do miernika

rezystancji

R

x

R

iz

iz

x

x

iz

iz

R

R

G

G







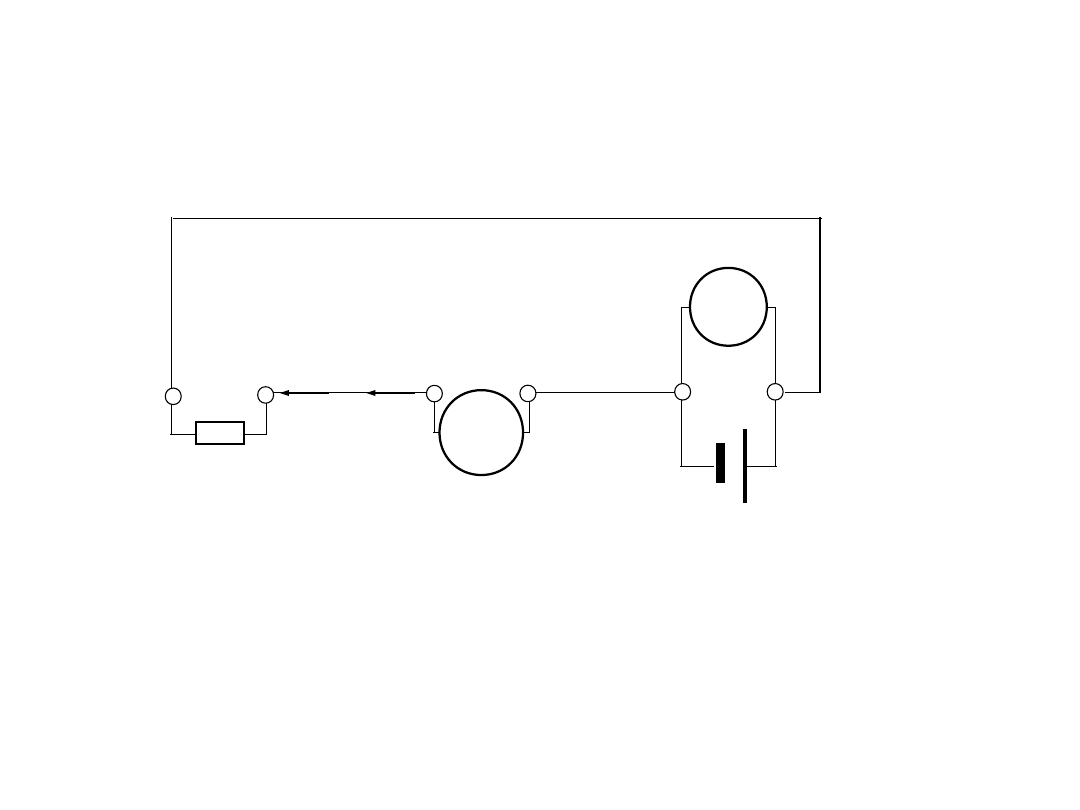
8. Pomiary dużych rezystancji

Rys.5. Zasada pomiaru rezystancji rezystancji

I

nA

R

x

U

zas

nA

I

x

V

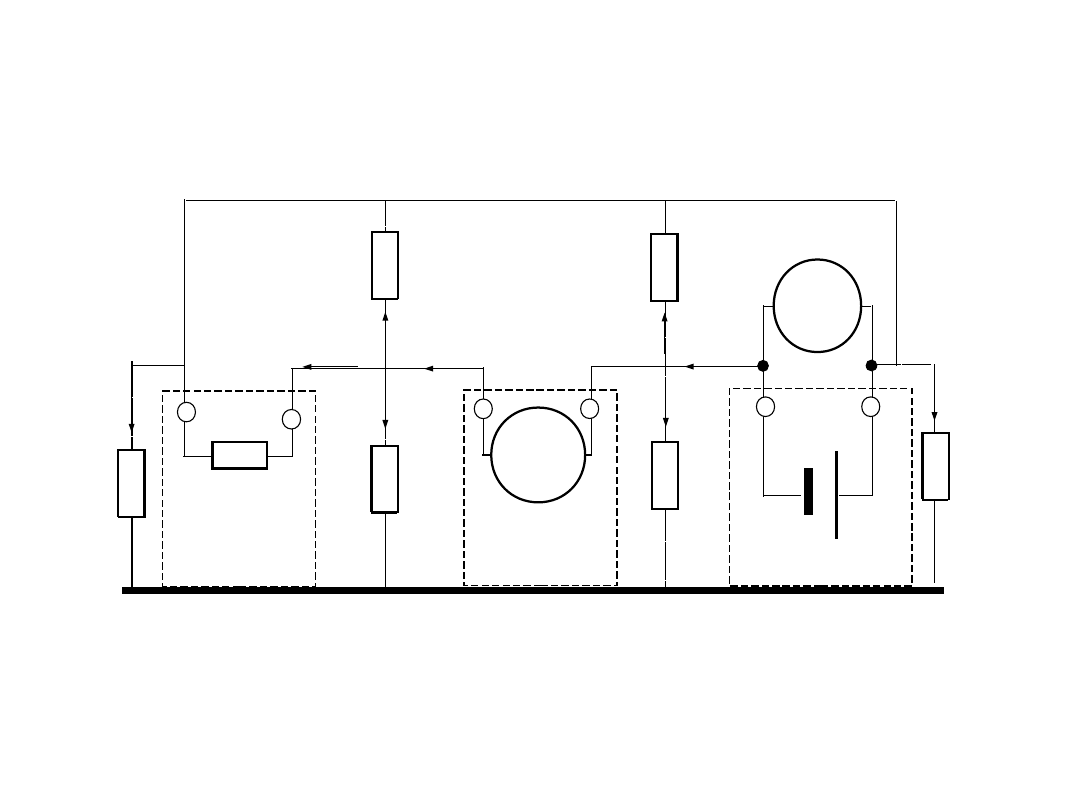
8. Pomiary dużych rezystancji

Rys. Układ zastępczy uwzględniający wpływ rezystancji izolacji

R

k2

I

nA

R

x

R

iz2

R

iz1

U

zas

nA

R

k1

I

x

I

zas

I

izU

I

izx

I

k2

I

iz2

I

iz1

I

k1

V

R

izU

R

izx

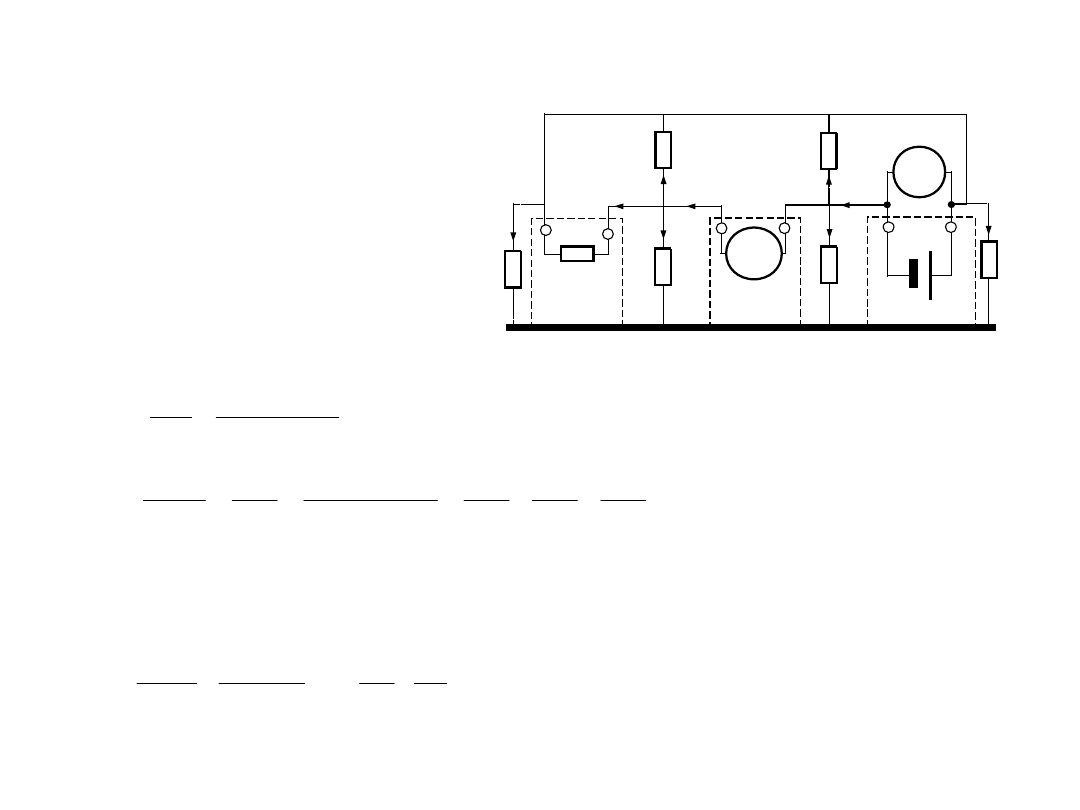
3. Pomiary dużych rezystancji

Wynik pomiaru prądu:

I

nA

=I

x

+I

iz2

+I

k2

Zamiast I

nA

=I

x

Prądy przez izolacje I

iz2

=U

zas

/R

iz2

oraz kabel I

k2

=U

zas

/R

k2

powodują powstanie błędu:

R

k2

I

nA

R

x

R

iz2

R

iz1

U

zas

nA

R

k1

I

x

I

zas

I

izU

I

izx

I

k2

I

iz2

I

iz1

I

k1

V

R

izU

R

izx

2

2

k

iz

x

zas

nA

zas

pom

,

x

I

I

I

U

I

U

R









2

2

2

2

2

2

1

k

iz

x

zas

k

zas

iz

zas

x

zas

k

iz

x

zas

nA

pom

,

x

pom

,

x

G

G

G

U

I

U

I

U

I

U

I

I

I

U

I

R

G























2

2

k

iz

pom

,

x

pom

,

x

G

G

G

G

G

pom

,

x

































2

2

2

2

1

1

k

iz

x

x

k

iz

x

G

G

R

R

R

G

G

G

G

pom

,

x

pom

,

x





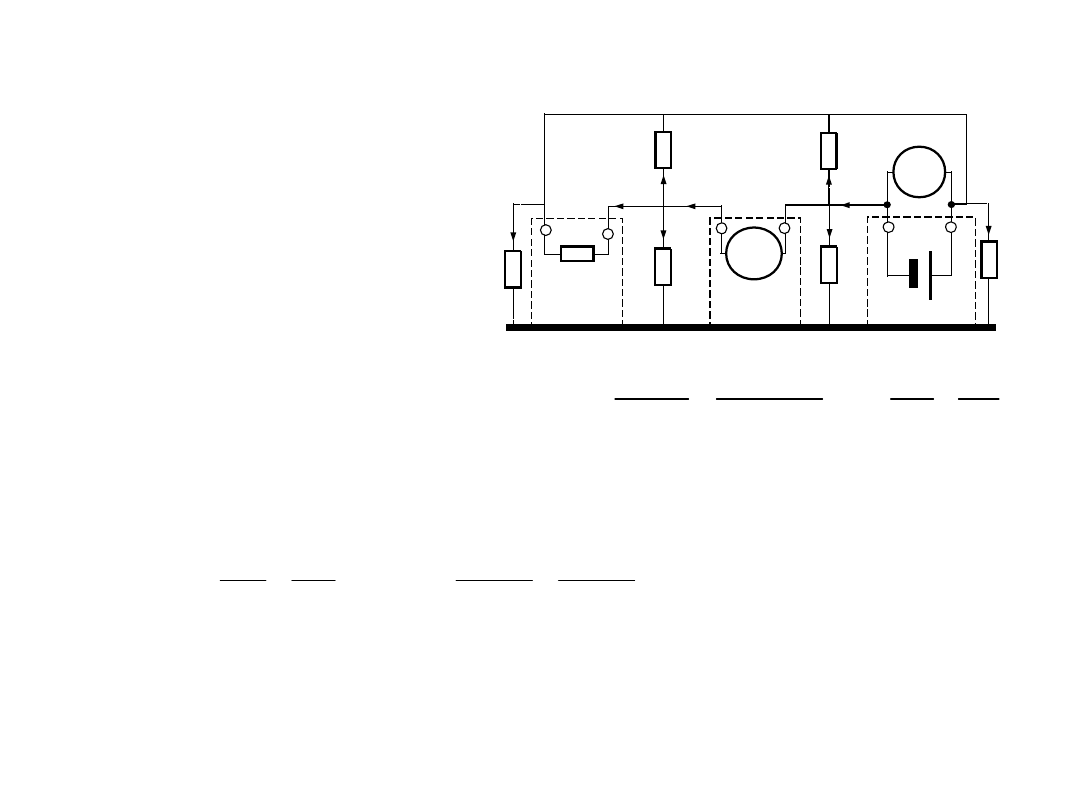
8. Pomiary dużych rezystancji

Prądy przez izolacje I

iz2

=U

zas

/R

iz2

oraz kabel I

k2

=U

zas

/R

k2

powodują powstanie błędu:

R

k2

I

nA

R

x

R

iz2

R

iz1

U

zas

nA

R

k1

I

x

I

zas

I

izU

I

izx

I

k2

I

iz2

I

iz1

I

k1

V

R

izU

R

izx

2

2

k

iz

pom

,

x

pom

,

x

G

G

G

G

G

pom

,

x

































2

2

2

2

1

1

k

iz

x

x

k

iz

x

G

G

R

R

R

G

G

G

G

pom

,

x

pom

,

x





Przykład: R

x

=1 GΩ; R

iz2

=R

k2

=10 GΩ=10

10

Ω

%

,

R

R

R

k

iz

x

G

pom

,

x

20

2

0

10

1

10

1

10

1

1

10

10

9

2

2













































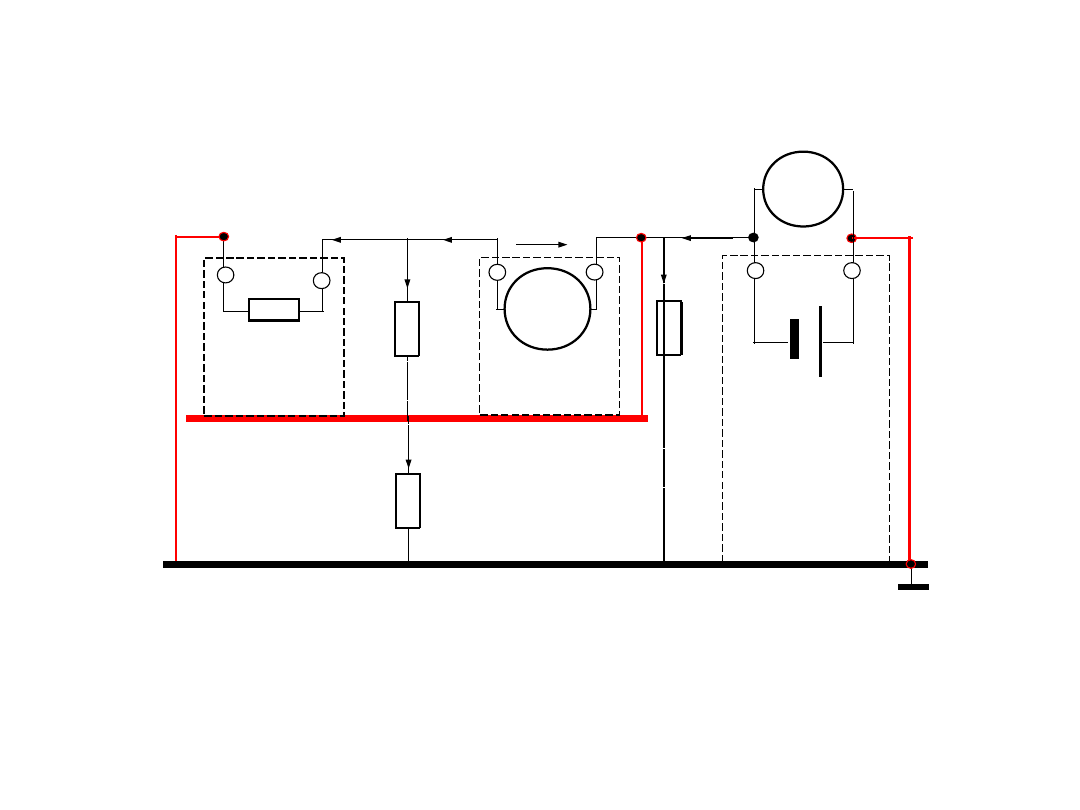
8. Pomiary dużych rezystancji

Rys. zasada ekwipotencjalnego zabezpieczenia podczas

pomiaru dużych rezystancji.

R

iz3

I

nA

R

x

R

iz2

R

iz1

U

zas

nA

I

x

I

zas

I'

iz2

I

iz3

I

iz1

V

U

nA

Ekran ekwipotencjalny

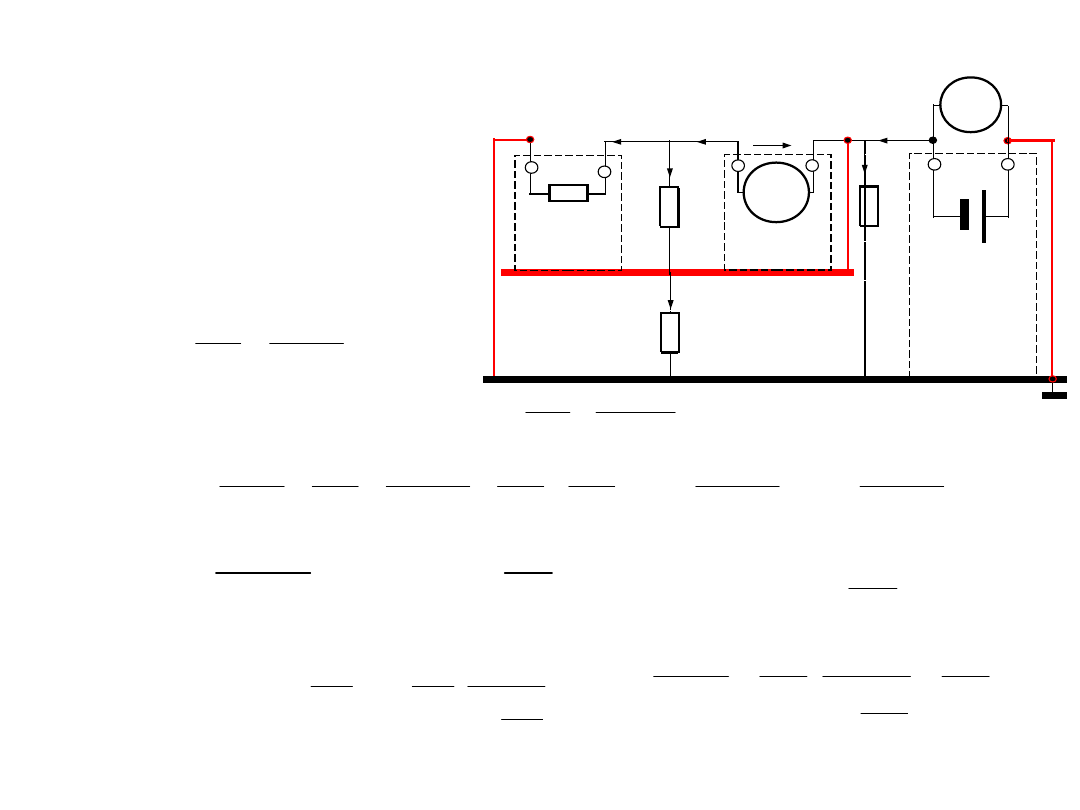
8. Pomiary dużych rezystancji

Wynik pomiaru prądu: I

nA

=I

x

+I'

iz2

Prąd przez izolację

Wynik pomiaru rezystancji:

Błąd

R

iz3

I

nA

R

x

R

iz

2

R

iz1

U

zas

nA

I

x

I

zas

I'

iz2

I

iz3

I

iz1

V

U

nA

Ekran ekwipotencjalny

2

2

2

iz

nA

nA

iz

nA

iz

R

R

I

R

U

I







2

iz

x

zas

nA

zas

pom

,

x

I

I

U

I

U

R









zas

iz

nA

nA

x

zas

iz

nA

x

zas

iz

zas

x

zas

iz

x

zas

nA

pom

x

pom

x

U

R

I

R

G

U

R

U

G

U

I

U

I

U

I

I

U

I

R

G

2

2

2

2

,

,

1

























pom

x

iz

nA

x

pom

x

zas

iz

nA

nA

x

pom

x

G

R

R

G

G

U

R

I

R

G

G

,

2

,

2

,



























2

,

1

iz

nA

pom

x

x

R

R

G

G

2

2

2

,

,

1

1

,

iz

nA

iz

nA

x

iz

nA

pom

x

x

pom

x

G

R

R

R

R

G

R

R

G

G

G

pom

x















2

2

2

1

1

,

,

iz

nA

iz

nA

iz

nA

x

G

G

R

R

R

R

R

R

G

pom

x

pom

x















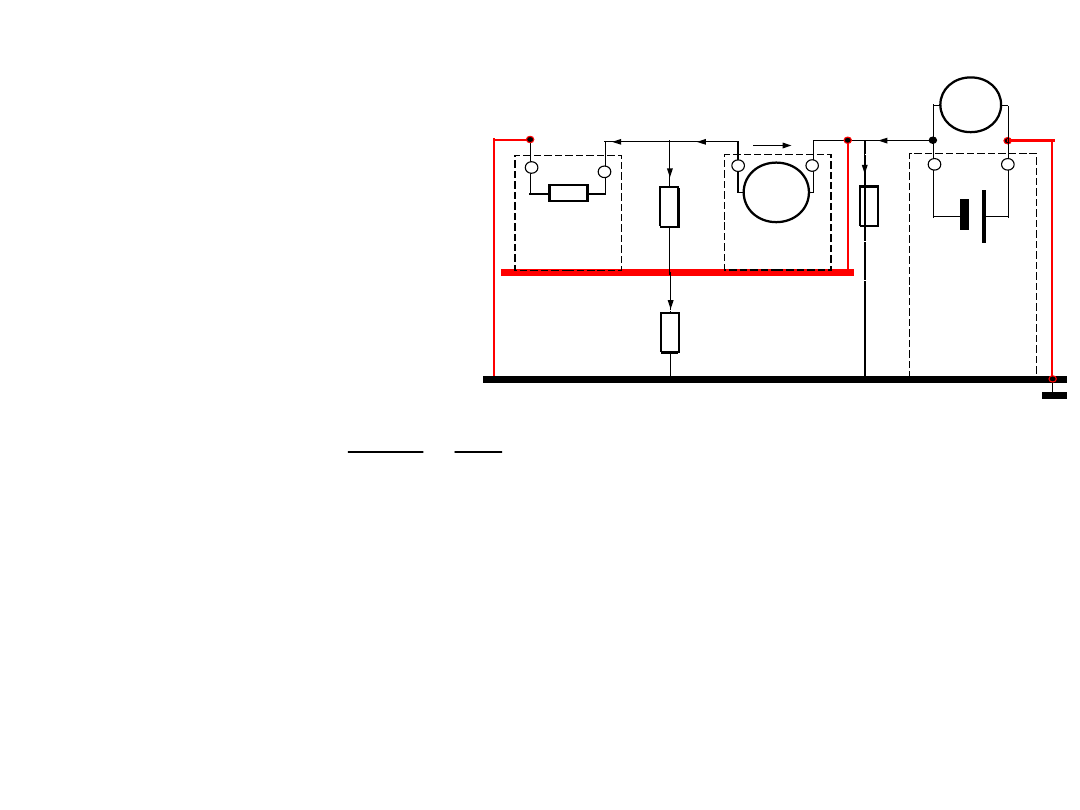
8. Pomiary dużych rezystancji

Błąd

Przykład: R

nA

=1000 Ω; R

iz2

=10 GΩ=10

10

Ω

δ

Gx,pom

≈(1000/10

10

)·100%= 10

-7

= 10

-5

%

R

iz3

I

nA

R

x

R

iz

2

R

iz1

U

zas

nA

I

x

I

zas

I'

iz2

I

iz3

I

iz1

V

U

nA

Ekran ekwipotencjalny

2

,

,

iz

nA

x

G

G

R

R

G

pom

x

pom

x









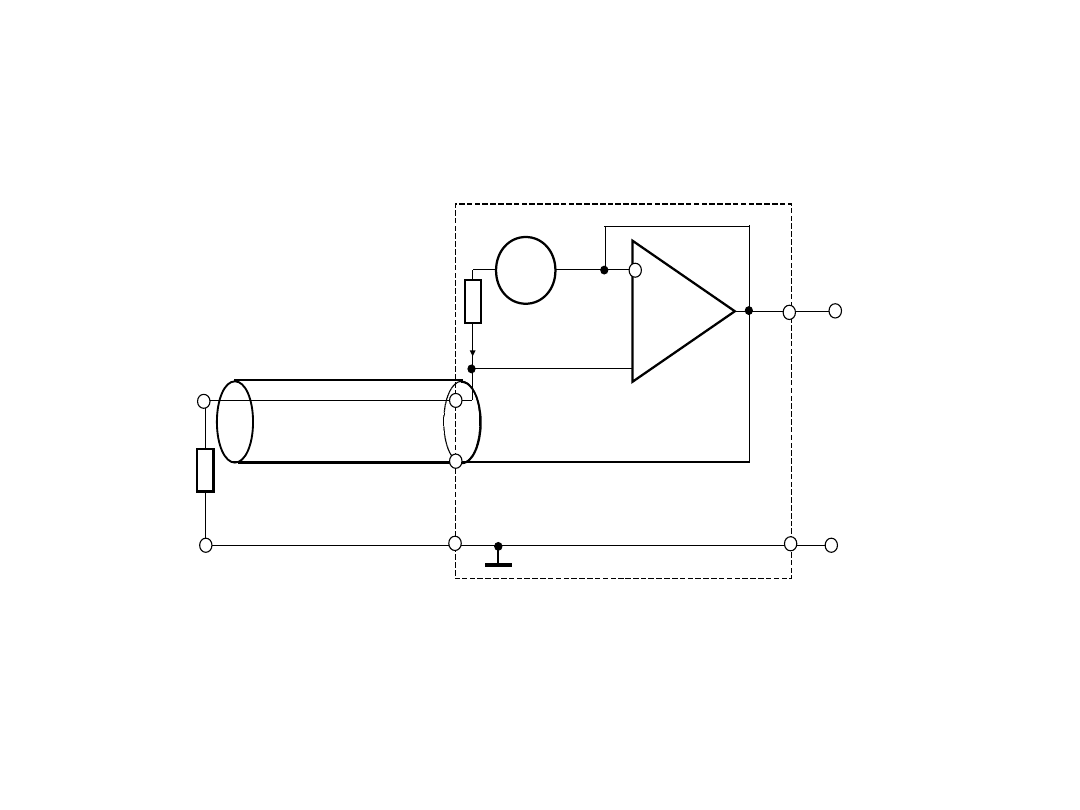
9. Omomierz do pomiaru dużych

rezystancji

Przetwornik rezystancji z ekranowaniem

ekwipotencjalnym

Rys.8. Schemat przetwarzania dużej wartości rezystancji

R

n

WO

-

+

I

x

U

wy

U

ref

R

x

Ekran

ekwipotencjalny

HI

LO

E -Ekran

Do A/C

WY

WE

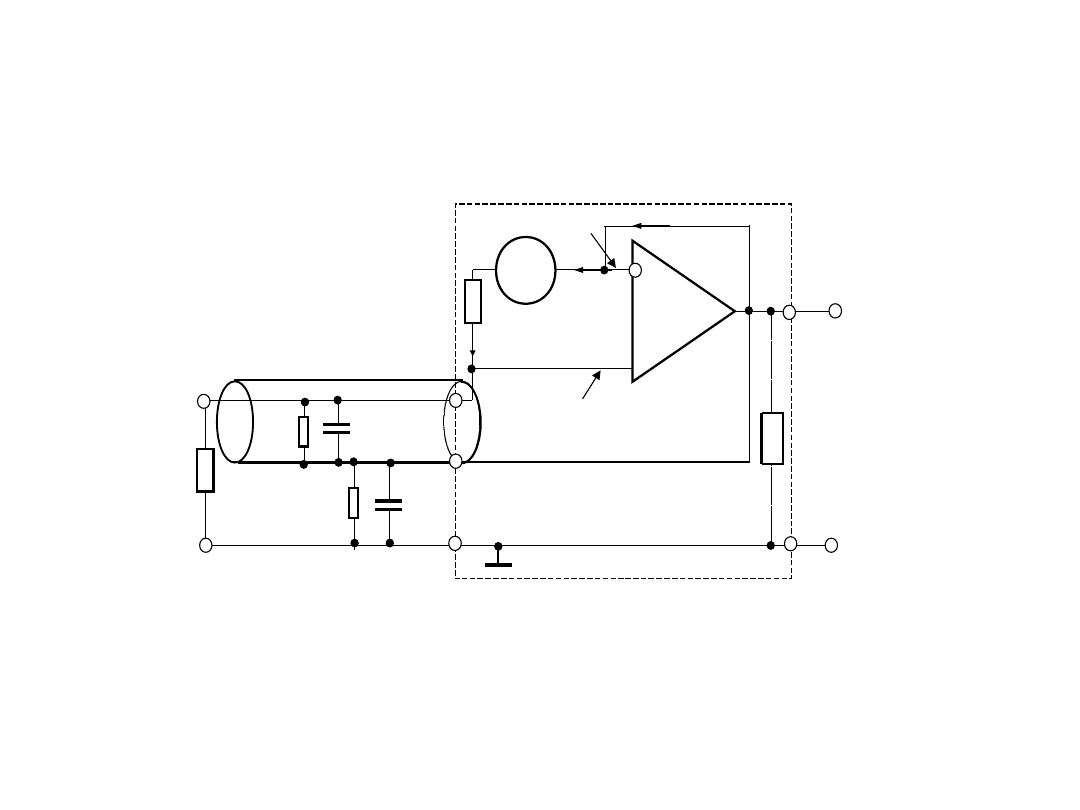
9. Omomierz do pomiaru dużych

rezystancji

- Przetwornik rezystancji z ekranowaniem

ekwipotencjalnym

Rys.8. Schemat przetwarzania dużej wartości rezystancji

R

n

WO

-

+

I

x

=I

n

U

wy

U

ref

I

n

=U

ref

/R

n

R

x

I

n

Ekran

ekwipotencjalny

U

e

=U

wy

=U

-

=U

+

=U

HI

R

iz

R

wy

C

iz

HI

LO

U

HI

E -Ekran

Do A/C

I

we+

=0

I

we-

=0

WY

WE

R

k

C

k

10. Pomiary parametrów izolacji

Podstawowymi obiektywnymi parametrami

materiałów dielektrycznych (izolacji) w stałym
polu elektrycznym są:

rezystywność skrośna ρ

s

oraz

powierzchniowa ρ

p

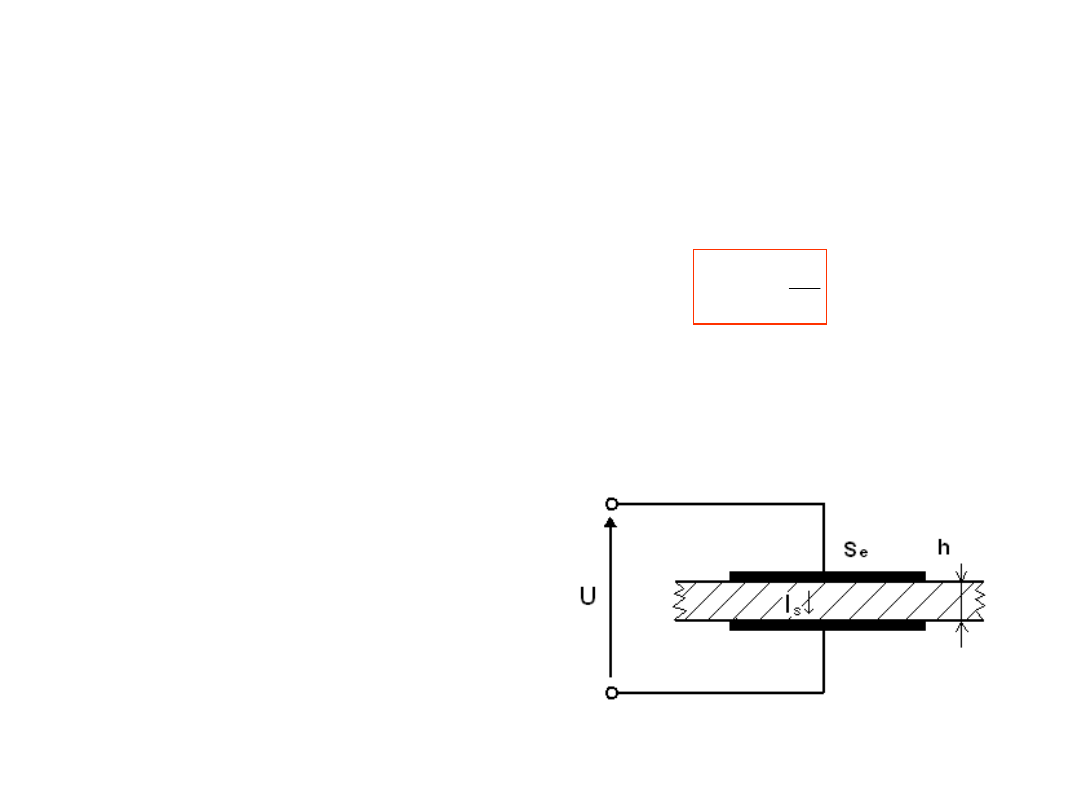
10. Pomiary parametrów izolacji

Rezystywność skrośna ρ

s

odwzoruje własności przepływu prądu

wewnątrz objętości dielektryka umieszczonego pomiędzy dwoma
elektrodami (o zadanej powierzchni), do których doprowadzone
jest napięcie stałe.

Rezystywność skrośna

ρ

s

wyznaczana jest ze wzoru:

[

Ω·m

] lub [

Ω·cm

]

gdzie

R

s

=U/I

s

jest zmierzona wartość rezystancji skrośnej przez

pomiar wartości doprowadzonego do elektrod napięcia

U

oraz

wartość płynącego wewnątrz objętości dielektryka prąd

I

s

;

S

e

jest efektywną powierzchnią elektrod;

h

– jest grubością izolacji (dielektryka).

h

S

R

e

s

s





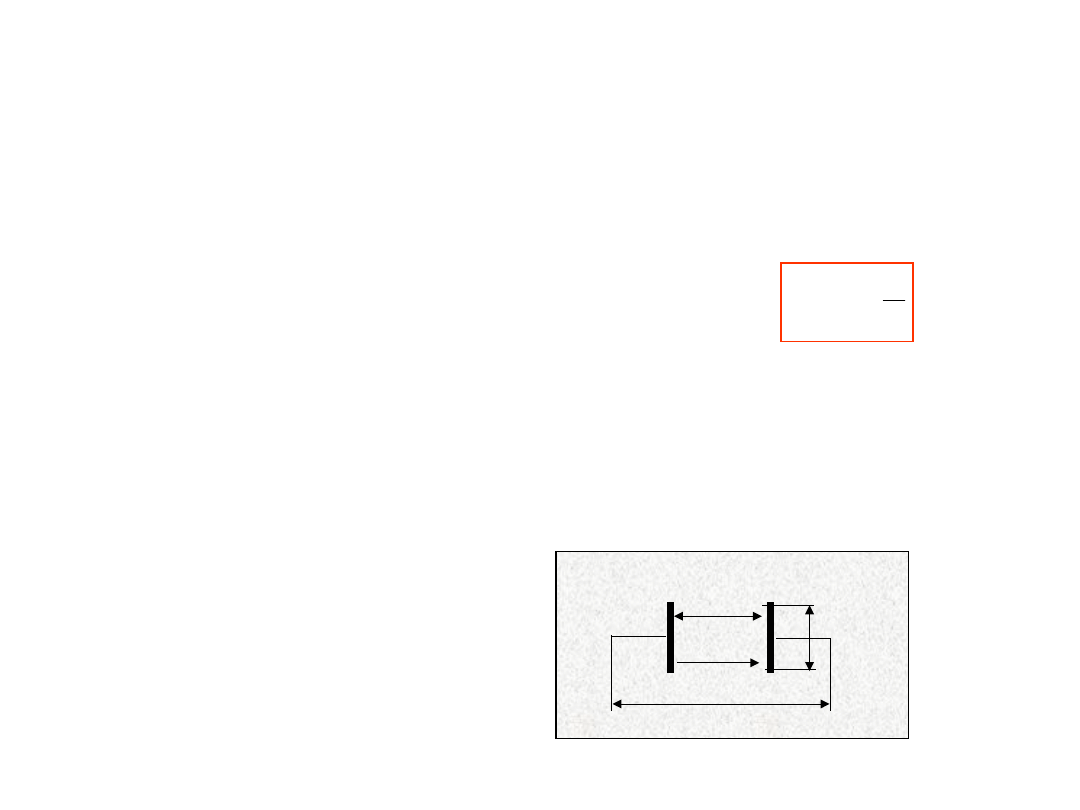
10. Pomiary parametrów izolacji

Rezystywność powierzchniowa ρ

p

odwzoruje własności

przepływu prądu po powierzchni dielektryka pomiędzy dwoma
elektrodami o zadanych wymiarach i odstępie usytuowanymi na
jego powierzchni, do których doprowadzone jest napięcie stałe .

Rezystywność powierzchniowa

ρ

p

wyznaczana jest ze wzoru:

[

Ω

]

gdzie

R

p

=U/I

p

jest zmierzona wartość rezystancji powierzchniowej

przez pomiar wartości doprowadzonego do elektrod napięcia

U

oraz wartość płynącego po powierzchni dielektryka prąd

I

p

;

L

jest odległością pomiędzy elektrodami;

g

– jest odstępem pomiędzy elektrodami

g

L

R

p

p





L

g

I

p

U

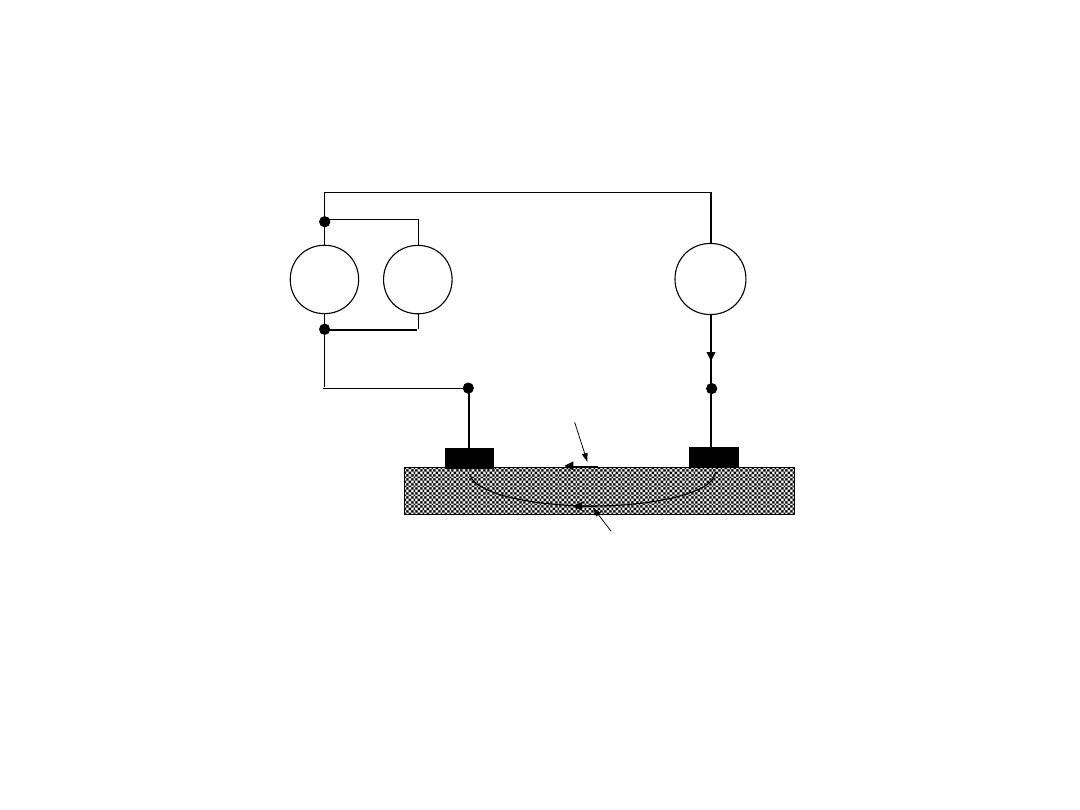
10. Pomiary parametrów izolacji

Przez materiał dielektryczny, do którego za pomocą elektrod

pomiarowych zostało podane napięcie, płyną jednocześnie prądy
wewnątrz jego objętości (

I

s

) oraz po powierzchnie (I

p

).

Dlatego zmierzona wartość rezystancji jest wypadkową rezystancją

skrośnej i powierzchniowej:

I

pom

=I

s

+I

p

.

W celu niezależnego pomiaru rezystancji skrośnej i powierzchniowej (i

dalej odpowiednich rezystywności) wykorzystuje się specjalne
elektrody pomiarowe (komórka pomiarowa)

U

V

μA

2

1

I

pom

I

s

I

p

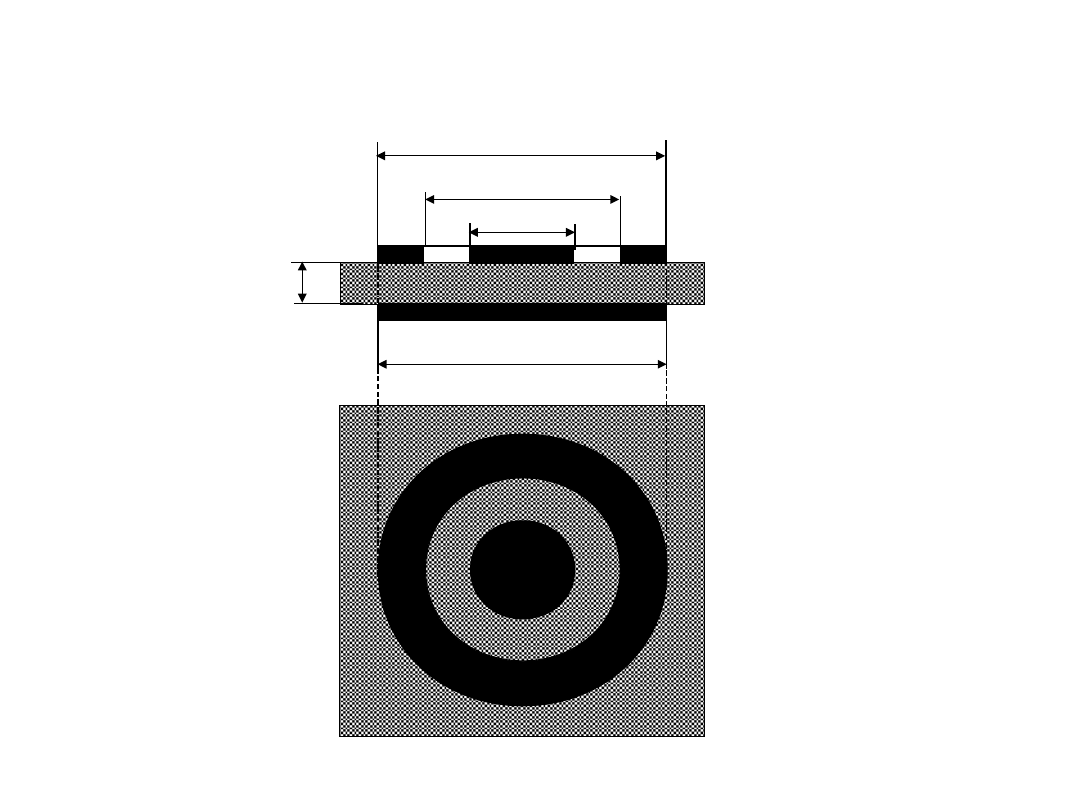
10. Pomiary parametrów izolacji

Układ elektrod pomiarowych (komórka pomiarowa) do niezależnego

pomiaru rezystancji skrośnej i powierzchniowej

d

4

d

3

d

1

d

2

h

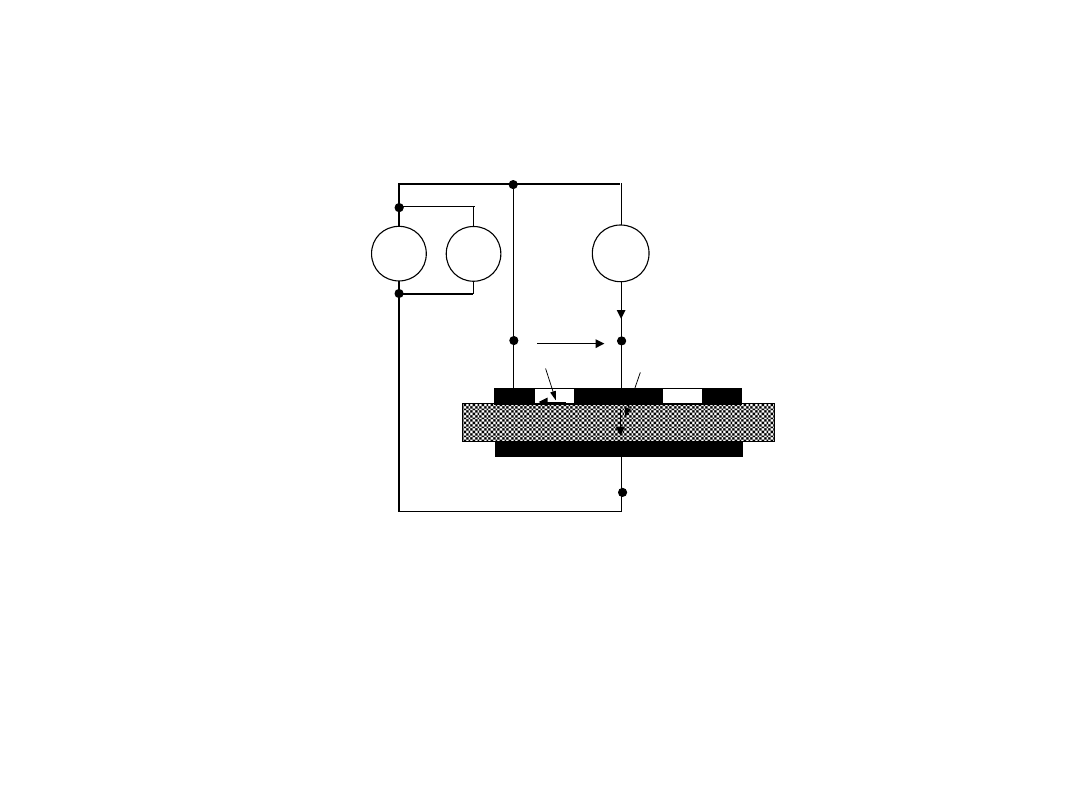
10. Pomiary parametrów izolacji

Pomiar rezystancji i rezystywności skrośnej

2

E

U

V

μ
A

3

1

I

pom

I

s

I

p

U

μA

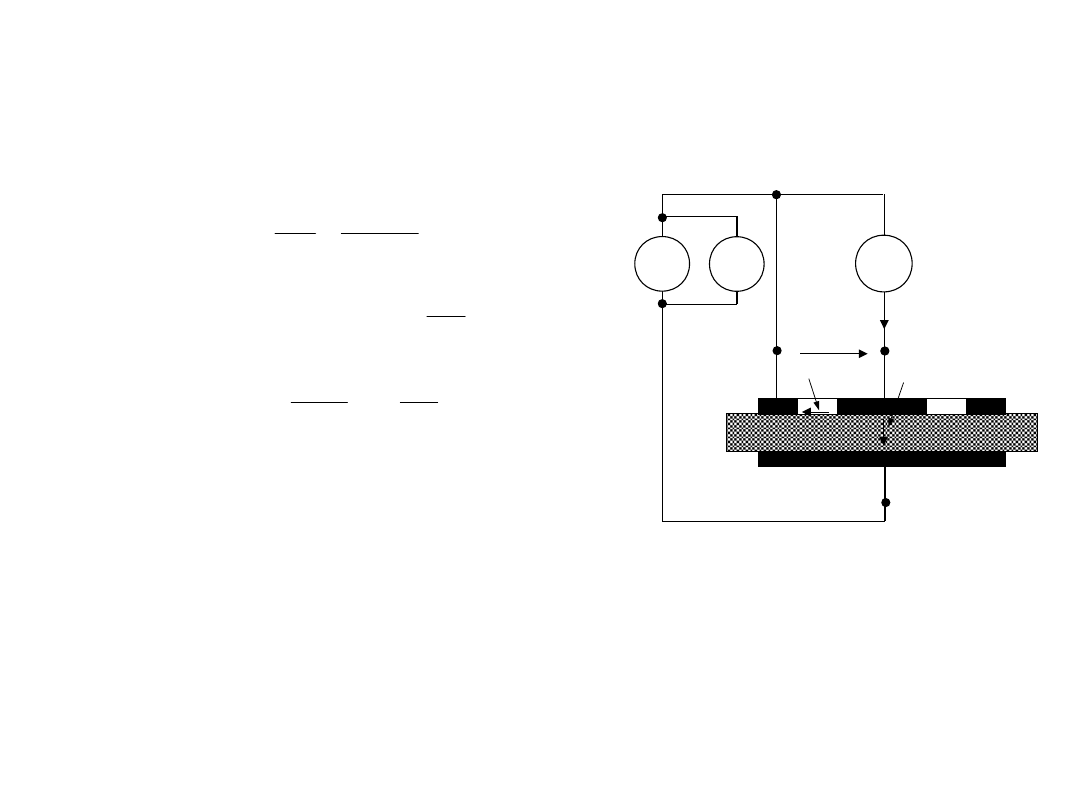
10. Pomiary parametrów izolacji

Pomiar rezystancji i rezystywności skrośnej

Wartość prądu powierzchniowego (powodującego błąd)

Błąd

R

μA

<<R

p

2

E

U

V

μ
A

3

1

I

pom

I

s

I

p

U

μA

p

A

pom

p

A

p

R

R

I

R

U

I































p

A

pom

p

pom

pom

R

R

I

I

I

I



1



 

p

A

pom

pom

p

pom

R

R

I

I

I

I











1



 

0



p

pom

I

I



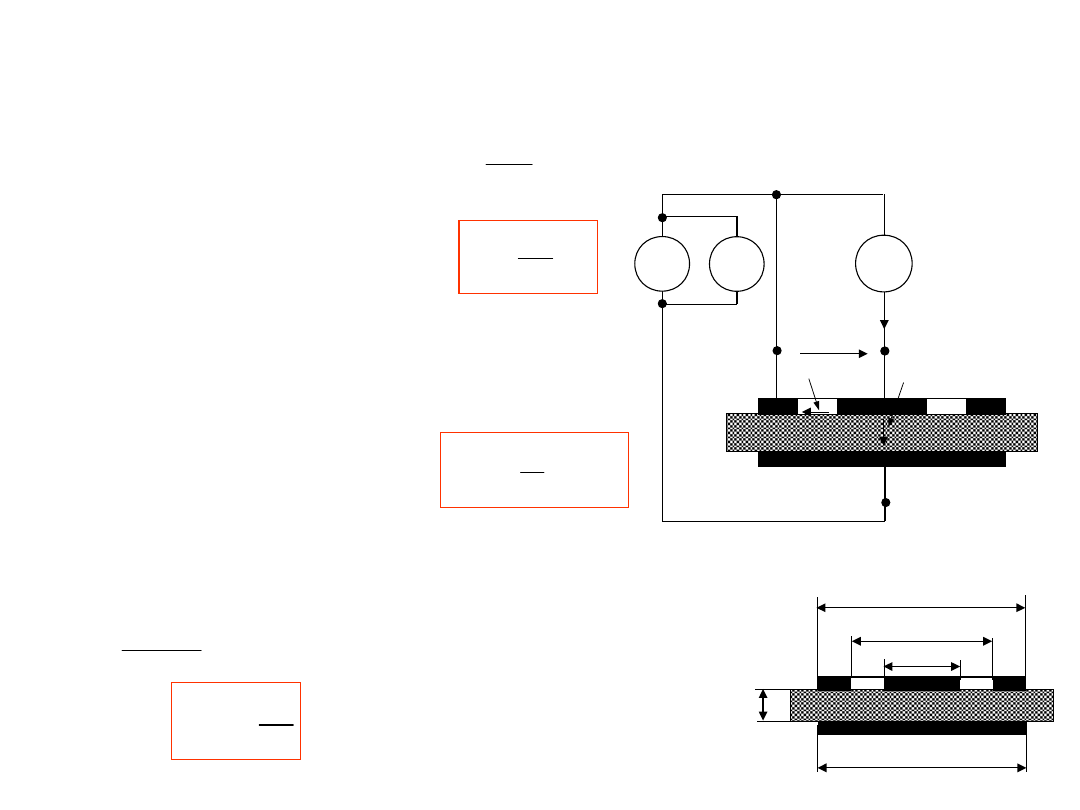
10. Pomiary parametrów izolacji

Pomiar rezystancji i rezystywności skrośnej

Wartość rezystancji skrośnej

Wartość rezystywności skrośnej

Wartość stałej K

s

komórki pomiarowej

z okrągłymi elektrodami pomiarowymi
do pomiaru rezystywności skrośnej ρ

s

wyznaczana jest ze wzoru:

gdzie

B

jest współczynnikiem efektywnej powierzchni elektrody

pomiarowej (można przyjąć

B=0

);

- jest połową odległości
elektrody wewnętrznej i zewnętrznej.
Otóż

2

E

U

V

μ
A

3

1

I

pom

I

s

I

p

U

μA

pom

i

I

U

R 

s

s

s

R

h

K







2

1

2



















g

B

d

K

s



2

1

2

d

d

g





4

2

1

d

K

s





d

4

d

3

d

1

d

2

h

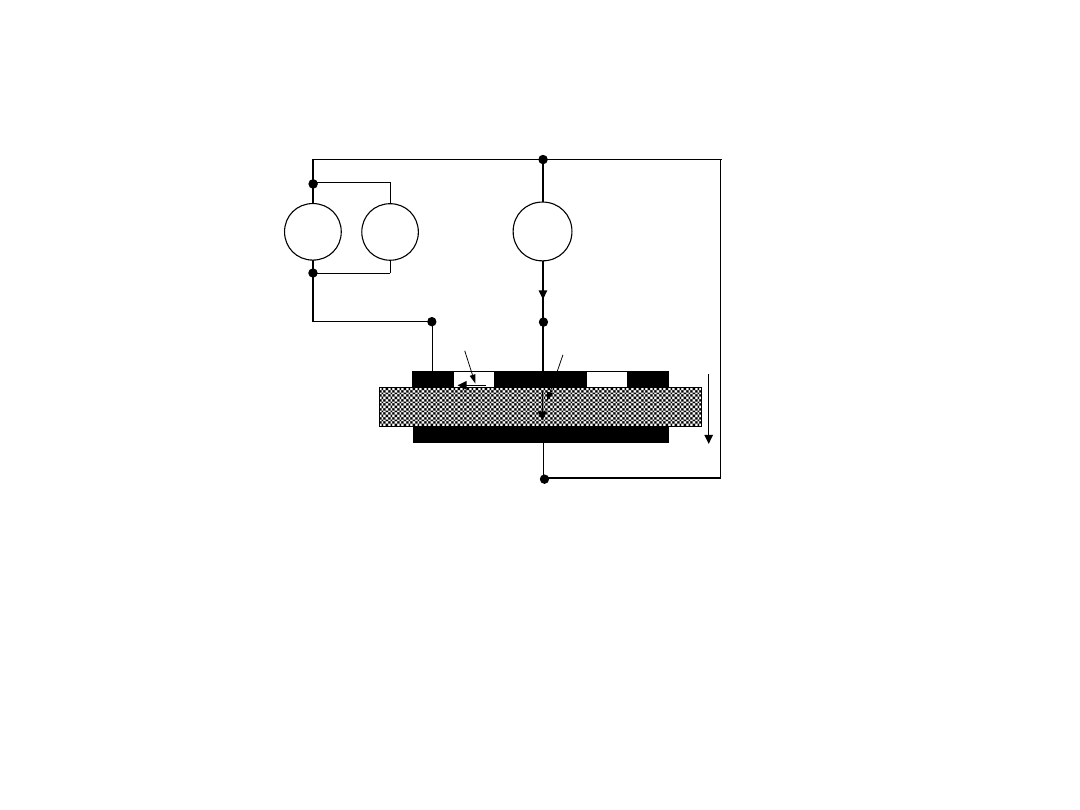
10. Pomiary parametrów izolacji

Pomiar rezystancji i rezystywności powierzchniowej

2

E

U

V

μA

3

1

I

pom

I

s

I

p

U

μA

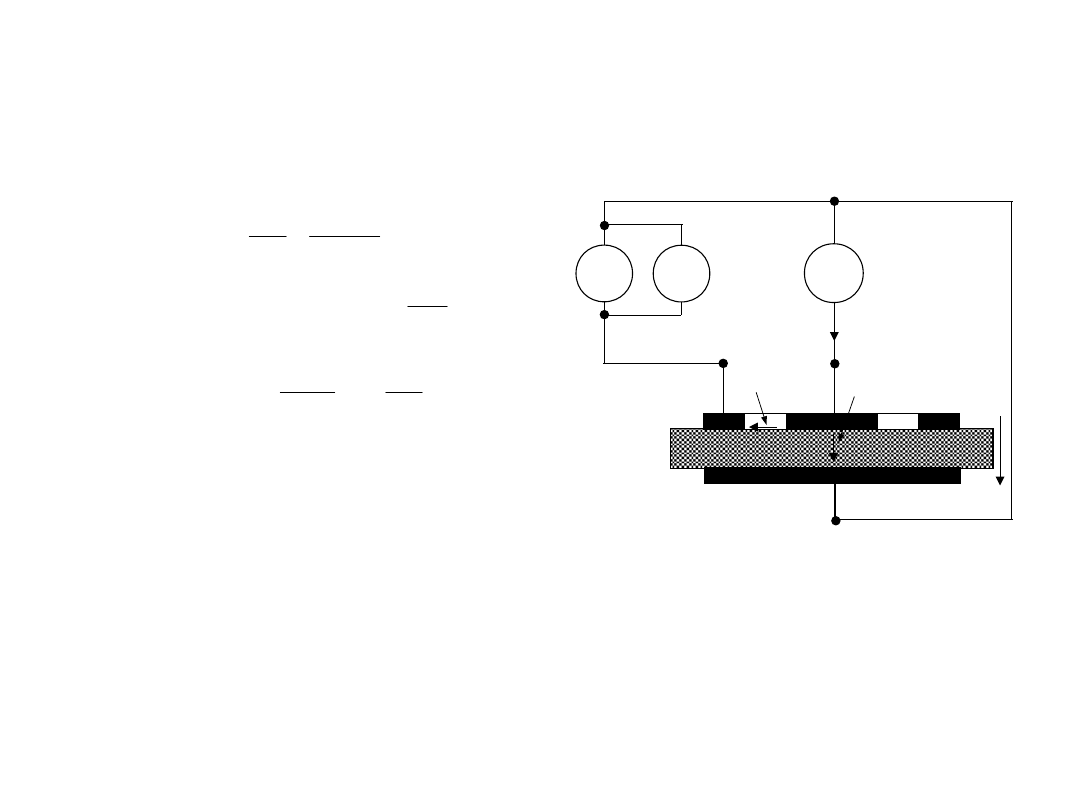
10. Pomiary parametrów izolacji

Pomiar rezystancji i rezystywności powierzchniowej

Wartość prądu skrośnego (powodującego błąd)

Błąd

R

μA

<<R

s

2

E

U

V

μA

3

1

I

pom

I

s

I

p

U

μA

s

A

pom

s

A

s

R

R

I

R

U

I





























s

A

pom

s

pom

pom

R

R

I

I

I

I



1



s

A

pom

pom

pom

R

R

I

I

I











1



 

0



s

pom

I

I



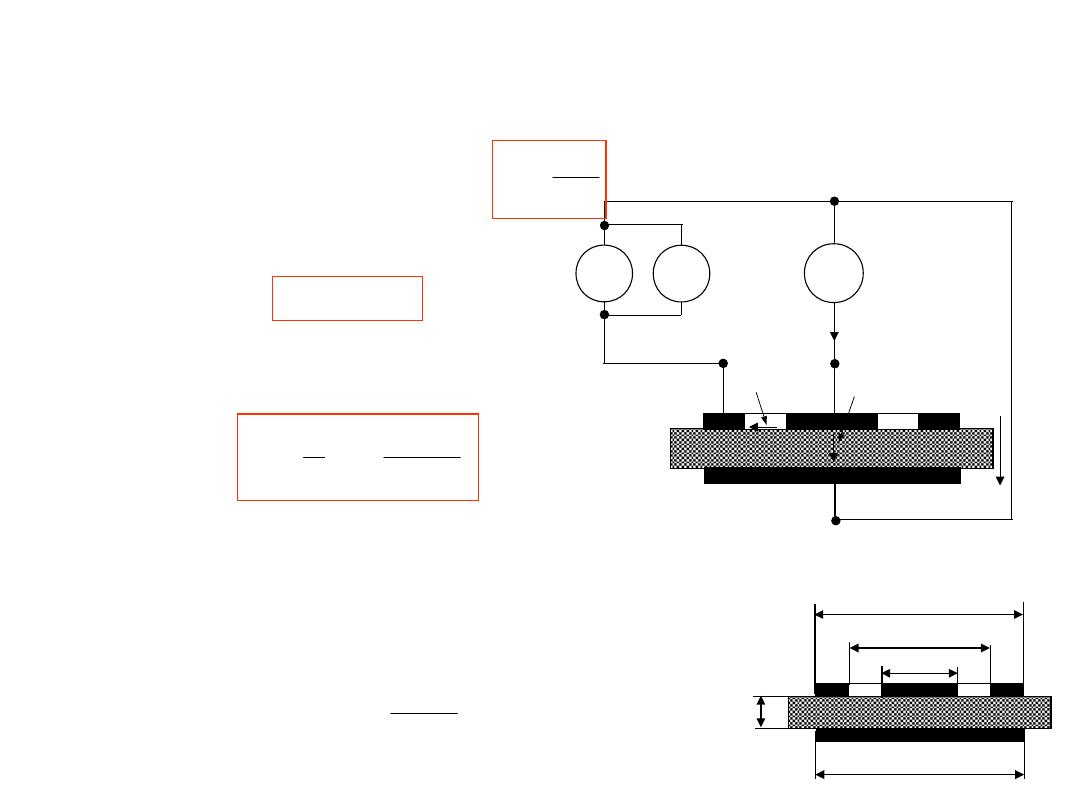
10. Pomiary parametrów izolacji

Pomiar rezystancji i rezystywności powierzchniowej

Wartość rezystancji powierzchniowej

Wartość rezystywności powierzchniowej

Wartość stałej K

p

komórki pomiarowej

do pomiaru rezystywności powierzchniowej

gdzie P jest efektywnym obwodem elektrody ekranującej:

g - jest połową odległości elektrody wewnętrznej i zewnętrznej:

2

E

U

V

μA

3

1

I

pom

I

s

I

p

U

μA

pom

p

I

U

R 

p

p

p

R

K 

























1

2

2

1

d

d

d

d

g

P

K

p







g

d

d

P







1

0





2

1

2

d

d

g





d

4

d

3

d

1

d

2

h

TŁUMIENIE ZAKŁÓCEŃ

W TRAKCIE ICH

PRZENIKANIA W

OBWÓD POMIAROWY

Plan wykładu

Plan:
3.1. Wstęp
3.2. Metody konstrukcyjno-technologiczne

zmniejszenia wpływu zakłóceń

3.2.1. Ekranowanie
3.2.2. Skręcanie par przewodów
3.2.3. Prawidłowe uziemienie
3.2.4. Ekwipotencjalne ekranowanie
3.3. Zabezpieczenie (ekranowanie)

ekwipotencjalne

3.3.1. Niektóry przykłady analizy wpływu

zakłóceń wspólnych

3.3.2. Współczynnik tłumienia zakłócenia

wspólnego

3.3.3. Ekranowanie ekwipotencjalne

Cel:

Zapoznać się z rodzajami zakłóceń w obwodach

pomiarowych

3.1. Wstęp

Zakłócenia, występujące w torze pomiarowym, powodują powstanie

dodatkowej niepewności wyników pomiaru. Przy tym wartość na

niepewności, spowodowanej zakłóceniami, zależy od wielu

czynników. Przy rozpatrywaniu zagadnień wpływu zakłóceń na wyniki

pomiaru należy uwzględniać trzy podstawowe składowe (rys. 1):

-

źródło

zakłóceń;

-

kanał przenikania

zakłócenia w tor pomiarowy oraz

-

obwód pomiarowy

wraz z urządzeniami pomiarowymi i

metodą

przetwarzania

sygnału pomiarowego.

Kanał

przenikania

zakłócenia

-wrażliwość

ξ

z

Źródło

zakłócenia

U

x

Obwód

pomiarowy

U

z

Źródło

sygnału

pomiarowego

Z

z

Wynik pomiaru

X i jego

niepewność

u

z

(Z)

3.1. Wstęp

W ogólnym podejściu niepewność wyniku pomiaru wielkości od wpływu

zakłócenia z zależy od

- jego

intensywności

Z,

- wrażliwości

obwodu pomiarowego na zakłócenie oraz

- operatora

(

algorytmu

) opracowania sygnału:

Dlatego można wyróżnić trzy podstawowe sposoby zwalczania

zakłóceń w układach pomiarowych:

1.

Tłumienie zakłóceń w miejscu ich powstania

(tłumienie „źródła”);

2.

Utrudnienie przenikania zakłóceń

w obwód pomiarowy –

zmniejszenia wrażliwości obwodu na zakłócenia;

3.

Podwyższenie odporności sygnałów

i układów pomiarowych na

zakłócenia

– zmniejszenie skutku oddziaływania zakłócenia.

z

X

z













Z

L

z





































Z

z

X

L

Z

L

z

X

u

z



,

3.2. Konstrukcyjno-technologiczne

metody zmniejszenia wpływu zakłóceń

Pierwszy

dwie metody są metodami konstrukcyjno-

technologicznymi

, a

trzecia metoda

jest powiązana z

odpowiednimi odpornym na zakłócenia przetwarzaniami

sygnałów

pomiarowych.

Podstawowymi konstrukcyjno-technologicznymi metodami zwalczania

wpływu zakłóceń są:

-

ekranowanie

oraz

-

prawidłowe uziemienie

,

a dla zmniejszenia przenikania zakłóceń także wykorzystanie
-

skręconych par przewodów linii

.

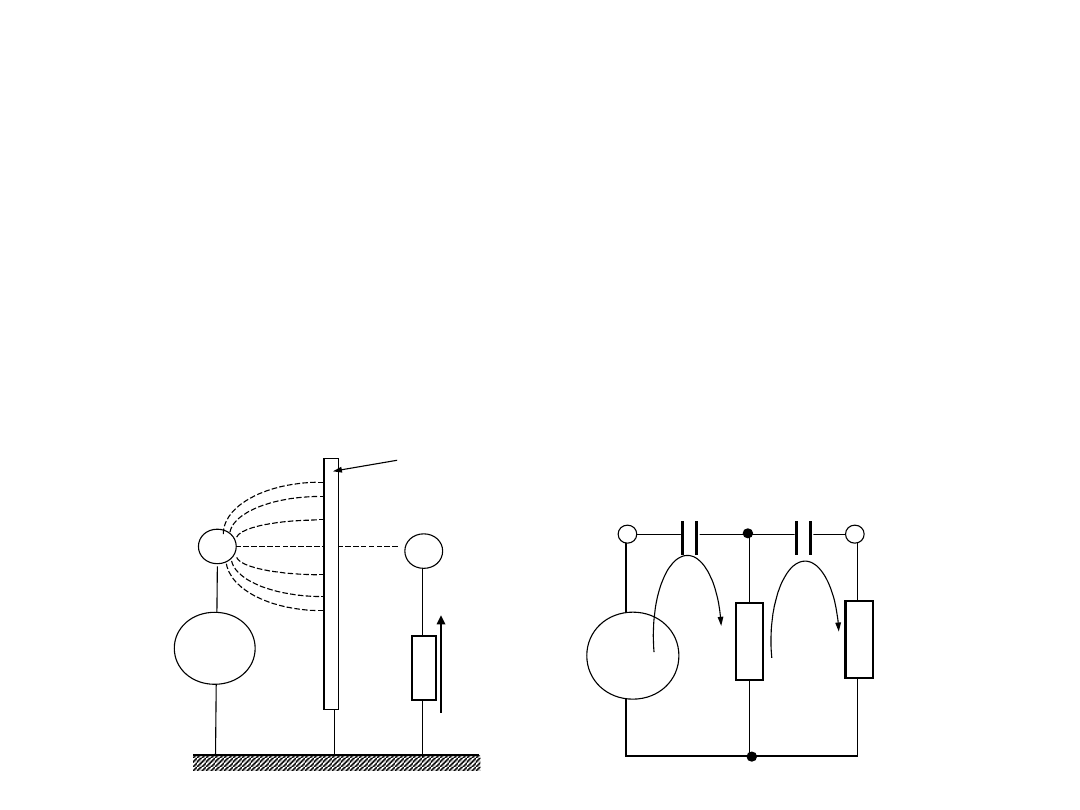
3.2.1. Ekranowanie

W zależności od rodzaju pola elektrostatycznego,

magnetostatycznego i elektromagnetycznego rozróżnia się

ekrany:

• elektrostatyczne

;

• magnetostatyczne

;

• elektromagnetyczne

.

Ekran elektrostatyczny.

Pole elektrostatyczne indukuje na powierzchni ekranu ładunki

elektryczne, na których kończą się linii pola, które

spowodowało powstanie tych ładunków. Przez co pole nie

wnika za ekran.

+

U

e

-

Uz

C

1e

C

e2

Ekran



e

, (r

e

)

C

1e

Uz

U

e

I

1e

1

2

C

e2

I

e2

Z

Z

e

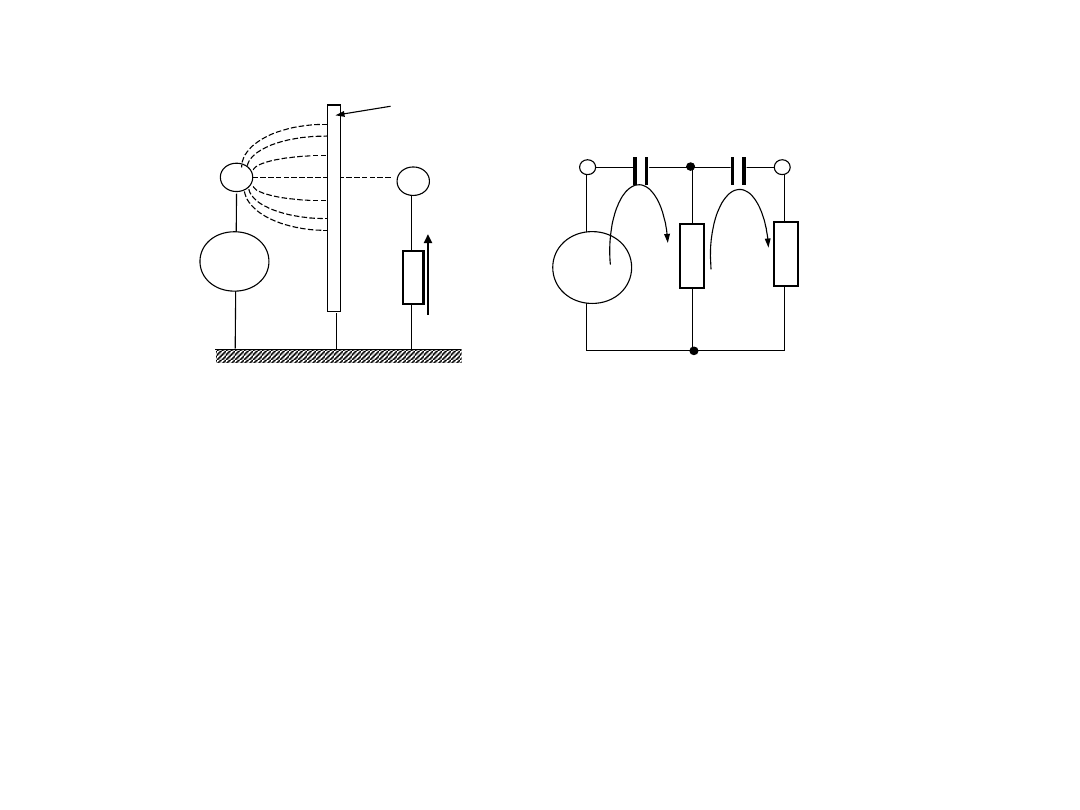
3.2.1. Ekranowanie

Skuteczność ekranu zależy od przewodności materiału ekranu

. Ona musi być

duża (materiał: miedź, aluminium, srebro, złoto, itp.).

Przy obecności ekranu prąd I

e1

płynąc będzie tylko w obwodzie źródło –

pojemność pasożytnicza C

e1

– ekran, powodując napięcie na rezystancji na

ekranie (gdzie uwzględniono, że rezystancja ekranu jest w dużym stopniu

mniejsza impedancją pojemności C

e1

(r

e

<<1/



C

e1

).

Napięcie U

ez

jest źródłem wtórnego prądu płynącego przez pojemność

pasożytnicza C

e2

do impedancji wejściowej Z, wywołując na niej napięcie

zakłócające , gdzie C

e

=C

e1



C

e2

.

Przykładowo, dla Us=230V, f=50Hz; C

e

=25pF (zwiększenie pojemności wskutek

zwiększenia powierzchni ekranu); r

e

=2,5, Z=1M wartość napięcia

zakłócenia wynosi około U

z

0,035 V.

Skuteczność ekranowania zależy od przewodności materiału ekranu i jej

zmniejszenie powoduje pogorszenie skuteczności ekranowania. Ekran może

być jako siatka

.

+

U

ez

-

Uz

C

1e

C

e2

Ekran



e

, (r

e

)

C

1e

Uz

U

ez

I

1e

1

2

C

e2

I

e2

Z

Z

e

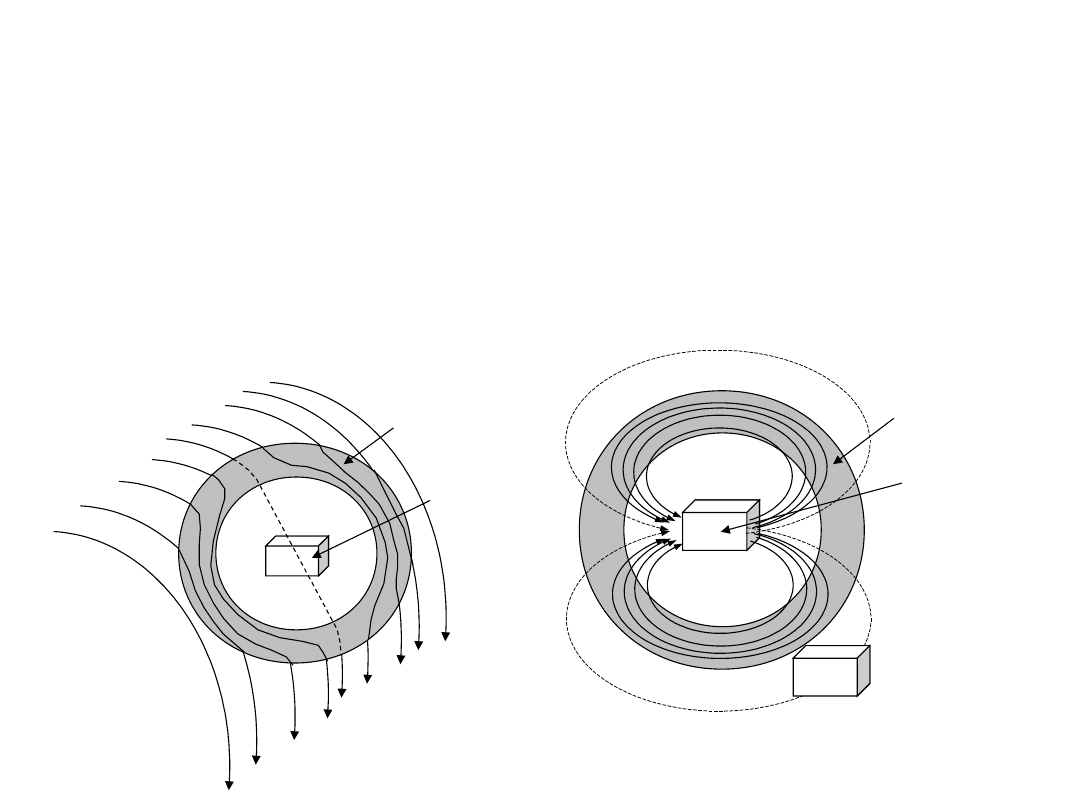
Magnetostatyczne ekranowanie

Linii pola magnetostatycznego trafiając na ekran z materiału

ferromagnetycznego wnikają weń i zbierają się w materiale

ekranu malejąc wewnątrz niego.

Ekranowany może być obwód pomiarowy (a) lub źródło

zakłócenia (b).

Skuteczność takiego ekranu tym większa im mniejszy opór

magnetyczny ekranu (im większa przenikalność magnetyczna

i grubość ekranu).

Ekran musi być jednolity, bez dziur.

Ekran

magnetycz

nyUkład

pomiarow

y

Pole

magnetostatyc

zne zewnętrzne

Ekran

magnetyczny

Układ

pomiarowy

Źródło zakłócenia

magnetycznego

wewnętrznego

Ekranowanie elektromagnetyczne

Pole elektromagnetyczne (EMP) zwykle przyjmuje się zmiennym sinusoidalnym,

ono powoduje powstanie siły elektromotorycznej (EMS) oraz prądów

wirowych w materiale przewodzącym.

Te prądy wywołując pole magnetyczne, które przeciwdziała polu zewnętrznemu.

Efektywność ekranu zależy od przewodności i przenikalności magnetycznej

materiału, grubości ekranu oraz długości fali (częstotliwości) EMP

Przenikalność EMP, mm

Grubość ekranu musi być co najmniej równa trzykrotnej głębokości wnikania fali

elektromagnetycznej.

Wymiary szczelin i dziur w ekranie też muszą być kilka razy mniejszymi od

długości fali elektromagnetycznej. Im większa częstotliwość EMP tym cieńszy

wymagany jest ekran.

Częstotliwoś

ć, Hz

Miedź Aluminium

Stal

50

9

11.5

0.91

100

6.6

8.5

0.66

1000=1kHz

2.1

2.7

0.20

10000=10k

Hz

0.66

0.84

0.08

100000=1M

Hz

0.08

0.08

0.008

Rekomendacje

Jeżeli obudowa przyrządu pomiarowego jest zrobiona z tworzywa wtedy

jako ekran może się wykorzystywać zewnętrzne przewodzące pokrycia

obudowy.

Dla zapewnienia zmniejszenia wpływu pól różnego rodzaju na praktyce

często stosuje się wielu warstwowe ekrany z różnych materiałów.

W niektórych przypadkach mogą być ekranowany każdy element układu

pomiarowego lub najważniejszy jego podzespoły.

W takich przypadkach ekrany powinny być dołączone do masy lub punktu

odniesienia

Rekomendacje [ZwAE]:
-

Ekran elektrostatyczny

: wysoka przewodność materiału, może być jako

siatka.

-

Ekran magnetostatyczny

: wysoka przenikalność materiału, musi być bez

dziur lub z niewielkimi dziurami. Dla zwiększenia skuteczności ekran

może być kilku warstwowym.

-

Ekran elektromagnetyczny

: efektywność ekranu zależy od przewodności i

przenikalności magnetycznej materiału, grubości ekranu oraz długości

fali (częstotliwości) EMP. Grubość ekranu musi być co najmniej równa

trzykrotnej głębokości wnikania fali elektromagnetycznej.

- Dla zapewnienia zmniejszenia wpływu pól różnego rodzaju na praktyce

często stosuje się

wielu warstwowe ekrany

z różnych materiałów.

3.2.2.Tłumienie pola

magnetycznego przez skręcanie

par przewodów

Pole zmienne magnetyczne o indukcyjności B powoduje powstanie w

obwodzie o powierzchnie S siły elektro motorycznej

gdzie Ф – jest strumień magnetyczny, B – jest gęstość strumieniu

magnetycznego. To znaczy, że wpływ zmiennego pola

magnetycznego jest proporcjonalny do powierzchni obwodu.

Dla zmniejszenia wpływu takiego pola należy unikać pętli przewodów

oraz długich dwu przewodowych kabli.

dt

dB

S

dt

d

e

B











S

e

B

=-SdB/dt

B

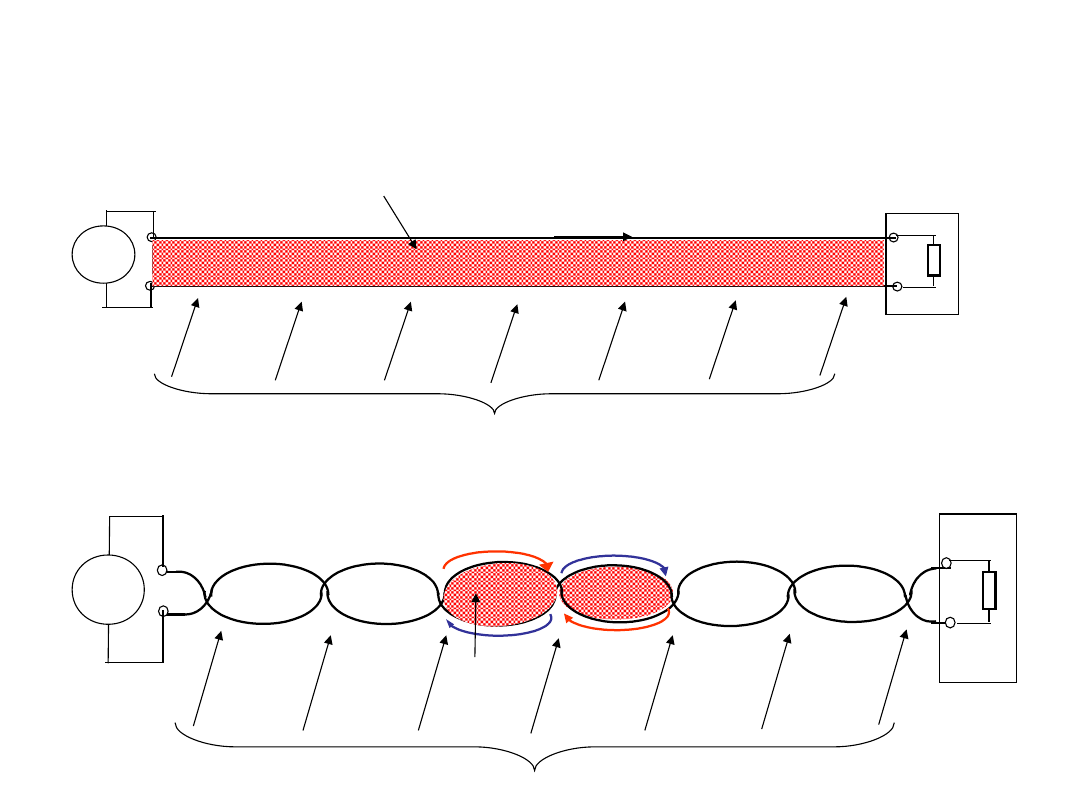
3.2.2.Tłumienie pola

magnetycznego przez skręcanie

par przewodów

Skutecznym przeciwdziałaniem wpływu pola magnetycznego jest

skręcanie par dwu przewodowych kabli

S

p

e

z

=S

dB/dt

Z

we

U

z

B

e

B

=-

SdB/dt

S

S

i

e

zi

=S

i

dB/

dt

Z

we

U

z

B

e

zi+1

=-

S

i+1

dB/dt

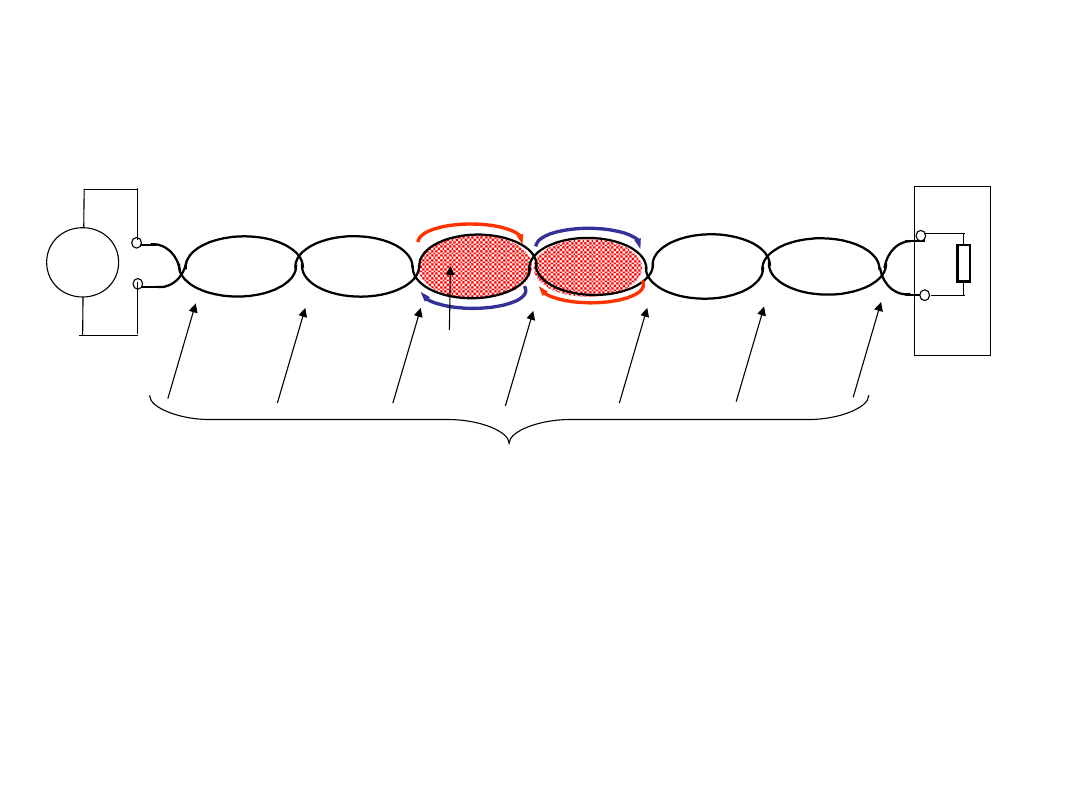
3.2.2.Tłumienie pola

magnetycznego przez skręcanie

par przewodów

Rekomendacje:
-

Unikać długi kabli

-

Unikać pętli

-

Separować linii zasilania

od linii sygnałów pomiarowych

- Wykorzystanie skręconych par przewodów

Efektywność skręcania zależy od jednakowości powierzchni

pętli, liczba pętli musi być dużą i parzystą.

S

i

e

zi

=S

i

dB/

dt

Z

we

U

z

B

e

zi+1

=-

S

i+1

dB/dt

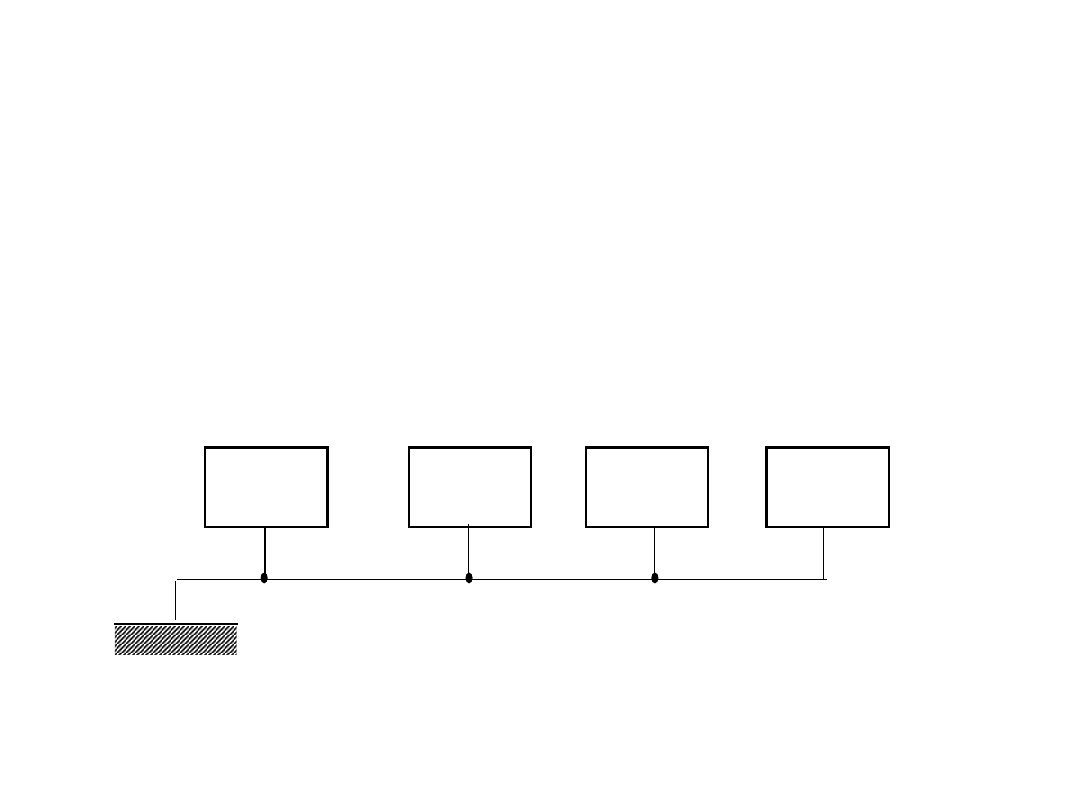
3.2.3. Uziemienie

Dla prawidłowej transmisji, przetwarzania i wykorzystania sygnałów

pomiarowych elektrycznych wymaganie jest istnienie punktów lub

płaszczyzn ekwipotencjalnych (stałych w czasie i niezależnych od

przepływających prądów).

Te punkty lub płaszczyzny odniesienia w danym układzie, zespole lub

systemie pomiarowym stanowią tzw. masę.

Nazywa się ona również uziemieniami dla sygnałów pomiarowych.
W praktyce płaszczyzny odniesienia posiada niezerową impedancją

(rezystywnością) (zależną od materiału, jej długości, szerokości i

grubości oraz częstotliwości sygnałów) i dla tego płaszczyzna

odniesienia przy obecności przepływających prądów nie jest

ekwipotencjalną.

W takiej sytuacji przy dołączeniu źródła sygnału oraz odbiornika do takiej

płaszczyzny w dostatecznych odległych punktach pomiędzy tymi

punktami powstaje różnica potencjałów, która powoduje blendy

transmisji (przetwarzania) sygnału pomiarowego.

Układ 1

Układ 2

Układ 3

Układ 4

Masa

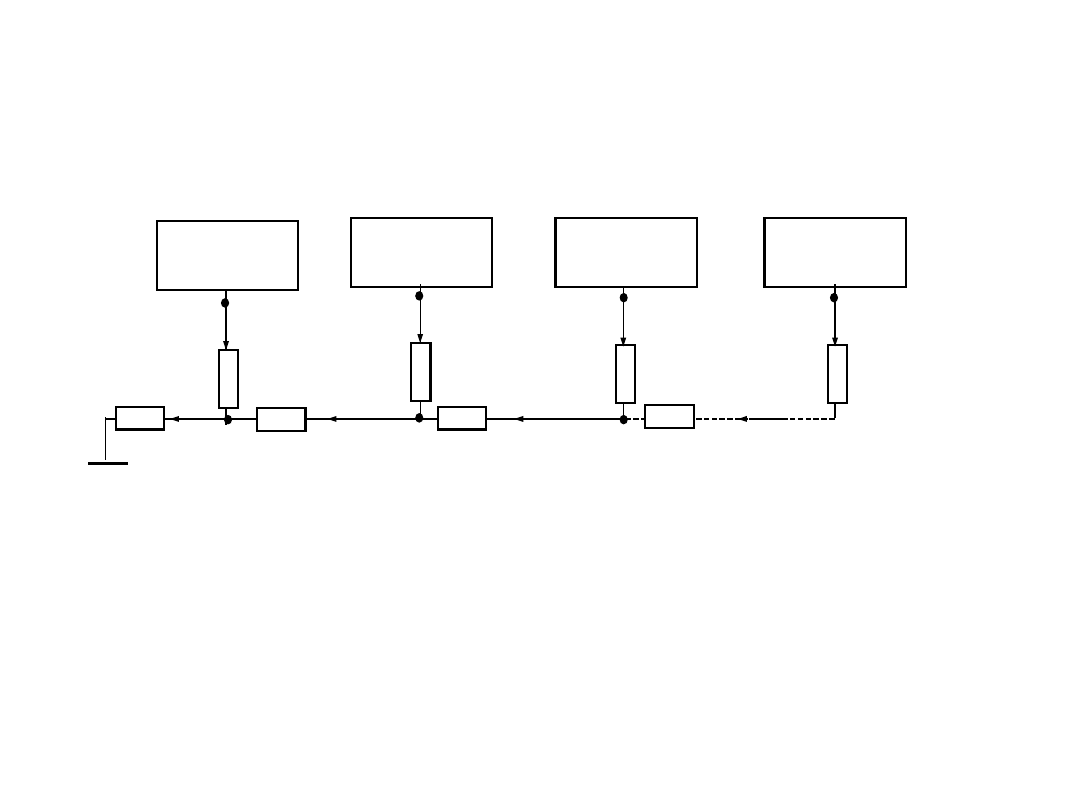
3.2.3. Uziemienie

Przykładem powstania nieekwipotencjalności jest uziemienie

jedno punktowe szeregowe, układ zastępczy jest pokazany

niżej.

Własny potencjał odniesienia pierwszego układu wynosi:

gdzie

- potencjał punkcie w pierwszym punkcie uziemienia.
Podobnie, własne potencjały odniesienia drugiego i trzeciego

punktów wynoszą:

Układ 1

Układ 2

Układ 3

Układ n

I

un

I

u1

I

u2

I

u3

Z

zn

Z

z1

Z

z2

Z

z3

U

1

U

2

U

3

U

n

Z

01

Z

02

Z

03

Z

0n

I

3

I

2

I

n

I

1

U

01

U

02

U

03

U

0n

1

1

1

01

z

u

Z

I

U

U









01

3

2

1

01

1

1

...

Z

I

I

I

I

Z

I

U

un

u

u

u















2

2

2

02

z

u

Z

I

U

U





3

3

3

03

z

u

Z

I

U

U





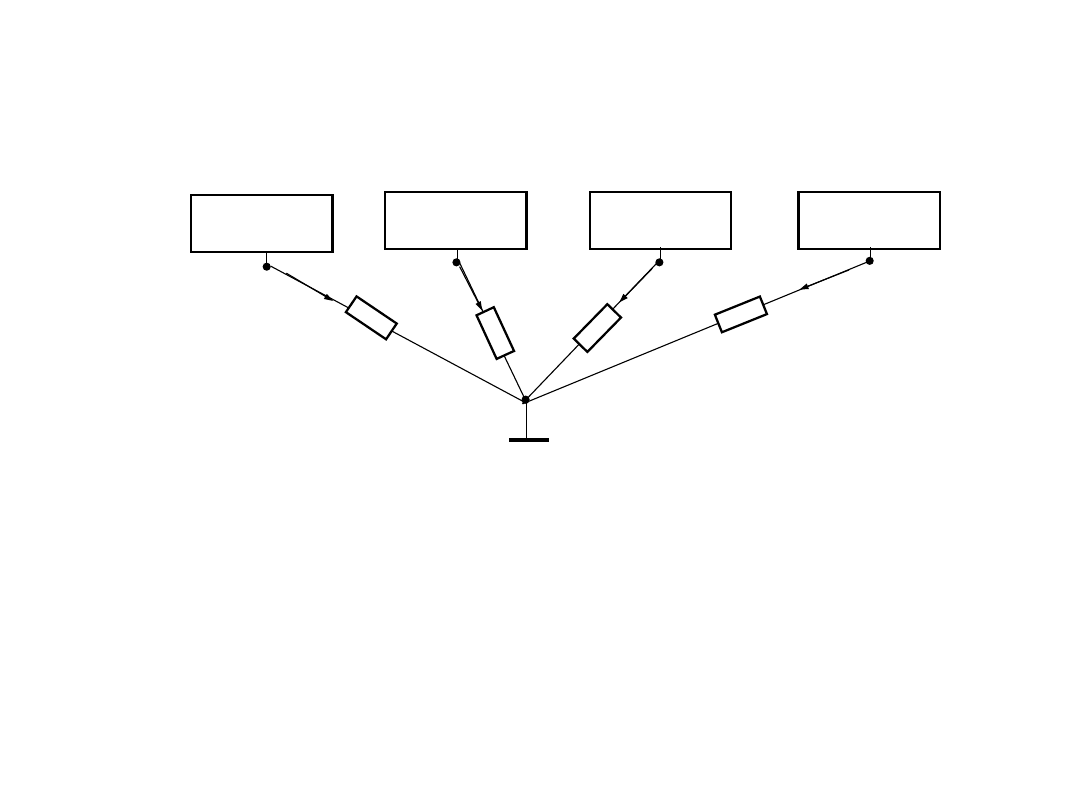
3.2.3. Uziemienie

Dla uniknięcia wzajemnych wpływów prądów od różnych

układów należy wykorzystać jednopunktowe uziemienie

równoległe

Przy takim uziemieniu potencjały odniesienia układów (U

01

, U

02

, U

03

,...,

U

0n

) są zależny tylko od wartości własnych prądów oraz rezystancji

uziemienia (Z

z1

, Z

z2

, Z

z3

,..., Z

zn

).

Mogą być stosowane jednopunktowe uziemienia mieszane (szeregowo-

równolegle).

Układ 1

Układ 2

Układ 3

Układ n

I

un

I

u1

I

u2

I

u3

Z

zn

Z

z1

Z

z2

Z

z3

U

01

U

02

U

03

U

0n

3.2.3. Uziemienie

Należy pamiętać że rezystancja uziemienia zależy nie tylko od

materiału i wymiarów geometrycznych (szerokość, długość, grubość)

jednak także w dużym stopniu od częstotliwości (długości fali)

sygnałów w danym obwodzie pomiarowym.

Przy stosunkowo małych (w porównaniu do długości fali)

odległościach pomiędzy punktami płaszczyzny

(L/<1/20=0.05) wartość impedancji równa się:

, [/],

gdzie R

DC

, [/] - rezystancja powierzchniowa dla prądu stałego;

k=R

RF

/R

DC

– współczynnik, wyrażający stosunek rezystancji na

prądzie zmiennym oraz stałym.

Przy L/=1/8=0,125 wartość impedancji równa się:

, [/].

A przy L/>1/8=0,125 wartość impedancji może mieć znacznie

większe wartości.

W

L

R

k

Z

DC





W

L

R

k

Z

DC



2

3.2.3. Uziemienie

Przykładowo, dla płaszczyzny odniesienia (uziemienia)

wykonanej z miedzi przy L0,5 m, szerokości W5 mm,

częstotliwości f100 kHz (3 km) obliczamy  [/],

L/=0.1710

-3

<1/20, dla tego

Taka sama płaszczyzna wykonana ze stali (

w

1000, 

w

0.1) ma

impedancję o wartości 100 razy większą.

Przy częstotliwości powyżej 10 MHz oraz dużej odległości

układów od wspólnego punktu uziemienia może okazać się że

niektóre z rezystancji uziemienia (Z

z1

, Z

z2

, Z

z3

,..., Z

zn

) są duże

(wzrost długości powoduje wzrost wpływu składowej

indukcyjnościowej) .















m

W

L

R

Z

RF

22

.

8

005

.

0

/

5

.

0

10

22

.

8

5

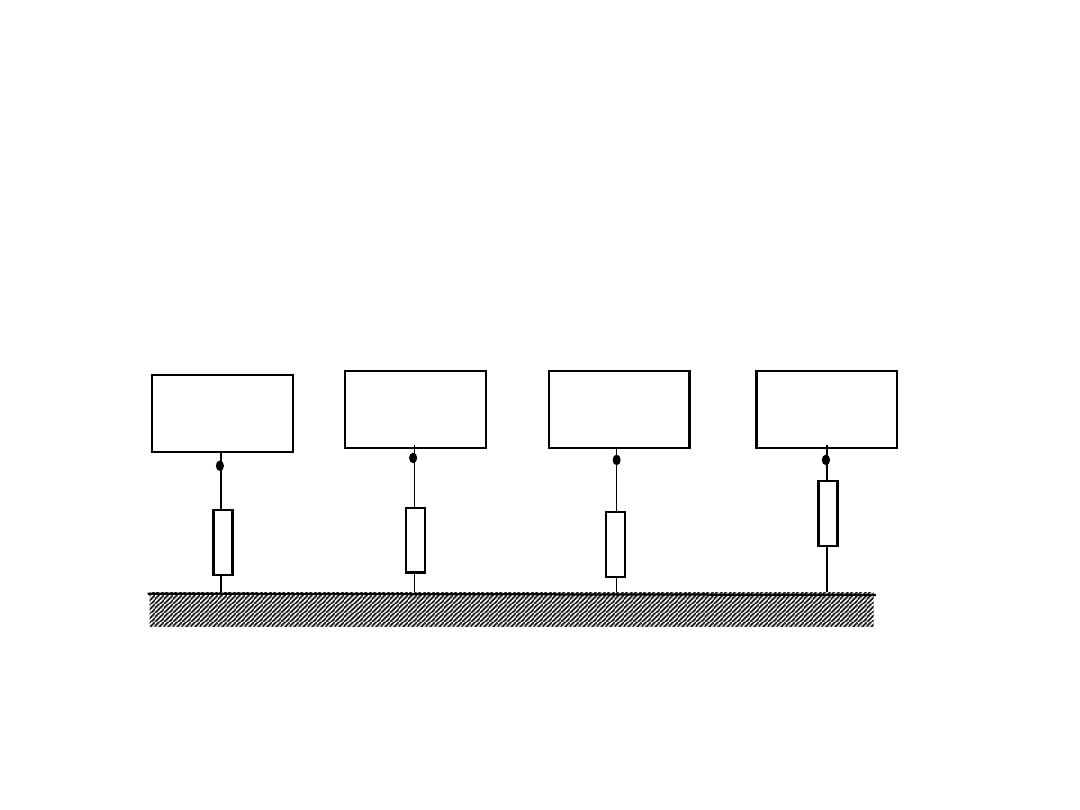
3.2.3. Uziemienie

W takich przypadkach jest rekomendowane uziemienie

wielopunktowe.

Przy tym płaszczyzny uziemienia obecnie są wykonywane z

cienkiej warstwy srebra lub nawet złota pokrywającej

praktycznie w całości elementy konstrukcyjne (tak zwane

chassis) układu.

Uziemienie jest wykonywane krótkimi przewodami o malej

indukcyjności.

Układ 1

Układ 2

Układ 3

Układ n

Z

zn

Z

z1

Z

z2

Z

z3

Chassi
s

3.2.3. Uziemienie

Dla zapewnienia skuteczności uziemienia w szerokim zakresie

częstotliwości wykorzystuje się uziemienie kombinowane:
jednopunktowe dla składowych niskoczęstotliwościowych,
oraz przez kondensatory (o pomijalnie małych
indukcyjnościach wyprowadzeń) wielopunktowe do chassis.

Rekomendacje:

- W realizacjach praktycznych systemów

pomiarowych powinny być przewidywane co
najmniej

trzy oddzielne systemy uziemienia

:

dla

sygnałów

(obwodów)

analogowych pomiarowych

;

dla

sygnałów

(obwodów)

cyfrowych

;

dla

uziemienia ochronnego

,

które mogą mieć połączenie tylko w jednym punkcie

.

3.2.3. Uziemienie

Dla zapewnienia skuteczności uziemienia w szerokim zakresie

częstotliwości wykorzystuje się uziemienie kombinowane:

jednopunktowe dla składowych niskoczęstotliwościowych, oraz

przez kondensatory (o pomijalnie małych indukcyjnościach

wyprowadzeń) wielopunktowe do chassis.

Rekomendacje:

-

Rezystancja przewodów oraz warstw uziemiających

zależy od ich materiału i parametrów

geometrycznych oraz częstotliwości sygnałów

.

-

W zakresie małych częstotliwości (do ok. 1 MHz)

rekomenduje się uziemienie jednopunktowe

równoległe.

-

W zakresie dużych częstotliwości (powyżej ok.

10 MHz) rekomenduje się uziemienie wielopunktowe

krótkimi przewodami do płaszczyzny odniesienia w

postaci cienkiej warstwy srebra

lub nawet złota

pokrywającej praktycznie w całości elementy

konstrukcyjne (tak zwane chassis) układu.

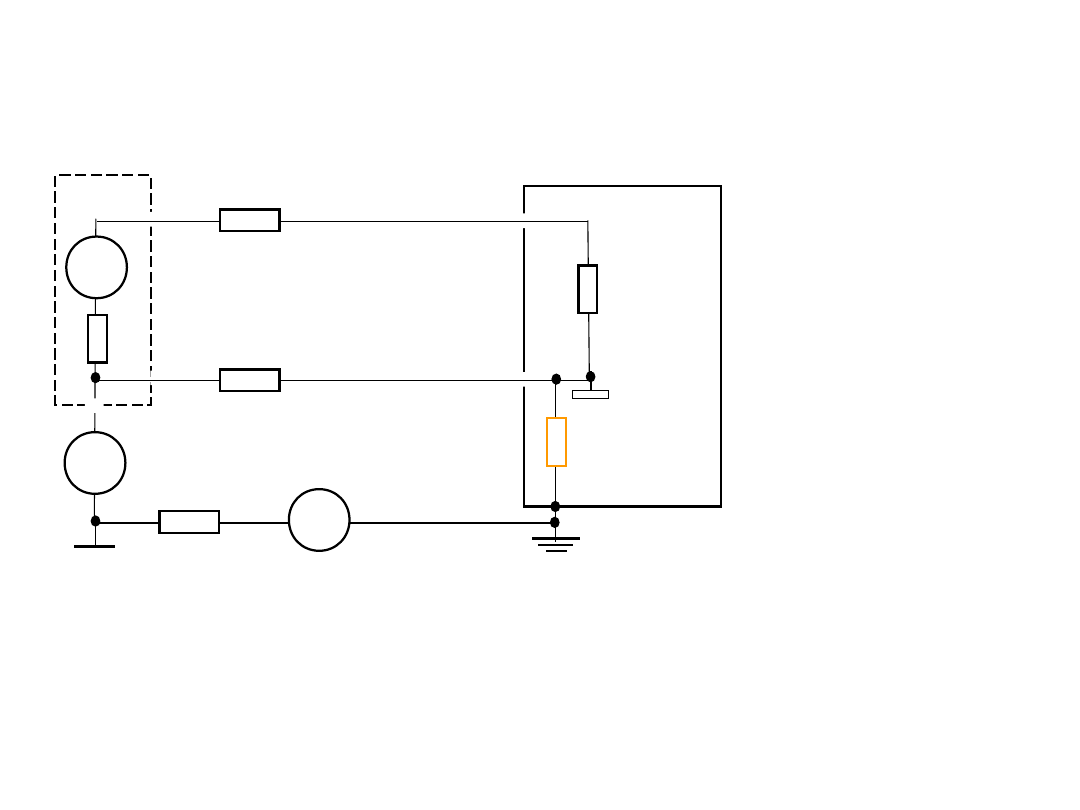
3.3. Zabezpieczenie (ekranowanie)

ekwipotencjalne

3.3.1.Typowe połączenie obiektu oraz narzędzi

pomiarowego

• R

x

- rezystancja źródła sygnału,

• R

l1

, R

l2

- rezystancja przewodów,

• R

we

- rezystancja wejściowa odbiornika sygnału

• R

iz

– rezystancja izolacji pomiędzy wejściami sygnałowymi i

obudową przyrządu

R

l2

R

we

U

x

R

iz

Układ 2

R

z

R

l1

ZU

ZŹ

ZO

R

x

Układ 1

U

cm

U

z

ZU – “ziemia” układu
ZO – “ziemia” odbiornika
ZŻ – “ziemia” źrudła
U

cm

– napięcie wspólne

U

z

– napięcie uziemienia

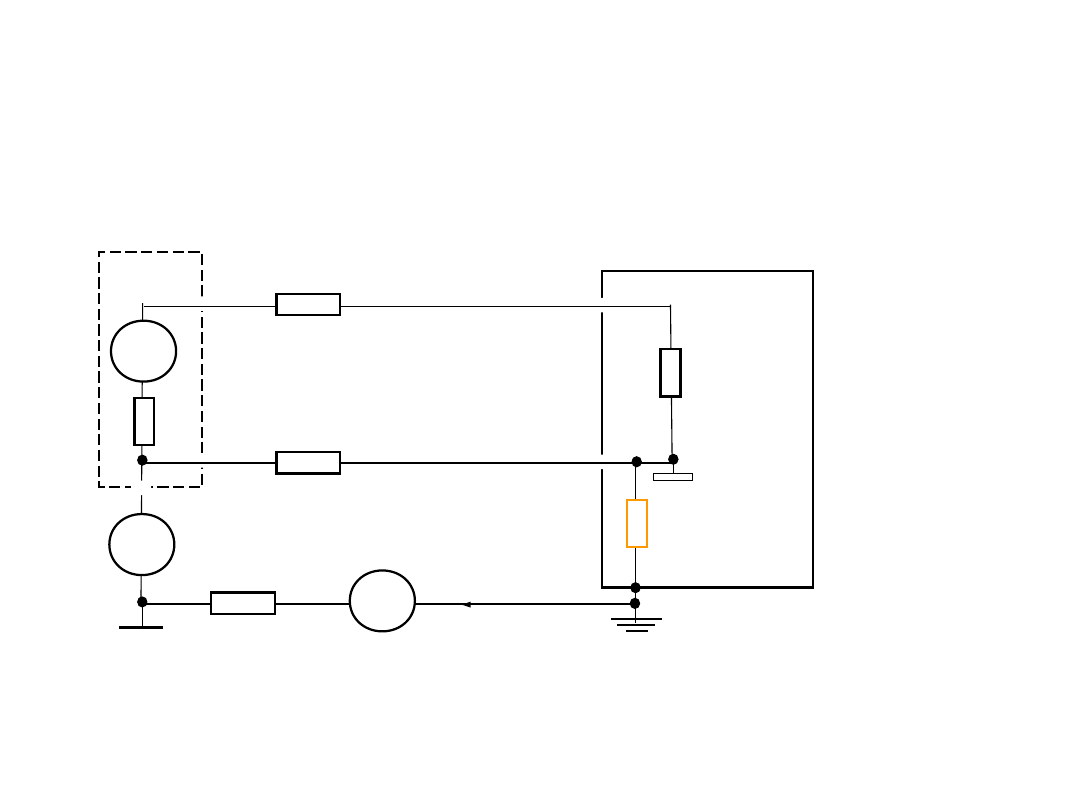
3.3.1.Analiza wpływu zakłócenia wspólnego przez R

iz

Typowy lub najgorsze wartości:

R

x

≈1…100 

;

R

l1

=R

l2

≈1…1000 ;

R

z

≈1…100 

R

we

≈>1…10 M; R

iz

≈>1…10 G; U

cm

≈230 V; U

z

 10V

Uproszczenia

: R

we

=10 M >>R

l2

+R

x

=1000 +100 

R

1sum

=R

we

+R

l2

+R

x

≈R

we

=

10 M; R

l1

R

1sum

R

l1

R

iz

>>R

l1

R

1sum

+R

z

R

l2

<1000



R

we

=10M

U

x

R

iz

10 G

Układ 2

R

z

10

R

l1

<1000

ZU

ZŹ

ZO

R

x

100

Układ 1

U

cm

230V

U

z

 10V

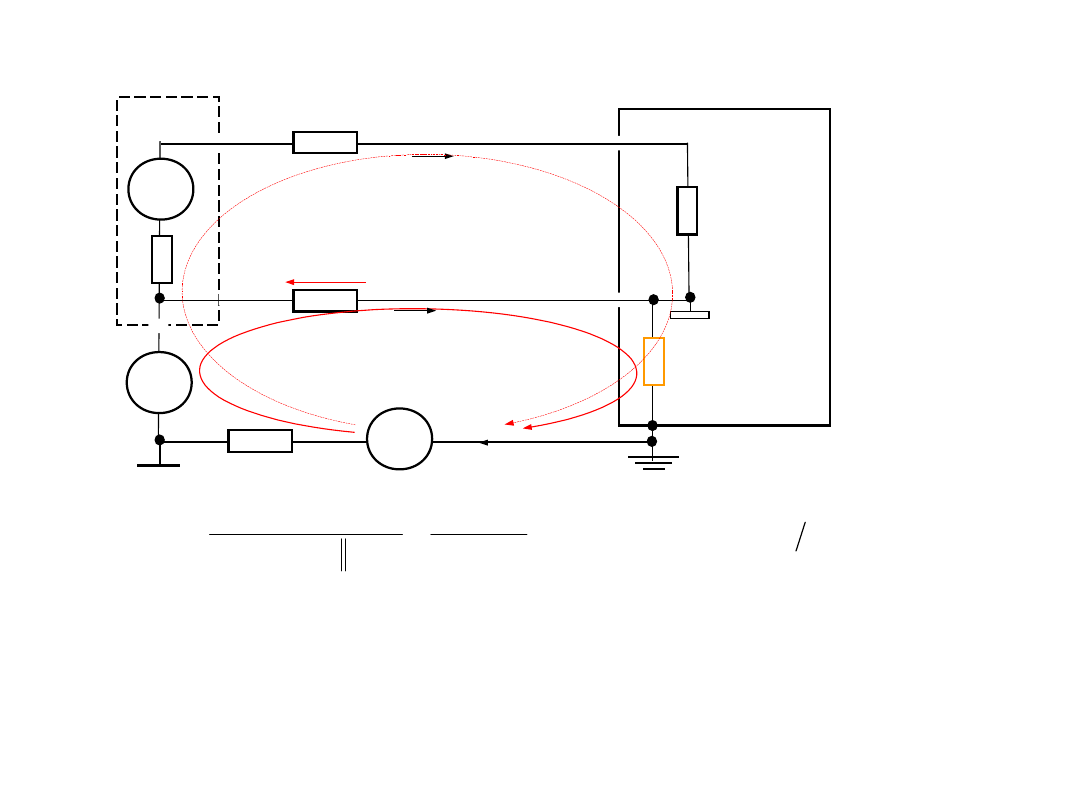
3.3.1.Analiza wpływu zakłócenia

wspólnego

I

2

=I

1

/10

4

<<I

1

R

l2

1000

R

we

=10M

U

x

I

Riz

=I

1

+I

2

25nA

R

iz

10 G

Układ 2

R

z

10

R

l1

1000

ZU

ZŹ

ZO

R

x

100

I

1

I

Riz

25nA

Układ 1

U

cm

230V

U

l1

=I

1

R

l1

25μV

U

z

 10V

iz

z

cm

sum

z

iz

z

cm

Riz

R

U

U

R

R

R

R

U

U

I

I















2

1

1





nA

G

V

I

Riz

25

10

10

230









U

l1

=25 nA1000 =25 

μV

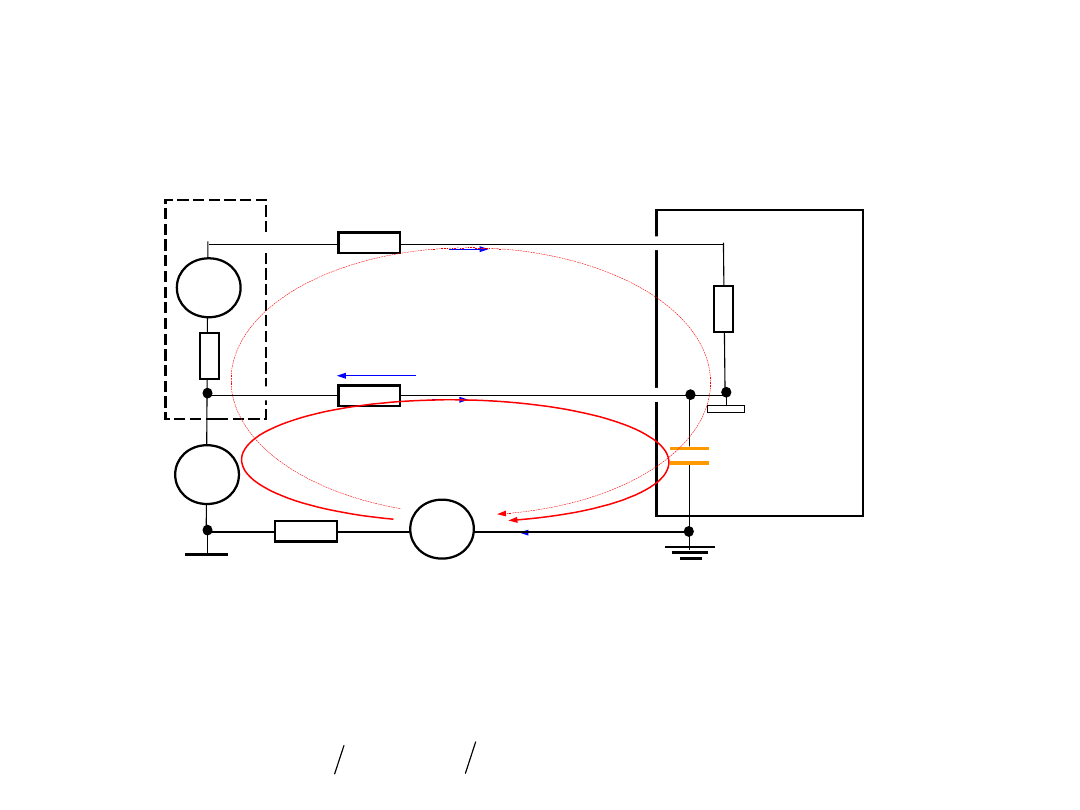
3.3.1.Analiza wpływu zakłócenia wspólnego

przez C

iz

Jeszcze gorsza sytuacja występuje w skutek działania pojemności
pasożytniczej C

iz

pomiędzy obudową odbiornika a obwodem

wspólnym

Typowa wartość pojemności wynosi około kilku dziesięć pikofarad:
przyjmiemy

C

iz

≈32 pF

.

Wtedy na częstotliwości sieciowej (f=50 Hz) impedancja tej
pojemności wynosi

U

z

10V

R

l2

1000

R

we

=10M

U

x

I

c

=I

1

+I

2

2,4A

C

iz

32pF

Układ 2

U

z

R

z

10

R

l1

1000

ZU

ZŹ

ZO

R

x

100

I

1

I

c

2,4A

Układ 1

U

cm

230V

U

l1c

=I

1

R

l1

2,4mV

I

2

=I

1

/10

4

<<I

1























M

fC

Z

iz

Ciz

100

10

32

314

1

2

1

12



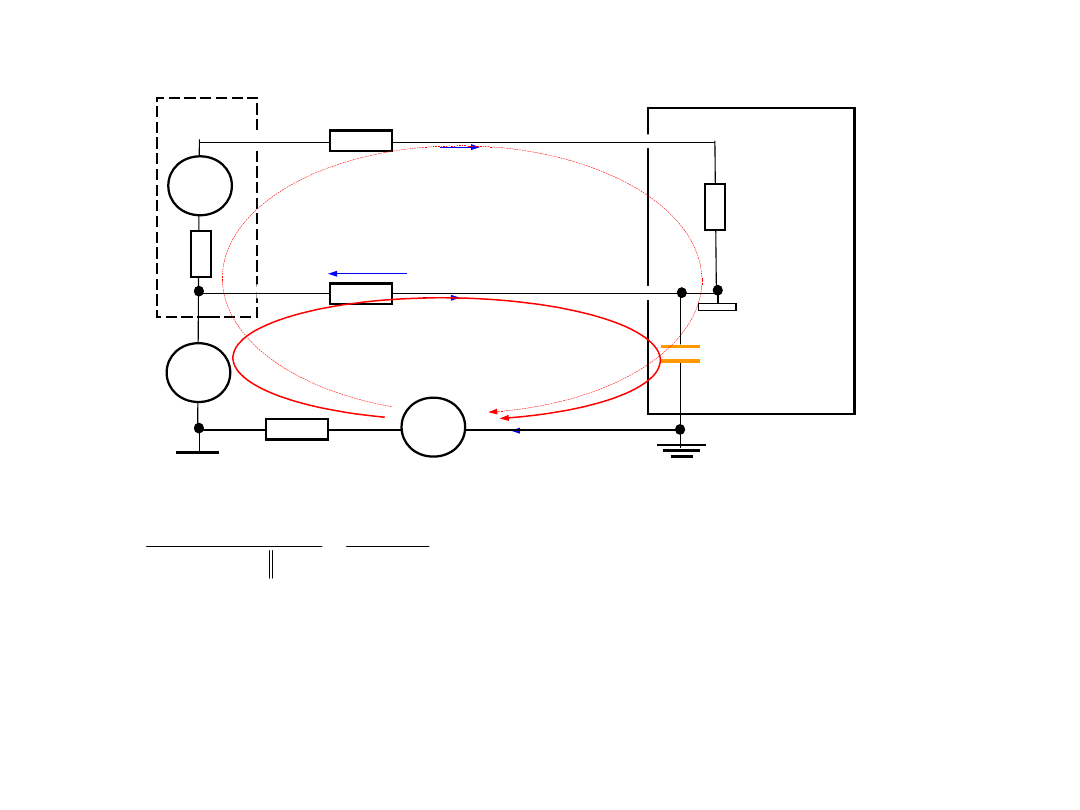
3.3.1.Analiza wpływu zakłócenia wspólnego

przez C

iz

Wartość napięcia zakłócającego normalnego wynosi

U

l1

≈2,4 



A



1000 



≈2,4 mV.

U

z

10V

R

l2

1000

R

we

=10M

U

x

I

c

=I

1

+I

2

2,4A

C

iz

32pF

Układ 2

U

z

R

z

10

R

l1

1000

ZU

ZŹ

ZO

R

x

100

I

1

I

ciz

2,4A

Układ 1

U

cm

230V

U

l1c

=I

1

R

l1

2,4mV

I

2

=I

1iz

/10

4

<<I

1





iz

z

cm

Ciz

z

cm

sum

z

Ciz

z

cm

Ciz

fC

U

U

Z

U

U

R

R

R

Z

U

U

I

I



2

2

1

1



















A

Sm

V

I

I

Ciz

l



4

,

2

10

240

8

1











3.2.2. Współczynnik tłumienia

zakłócenia wspólnego

Stopień szkodliwości zakłócenia wspólnego zależy od stopnia
jego przekształcenia w zakłócenie normalne.
•Stopień takiego przekształcenia charakteryzuje się przez

współczynnik tłumienia zakłócenia wspólnego

(

C

ommon

M

ode

R

ejection

R

atio,

CMRR

).

•CMRR jest to stosunek wartości maksymalnej zakłócenia
wspólnego do wartości maksymalnej spowodowanego nim
zakłócenia normalnego obecnie wyrażana w decybeli





cm

nm

cm

U

U

U

CMRR

max

,

max

,

lg

20



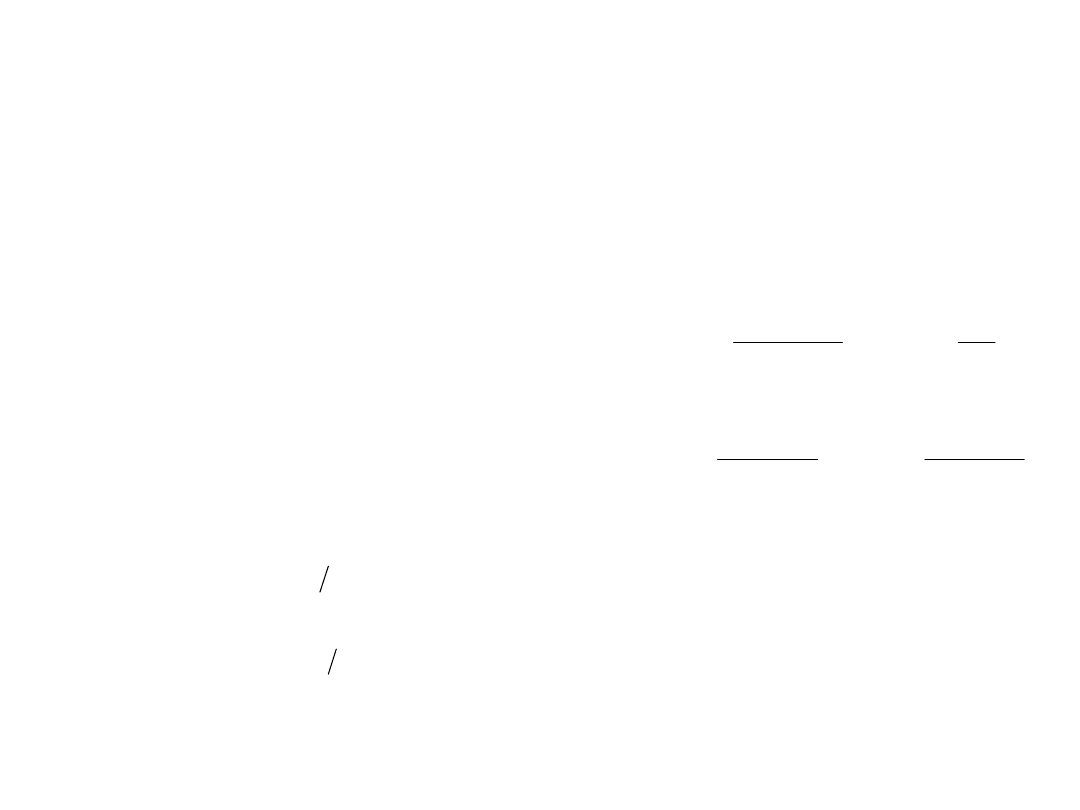
3.2.2. Współczynnik tłumienia

zakłócenia wspólnego

•Współczynniki tłumienia zakłóceń wspólnych są wyrażany

tylko przez

wartości rezystancji oraz pojemności izolacji

(z

jednej strony ) i

rezystancji linii pomiędzy źródłem odbiornikiem

sygnału

(z innej strony) parametry, a mianowicie:

•na prądzie stałym:

•na prądzie przemiennym

• (tłumienie 5

mln razy),

• (tłumienie

100 tys. razy).



































1

,

lg

20

lg

20

l

iz

n

Riz

z

cm

Riz

R

R

U

U

U

CMRR



































1

,

2

1

lg

20

lg

20

l

iz

n

Ciz

z

cm

Ciz

R

fC

U

U

U

CMRR











dB

G

CMRR

Riz

134

10

5

lg

20

1000

5

lg

20

6





















dB

M

CMRR

Ciz

100

100000

lg

20

1000

100

lg

20











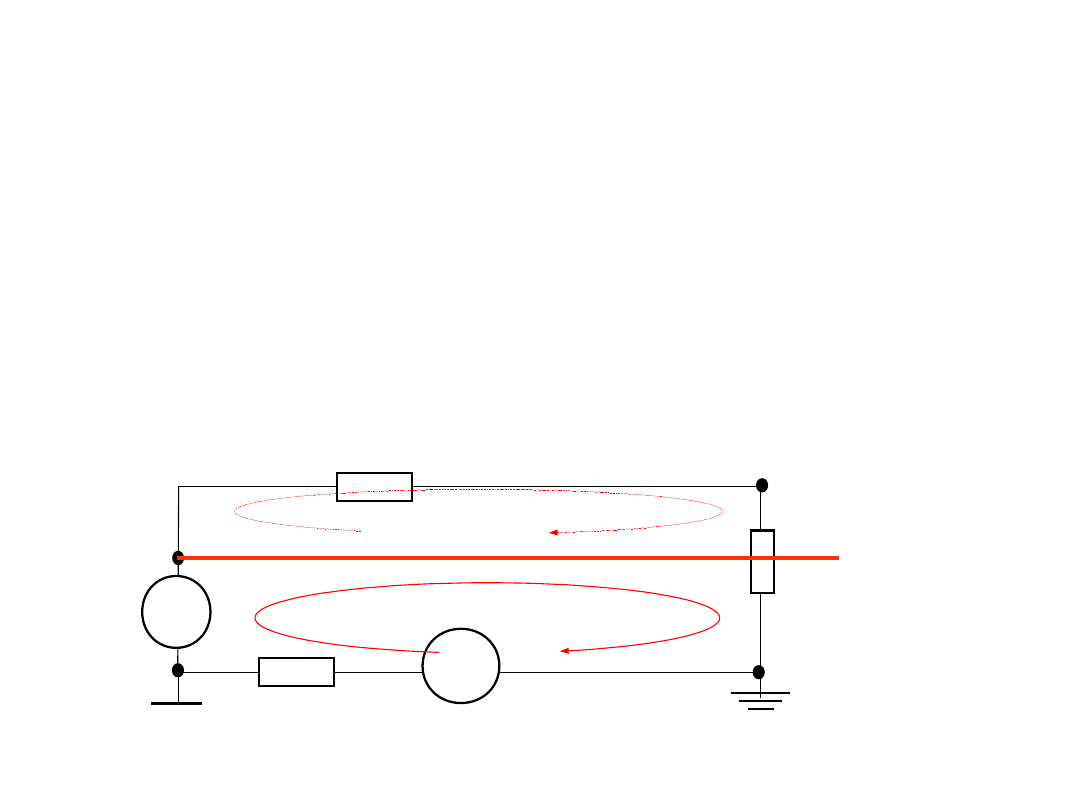
3.3.3. Ekranowanie ekwipotencjalne

•Jeżeli za pośrednictwem przewodu z zerowa rezystancją

(R

E

=0) połączyć punkt A (punkt oddziaływania zakłócenia

wspólnego) z płaszczyzną B (która tez ma zerową rezystancję i
przecina izolację pomiędzy obudową i nisko potencjalnym
wejściem), jak jest pokazano na rys. , wtedy prąd (I

Riz2

) od źródeł

zakłócających będzie płynąć w obwodzie utworzonym tymi
przewodem i płaszczyzną, omijając obwód z przewodem
sygnałowym (I

l1

=0).

R

iz1

I

1

0

U

cm

U

R1

0

I

Riz2

R

z

ZŹ

ZO

U

z

A

B

R

iz2

R

l1

R

AB

=R

E

0

U

AB

0

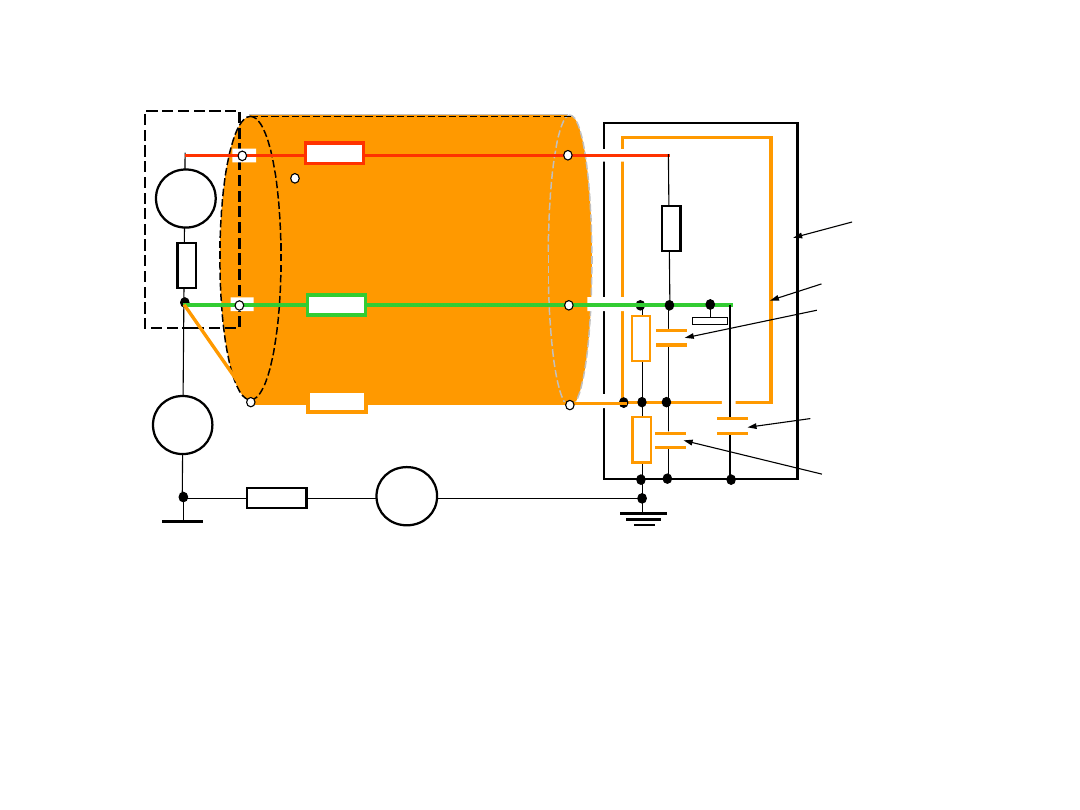
3.3.3. Ekranowanie ekwipotencjalne

•W układzie z ekranowaniem ekwipotencjalnym ma miejsce

się

dwustopniowe przekształcenie zakłócenia

wspólnego w

zakłócenie normalne

.

Ekran

ZŹ

C

iz

, R

iz

R

l2

U

x

C

iz

, R

iz

Układ 2

R

l1

R

x

Układ 1

LO

HI

C

p

=1...2p

F

R

we

ZU

1

2

3

Ekran

Obudow
a

U

z

R

z

ZO

U

uz

E

R

e

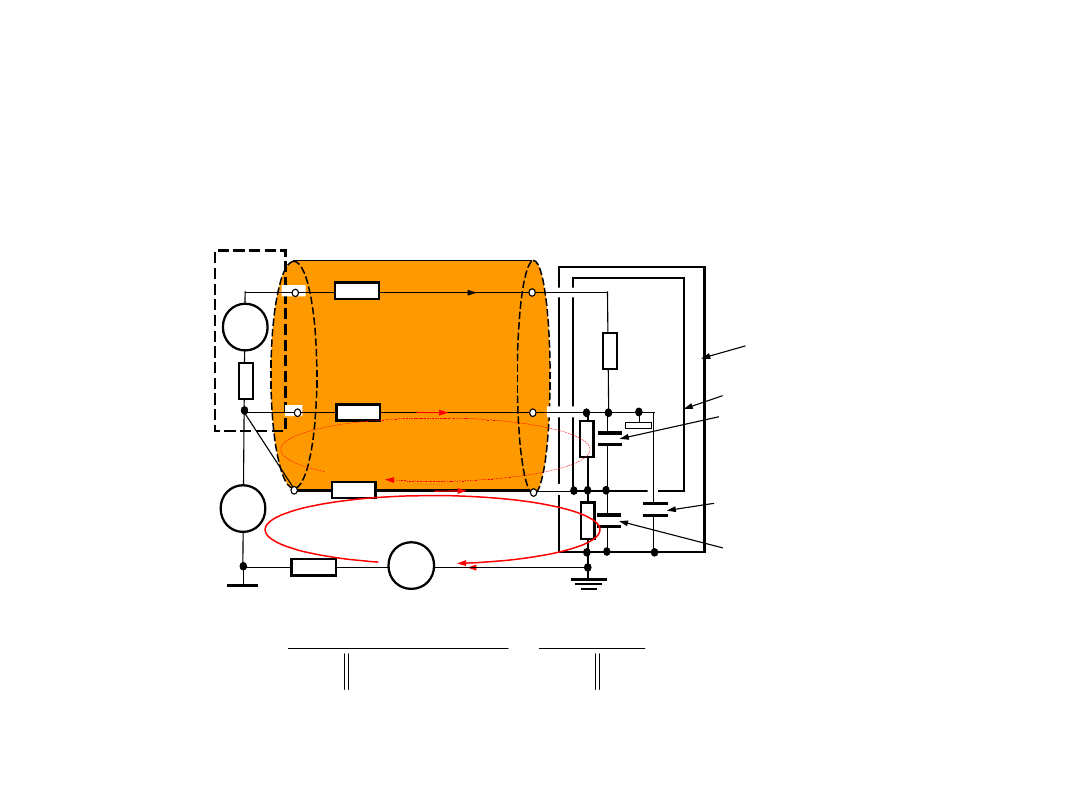
3.3.3. Ekranowanie ekwipotencjalne

Na drugim stopniu zakłóceniem wspólnym staje się spadek

napięcia na ekranie, które powoduje prąd zakłócający przez
rezystancję linii R

l1

zależny od wartości impedancji połączenia

poprzez pojemność izolacji C

iz2

oraz rezystancję izolacji R

iz2

U

l1

=0,1 nA



1000 



=0,1 μV

C

iz1

, R

iz1

R

l2

1000



U

x

C

iz2

, R

iz2

Układ 2

R

l1

1000

R

x

100

I

2

<<I

1

Układ 1

LO

HI

C

p

=

1...2pF

R

we

=

10M

ZU

1

2

3

U

e

5mV

Ekran

Obudow
a

I

iz



5A

Uz

=10 V

R

z

10

ZŹ

ZO

U

uz

230V

I

e

I

iz



5A

E

R

e

1000

I

Rle

U

e

/Z

iz2

0,1nA

U

e1

0,1 V

2

2

2

1

2

2

1

2

iz

e

iz

Ciz

e

l

e

iz

Ciz

e

e

Rl

fC

U

R

Z

U

R

R

R

Z

U

I













nA

Sm

mV

I

e

Rl

1

,

0

10

2

5

8

1











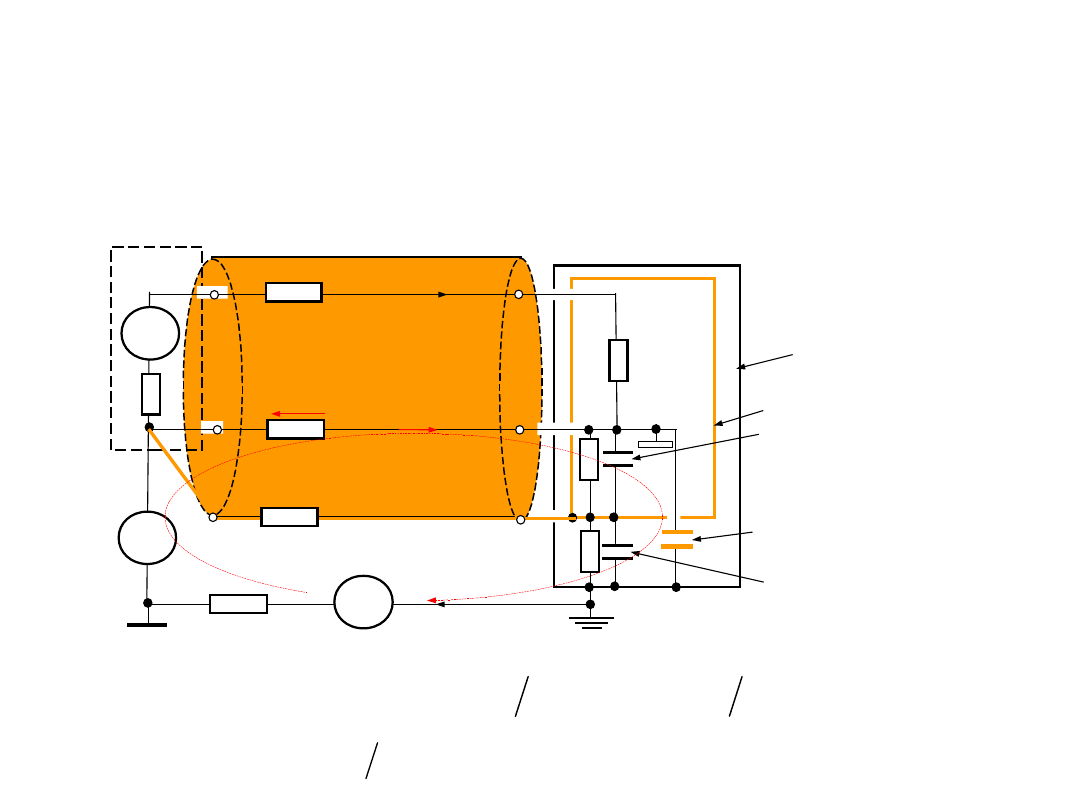
3.3.3. Ekranowanie ekwipotencjalne

Jednak w tym przypadku oprócz rezystancji i pojemności izolacji

pomiędzy linią sygnałową a ekranem (R

iz2

, C

iz2

) oraz pomiędzy

ekranem i obwodami źródeł zakłócających (R

iz1

, C

iz1

) występuje

pasożytnicza (przejściowa) pojemność C

p

) pomiędzy linią sygnałową a

obwodami źródeł zakłócających (obudową).













1

2

1

20

20

l

p

n

,

Cp

z

cm

Cp

R

fC

lg

U

U

U

lg

CMRR









C

iz2

,

R

iz2

R

l2

1000



U

x

C

iz1

,

R

iz1

Układ 2

R

l1

1000

R

x

I

2

<<I

1

Układ 1

LO

HI

C

p

=

1...2pF

R

we

=

10M

ZU

1

2

3

I

Cp

(U

uz

+U

z

)/Z

cp

0,15 A

U

Rl1Cp

I

Cp

R

l1

0,15mV

Ekran

Obudow
a

Uz10 V

R

z

10

ZŹ

ZO

U

uz

230V

E

R

e

1000



I

Cp









dB

Sm

,

lg

CMRR

Cp

125

1000

10

28

6

1

20

10













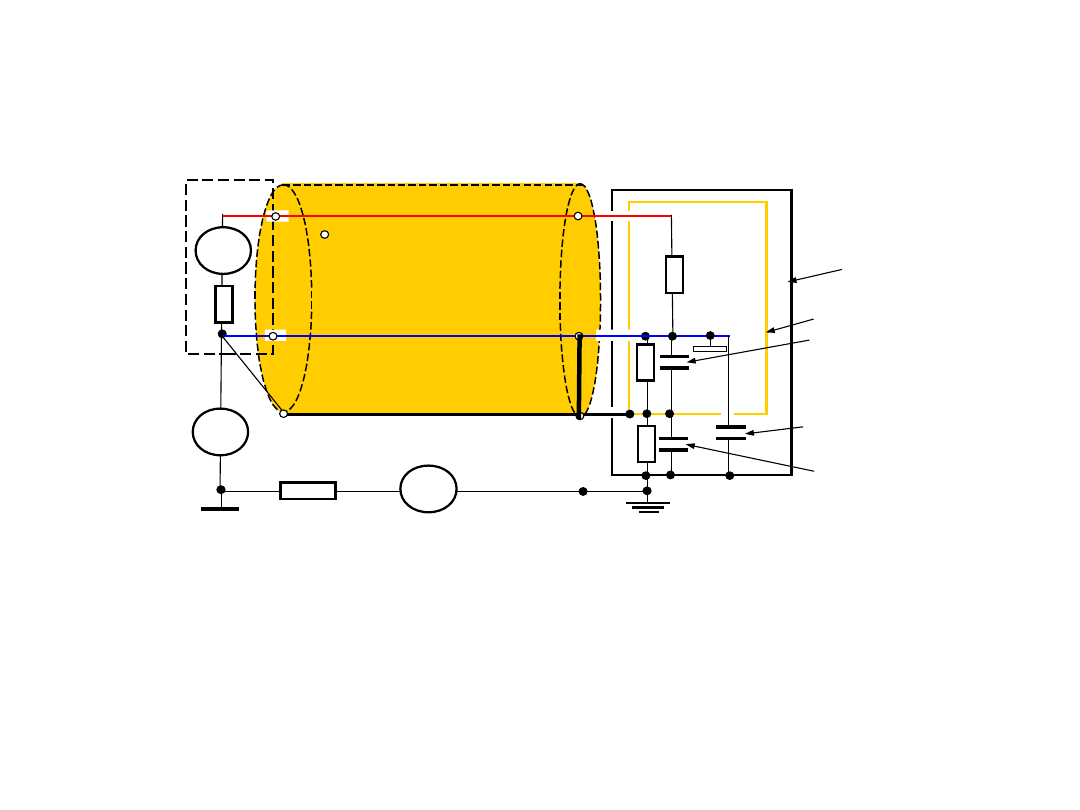
Nieprawidłowe połączenie obiektu i

miernika

Często podczas pomiarów w celu „uproszczenia” połączeń

obiektu badanego i miernika w ostatnim łączą zaciski LO
(potencjał niski) oraz E (ekran)

Przy takim połączeniu traci się skuteczność ekranowania

ekwipotencjalnego.

Ponieważ wtedy oddziaływanie napięcia wspólnego odbywa się

przez izolację C

iz2

, R

iz2

zamiast pojemności przejściowej C

p

, która

w kilku dziesięć razy jest mniejsza od pojemności C

iz2

.

ZŹ

C

iz2

, R

iz2

U

x

C

iz1

, R

iz1

Układ 2

R

x

Układ 1

LO

HI

C

p

=1...2pF

R

we

ZU

1

2

3

Ekran

Obudowa

Uz

R

z

ZO

U

uz

E

Ekran

Nieprawidłowe połączenie obiektu i

miernika

Rekomendację:

- w celu skutecznego tłumienia zakłóceń wspólnych należy

stosować ekranowanie ekwipotencjalne;

- na obiekcie badanym ekran należy podłączać w jak

najbliższym punkcie do oddziaływania zakłócenia wspólnego;

- po stronie miernika nie można łączyć zaciski LO (potencjał

niski) oraz E (ekran), w wyniku czego traci się skuteczność
ekranowania ekwipotencjalnego.

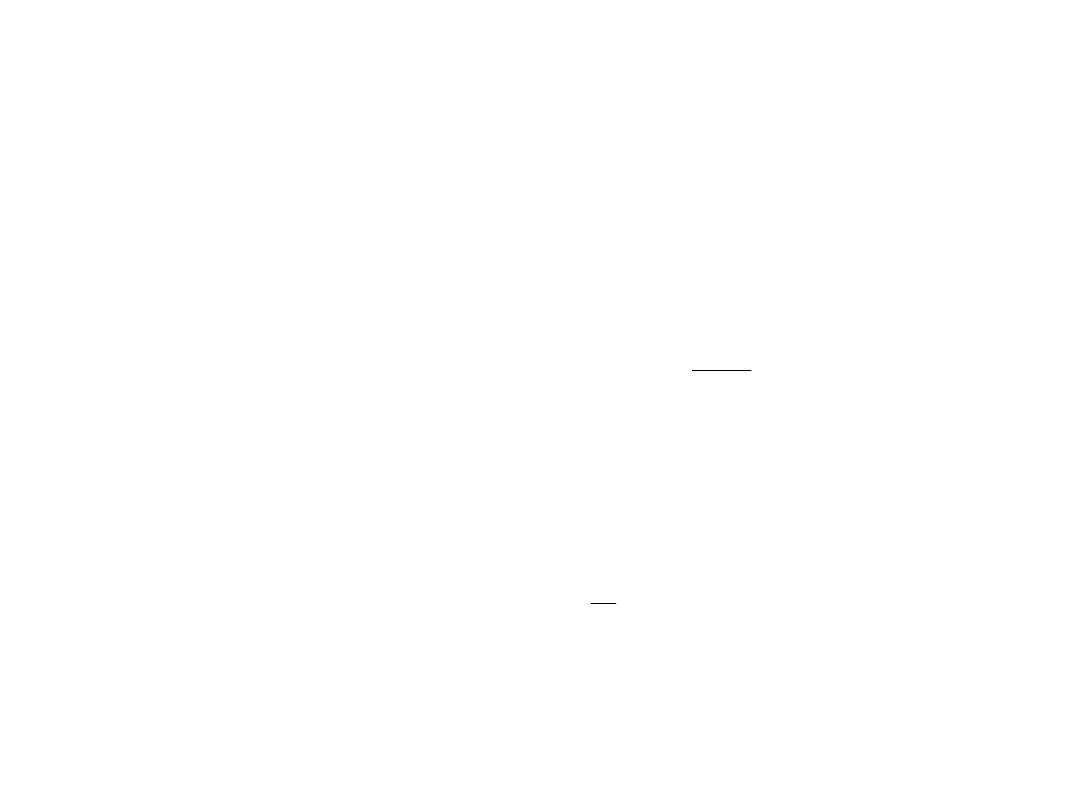
Obliczanie wartości błędu przez

ograniczona wartością współczynnika

tłumienia zakłócenia wspólnego

Jeżeli wartość maksymalna sygnału wspólnego

wynosi wtedy przy

współczynniku tłumienia CMRR maksymalna

wartość napięcia normalnego , w które

zostało transformowane napięcie wspólne równa

się

Na przykład, przy oraz CMRR=100 dB

maksymalna wartość napięcia normalnego

, w które zostało transformowane napięcie

wspólne równa się

wsp

U

max,

norm

U

max,

20

max,

max,

10

CMRR

wsp

norm

U

U







V

U

wsp

230

max,



norm

U

max,

mV

V

U

norm

3

,

2

10

230

20

100

max,









Sumaryczny współczynnik tłumienia

zakłócenia (napięcia) wspólnego

Jeżeli karta pomiarowa zapewnia tłumienie napięć

wspólnego oraz normalnego (szeregowego) wtedy

sumaryczny współczynnik napięcia wspólnego

równa się sumie współczynników

CMMR+NMRR

dla którego maksymalna wartość błędu,

spowodowanego tym zakłóceniem równa się

Na przykład, przy oraz CMMR=100 dB i

NMRR=40 dB maksymalna wartość maksymalna

wartość błędu, spowodowanego zakłóceniem

wspólnym równa się

20

max,

max

10

NMRR

CMRR

wsp

U











V

U

wsp

230

max,



mkV

V

23

10

230

20

40

100

max













 RÓWNOMIERNE

CYFROWE

UŚREDNIANIE

SYGNAŁÓW

Plan wykładu

1. Wstęp. Uśrednianie zwykłe (równoważne).
2.  Tłumienie (eliminacja) składowych

harmonicznych

Cel: Zapoznać się z zasadami oraz wyznaczaniem
podstawowych parametrów uśredniania cyfrowego

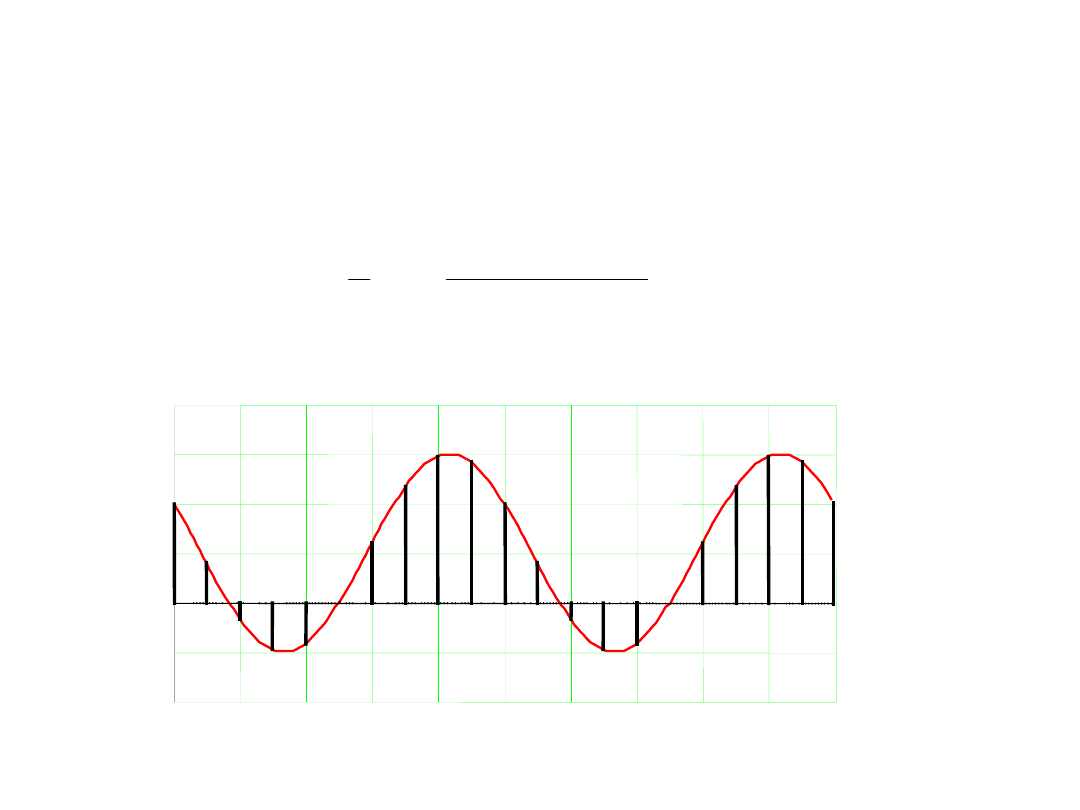
1. Wstęp

Zasada cyfrowego uśredniania polega na wstępnym

przetwarzaniu analogowo-cyfrowym sygnału wejściowego -

skrót: pobranie próbek U

1

, U

2

,…, U

n

) w dyskretny momenty

czasowe t

1

, t

2

,…, t

n

i następnym wyznaczaniu wartości średniej

z N próbek

1

2

4

6

8

10

12

14

16

18

20

u(t)

U

i

i

N

U

U

U

U

U

N

U

N

N

i

i

sr

















...

1

3

2

1

1

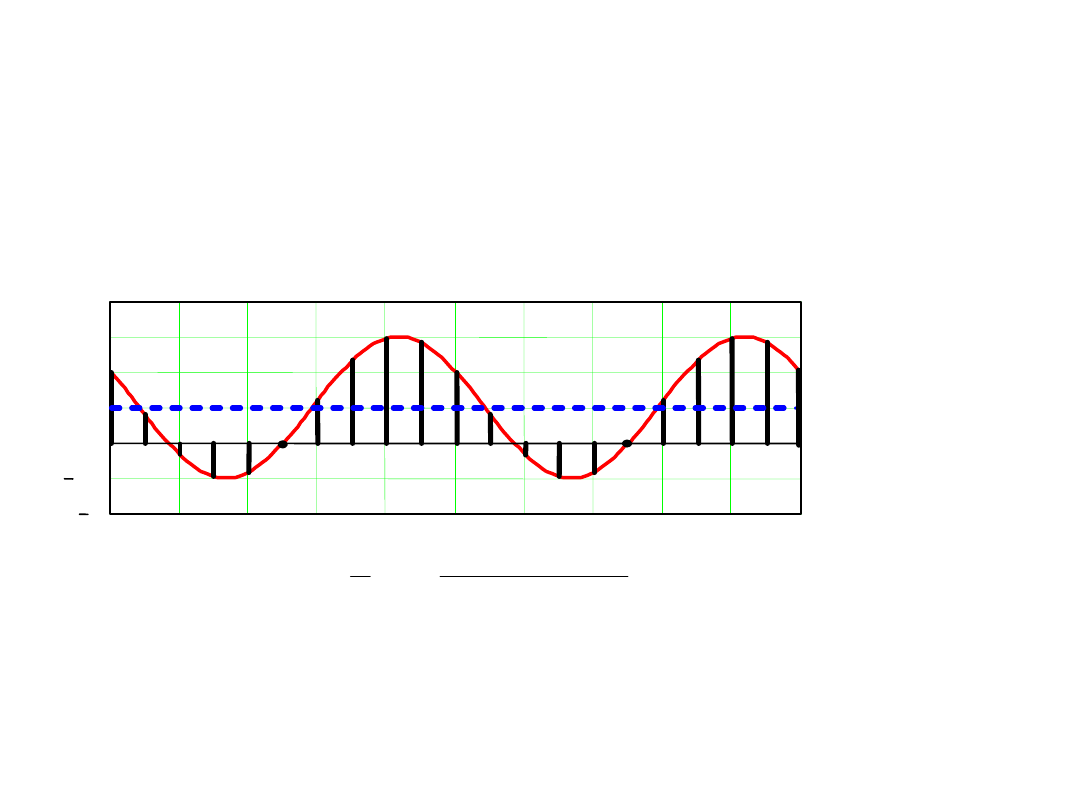
1. Wstęp

W praktyce pomiarowej na drodze uśredniania często są mierzone

parametry sygnałów przemiennych, będących wartościami średnimi

pewnych funkcji wartości chwilowych sygnału:

Wartość składowej stałej sygnału

0

2

4

6

8

10

12

14

16

18

20

1

0.5

0

0.5

1

1.5

2

u(t)

U

i

Us

i

N

U

U

U

U

U

N

U

U

N

N

i

i

DC



















...

1

3

2

1

1

0

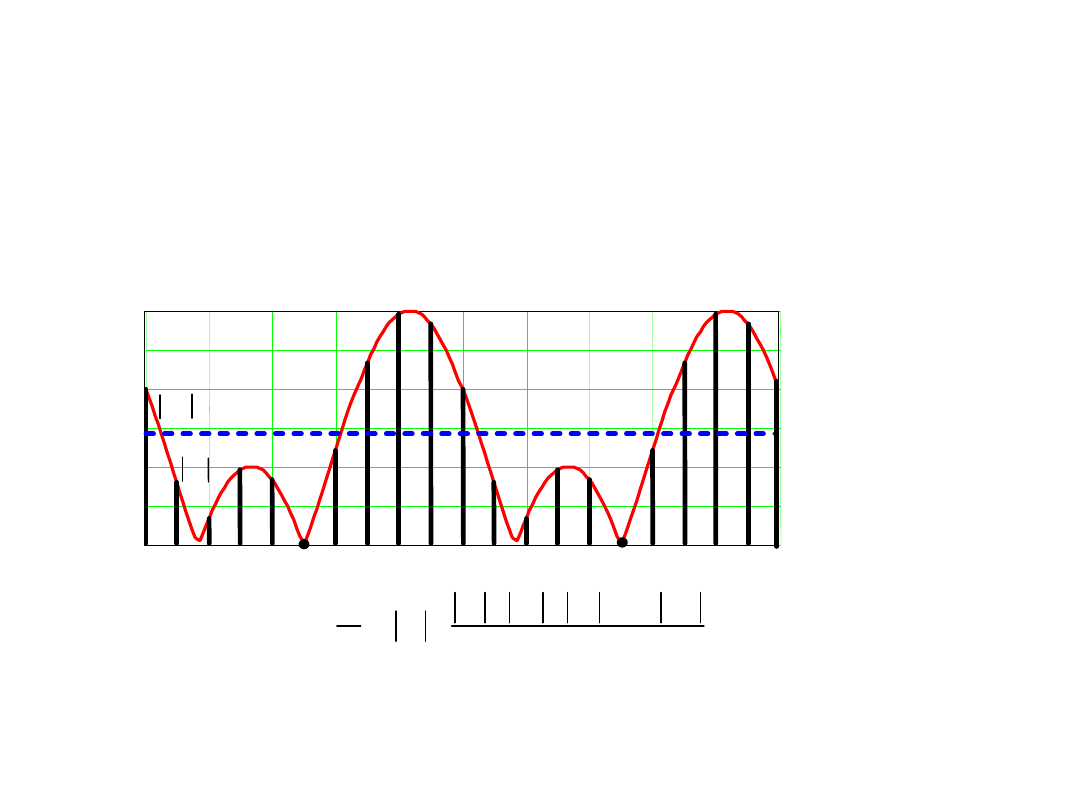
1. Wstęp

W praktyce pomiarowej na drodze uśredniania często są mierzone

parametry sygnałów przemiennych, będących wartościami średnimi

pewnych funkcji wartości chwilowych sygnału:

Wartość średnia wyprostowana sygnału

0

2

4

6

8

10

12

14

16

18

20

0

0.25

0.5

0.75

1

1.25

1.5

u(t)

U

s

i

U

i

N

U

U

U

U

U

N

U

N

N

i

i

SW

















...

1

3

2

1

1

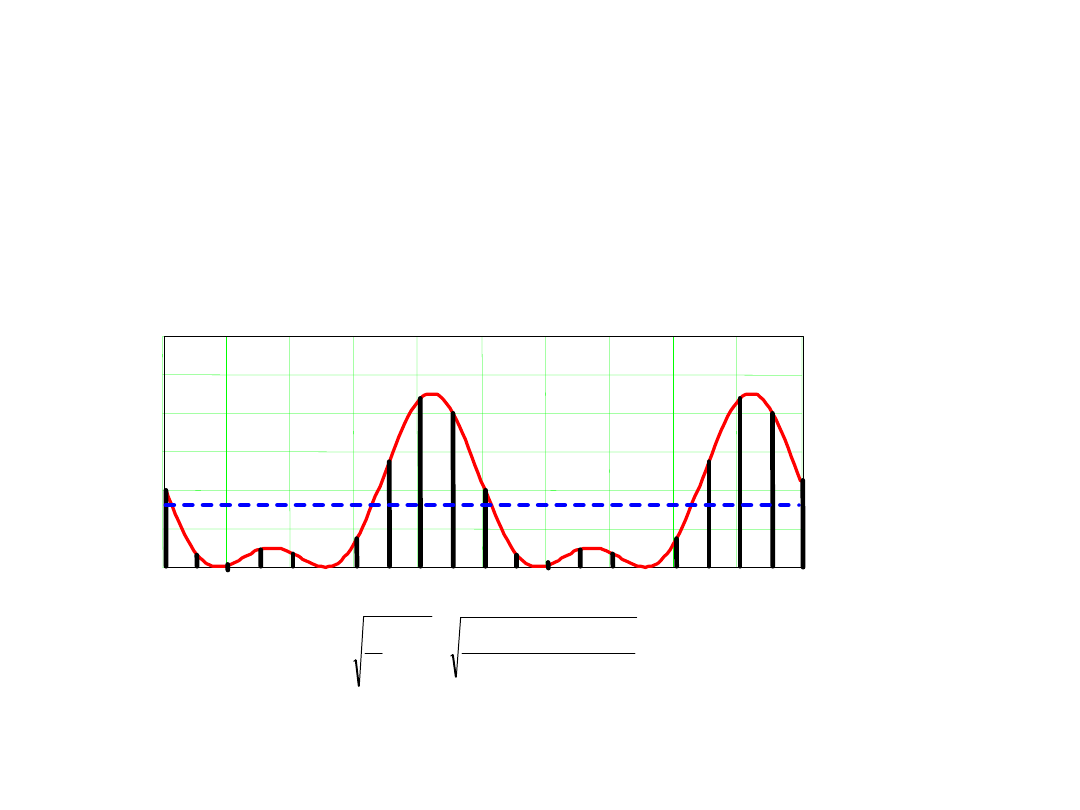
1. Wstęp

W praktyce pomiarowej na drodze uśredniania często są mierzone

parametry sygnałów przemiennych, będących wartościami średnimi

pewnych funkcji wartości chwilowych sygnału:

Wartość skuteczna sygnału

0

2

4

6

8

10

12

14

16

18

20

0

0.5

1

1.5

2

2.5

3

u

(

t)

2

U

i

2

U

RMS

i

2

N

U

U

U

U

U

N

U

U

N

N

i

i

TrueRMS

2

2

3

2

2

2

1

1

2

...

1



















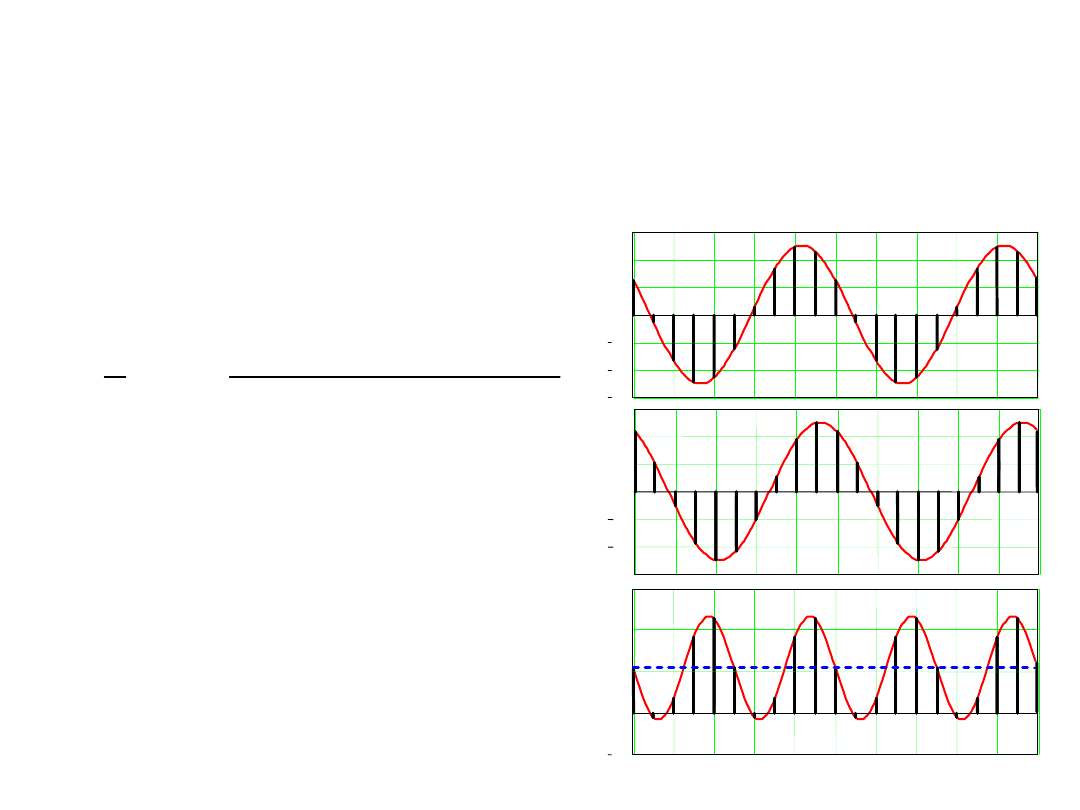
1. Wstęp

W praktyce pomiarowej na drodze uśredniania często są mierzone

parametry sygnałów przemiennych, będących wartościami średnimi

pewnych funkcji wartości chwilowych sygnału:

Wartość mocy czynnej

-0.6

0

2

4

6

8

10

12

14

16

18

20

0.4

0.2

0

0.2

0.4

0.6

i(t)

I

i

i

0

2

4

6

8

10

12

14

16

18

20

1.2

0.8

0.4

0

0.4

0.8

1.2

u(t)

U

i

i

0

2

4

6

8

10

12

14

16

18

20

0.2

0

0.2

0.4

0.6

i

P

i

P

p(t)

a

b

c

N

I

U

I

U

I

U

I

U

I

U

N

P

N

N

N

i

i

i



























...

1

3

3

2

2

1

1

1

2. Tłumienie (eliminacja) składowych

harmonicznych w trakcie ich

uśredniania

2.1. Skuteczność uśredniania.

We wszystkich algorytmach pomiarów parametrów sygnałów

zmiennych po odpowiednim przetwarzaniu sygnału
wejściowego istnieją:

- korzystna składowa

w postaci

składowej stałej

Ux;

- niekorzystna składowa

w postaci

składowych harmonicznych

Uh(t) przetworzonego sygnału

)

(

i

h

x

i

t

U

U

U





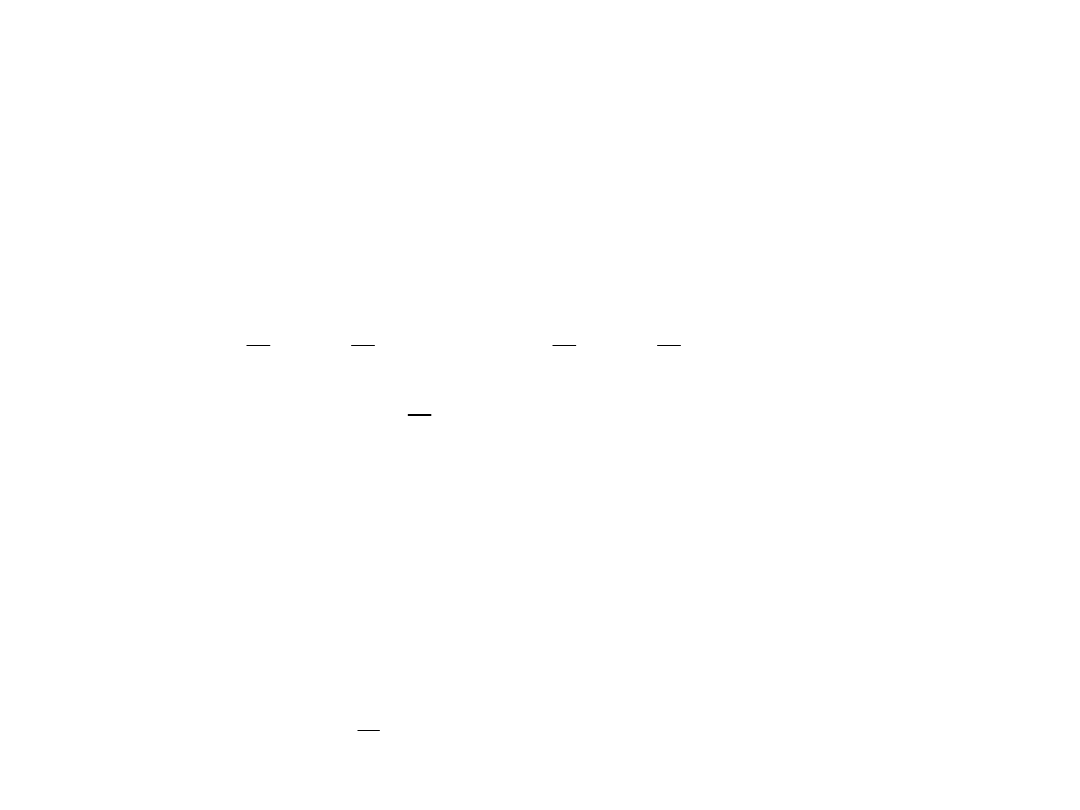
2. Tłumienie (eliminacja) składowych

harmonicznych w trakcie ich

uśredniania

2.1. Skuteczność uśredniania.

Według definicji parametrów sygnałów zmiennych zadaniem

operacji uśredniania

-

wyznaczanie składowej stałej

przetworzonego odpowiednio do

mierzonego parametru sygnału;

-

eliminacja (tłumienie) składowych harmonicznych

,

wynikających podczas odpowiedniego przetwarzania
sygnału.







































N

i

i

h

x

N

i

i

h

N

i

x

N

i

i

h

x

N

i

i

t

U

N

U

t

U

N

U

N

t

U

U

N

U

N

1

1

1

1

1

)

(

1

)

(

1

1

)

(

1

1

0

)

(

1

1











h

N

i

i

h

U

t

U

N

2. Tłumienie (eliminacja) składowych

harmonicznych w trakcie ich

uśredniania

2.1. Skuteczność uśredniania.

Skuteczność eliminacji (tłumienia) niekorzystnych składowych

harmonicznych

na drodze uśredniania próbek sygnału może

być scharakteryzowana

- błędem uśredniania , który powinien dążyć do zera ,

- współczynnikiem tłumienia K

tł

, jako stosunek amplitudy

składowej harmonicznej do modułu maksymalnego błędu

0





h

U

m

h

U

,

max

,

h

U



max

,

,

h

m

h

tl

U

U

K























max

,

,

,

lg

20

h

m

h

dB

tl

U

U

K

2. Tłumienie (eliminacja) składowych

harmonicznych w trakcie ich

uśredniania

Podstawowe zagadnienia cyfrowego uśredniania

sygnałów :

•

Wyznaczanie minimalnej liczby N

min

uśrednianych

próbek sygnału niezbędnych dla teoretycznie całkowitej
eliminacji składowych harmonicznych; oraz

•

Wyznaczanie okresu T

d

(częstotliwości f

d

) próbkowania.

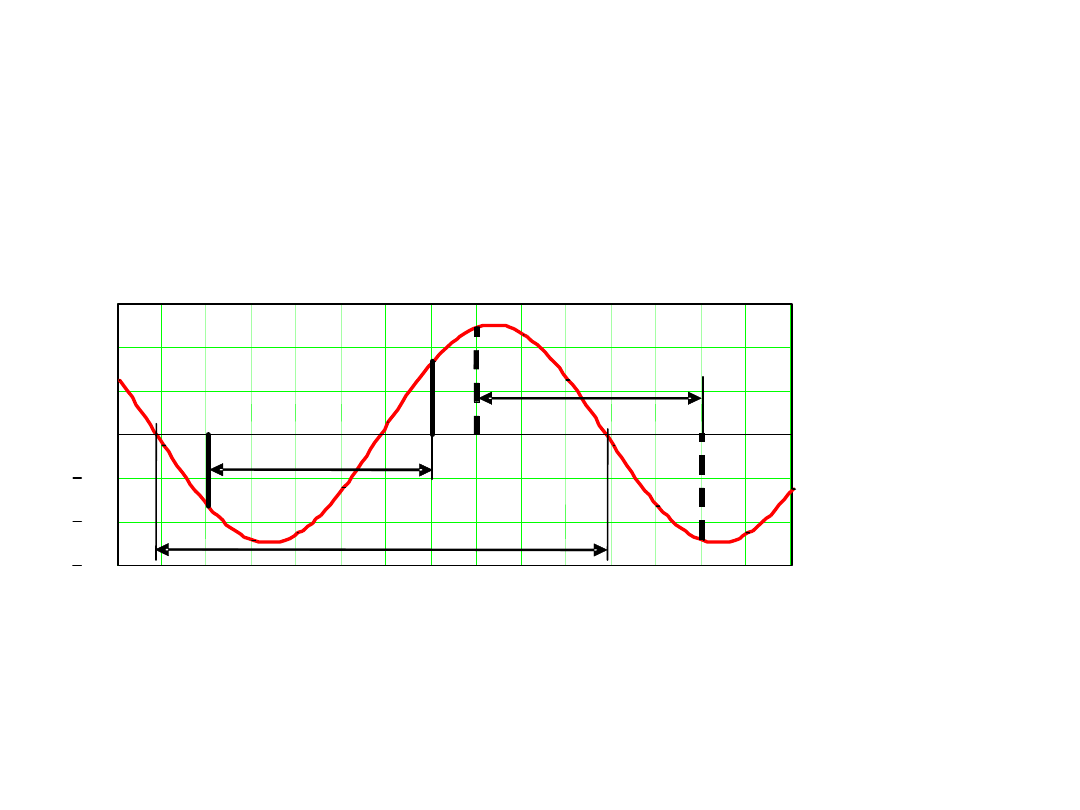
2. Tłumienie (eliminacja) składowych

harmonicznych w trakcie ich

uśredniania

2.2. Jedna składowa harmoniczna sygnału przetworzonego.

•Minimalna liczba uśrednianych próbek

N

min

=2

•Okres próbkowania

T

d

=T/2

Jest to możliwie dzięki temu, że dwie wartości (próbki) sygnału

harmonicznego pobrane w momenty czasowe

t1

oraz

t2

z odstępem

czasowym pół okresu (

Td=T/2

):

t2=t1+T/2

różnią się znakiem przy

równych wartościach modułów

U2=-U1, U4=-U3

1.2

0.8

0.4

0

0.4

0.8

1.2

u(t)

U

1

U

2

=-U

1

T

d

=T/2

T

t

1

t

2

=t

1

+T/2

T

d

=T/2

U

3

t

3

t

4

=t

3

+T/2

U

4

=-U

3

2. Tłumienie (eliminacja) składowych

harmonicznych w trakcie ich

uśredniania

2.3. 

Podstawowa + k-ta składowa harmoniczna sygnału przetworzonego

.

częstotliwość składowej harmonicznej:

f

k

=k·f

1

,

okres której równa się:

T

k

=1/f

k

=1/(k·f

1

)=T/k

,

f

1

=1/T-

częstotliwość podstawowej składowej harmonicznej

Jeżeli postępować analogicznie jak w poprzednim przypadku, można wnioskować, że dla eliminacji

(tłumienia) wpływu

k

-tej składowej harmonicznej na każdy jej okres należy pobrać minimalnie

N

k,min

=2

próbki

z odstępem pół okresu tej składowej:

T

d

=T

k

/2=T/2·k

,

Dla jednoczesnej eliminacji (tłumienia) wpływu podstawowej harmonicznej należy pobrać i uśrednić

N=k·N

k,min=

2·k

próbek w ciągu okresu sygnału

T

Jest to możliwie dzięki temu, że dwie wartości (próbki) sygnału harmonicznego pobrane w momenty

czasowe

t1

oraz

t2

z odstępem czasowym pół okresu (

Td=T/2

):

t2=t1+T/2

różnią się znakiem przy

równych wartościach modułów

U2=-U1, U4=-U3

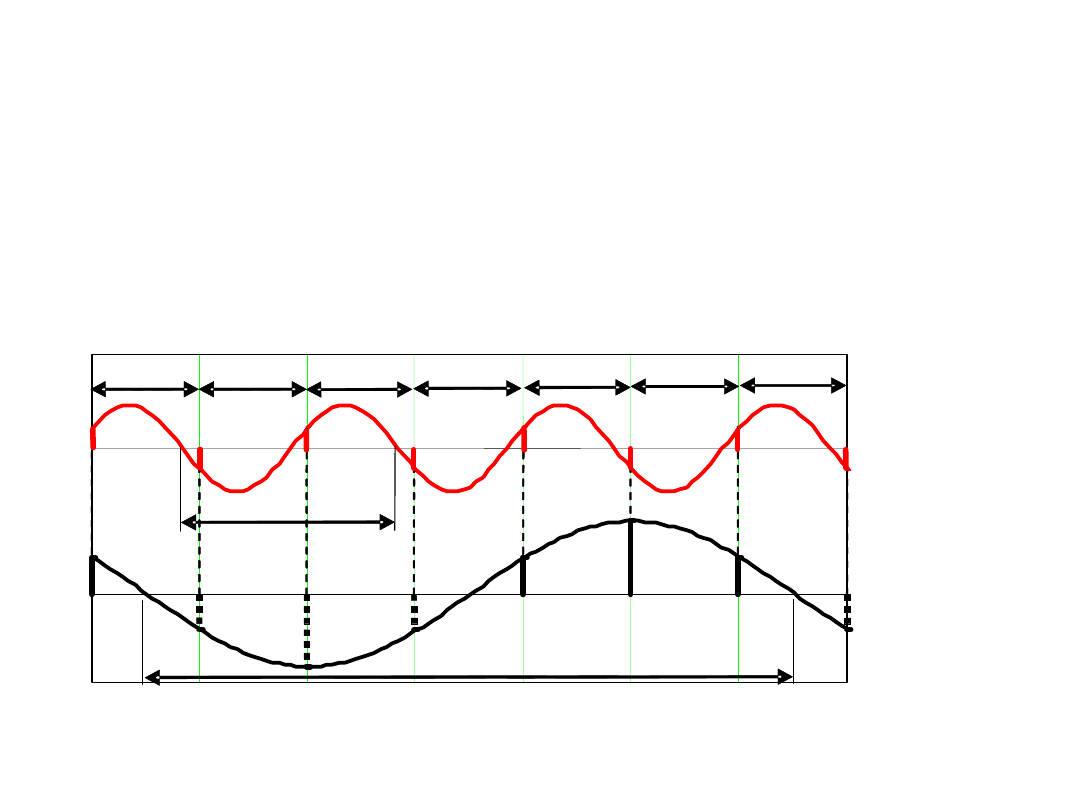
2. Tłumienie (eliminacja) składowych

harmonicznych w trakcie ich

uśredniania

2.3. 

Podstawowa + k-ta składowa harmoniczna sygnału

przetworzonego

.

0

u

3

(t)

u

1

(t)

U

3,1

T

d

=T

3

/2

T

d

T

d

T

d

T

d

T

d

T

d

U

3,2

U

3,3

U

3,4

U

3,5

U

3,6

U

1,1

U

1,2

U

1,3

U

1,4

U

1,5

U

1,6

t

1

t

2

t

3

t

4

t

5

t

6

t

7

U

1,7

U

3,7

T

3

T=3·T

3

Eliminacja wpływu podstawowej oraz 3-ej składowej harmonicznej

(k=3)

2. Tłumienie (eliminacja) składowych

harmonicznych w trakcie ich

uśredniania

Z ostatnich wzorów wynika, ze dla całkowitej eliminacji

podstawowej składowej harmonicznej oraz składowej z

numerem

k

należy pobrać minimalnie

N

min

=2k

próbek z

odstępem pół okresu

T

d

=T

k

/2=T/2k

k

-tej składowej i następnie uśrednić ich.

Częstotliwość próbkowania powinna być dwukrotnie większą

od częstotliwości wyższej składowej harmonicznej

f

d

=2f

k

=2kf

1

co się zgadza z twierdzeniem

Kotelnikowa-Shennona

.

Jednak takie wymaganie jest zbyt ostre, i

dla tłumienia

wszystkich całkowych harmonicznych od 1-ej do k-tej

częstotliwość próbkowania może być mniejsza oraz liczba

uśrednianych próbek tez może być mniejszą

.

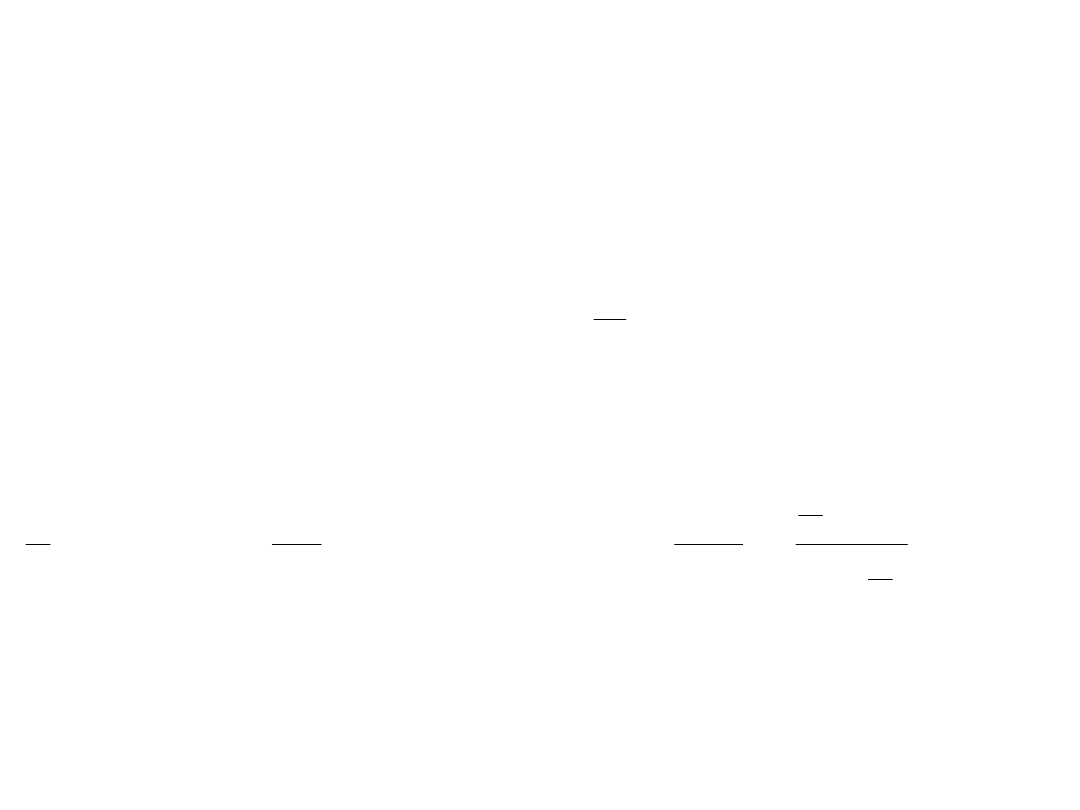
2.4. Uogólnione wyrażenia tłumienia

składowych harmonicznych podczas

uśredniania spróbkowanego sygnału

Wartość średnia próbek sygnału harmonicznego

o amplitudzie U

h,m

, częstotliwości

przy okresie próbkowania wynosi

T

d

=T/N





2



f













ft

U

t

u

m

h

h

2

cos

)

(

,









 

.

sin

sin

1

1

cos

2

cos

)

(

)

(

1

,

1

,

1

















































N

T

f

fT

N

N

N

fT

U

i

fT

N

U

f

U

t

u

N

m

h

N

i

d

m

h

h

N

i

i

h













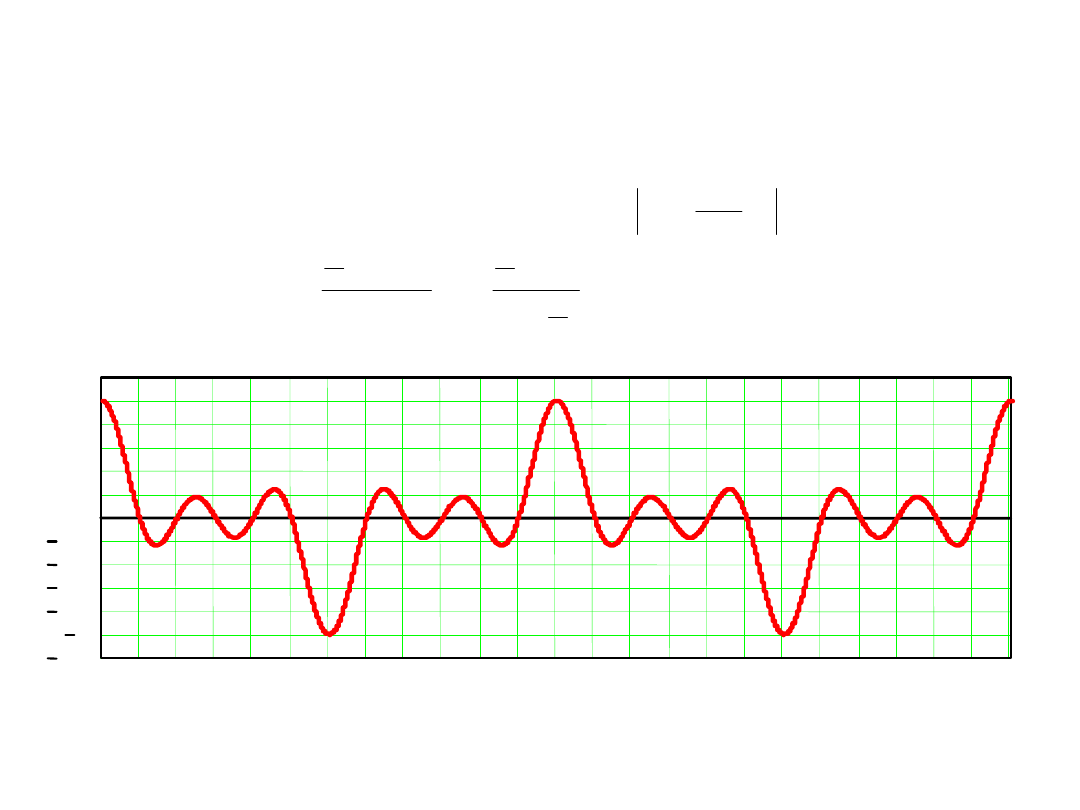
2.4. Uogólnione wyrażenia tłumienia

składowych harmonicznych podczas

uśredniania spróbkowanego sygnału

Wartość maksymalna błędu









 

.

sin

sin

1

sin

sin

1

,

,

max

,



















N

T

f

fT

N

U

fT

N

fT

N

U

U

m

h

d

d

m

h

h













1

1

cos

max























N

N

fT

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

1.2

1

0.8

0.6

0.4

0.2

0

0.2

0.4

0.6

0.8

1

1.2

ΔU

h,max

(f)

fT

Zależność maksymalnej wartości błędu składowych harmonicznych
przy uśrednianiu

N=6

próbek sygnału wciągu jego okresu T

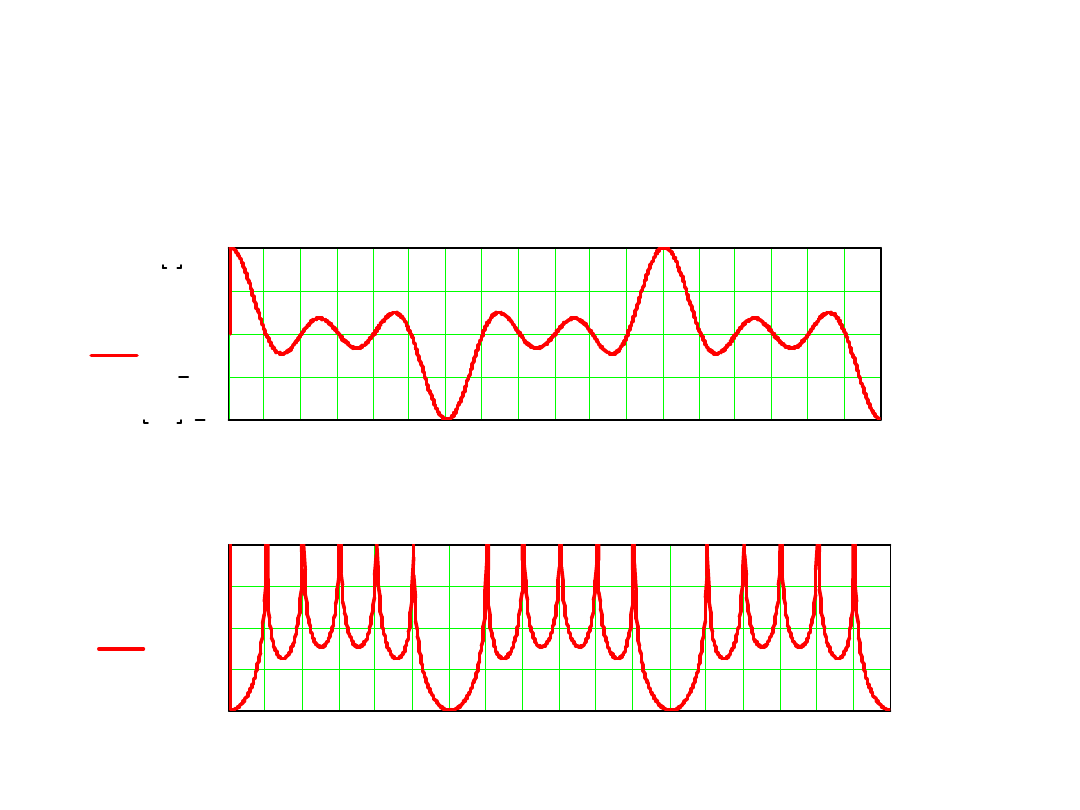
2.4. Uogólnione wyrażenia tłumienia

składowych harmonicznych podczas

uśredniania spróbkowanego sygnału

Wartość maksymalna

błędu

Współczynnik tłumienia

x=fT

0

1

2

3

4

5

6

7

8

9 10 11 12 13 14 15 16 17 18

0

10

20

30

40

40

0

Ktl 6 x



(

)

18

0

x

0

1

2

3

4

5

6

7

8

9 10 11 12 13 14 15 16 17 18

1

0.5

0

0.5

1

1

1



Usr 6 x



(

)

18

0

x

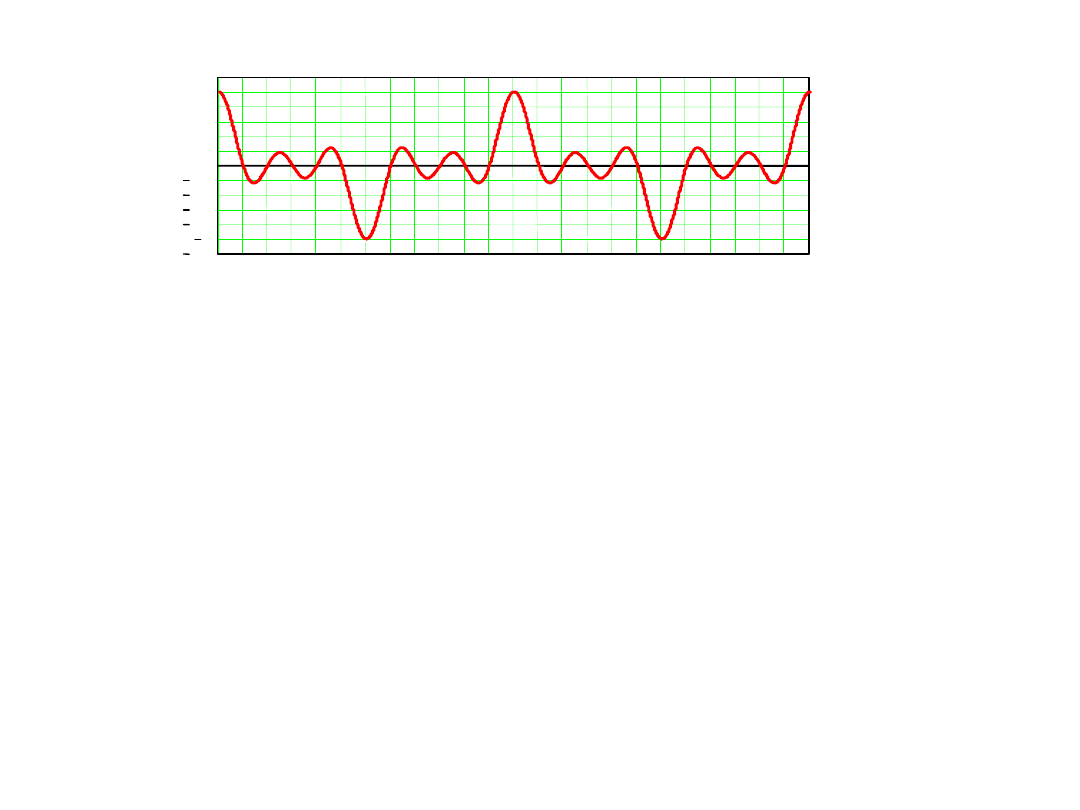
Parametry uśredniania spróbkowanego

sygnału

Przy częstotliwości próbkowania

f

d

=N·f

1

w ciągu jednego

okresu T są uśredniane N próbek sygnału, w wyniku czego będą

eliminowany wpływ (stłumiony) wszystkich harmonicznych z

numerami

od k=1 do k=N-1

.

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

1.2

1

0.8

0.6

0.4

0.2

0

0.2

0.4

0.6

0.8

1

1.2

ΔU

h,max

(f)

fT

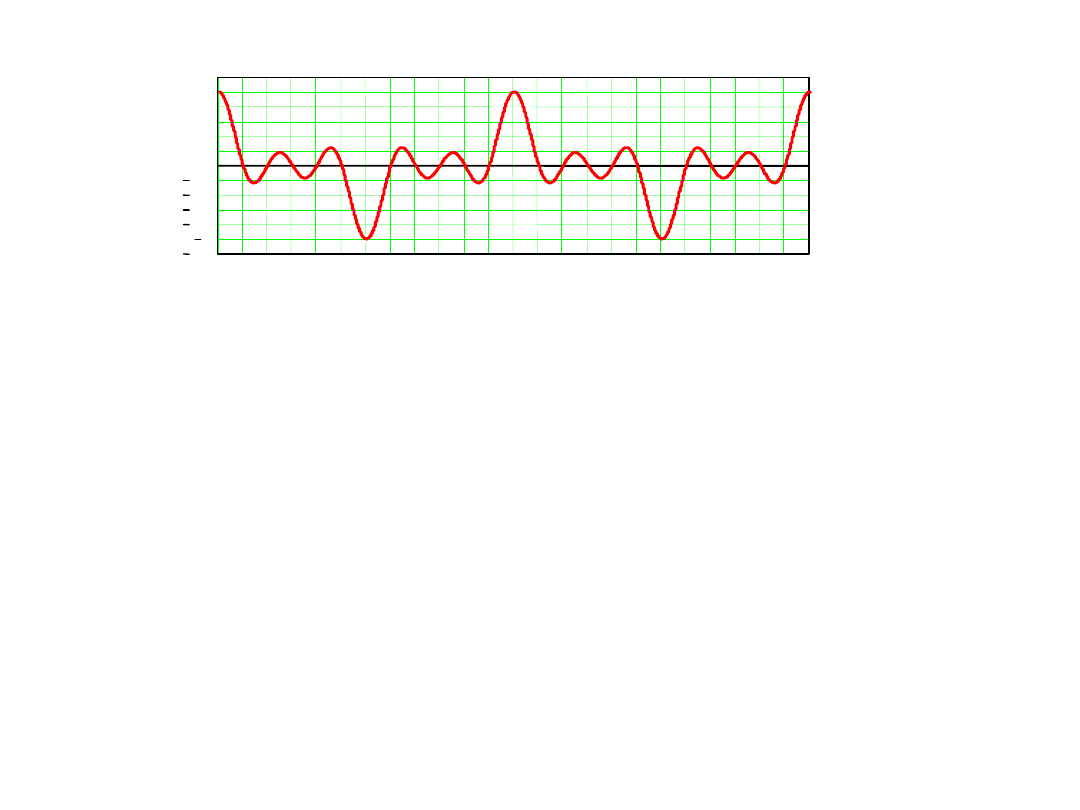
Parametry uśredniania spróbkowanego

sygnału

Innymi słowami, dla eliminowania wpływu (tłumienia)

składowych harmonicznych do

k

-ej włącznie (przy

f

m

=k·f

1

) liczba

uśrednianych próbek (pobranych w jednym okresie sygnału)

powinna być o jeden większą

N

min

=k+1

zamiast N=2k

jak to wynika z

twierdzenia Kotelnikowa

Schannona

.

Minimalna częstotliwość próbkowania powinna równać się

f

d,min

=f

1

·N

min

=f

1

·(k+1)=f

m

+f

1

.

to znaczy, że ona powinna być tylko o

(k+1)

razy zamiast

2·k

razy większą od częstotliwości podstawowej składowej.

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

1.2

1

0.8

0.6

0.4

0.2

0

0.2

0.4

0.6

0.8

1

1.2

ΔU

h,max

(f)

fT

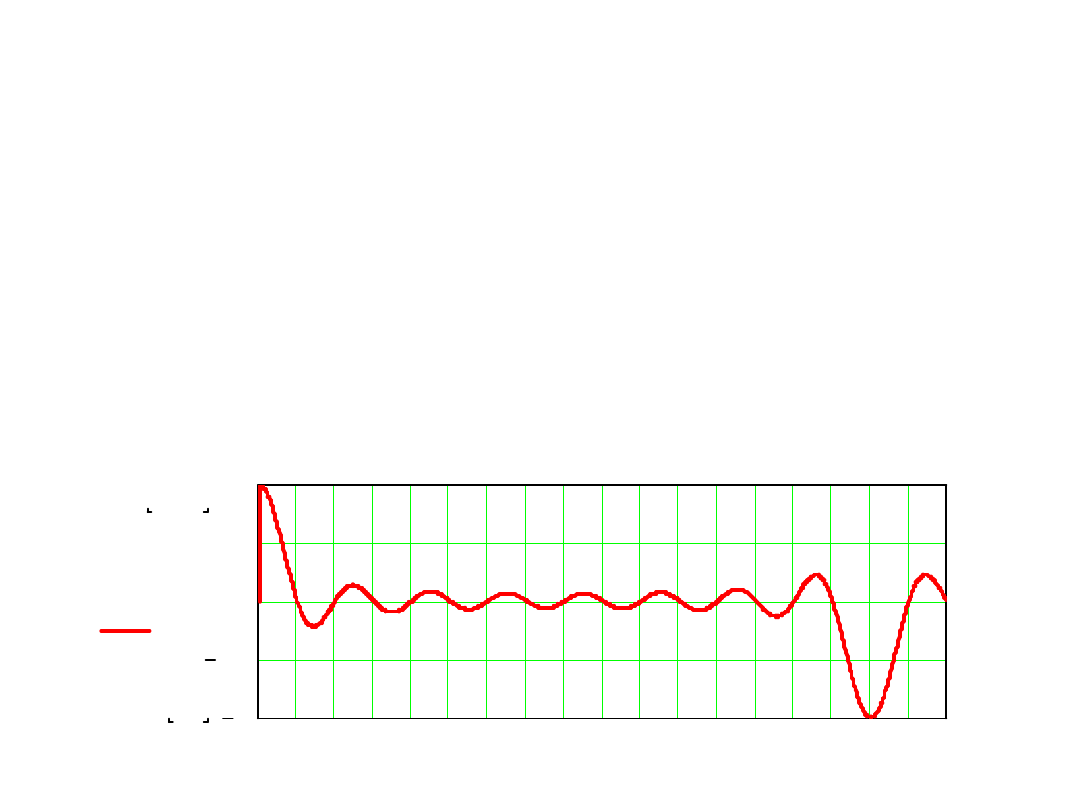
Przykład 1

Wyznaczyć minimalną liczbę próbek oraz częstotliwość

próbkowania sygnału z warunku zapewnienia tłumienia wszystkich

składowych harmonicznych

od 1-ej do 15-tej

, stosując uśrednianie

próbek.

Rozwiązanie. Ponieważ numer maksymalnej składowej

harmonicznej równa się k=15, wtedy minimalna liczba próbek wynosi

N

min

=k+1=15+1=16

.

Częstotliwość próbkowania powinna być o

16

razy większą od

częstotliwości podstawowej składowej zamiast

2·15=30

razy.

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

1

0.5

0

0.5

1

0.999

1



Usr16 x



(

)

18

0

x

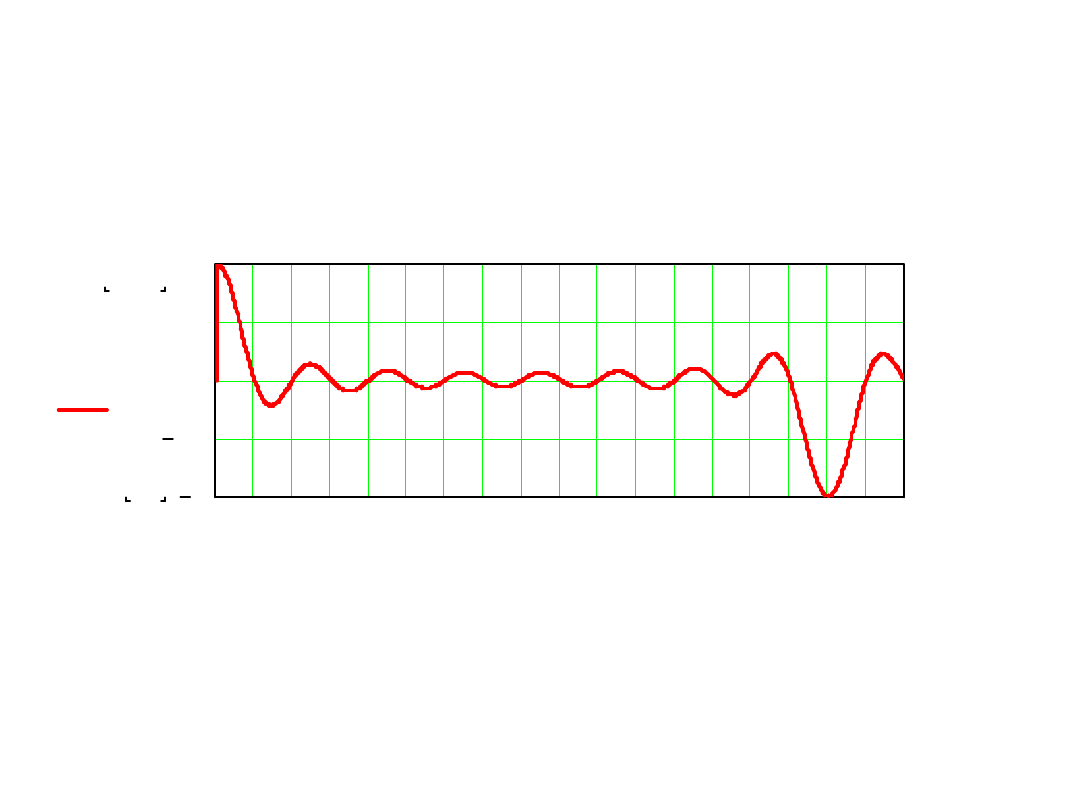
Przykładowo, jeżeli

f

1

=2 kHz

oraz

k=15

maksymalna

częstotliwość

f

m

=15·2 kHz=30 kHz

. Częstotliwość próbkowania

powinna równać się

f

d

=f

m

+f

1

=32 kHz

, zamiast

2·30 kHz=60 kHz

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

1

0.5

0

0.5

1

0.999

1



Usr16 x



(

)

18

0

x

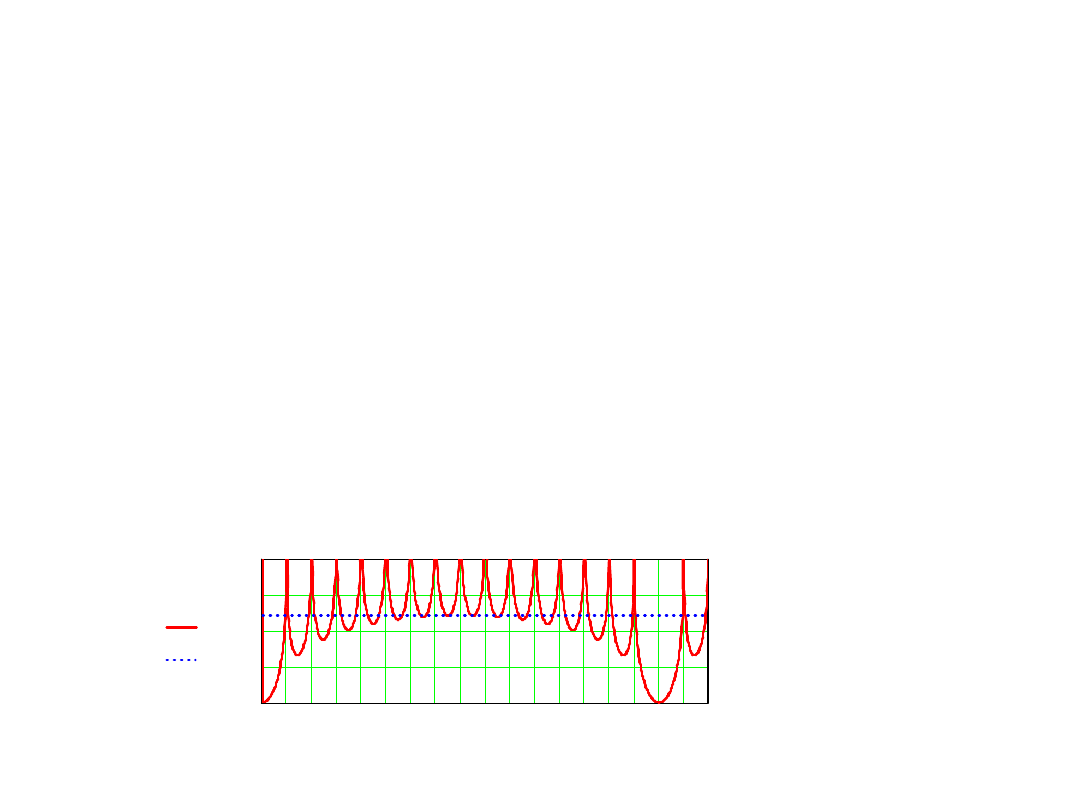
Poziom tumienia

Maksymalny poziom obwiedni współczynnika tłumienia ma
miejsce na częstotliwości równej połowie częstotliwości
próbkowania

f=f

d,min

/2

i ten poziom równa się liczbie próbek N (maksymalny błąd

Δ

u,m

=U

m

/N

):

K

tl

=N

lub

20lg(N)

w decybeli.

Przykładowo, przy

N=16

K

tl,db

=20lg(16)=24 dB

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

0

10

20

30

40

40

0

Ktl 16 x



(

)

KN x

( )

18

0

x

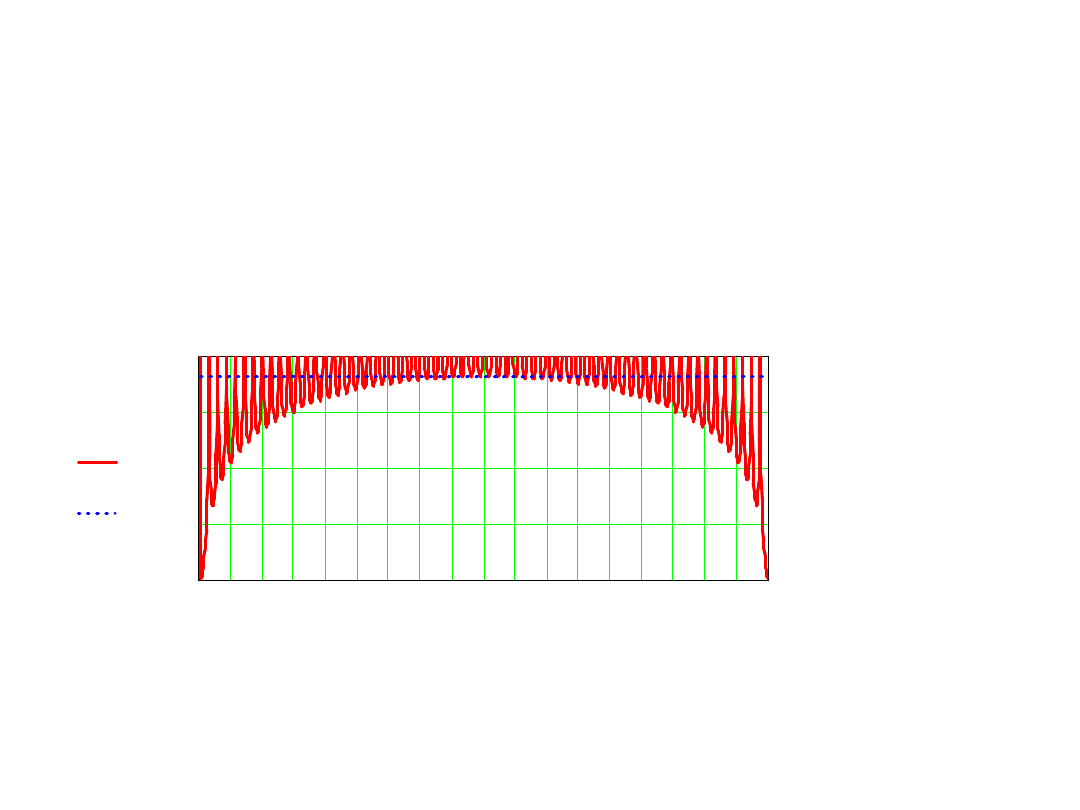
Poziom tumienia

Przy

N=64

K

tl,db

=20lg(64)=36 dB

0 3.567.11

10.67

14.22

17.78

21.33

24.89

28.443235.56

39.11

42.67

46.22

49.78

53.33

56.89

60.4464

0

10

20

30

40

40

0

Ktl 64 x



(

)

KN x

( )

64

0

x

3. Zwiększenie stopnia tłumienia

składowych harmonicznych.

Uśrednianie wagowe

W rzeczywistości

okres sygnału oraz częstotliwości

składowych harmonicznych mogą się zmieniać

lub ich wartości

mogą odbiegać od wartości nominalnych.

W takich przypadkach w wyniku uśredniania składowe

harmoniczne nie będą stłumione (eliminowane) całkowicie, a

pozostanie błąd uśredniania, wartość którego zależy od stopnia

odchylenia okresu (częstotliwości) od nominalnej wartości i jego

można obliczyć według wzoru

 

.

sin

sin

1

,

max

,

















N

T

f

fT

N

U

U

m

h

h





3.1. Małe odchylenia okresu sygnału od

nominalnej wartości

Do małych względnych odchyleń okresu (dla odchyleń

częstotliwości ) będziemy zaliczać taki, dla których są

spełniane warunki:

Założymy, że trwałość rzeczywista okresu sygnału różni się

od nominalnej o :

Ponieważ względne odchylenia okresu i częstotliwości

posiadają różne znaki , to przy nominalnej częstotliwości

podstawowej składowej jej wartość rzeczywista różni na się na :

w takim razie częstotliwości k-tej składowej harmonicznej

sygnału równają się

1

,

1













n

f

n

T

f

f

T

T





T



T

f













T

n

T

T





 1

n

n

T

f

/

1

,

1















f

n

T

n

T

n

f

f

T

f



















1

1

1

1

,

1

,

1

,

1

1





f

n

k

kf

kf

f









1

,

1

1

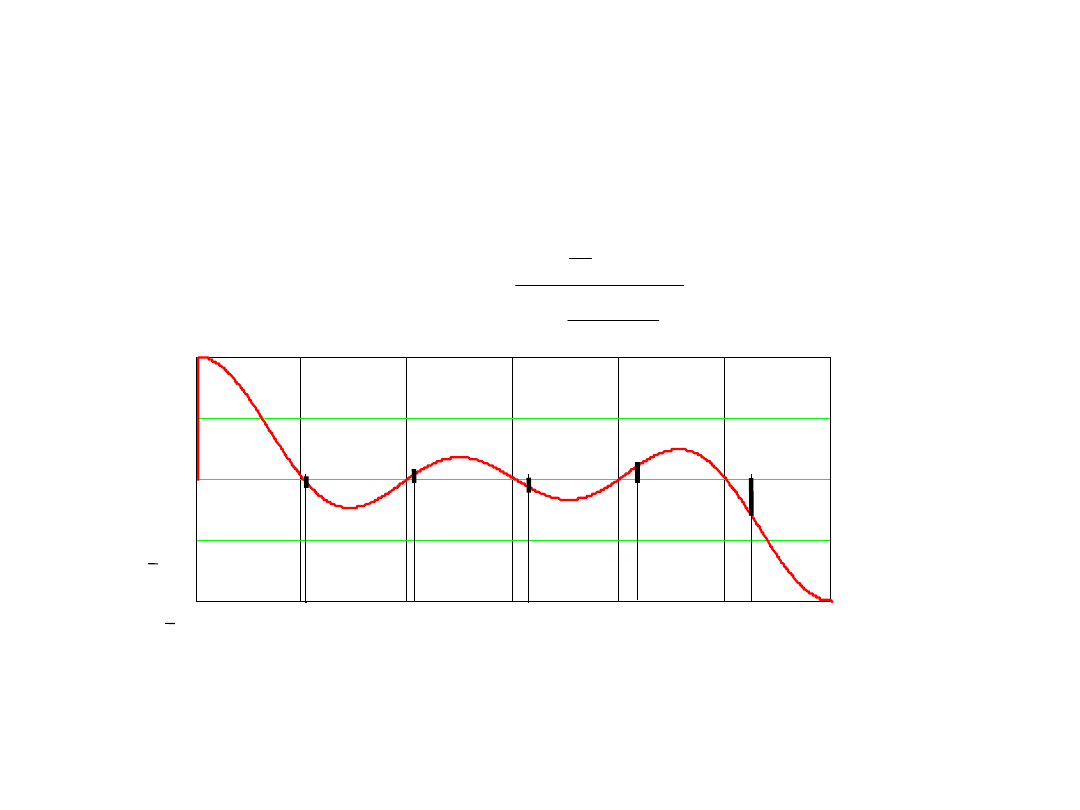
3.1. Małe odchylenia okresu sygnału od

nominalnej wartości

Wtedy przy oraz
wartość maksymalna błędu uśredniania wynosi

Przy δ

f

=+5%

w

artości błędu stanowią:

Δ

1

=-0.05; Δ

2

=0.058; Δ

3

=-0.076; Δ

4

=0.121; Δ

5

=-0.308

 





























N

k

k

N

U

U

f

f

k

m

h

h









1

sin

sin

1

1

,

max

,

1

,

1



n

n

T

f











  





f

k

T

f

n

n

k

k

k

T

kf















sin

1

sin

1

sin

,

1











0

1

2

3

4

5

6

1

0.5

0

0.5

1

Δ

1

Δ

Usr

f·T

Δ

2

Δ

3

Δ

4

Δ

5

1δ

f

2δ

f

3δ

f

4δ

f

5δ

f

3.1. Małe odchylenia okresu sygnału od

nominalnej wartości

Jeżeli, co ma miejsce dla małych

k

(pierwsze

składowe harmoniczne), oraz

przy

k<<N

maksymalna wartość błędu równa się

Przy tym wartość błędu uśredniania pierwszych składowych

harmonicznych jest proporcjonalna do względnego odchylenia

częstotliwości (okresu).

1



f

k









N

k

N

k

f























1

sin

f

m

h

h

U

U



,

max

,





W7. UŚREDNIANIE CYFROWE

WAGOWE W SZEROKIM PAŚMIE

CZĘSTOTLIWOŚCI.

Funkcja wagowa (okno)

Dolpha-Czebyszewa

Plan wykładu

1. Tłumienie składowych harmonicznych szerokim

paśmie częstotliwościowym. Funkcja wagowa

(okno) Dolpha-Czebyszewa

2. Projektowanie funkcji (okna) Dolpha–Czebyszewa

3. Algorytm obliczania współczynników funkcji

(okna) Dolpha-Czebyszewa z przykaładem

4. Porównanie uśredniania wagowego oraz filtracji

średniej wartości.

5. Parametry częstotliwościowe do projektowania

FW Dolpha-Czebyszewa do pomiaru wybranych

parametrów sygnałów przemiennych

Cel: Zapoznać się z zasadami projektowania uśredniania
z wykorzystaniem funkcji wagowej Dolpha_Czebyszewa

Tłumienie składowych harmonicznych

szerokim paśmie częstotliwościowym.

Funkcja wagowa (okno) Dolpha-

Czebyszewa

Jeżeli

częstotliwość składowych harmonicznych

nie jest stałą i może się zmieniać
niekontrolowanie w szerokim paśmie

, wtedy

wykorzystanie

zwykłych metod uśredniania,

które tłumią zakłócenia okresowe,
częstotliwość których krotna odwrotności czasu
uśredniania,

nie jest wystarczająco

skutecznym.

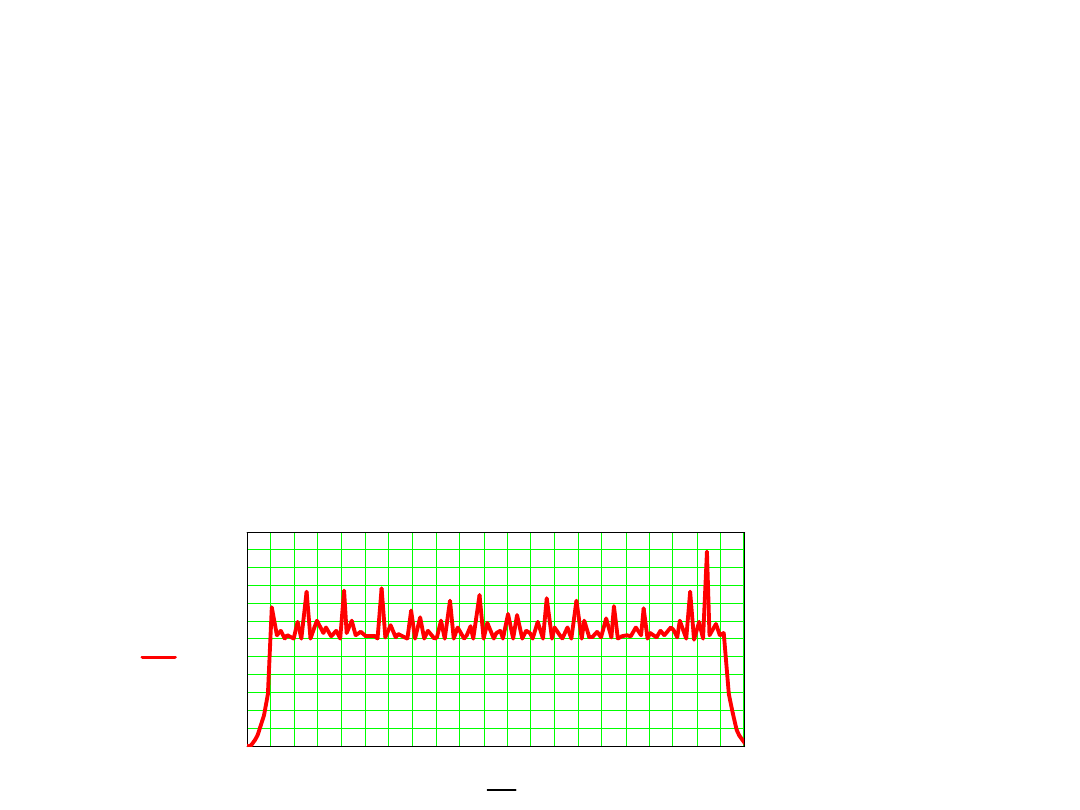
Tłumienie składowych harmonicznych

szerokim paśmie częstotliwościowym.

Funkcja wagowa (okno) Dolpha-

Czebyszewa

Dla tłumienia składowych harmonicznych o nieznanych
częstotliwościach oraz przy ich zmianie w szerokim zakresie – co
ma miejsce przy cyfrowych pomiarach parametrów sygnałów
(wartości średnia wyprostowana, skuteczna, moc czynna oraz
bierna itp.) najlepszy efekt daje zastosowanie funkcji wagowej
(okna) Dolpha- Czebyszewa.
Z pośród innych funkcji wagowych jest to “

najlepsza

” funkcja

wagowa (okno). Jej wykorzystanie zapewnia

zadany poziom

tłumienia Ktl

zakłóceń w

zadanym skończonym zakresie

częstotliwości od dolnej fd do górnej fg. przy minimalnie
możliwym czasie uśredniania Tus

.

0 20 40 60 80100120140160180200220240260280300320340360380400420

0

10

20

30

40

50

60

70

80

90

100

110

120

120

0

Ktl_dBx

( )

420

0

x fd



v0

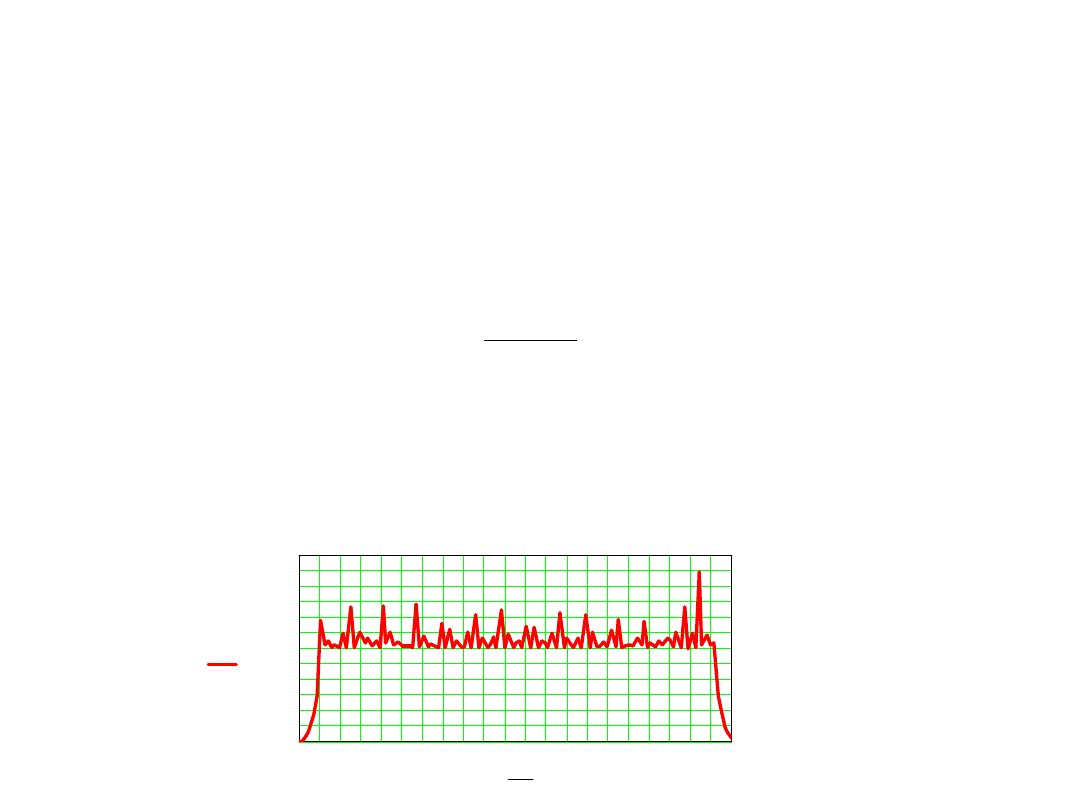
Funkcja wagowa (okno) Dolpha-

Czebyszewa

•Na tym rysunku funkcja wagowa zapewnia tłumienie 60 dB (1000
razy) w zakresie częstotliwości od dolnej fd =20 Hz do górnej
fg=400 Hz.
•Trwałość uśredniania praktycznie zależy tylko od poziomu
tłumienia oraz wartości fd i jest minimalnie możliwą:

•i równa się około

121 ms

dla zadanych wyżej parametrów.

•Nie istnieje innej funkcji wagowej, która zapewni tłumienie minimalnie
60 dB w interwale czasowym mniej niżeli 121 ms

.

0 20 40 60 80100120140160180200220240260280300320340360380400420

0

10

20

30

40

50

60

70

80

90

100

110

120

120

0

Ktl_dBx

( )

420

0

x fd



v0

d

tl

us

f

K

T



)

2

ln(



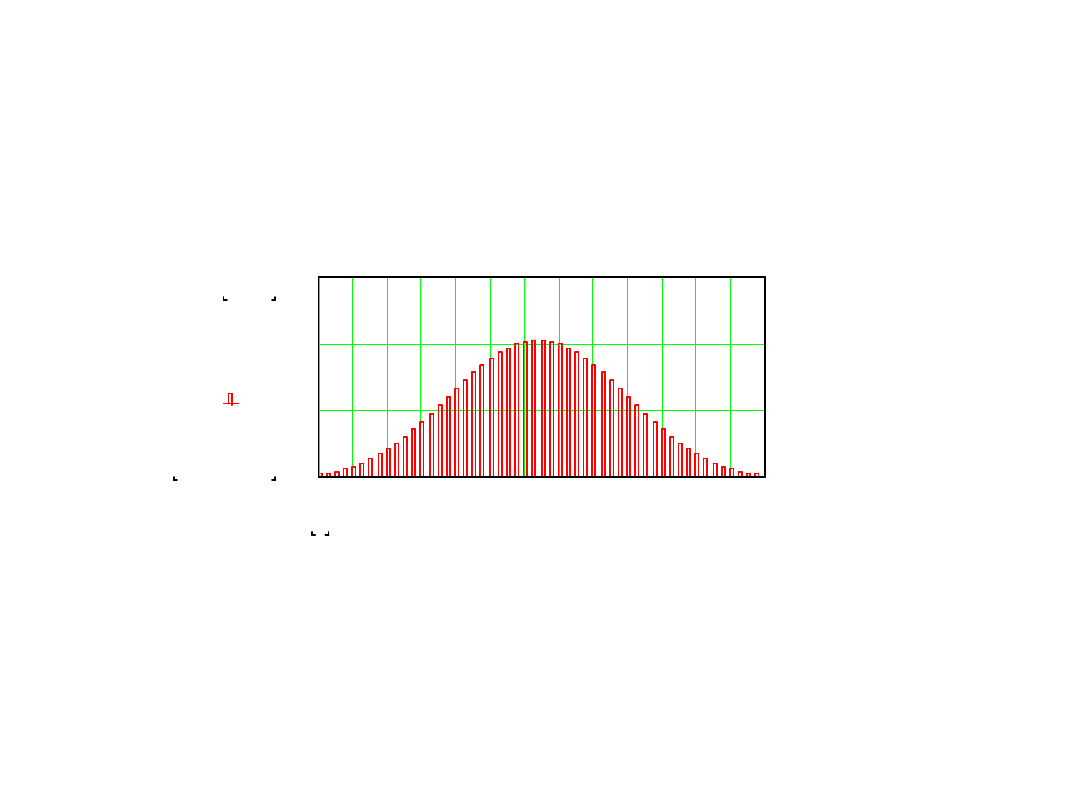
Funkcja wagowa (okno) Dolpha-

Czebyszewa

•Charakterystyczny widok FW Dolpha-Czebyszewa jest pokazana
na rysunku niżej

0 4 8 12 16 20 24 28 32 36 40 44 48 52

0

0.02

0.04

0.06

0.041

8.79110

4





g

in

N

0

in

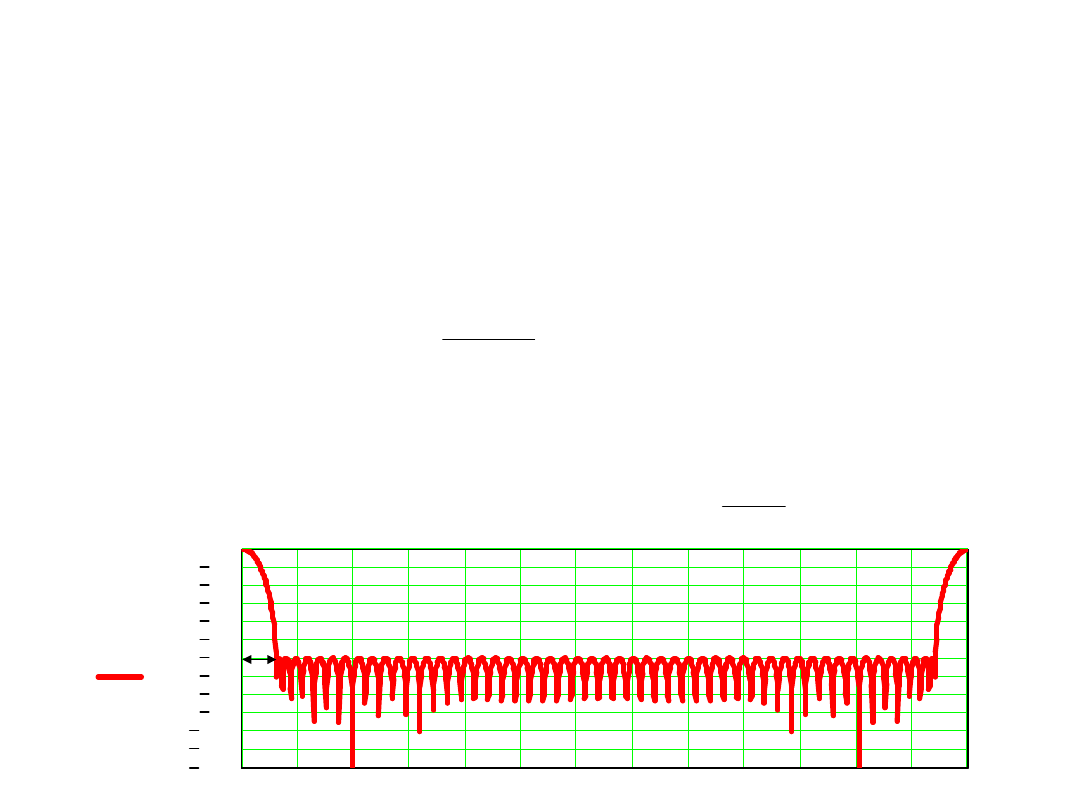
Funkcja wagowa (okno) Dolpha-

Czebyszewa

v0

ln 2Ktl

(

)





v0 2.419



•W dziedzinie częstotliwości FW Dolpha-Czebyszewa minimalizuje
się szerokość listka głównego widma przy założeniu określonej
długości okna oraz przy ograniczeniu dopuszczalnej wysokości
maksymalnego listka bocznego widma .
•
•Przykładowo na rys. niżej pokazano moduł widma FW Dolpha-
Czebyszewa zapewniającej stały minimalny poziom tłumienia 60
dB (1 tysiąc razy) w paśmie częstotliwości od 20 Hz do 400 Hz
wartość szerokości głównego listka równa się:



)

2

ln(

0

tl

K

v 

0

4

8

12

16

20

24

28

32

36

40

44

48

52

120

110

100

90

80

70

60

50

40

30

20

10

0

0

120



WF_dBx

( )

n

0

x

v0

2. Projektowanie optymalnej

FW Dolpha–Czebyszewa

Z punktu widzenia realizacji praktycznej uśredniania wagowego

zadanymi parametrami są:
1) poziom tłumienia Ktl

oraz

2) pasmo częstotliwości od fd do fg

;

a

poszukiwanymi parametrami

są:

1) Rząd FW n

;

2) liczba N

(długość) współczynników FW;

3) wartości współczynników w

i

(i=1,2,…,N),

4) częstotliwość próbkowania fs

oraz

5) czas uśredniania Tus

.

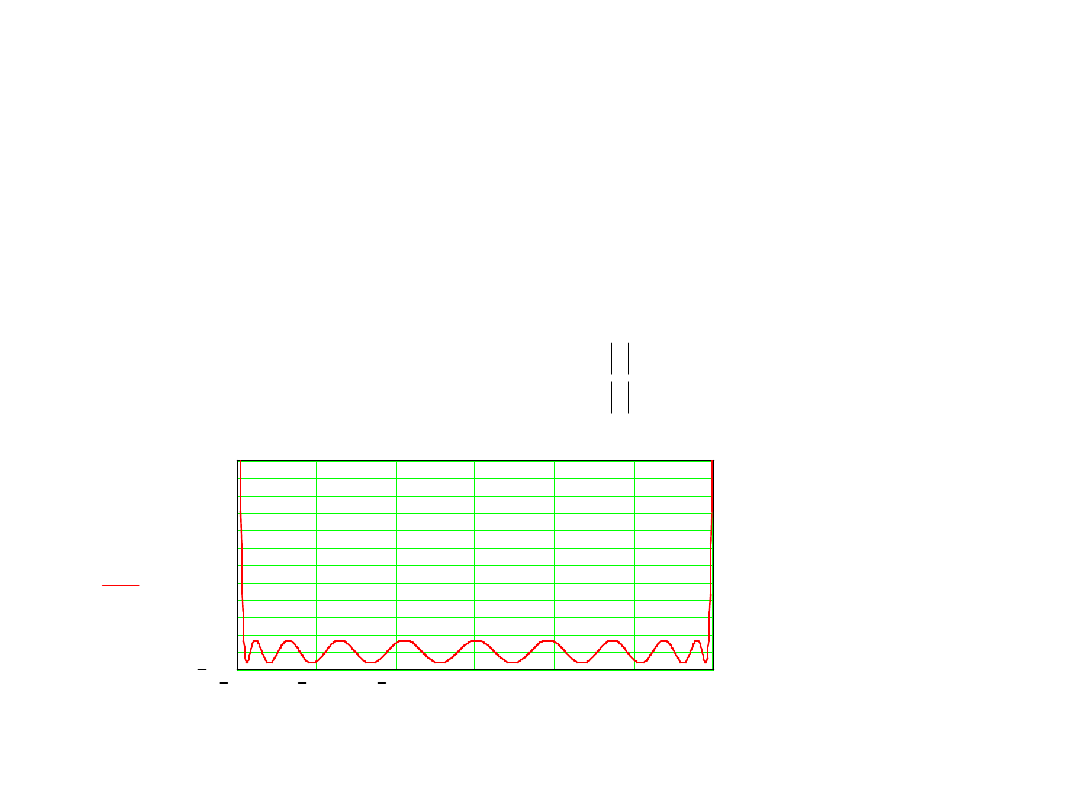
2. Projektowanie optymalnej

FW Dolpha–Czebyszewa

Charakterystyka widmowa funkcji wagowej Dolpha-Czebyszewa o

N współczynnikach gi jest konstruowana na podstawie
wielomiana Czebyszewa rzędu

n=N-1:









1

1

,

)

(

h

arccos

cosh

,

)

arccos(

cos

)

(

















x

x

dla

dla

x

n

x

n

x

T

n

1.02

0.68

0.34

0

0.34

0.68

1.02

1.5

0

1.5

3

4.5

6

7.5

9

10.5

12

13.5

15

16.5

16.5

1.5



Tcheb20 x



(

)

1.025

1.025



x

2. Projektowanie optymalnej

FW Dolpha–Czebyszewa

Wartości współczynników tej FW można obliczyć wg wzoru

Gdzie:

parametr, który jest powiązany z szerokością głównego listka

widma zależnością:

 



























1

0

2

0

2

0

)!

1

(

)!

1

(

!

)!

1

(

1

2

i

j

j

j

tl

i

j

i

i

j

n

j

x

j

n

n

K

x

g















n

K

x

tl

)

(

h

arccos

cosh

0













)

2

ln(

)

(

h

arccos

cosh

1

arccos

1

arccos

0

0

tl

tl

K

n

K

n

x

n















































2. Projektowanie optymalnej

FW Dolpha–Czebyszewa

Częstotliwość próbkowania sygnału równa się:

fs=fd+fg=fd (D+1)

gdzie

D=fg/fd

jest względnym zakresem częstotliwości

Rząd WF wyznacza się wg. wzoru:





 













































1

cos

1

h

arccos

h

arccos

1

0

D

K

D

n

tl





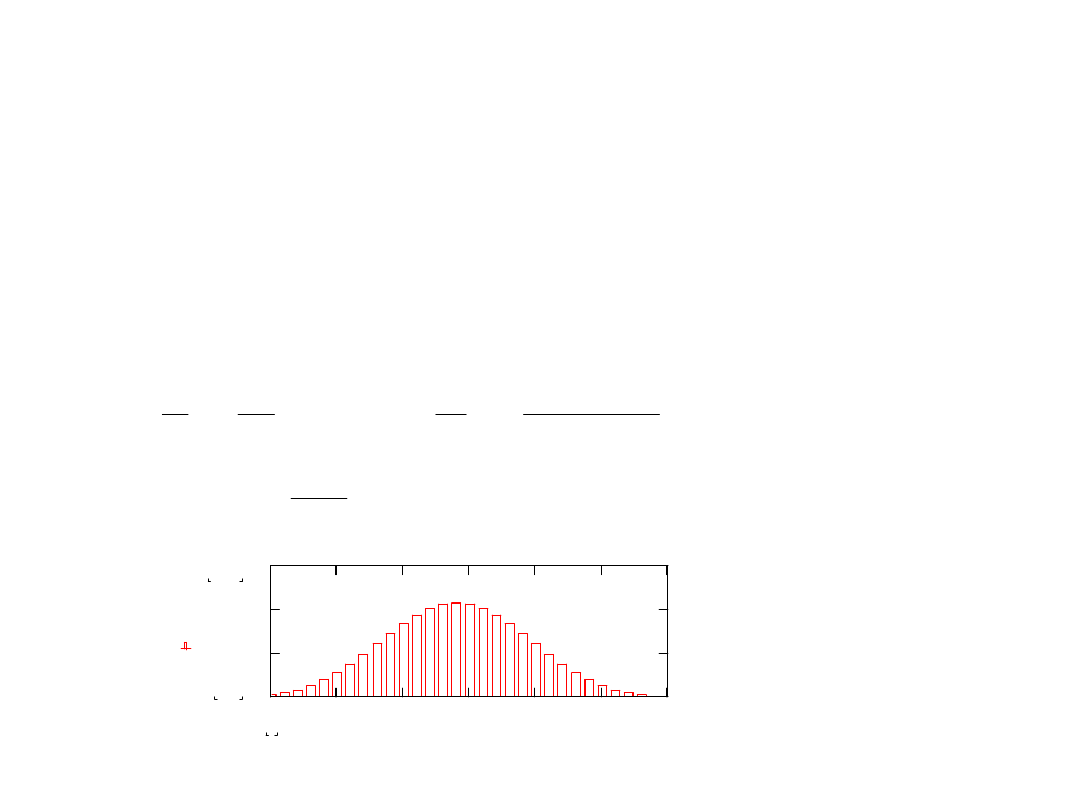
2. Projektowanie optymalnej

FW Dolpha–Czebyszewa

Liczba próbek FW Dolpha-Czebyszewa równa się:

N=n+1

Lepsza dokładność obliczeń (zwłaszcza przy dużych N) otrzymuje

się wykorzystująć odwrotne przekształcenie Fouriera

wielomianu Czebyszowa





































N

M

m

k

N

k

x

T

K

N

w

M

k

N

tl

in

)

(

2

cos

cos

2

1

1

0

1

1





2

1





N

M

1

2

0









N

M

m

0

5

10

15

20

25

30

0

1

2

3

2.135

0.04

w

in

n 1



(

)



N 1



0

in

3. Algorytm obliczania współczynników

funkcji (okna) Dolpha-Czebyszewa z

przykaładem

1) Zadano:

2) Obliczanie względnej szerokości pasma tłumienia

3) Obliczanie rzędu wielomianu Czebyszewa

Po zaokrągleniu do wartości całkowitej większej

n=51

4) Obliczanie długości (liczby próbek) FW Dolpha-Czebyszewa

Ktl 1000



fd 20



fg 400



D

fg
fd



D 20



n

acoshKtl

(

)

acosh

1

cos



D 1





























N 1 n





N 52



5) Obliczanie wartości parametru

x0

6) Obliczanie wartości współczynników FW Dolpha-Czebyszewa

3. Algorytm obliczania współczynników

funkcji (okna) Dolpha-Czebyszewa z

przykaładem

x0 cosh

acoshKtl

(

)

n











x0 1.011



M

n
2



M 26



in 0 n





w

in

1

n 1



(

)

1

2

Ktl

1

M

k

Tcheb n x0cos 

k

n 1

























cos

2 

 k

 in M



(

)



n 1













�



























0.046

0.050

0.077

0.110

0.152

0.202

0.262

0.332

0.412

0.502

0.710

0.825

0.947

1.073

1.201

1.329

1.456

1.578

1.692

1.797

1.970

2.034

2.081

2.109

2.119

2.109

2.081

2.034

1.970

1.891

1.692

1.578

1.456

1.329

1.201

1.073

0.947

0.825

0.710

0.602

0.412

0.332

0.262

0.202

0.152

0.110

0.077

0.050

0.046

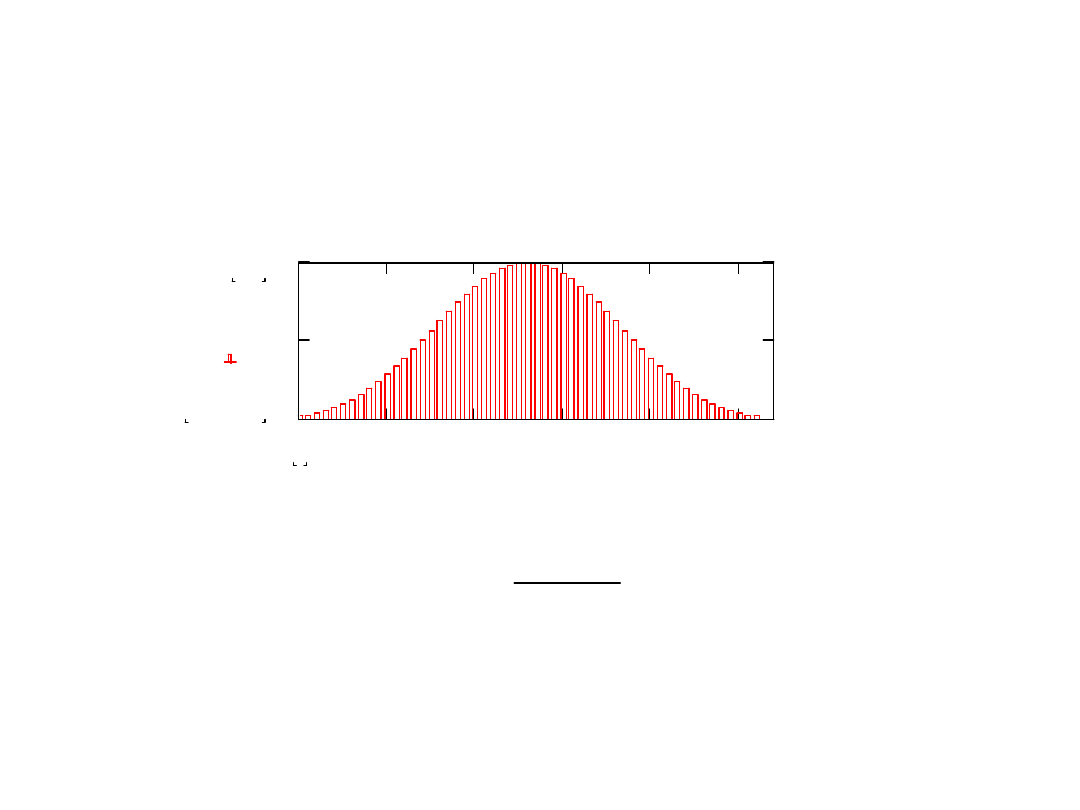
7) Wykres funkcji wagowej

8) Obliczanie charakterystyki widmowej: x=f·T

us

3. Algorytm obliczania współczynników

funkcji (okna) Dolpha-Czebyszewa z

przykaładem

0

10

20

30

40

50

0

0.02

0.04

0.04

8.69710

4





g

in

N 1



0

in

WF x

( )

0

n

in

w

in

cos 2

x in M



(

)



n













�





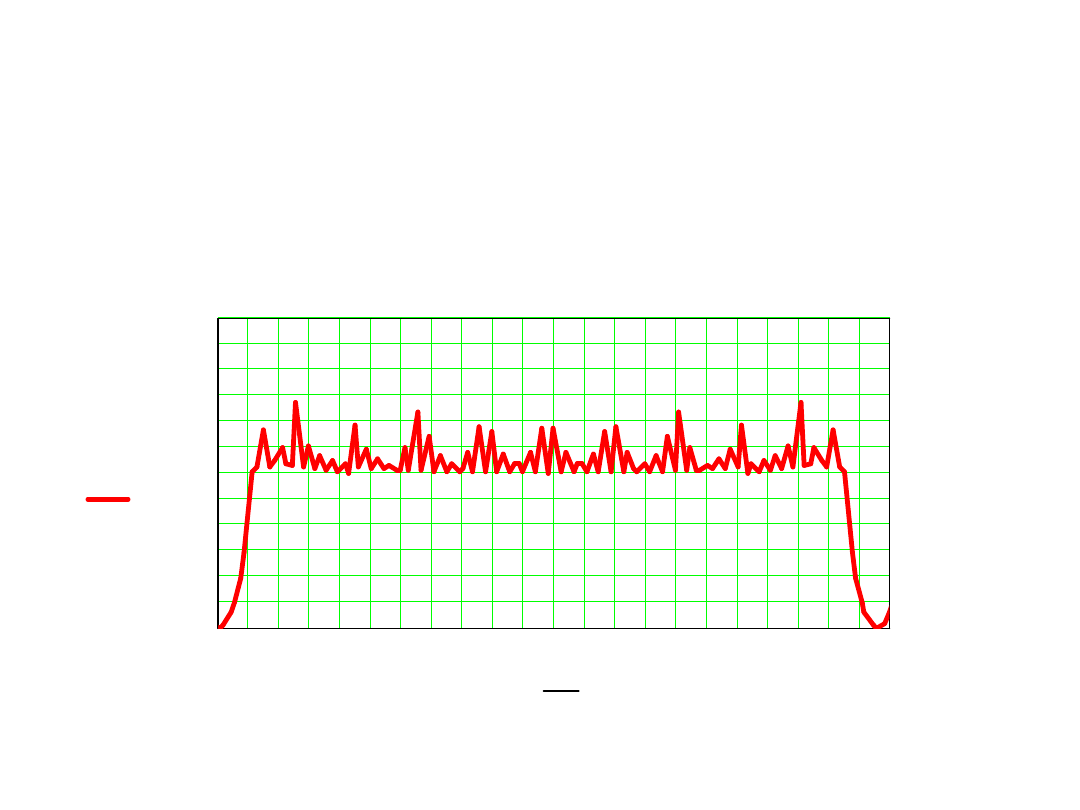
9) Obliczanie współczynnika tłumienia w decybeli

3. Algorytm obliczania współczynników

funkcji (okna) Dolpha-Czebyszewa z

przykaładem

Ktl_dBx

( )

WF_dBx

( )





0 20 40 60 80100120140160180200220240260280300320340360380400420440

0

10

20

30

40

50

60

70

80

90

100

110

120

120

0

Ktl_dBx

( )

440

0

x fd



v0

10) Obliczanie względnej trwałości uśredniania FW Dolpha-

Czebyszewa

11) Obliczanie trwałości uśredniania FW Dolpha-Czebyszewa

12) Obliczanie częstotliwości próbkowania

•

Obliczanie wyniku przetwarzania jeżeli x

1

,x

2

, x

3

,…,x

N

są

wartościami zarejestrowanymi sygnału badanego

3. Algorytm obliczania współczynników

funkcji (okna) Dolpha-Czebyszewa z

przykaładem

v0

n


acos

1

cosh

acoshKtl

(

)

n





























v0 2.411



Tus

v0

fd



Tus 0.121



fp n

fd

v0





fp 431.379









N

i

i

i

X

w

x

N

1

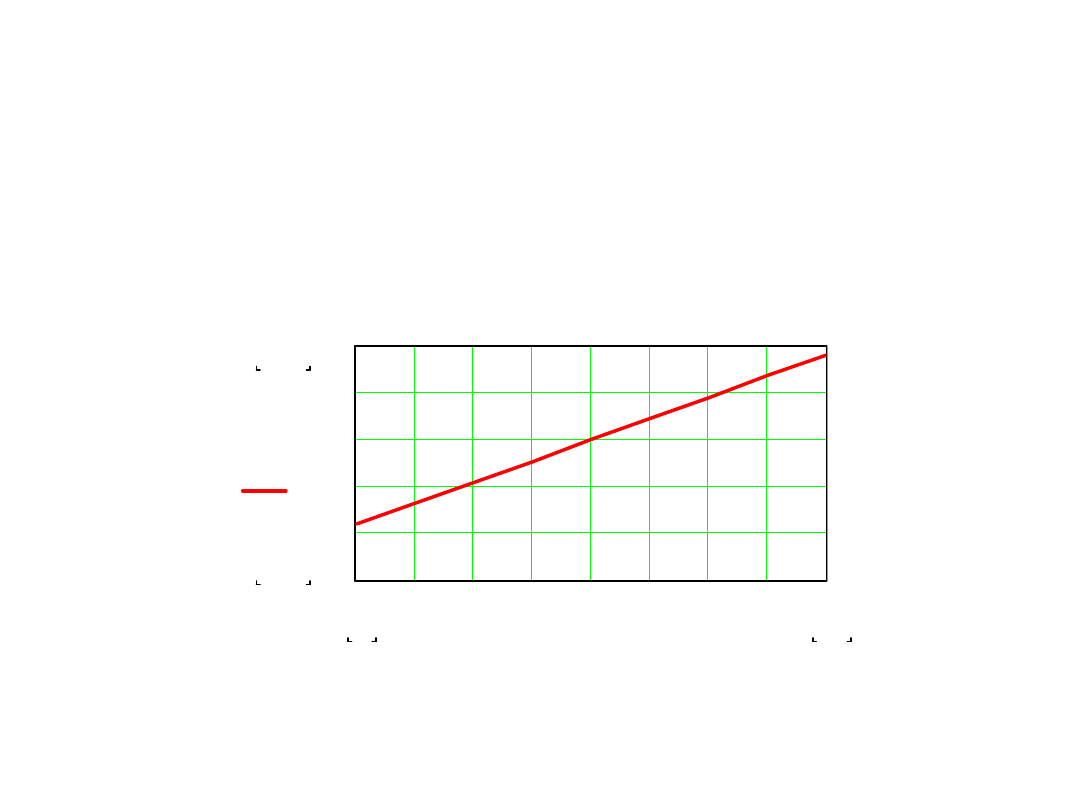
Zależność

względnego

czasu

uśredniania

od

wartości

współczynnika tłumienia

Przy Ktl=50 dB v0=2,054 Tus=v0/fd=41ms

4. Porównanie uśredniania wagowego

oraz filtracji średniej wartości

v_0 0.221 Kdb 0.03665







20

30

40

50

60

70

80

90

100

0

0.8

1.6

2.4

3.2

4

3.834

0.941

v_0

0 ij



100

20

ij 10



20



Pomiar wartości skutecznej

W sygnale pomiarowym jest:

1)

Tylko jedna składowa harmoniczna

o częstotliwości f1w

paśmie od f

dx

do f

gx

:

Przy obliczaniu kwadratu wartości próbek powstaje druga

składowa harmoniczna

Sygnał kwadrowany będzie się mieścić w paśmie

od f

d

=2f

dx

do f

g

=2f

gx

.

2)

Stała składowa U0+ podstawowa składowa harmoniczna o

częstotliwości f

1

+ k składowych wyższych (kf

1

)

w paśmie

od f

dx

do fg: kf

1

<f

gx

.

Sygnał kwadrowany będzie się mieścić w paśmie

od f

d

=f

dx

do f

g

= 2f

gx

.













k

t

kf

Um

t

f

Um

t

f

Um

U

t

u





























1

1

2

1

1

1

1

1

2

cos

...

2

2

cos

2

cos

0

)

(

Pomiar mocy czynnej

• W razie cyfrowego pomiaru mocy

parametry

częstotliwościowe analogiczne

jak dla pomiaru

wartości skutecznej

N

I

U

I

U

I

U

I

U

I

U

N

P

N

N

N

i

i

i



























...

1

3

3

2

2

1

1

1

Pomiar wartości średniej wyprostowanej

W razie cyfrowego pomiaru wartości średniej wyprostowanej:
1)

Tylko jedna składowa harmoniczna

o częstotliwości f

1

w

paśmie od f

dx

do f

gx

:

Przy obliczaniu modułu (dwu połówkowego prostowania)

wartości próbek powstaje druga składowa harmoniczna +

wyższe składowe harmoniczne, amplituda których maleje

proporcjonalnie do kwadratu numeru harmonicznej.

Jeżeli uwzględniane są k=10 składowych harmonicznych

(poziom 10-j nie przekracza 0,01 od wartości średniej

wyprostowanej) wtedy sygnał wyprostowany będzie się

mieścić w paśmie

od f

d

=2f

dx

do f

g

=2kf

gx

.

2)

Stała składowa U0+ podstawowa składowa harmoniczna o

częstotliwości f

1

+ k składowych wyższych (kf

1

)

w paśmie od

f

dx

do fg: kf

1

<f

gx

.

Po dwu połówkowym prostowaniu sygnału składowe

harmoniczne będą się mieścić w paśmie

od f

d

=f

dx

do f

g

=2kf

gx

.