METODY PRZESUWANIA

BIEGUNÓW

Jak wynika z poprzednich rozważań istnieje związek pomiędzy wartościami

własnymi (a tym samym i biegunami) układu zamkniętego a jakością

układu. Bieguny pi (i=1,2,…,n) stabilnego układu zamkniętego leżą w lewej

półpłaszczyźnie zmiennej zespolonej s=α+jω. Bieguny mogą być

rzeczywiste lub zespolone: pi= αi+jωi. Jeśli bieguny rzeczywistego układu

zamkniętego mają części urojone, to wówczas występują parami jako

zespolone sprzężone, czyli: pi1,2= αi±jωi. Bieguny układu stabilnego mają

ujemną część urojoną α.
Jak wiemy odpowiedź układu liniowego jest sumą odpowiedzi wszystkich

modów, z których każdy jest związany z jedną z wartości własnych

(biegunów) układu, czyli:

.

Z powyższej zależności wynika, że dla układów stabilnych każda αi musi

być ujemna, aby odpowiedź zanikała w czasie. Co więcej, jeśli będzie co do

modułu (wartości bezwzględnej) rosła, to proces przejściowy będzie ulegał

skróceniu. Z drugiej strony ω decyduje o częstości oscylacji odpowiedzi

układu. Dla rosnącego ω rośnie częstość oscylacji (układ ma coraz mniejsze

stałe czasowe). Bieguny leżące na osi rzeczywistej generują odpowiedź

aperiodyczną, podczas, gdy bieguny leżące na urojonej dają składowe

odpowiedzi o nie gasnących oscylacjach (rys.).

)

cos

(sin

1

1

t

j

t

e

A

e

C

y

i

i

n

i

t

i

n

i

t

p

i

ii

i





















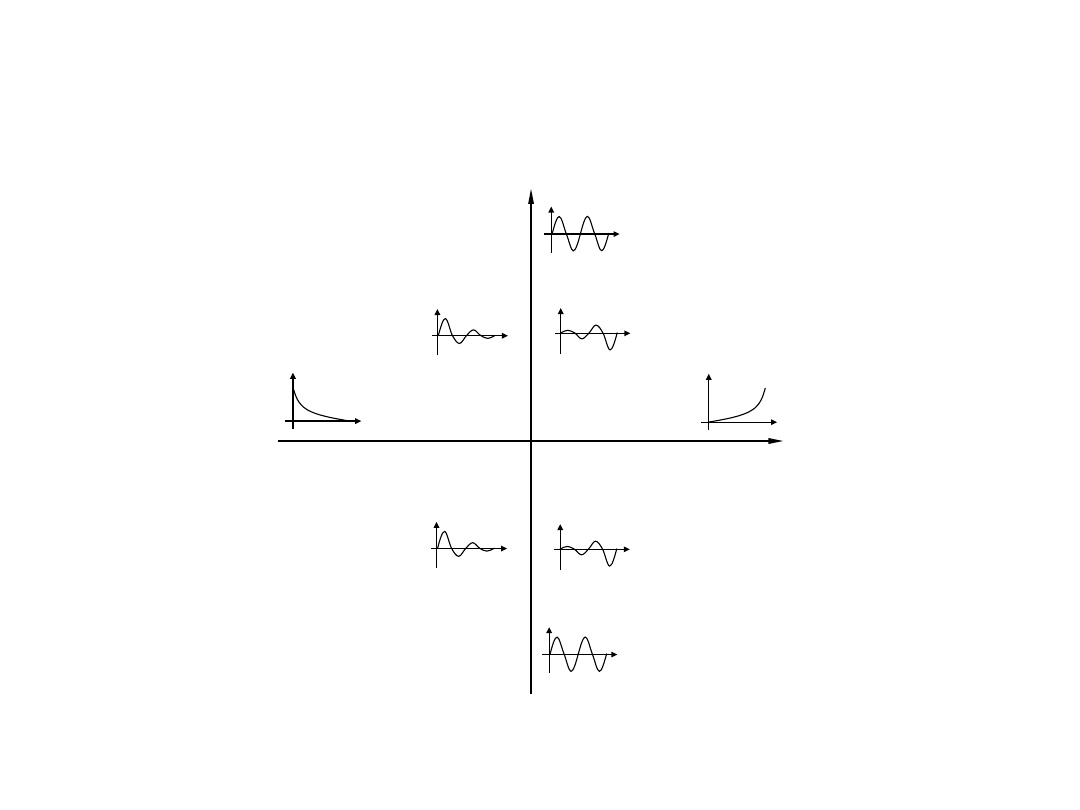
Przebieg procesu przejściowego w

zależności od położenia bieguna

x

x

x

x

x

x

x

x

α

jω

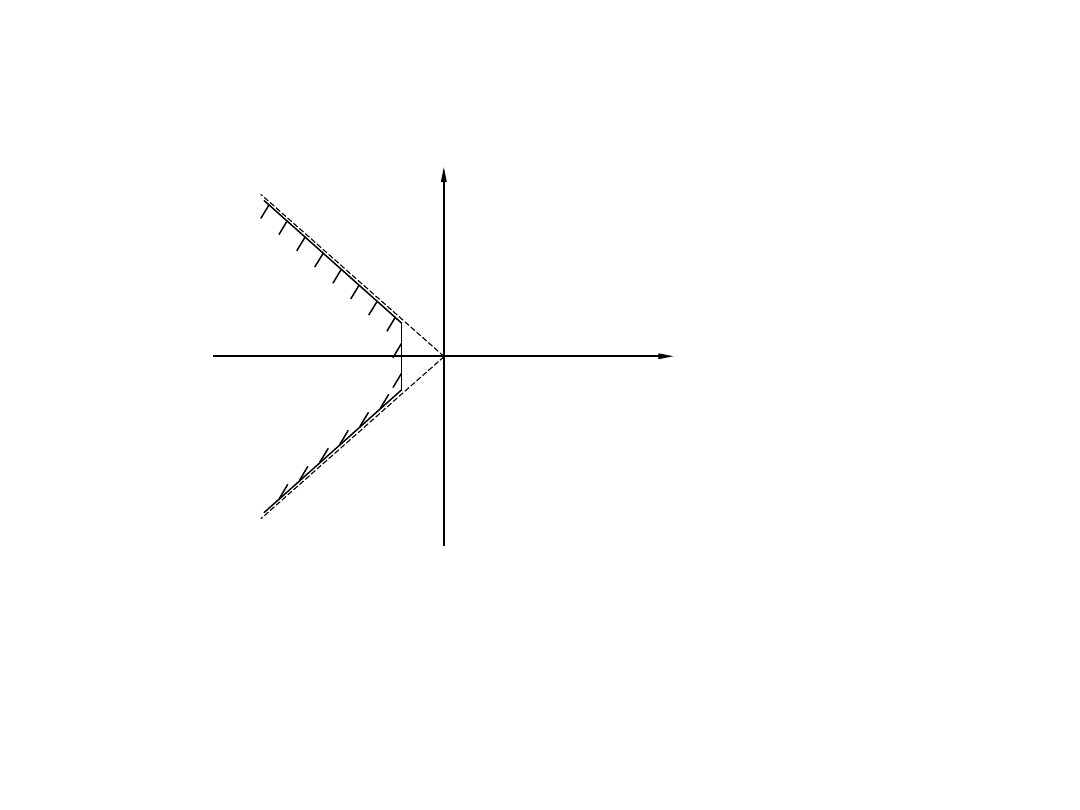
Położenia biegunów

•

Rys. Pożądana lokalizacja biegunów układu zamkniętego

• Od projektowanego układu sterowania zazwyczaj wymaga się, aby bieguny układu

zamkniętego leżały w narzuconej części lewej półpłaszczyzny zmiennej zespolonej s.

Najczęściej ta podprzestrzeń ma charakter pokazany na rys. Dla układu liniowego

wyższego rzędu odpowiedź układu jest superpozycją poszczególnych składowych

odpowiedzi. Często zdarza się, że układ ma dominującą odpowiedź drugiego rzędu. W tym

przypadku rozmieszczenie wartości własnych (biegunów) jest następujące: dwie wartości

własne zespolone sprzężone leżą stosunkowo blisko osi urojonych, podczas gdy pozostałe

leżą daleko na lewo w lewej półpłaszczyźnie. Im większa jest separacja tym lepsza jest

aproksymacja układu przez układ drugiego rzędu.

x

x

α

j
ω

x

Dobre
lokalizacj
e

0

0

Metoda linii

pierwiastkowych

• Rozważmy przypadek, gdzie jeden parametr układu regulacji

jest nieznany. Tym parametrem może być współczynnik

wzmocnienia regulatora lub dowolny inny jego parametr. Ale

równie dobrze może być to dowolnie wybrany parametr

obiektu, przy założeniu, że parametry regulatora są znane. W

tym ostatnim przypadku możemy badać wrażliwość układu

zamkniętego na zmiany tego parametru. Zauważmy, że

wszystkie bieguny układu zamkniętego są funkcją tego

parametru. Można funkcje te przedstawić na płaszczyźnie

zmiennej zespolonej s. Otrzymane linie nazwiemy liniami

pierwiastkowymi, gdyż po nich poruszają się pierwiastki

równania charakterystycznego (bieguny) układu

zamkniętego wraz ze zmianą parametru. Takie linie nazywa

się również miejscami geometrycznymi wartości własnych.

To ostatnie jest słuszne, przy założeniu, że układ jest

całkowicie sterowalny i obserwowalny.

Wyznaczanie linii pierwiastkowej

• Graficzna metoda wykreślania linii pierwiastkowych została

zaproponowana przez Evansa i zostanie ona przedstawiona w tym

rozdziale. Rozważmy transmitancję układu otwartego w postaci

kanonicznej czynnikowej:

• gdzie:

• Współczynnik K jest tą zmienną, której wartość (spełniającą

narzucone wymagania) należy określić. Równanie

charakterystyczne układu zamkniętego przybiera postać:

• lub

•
• przy czym:

 























n

j

j

m

i

i

p

s

z

s

K

s

G

1

1

.

,

j

j

j

i

i

i

j

p

j

z

















0

)

(

1





s

KG

o

,

0

dla

,

1

)

(







K

K

s

G

o

 









.

,

1

1

m

n

p

s

z

s

s

G

n

j

i

m

i

i

o

















• W ogólnym przypadku jest liczbą zespoloną, czyli wektorem na

płaszczyźnie zmiennej zespolonej s. Na bazie równań transmitancja

powinna więc spełniać dwa warunki; na kąt położenia wektora:

• i na jego moduł:

•

• Z tych warunków wynika następująca trzyetapowa procedura znajdowania

pierwiastka równania.

• 1. Na płaszczyźnie zmiennej zespolonej s nanosimy zera i bieguny układu

otwartego. Bieguny zazwyczaj zaznacza się krzyżykiem, a zera - kółkiem

Liczba zer fizycznie realizowalnego układu otwartego jest równa lub

mniejsza od liczby biegunów, czyli m≤n.

• 2. Metodą prób i błędów szukamy na płaszczyźnie s punktu P, który

spełnia warunek na kąt. W każdej z prób dodajemy (dla zer) i odejmujemy

(dla biegunów) kąty mierzone na płaszczyźnie s. Kąty odmierzane są od

osi rzeczywistej w kierunku przeciwnym do ruchu wskazówek zegara.

• 3. Po znalezieniu punktu P spełniającego w przybliżeniu warunek na kąt

możemy policzyć K z warunku na moduł. Obliczanie K sprowadza się do

mnożenia (od biegunów) i dzielenia (od zer) odcinków na płaszczyźnie s.

Linie pierwiastkowe wykreślamy łącząc kilka w ten sposób otrzymanych

punktów P. Typowe kształty krzywych pierwiastkowych pokażemy na kilku

przykładach.

calkowita

liczba

-

N

,

360

180

)

(

arg

N

s

G

o

o

o







.

1

)

(

K

s

G

o



)

(s

G

o

)

(s

G

o

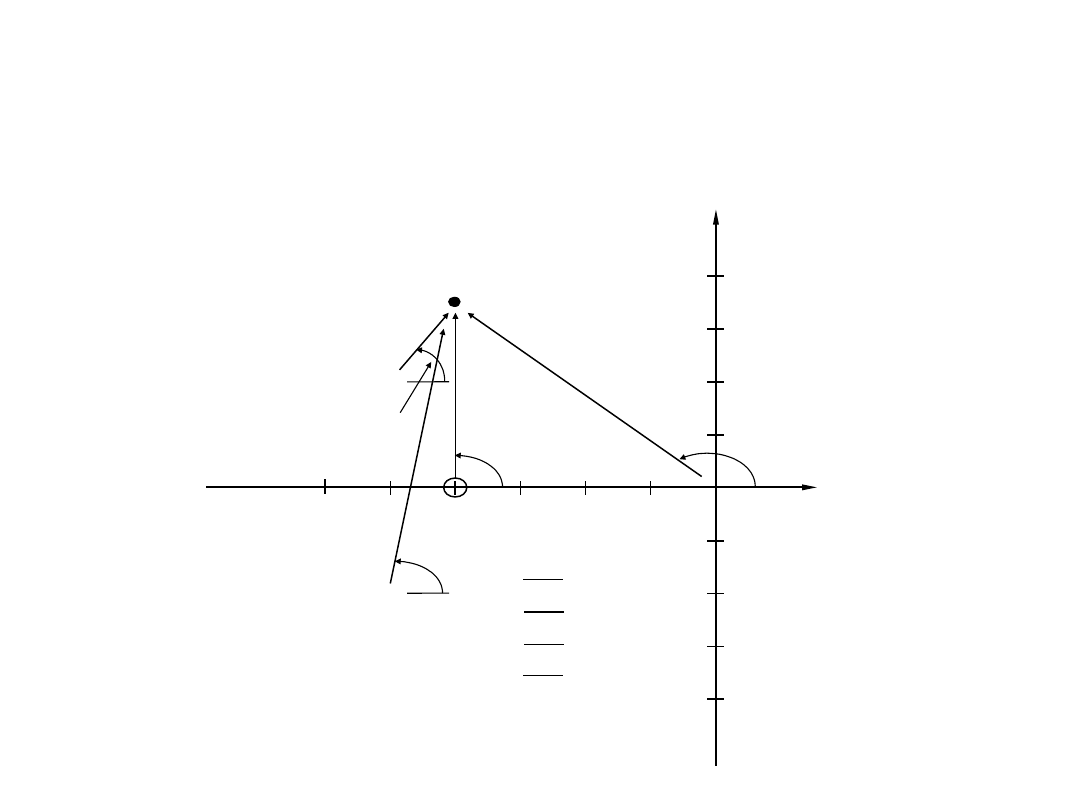
Poszukiwanie punktu na l. p.

• Rys

Re

Im

x

x

x

P

2

4

-2

-4

-2

-6

z

1

β

1

β

2

β

3

α

p

1

p

3

p

2

(s-p

1

)=s

(s-p

2

)

(s-p

3

)

(s-z

1

)

z

1

P = 3,4

p

1

P = 5,2

p

2

P = 1,6

p

3

P = 5,5

Przykład 19.1

•

Iloczyn transmitancji obiektu i regulatora wyraża wzór:

•

Wykreślić linie pierwiastkowe dla powyższego obiektu. Równaniem charakterystycznym

układu zamkniętego jest:

•

,

•

.

•

Rozwiązując równanie kwadratowe otrzymujemy wzór na obliczanie pierwiastków

równania charakterystycznego:

•

•

M-plik do przykładu 19.1

•

clear;clc;clf;

•

s=zpk('s');

•

%rlocfind(Gm)

•

Kc=1;

•

Gm=Kc/((2*s+1)*(5*s+1));

•

%pierwiastki równania charkaterystycznego

•

eig(Gm)

•

%wykres linii pierwiastkowych

•

figure(1);

•

rlocus(Gm,'b-');grid;%axis('image');

•

r = rlocus(Gm,[0,0.2,0.5]);hold on;

•

id1=plot(r,'rs');set(id1,'LineWidth',1.5);hold off;

•

df=char('Kc=0','Kc=0.2','Kc=0.5');

•

for i=1:1:(length(r)*length(eig(Gm)));

•

j=[1,1,2,2,3,3];

•

text(real(r(i))-real(r(i))*0.05, imag(r(i)),df(j(i),:),'FontSize',11,'Color','k','FontWeight','bold');

•

end;

( )

( )

(2 1)(5 1)

c

M

K

B s G s

s

s

=

+

+

0

)

(

)

(

1





s

G

s

B

M

1

0

(2 1)(5 1)

c

K

s

s

+

=

+

+

2

10

7 1

0

c

s

s

K

+ + +

=

3 1

4 5

5 5

c

s

K

=- �

-

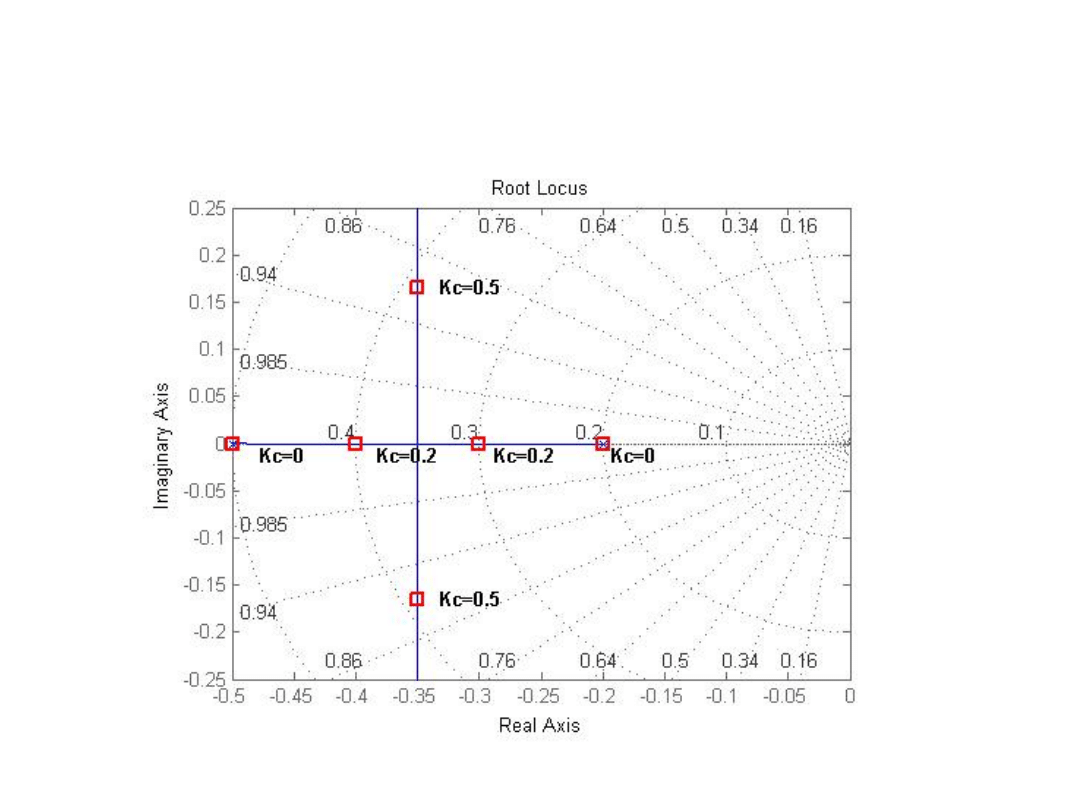
Lokalizacja biegunów i zer

Komentarz do przykładu 1

• Gdy Kc = 0, pierwiastki równania charakterystycznego wynoszą: –

1/5, –1 (są to bieguny transmitancji układu w stanie otwartym). Gdy

Kc = 0÷4/5, oba pierwiastki są rzeczywiste i leżą na ujemnej półosi

rzeczywistej. Układ zamknięty ma tłumienie krytyczne przy

wzmocnieniu Kc = 4/5, gdyż oba pierwiastki są rzeczywiste i równe.

Dla każdej większej wartości Kc pojawiają się pierwiastki zespolone.

Gdy Kc zmienia się w granicach od 4/5 do -∞, wówczas części

rzeczywiste obu pierwiastków są stałe i równe –3/5, a części urojone

przybierają wartości od plus do minus nieskończoności. W miarę

wzrostu Kc, układ staje coraz bardziej niedotłumiony. Rozpatrywany

układ zamknięty zawsze jest stabilny, gdyż pierwiastki równania

charakterystycznego nigdy nie przechodzą do prawej półpłaszczyzny

zespolonej.

• Przypuśćmy teraz, że należy zaprojektować układ o współczynniku

tłumienia równym 0,707. Z równania (8.22) otrzymujemy:0,707 =

450. Aby znaleźć odpowiednią wartość wzmocnienia regulatora,

musimy wyznaczyć punkt przecięcia wykresu linii pierwiastkowych z

prostą wychodzącą z początku układu współrzędnych i nachyloną

pod kątem 450 do ujemnej półosi rzeczywistej. Części urojona i

rzeczywista szukanego pierwiastka muszą być równe, stąd Kc =

13/5. Stała czasu układu zamkniętego odpowiadająca tej wartości

wzmocnienia wynosi T=5/3.

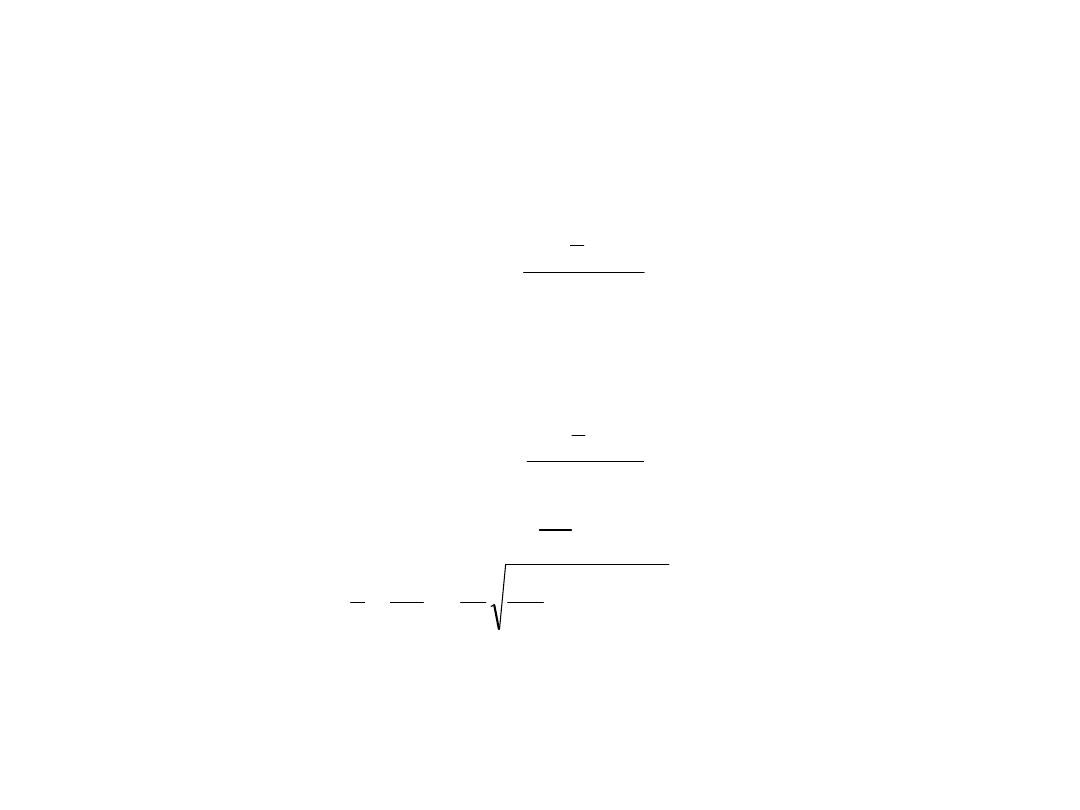
Przykład 2

• Załóżmy, że transmitancja pewnego układu zamkniętego różni się od poprzedniej

dodatkowym zerem (obecnością członu przyspieszającego fazę):

• Zbudować wykresy linii pierwiastkowych. Przeprowadzić dyskusję celem wybrania

wzmocnienia zapewniającego pożądane właściwości dynamiczne.

• Rozwiązanie

• Równanie charakterystyczne układu zamkniętego jest postaci:

• .

• Pierwiastkami równania są:

• Dla małych wartości wzmocnienia Kc wyrażenie podpierwiastkowe będzie dodatnie

i oba pierwiastki będą rzeczywiste. Podobnie dla bardzo dużych wartości

wzmocnienia dominować będzie wyraz zawierający i znów oba pierwiastki będą

rzeczywiste. Dla pośrednich wartości Kc wyrażenie podpierwiastkowe będzie

ujemne, a pierwiastki przyjmą wartości zespolone.

)

1

5

)(

1

(

)

1

2

1

(

)

(

)

(









s

s

s

K

s

G

s

B

c

M

1

(

1)

2

1

( )

( ) 1

(

1)(5 1)

c

M

K

s

B s G s

s

s

+

+

= +

+

+

2

5

(6

)

1 0

2

c

c

K

s

s K

+ +

+

+ =

16

14

4

10

1

20

5

3

2

2

,

1

















 





c

c

c

K

K

K

s

2

c

K

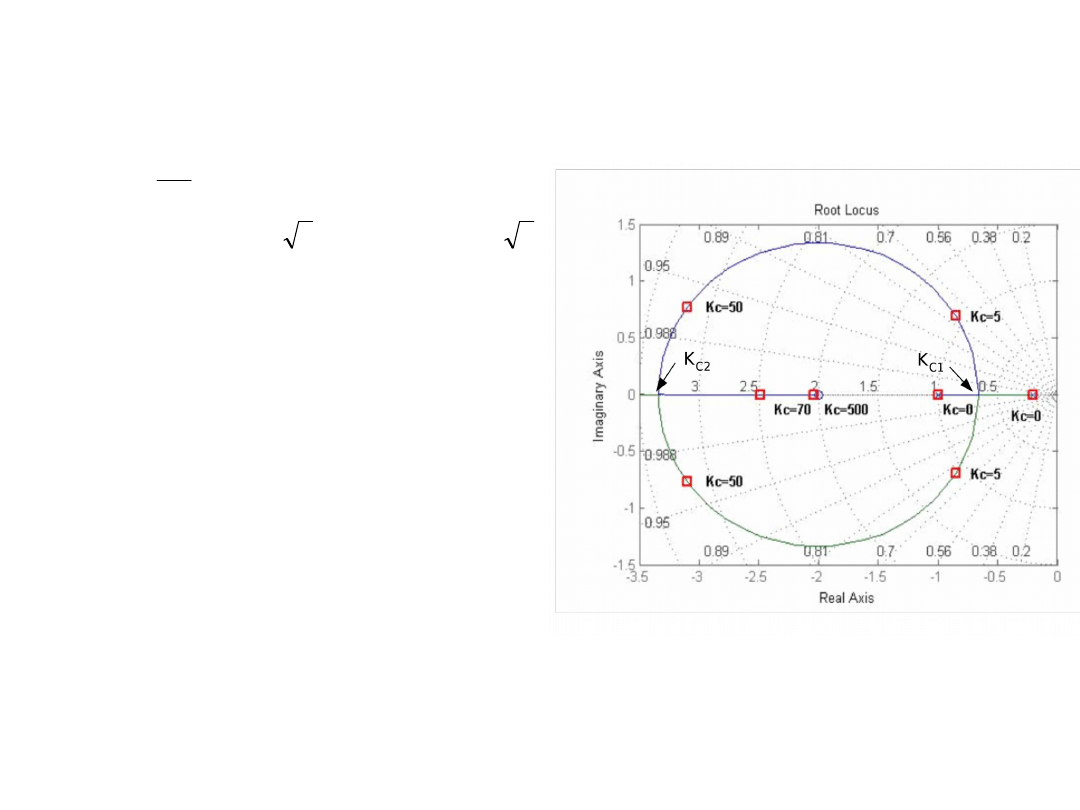
Przykład 2

•

Zakres wartości Kc, dla których równanie charakterystyczne będzie miało pierwiastki zespolone, znajdujemy

rozwiązując równanie:

•

gdzie: Kc1 – mniejsza wartość Kc, dla której wyrażenie

•

podpierwiastkowe równa się zeru; Kc2 – większa wartość Kc,

•

dla której wyrażenie podpierwiastkowe równa się zeru.

•

Wykres linii pierwiastkowych pokazano na rys.

•
•

Zauważmy, że dodanie do układu członu przyspieszającego fazę przesuwa wykres linii pierwiastkowych w głąb lewej

półpłaszczyzny zespolonej, a więc w kierunku poprawy stabilności układu. Gdy wzmocnienie dąży do

nieskończoności, dwie gałęzie linii pierwiastkujących dążą do minus nieskończoności i do wartości s = -2, czyli zera

transmitancji. Dla Kc równego zeru pierwiastki równania charakterystycznego równają się biegunom transmitancji

układu w stanie otwartym. Układ w stanie zamkniętym pozostaje stabilny dla wszystkich wartości wzmocnienia.

Najszybsze odpowiedzi dynamiczne układu można otrzymać stosując wzmocnienie Kc = Kc2, dla którego oba

pierwiastki są rzeczywiste i równe.

0

16

14

4

2







c

c

K

K

;

5

12

28

1





c

K

5

12

28

2





c

K

Przykład.3

• Wyznaczanie linii pierwiastkowym z członem przyśpieszającym i opóźniającym fazę

• Do układu rozważonego w przykładzie 19.2 dołączymy człon opóźniający fazę

(dodajmy dodatkowy biegun):

• Przedstawić zachowanie dynamiczne układu dla różnych wartości wzmocnienia Kc.

• Równanie charakterystyczne układu zamkniętego:

•

,

•

.

• Wykres linii pierwiastkowych pokazano na rys. Sposób obliczania pierwiastków

powyższego równania charakterystycznego wyjaśnimy w następnej części.

• Efektem dołączenia do układu członu opóźniającego fazę jest przesunięcie linii

pierwiastkowych w prawo, czyli w kierunku niestabilności. Wykres pierwiastków

równania charakterystycznego składa się z trzech linii. Dwie z nich o początku w

punktach s = 1/5 i s = -1 przyjmują zespolone wartości sprzężone i przechodzą do

prawej półpłaszczyzny. Układ w stanie zamkniętym staje się więc niestabilny dla

wartości Kc > Ku.





















1

2

1

)

1

5

)(

1

(

)

(

s

s

s

K

s

KG

c

o

























1

2

1

)

1

5

)(

1

(

1

)

(

1

s

s

s

K

s

KG

c

o

0

1

2

13

8

2

5

2

3











c

K

s

s

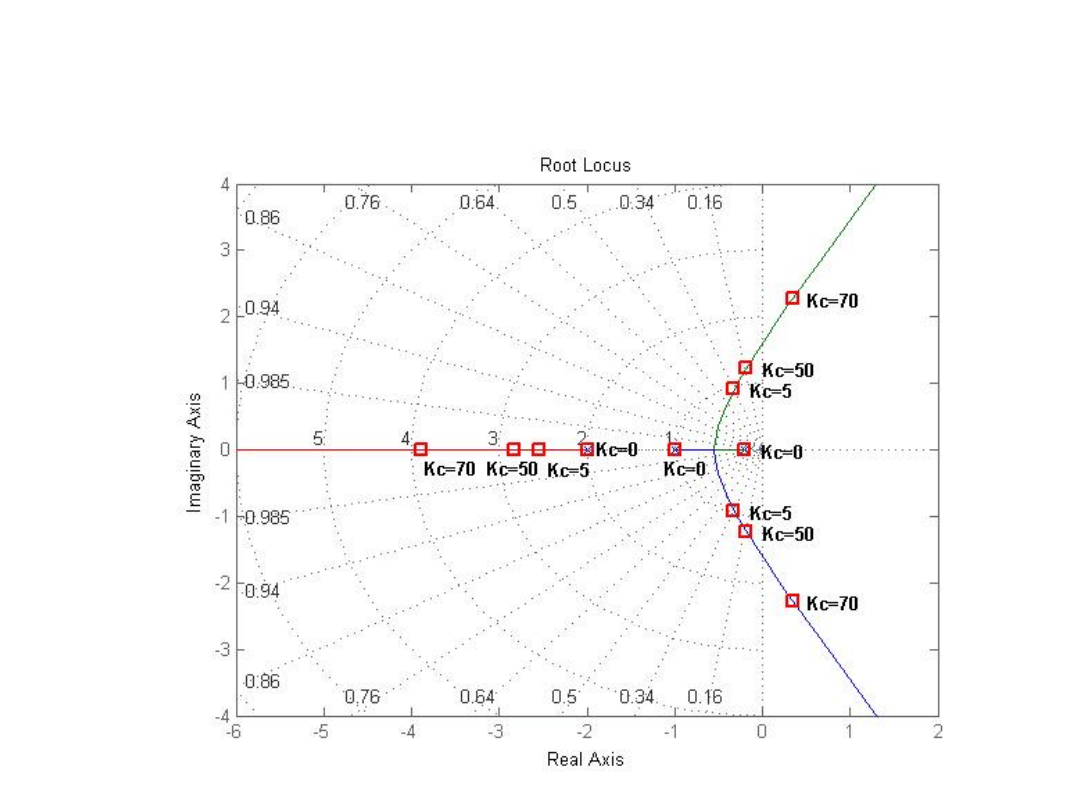
Przykład 3

Konstrukcja linii pierwiastkowych

•

Kreślenie linii pierwiastkowych dla układów pierwszego i drugiego rzędu nie

przedstawia większych trudności, gdyż pierwiastki odpowiadających im równań

charakterystycznych dają się wyznaczyć jako funkcje wzmocnienia regulatora. Dla

układów wyższych jest to żądanie trudniejsze. W tym przypadku korzystamy z

metody Evansa, który opracował podstawowe reguły wykreślania linii

pierwiastkowych.

1.

Krzywe pierwiastkowe są symetryczne względem osi rzeczywistej.

2.

Linie pierwiastkowe zaczynają się zawsze (Kc = 0) w punktach odpowiadających

biegunom transmitancji układu otwartego.

3.

Linie (w ilości m) kończą się (Kc = ∞) w punktach odpowiadających zerom Go(s). Gdy

m<n, to mamy n-m asymptot wychodzących ze wspólnego punktu, do których

zmierzają (do nieskończoności) pozostałe krzywe.

4.

Liczba linii pierwiastkowych równa się rzędowi układu, czyli liczbie biegunów Go(s).

Niektóre gałęzie linii pierwiastkowych mogą się wzajemnie przecinać, lecz nie

nakładają się nigdy w skończonym zakresie wartości Kc.

5.

Części linii będące wykresami pierwiastków zespolonych występują w postaci par

sprzężonych.

6.

Kąty nachylenia asymptot linii (gdy s → ∞) równają się ± 1900/(N-M), gdzie N jest

liczbą biegunów Go(s), a M jest liczbą zer Go(s). W przykładzie 1 N-M =2, więc

asymptoty tworzyły z osią rzeczywistą kąty ± 900. W przykładzie 2 N-M=1, więc kąty

nachylenia asymptot równały się ± 1900. W przykładzie 3 N-M=3, stąd kąty wynoszą

odpowiednio ± 600.

7.

Punkt początkowy asymptot, gdy n-m≥2, znajduje się
na osi rzeczywistej w punkcie o współrzędnej:

1.

Jeśli n-m≥2, to środek ciężkości biegunów układu zamkniętego

2.

, obliczany ze wzoru:

•

jest niezależny od K, czyli pozostaje nieruchomy na płaszczyźnie s przy zmianie K.

m

n

z

p

h

n

i

m

i

j

i















1

1







n

i

i

n

P

S

1

Konstrukcja linii pierwiastkowych

9 Udział w sumarycznej fazie transmitancji Go(s), wynikający z biegunów i

zer układu otwartego na prawo od punktu rozwidlenia i odejścia krzywej

pierwiastkowej od osi rzeczywistej, jest zrównoważony przez sumaryczną

fazę biegunów i zer po stronie lewej. Jeśli wszystkie bieguny i zera układu

otwartego są rzeczywiste, współrzędna punktu rozwidlenia może zostać

ustalona poprzez rozwiązanie następującego równania na b metodą prób:

•

10 Kąty θi odejścia linii od bieguna zespolonego układu otwartego pi są

podane wzorem:

• przy czym ψj jest kątem na który składają się kąty od innych biegunów

(mierzone dodatnio) i zer (mierzone ujemnie) układu otwartego. Podobnie

można obliczyć kąt osiągnięcia zespolonego zera układu otwartego.

• Wymienione reguły są bardzo proste do zapamiętania i umożliwiają

szybkie określenie przybliżonego przebiegu linii pierwiastkowych. Bardziej

szczegółowe wskazówki dotyczące wykreślenia linii pierwiastkowych oraz

inne metody ich konstrukcji można znaleźć w wielu opracowaniach.















m

j

j

n

i

i

z

b

p

b

1

1

.

1

1

j

i

,

180









j

o

i





Metoda przesuwania biegunów w

przestrzeni stanów dla układów SISO

•

Metoda przestrzeni stanów zapewnia bezpośrednie podejście do projektowania i analizy

wielowymiarowych układów sterowania. Projektowanie jest łatwe, jeżeli istnieją macierze

odwrotne względem macierzy B i C występujących w równaniach:

•

y = Cx,

•

opisujących liniowy obiekt sterowany o parametrach skupionych. Aby nieco uprościć ten

problem, przyjmujeliśmy, że nie ma bezpośredniego przejścia od u do y (tj. D = 0). Jeżeli

istnieją macierze B-1 i C-1, to B i C muszą być macierzami kwadratowymi o wymiarach n×n.

W następstwie tego wektor sterowań u i wektor wyjść y mają ten sam wymiar n co wektor

stanu x. Gdy pożądane zachowanie się obiektu jest określone przez [n×n] – wymiarową

macierz Ad, to można jednoznacznie wyznaczyć wektorowe prawo sterowania K ze

sprzężeniem zwrotnym w postaci

• u = - Ky

•

takie, że równania obiektu będą zapewniać pożądane właściwości dynamiczne obiektu w

układzie zamkniętym:

•

•

Aby znaleźć K, podstawimy najpierw drugie z równań obiektu do pierwszego równania, co

pozwala wyrazić wektor sterowania jako funkcję stanu:

•

u = - KCx

•

Jeżeli powyższe równanie (19.14) podstawimy teraz do równania stanu i wynik przyrównamy do

równania układu zamkniętego, to otrzymamy:

•

Ax – BKCx = Adx,

•

skąd wynika zależność:

•

A – BKC = Ad,

•

Czyli K = B-1(A – Ad) C-1

•

 

)

(

)

(

t

t

dt

t

d

Bu

Ax

x





x

A

x

d

dt

d



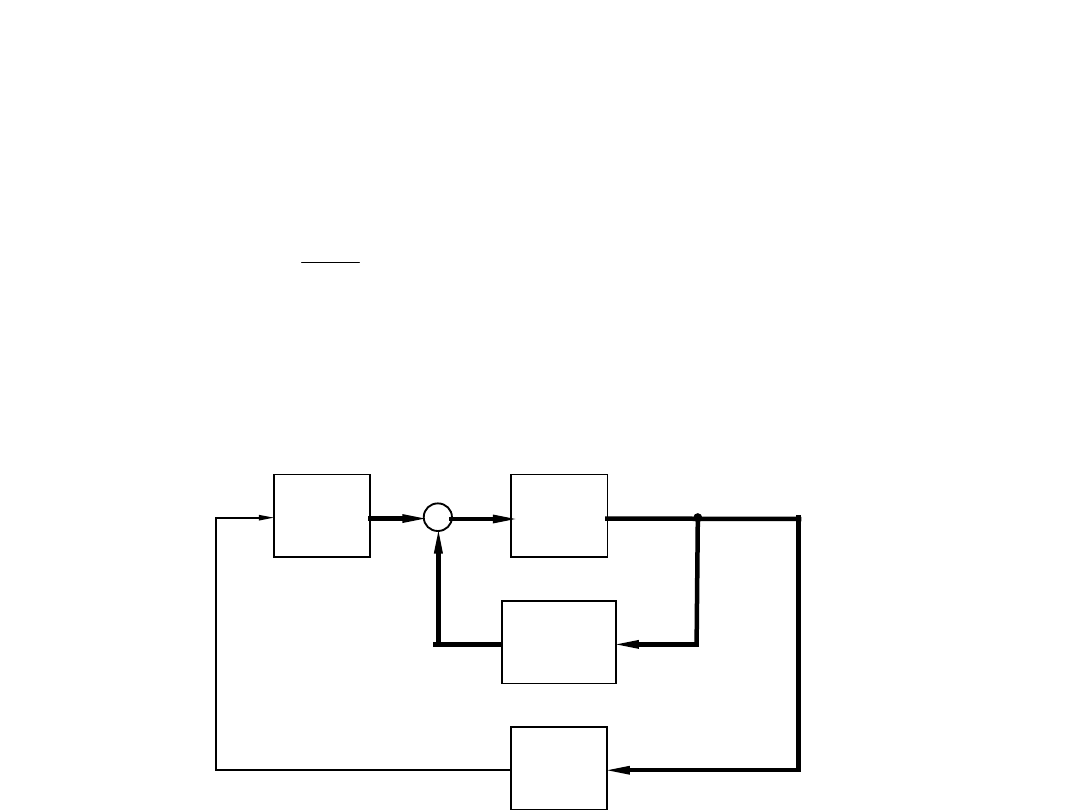
Zarys metody przesuwania

biegunów

• Istnieje możliwość, przez wprowadzenie odpowiedniej skalarnej zmiennej

sterującej u(t), zaprojektowania wielowymiarowego układu sterowania ze

sprzężeniem zwrotnym, w którym wszystkie bieguny układu zamkniętego będą

ustalone w wybranych dowolnych punktach na płaszczyźnie zespolonej s.

Potrzebne do tego warunki konieczne są następujące: (1) musi być możliwy

bezpośredni i całkowity pomiar stanu (tj. musi istnieć macierz C-1) i (2) obiekt

musi być sterowalny. Równanie stanu obiektu w tym przypadku ma postać:

•

• przy czym x jest wektorem stanu n-wymiarowym, A jest stałą macierzą o

wymiarach (n×n), a b jest wektorem n-wymiarowym. Ponieważ C-1 istnieje z

założenia, więc uprościmy dalsze rozważania przyjmując, że C = I, czyli: y = x;

co oznacza, że jest możliwy bezpośredni pomiar lub estymacja wektora stanu.

Prawo sterowania dla tego przypadku może być reprezentowane przez wektor

wierszowy kT, prowadząc do skalarnego sterowania:

• u(t) = - kTx(t)

 

)

(

)

(

t

t

dt

t

d

Bu

Ax

x





















5

4

2

3















0

1

















2

1

x

x

x















s

s

0

0

 

2

1

k

k

związek między biegunami układu

otwartego i zamkniętego

•

Wektor uchybu E(s) jest równy – X(s). Gdy wartość zadana jest zerowa, na wektor ten działa

stały wektor wierszowy kT, który zapewnia sterowanie skalarne U(s). Wektor wierszowy jest

zbiorem sterowań proporcjonalnych:

•

kT = [k1,k2, ..., kn]

•

Skalarne wejście sterujące jest zatem dane jako:

•

U(s) = = kTX (s)

lub

u(t) = - kTx(t)

•

Podstawiając liniowe prawo sterowania do równania obiektu, otrzymamy równanie układu

zamkniętego :

•

=(A-bkT)x(t).

•

Tym samym wielomian charakterystyczny układu zamkniętego przyjmuje postać:

•

ΔZ = det(sI – A+ bkT) = det{sI – A) [I + (sI – A)-1 bkT]} =

•

= det [sI – A) det [I + (sI – A)-1 bkT] =

•

= Δ (s) det {I + h(s)kT},

•

przy czym Δ(s) jest wielomianem charakterystycznym układu otwartego:

•

Δ(s) = |sI-A| = a0 + a1 s + ... + an-1 sn-1 + an sn , an = 1,

•

natomiast wektor h(s) ma postać:

•

h(s) = (sI – A)-1 b

•

i jest wektorem n-wymiarowym. Z rachunku macierzowego wiemy, że drugi wyznacznik ze

wzoru redukuje się do:

•

det (I + h(s) kT) = 1 + kTh (s)

•

Ostatecznie wielomian charakterystyczny układu zamkniętego przyjmuje postać:

•

Δz(s) = Δ(s) (1 + kTh(s) = Δ(s) + Δ(s) kT h(s).

•

Widzimy, że równanie Δz(s) = Δ(s) (1 + kTh(s) = Δ(s) + Δ(s) kT h(s) wiąże ze

sobą równania charakterystyczne układu zamkniętego i otwartego. Drugi

wyraz po prawej stronie równania można teraz wyrazić w sposób jawny jako

wielomian zmiennej s,

•

Δ(s) kT h(s) = Δ(s) kT (sI – A)-1 b = Δ(s) kT δi b = kT δi b,

•

Stąd:

•

Δc(s) = Δ(s) + kTδi b.

•

Wielomian charakterystyczny układu otwartego był wyrażony w zależności od

współczynników a0, a1, ..., an. Wracając doń, mamy teraz:

•
•

Δ(s) = a0 + a1 s + … + an sn ; an = 1.

•

Niech wielomian charakterystyczny układu zamkniętego będzie następujący:

•

Δc(s) = a0c + a1c s + … + anc sn ; anc = 1

•

Wówczas współczynniki dwu wielomianów charakterystycznych są powiązane

jak następuje:

•

ajc = aj + kTδj+1b ;

j = 0, ..., n

Przykład

•

Rozważmy układ pokazany na rys.. Obiekt sterowany jest opisany przez równanie:

•

Znaleźć wektor sterowania, czyli wektor [k1,k2] (patrz Rys.) metodą przesuwania biegunów.

•

Liniowe prawo sterowania ma postać:

•

Wielomian charakterystyczny układu otwartego jest równy:

•

Δ (s) = |(sI – A)| = 7 + 8s + s2

•

i stąd:

•

a0 = 7 , a1 = 8 , a2 = 1.

•

Wzór daje:

•

δ1 = a1I + a2 A =, δ2 = a2 I = I,

•

skąd:

•

a0c = a0 + kTδ1 b = 7 + 5k1 + 4k2,

•

a1c = a1 + kTδ2 b = 8 + k1,

•

a2c = a2 = 1

•

i wobec tego wielomian charakterystyczny układu zamkniętego przyjmuje postać:

•

Δc(s) = (7 + 5k1 + 4k2) + (8 + k1)s + s2.

•

Jeżeli np. chcemy, aby układ zamknięty miał dwa ujemne bieguny rzeczywiste, obydwa

równe –10, to musimy wtedy mieć:

•

Δc(s) = (s + 10)2 = 100 + 20s + s2.

•

Możemy wyznaczyć k1 i k2 dla spełnienia tego warunku przez rozwiązanie dwu równań:

•

8 + k1 = 20,

7 + 5k1 + 4k2 = 100

•

zatem:

•

k1 = 12, k2 =33/4 .

.

0

1

5

4

2

3

2

1

2

1

u

x

x

x

x

dt

d





































































3

4

2

5

Zapis macierzowy metody

przesuwania biegunów

•

Obecnie pokażemy, że jednoznaczne rozwiązanie na prawo sterowania kT istnieje i że

daje ono pożądany zbiór biegunów układu zamkniętego, gdy obiekt jest sterowalny. Jako

pierwszy krok rozwiązania problemu wyprowadzamy równanie macierzowe z równania

(19.29). Przepisując równanie (19.29) dla kolejnych j w następującej postaci:

•

a0c – a0 = kTδ1b = (δ1b)Tk,

»

………………….

•

a(n-1)c – an-1 = (δnb)Tk,

•

łączymy ten układ równań w jedno równanie macierzowe:

•

a macierz z prawej strony powyższego równania oznaczymy:

•

Równanie można rozwiązać względem k, jeżeli jest znana macierz D-1. Aby znaleźć

D-1, wprowadzamy stały wektor n-wymiarowy p, takie że:

•

PTb = 0, pTAb = 0, ..., pTAn-2b = 0, pTAn-1b = 1.

•

Wówczas wynika stąd, że:

•

PT[b Ab ... An-1b] = pTP = [0 0 ... 0 1],

•

a po transpozycji: PTp = en,

•
•

przy czym en jest n-tą kolumną macierzy I, a macierz P jest zdefiniowana jako:

•

P = [b Ab ... An-1b].

•

Jest to macierz decydująca o sterowalności, jak to wykazano wcześniej. Jeżeli obiekt jest

sterowalny, to |P| = 0 i możemy wyznaczyć wektor p z równania

•

P = (P-1)Ten.

 









,

1

1

0

0

1



















































n

c

n

c

n

a

a

a

a

k

b

S

b

S





 

 























b

S

b

S

D

n



1

•

Obliczamy teraz iloczyn macierzy:

•

[p ATp ... (AT)n-1 p] b = [p ATp ... (AT)n-1p] Db =

•

= p (δ1 b)Tb + ATp(δ2 b)Tb + ... + (AT)n-1 p (δn b)Tb =

•

= [δ1 bpT + δ2 bpTA + ... + δn bpT(A)n-1]Tb =

•

= Ib

•

Redukcja ta opiera się na równości iloczynów wektora kolumnowego i wektora wierszowego:

•

p (δi b)T = [(δi b)T], na podstawie własności wektora p: pTAib = 0- dla wszystkich i z

wyjątkiem i = (n-1) oraz na fakcie, że: δnb(pTAn-1 = δnb = Ib

•

Ponieważ Sn = I., to z równania (19.39) otrzymujemy:

•

[pATp ... (AT)n-1p] D = I,

•

przeto:

•

D-1 = [p ATp ... (AT)n-1p]

•

i równanie ma następujące rozwiązanie:

•

k = [p ATp ... (AT)n-1p]

•

•

= (a0c – a0) + (a1c – a1) ATp +(a(n-1)c – an-1)(AT)n-1 p =

•

= (aic – ai)(A)i p.

•

Prawo sterowania ze sprzężeniem zwrotnym od zmiennej stanu (wektor wierszowy) kT

można obliczyć za pomocą wzoru (19.34) (zazwyczaj posługując się komputerem) dla

sterowania skalarnego danego obiektu, gdy wszystkie bieguny układu zamkniętego są dane

z góry.









































1

)

1

(

1

0

n

c

n

k

k

a

a

a

a

a

a





Przykład

•

Rozważymy ponownie układ, który projektowaliśmy w ostatnim

• przykładzie, czyli obiekt opisany macierzami: A = b =

• z prawem sterowania: . Ponownie wyznaczymy parametry

regulatora; tym razem metodą macierzową.

• Rozwiązanie

• Jeśli pożądane bieguny układu zamkniętego są biegunem podwójnym

równym –10, mamy:

• ∆c(s) = (s + 10)2 = a0c + a1c s + s2, przy czym: a0c = 100, a1c = 20.

Obliczamy:

•

P =[ b Ab] =

P-1 =

(P-1)T =

•

•

p = (P-1)T en =

•

•

k = (a0c - a0)p + (a1c – a1) AT p = (100-7)p + (20-8) p

= .

• Wyniki są takie same, jak w poprzednim przykładzie, ale rozwiązanie jest

teraz w zwartej postaci, nadającej się bezpośrednio do obliczeń na

komputerze cyfrowym.

,

5

4

2

3





























0

1















2

1

k

k

k

;

4

/

1

4

/

3

4

/

3

1













;

4

0

3

1















.

4

/

1

4

/

3

0

1





























5

2

4

3













4

/

33

12

,

4

/

1

1

0

1

4

/

1

4

/

3

0

1





































Zastosowanie postaci kanonicznej

sterowalnej

• W poprzednim punkcie można zauważyć ważną rolę jaką spełnia postać

kanoniczna sterowalna w projektowaniu regulatora metodą przesuwania biegunów.

Obecnie pokażemy jak można wykorzystać tą postać do skonstruowania prawa

sterowania. Jak wiemy z rozdziału 6 postać kanoniczną uzyskuje się przez obrót

układu współrzędnych stanu z wykorzystaniem odpowiedniej postaci macierzy

transformacji T. Zdefiniujmy macierz transformacji jako iloczyn dwóch macierzy:

• Gdzie H jest macierzą obserwowalności:

• Natomiast macierz W zbudowana jest ze współczynników wielomianu

charakterystycznego:

• Jak pamiętamy z rozdziału 6 wielomian charakterystyczny ma postać:

• Δ(s) = |sI-A| = a0 + a1 s + ... + an-1 sn-1 + an sn , an = 1,

• Wprowadzenie transformacji (obrotu) prowadzi do nowego wektora stanu i

równania stanu układu otwartego:

• gdzie:

HW

T 





B

A

B

A

AB

B

H

1

2





n













































0

0

0

1

0

0

1

0

1

1

1

3

1

1

2

1

















a

a

a

a

a

a

n

n

n

n

W

,

~

~

1

1

u

B

T

x

AT

T

x











• Wprowadzenie transformacji (obrotu) prowadzi do nowego wektora stanu i

równania stanu układu otwartego:

• gdzie:

• , .

• Przyjmiemy teraz, że pożądanymi wartościami własnymi układu zamkniętego

są bieguny: . Tym samym równanie charakterystyczne

układu zamkniętego przyjmie postać:

• Macierz wzmocnienia regulatora K również poddamy transformacji:

• a prawo sterowania będzie miało postać:

• Po wprowadzeniu powyższego prawa sterowania do równania stanu obiektu

otrzymujemy równanie stanu układu zamkniętego:

• Równanie charakterystyczne macierzy stanu układu zamkniętego przyjmie

więc postać:

,

~

~

1

1

u

B

T

x

AT

T

x























































a

a

a

a

n

















1

0

0

0

0

0

0

0

0

0

1

0

1

AT

T





































1

0

0

0

1



B

T

n

p

p

p

,

,

,

2

1



0

)

(

)

)(

(

1

2

2

1

1

2

1



























n

n

n

n

n

n

s

s

s

s

p

s

p

s

p

s

















1

1

~

~

~

~

k

k

k

n

n







KT

K

x

KT

x

K

~

~

~









u

,

~

)

(

~

~

~

1

1

1

1

x

BKT

T

AT

T

x

BKT

T

x

AT

T

x



















.

0

)

(

1

1

1

























BK

A

I

T

BK

A

I

T

BKT

T

AT

T

I

s

s

s

•

Równanie charakterystyczne odpowiada więc następującemu równaniu stanu układu zamkniętego:

•

(19.53)

•

i prawu sterowania:

•

(19.54)

•

Widzimy więc , że powyższe prawo sterowania jest równoznaczne z prawem sterowania dla układu

opisanego w postaci fizycznej (z wykorzystaniem paw fizyki).

•

Obecnie rozwiniemy (uprościmy) równanie charakterystyczne wykorzystując zależności

(19.47), (19.52):

•

=

•

=

•

(19.55)

•

Otrzymaliśmy równanie charakterystyczne układu ze sprzężeniem od wektora stanu. Równanie te

musi być równoważne równaniu charakterystycznemu (19.48). Po porównaniu współczynników przy

tych samych potęgach s mamy:

•

(19.56)

•

Na bazie tych równań w prosty sposób wyznaczmy elementy macierzy wzmocnienia regulatora:

•

,

•

czyli:

•

K

(19.57)

•

Tym samym uzyskaliśmy stosunkowo prostą zależność na wyznaczanie macierzy wzmocnienia w

prawie sterowania (19.54). Aby wyznaczyć macierz wzmocnienia korzystamy ze współczynników

równania charakterystycznego obiektu (19.45), współczynników równania charakterystycznego

układu zamkniętego (19.48) oraz macierzy transformacji podanej wzorami (19.42), (19.43), (19.44).