



Analiza liczby

Analiza liczby

posiadanych kontaktów w

posiadanych kontaktów w

telefonie.

telefonie.





Badanie występowania

Badanie występowania

korelacji pomiędzy liczbą

korelacji pomiędzy liczbą

kontaktów w telefonie, a ilością

kontaktów w telefonie, a ilością

wysyłanych przez miesiąc

wysyłanych przez miesiąc

smsów

smsów

.

.



miary tendencji centralnej

miary tendencji centralnej



miary zróżnicowania

miary zróżnicowania



typowe przedziały zmienności

typowe przedziały zmienności



wskaźnik asymetrii

wskaźnik asymetrii



współczynnik korelacji

współczynnik korelacji

Studenci studiów stacjonarnych i

Studenci studiów stacjonarnych i

niestacjonarnych:

niestacjonarnych:



przedział wiekowy od 19 do

przedział wiekowy od 19 do

22 lat

22 lat



zamieszkali na terenie

zamieszkali na terenie

miasta Łodzi

miasta Łodzi

Próba statystyczna:

Próba statystyczna:

20

20

studentów

studentów

Zbiorowość

Zbiorowość

statystyczna:

statystyczna:

Zebrane dane:

Zebrane dane:

Liczba kontaktów w telefonie:

130,200,300,70,74,50,41,125,450,70,25,10,250,270,2

00,15,220,110,50,150

Ilość wysłanych w ciągu miesiąca smsów:

300,300,1000,400,750,526,250,100,600,2000,2500,15

35,1300,1000,250,700,650,300,350.

Liczba kontaktów w telefonie

l. kontaktów

l. studentów

0

100

9

100

200

4

200

300

5

300

400

1

400

500

1

L. wysyłanych smsów w miesiącu

Ilość smsów

l. studentów

0

500

9

500

1000

5

1000

1500

3

1500

2000

1

2000

2500

2

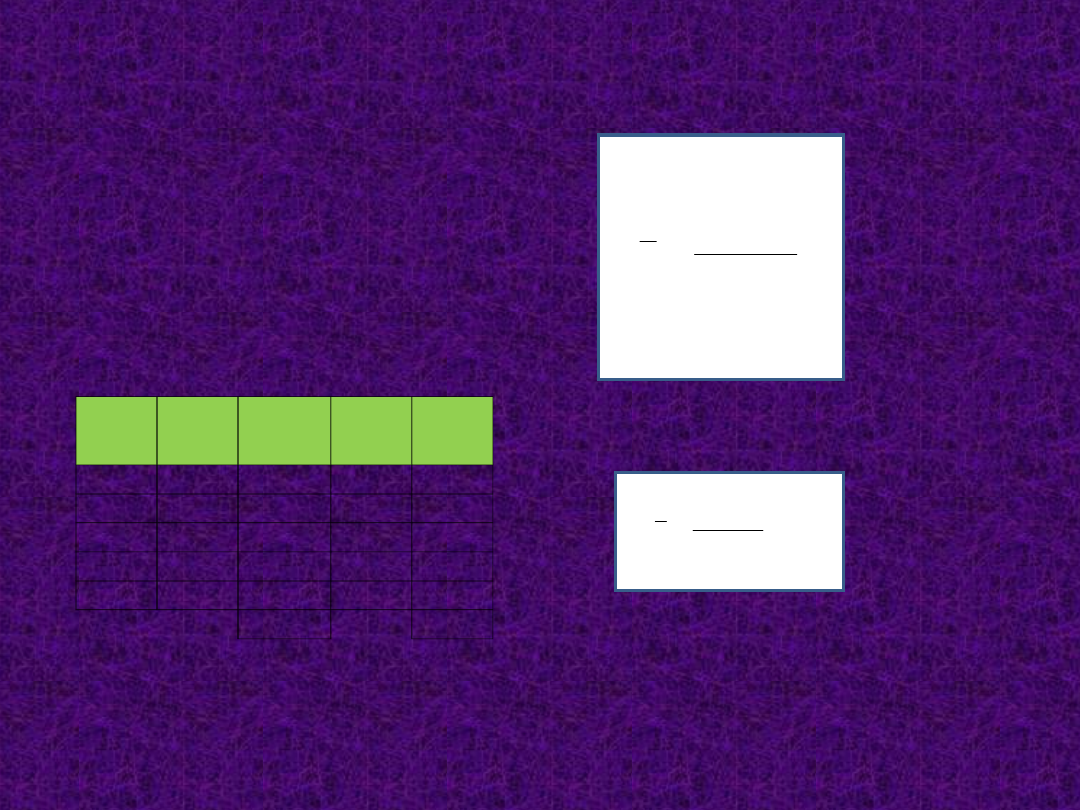
Szereg rozdzielczy z przedziałami

Szereg rozdzielczy z przedziałami

klasowymi

klasowymi

Do analizy

Do analizy

użyjemy

użyjemy

Liczby

Liczby

kontaktów w

kontaktów w

telefonie.

telefonie.

Miary tendencji

Miary tendencji

centralnej

centralnej











k

i

i

k

i

i

i

n

n

x

x

1

1



l.

kontakt

ów

 

l.

studentó

w

Xi

Xi*ni

0

100

9

50

450

100

200

4

150

600

200

300

5

250

1250

300

400

1

350

350

400

500

1

450

450

20

3100

Średnia
arytmetyczna

Obliczenia

155

20

5

,

3104





x

Średnia liczba kontaktów w telefonie wynosi w przybliżeniu

Średnia liczba kontaktów w telefonie wynosi w przybliżeniu

155 wpisów przypadające na jednego studenta.

155 wpisów przypadające na jednego studenta.

Dominanta

Najwięcej studentów posiada od 0 do 100 liczby kontaktów w
telefonie, a ponieważ jest to pierwszy przedział, dominanty się
nie oblicza.

Mediana





1

0

0

0









sk

Me

n

N

n

h

x

Me

250

)

13

10

(

5

100

200









Me

50% studentów posiada

50% studentów posiada

250 wpisów lub mniej,

250 wpisów lub mniej,

pozostałe 50%

pozostałe 50%

studentów posiada 250

studentów posiada 250

wpisów lub więcej.

wpisów lub więcej.

Miary zróżnicowania

Miary zróżnicowania

0819

,

116

20

269500

)

(

1

1

2

















k

i

i

k

i

i

i

x

n

n

x

x





Wariancja

l. kontaktów

l. smsów

Xi

Xi*ni

Xi-x

(Xi-x)^2

((Xi-x)^2)*ni

0

100

9

50,5

450

-105

11025

99225

100

200

4

150

600

-5

25

100

200

300

5

250

1250

95

9025

45125

300

400

1

350

350

195

38025

38025

400

500

1

450

450

295

87025

87025

20

3100

suma

269500

Obliczenia:

%

75

%

100

155

0819

,

116

%

100









x

V

x

x





Liczba kontaktów

Liczba kontaktów

poszczególnych

poszczególnych

studentów

studentów

odchylała się od

odchylała się od

średniej przeciętnie

średniej przeciętnie

o 116 wpisów, co

o 116 wpisów, co

stanowi 75%

stanowi 75%

średniej.

średniej.

Typowe przedziały

Typowe przedziały

zmienności

zmienności

x

typ

x

x

x

x













0819

,

116

155

0819

,

116

155









typ

x

0819

,

271

9181

,

39





typ

x

Typowa liczba

Typowa liczba

kontaktów

kontaktów

posiadanych przez

posiadanych przez

studentów mieści

studentów mieści

się w przedziale od

się w przedziale od

39 wpisów do 271

39 wpisów do 271

wpisów, dane

wpisów, dane

zostały podane w

zostały podane w

przybliżeniu.

przybliżeniu.

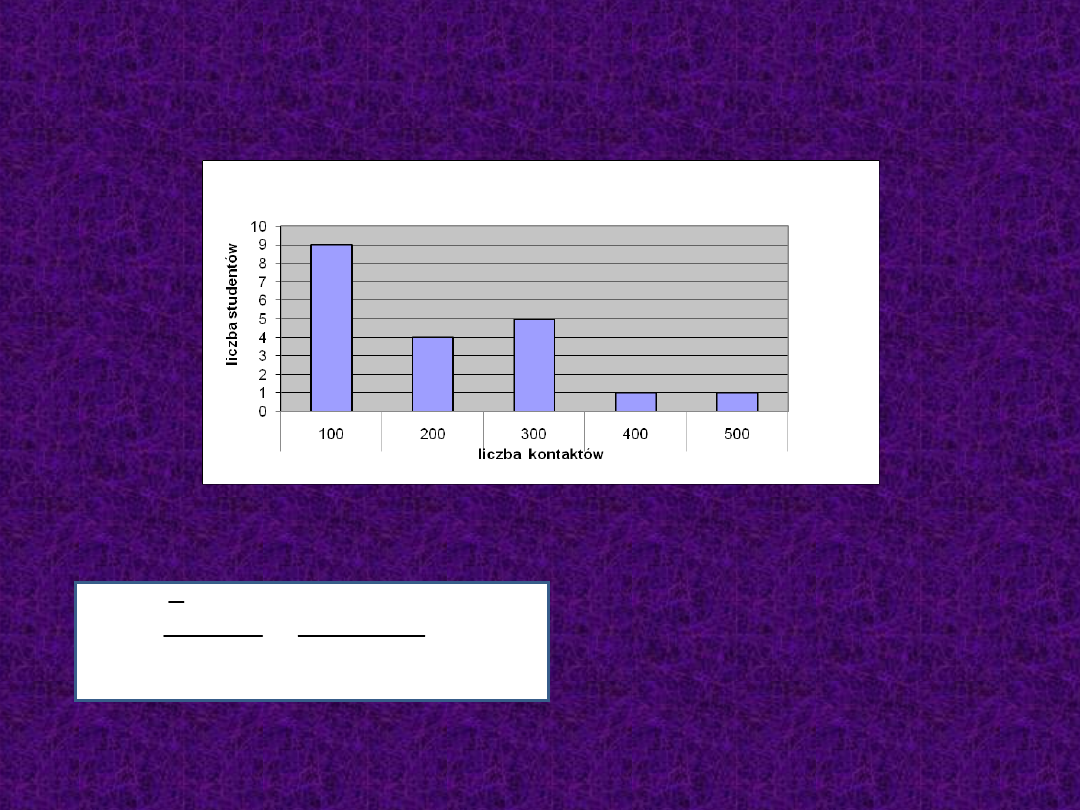
Wskaźnik asymetrii

Wskaźnik asymetrii

Rozkład

liczby

posiadanych

przez

studentów

kontaktów w telefonie

948

,

0

0819

,

116

45

155











x

Mo

x

A





Wartość współczynnika

Wartość współczynnika

asymetrii wskazuje na to,

asymetrii wskazuje na to,

że szereg przedstawiający

że szereg przedstawiający

liczbę kontaktów 20

liczbę kontaktów 20

losowo wybranych osób w

losowo wybranych osób w

wieku 19 - 22 lat

wieku 19 - 22 lat

charakteryzuje się silną

charakteryzuje się silną

asymetrią prawostronną.

asymetrią prawostronną.

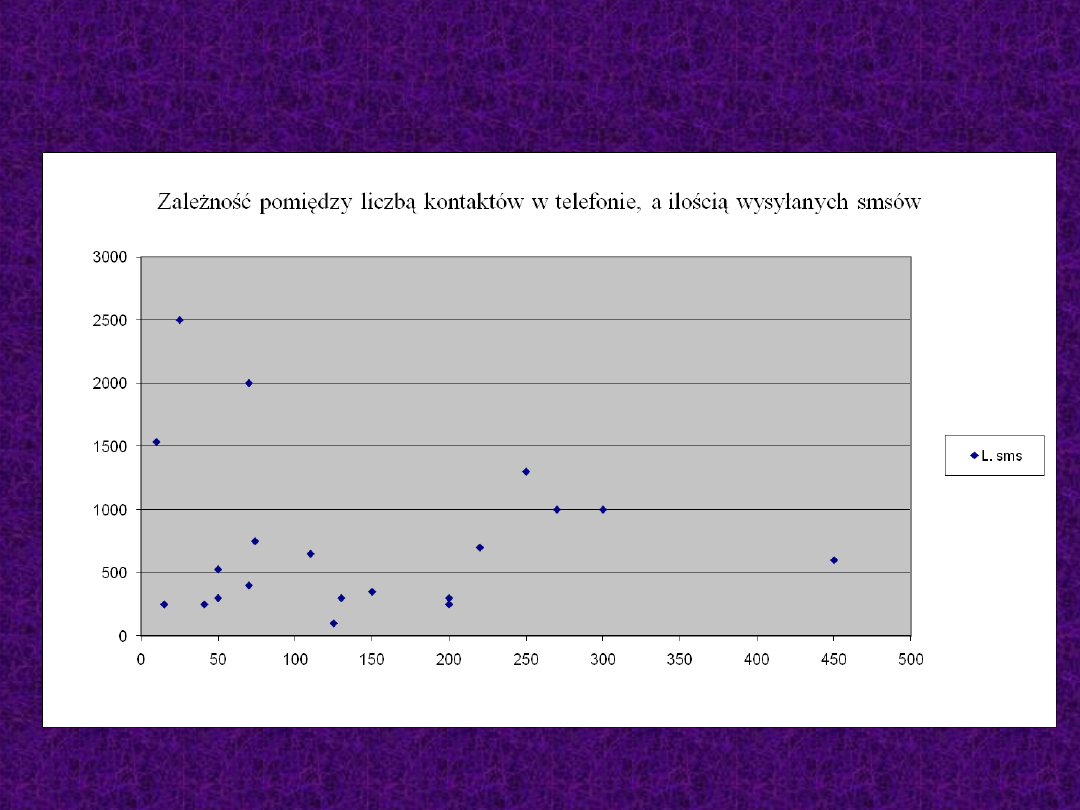
Badanie korelacji

Badanie korelacji

L. kontaktów

L. sms

xi-x

y-yi

 

x-xi^2

y-yi^2

130

300

-10,5

-453,05

4757,025

110,25

205254,3

200

300

59,5

-453,05

-26956,5

3540,25

205254,3

300

1000

159,5

246,95

39388,53

25440,25

60984,3

70

400

-70,5

-353,05

24890,03

4970,25

124644,3

74

750

-66,5

-3,05

202,825

4422,25

9,3025

50

526

-90,5

-227,05

20548,03

8190,25

51551,7

41

250

-99,5

-503,05

50053,48

9900,25

253059,3

125

100

-15,5

-653,05

10122,28

240,25

426474,3

450

600

309,5

-153,05

-47369

95790,25

23424,3

70

2000

-70,5

1246,95

-87910

4970,25

1554884

25

2500

-115,5

1746,95

-201773

13340,25

3051834

10

1535

-130,5

781,95

-102044

17030,25

611445,8

250

1300

109,5

546,95

59891,03

11990,25

299154,3

270

1000

129,5

246,95

31980,03

16770,25

60984,3

200

250

59,5

-503,05

-29931,5

3540,25

253059,3

15

250

-125,5

-503,05

63132,78

15750,25

253059,3

220

700

79,5

-53,05

-4217,48

6320,25

2814,303

110

650

-30,5

-103,05

3143,025

930,25

10619,3

50

300

-90,5

-453,05

41001,03

8190,25

205254,3

150

350

9,5

-403,05

-3828,98

90,25

162449,3

140,5

753,05  

 

-154921

251527

7816215

Obliczenia

r

r

xy

xy

=

=

-0,11049

-0,11049

Nie występuję zależność korelacyjna

Nie występuję zależność korelacyjna