BADANIE

KORELACJI

ZMIENNYCH

SPIS TREŚCI:

1. Zapis współzależności zjawisk:

1.1. Wykresy korelacyjne.

1.2. Tablice korelacyjne.

2. Analiza zależności dwóch cech:

2.1. Współczynnik korelacji liniowej

Pearsona.

2.2. Współczynnik korelacji

rangowej

Spearmana.

2.3. Test niezależności chi-kwadrat.

2.4. Współczynnik V Cramera.

Korelację w statystyce można

przedstawić na trzy sposoby:

1. Graficznie,

2. Tabelarycznie,

3. Liczbowo, jako współczynnik

korelacji

ZAPIS

WSPÓŁZALEŻNOŚCI

ZJAWISK

Do zapisu współzależności zjawisk

zaliczamy:

• Wykresy korelacyjne,

• Tablice korelacyjne.

WYKRESY KORELACYJNE

Analizę związku korelacyjnego między

badanymi cechami rozpoczynamy

zawsze od sporządzenia wykresu.

Wykresy, które reprezentują obrazowo

związek pomiędzy zmiennymi, nazywane

są wykresami rozrzutu (scatterplot).

Wzrokowa ocena ułatwia określenie siły

i rodzaju zależności.

Przyjmijmy, że zbiorowość jest badana

ze względu na dwie zmienne X i Y, a

wartości tych zmiennych w populacji

lub próbie n - elementowej są

zestawione w postaci dwóch szeregów

szczegółowych lub rozdzielczych.

W prostokątnym układzie

współrzędnych na osi odciętych

zaznaczamy wartości jednej

zmiennej, a na osi rzędnych -

wartości drugiej zmiennej.

Punkty odpowiadające poszczególnym

wartościom cech tworzą korelacyjny

wykres rozrzutu.

Rzadko się zdarza, że zaznaczone punkty

leżą dokładnie na linii prostej (pełna

korelacja); częściej spotykana

konfiguracja składa się

z wielu zaznaczonych punktów leżących

mniej więcej wzdłuż konkretnej krzywej

(najczęściej linii prostej).

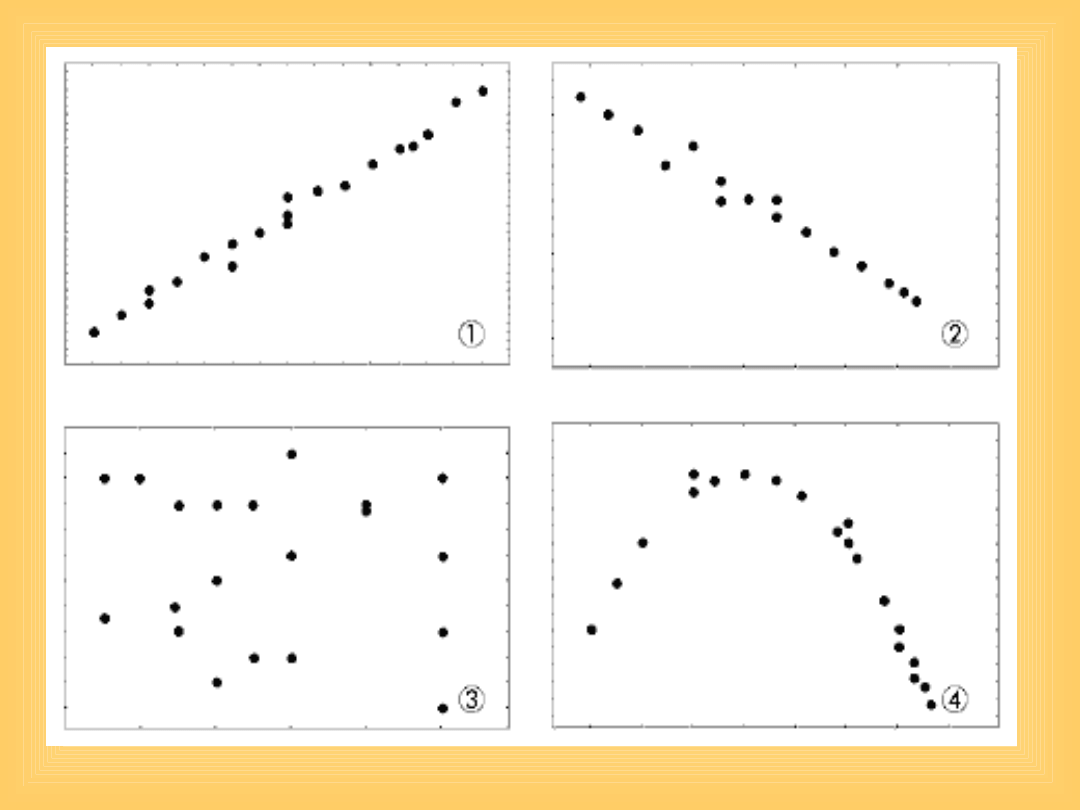
Taka sytuacja przedstawiona jest jako

przypadek 1. i 2. na rysunku 1. Przy

silnie skorelowanych zmiennych

odnosimy wrażenie, jakby te punkty

równocześnie się poruszały.

Gdy korelacja staje się coraz słabsza,

wówczas punkty zaczynają się

rozpraszać i przesuwać, tworząc w

pewnym momencie bezkształtną

chmurę punktów (brak korelacji).

Taka sytuacja ma miejsce w

przypadku 3. na rysunku 1.

Korelacja dodatnia występuje wtedy, gdy

wzrostowi wartości jednej zmiennej

odpowiada wzrost średnich wartości

drugiej zmiennej (przypadek 1. na rys. 1).

Korelacja ujemna występuje wtedy, gdy

wzrostowi wartości 耠 jednej zmiennej

odpowiada spadek średnich wartości

drugiej zmiennej (przypadek 2. na rys. 1).