Analiza matematyczna -

Analiza matematyczna -

Badanie przebiegu

Badanie przebiegu

zmienności funkcji

zmienności funkcji

wykład IV

wykład IV

Autor wykładu :

Prof. nadzw. dr Bożena PALUCHIEWICZ

Autor slajdów:

Inż. Krzysztof Broczkowski

Spis treści:

Spis treści:



Założenia



Asymptoty



Przykłady obliczania asymptoty funkcji



Monotoniczność funkcji



Ekstrema funkcji



Wypukłość i wklęsłość wykresu, punkty przegięcia



Badanie funkcji

Założenia

Założenia

wyczerpującej informacji o funkcji.

W celu badania przeprowadza się

Badanie przebiegu zmienności funkcji pozwala na uzyskanie

:

- analizę funkcji

- analizę pierwszej pochodnej

- analizę drugiej pochodnej

Na podstawie uzyskanych wyników sporządza się

tabelę zmienności funkcji i wykres funkcji

.

,

,

.

Analiza funkcji

Analiza funkcji

1). Znalezienie dziedziny

2). Obliczenie granic na końcach przedziałów określoności

3). Obliczenie asymptot

4). Znalezienie punktów przecięcia z osiami

5). Określenie parzystości, okresowości, ciągłości

;

;

;

;

.

Analiza pierwszej

Analiza pierwszej

pochodnej

pochodnej

1). Znalezienie ekstremów

2). Określenie przedziałów monotoniczności

;

.

Analiza drugiej pochodnej

Analiza drugiej pochodnej

1). Znalezienie punktów przegięcia

2). Określenie przedziałów wypukłości i wklęsłości

;

.

Asymptoty

Asymptoty



Pionowe



Poziome



Pochyłe (ukośne)

,

,

.

twierdze

nie

Asymptoty pionowe

Asymptoty pionowe

Zakłada się, że dziedzina funkcji zawiera pewne sąsiedztwo

prawostronne lub lewostronne punktu

.

Definicja:

Prostą o równaniu nazywa się asymptotą pionową

funkcji

wtedy i tylko wtedy

a

x 

a

)

f(x

y 

,

gdy istnieje granica niewłaściwa

 









x

a

x

f

lim

asymptota pionowa lewostronna

lub

 









x

a

x

f

lim

asymptota pionowa prawostronna

,

.

Jeżeli prosta jest jednocześnie asymptotą pionową lewo i prawostronną

a

x 

-

-

mówi się, że jest asymptotą pionową obustronną

.

Asymptoty poziome

Asymptoty poziome

Zakłada się, że dziedzina funkcji zawiera przedział lub

Definicja:

Prostą o równaniu lub nazywa się

asymptotą poziomą funkcji

wtedy i tylko wtedy

c

y 

)

f(x

y 

,

gdy istnieje granica niewłaściwa

 

c

x

x









f

lim

asymptota pozioma lewostronna

lub

 

d

x

x









f

lim

asymptota pozioma prawostronna

,

.

Jeżeli to mówi się, że

d

c 

-

-

jest asymptotą poziomą obustronną

.

.





a

,











,

b

d

y 

c

y 

Asymptoty pochyłe (ukośne)

Asymptoty pochyłe (ukośne)

Zakłada się, że dziedzina funkcji zawiera przedział lub

Definicja:

Prostą o równaniu dla nazywa się

asymptotą pochyłą funkcji

wtedy i tylko wtedy

k

x

m

y







)

f(x

y 

,

gdy istnieje granica niewłaściwa

 





0

f

lim













k

x

m

x

x

asymptota pozioma lewostronna

lub

 





0

f

lim













k

x

m

x

x

asymptota pozioma prawostronna

,

.

-

-

.





a

,











,

b

0



m

Jeżeli asymptota pochyła jest jednocześnie asymptotą lewo i prawostronną

To prostą nazywa się asymptotą pochyłą obustronną

.

k

x

m

y







Asymptoty pochyłe

Asymptoty pochyłe

(ukośne)

(ukośne)

- twierdzenie

- twierdzenie

Jeżeli funkcja o równaniu ma asymptotę pochyłą

o równaniu

 

x

y f



,to

 

x

x

m

x

f

lim









oraz

 





x

m

x

k

x













f

lim

k

x

m

y







.

Przykłady obliczania asymptot

Przykłady obliczania asymptot

funkcji

funkcji

a)

b)

c)

d)





2

3

1

x

x

y





,

x

x

y

ln

1



,

3

2



x

y

,

1

1

2







x

x

y

.

Obliczanie asymptot funkcji -a

Obliczanie asymptot funkcji -a

3

2



x

y

R

D  















,

x

Ponieważ asymptoty pionowej brak

.

R

D 

















3

lim

2

x

x

- lewostronnej asymptoty poziomej brak

.

















3

lim

2

x

x

- prawostronnej asymptoty poziomej brak

.

Obliczanie asymptot funkcji -

Obliczanie asymptot funkcji -

a asymptota ukośna

a asymptota ukośna

Ponieważ nie ma asymptoty poziomej sprawdza się istnienie asymptoty

.

k

mx

y

































x

x

m

x

3

lim

2

- asymptoty ukośnej brak

.

Wykres funkcji nie ma asymptot

.

3

2



x

y

Obliczanie asymptot funkcji -b

Obliczanie asymptot funkcji -b

x

x

y

ln

1



0

: 

x

D

0

ln

1





x













e

x

x 0



 











,

,

0

e

e

x

x

x

x

ln

1

lim

0





























0

0

0

1

0



0

- asymptoty pionowej prawostronnej brak.

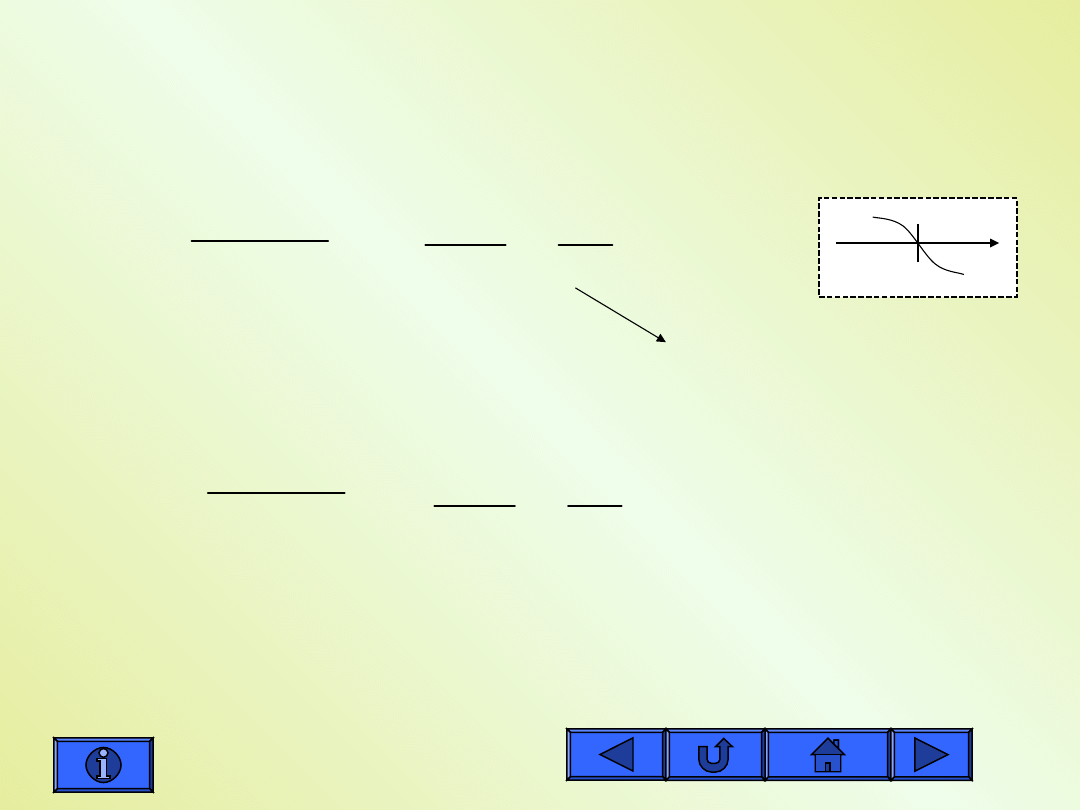
Obliczanie asymptot funkcji -b

Obliczanie asymptot funkcji -b

asymptota pionowa

asymptota pionowa

x

x

e

x

ln

1

lim























0

1

1

e

e







x

ln

1





e

x

x

e

x

ln

1

lim























0

1

1

e

e

 



- prosta jest obustronną asymptotą pionową.

e

x 

Obliczanie asymptot funkcji -b

Obliczanie asymptot funkcji -b

asymptota pozioma

asymptota pozioma

x

x

x

ln

1

lim

























x

x

1

1

lim









 



- prawostronnej asymptoty poziomej brak

.



H

Obliczanie asymptot funkcji -b

Obliczanie asymptot funkcji -b

asymptota ukośna

asymptota ukośna





x

x

x

x

ln

1

lim





















1





















x

x

x

x

0

ln

1

lim





- prawostronnej asymptoty ukośnej brak.



k

mx

y





m





x

x

ln

1

1

lim











0

k



x

x

x

ln

1

lim











Obliczanie asymptot funkcji -c

Obliczanie asymptot funkcji -c

asymptota

asymptota

pionowa

pionowa





2

3

1

x

x

y





0

: 

x

D



 















,

0

0

,

x





2

3

0

1

lim

x

x

x















 

0

1



x







0

- lewostronna

asymptota pionowa





2

3

0

1

lim

x

x

x















 

0

1



x







0

- prawostronna

asymptota pionowa

- prosta jest obustronną asymptotą pionową.

0



x

Obliczanie asymptot funkcji -c

Obliczanie asymptot funkcji -c

asymptota pozioma

asymptota pozioma





2

3

1

lim

x

x

x





























x

x

x

2

1

3

lim

2









 



- lewostronnej

asymptoty poziomej brak

Łatwo sprawdzić, że prawostronnej asymptoty poziomej brak

.





















2

1

6

lim







x

x

H

H

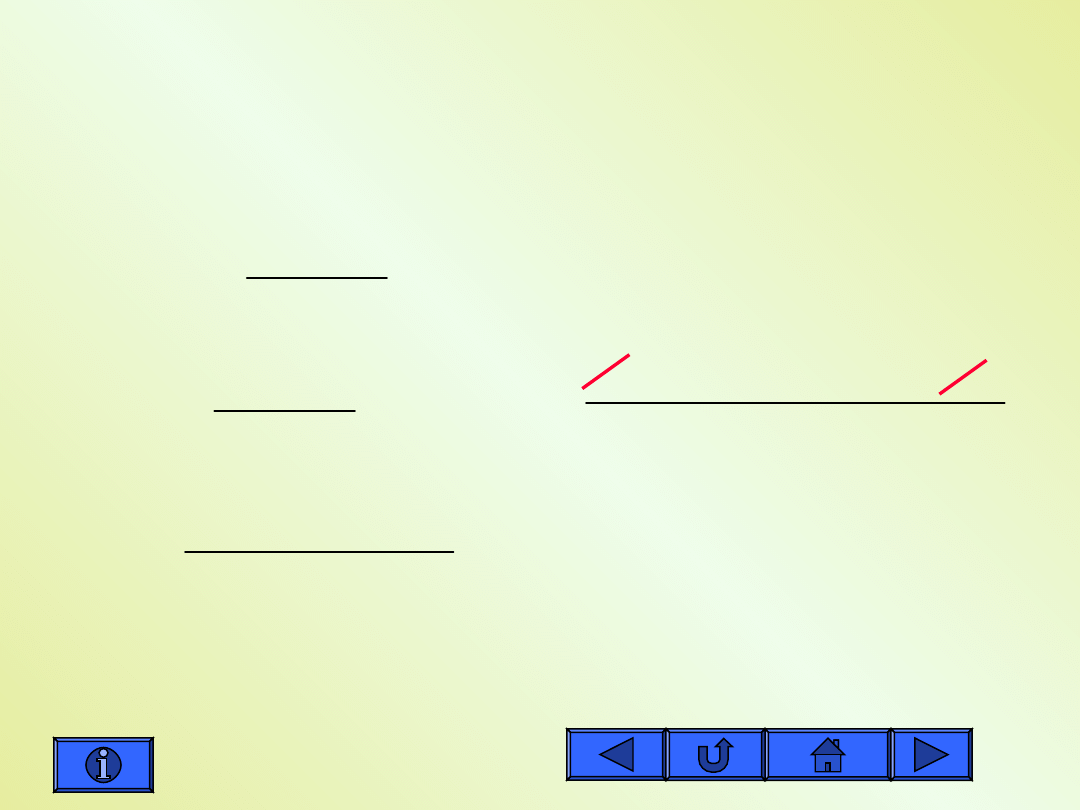
Obliczanie asymptot funkcji -c

Obliczanie asymptot funkcji -c

asymptota ukośna

asymptota ukośna





3

3

1

lim

x

x

x



































x

x

x

x

2

3

1

lim

- lewostronna

asymptota ukośna

.



k

mx

y





m





1

k



2

3

2

3

1

3

3

lim

x

x

x

x

x

x



















2

2

1

3

3

lim

x

x

x

x















3



3



x

y

Łatwo sprawdzić, że jest obustronną asymptotą ukośną

.

3



x

y

Obliczanie asymptot funkcji -d

Obliczanie asymptot funkcji -d

1

1

2







x

x

y

R

D:















,

x

Asymptoty pionowej brak

1

1

lim

2











x

x

x

 0

Łatwo sprawdzić, że jest obustronną asymptotą poziomą

.

0



y

R

D 

.

- lewostronna

asymptota pozioma

.

0



y

Monotoniczność funkcji

Monotoniczność funkcji

Na to, by funkcja była stała w przedziale

 

x

y f







b

a,

potrzeba i wystarcza, aby dla każdego





b

a

x

,



 

0

f



x

Jeżeli w każdym punkcie przedziału

 

0

f



 x





b

a,

,

to funkcja jest na tym przedziale

rosnąca

 

x

f

.

Jeżeli w każdym punkcie przedziału

 

0

f



 x





b

a,

,

to funkcja jest na tym przedziale

malejąca

 

x

f

.

.

Przykłady obliczania

Przykłady obliczania

monotoniczności funkcji

monotoniczności funkcji

a)

b)

c)

d)

4

3

2

3

8

6

x

x

x

y







x

x

y

2

5

3





x

x

y

ln



x

x

y

arctg





;

;

;

.

Przykłady obliczania

Przykłady obliczania

monotoniczności funkcji -

monotoniczności funkcji -

a

a

4

3

2

3

8

6

x

x

x

y







3

2

12

24

12

x

x

x

y









R

D

D

f

f







0

12

24

12

3

2







x

x

x

12

:

0

2

2

3







x

x

x





0

1

2

2





 x

x

x







0

1

2





x

x





0



Funkcja jest malejąca w przedziale





0

,





.

Funkcja jest rosnąca w przedziałach oraz

 

1

,

0

.









,

1

1

Przykłady obliczania

Przykłady obliczania

monotoniczności funkcji -

monotoniczności funkcji -

b

b

x

x

y

2

5

3





2

15

2







x

y

R

D

D

f

f







0

2

15

2





x



R

x

Funkcja jest rosnąca w całym przedziale określoności

.

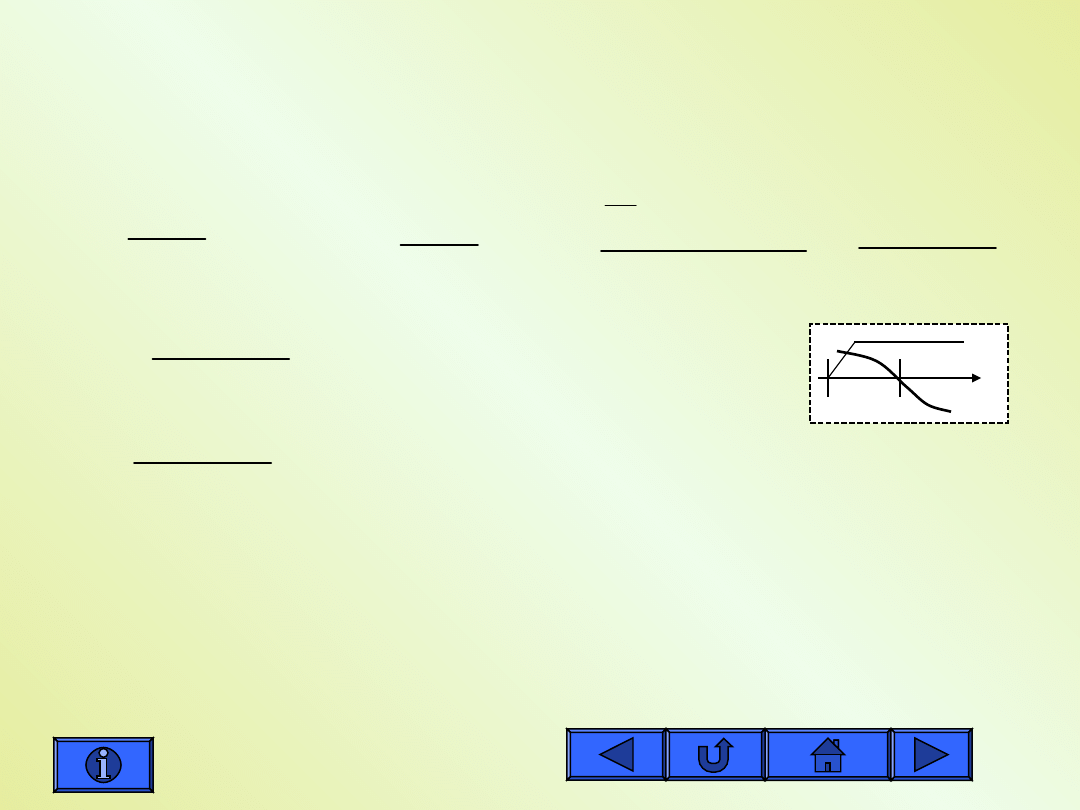
Przykłady obliczania

Przykłady obliczania

monotoniczności funkcji -

monotoniczności funkcji -

c

c

x

x

y

ln





















x

x

y

ln

2

ln

1

x

x

x

x













R

D

D

f

f

2

ln

1

x

x





0

ln

1

2





x

x







0

ln

1

i

0

2







x

x



0



Funkcja jest rosnąca w przedziale

 

e

,

0

.

Funkcja jest malejąca w przedziale









,

e

.

e









2

ln

1

x

x



e

x 

Przykłady obliczania

Przykłady obliczania

monotoniczności funkcji -

monotoniczności funkcji -

d

d

2

1

1

1

x

y









R

D

D

f

f







2

2

1 x

x



0

1

2

2



 x

x







0

1

i

0

2

2

2







x

x

x

Funkcja jest rosnąca w przedziałach oraz





0

,





.



2

2

1

1

1

x

x









0



x

x

x

y

arctg















,

0

Ekstrema funkcji

Ekstrema funkcji



WKE - Warunek Konieczny Ekstremum



WWE - Warunek Wystarczający Ekstremum

,

,

Maksima i minima funkcji nazywa się ekstremami

.



WWE - Warunek Wystarczający Ekstremum

- druga pochodna

.

WKE

WKE

-

-

W

W

arunek

arunek

K

K

onieczny

onieczny

E

E

kstremum

kstremum

Warunek jest warunkiem koniecznym na to

 

0

f

0



x

0

x

,

aby funkcja różniczkowalna w punkcie

ekstremum

 

x

y f



.

miała w tym punkcie

0

Funkcja może mieć ekstremum jedynie

 

x

y f



w tych punktach, w których bądź pochodna nie istnieje,

.

bądź jest równa

WWE-W

WWE-W

arunek

arunek

W

W

ystarczający

ystarczający

E

E

kstremum

kstremum

zmienia znak z ujemnego na dodatni gdy

 

x

f

x

,

rosnąc przechodzi przez , to w punkcie funkcja ma

minimum

0

x

.

Jeżeli

, a ponadto

 

0

f

0



x

:

0

x

zmienia znak z dodatniego na ujemny, gdy

 

x

f

x

,

rosnąc przechodzi przez , to w punkcie funkcja ma

maksimum

0

x

.

0

x

WWE-W

WWE-W

arunek

arunek

W

W

ystarczający

ystarczający

E

E

kstremum

kstremum

za pomocą drugiej pochodnej

za pomocą drugiej pochodnej

drugą pochodną, która jest ciągła w punkcie i

 

0

f

0



x

Jeżeli funkcja

, ma w pewnym otoczeniu punktu

 

0

f x

y 

0

x

0

x

 

0

f

0





 x

i

,to funkcja w punkcie ma

0

x

:

minimum

maksimum

,gdy

,gdy

 

0

f

0





 x

 

0

f

0



 x

Przykłady obliczania

Przykłady obliczania

ekstremum funkcji

ekstremum funkcji

a)

b)

c)

d)

10

2

3

5









x

x

x

y

3

1

x

y





x

x

y

arctg

2









1

1

ln







x

x

y

;

;

;

.

Przykłady obliczania

Przykłady obliczania

ekstremum funkcji - a

ekstremum funkcji - a

10

2

3

5









x

x

x

y

R

D

f



2

3

5

2

4









x

x

y

R

D

f





WKE:

0

2

3

5

2

4





 x

x















0

2

3

5

2

2

t

t

t

x



40

9





 31



Nie ma spełniającego WKE.

R

x



Funkcja nie ma ekstremum

.

Przykłady obliczania

Przykłady obliczania

ekstremum funkcji - b

ekstremum funkcji - b

3

1

x

y





R

D

f























3

1

1 x

y

 

0

\

R

D

f





WKE:

0





y

- należy do dziedziny funkcji

0



x

ale nie należy do dziedziny pochodnej.



3

2

3

1





x



3

2

1

x



- nie ma takiego x w R.

,

WWE:

Zarówno dla x > 0 jak i x < 0 nie zmienia się znak pochodnej.

Funkcja w punkcie x = 0 nie ma ekstremum.

Wypukłość i wklęsłość

Wypukłość i wklęsłość

wykresu,

wykresu,

punkty przegięcia

punkty przegięcia



Wypukłość



Wklęsłość



Punkty przegięcia

,

,

.

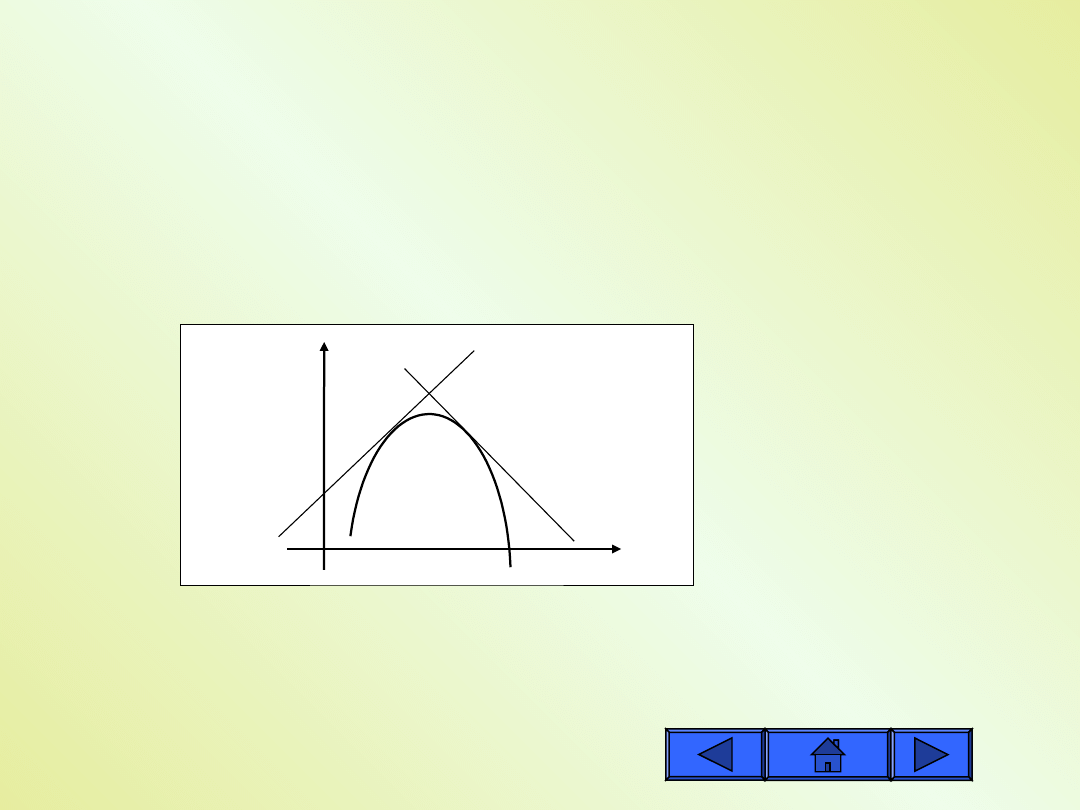
Wypukłość wykresu

Wypukłość wykresu

funkcji

funkcji

Krzywa jest wypukła w pewnym przedziale,

jeśli we wszystkich punktach tego przedziału

leży ona poniżej swych stycznych.

y

x

Jeśli w pewnym przedziale , to krzywa jest w tym przedziale

0







y

wypukła.

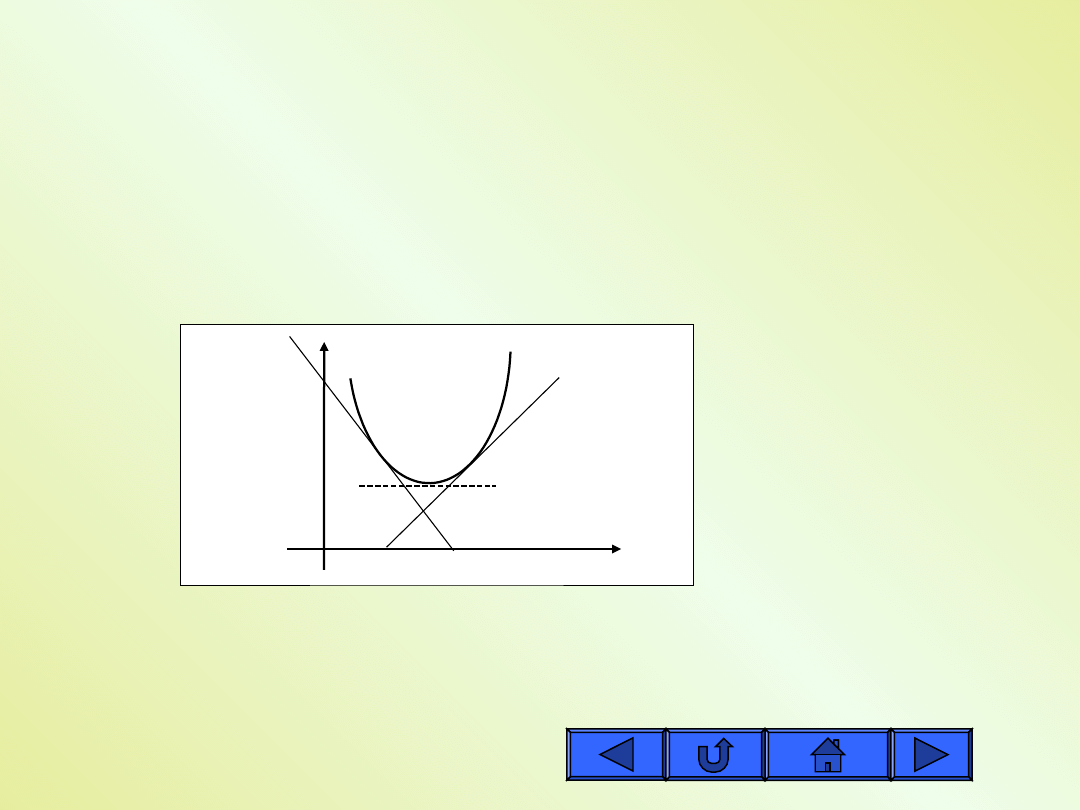
Wklęsłość wykresu funkcji

Wklęsłość wykresu funkcji

Krzywa jest wklęsła w pewnym przedziale,

jeśli we wszystkich punktach tego przedziału

leży ona powyżej swych stycznych.

y

x

Jeśli w pewnym przedziale , to krzywa jest w tym przedziale

0







y

wklęsła .

Punkty przegięcia

Punkty przegięcia

WKPP

- Warunek Konieczny Punktu Przegięcia

0





y

y



albo nie istnieje w dziedzinie funkcji

.

:

WWPP

- Warunek Wystarczający Punktu Przegięcia

Zmiana krzywej z wypukłej na wklęsłą lub odwrotnie

wokół punktu z WKPP

.

:

Przykład obliczania

Przykład obliczania

punktu przegięcia

punktu przegięcia





2

1

ln

x

y





R

D

f



x

x

y

2

1

1

2











2

1

2

x

x



R

D

f



























2

1

2

x

x

y











2

2

2

1

2

2

1

2

x

x

x

x















2

2

2

2

1

4

2

2

x

x

x













2

2

2

1

2

2

x

x





R

D

f









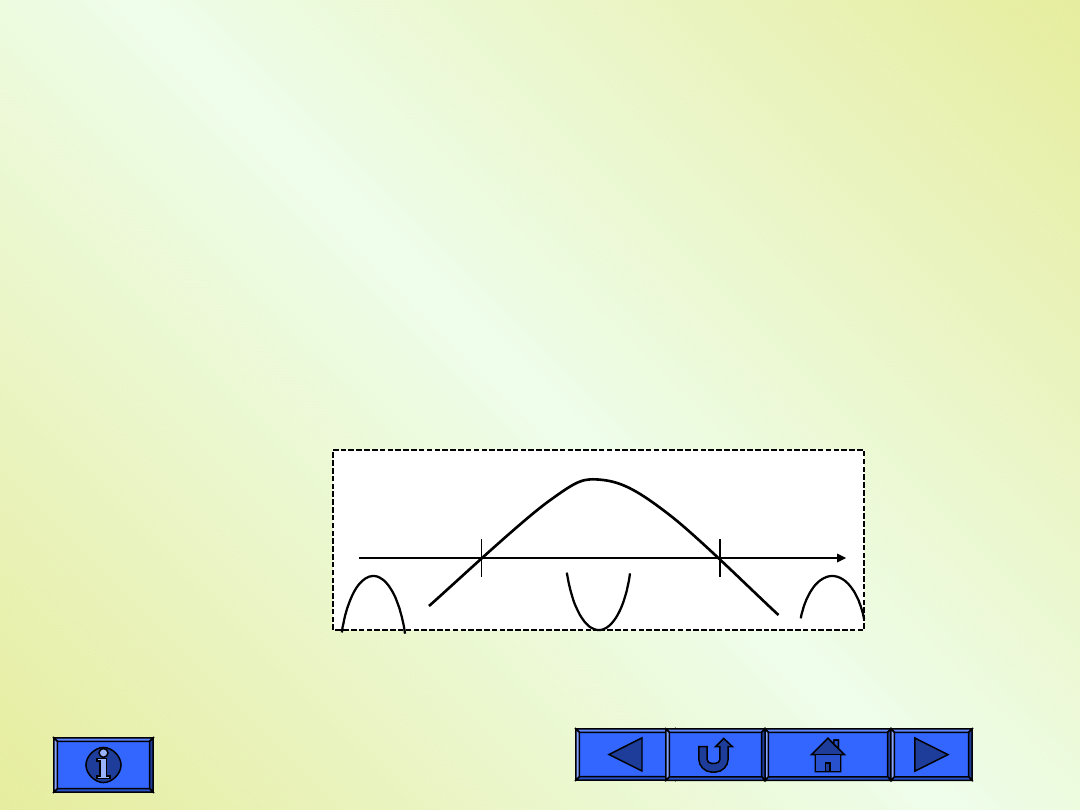
Przykład obliczania PP -cd

Przykład obliczania PP -cd

0







y

0





0

1

2

2



 x



 



1

,

1

0

1

1

2

1















x

x

x

x





0

1

2

2



 x

WKPP:



2

2

2

x







WWPP:

f

D

x









i nie wpływa na znak pochodnej



1





1



Funkcja ma w punktach x = -1 oraz x = 1 punkty przegięcia

.

Badanie funkcji

Badanie funkcji

x

x

x

y

ln





1). Znalezienie dziedziny

2). Obliczenie granic na końcach przedziałów określoności

3). Obliczenie asymptot

4). Znalezienie punktów przecięcia z osiami

5). Określenie parzystości, okresowości

.

.

.

.

.

6). Znalezienie ekstremów

.

7). Znalezienie punktów przegięcia

.

8). Tabela.

9). Wykres funkcji.

Badanie funkcji - przykład

Badanie funkcji - przykład

Znalezienie dziedziny

Znalezienie dziedziny

x

x

x

y

ln





D

0



x

0



x











 ,

0

x

:

i

Obliczenie granic na

Obliczenie granic na

końcach przedziałów

końcach przedziałów

określoności

określoności

x

x

x

y

ln















 





x

x

x

x

ln

lim

0

















0

0































0

1



















 







x

x

x

x

ln

lim



x

x

x

x

ln

lim

2



























1

1

2

lim

x

x

x















0

H

Obliczenie asymptot

Obliczenie asymptot

x

x

x

y

ln





m

kx

y







1

x

x

x

x

2

1

2

lim

































x

x

x

x

x

ln

lim



1

1

lim x

x







0

0

H

x = 0 - asymptota pionowa prawostronna

























2

2

ln

lim

x

x

x

k

x



H

0

m



y = x - asymptota ukośna prawostronna.

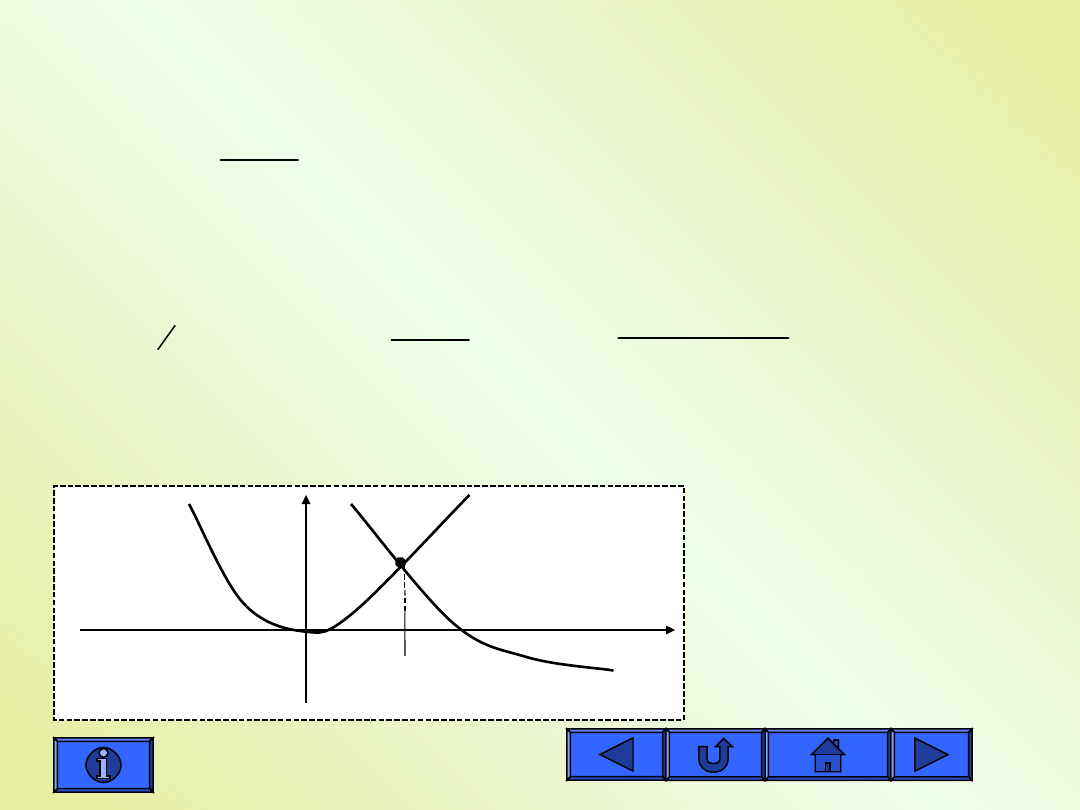
Znalezienie punktów

Znalezienie punktów

przecięcia z osiami

przecięcia z osiami

x

x

x

y

ln

















0

0

y

D

x

0

ln

2





x

x

x

0

ln

2





x

x















0

ln

0

x

x

x

y









x

x

ln

2





2

x

y 

1

0



x

x

y

ln









0

,

0

x

wartość przybliżona

Określenie parzystości,

Określenie parzystości,

okresowości

okresowości

x

x

x

y

ln





Funkcja jest nieokresowa.

Funkcja nie jest ani parzysta ani nieparzysta,
gdyż D: x > 0.

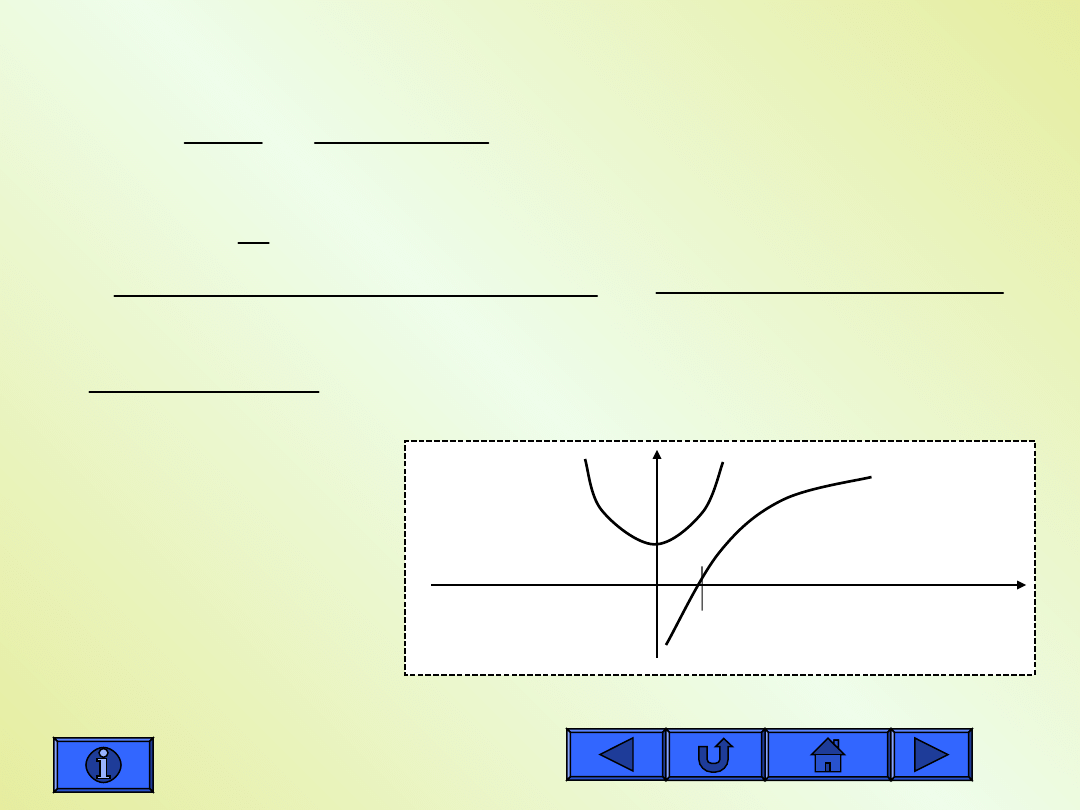
Znalezienie ekstremów

Znalezienie ekstremów

x

x

x

x

x

x

y

ln

ln

2













2

2

1

ln

1

2

x

x

x

x

x

x

y



























1



2

2

2

ln

1

2

x

x

x

x











2

2

ln

1

x

x

x





0





y

x

x

ln

1

2







funkcja

stale rosnąca

.

Nie ma ekstremum

.

0





y



WKE:

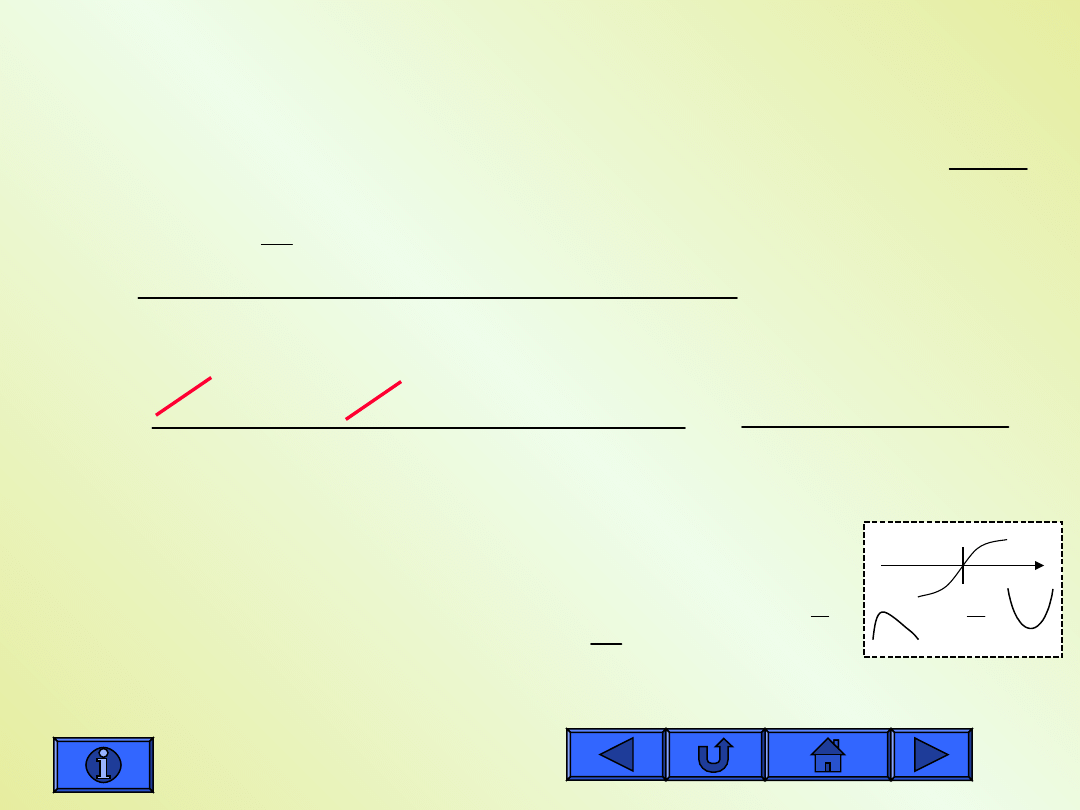
Znalezienie punktów

Znalezienie punktów

przegięcia

przegięcia

x

x

x

y

ln









4

2

2

2

ln

1

1

2

x

x

x

x

x

x

x

y

































4

3

3

ln

2

2

2

2

x

x

x

x

x

x

x















4

ln

2

3

x

x

x





0







y

0

ln

2

3







x

WKPP:

0

i





x

2

3

ln 

x



2

3

e

x 





2

3

e





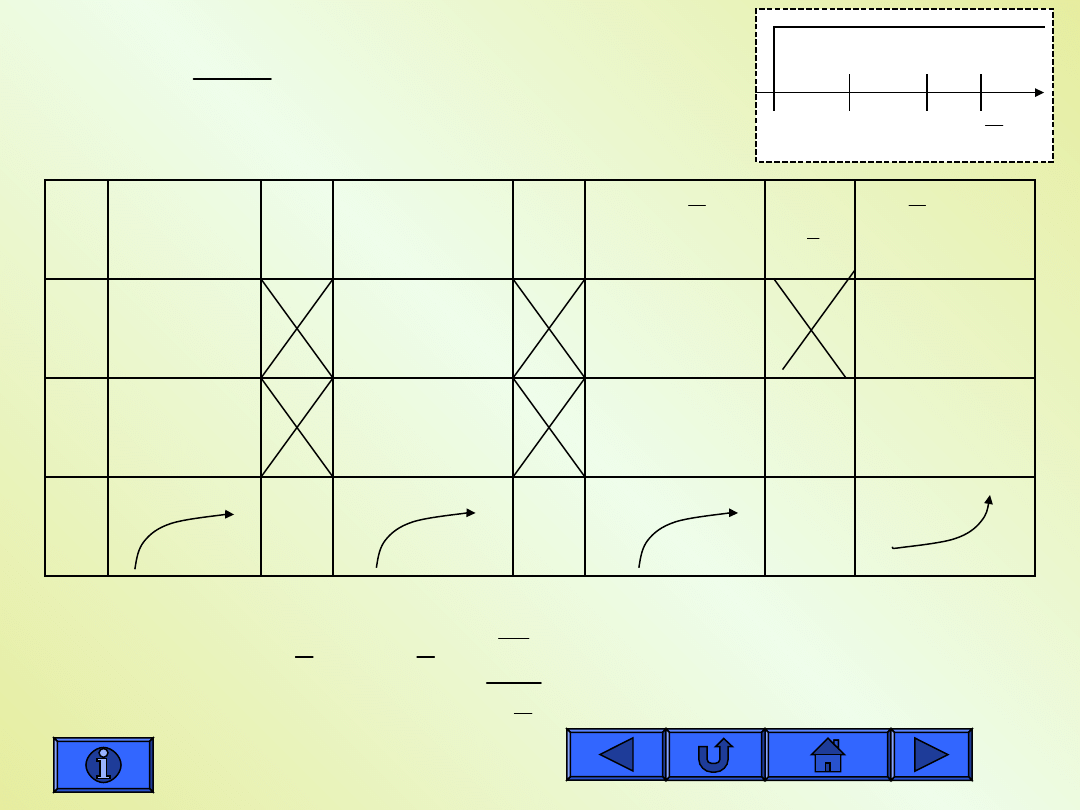
Tabela

Tabela

x

x

x

y

ln





x

0

7

,

0

x



y

y



y

0

1

1

2

3

48

,

4

e



0

8

,

4





0

,

0 x





1

,

0

x













2

3

,

1 e















,

2

3

e

















0

0

x

1

2

3

e

8

,

4

2

3

f

2

3

2

3

2

3



















e

e

e

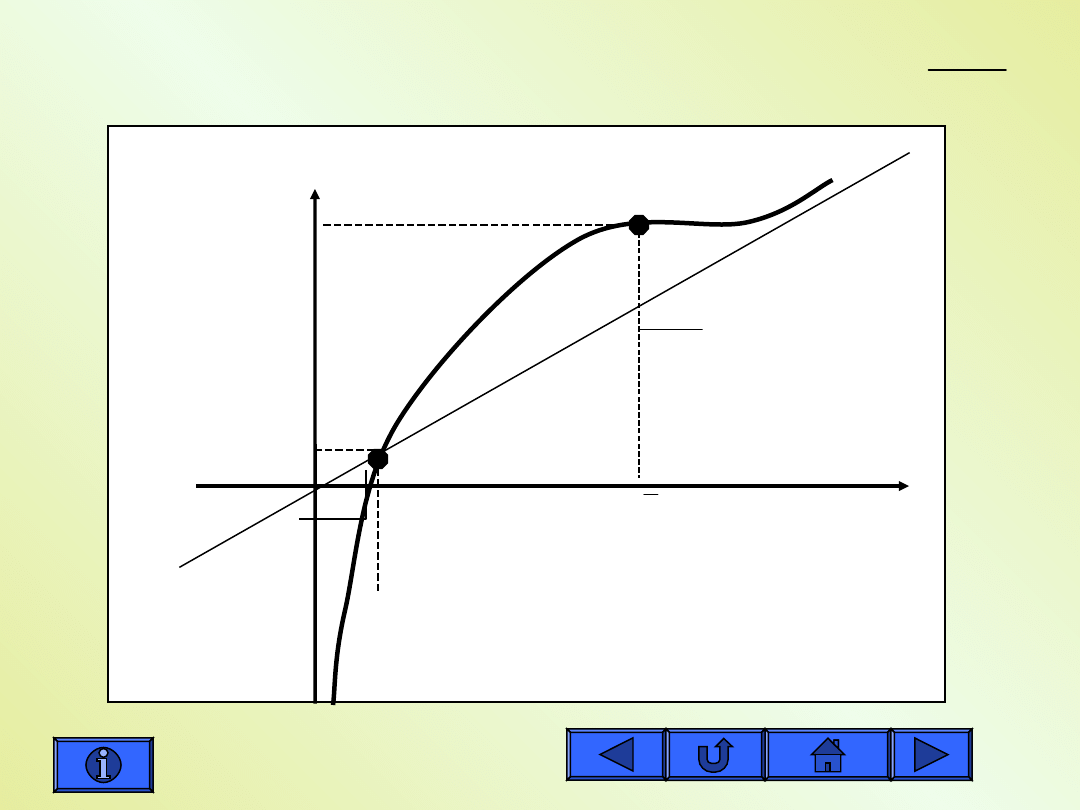
Wykres funkcji

Wykres funkcji

x

x

x

y

ln





8

,

4

y

x

x

x

y

ln





1

x

1

2

3

48

,

4

e



PP

0

x

x

y 