DZIAŁANIA

NA

ZDARZENIAC

H

Rzucamy raz kostką do gry.

Zbiór wszystkich możliwych wyników
doświadczenia to zbiór:

�

= {1, 2, 3, 4, 5, 6}

Opiszmy zdarzenia:

A – otrzymano mniej niż 5 oczek

B – otrzymano co najmniej 4 oczka

C – otrzymano szóstkę

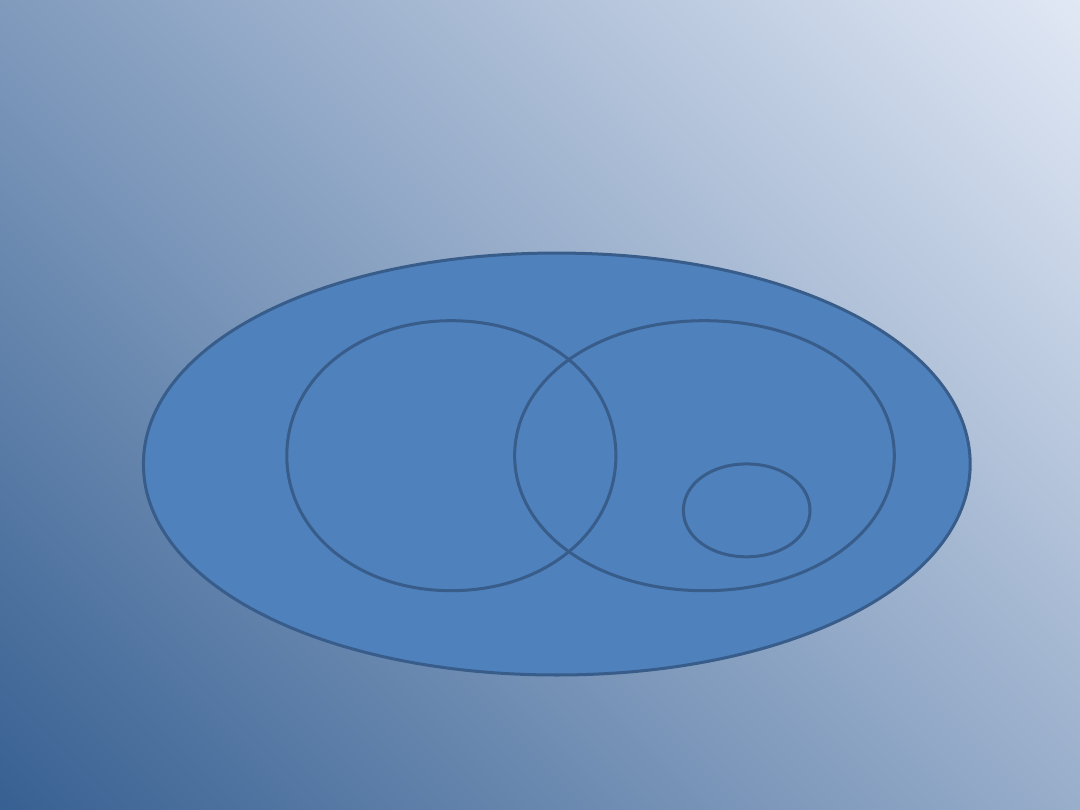
Wypiszmy wyniki sprzyjające tym zdarzeniom A, B,
C i narysujmy odpowiednie zbiory.

A = {1,2,3,4}
B = {4,5,6}
C = {6}

2 5

3 4
1

6

B

A

C

�
�

Iloczynem zdarzeń A i B

nazywamy zdarzenie

złożone z wyników, które sprzyjają zdarzeniu A i
jednocześnie zdarzeniu B.

A ∩ B – iloczyn zdarzeń A i B

A

∩

B = {4} – wynik 4 sprzyja iloczynowi zdarzeń

A

∩

C =

∅

-

zdarzenie niemożliwe

- to takie,

któremu

nie sprzyja żaden wynik

B

∩

C = {6} = C

Sumą zdarzeń A i B

jest zdarzenie złożone z

wyników, które sprzyjają zdarzeniu A lub zdarzeniu
B.

A ∪ B – suma zdarzeń A i B

A ∪ B = {1,2,3,4,5,6} =

�

A ∪ C = {1,2,3,4,6}

B

∪

C = {4,5,6} = B

Różnicą zdarzeń A i B

jest zdarzenie złożone

z wyników, które sprzyjają zdarzeniu A, ale nie
sprzyjają zdarzeniu B.

A \ B – różnica zdarzeń A i B

A \ B = {1,2,3} A \ C = {1,2,3,4} = A

B

\

C = {4,5}

�

\ A = {5,6}

A’ – zdarzenie przeciwne do zdarzenia A

(są to wszystkie wyniki, które sprzyjają ,

�

ale nie

sprzyjają zdarzeniu A)

A’=

�

\ A

Przykład 1:
W pudełku są: 2 kule białe, 3 czarne, 2 zielone.
Losujemy jednocześnie dwie kule. Opiszmy
zdarzenia:
A – otrzymano kule białe
B – otrzymano kule różnego koloru
C – otrzymano kule tego samego koloru
D – nie otrzymano kuli białej

�

= {(b,b),(b,c),(b,z),(c,c),(c,z),

(z,z)}

Wypiszmy wyniki sprzyjające zdarzeniom:

A = {(b,b)}

B = {(b,c),(b,z),(c,z)}

C = {(b,b),(c,c),(z,z)}

D = {(c,c),(c,z),(z,z)}

A’ = {(b,c),(b,z),(c,c),(c,z),(z,z)}

B’ = {(b,b),(c,c),(z,z)}

C’ = {(b,c),(b,z),(c,z)}

D’ = {(b,b),(b,c),(b,z)}

A

∩

B = ∅

B

∩

C = ∅

A

∩

C = {(b,b)}

A

∪

B = {(b,b),(b,c),(b,z),(c,z)}

A

∪

C = {(b,b),(c,c),(z,z)}

A \ B = {(b,b)}

D’ \ B = {(b,b)}

Przykład 2:
Rzucamy sześcienną kostką i monetą.
A – otrzymano parzystą liczbę oczek
B – otrzymano reszkę
C – otrzymano liczbę pierwszą oczek i orła
D – otrzymano co najmniej 5 oczek r -
reszka

o -

orzeł

�

= {(1,o),(2,o),(3,o),(4,o),(5,o),(6,o),

(1,r),(2,r),(3,r),(4,r),(5,r),(6,r)}

Wypiszmy wyniki sprzyjające zdarzeniom:

A = {(2,o),(2,r),(4,o),(4,r),(6,o),(6,r)}

B = {(1,r),(2,r),(3,r),(4,r),(5,r),(6,r)}

C = {(2,o),(3,o),(5,o)}

D = {(5,r),(5,o),(6,r),(6,o)}

A’ = {(1,o),(3,o),(5,o),(1,r),(3,r),(5,r)}

D’ = {(1,o),(2,o),(3,o),(4,o),(1,r),(2,r),(3,r),(4,r)}

A

∩

B = {(2,r),(4,r),(6,r)}

A

∩

C = {(2,o)}

C

∪

D = {(2,o),(3,o),(5,o),(6,o),(5,r),(6,r)}

B \ D = {(1,r),(2,r),(3,r),(4,r)}

D \ A = {(5,o),(5,r)}

Przykład 3:
Doświadczenie polega na rzucie kostką i monetą.
Wiedząc, że:

A

∩

B = {(4,o)}

A ∪ B = {(2,o),(3,o),(4,o),(6,o),(4,r)}

A \ B = {(2,o),(6,o)}

Określ zdarzenia A i B.

Zaczniemy od wyznaczenia zbioru wszystkich
możliwych wyników doświadczenia:

�

= {(1,o),(2,o),(3,o),(4,o),(5,o),(6,o),(1,r),

(2,r),(3,r),(4,r),(5,r),(6,r)}

Do zadania narysujmy zbiory i umieśćmy w nich
odpowiednie wyniki:

Z rysunku odczytamy wyniki sprzyjające

zdarzeniom:

A = {(2,o),(4,o),(6,o)}

B = {(3,o),(4,o),(4,r)}

A

B

(2,o) (4,o)
(3,o)

(6,o)
(4,r)

Przykład 4
Rzucamy dwa razy kostką do gry.
A – wypadnie parzysta liczba oczek w I i II rzucie
B – suma oczek jest liczbą mniejszą od 5
C – suma oczek jest liczbą podzielną przez 3

�

= {(1,1),(1,2),(1,3),(1,4),...,(6,5),(6,6)}

Wypiszmy wyniki sprzyjające zdarzeniom:

A = {(2,2),(2,4),(2,6),(4,2),(4,4),(4,6),(6,2),(6,4),

(6,6)}

B = {(1,1),(1,2),(1,3),(2,1),(2,2),(3,1)}

C = {(1,2),(1,5),(2,1),(2,4),(3,3),(3,6),(4,2),(4,5),

(5,1),

(5,4),(6,3),(6,6)}

A

∩

B = {(2,2)}

A

∩

C = {(2,4),(4,2),(6,6)}

A \ B = {(2,4),(2,6),(4,2),(4,4),(4,6),(6,2),(6,4),(6,6)}

A \ C = {(2,2),(2,6),(4,4),(4,6),(6,2),(6,4)}

B

∩

C = {(1,2),(2,1)}

B \ C = {(1,1),(1,3),(2,2),(3,1)}

C \ A = {(1,2),(1,5),(2,1),(3,3),(3,6),(4,5),(5,1),(5,4),

(6,3)}

Przykład 5:

Kręcimy trzy razy bączkiem w kształcie

siedmiokąta foremnego z zaznaczonymi

literkami: a, b

A –za pierwszym razem otrzymano literkę a

B – za drugim razem otrzymano literkę b

Wypiszmy zbiór

�

oraz wyniki sprzyjające zdarzeniom:

�

={(a,a,a),(a,a,b),(a,b,a),(a,b,b),(b,a,a),

(b,a,b),

(b,b,a),(b,b,b)}

A = {(a,a,a),(a,a,b),(a,b,a),(a,b,b)}

B = {(a,b,a),(a,b,b),(b,b,a),(b,b,b)}

A

∩

B = {(a,b,a),(a,b,b)}

A ∪ B = {(a,a,a),(a,a,b),(a,b,a),(a,b,b),(b,b,a),

(b,b,b)}

A \ B = {(a,a,a),(a,a,b)}

B \ A = {(b,b,a),(b,b,b)}

A’ = {(b,a,a),(b,a,b),(b,b,a),(b,b,b)}

B’ = {(a,a,a),(a,a,b),(b,a,a),(b,a,b)}

A’

∩

B’ = {(b,a,a),(b,a,b)}