ANTIDERIVATIVES

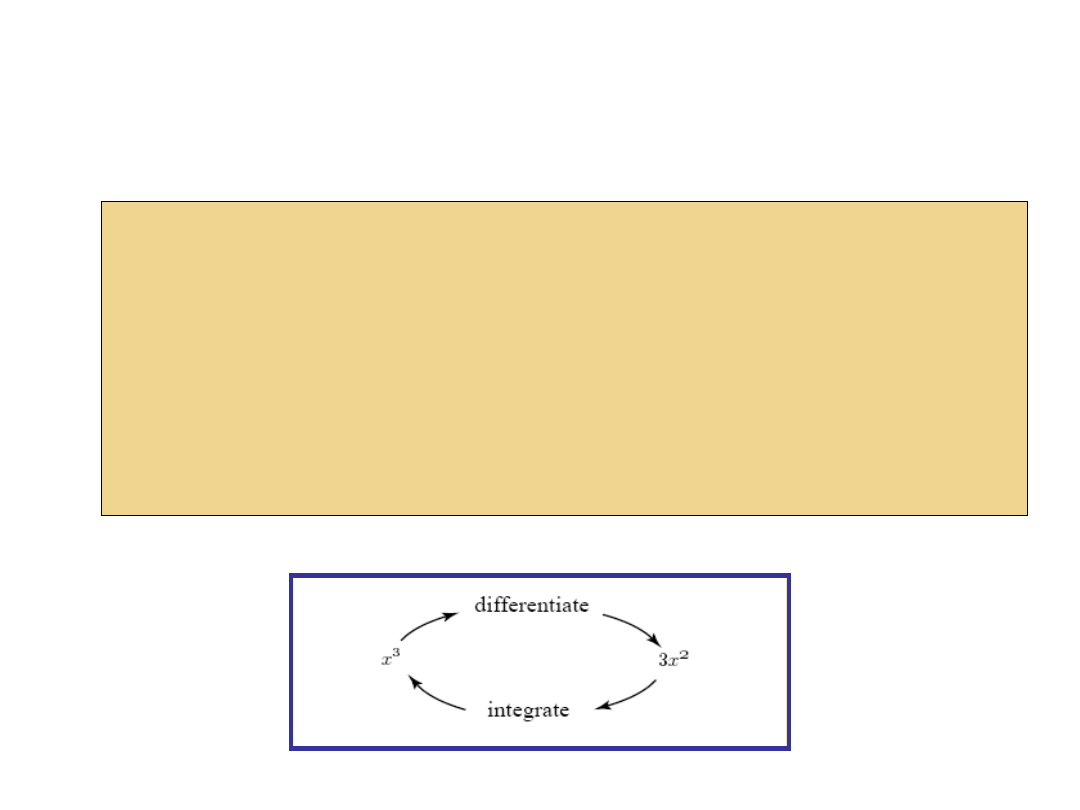
An antiderivative, (primitive or indefinite integral) of a
function f is a function F whose derivative is equal to f,
i.e., F ′ = f.

Definition

A differentiable function F defined on (a, b), for which:

F '(x) = f (x),

for every x 

(a, b)

is called an

antiderivative

of the function f on the interval (a, b).

Remark
If F is some specific antiderivative of a function f on (a, b),
then all the antiderivatives are given by the formula

The graphs of antiderivatives of a given function are vertical
translations of each other; each graph's location depending upon the
value of C.

The constant C is called the arbitrary constant of integration.

G(x) = F(x) + C, where C is a real constant.

Antiderivative of y = 2x,
they fill up the whole plane without
overlapping.

We identify a curve as the one which
passes through the given point, i.e. (0,0)

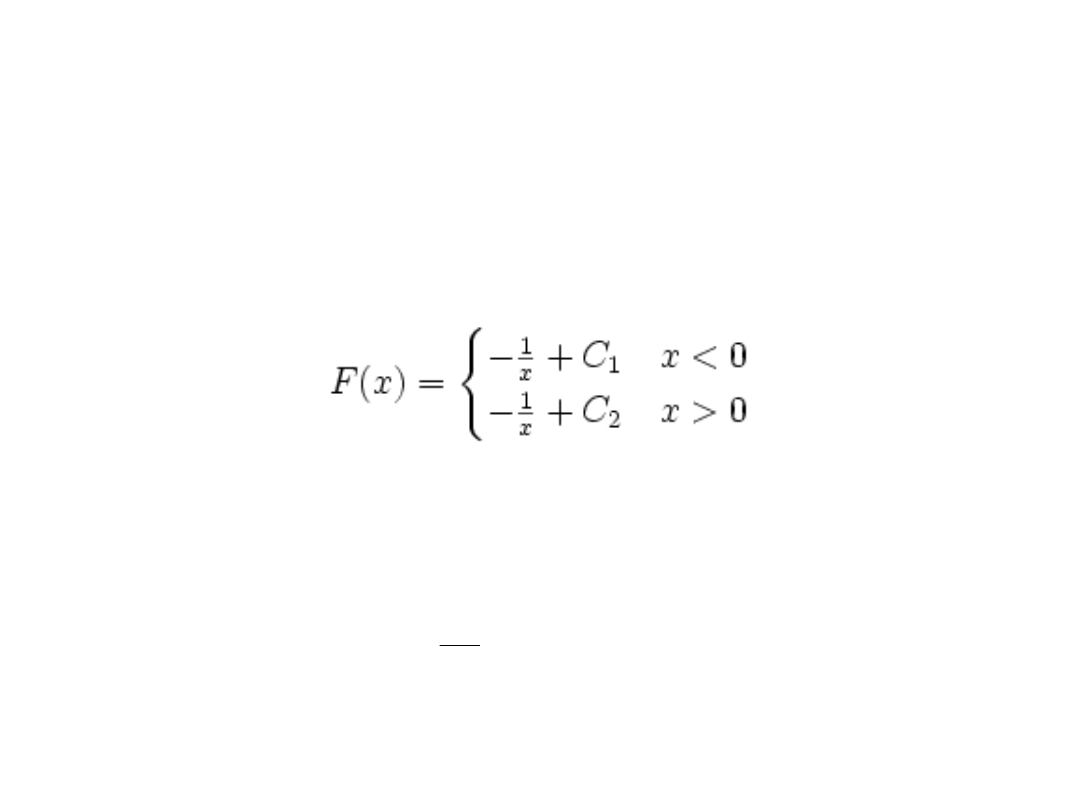
If the domain of F is a disjoint union of two or more
intervals, then a different constant of integration may be
chosen for each of the intervals. For instance

is the most general antiderivative of

)

,

0

(

)

0

,

(

,

1

)

(

2











x

x

x

f

Definition

The set of all antiderivatives of a function f is called an
indefinite integral of a function f on (a, b) and is denoted by

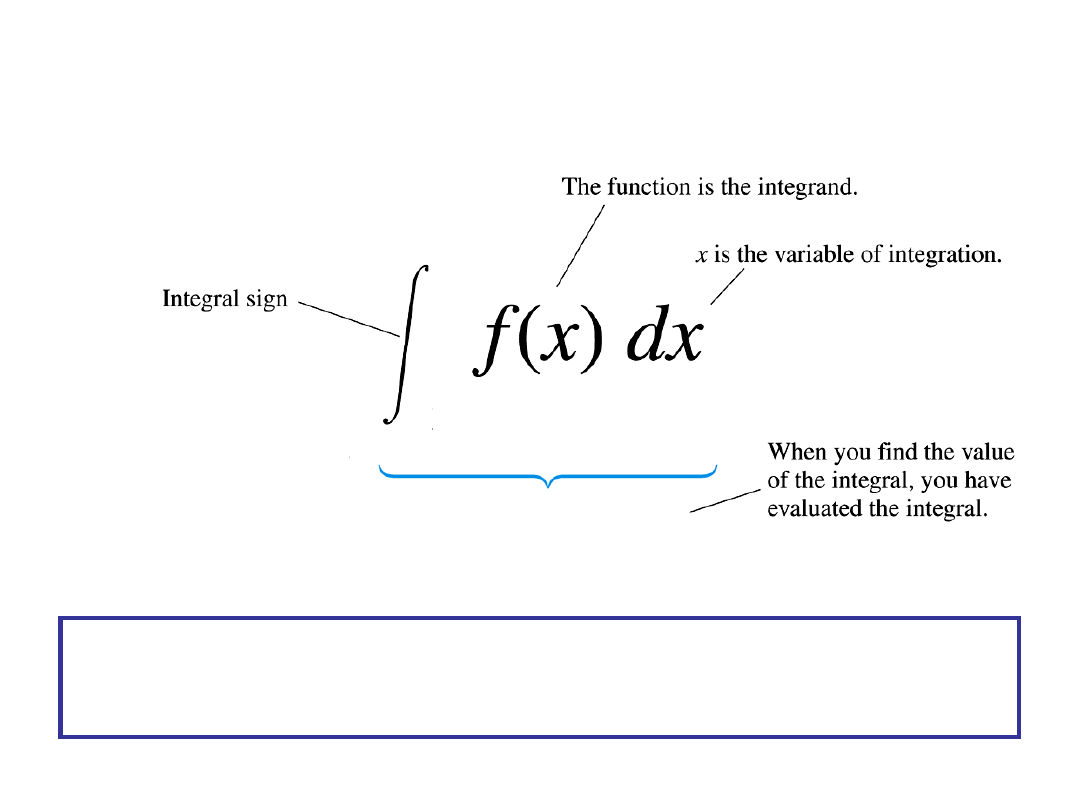
This the above symbol is read as: "an integral of f of x over dx".

•The function f is called the integrand

•The variable x is called the integration variable

•The expression dx is called the differential of the integration variable.



dx

x

f )

(

Definition

A function, for which the indefinite integral in a given
interval exists, is said to be integrable on this interval

Definition

A function, for which the indefinite integral in a given
interval exists, is said to be integrable on this interval

Integral of f of x over dx

THEOREM

If a function f is continuous on an interval (a, b),
it is also integrable on this interval.

Fact

There are many functions whose antiderivatives, even though
they exist, cannot be expressed in terms of elementary
functions. These functions are called are not

elementary

integrable

e.g.

3

2

1

)

(

,

sin

)

(

,

ln

1

)

(

),

sin(

)

(

,

)

(

2

x

x

f

x

x

x

f

x

x

f

x

x

f

e

x

f

x



























C

x

dx

x

n

n

n

1

1

1









C

x

xdx

2

2

1







C

x

x sin

cos









C

x

xdx

cos

sin







C

a

a

dx

a

x

x

ln

/







C

x

dx

x

|

|

ln

1







C

e

dx

e

x

x









C

x

dx

x

arcsin

1

1

2











C

x

dx

x

arccos

1

1

2









C

x

dx

x

arctan

1

1

2











C

x

arcc

dx

x

tan

1

1

2







C

x

dx

1

BASIC ANTIDERIVATIVES

Theorem (on linearity of an indefinite integral)

If functions f and g are integrable on some interval P, then the
functions f + g and A f , where A denotes any real constant, are
also integrable on this interval too, and

"an integral of a sum equals a sum of integrals",

"a constant can be factored out of the integral".

dx

x

g

dx

x

f

dx

x

g

x

f













)

(

)

(

)]

(

)

(

[

dx

x

f

A

x

f

A











)

(

)

(

Theorem (Integration by Parts)

Suppose f (x) and g(x) are two functions that are
continuously differentiable on some open interval, then in
this interval

In other notation

dx

x

g

x

'

f

x

g

x

f

dx

x

g'

x

f









)

(

)

(

)

(

)

(

)

(

)

(









df

g

g

f

dg

f

[f (x) g(x)]’ = f ’(x) g(x) + f (x) g’(x)

f (x) g’(x) = [f (x) g(x)]’ - f’ (x) g(x)











dx

x

f

x

g

dx

x

g

x

f

dx

x

g

x

f

)

(

'

)

(

)]'

(

)

(

[

)

(

'

)

(









dx

x

f

x

g

x

g

x

f

dx

x

g

x

f

)

(

'

)

(

)

(

)

(

)

(

'

)

(

Proof

QED

Examples









g

f

g

f

'

'

according to Gewert, Skoczylas

Theorem (Integration by Substitution - change of
variable)

Suppose the function f is integrable on an interval P, and t(x)
is a continuously differentiable function which is defined on the
interval [a, b] and whose image (also known as range) is
contained in the domain P of f then







dt

t

f

dx

x

t

x

t

f

)

(

)

(

'

))

(

(

C

x

F

dx

x

f







)

(

)

(

dx

x

t

dt

)

(

'



)

(

'

))

(

(

'

))

(

(

)

(

x

t

x

t

F

x

t

F

dx

d

x

f

F

dx

d





Remarks

•The constant of integration C should be written last

,

after finding the antiderivative. As long as on the right hand
side there is at least one indefinite integral, the constant of
integration doesn't have to appear explicitly, since it is hidden
in the symbol of an indefinite integral.

•The correctness of the result, i.e. of the antiderivative
which was found, can always be

verified by

differentating

the antiderivative; as a result we should

get the integrand.

RATIONAL FUNCTIONS

)

(

)

(

)

(

x

Q

x

P

x

f



INTEGRATION OF RATIONAL FUNCTIONS

Definition

A rational function is a quotient of two polynomials, i.e., a function of the form

where P (x) and Q (x) are polynomials of degree n and m.

If the degree of the numerator is less than the degree of the
denominator, the function is called

a proper rational

function.

Theorem

Any proper rational function can be represented as a sum of the
so called partial fractions of the first kind

and partial fractions of the second kind

where A, B, C, a, p, q are real numbers,

p

2

- 4q < 0

, and k is a natural number

-

irreducible

.

k

a

x

A

)

( 

k

q

px

x

C

Bx

)

(

2







PRACTICALLY,
If the degree of P(x) is greater than or equal to the degree of
Q(x), then by

long division

we can express the rational function

by

where q(x) is the quotient and r(x) is the remainder whose
degree is less that the degree of Q(x).

Then Q(x) is factored as a product of powers of linear and
quadratic factors. Finally r(x)/ Q(x) is split into a sum of fractions
which consist of ones of type

and

)

(

)

(

)

(

)

(

)

(

x

Q

x

r

x

q

x

Q

x

P





n

n

a

x

A

a

x

A

a

x

A

)

(

)

(

2

2

1













n

n

n

q

px

x

C

x

B

q

px

x

C

x

B

q

px

x

C

x

B

)

(

)

(

2

2

2

2

2

2

1

1



























irreducible quadratic factors

Each factor (x - a)

m

in the denominator of the proper

rational function suggests repeated linear factors

m

i

a

x

A

a

x

A

a

x

A

)

(

)

(

2

2

1













Note that the degree of the terms is from 1 to m.

Each factor (x

2

+ px + q)

m

in the denominator of the

proper rational function suggests repeated irreducible
quadratic facors:

m

m

m

q

px

x

C

x

B

q

px

x

C

x

B

q

px

x

C

x

B

)

(

)

(

2

2

2

2

2

2

1

1



























Note that the degree of the terms is from 1 to m.

Examples

http://calc101.com/webMathematica/partial-fractions.jsp

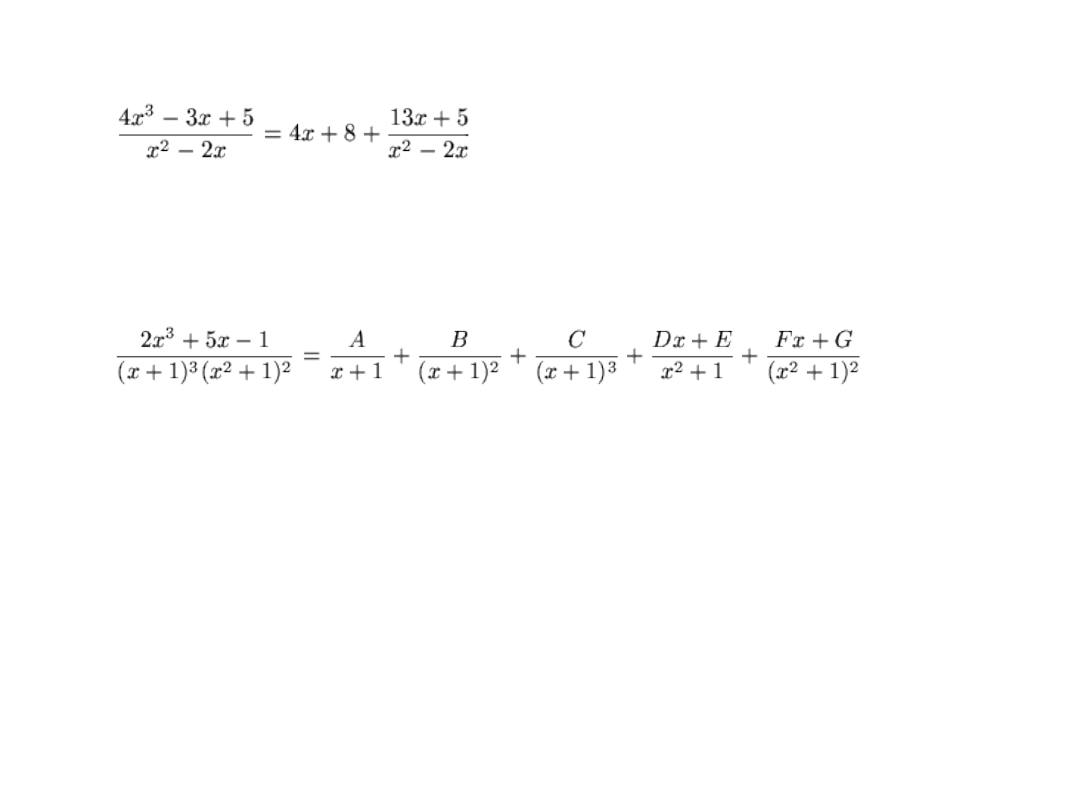
To find the coefficients A

i

.

INTEGRATION OF PARTIAL FRACTIONS

Integration of partial fractions of the first kind

For k = 1

For k > 1

C

a

x

A

dx

a

x

A











ln











































C

a

x

k

A

C

k

t

A

dt

t

A

dx

dt

a

x

t

dx

a

x

A

k

k

k

k

1

1

)

)(

1

(

1

1

)

(

n

n

b

ax

A

b

ax

A

b

ax

A

)

(

)

(

2

2

1













We express the integral as a sum of two integrals in such a
way that the numerator of the integrand in the first integral is
the derivative of the denominator:

The first integral on the right hand side can be evaluated by substituting





















 

















dx

q

px

x

Bp

C

dx

q

px

x

p

x

B

dx

q

px

x

C

Bx

k

k

k

)

(

1

2

)

(

2

2

)

(

2

2

2

t = x

2

+ px + q,

Integration of partial fractions of
the second kind

m

m

m

c

bx

ax

c

x

B

c

bx

ax

c

x

B

c

bx

ax

c

x

B

)

(

)

(

2

2

2

2

2

2

1

1



























For k = 1, we complete the square to represent the trinomial in
the canonical form

Substituting

we obtain the elementary integral

For k > 1, the integral is found by use of an appropriate
recurrence formula (which shall be not considered here).

4

2

2

2

p

q

q

p

x

q

px

x





























dt

t

2

1

1

4

2

2

p

q

t

p

x





