Zasady tworzenia modelu

matematycznego dynamiki w

oparciu o model fizyczny:

wyodrębnienie układu z otoczenia,

założenia upraszczające

Prezentację przygotował:

Tomasz Paciepnik
149473

Co to jest model
matematyczny?

Przez model matematyczny rozumiemy
opis wzorów i wyników ilościowych
opisujących, statyczne, dynamiczne,
niezawodnościowe, energetyczne,
strukturalne, funkcjonalne i logiczne
związki pomiędzy wielkościami
występującymi w opisywanym obiekcie
(urządzeniu, systemie, procesie)

W jaki sposób powstaje model

matematyczny?

Model

matematyczny

powstaje

na

podstawie znajomości praw fizycznych i
chemicznych

rządzących

układem.

Powinien on potem ulec weryfikacji
doświadczalnej (identyfikacja).

Fazy procesu modelowania
matematycznego

I Przyjęcie założeń upraszczających (hipotez roboczych)

II Ułożenie modelu matematycznego w postaci ukł. równań,
schematów bloko-
wych, grafów, itp.

III Realizacja modelu matematycznego

IV Weryfikacja opracowanego modelu

V Wykorzystanie modelu do celów związanych z procesami
projektowania

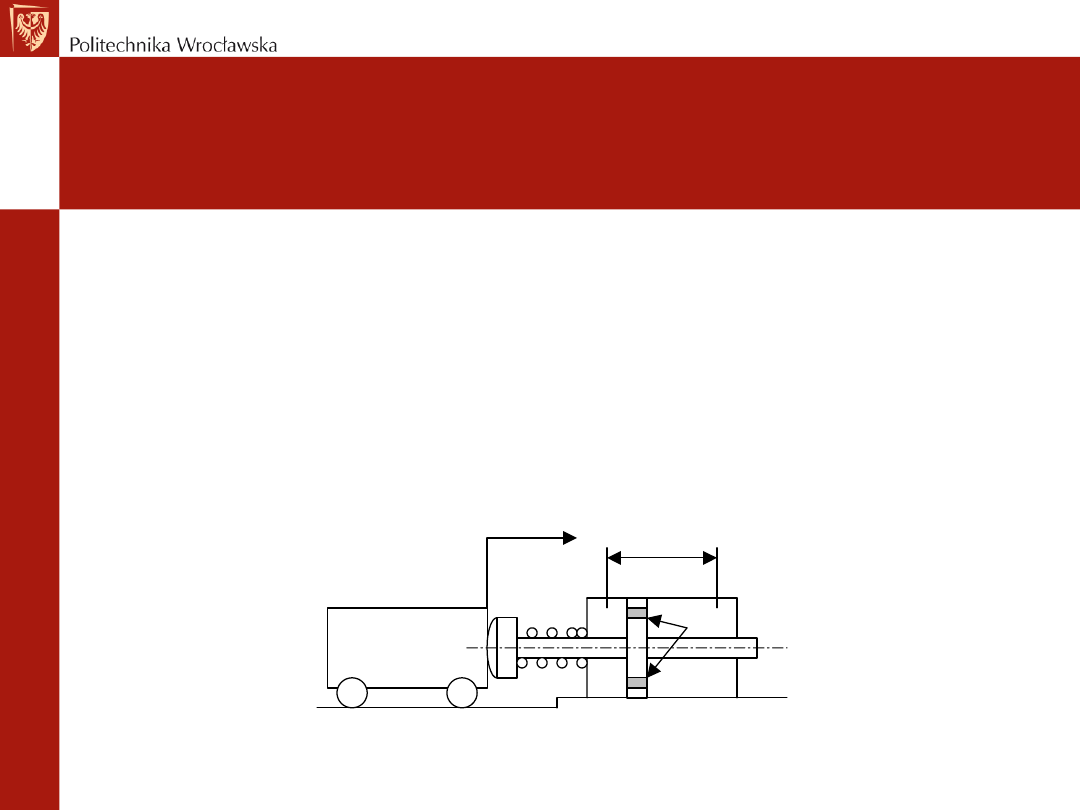
Założenia upraszczające – pomijanie
małych wpływów

Pomijanie małych wpływów upraszcza analizę zmiennych i stopień
skomplikowania równań ruchu. Komplikacja analizy rośnie wraz z
większą liczbą części „ruchomych” układu.

PRZYKŁAD : Zderzak

hydrauliczny:

mẍ + kx + S

0

= A∆p

S

0

- pomijalnie mały wpływ napięcia wstępnego sprężyny

x

p

k ,S

0

A G

m

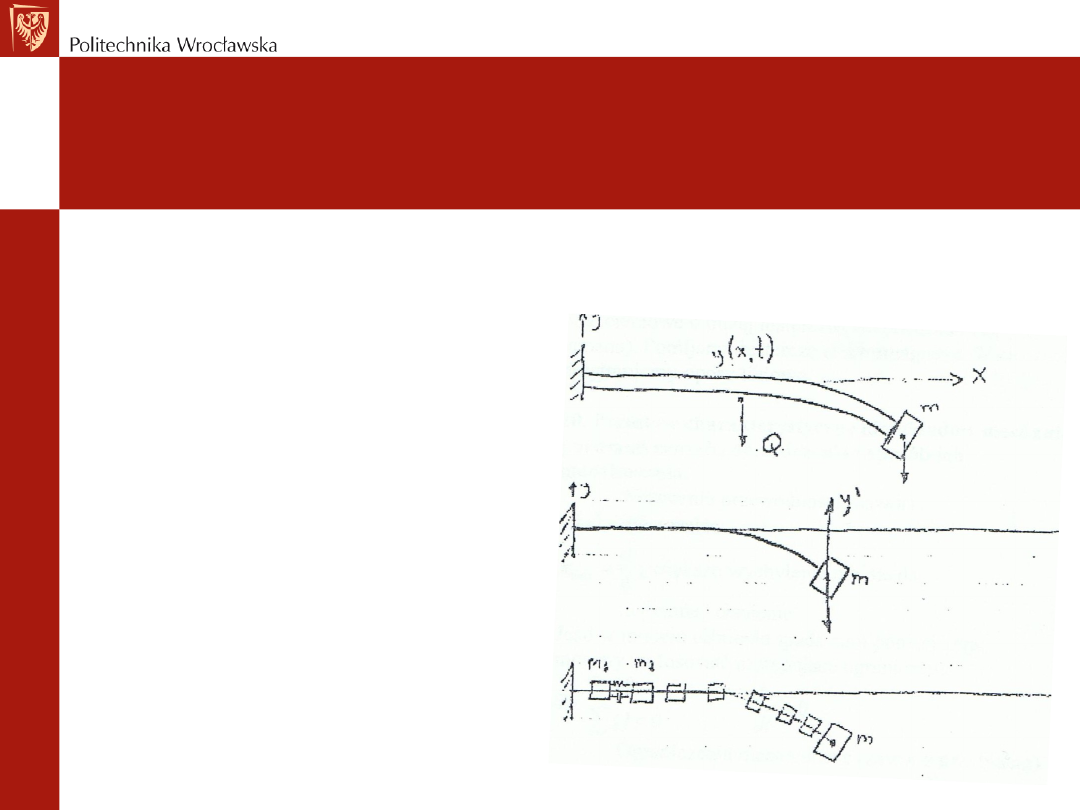
Założenia upraszczające – zastępowanie
parametrów rozłożonych skupionymi

Zamiast równań różniczkowych o pochodnych cząstkowych
można opisać układ równaniami różniczkowymi
zwyczajnymi.

Przykład:
Masa ciągła na belce jest
zamieniana na kilka mas
skupionych (równych sobie i w
jednakowych odstępach). W
zderzeniu

wagonów

przyjmujemy masę skupioną
żeby nie brać pod uwagę
żadnych

momentów

siły

(skupiona masa w centralnym
punkcie

wagonu).

Masa

rozłożona

powoduje

duże

trudności

przy

obliczaniu

momentów bezwładności).

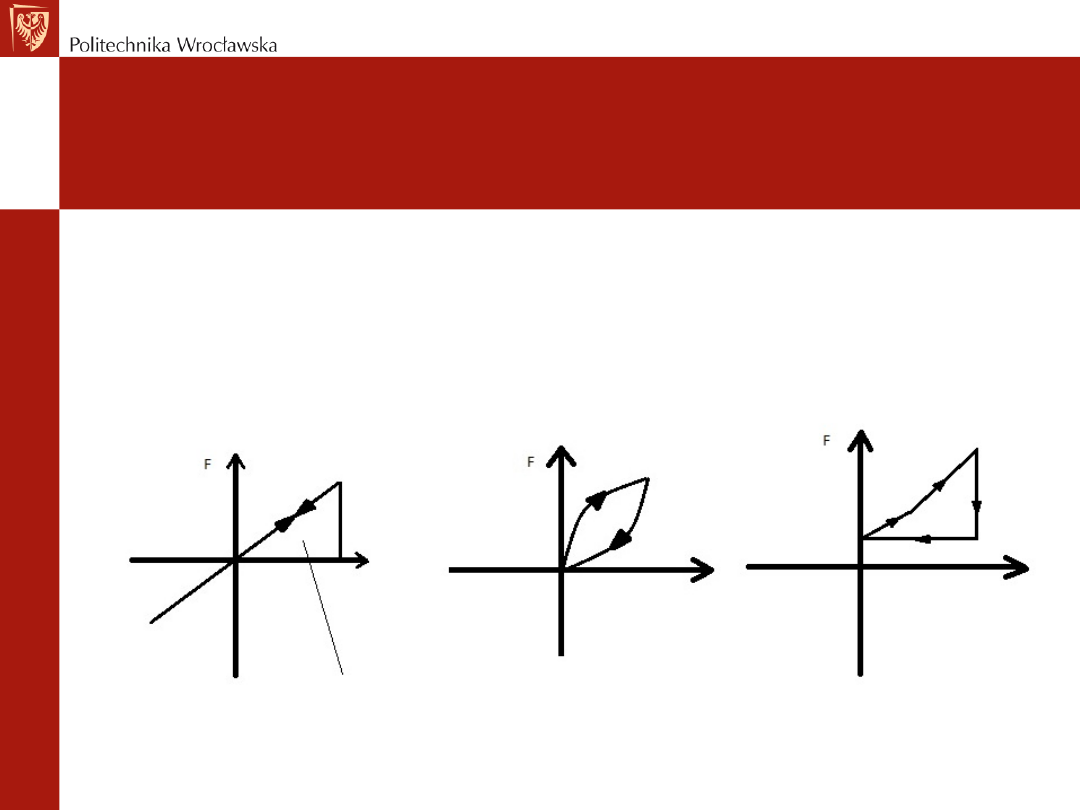
Założenia upraszczające – zakładanie
prostych zależności liniowych

Liniowość – superpozycja. Zakładanie
liniowych zależności w prostych
przypadkach umożliwia uzyskanie
rozwiązania o charakterze ogólnym.

Histereza
sprężyny

Pole pracy
sprężyny

Charakterystyka
sprężyny

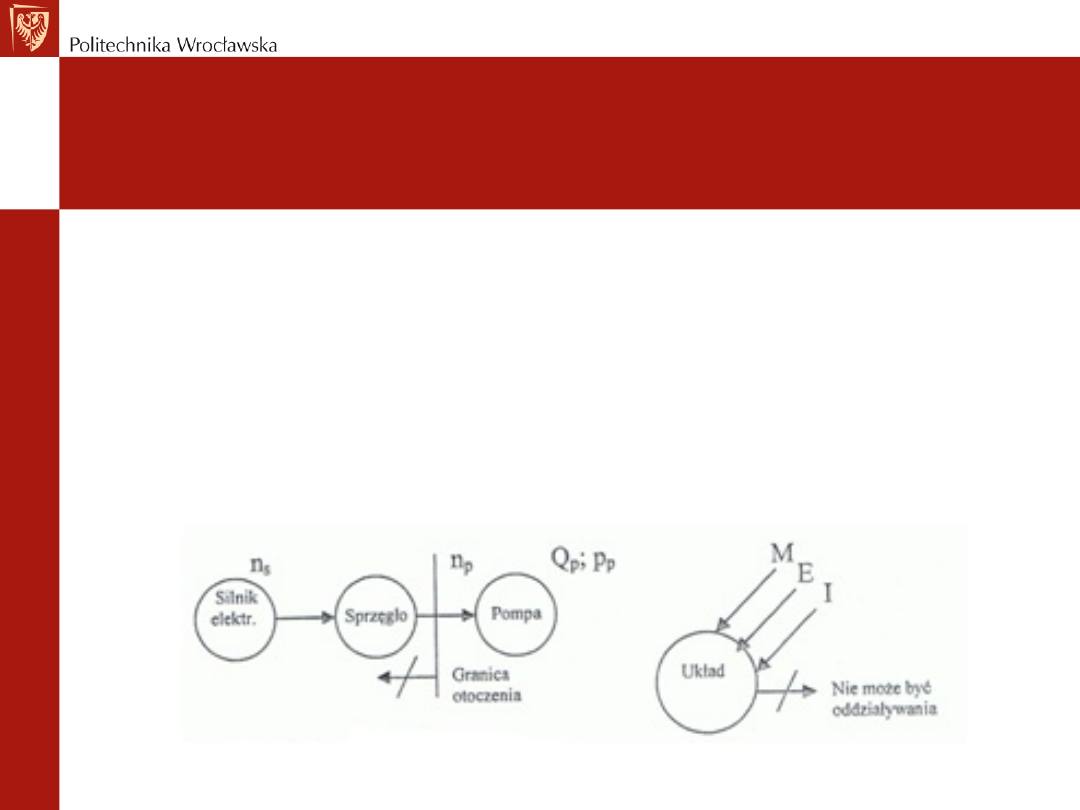
Założenia upraszczające – niezależność
otoczenia badanego układu

Środowisko otaczające układ nie ulega wpływom pochodzącym
z układu.

Przykład:

Pomijamy sprawność sprzęgła, dynamikę silnika oraz
przyjmujemy stałą prędkość silnika. Daje to granicę pomiędzy
sprzęgłem, a pompą, która jest granicą z otoczeniem.
Zależności przechodzą w jedną stronę.

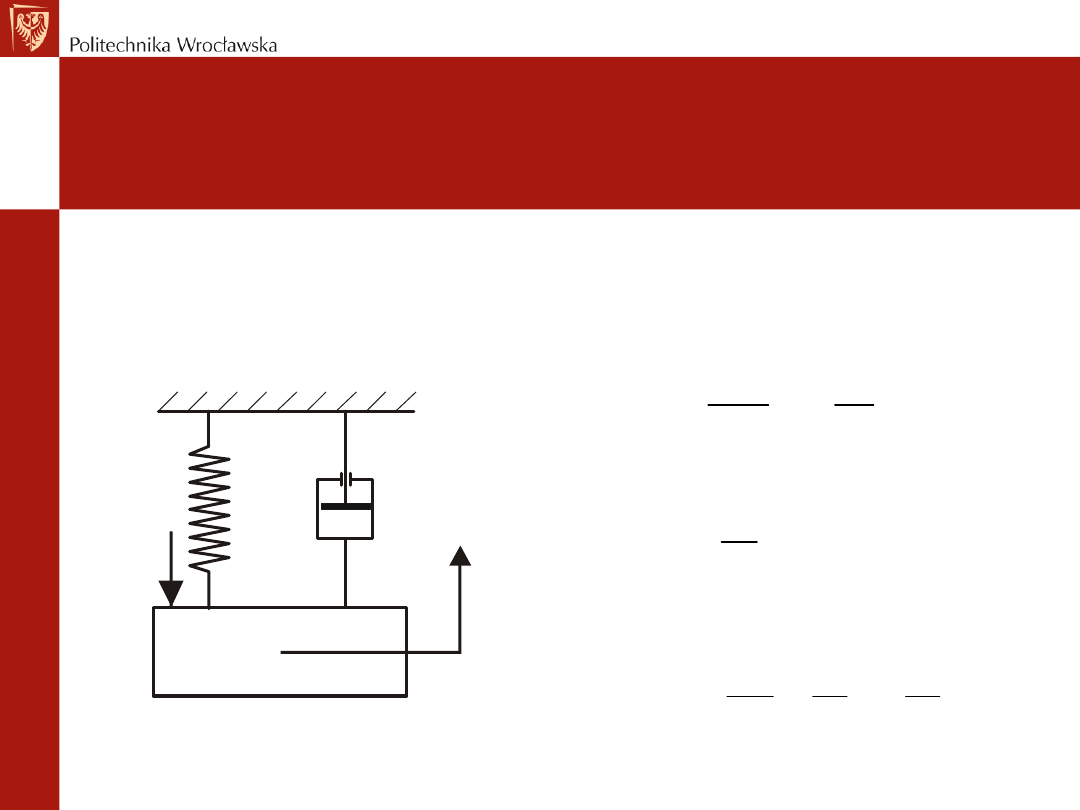
Przykład – oscylator harmoniczny

m

k

f

x

F

Model
fizyczny:

Model
matematyczny:

F

kx

dt

dx

f

dt

x

d

m







2

2

*

)

*

(

1

..

0

..

kx

x

f

F

m

x







x

m

k

x

m

f

m

F

x

*

.

0

..







Przykład – zawieszenia samochodu

M

m

z

y

x

K

k

f





































mg

k

y

z

K

y

z

f

y

m

Mg

y

z

K

y

z

f

z

M

x)

F(y

)

(

)

(

)

(

)

(













Model
fizyczny:

Równania
ruchu:









































g

m

k

y

z

m

K

y

z

m

f

y

g

y

z

M

K

y

z

M

f

z

x)

(y

F

)

(

)

(

)

(

)

(













Model
matematyczny:

Dziękuję za

uwagę