
Zastosowanie
rachunku
operatorowego do
analizy obwodów
liniowych w stanie
nieustalonym
Niech funkcja f(t) będzie określona w przedziale
). Przekształceniem lub transformatą
Laplace’a funkcji f(t) nazywamy wyrażenie:
gdzie:
jest zmienną zespoloną.
funkcja pierwotna (oryginał)
transformata Laplace’a
funkcji f(t)
,
0
t
e
t
f
s
F
t
f
st
d
)
(
)
(
)
(
0
L
j
s
Przykład 1
Wyznaczenie transformaty funkcji stałej
f(t) = a
zakładamy:
Dla całka Laplace’a nie jest zbieżna
można stosować dla każdego
0
0
d
st
st
e
s
a
t
e
a
a
L
t
t
t
st
t
e
e
e
j
lim
lim
0
s
a
a
L
0
0
s
definicja funkcji jednostkowej
Dla t=0 przyjmuje się różne
wartości:
0
gdy
1
0
gdy
0
1
t
,
t
,
)
t
(
1(t)
1
0
t
s
t
1
)
(
1
L
1
,
2
1
,
0
Przykład 2
wyznaczenie transformaty funkcji
wykładniczej
gdzie:
zakładamy
można stosować dla
każdego
at
e
t
f
)
(
j
a
0
j
0
1
d
t
t
st
t
a
t
a
e
e
s
a
t
e
e
e
L
a
s
e
t
a
1
L
0
s
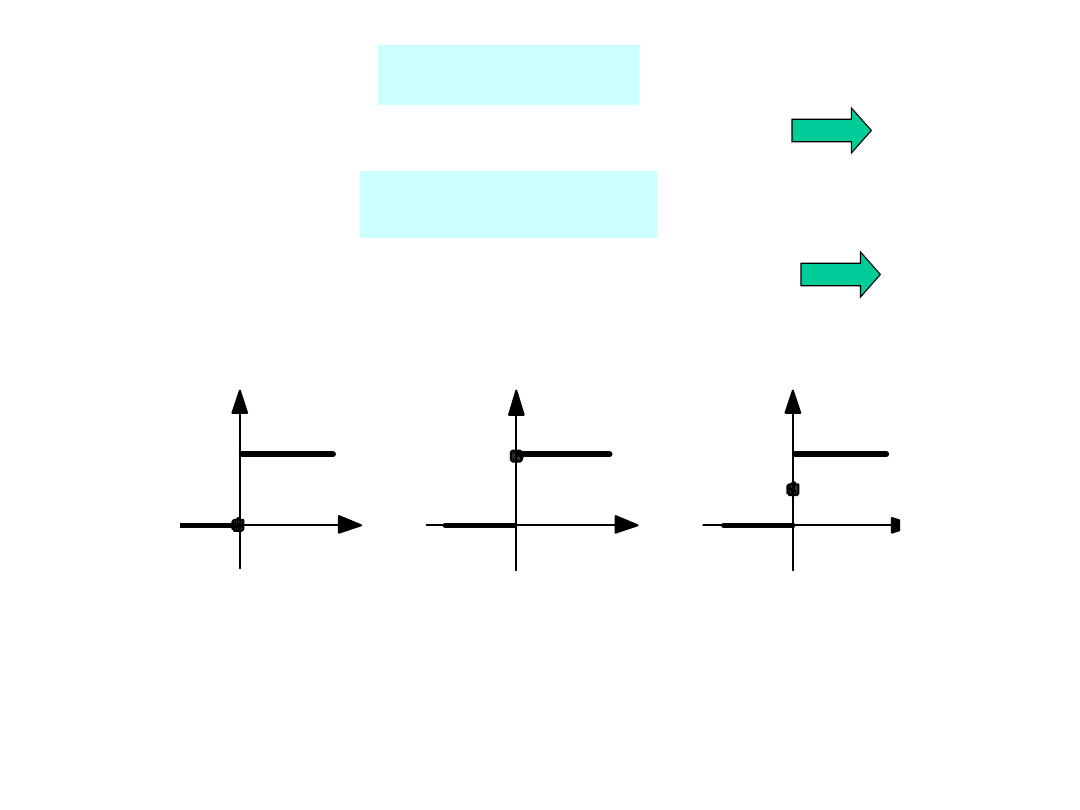
to jednoznaczne przyporządkowanie f(t)
F(s)
to jednoznaczne przyporządkowanie F(s)
f(t)
jeżeli dwie funkcje f(t) i g(t) określone w
przedziale mają tę samą transformatę F(s), to
funkcje te różnią się tylko o funkcję zerową
)
(
)
(
s
F
t
f
L
)
(
)
(
1
s
F
t
f
L
f (t)
1
t
1
t
1
g (t)
h (t)
0.5
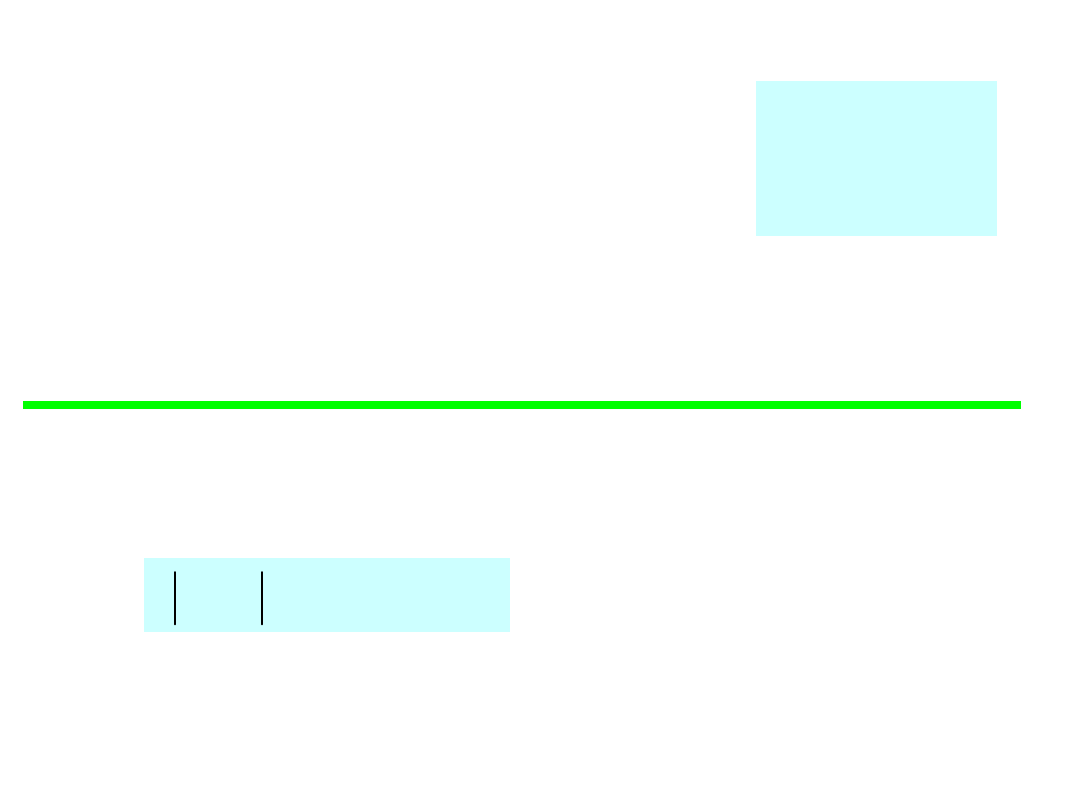
Funkcją zerową N(t) nazywamy funkcję prawie
wszędzie
równą zeru, a więc taką funkcję dla której
dla każdego t. Funkcja zerowa może więc mieć
wartości różne od zera tylko w punktach
nieciągłości.
Każda funkcja f(t), dla której istnieją stałe
dodatnie M >0 oraz c > 0 takie, że
dla każdego t > 0
ma transformatę Laplace’a.
t
)
(
N
0
0
d
ct
Me
t
f
Twierdzenie o liniowości
jeżeli a i b są dowolnymi stałymi to:
Przykład 3
)
(
)
(
)
(
)
(
s
G
b
s
F
a
t
g
b
t
f
a
L
.
j
1
j
1
j
2
1
j
2
1
j
2
1
j
2
sin
2
2
j
j
j
j
s
s
s
e
e
e
e
t
t
t
t
t
L
L
L
L
2
2
sin
s
t
L
2
2
cos
s
s
t
L

Twierdzenie o podobieństwie
Jeżeli a jest liczbą rzeczywistą dodatnią,
to
Dowód
a
s
F
a
at
f
1
L
a
s
F
a
at
a
e
at
f
t
e
at
f
at
f
t
a
a
s
st
1
)
(
d
1
)
(
d
)
(
)
(
0
0
L
Twierdzenie o przesunięciu w dziedzinie
zespolonej
Jeżeli k jest dowolną liczba rzeczywistą lub
zespoloną, to
Dowód
k
s
F
t
f
e
t
k
)
(
L
k
s
F
t
e
t
f
t
f
e
t
k
s
t
k
d
0
L

Przykład 4
obliczymy transformatę funkcji
gdzie F(s) jest transformatą
funkcji
t
e
t
sin
s
F
t
e
t
sin
L
2
2
sin
s
t
e
t
L
t
)
t
(
f
sin
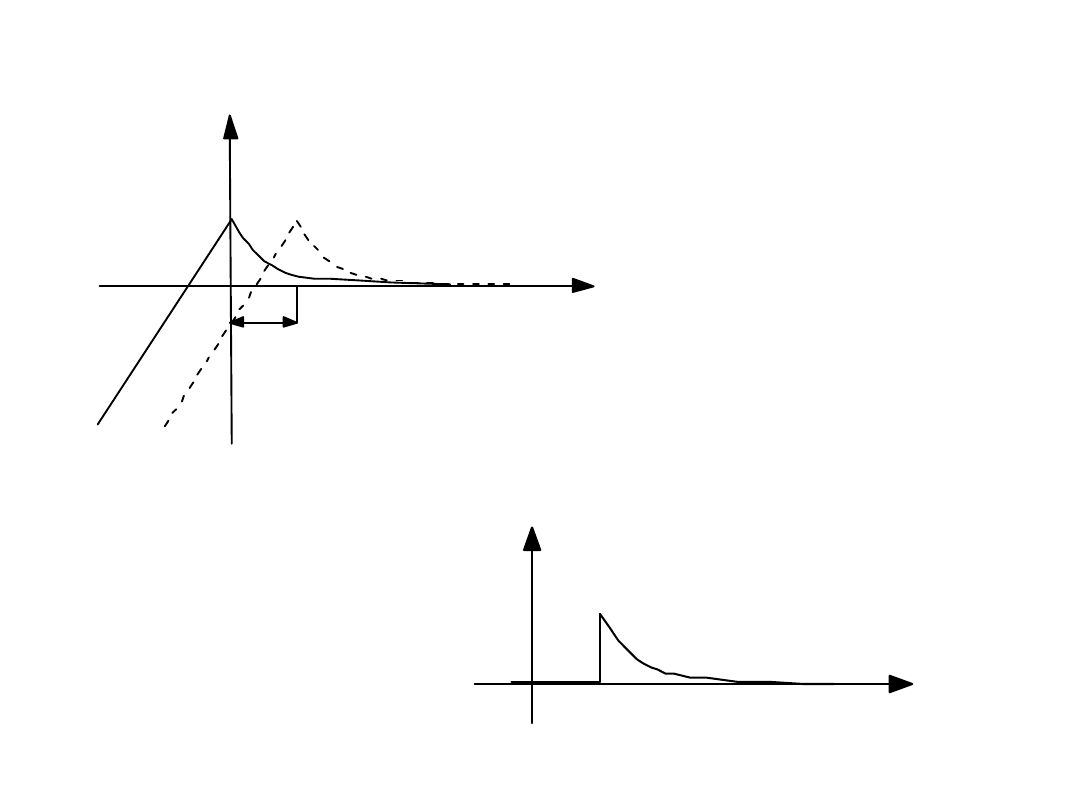
t
h
f(t), f(t-h)
f(t)
f(t-h)
f(t-h)1(t-h)
h
0
f(t-h)1(t-h)
Twierdzenie o opóźnieniu
Jeżeli h jest stałą rzeczywistą dodatnią, to
Dowód
niech: wtedy:
s
F
e
h
t
h
t
f
sh
-
1
L
t
e
h
t
h
t
f
h
t
h
t
f
st
d
1
-
1
0
L
h
t
.
d
d
1
d
1
τ
0
τ
0
)
s
(
F
e
e
f
e
e
e
f
t
e
h
t
h
t
f
sh
s
sh
s
sh
h
st
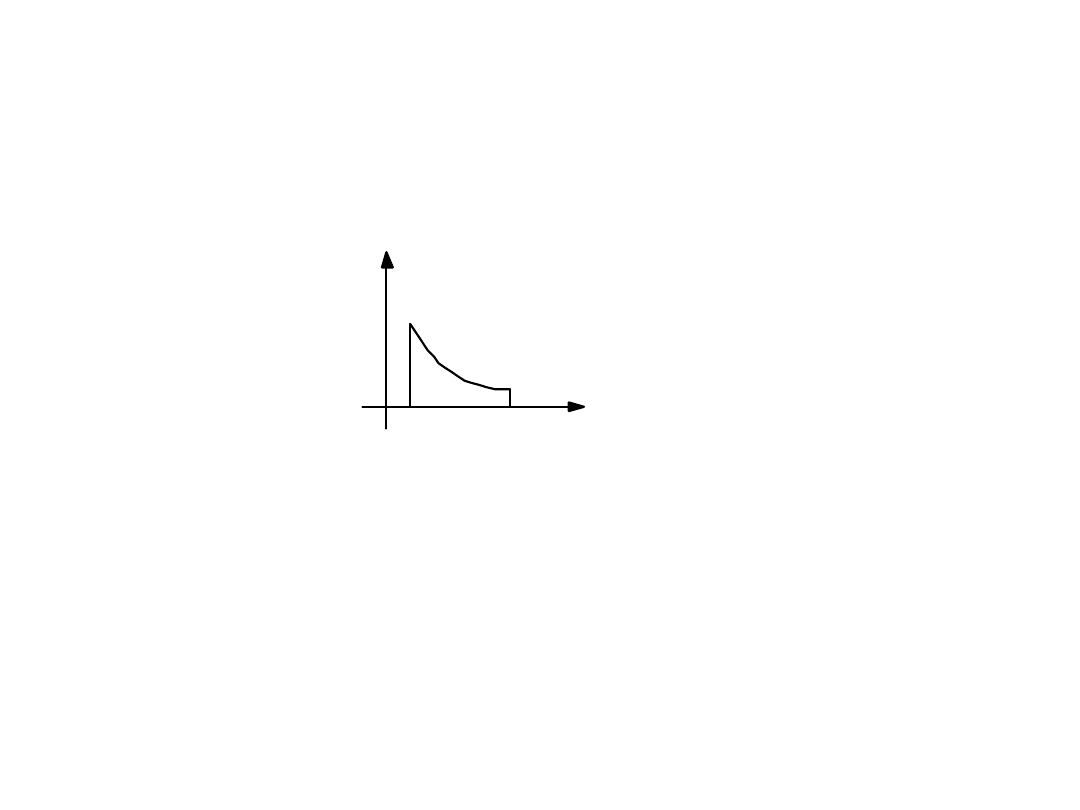
Przykład 5
Wyznaczymy transformatę funkcji
przedstawionej na rysunku
f(t)
.
dla
0
,
dla
,
dla
0
2
2
1
1
h
t
h
t
h
e
h
t
)
t
(
f
at

Równanie funkcji f (t) jest następujące:
2
1
1
1
h
t
h
t
e
)
t
(
f
at
2
1
1
1
)
(
2
2
1
1
h
t
e
e
h
t
e
e
t
f
h
t
a
h
a
h
t
a
h
a
a
s
e
e
a
s
e
e
a
s
e
e
)
s
(
F
h
s
a
h
s
a
h
s
h
a
h
s
h
a
1
1
1
2
1
2
2
1
1
Twierdzenie o transformacie
pochodnej
Dowód
W powyższych przekształceniach przyjęto
Re(s) większe od odciętej zbieżności tak, że
(0)
f
-
(s)
F
d
d
s
t
f
L
)
0
(
)
(
d
)
(
)
(
d
d
d
d
d
0
-
0
0
f
s
F
s
t
e
s
t
f
t
f
e
t
e
t
f
t
f
st
st
st
L
0
)
(
lim
t
f
e
t
s
t
0
2
2
d
d
)
0
(
)
(
d
d
d
d
d
d
t
t
f
f
s
sF
s
t
f
t
t
f
L
L
0
)
1
(
d
d
)
0
(
t
t
f
f
(0)
)
0
(
)
(
d
d
(1)
2
2
2
f
f
s
s
F
s
t
f
L

Przykład 6
Rozwiążemy równanie
-0,5
(0)
sin
d
d
x
t
x
t
x
1
1
)
(
-
0,5
)
(
2
s
s
X
s
X
s
1
1
5
0
1
5
0
1
5
0
5
0
1
1
)
(
2
2
2
2
s
,
s
s
,
s
s
,
,
s
s
X
t
t
,
t
x
sin
0,5
-
cos
5
0
)
(
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
Wyszukiwarka
Podobne podstrony:
OPERAT DOM metoda porównania parami
OPERAT dom metoda korygowania ?ny średniej
GP I rok nst Dolata M , Hutnik S , Piechota M Operat szacunkowy metodą porównywania prarami podejści
Metoda magnetyczna MT 14
Metoda animacji społecznej (Animacja społeczno kulturalna)
Metoda Weroniki Sherborne[1]
Metoda Ruchu Rozwijajacego Sherborne
Projet metoda projektu
METODA DENNISONA
PFM metodaABC
Metoda z wyboru usprawniania pacjentów po udarach mózgu
metoda sherborne
Metoda symultaniczno sekwencyjna
The uA741 Operational Amplifier[1]
więcej podobnych podstron