Ćwiczenia

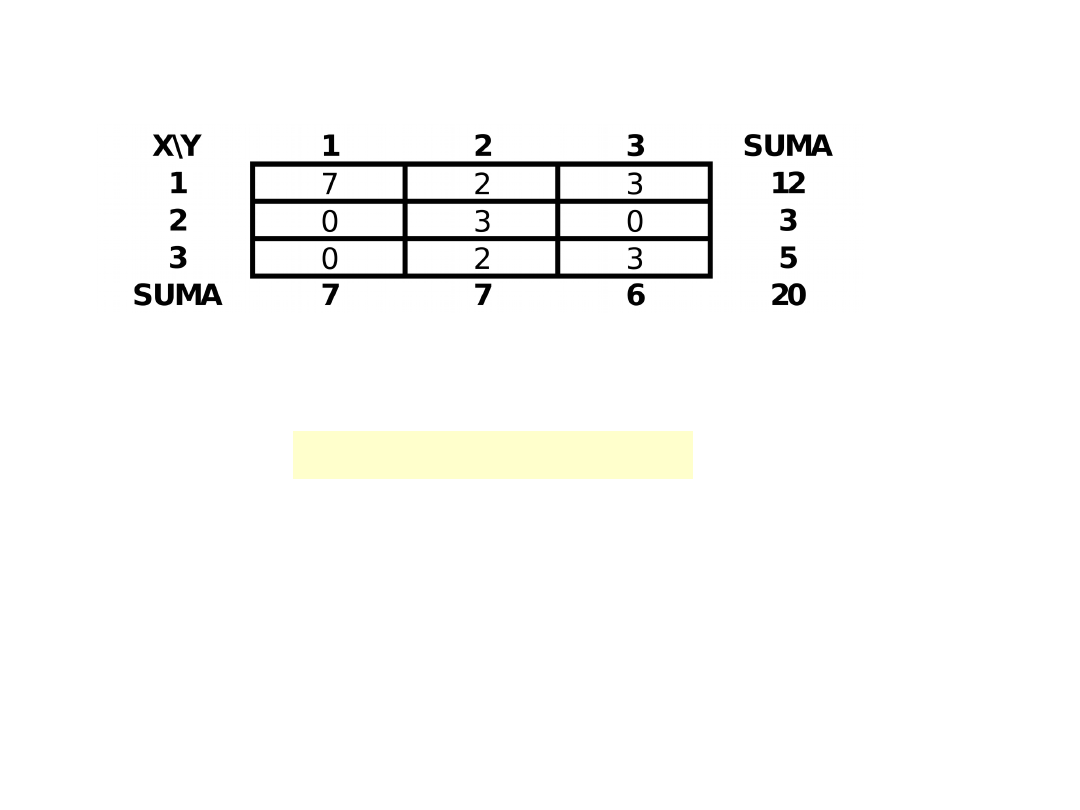
Wejściówka – 10-o minutowa

Oblicz:

C(X,Y) =
E(X|Y=2) =
Mo(X|Y=3) =
E(Y|X=2) =

 

   

Y

E

X

E

XY

E

XY

C





)

(

Niezależność stochastyczna

Warunki zachodzenia niezależności

stochastycznej









i

j

i

x

X

P

y

Y

x

X

P







 |



 



j

i

j

y

Y

P

x

X

y

Y

P









|













j

i

j

i

y

Y

P

x

X

P

y

Y

x

X

P















Zmienna X jest niezależna stochastycznie od zmiennej Y zawsze i tylko wtedy, gdy częstość
warunkowa występowania żadnej wartości zmiennej X nie zależy od wartości, jaką przyjmuje
zmienna Y.
Inaczej: wszystkie rozkłady warunkowe zmiennej X pod warunkiem, że zmienna Y przyjmuje
pewną wartość, są jednakowe, tj. nie zależą od wartości zmiennej Y. Oznacza to że są one
identyczne z rozkładem zmiennej X w całej zbiorowości.

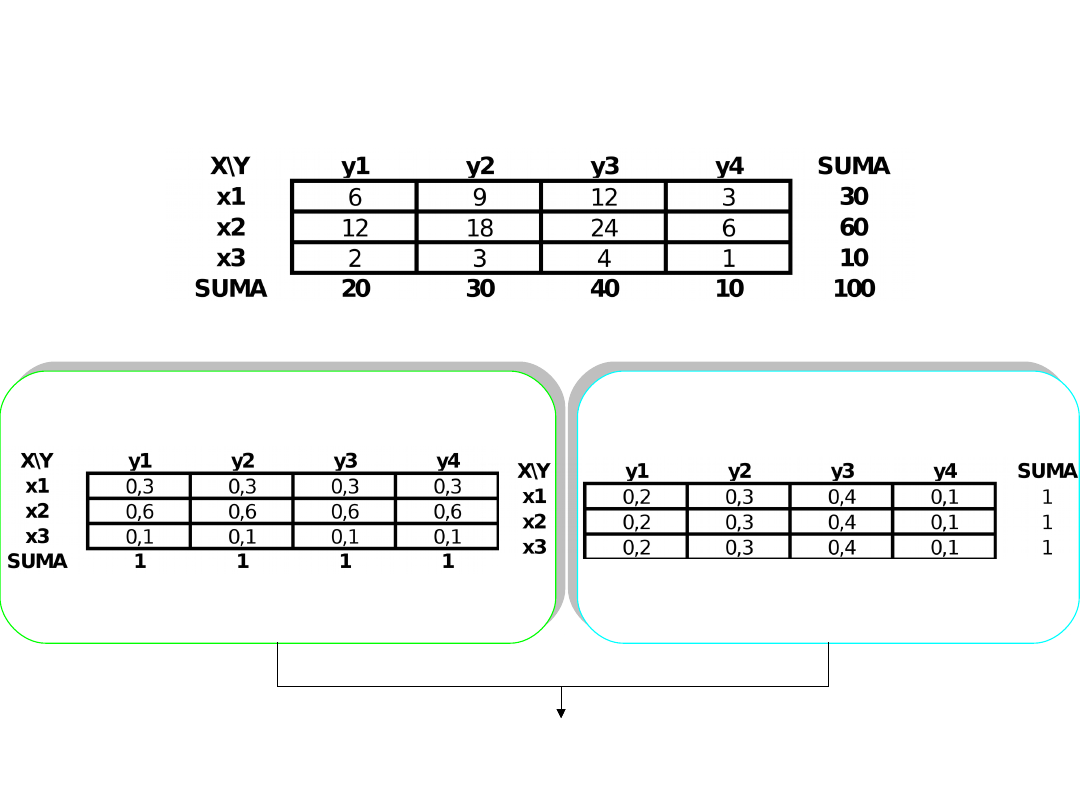
Warunki zachodzenia niezależności

stochastycznej

Łączny rozkład liczebności zmiennej X i Y.

Rozkłady warunkowe X ze względu na Y

Rozkłady warunkowe Y ze względu na X

Zmienna X jest niezależna stochastycznie od zmiennej Y zawsze i tylko wtedy

gdy zmienna Y jest niezależna stochastycznie od zmiennej X

Warunki zachodzenia niezależności

stochastycznej





 









 

 





 









X

Y

H

E

Y

H

Y

X

H

Y

H

X

H

Y

X

H

E

X

H

Y

X

I

|

,

|

:





















 

)

(

)]

|

(

[

)

(

:

|

X

H

Y

X

H

E

X

H

X

H

Y

X

I

Y

X









1

0

|





Y

X



Natężenie zależności stochastycznej

•

I(X:Y) – ilość dostarczanej informacji o zmiennej X przez zmienną Y

•

Miernik siły zależności stochastycznej –

(kappa)

– 0, gdy zmienne są niezależne;
1, gdy są maksymalnie zależne stochastycznie – X jest funkcją Y.

L

P

L

P

A

B

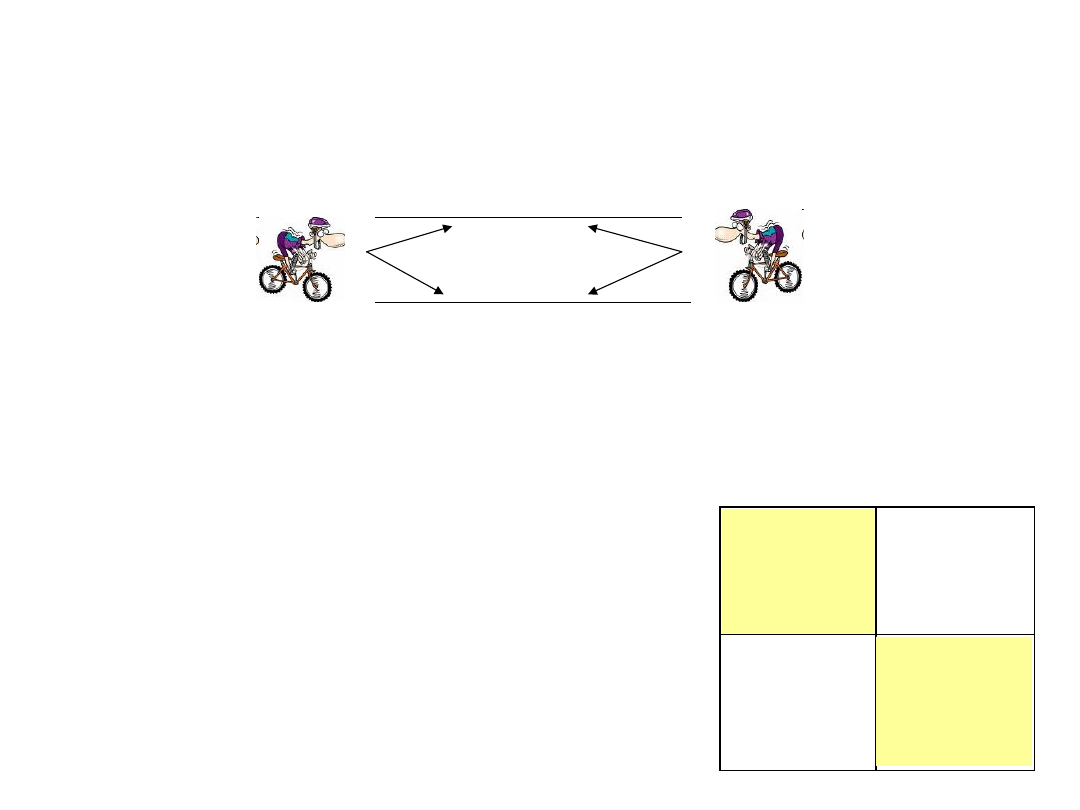
Interakcja społeczna

(gra)

A,B – „gracze”
L,P – opcje (wyboru)
P(L) – strategia P(L)[0,1], P(P)=1-P(L)

L

P

L

P

A

B

OK.
(+N)

OK.
(+N)

Katastrofa

(źle)

(-K)

Katastrofa

(źle)

(-K)

unikaj

unikaj

Działanie społeczne Max Weber

L

P

L

P

L

P

L

P

A

B

A

B

0,8

0,2

0,8

0,2

0,64

0,04

0,16

0,16

L

P

L

P

A

B

0,8

0,2

1

1

0,8

0,2

0,8

0,2









 

B

B

A

B

A

L

P

L

L

P

L

L

P



 

A

L

P

 

B

L

P





 

A

B

A

L

P

L

L

P







   

B

A

B

A

L

P

L

P

L

L

P

*



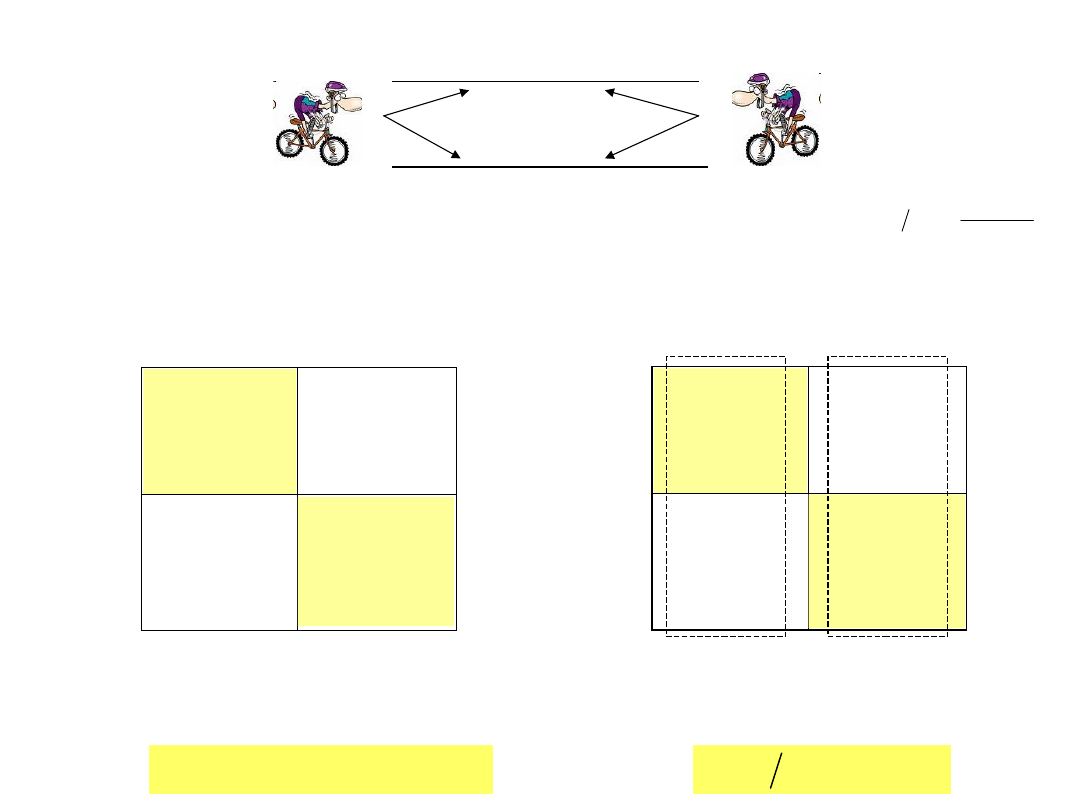
Prawdopodobieństwo łączne

Prawdopodobieństwo warunkowe

Niezależność

stochastyczna

Interakcja społeczna

(gra)

L

P

L

P

A

B

0,8

0,2

0,8

0,2

0,6

0

0,2

0,2

L

P

L

P

A

B

0,8

0,2

1

1

0,75

0

1

0,25









 

75

,

0

8

,

0

6

,

0







B

B

A

B

A

L

P

L

L

P

L

L

P

 

A

L

P

 

B

L

P





 

A

B

A

L

P

L

L

P







   

B

A

B

A

L

P

L

P

L

L

P

*



Prawdopodobieństwo łączne

Prawdopodobieństwo warunkowe

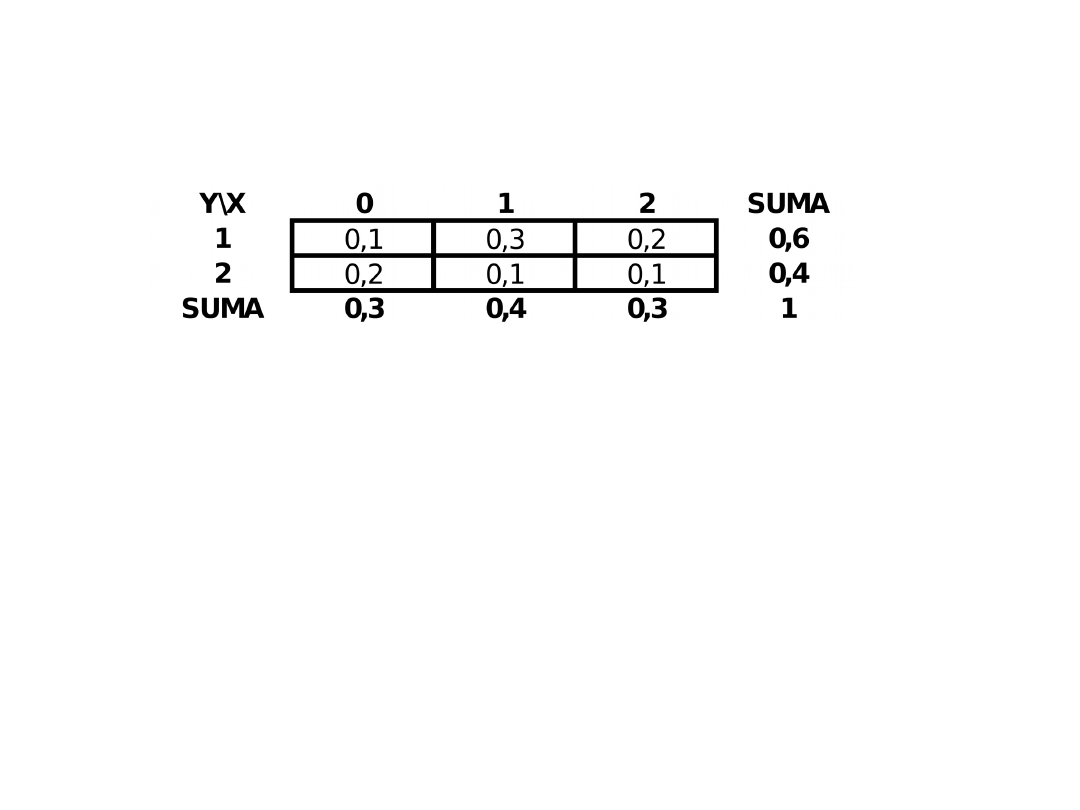
Zadanie 1

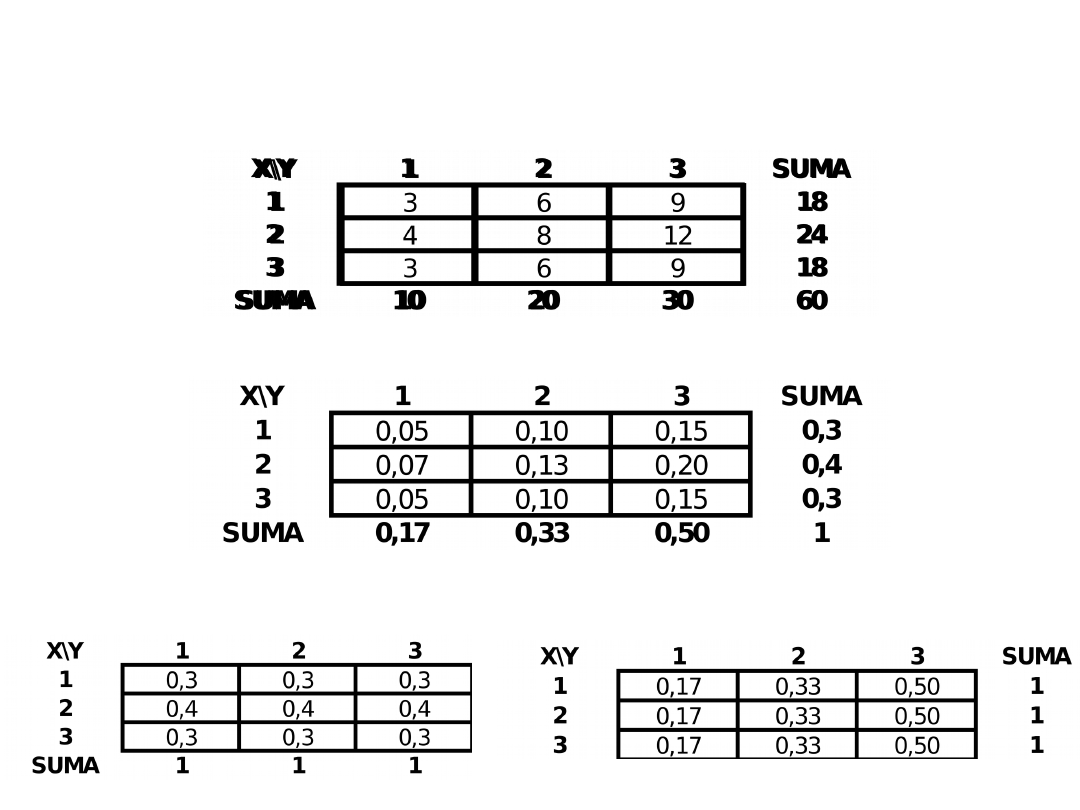
Uzupełnij rozkład łączny liczebności zmiennych X i Y w taki sposób, by zmienne te były
Niezależne stochastycznie.

Łączny rozkład częstości zmiennej X i Y

Rozkłady warunkowe X ze względu na Y

Rozkłady warunkowe Y ze względu na X

0,3
0,4
0,3

Zadanie 2

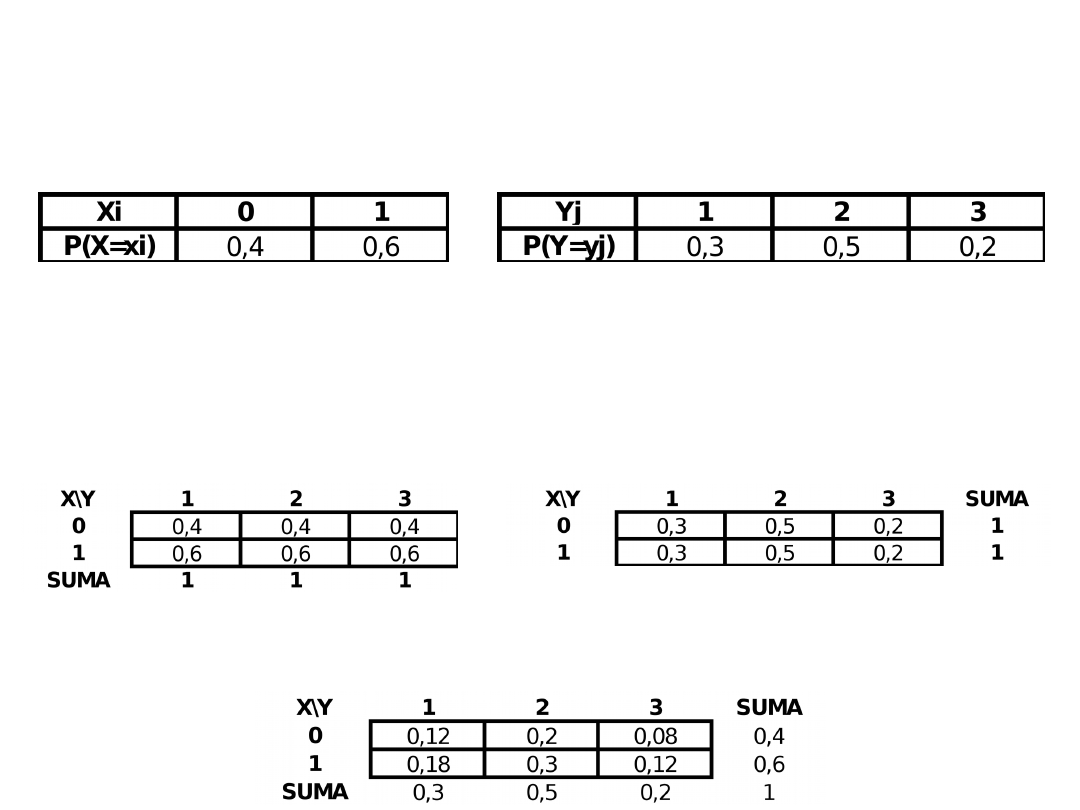
W pewnej populacji określone są dwie zmienne statystyczne stochastycznie niezależne
X (płeć; 0- kobieta, 1- mężczyzna) i Y (kolor oczu; 1- czarne; 2 – piwne; 3- zielone)
o następujących rozkładach:

a) Jaki odsetek mężczyzn stanowią osoby piwnookie?

b) Jaki odsetek zielonookich stanowią kobiety?

c) Jaką część badanej populacji stanowią czarnookie kobiety?

d) Wyznacz łączny rozkład częstości zmiennych X i Y.

Łączny rozkład częstości zmiennej X i Y

Rozkłady warunkowe X ze względu na Y

Rozkłady warunkowe Y ze względu na X

Parametry funkcji dwóch

zmiennych

Parametry funkcji dwóch zmiennych





)

(

)

(

Y

E

X

E

Y

X

E







1. Średnia sumy dwóch zmiennych:

2. Średnia różnicy dwóch zmiennych:





)

(

)

(

Y

E

X

E

Y

X

E







3. Średnia iloczynu i ilorazu dwóch zmiennych:

Jeśli zmienne są niezależne stochastycznie to:

 

)

(

*

)

(

Y

E

X

E

XY

E



)

(

)

(

Y

E

X

E

Y

X

E

H















4. Wariancja sumy (różnicy) dwóch zmiennych:

 

 

 

XY

C

Y

D

X

D

Y

X

D

2

)

(

2

2

2









 

 

 

XY

C

Y

D

X

D

Y

X

D

2

)

(

2

2

2









Parametry funkcji dwóch zmiennych

0
1
2
3

1

2
3
4

2
3
4
5

3
4
5
6

Parametry funkcji dwóch zmiennych

0
1
2
3

1

2
3
4

2
3
4
5

3
4
5
6

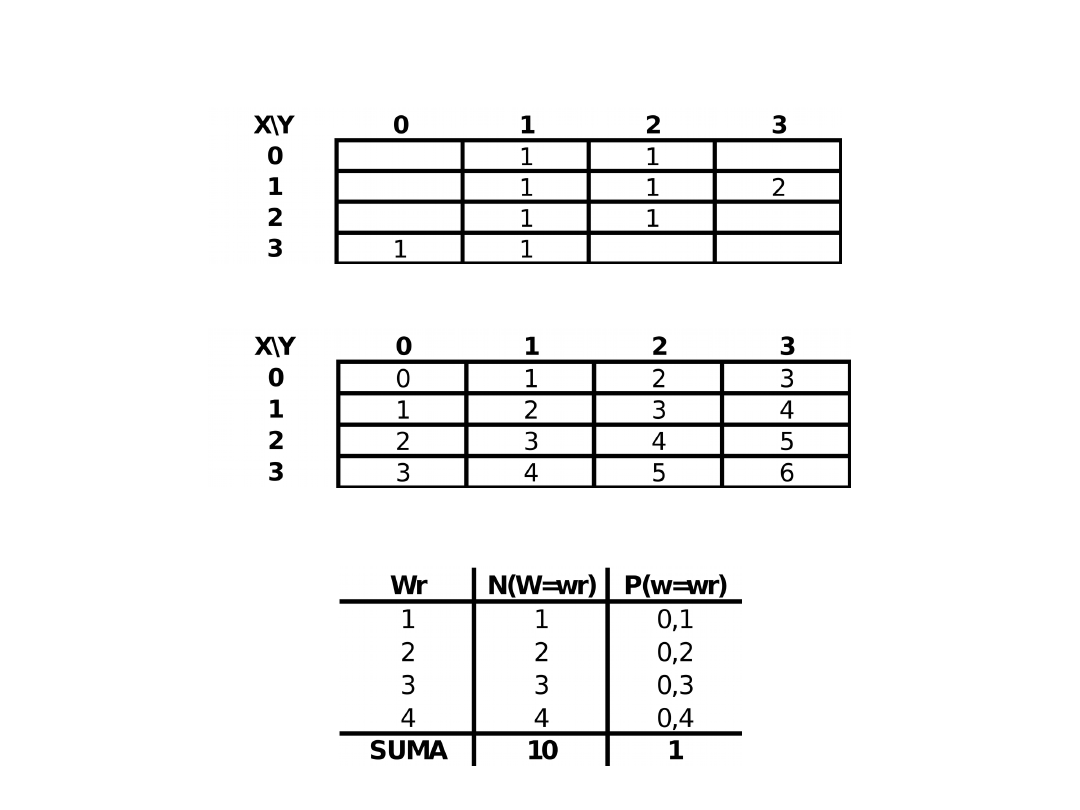
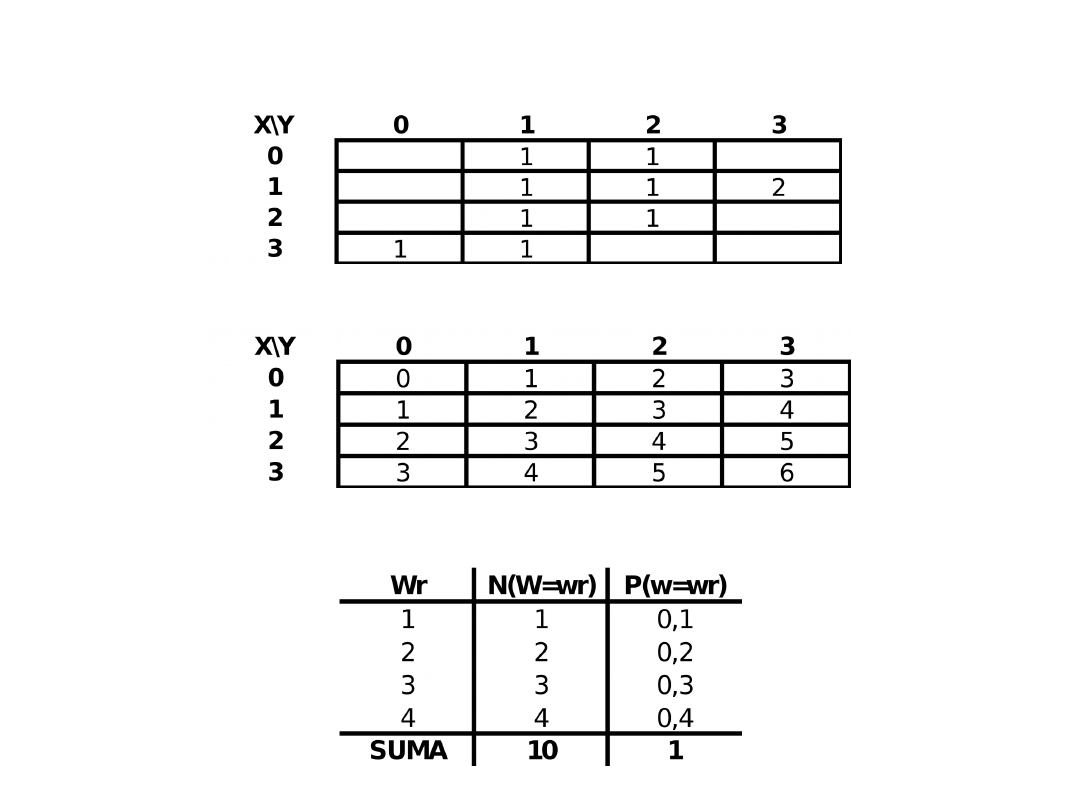
Ćwiczenie 1

Dany jest następujący rozkład łączny zmiennych X i Y:

a) Wyznacz rozkład częstości, średnie, oraz wariancje następujących zmiennych

• Z=X+Y

• W=X-Y

• S=XY

b) Korzystając z obliczeń wykonanych w punkcie a) wyznacz kowariancję zmiennych X i Y