Wykład IV

Teoria pasmowa ciał stałych

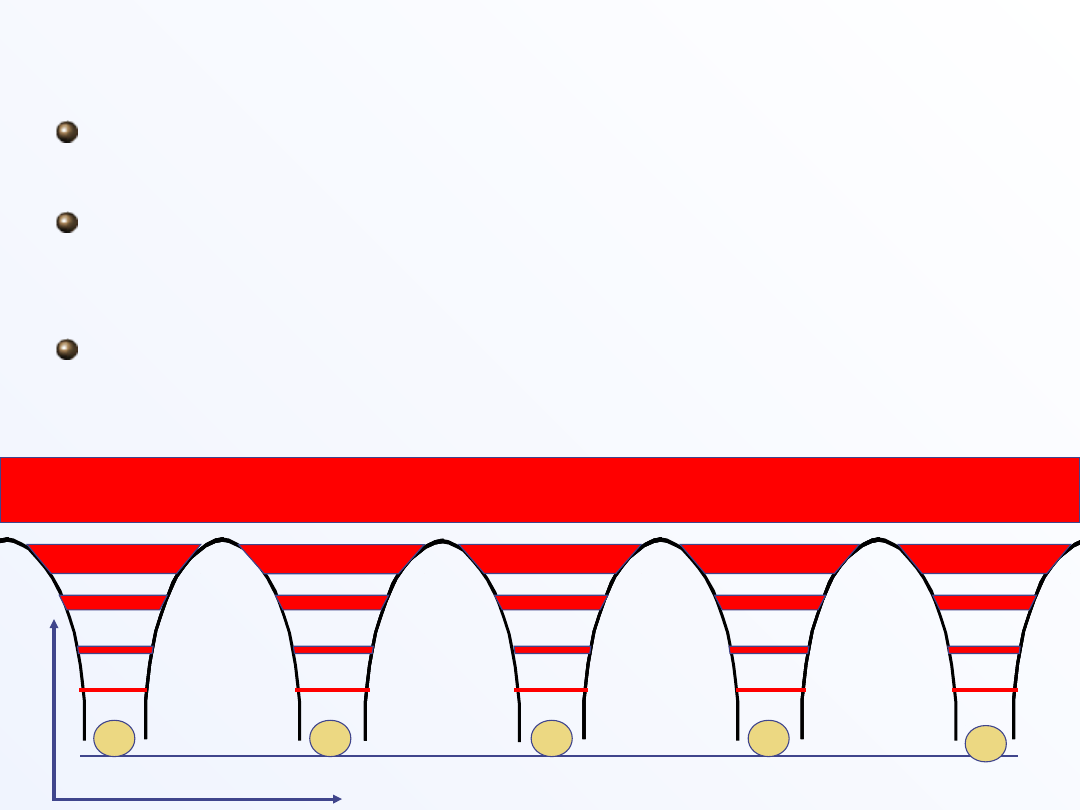
Periodyczność sieci i dozwolone pasma

energii

Izolowane atomy mają dyskretne dozwolone poziomy

energetyczne

Periodyczność sieci w ciele stałym prowadzi do

pojawienia się pasm energetycznych oddzielonych
obszarami wzbronionymi

Dozwolone stany elektronowe mogą być tworzone albo

jako kombinacja stanów elektronów swobodnych ( model
elektronów prawie swobodnych) albo jako liniowa
kombinacja stanów izolowanych atomów ( model LCAO)

+

E

+

+

+

+

położe
nie

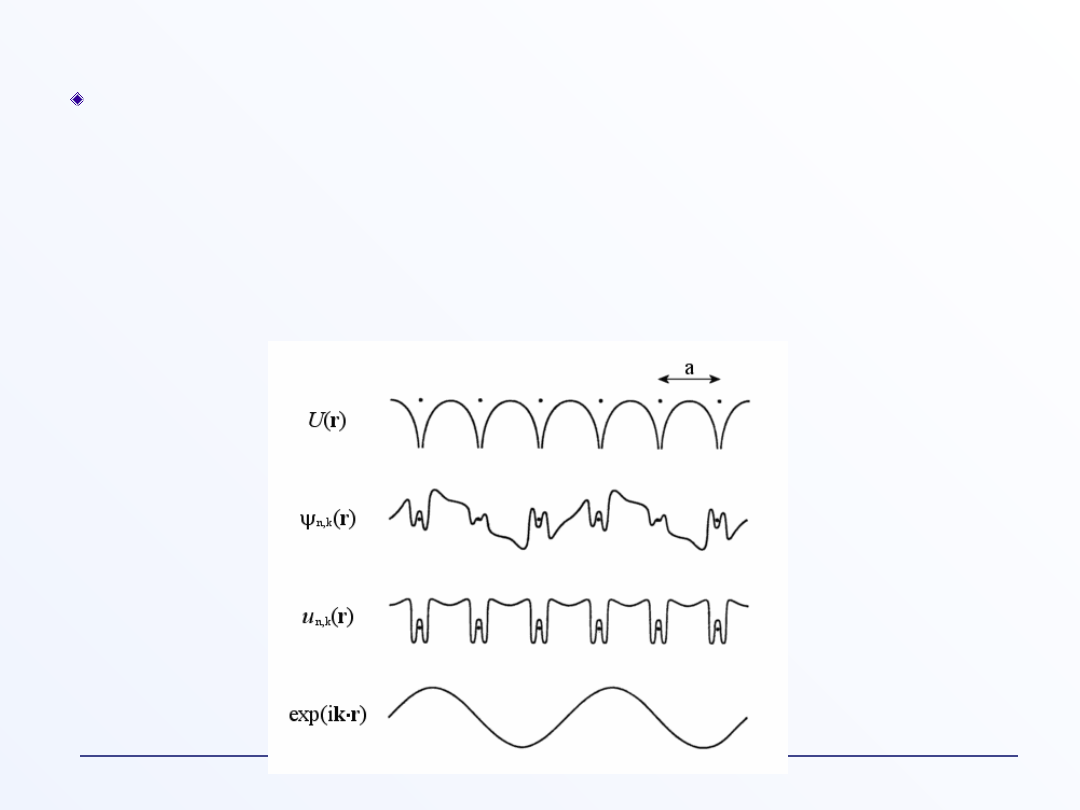
Twierdzenie Blocha

Funkcje falowe będące rozwiązaniem równania Schrödingera
z potencjałem periodycznym U(r) są iloczynem zespolonej
fali płaskiej exp(i k·r) i funkcji periodycznej u

n

k(r) (n – liczba

całkowita).

( )

( )

i

nk

nk

e u

Y

=

kr

r

r

Niejednoznaczność wektora k. Strefy
Brillouina

Funkcje Blocha posiadają dziwną własność: zarówno same
funkcje

jak i odpowiadające im wartości własne energii E

obliczone dla k oraz k+G są identyczne:

3

2

1

3

2

1

3

2

1

3

2

1

a

a

a

a

a

b

a

a

a

a

a

b

a

a

a

a

a

b

























2

1

3

2

3

2

2

2

2







Y

.

.

( )

( )

( )

(

)

n

n

n

n

n

E

E

+

Y

=Y

=

+

k

k G

r

r

k

k G

gdzie G jest

wektorem sieci odwrotnej:

n

1

,n

2

i n

3

– liczby całkowite, a

i

są wektorami podstawowymi sieci

krystalicznej, b

i

są wektorami podstawowymi sieci odwrotnej.

3

2

1

b

b

b

G

3

2

1

n

n

n







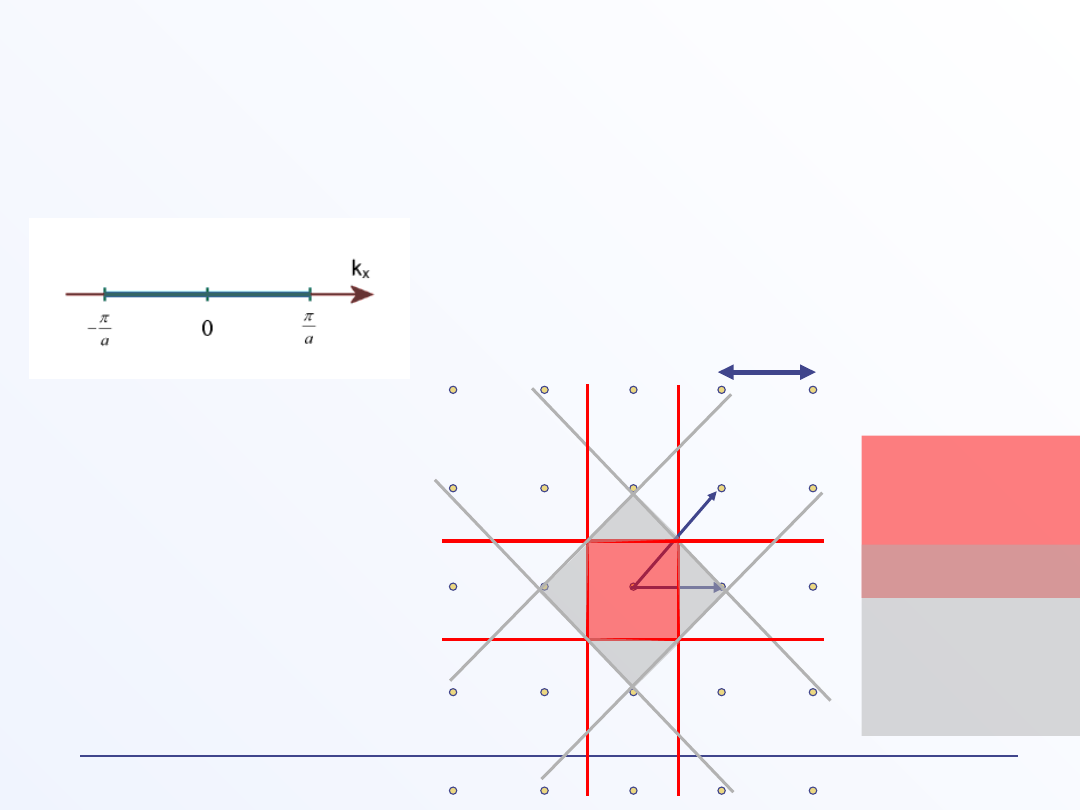
Strefa Brillouina

Strefa Brillouina jest figurą gemetryczną, która
powstaje z przecięcia symetralnych wektorów
łączących sąsiednie punkty sieci odwrotnej.

1

strefa

Brilloui
na

2

strefa

Brillouin
a

2/

a

1D

2D sieć regularna.

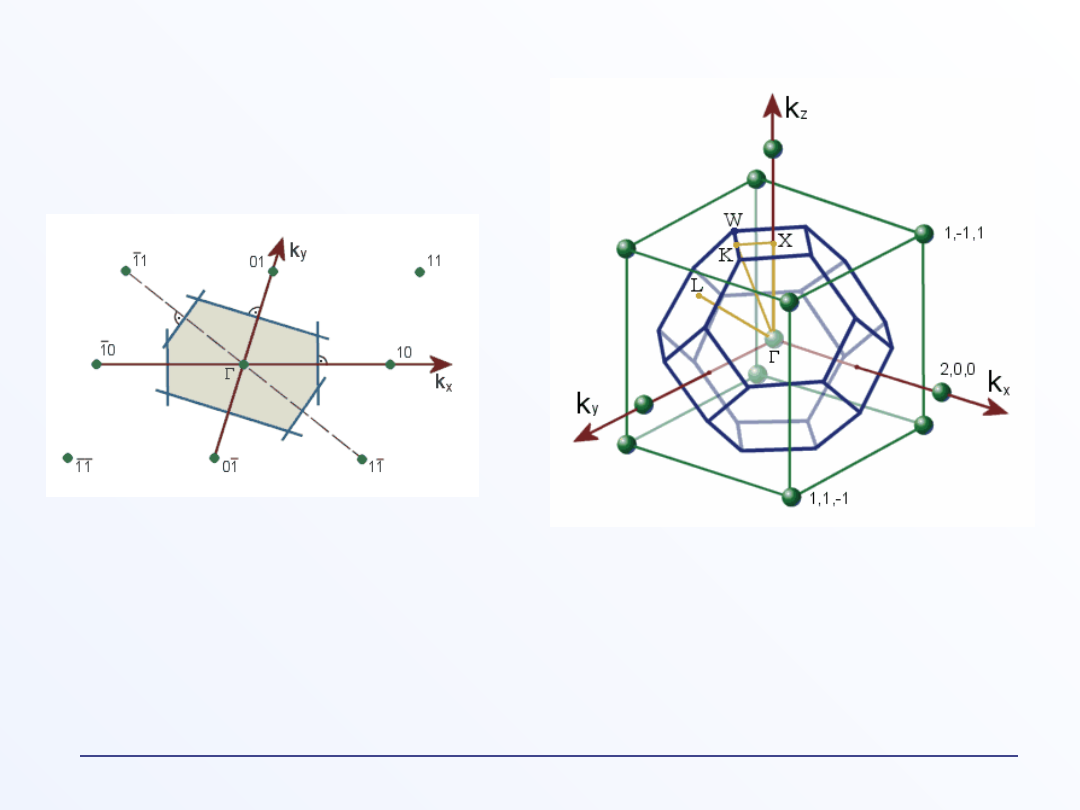
I strefa Brillouina

Konstrukcja I strefy Brillouina w
przestrzeni 2D, sieć
ukośnokątna.

I strefa Brillouina dla sieci
kubicznej powierzchniowo
centrowanej (fcc).

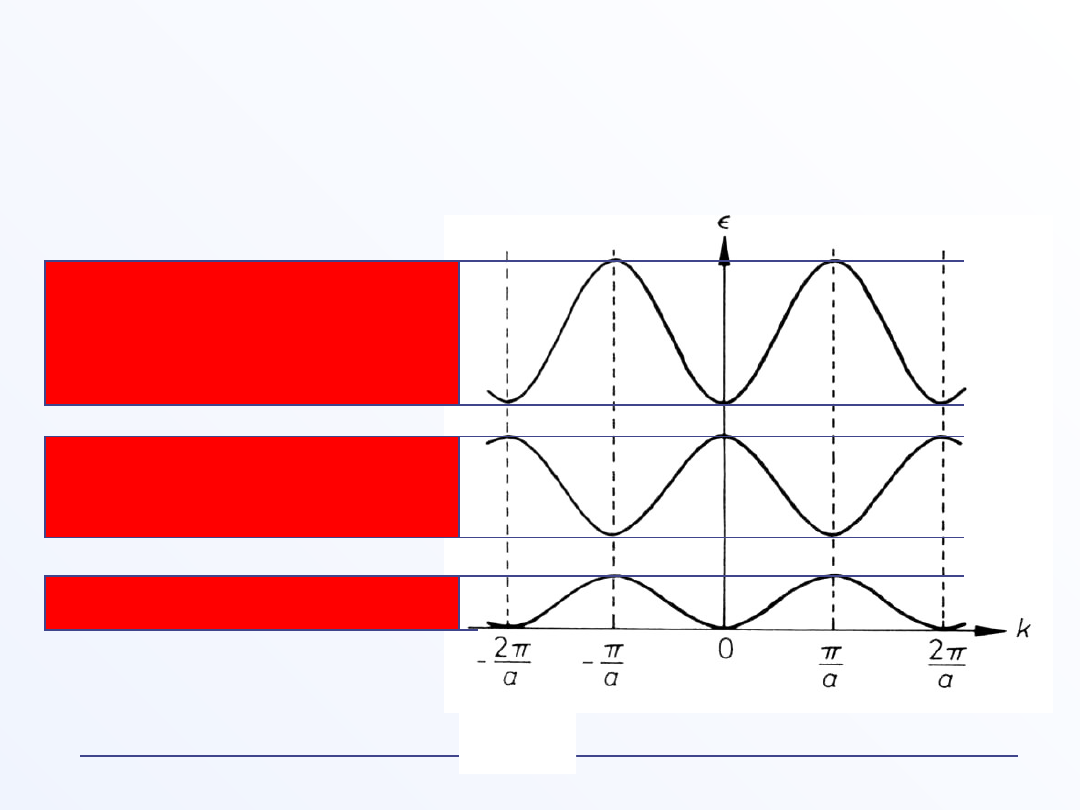
Pasmo dozwol. stanów

Pasmo dozwolonych
stanów

Pasmo dozwolonych
stanów

Przerwa
wzbroniona

Przerwa
wzbroniona

( )

(

)

n

n

E

E

=

+

k

k G

Ze względu na tę periodyczność, wystarczy ograniczyć się do I-
szej strefy Brillouina

Periodyczność E(k)

1D

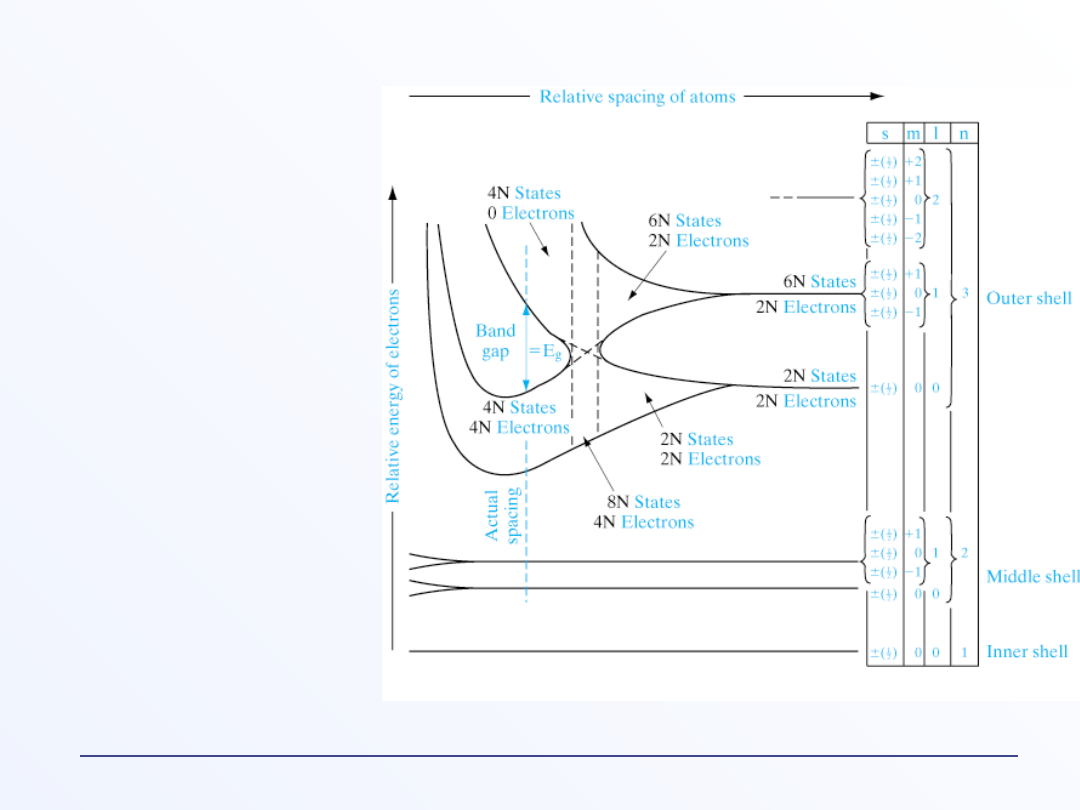
Krzem

Podpasma mogą łączyć się, jak np. w Si, gdzie 4 podpasma łączą się
w pasmo walencyjne

Konfiguracja w izolowanym atomie

Si:

1s

2

2s

2

2p

6

3s

2

3p

2

-Każdy atom ma dwa
stany1s dwa 2s, 6sześć
stanów 2p, dwa 3s,
sześć 3p i wyższe

-Dla N atomów, dostępnych
jest 2N stanów 1s, 2N
stanów 2s, 6N stanów
2p, 2N stanów 3s i 6N
stanów 3p

-Po zbliżeniu atomów
największemu
rozszczepieniu ulegają
stany 3s i 3p. Stany te
mieszają się dając 8N
stanów.

-Przy odległości
równowagowej, pasmo
to rozszczepia się na
dwa pasma oddzielone
przerwą E

g

. Górne pasmo

– przewodnictwa zawiera
4N stanów i dolne –
walencyjne, też 4N
stanów.

Łańcuch jednoatomowy

Periodyczny warunek brzegowy oznacza równość

funkcji Blocha w punktach krańcowych x = 0 oraz

x = Na,

Z periodyczności : i
więc

(0)exp( 0)

(

)exp(

)

u

ik

u Na

ikNa

=

(0)

(

)

exp( 0) 1

u

u Na

ik

=

=

exp(

) 1

2

ikNa

kNa

m

p

=

=

2

k

m

Na

p

=

„Wytnijmy" z nieskończonego kryształu pewną część o skończonej
objętości, co umożliwia policzenie przypadających na tę objętość
stanów. Zaletą tak wyimaginowanego skończonego kryształu jest, że
nie ma on atomów powierzchniowych. Funkcja Blocha:

Dla 1D:

( )

( )

ikx

x

u x e

Y

=

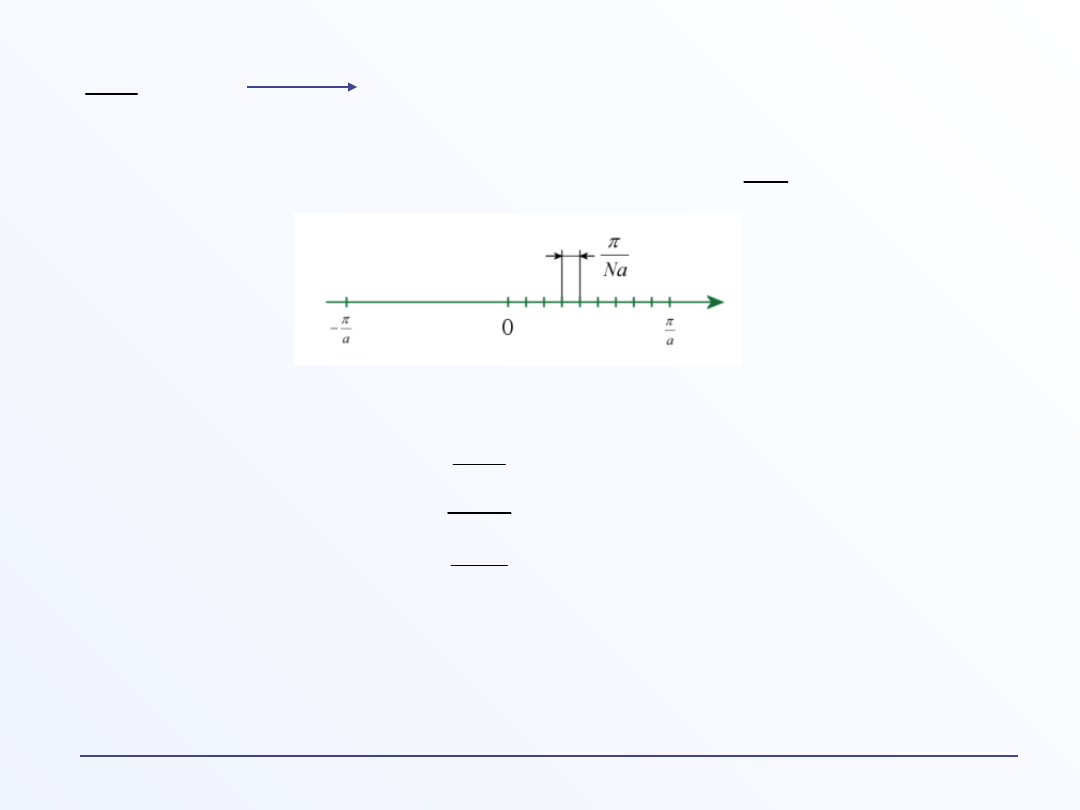
Łańcuch jednoatomowy

2
Na

p

dozwolone wartości k leżą w odległości

2

k

m

Na

p

=

Liczba dozwolonych wektorów falowych w I
strefie Brillouina:

jest równa liczbie komórek prymitywnych w
objętości kryształu

2

2

a

N

Na

p

p

=

WNIOSKI

strefa Brillouina nie jest przestrzenią ciągłą,

ilość dozwolonych wartości wektora falowego jest
ograniczona ze względu na skończoną liczbę N

ilość możliwych punktów, w których kończy się wektor k, czyli
ilość możliwych stanów wynosi N, tzn. tyle, ile jest komórek
elementarnych.

Zatem każda komórka elementarna daje jeden stan k w
każdym paśmie.

Po uwzględnieniu spinu mamy 2N niezależnych stanów w
każdym paśmie.

Ten wynik jest słuszny również dla kryształu trójwymiarowego.

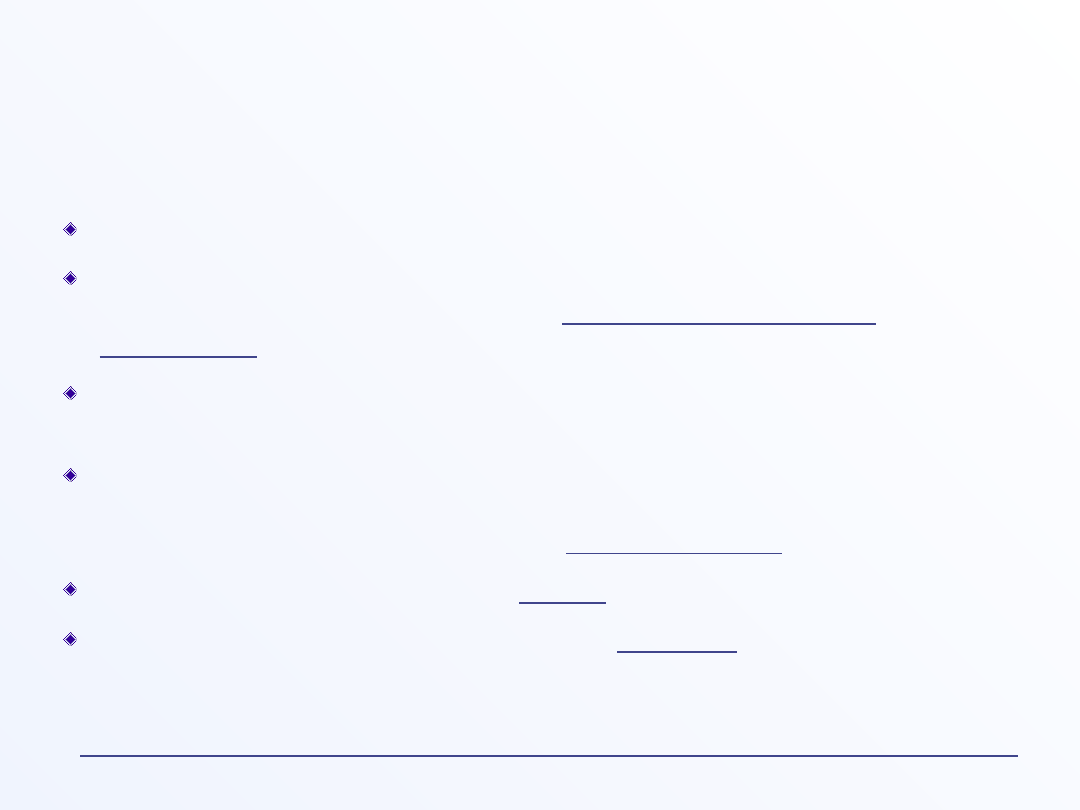
Metale i półprzewodniki

częściowo zapełnione pasmo może przewodzić prąd; pełne – nie.

jeden elektron walencyjny w komórce elementarnej – pasmo do
połowy wypełnione elektronami – metal (litowce i metale
szlachetne)

w pełnym paśmie zawierającym 2N elektronów wszystkie stany w
I strefie B są zajęte. Suma wszystkich wektorów k w paśmie = 0.

liczba elektronów walencyjnych w komórce elementarnej jest
całkowita i parzysta i pasma nie przekrywają się - pasmo
walencyjne całkowicie zapełnione - półprzewodnik;

jeśli pasma przekrywają się - metal.

pasma przekrywają się tylko trochę - półmetal

.

mamy 2N niezależnych stanów w każdym paśmie.

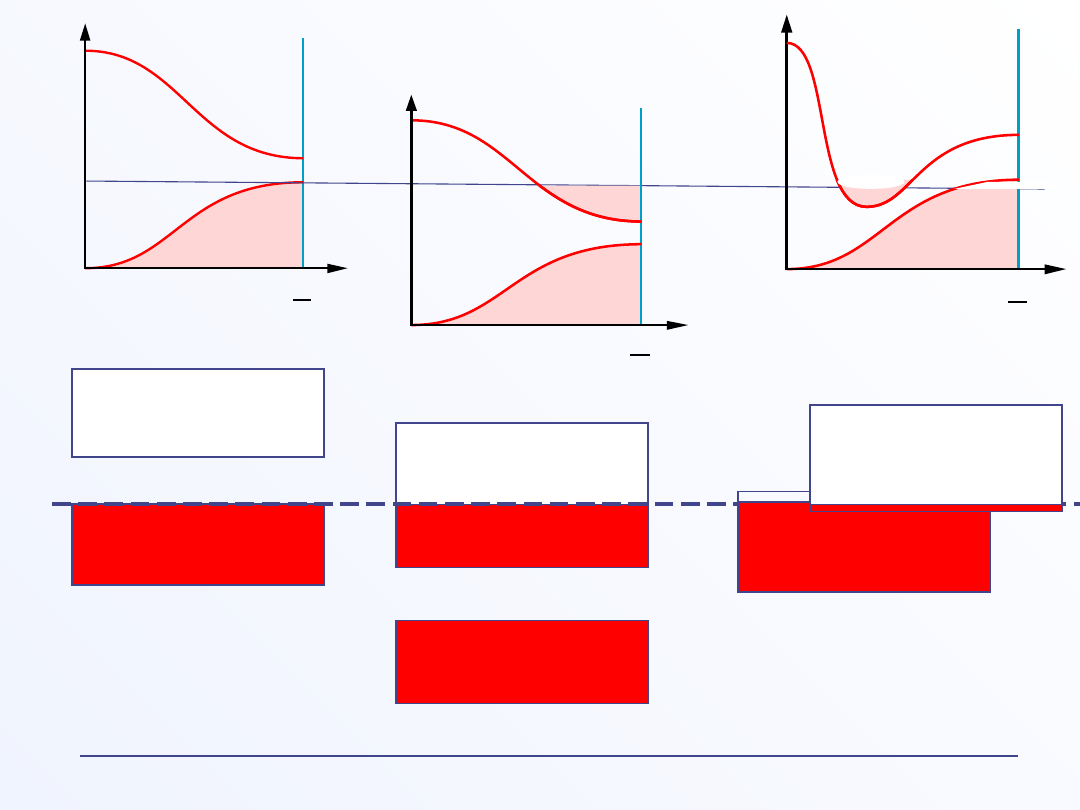
Pełne pasmo

Puste pasmo

Przerwa wzbr.

Pełne pasmo

Częściowo
pełne pasmo

Przerwa wzbr.

Częściowo pełne
p.

Częściowo pełne
pasmo

E

F

IZOLATOR

METAL

METAL
lub półprzewodnik

lub

półmetal

E

k

0

p

a

E

F

E

k

0

p

a

E

k

0

p

a

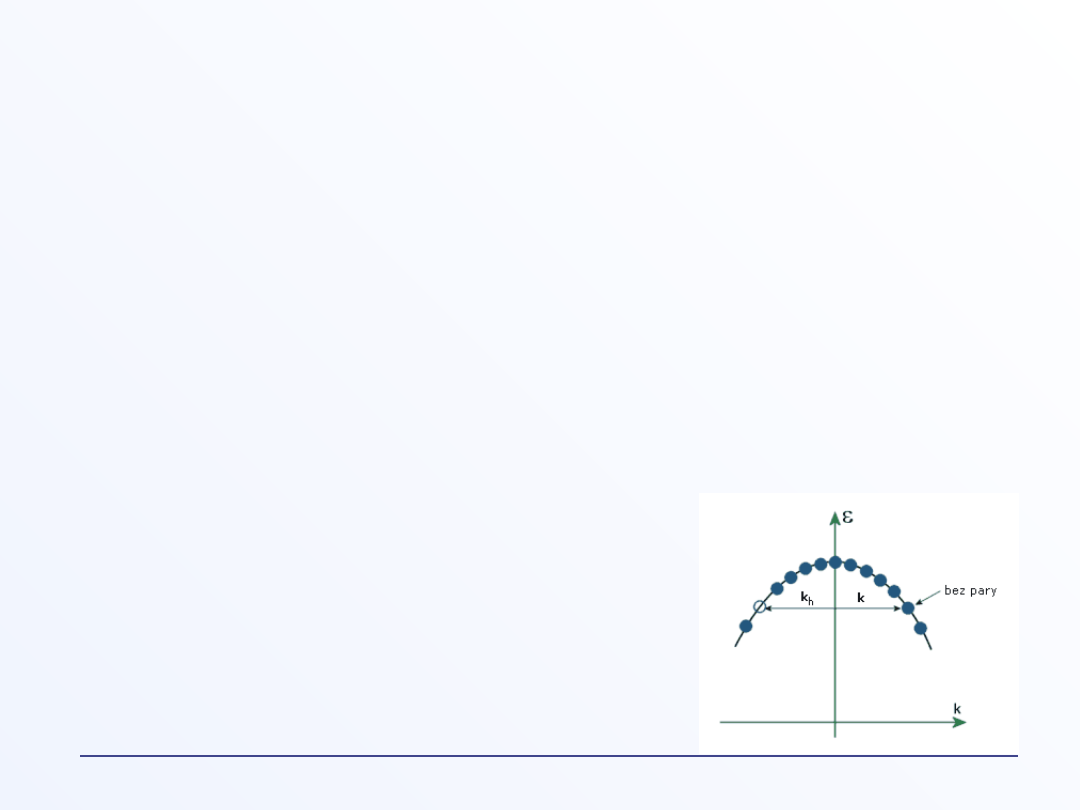
Koncepcja dziury

Elektron opisany funkcją Blocha jest naładowaną cząstką
biegnącą przez kryształ. W obrazie klasycznym reprezentuje
prąd elektryczny. W paśmie całkowicie zapełnionym każdemu
elektronowi o wektorze falowym k towarzyszy elektron z -k i
odpowiednie przyczynki do prądu znoszą się.

Jeśli zabierzemy jeden elektron, to wytworzymy

dziurę, ale prąd będzie wówczas różny od zera:

( )

0

N

i

i

J

e

= -

=

�

V

( )

( )

N

i

i

J

e

e

e

= -

- -

=

�

j

j

V

V

V

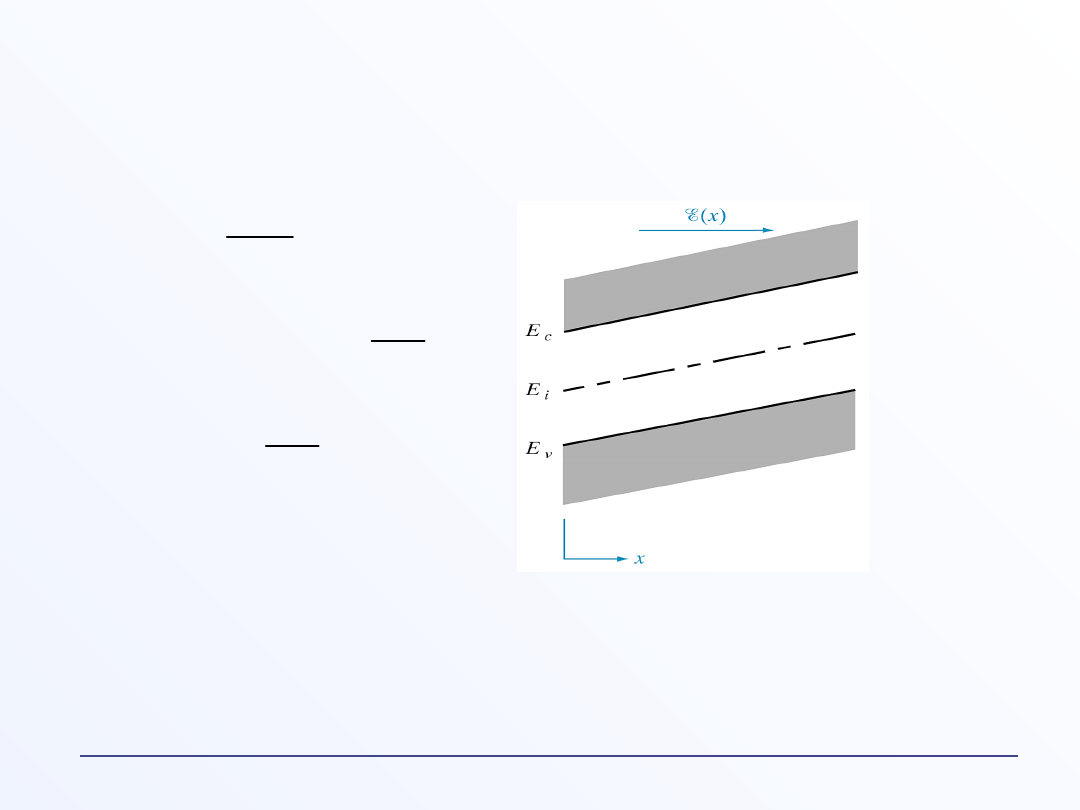
Półprzewodnik w polu elektrycznym

( )

( )

( )

( )

p

p

dE

F

dx

dV

e x

e

dx

dV

x

dx

x

const c

V

cx

E

cex

e

e

e

=-

-

=- -

=-

=

= �

=-

�

=

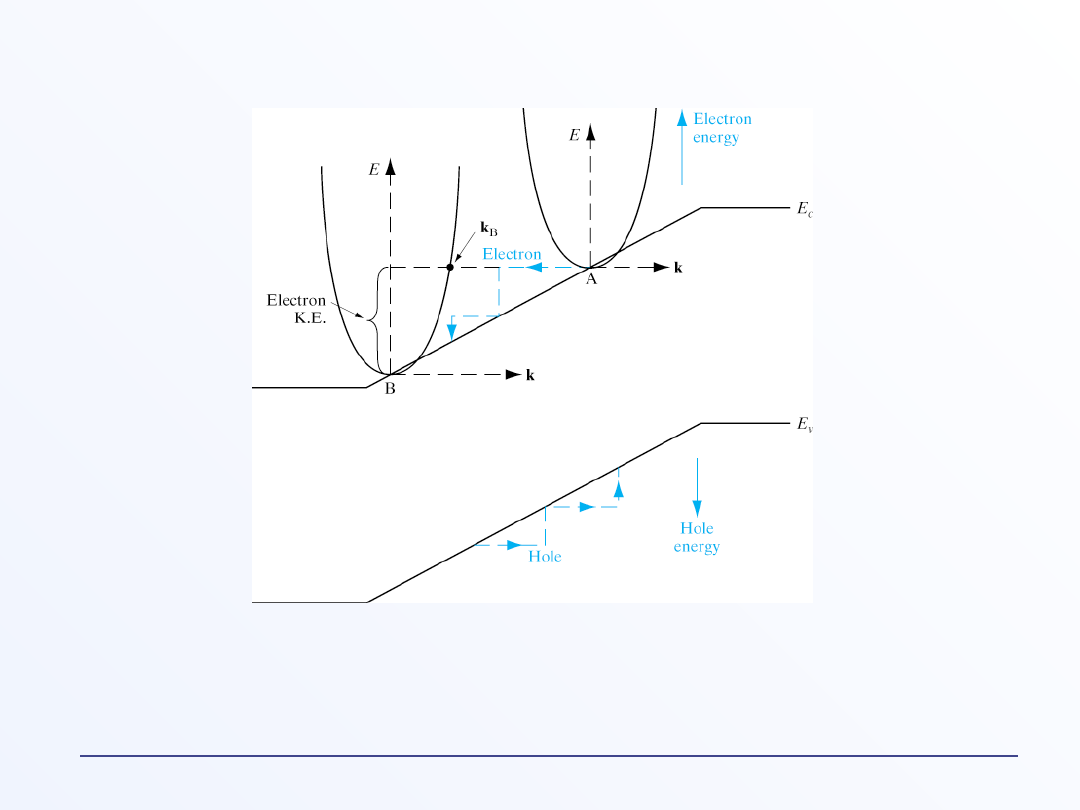
E(k) i E(x) w polu elektrycznym

h

e

E

E

=-

Energia elektronu rośnie w górę diagramu, dziury – w dół;

Elektrony poruszają się w lewo, dziury w prawo.

Zabranie jednego elektronu jest równoważne wzrostowi energii
o .
Zatem dziura ma energię:

e

E

h

e

E

E

=-

Masa efektywna

Dla elektronu swobodnego:

Dla elektronu w sieci krystalicznej:

Dla dziury w sieci krystalicznej:

2

2

2

d E

dk

m

=

h

2

2 2

2

2

p

k

E

m

m

=

=

h

2

dE

k

dk

m

=

h

1

2

2

2

d E

m

dk

-

�

�

= �

�

�

�

h

1

2

2

2

*

n

d E

m

dk

-

�

�

= �

�

�

�

h

h

e

E

E

=-

h

e

= -

k

k

*

*

p

n

m

m

=-

p

e

=

v

v

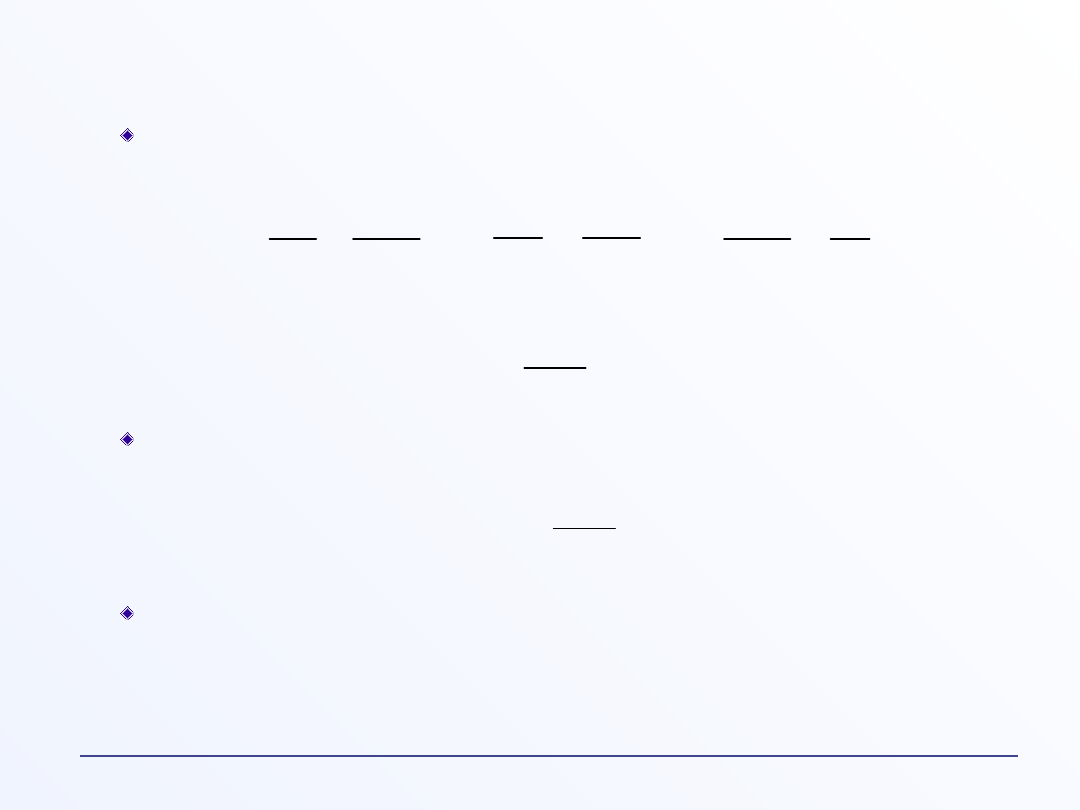
Krzywizna pasma decyduje o masie efektywnej

-

Masa efektywna elektronów w GaAs w pasmie przewodnictwa jest

mniejsza w punkcie  (silna krzywizna - duża )

niż w punkcie L lub X (słabsza krzywizna - mała )

- Elektrony przy wierzchołku pasma walencyjnego mają masę
efektywną ujemną (dziury – dodatnią).

2

2

dk

E

d

2

2

dk

E

d

Prawdziwe (m

e

, m

h

) i efektywne masy (m

e

*,

m

h

*)

- masy efektywne są różne dla różnych półprzewodników
- prawdziwe – równe masie elektronu swobodnego
- dlaczego ?

dp/dt =d(mv)/dt = F : II zasada dynamiki Newtona !

F = F

wewn

+ F

zewn

F

zewn

= siła zewnętrzna

F

wewn

= siła wynikająca z istnienia potencjału periodycznego; to

oddziaływanie prowadzi do zależności E(k), z której z kolei wynika
masa efektywna, m

e

*.

dp/dt =d(m

e

*

v)/dt = F

zewn

Zatem elektron zachowuje się w polu siły

zewnętrznej, tak jakby miał nową masę, m

e

*.

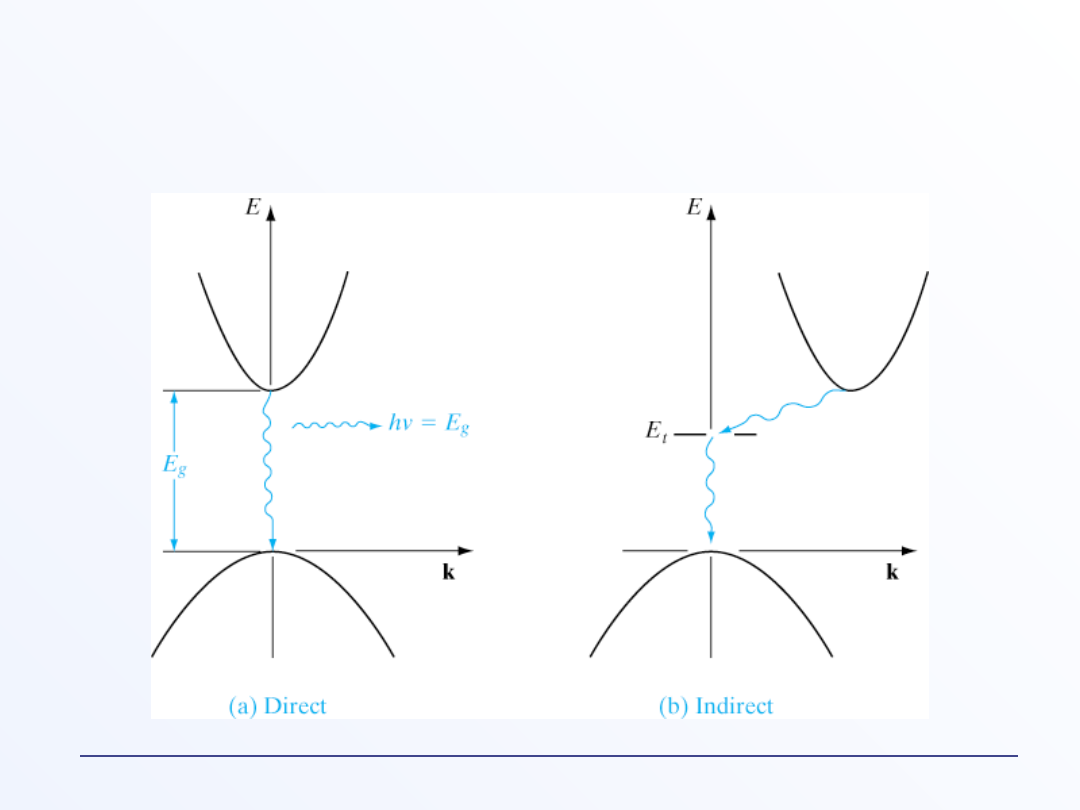
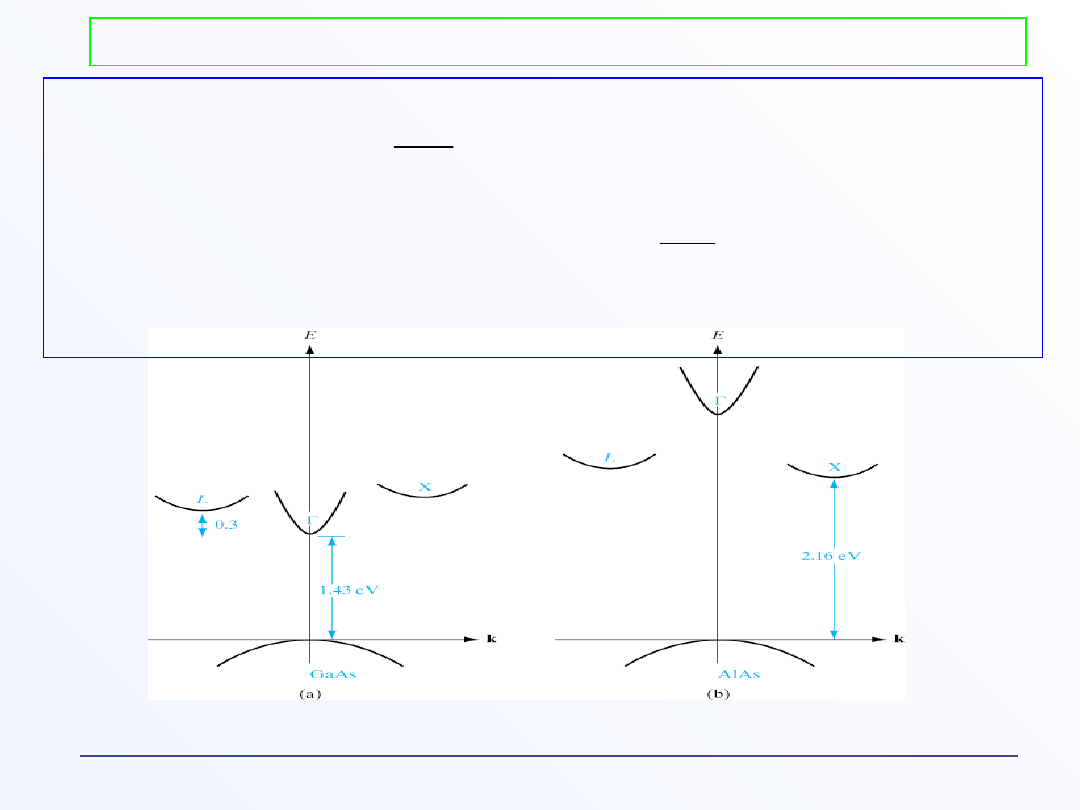
Półprzewodniki z prostą i skośną przerwą

wzbronioną

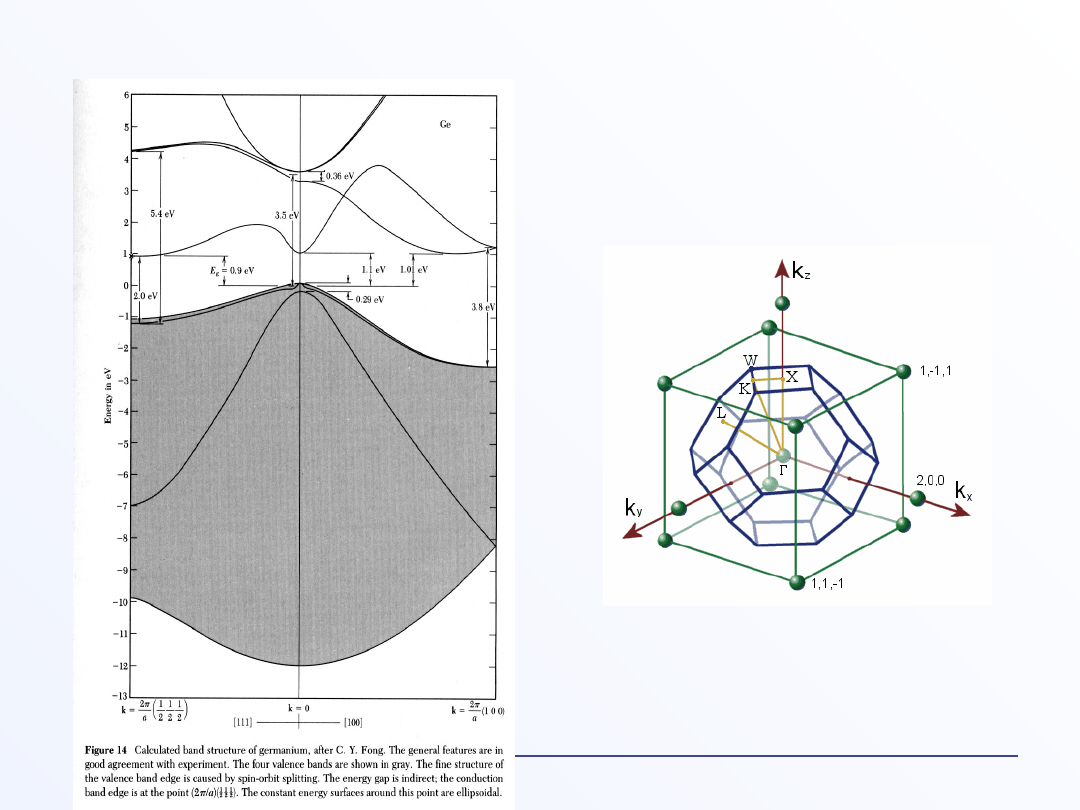
E(k) (relacja dyspersji) dla germanu

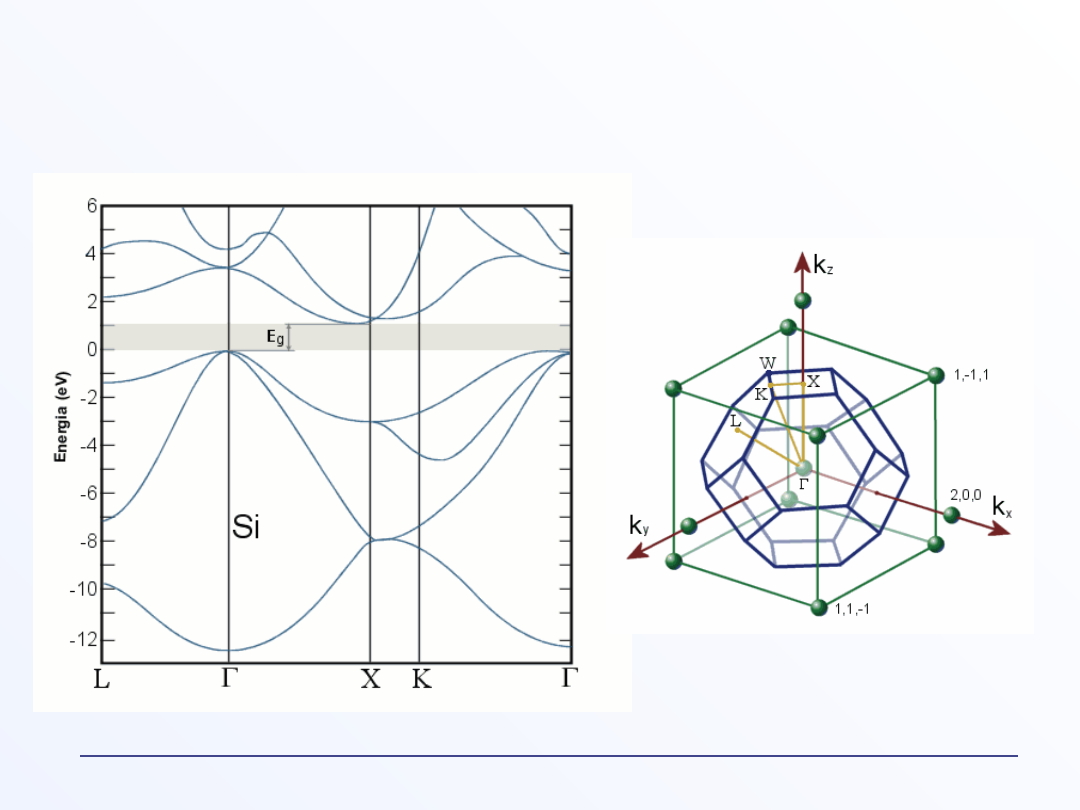
E(k) (relacja dyspersji) dla krzemu

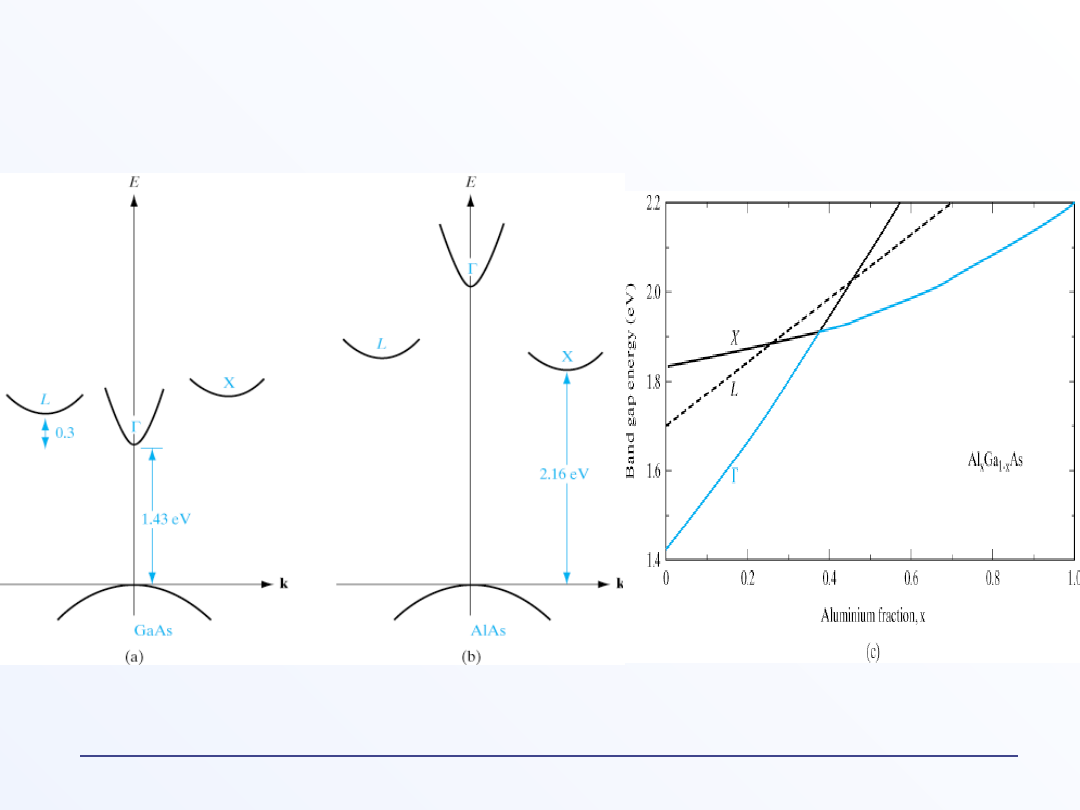
E(k) (relacja dyspersji) dla GaAs i AlAs

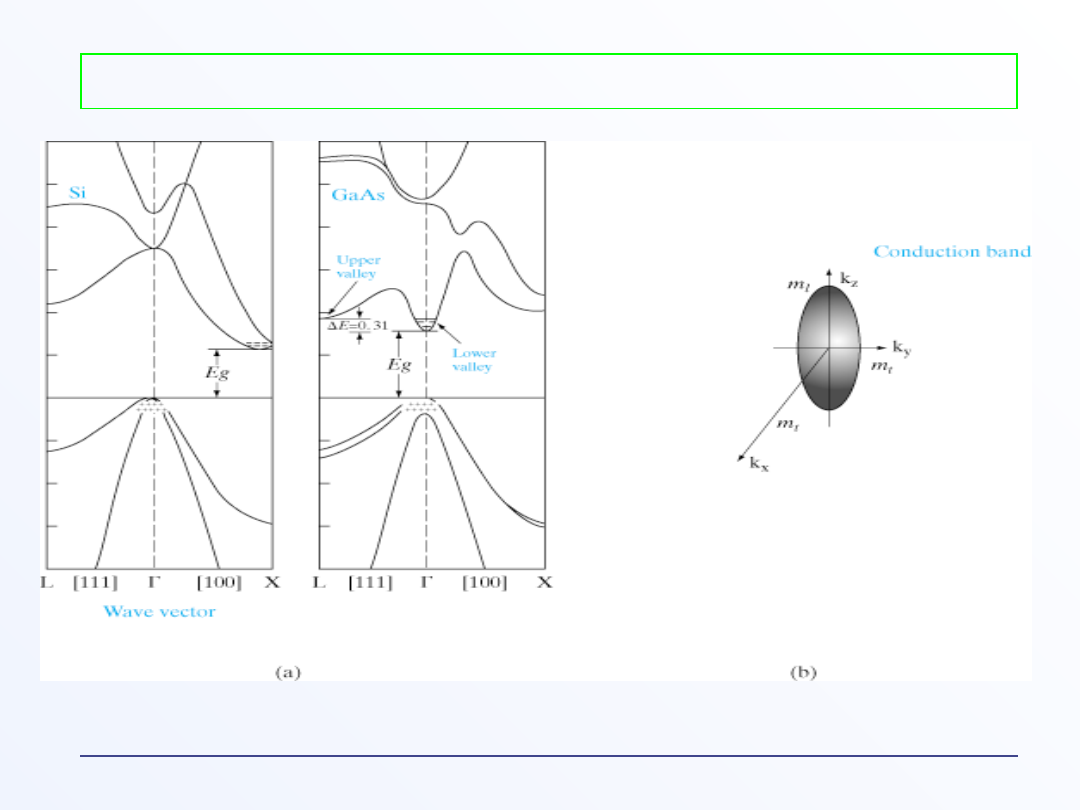
a) E(k) dla Si i GaAs
b)Powierzchnia stałej energii dla Si, w pobliżu 6 minimów pasma
przewodnictwa w kierunku punktu X..

E(k) dla Si i GaAs)