Metody ab initio 

uwzględniające 

korelację elektronów

Wykład 9

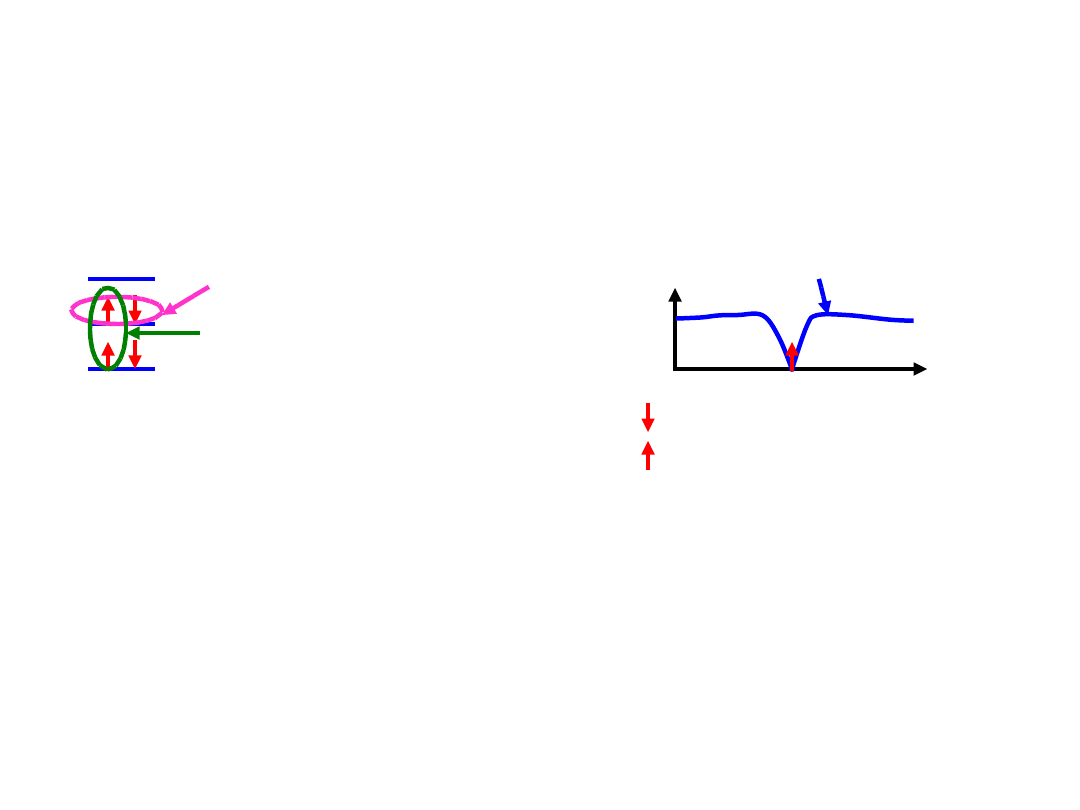
Elektrony wzajemnie  się unikają

Energia korelacji 

elektronów

korelacja elektronów
 na jednym orbitalu

korelacja elektronów
 z jednakowym spinem

x

(x)

Prawdopodobieńst
wo znalezienia 
drugiego elektronu

Dla   : dziura coulombowska 
(korelacyjna)
Dla   : dziura Fermi’ego 
(wymienna) 

Energia korelacji elektronów

E

corr

 = E

exact

  E

HF

Metoda Hartree-Focka nie uwzględnia korelacji 

elektronów.

2

Po co nam ta korelacja?

Metoda HF daje co prawda ok. 99% energii całkowitej 
układu ale:



 tylko dzięki korelacji elektronowej gazy szlachetne się przyciągają, w 

zgodzie z doświadczeniem (skraplanie gazów)



 wg. metody HF cząsteczka F

2

 w ogóle nie powinna istnieć (a istnieje, 

dośw. energia wiązania 38 kcal/mol)



 około 

połowy

 energii oddziaływania wielkich cząsteczek (np. białek) 

pochodzi z efektu czysto korelacyjnego



 metoda RHF w opisie dysocjacji wiązania daje wyniki bardzo złe, 

jakościowo

 niezgodne z doświadczeniem

3

Dlaczego energia Hartree-

Focka jest za wysoka? 

W metodzie HF używa się funkcji falowej w postaci 

jednego wyznacznika Slatera.



oddziaływania elektronów są traktowane w sposób uśredniony



każdy elektron „czuje” uśrednione odpychanie wynikające ze 

statycznego, uśrednionego rozkładu gęstości pozostałych N-1 
elektronów. 



chwilowe, dynamiczne oddziaływanie elektronów jest 

zaniedbane



to powoduje, że energia oddziaływanie coulombowskiego jest 

za wysoka. 



uwzględnione jest jedynie oddziaływanie wymienne, pomiędzy 

elektronami z tym samym spinem

4

Dwa rodzaje korelacji 

elektronów

1. Dynamiczna korelacja :

●

bierze pod uwagę fakt, że elektrony poruszają się w 
taki sposób aby się do siebie zanadto nie zbliżać

●

to ciągłe, dynamiczne oddziaływanie elektronów 
jest zaniedbywane w metodzie HF

2. Statyczna korelacja

:

●

w układach z wieloma stanami rezonansowymi 
elektrony mogą się unikać przez zajmowanie 
różnych „stanów rezonansowych”

●

pojedynczy wyznacznik Slatera reprezentuje tylko 1 
stan rezonansowy, więc metoda HF nie może 
opisywać tego typu korelacji

●

nazywana też bywa korelacją nie-dynamiczną

5

Dynamiczna korelacja

metoda HF nie uwzględnia tego efektu, co jest 
konsekwencją stosowania średniego rozkładu gęstości elektronowej 
i jednego wyznacznika Slatera jako funkcji falowej

Rozwiązanie:

zmienić formę funkcji falowej

2. Metoda zaburzeń

1. Wielowyznacznikowa funkcja falowa

nazywane metodami
post -HF

●

elektrony mają ładunek elektryczny i poruszają się w przestrzeni

●

ich ruch jest skorelowany więc się wzajemnie unikają

6

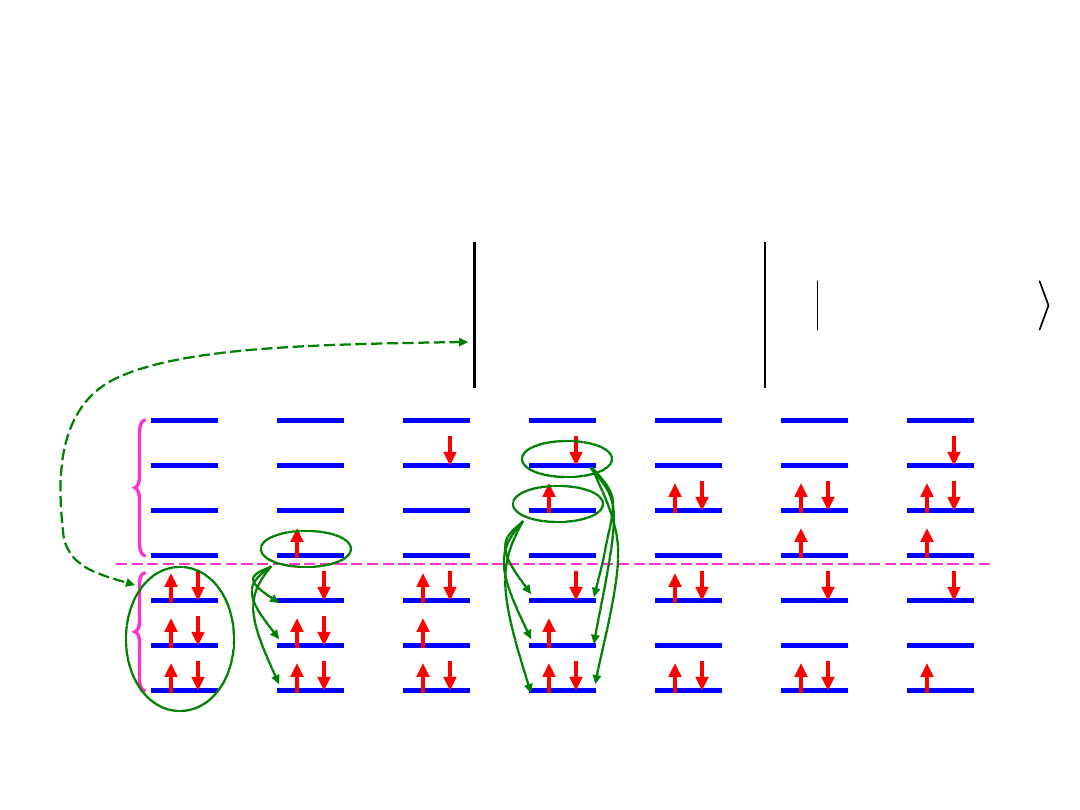
Zamieniamy zajęte orbitale w wyznaczniku uzyskanym w 
metodzie HF przez niezajęte orbitale

Wyznaczniki Slatera stanów 

wzbudzonych

Pu

st

e

Z

a

ję

te

HF

S-typ

S-typ

D-typ

D-typ

T-typ

Q-typ



i

(x

1

)



j

(x

1

)  …



k

(x

1

)



i

(x

2

)



j

(x

2

)  …



k

(x

2

)

…        …    …    …



i

(x

N

)



j

(x

N

)  …



k

(x

N

)

(x

1

, x

2

, …, x

N 

) = (1/N!)

½

  

N

N









1

2

1







7



































0

D

T

T

T

D

D

S

S

S

HF

0

...

i

i

i

a

a

a

a

a

1. Jak dużo i które wyznaczniki uwzględnić? 

2. Jak zbudować te wyznaczniki?

3. Jak wyznaczyć współczynniki rozwinięcia a

i

?

Metody ab initio uwzględniające 

korelację  elektronów:

Metoda oddziaływania konfiguracji (

CI

)

Wielokonfiguracyjna metoda SCF (

MCSCF

)

Wielociałowy rachunek zaburzeń Möllera-Plesseta (

MPn

)

Metoda sprzężonych klasterów (

CC

)

Wielowyznacznikowa funkcja

8

Metoda oddziaływania konfiguracji CI

Wyznaczniki Slatera w wielowyznacznikowej funkcji falowej są 

wzięte z metody Hartree-Focka



‘zamiana’ orbitali odpowiada 
wzbudzaniu elektronów do stanów o 
wyższej energii



możemy  stosować tylko pojedyncze 
wzbudzenia

e

n

e

rg

ia

zajęte

wirtualne

oznaczane i, j,…

oznaczane r, s, …



możemy używać podwójnych 
wzbudzeń



możemy wzbudzać elektrony ze 
wszystkich N zajętych orbitali na 2K-N 
wirtualne orbitale



to daje całą serię nowych 
wyznaczników Slatera



ważne: orbitale molekularne 
Hartree-Fock, 



i

 

 

w tej metodzie 

nie są ponownie 
optymalizowane

N

j

r

r

i

Φ













1



N

s

r

rs

ij

Φ













1



9

10

W jaki sposób dodanie „wzbudzonych” wyznaczników 
Slatera 
polepsza funkcję falową? 

1. mamy więcej parametrów wariacyjnych

• więcej parametrów funkcji próbnej w metodzie 

wariacyjnej oznacza że otrzymamy rozwiązanie o niższej 
energii

2. włączenie dodatkowych 
orbitali daje elektronom 
więcej możliwości unikania 
się

Na przykład anion allilowy::



1



2



3

• wzbudzenie pozwala 

jednemu z elektronów na 
orbitalu 

2

 uciec na 

orbital 

3

Metoda CI



















rs

ij

zaj

j

i

wirt

s

r

rs

ij

r

i

zaj

i

wirt

r

r

i

HF

Φ

a

Φ

a

Φ

a

Φ

0

HF

Φ

3

2

Φ

Jak wielowyznacznikowa funkcja jest używana w 

praktyce?

Pełne oddziaływanie konfiguracji :

• nazywane również  ‘pełne CI’

• zawiera pełen zestaw wzbudzeń z N zajętych orbitali na 

wszystkie możliwe kombinacje 2K – N wirtualnych orbitali

• to dałoby „dokładną”  funkcję falową dla 

wybranej bazy funkcyjnej 

• liczba wyznaczników Slatera jest gigantyczna !

• koszt obliczeniowy jest olbrzymi i obliczenia metodą 

pełnego CI wykonywane są jedynie dla bardzo małych 
cząsteczek. 

)

2

(

2

(

)

2

(

0

N

K

rs

N

ij

zaj

N

j

i

wirt

N

K

s

r

N

K

rs

N

ij

rs

ij

zaj

j

i

wirt

s

r

rs

ij

r

i

zaj

i

wirt

r

r

i

HF

CI

Pełeł

Φ

a

Φ

a

Φ

a

Φ

a

























































)!

2

(

)!

2

(

N

K

K

n

ów

wyznacznik





Metoda CI

11

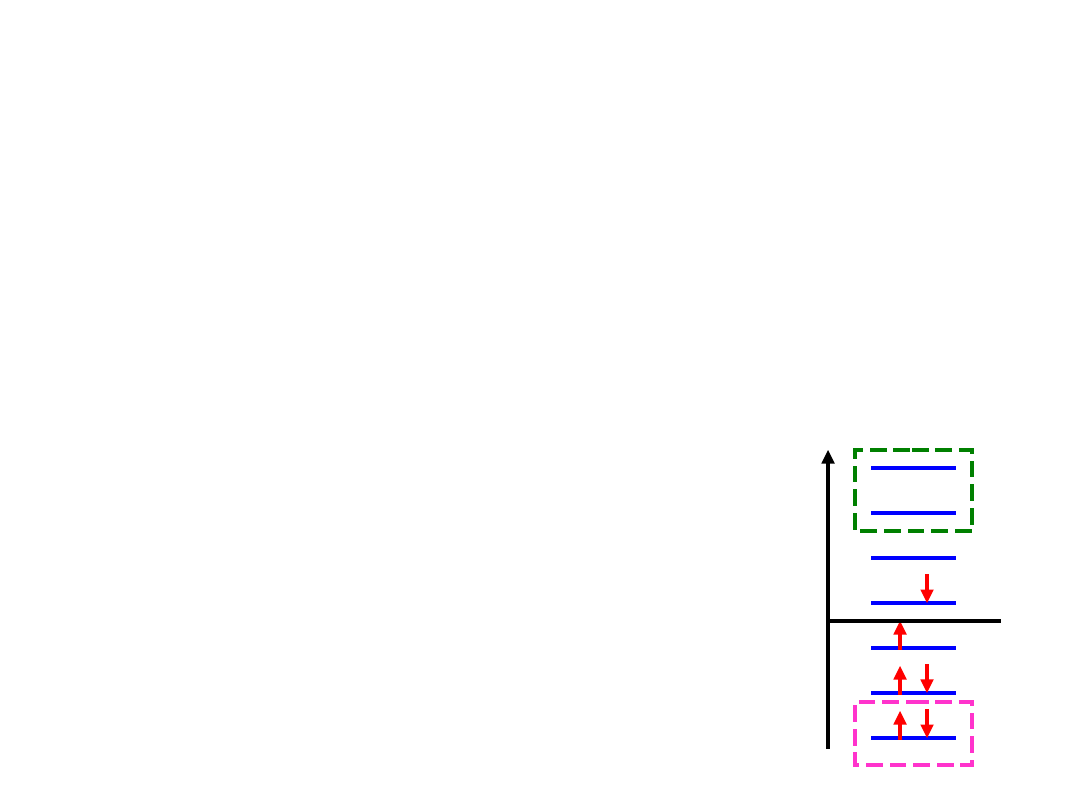
Ile wyznaczników w metodzie 

CI? 

Liczba wyznaczników rośnie dramatycznie!



H

2

O z bazą 6-31G(d) : 10 elektronów i 38 orbitali

Całkowita # wyznaczników = 38! / 10!(38-10)!
Całkowita # pojedynczo wzbudzonych (S = ½) wyznaczników = 310

7



H

2

O z bazą 6-311G(2d,2p) : 10 elektronów i 82 orbitali

Całkowita # wyznaczników = 82! / 10!(82-10)!
Całkowita # pojedynczo wzbudzonych (S = ½) wyznaczników = 110

11



C

2

H

4

 z bazą 6-31G(d) : 16 elektronów i 76 orbitali

Całkowita # wyznaczników = 76! / 16!(76-16)!
Całkowita # pojedynczo wzbudzonych (S = ½) 
wyznaczników = 310

14

Można brać pod uwagę tylko wzbudzenia
 z wysokoenergetycznych orbitali zajętych
 na niskoenergetyczne orbitale wirtualne, 
a pozostałe orbitale „zamrozić”. (ang.  

Frozen core

 and 

frozen virtuals 

approximations)

E

0

O: 

1s

2

 

2s

2 

2p

4 

3s

0 

3p

0 

3d

0 

4s

0 

4p

0

Wielowyznacznikowa 

funkcja próbna

Im więcej wyznaczników, tym lepsza funkcja falowa



































0

D

T

T

T

D

D

S

S

S

HF

0

...

i

i

i

a

a

a

a

a

Wielkość bazy funkcyjnej

Granica bazy = 
najlepszy 
jednoelektronowy 
orbital 
cząsteczkowy

Liczba 
wyznacznikó
w

Pełne rozwinięcie CI = 
Najlepsza wieloelektronowa 


Kompletne rozwinięcie CI = 
Dokładne rozwiązanie 
elektronowego równania 
Schrödingera

HF

Minimalna baza 
funkcyjna

14

Obcięte rozwinięcie CI



bierzemy pod uwagę tylko pewne rodzaje wzbudzeń



najbardziej popularny typ tej metody  - włączamy 

wszystkie pojedyncze i podwójne wzbudzenia (CISD)



zmniejsza to znacznie liczbę wyznaczników w 

funkcji falowej i czas obliczeń



w ten sposób ciągle jesteśmy w stanie obliczyć ~95 

% energii  korelacji



ta metoda ma problem z 

konsystencją 

rozmiarową



wzbudzenia podwójne są najważniejsze przy 

obliczaniu energii korelacji

rs

ij

zaj

j

i

wirt

s

r

rs

ij

r

i

zaj

i

wirt

r

r

i

HF

CISD

Φ

a

Φ

a

Φ

a

Φ















0

15

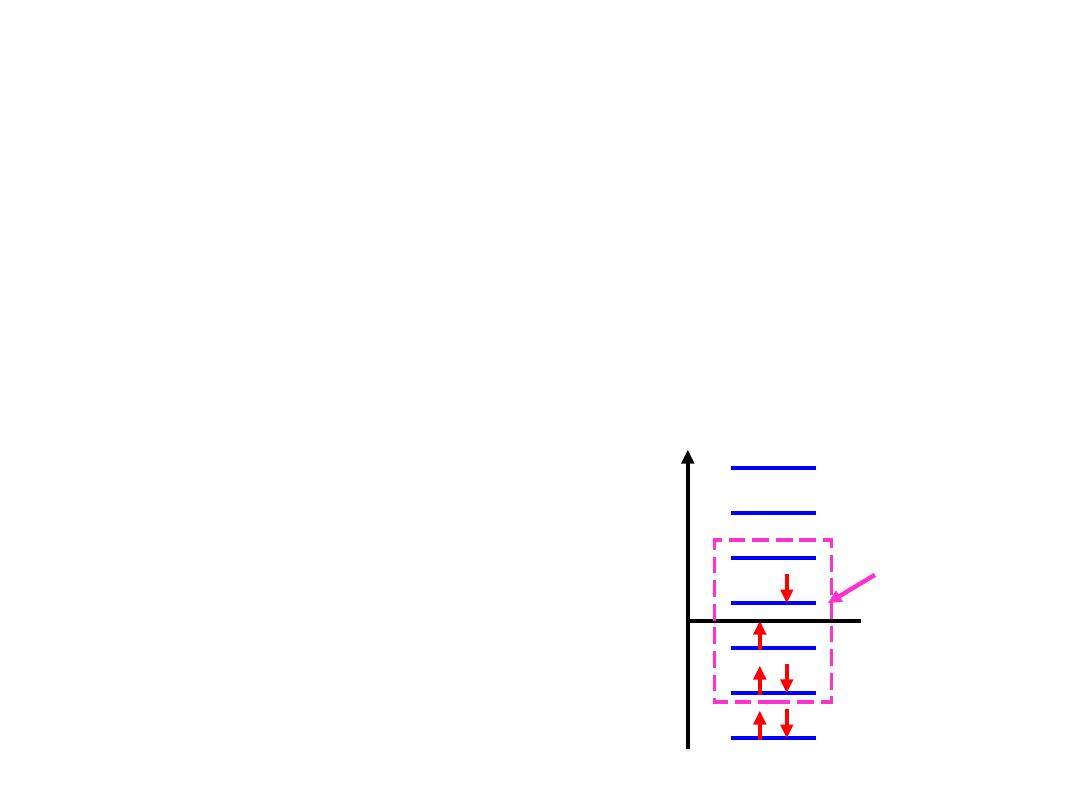
Konsystencja rozmiarowa

energia dwóch oddalonych cząsteczek powinna być sumą ich energii 

(

)

( )

( )

E A B

E A

E B

=

+

L

• obcięta metoda CI 

nie jest konsystentna rozmiarowo

A

• na przykład podwójne wzbudzenia dla układu A B

• bierzemy pod uwagę wszystkie podwójne wzbudzenia 

z zajętych orbitali A na wirtualne orbitale A

B

• bierzemy pod uwagę wszystkie podwójne wzbudzenia 

z zajętych orbitali B na wirtualne orbitale B

A

B

50 Å

• niektóre wzbudzenia są z zajętych orbitali A na wirtualne orbitale A
• niektóre wzbudzenia są z zajętych orbitali B na wirtualne orbitale B

• niektóre wzbudzenia są z zajętego orbitalu A na wirtualny 

orbital A 

i jednocześnie 

z zajętego orbitalu B na wirtualny orbital B

W obciętej metodzie CI więcej 

wzbudzeń występuje w układzie A+B 

niż w sumie oddzielnych cząsteczek 

A i B

Wielokonfiguracyjna metoda 

SCF MC SCF

• Wariacyjnie optymalizowane są nie tylko współczynniki 

rozwinięcia a

i

, ale również optymalizowane są orbitale 

molekularne () tak jak w metodzie HF. To znaczy 

optymalizowane są współczynniki 

pomiędzy

 jak i 

wewnątrz

 

.

• Które orbitale molekularne wziąć pod uwagę – zależy od 

chemii danego problemu.



































0

D

T

T

T

D

D

S

S

S

HF

0

...

i

i

i

a

a

a

a

a

• Ważnym przypadkiem 

szczególnym  metody MC SCF 
jest metoda CAS SCF 

(ang. 

Complete active space self-consistent 
field

) są to obliczenia MCSCF z 

pełnym rozwinięciem CI dla 
wybranej przestrzeni atywnej

[n,m]-CASSCF:  n elektronów na m 

orbitalach aktywnej przestrzeni

E

0

Pełne-CI 
rozwinięcie
dla 
przestrzeni 
atywnej

16

MC SCF vs. HF



Zarówno w metodzie HF jak i w MC SCF optymalizuje się 
orbitale molekularne (MO).



Metoda HF używa 

pojedynczego 

wyznacznika, natomiast MC 

SCF używa 

wielu

 wyznaczników.



Bardziej zaawansowane metody korelacji elektronów budują 
funkcję falową na podstawie:

●

zoptymalizowanych orbitali molekularnych HF — 

jedno-

referencyjne

 metody, np. CI.

●

zoptymalizowanych orbitali molekularnych MCSCF— 

wielo-

referencyjne

 metody, np. MR-CI.



Kiedy jedno-wyznacznikowa metoda HF zawodzi nie dając 
poprawnego opisu warto spróbować MC SCF.

O

+

O



O

O

O

O

17

Metody Sprzężonych 

Klasterów 

(ang. Coupled Cluster)

18

jeżeli weźmiemy pod uwagę odpowiednie wzbudzenia, możemy 

używać obciętej metody CI i jednocześnie zachować konsystencję 

rozmiarową

operator klasterowy :

1

2

3

ˆ ˆ ˆ

ˆ

ˆ

N

T T T T

T

= + + + +

L

generuje wszystkie 
pojedyncze wzbudzenia

generuje wszystkie podwójne wzbudzenia

generuje wszystkie N-te wzbudzenia

Klasterowa funkcja falowa :

2

3

2

3

2

3

ˆ

1

1

2

2

1

2

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

1

2! 3!

2! 3!

2! 3!

T

HF

N

N

HF

N

T

T

T

T

T

T

e

T

T

T

�

�

Y = Y

= + +

+

+ + +

+

+ + +

+

+

Y

�

�

�

�

L

L

L

2

ˆ

occ virt

HF

rs

rs

ij

ij

i j r s

T

a

<

<

Y

=

Y

��

19

Metoda Sprzężonych Klasterów

Obcięta klasterowa funkcja falowa :

2

ˆ

1

1

2

ˆ

ˆ

ˆ

1

2!

T

HF

HF

T

e

T

T

�

�

Y = Y

= + +

+

Y

�

�

�

�

• zawiera wszystkie możliwe pojedyncze i podwójne wzbudzenia

• polega na działaniu dwukrotnym operatora T

1 

na funkcję falową

• daje dodatkowe wzbudzenia których brakuje w metodzie CISD 

i co sprawia, że nie jest konsystentna rozmiarowo

2

1

ˆ

2!

HF

T

Y

obecnie metoda CCSD(T) jest „złotym standardem’” 

kwantowych metod obliczeniowych

• zawiera wszystkie możliwe pojedyncze, podwójne 

i niektóre potrójne wzbudzenia

• funkcja falowa zawiera olbrzymią liczbę wyznaczników Slatera. 

• jest bardzo wymagająca obliczeniowo, daje się ją 

zastosować do układów mających najwyżej 20 atomów

Należy podzielić dokładny Hamiltonian H na dwie części : 
niezaburzony H

0

 i zaburzenie H

′.

Teoria zaburzeń

H = H

0

 + H′

H

0

 

i

0

 = E

i

0 



i

0

,

      

(i = 0, 1, 2, ...)

Dla niezaburzonego  Hamiltonianu H

0

, rozwiązanie równania 

Schrodingera jest znane:

Dla dokładnego Hamiltonianu H, rozwiązanie równania 
Schrodingera można otrzymać jako:

H 

i

 = 



i

 

i



i

 = 

i

0 

+ 

i

1

 + 

i

2

 

+ ...



i

 = E

i

0 

+ E

i

1

 + E

i

2

 

+ ...

Poprawki

Poprawki mogą być wyrażone w zależności H

′

, 

i

0

 i E

i

0

.

Hamiltonian H dokładnego elektronowego równania 
Schrödingera został podzielony na dwie części:

Teoria zaburzeń Møllera-Plesseta

H = H

0

 + H′

Poprawki 

n-tego 

rzędu nazywane są metodą MP

n

 :

H 

i

 = 



i

 

i



i

 = 

i

0 

+ 

i

1

 + 

i

2

 

+ ...



i

 = E

i

0 

+ E

i

1

 + E

i

2

 

+ ...

Poprawki



 

Metoda MP2 uwzględnia około 

90% 

energii korelacji



 Nie jest to metoda wariacyjna 

― energia obliczona może być 

niższa niż energia dokładna.

 

Nie zawsze im większe n tym dokładniejszy wynik

.

Suma operatorów Focka F

i

Wszystkie pozostałe 
składniki  ― 
potencjał 
fluktuacyjny

22

Korelacja statyczna

strukturę elektronową niektórych układów najlepiej opisywać 

jako kombinację kilku stanów (myślimy o strukturach 

rezonansowych)

• pozwala to elektronom rozszerzyć się bardziej i zmniejszyć 

odpychanie między nimi. 

• nazywa się to korelacją statyczną

Przykład:

• nie ma nic wspólnego z skorelowanym ruchem 

elektronów. 

 system trimetylenometan multipletowość 1

H

H

H

H

H

H

• 4 elektrony 

• 2 zdegenerowane 

orbitale 
walencyjne

e

n

e

rg

ia



1



2



3



4

• 4 orbitale  

jak rozdzielić elektrony 

?

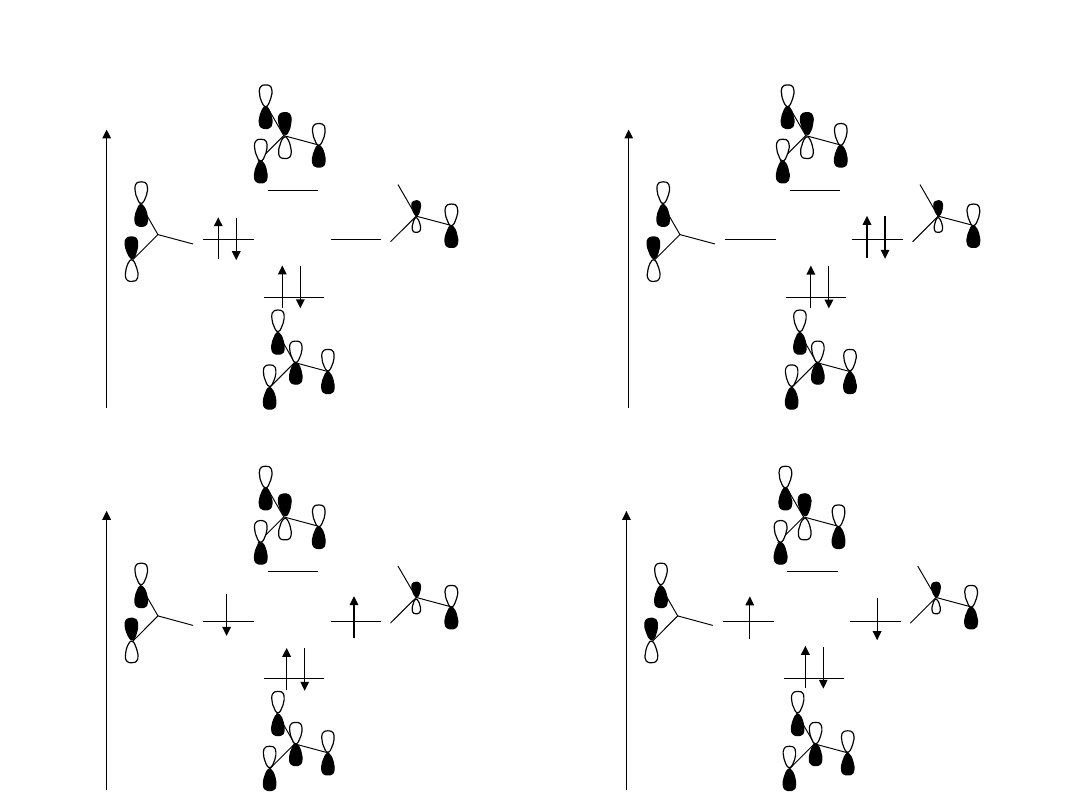
23

e

n

e

rg

ia

e

n

e

rg

ia

e

n

e

rg

ia

e

n

e

rg

ia

możliwe konfiguracje elektronowe
każda ma własny wyznacznik Slatera

Korelacja statyczna

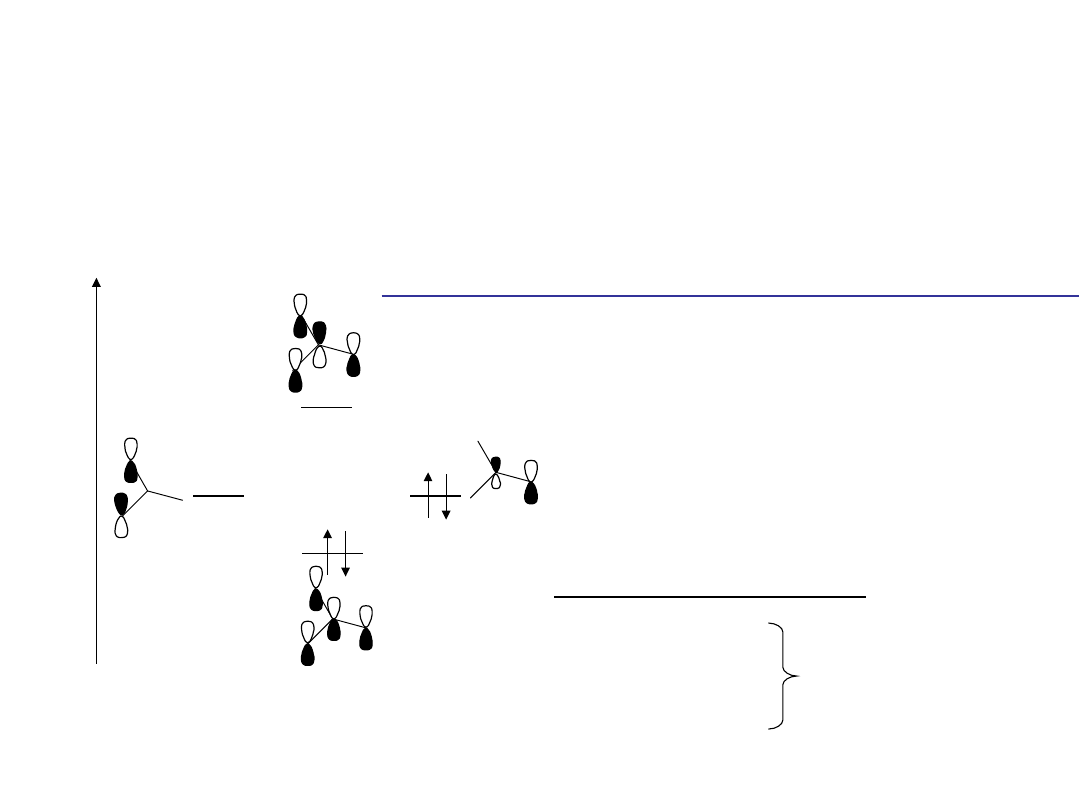
24

które wyznaczniki Slatera wziąć pod uwagę?

Metody wielo-referencyjne

• chcemy włączyć wszystkie wyznaczniki Slatera odpowiadające 

odpowiednim stanom rezonansowym w wielowyznacznikowej 
funkcji falowej

e

n

e

rg

ia



1



2



3



4

CAS SCF (metoda kompletnej przestrzeni aktywnej)

• wybierz liczbę orbitali, które mogą 

być obsadzane w różnych stanach 
rezonansowych

• wybierz ile elektronów może się 

znajdować na tych orbitalach

• uwzględnij wszystkie możliwe 

kombinacje

np. trimetylenomethan:

4  elektrony

4  orbitale

20 możliwych 
kombinacji

• Kiedy jednowyznacznikowa metoda HF zawodzi należy 

spróbować metody MC SCF

• Obcięte CI nie jest 

konsystentne rozmiarowo

, i zwykle 

nie jest polecane o ile inne metody są dostępne. 

• Metody MPn i CC nie radzą sobie dobrze z 

elektronowymi 

stanami wzbudzonymi

, znacznie lepsze są MC SCF i CI 

(zwłaszcza MR-CI).

• Metoda CCSD(T) z odpowiednia bazą funkcyjną może 

osiągnąć 

dokładność chemiczną 

 (~ 1kcal/mol).

Którą metodę wybrać? 

HF

MP2

CISD, CCSD

MP4

CCSD(T)

Dokładność i koszt obliczeń

Pytania

1.Co to jest energia korelacji i jaki metodami można ją 

obliczać? 

2.Co to są wzbudzone wyznaczniki Slatera typu S i typu D? 

3. Jaka jest główna różnica pomiędzy metodami CI i 

MCSCF

?

4. Co to znaczy, że metoda jest jedno-refencyjna, o co że 

wielo-referencyjna?