Wykład 3: Rozkłady

zmiennych losowych

Biometria i

Biostatystyka

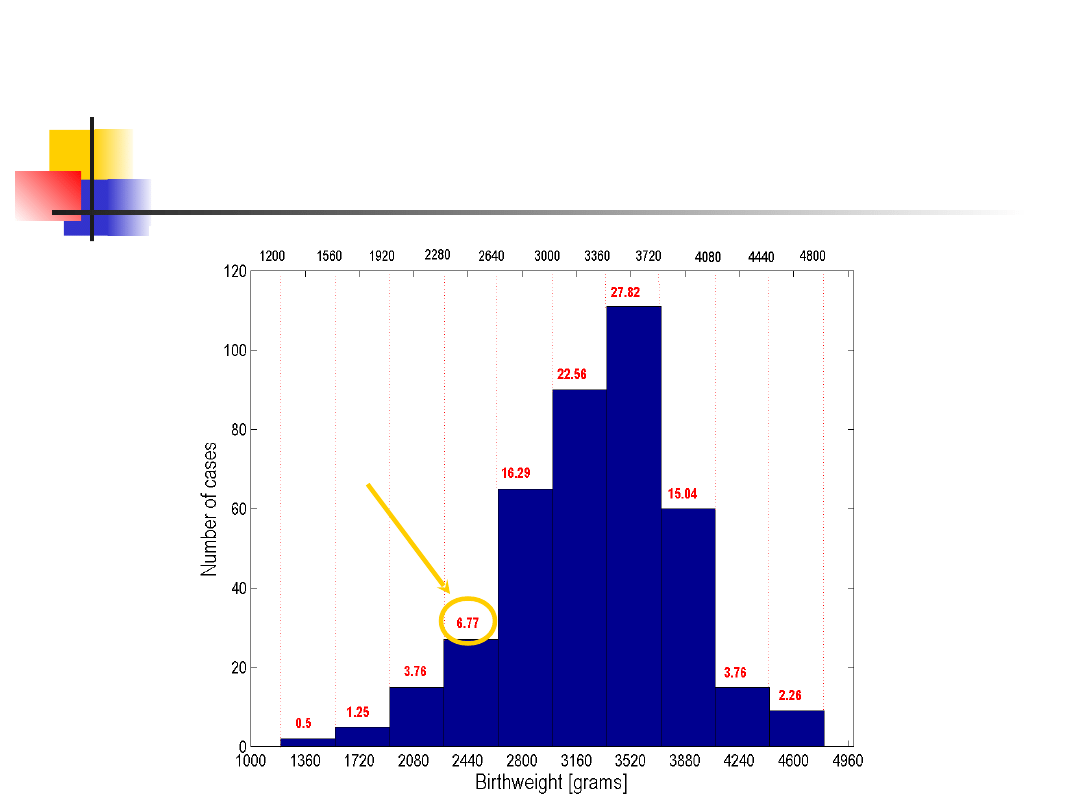
Rozkład częstości

Jakie jest prawdopodobieństwo, że waga

urodzeniowa dziecka będzie w przedziale klasy

2440g?

p=0.0677

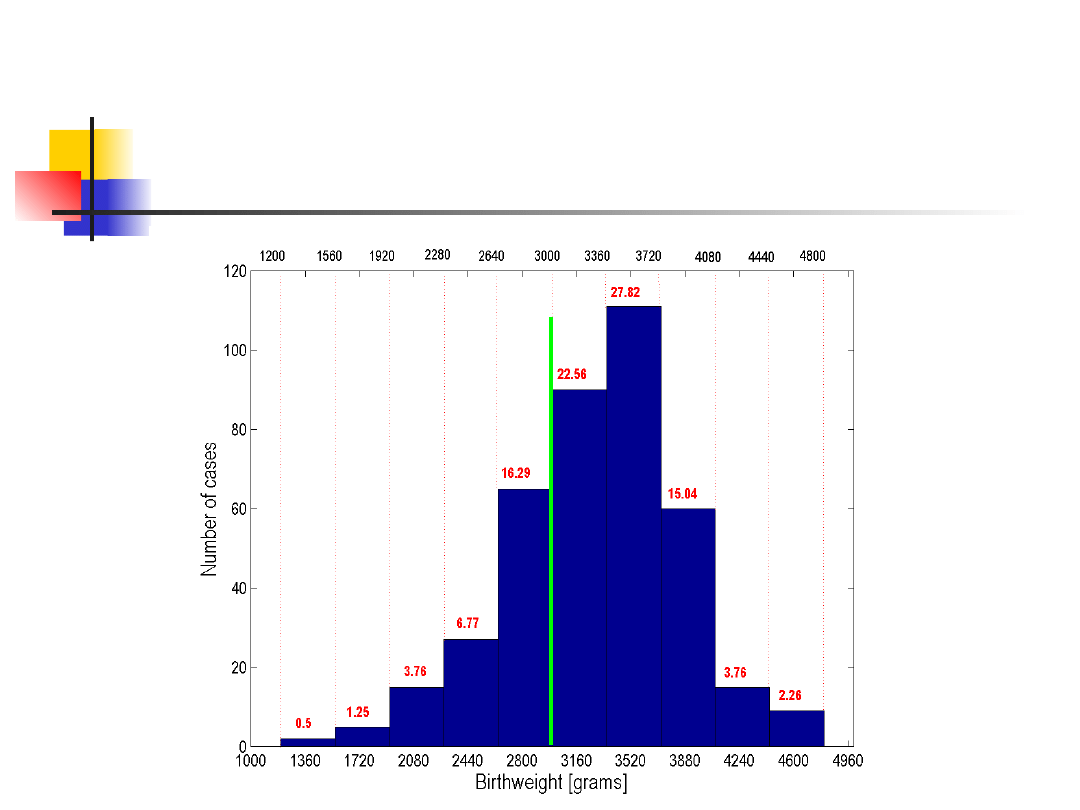
Rozkład częstości

Waga urodzeniowa < 3000 g

Jaki procent dzieci?

28.57%

Rozkład częstości

Dokonujemy pomiaru wagi urodzeniowej
dziecka losowo wybranego z nieznanej populacji
i ma ono wagę urodzeniową równą 6000 g.

Czy ta nieznana populacja ma rozkład częstości
taki sam jaka nasza?

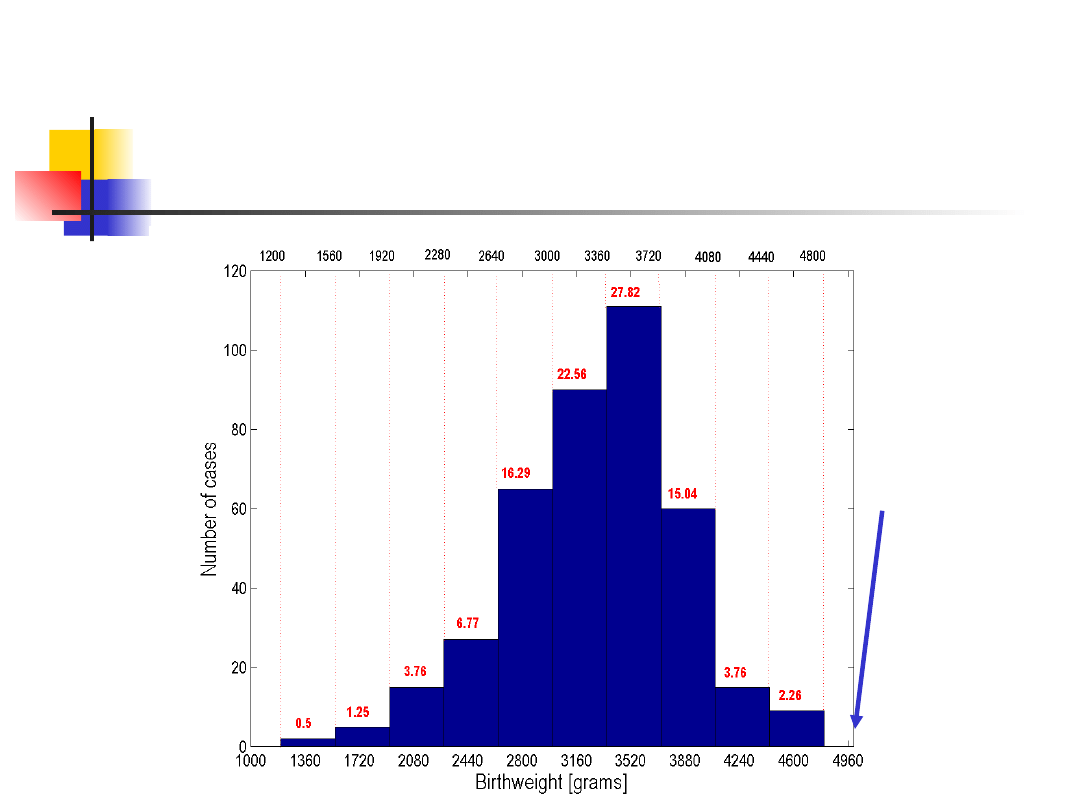
Rozkład częstości

P(Birthweight~6000) →
0

Rozkład częstości

Najprawdopodobniej odrzucilibyśmy hipotezę, iż

nieznana populacja ma rozkład taki sam jak

nasza, gdyż prawdopodobieństwo przynależności

do klasy 6000 g jest prawie równe zeru (mniejsze

niż 10

-12

).

Wnioskowalibyśmy, że nieznana populacja ma

prawdopodobnie inną wartość średnią i/albo

wariancję.

Rozkład częstości

Wykorzystaliśmy empiryczny rozkład częstości
do oceny i wnioskowania o przynależności do
naszej populacji. W wielu przypadkach
będziemy się jednak opierać nie na rozkładach
empirycznych, lecz na teoretycznych
założeniach. Często mamy przesłanki, by
założyć iż dane powinny mieć ściśle określony
rozkład częstości. Jeśli nasze przypuszczenia się
nie potwierdzą eksperymentalnie, powinniśmy
ponownie zastanowić się nad tymi założeniami i
wnioskami wyciągniętymi na ich podstawie.

Funkcja gęstości
prawdopodobieństwa

Rozkład teoretyczny częstości
nazywamy

funkcją gęstości

prawdopodobieństwa.

Funkcje gęstości dyskretnych
zmiennych losowych



Rozkład dwumianowy



Rozkład geometryczny



Rozkład hipergeometryczny



Rozkład Poissona

Rozkład dwumianowy



Załóżmy, że przeprowadzono n
niezależnych eksperymentów lub prób (n
jest znaną liczbą) i w każdej z prób wynik
jest

„sukcesem”

z prawdopodobieństwem

p

a

„porażką”

z prawdopodobieństwem

q=1-p

.



Całkowita liczba sukcesów w n próbach, X,
jest zmienną losową o rozkładzie
dwumianowym o parametrach n i p.

Rozkład dwumianowy

Prawdopodobieństwo, że X=k, oznaczane

jako p(k), można wyliczyć w następujący
sposób:



Konkretna konfiguracja niezależnych k
sukcesów i (n-k) porażek wystąpi z
prawdopodobieństwem



Całkowita liczba takich konfiguracji

k

n

k

p

p



 )

1

(













k

n

k

n

k

k

n

k

p

p

k

n

k

n

p

p

k

n

k

p



























)

1

(

)!

(

!

!

)

1

(

)

(

Rozkład dwumianowy

Wartość średnia to:

p

n

)

x

(

p

x

)

X

(

E

x

n

1

i

i

i













Wariancja:

q

p

n

)

x

(

p

)

x

x

(

)

X

(

Var

s

n

1

i

i

2

i

2

















Rozkład dwupunktowy
(Bernoulliego) z
prawdopodobieństwem sukcesu
p

Zmienna losowa przyjmuje tylko dwie różne wartości a i b (np.
pojedynczy rzut monetą, n=1). Oznaczmy prawdopodobieństwo
przyjęcia wartości a przez p, a prawdopodobieństwo przyjęcia
wartości b przez q = 1 – p. Kodując zmienną losową w postaci:
‘sukces’ – wartość a – jako 1 a ‘porażka’ – wartość b – jako 0
wyliczamy wartość średnią:

p

p

1

q

0

)

x

(

p

x

)

X

(

E

x

1

0

i

i

i



















natomiast wariancja znaleziona być może jako:

pq

)

q

p

(

pq

p

q

q

p

p

)

p

1

(

q

)

p

0

(

s

2

2

2

2

2

























Rozkład dwumianowy

Wartość średnia i wariancja
rozkładu dwumianowego przy n
próbach to

n-krotność

wartości

średniej i wariancji w pojedynczej
próbie (rozkładu Bernoulliego)

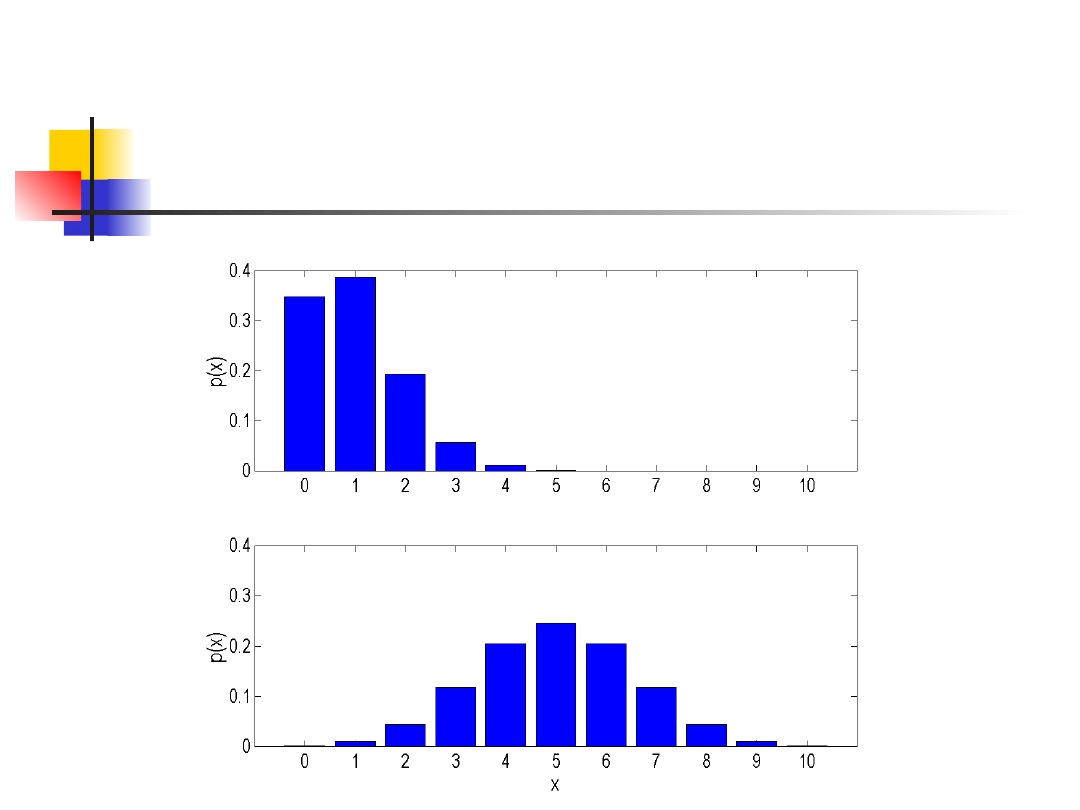
Rozkład dwumianowy

n=10, p=0.5

n=10, p=0.1

Przykład



Choroba Tay-Sachsa jest rzadką chorobą

o podłożu genetycznym ujawniającą się

w wieku niemowlęcym i

wczesnodziecięcym. Jeśli matka i ojciec

są nosicielami mutacji genetycznej Tay-

Sachsa, ich dziecko będzie chore z

prawdopodobieństwem równym 0.25.



Jeśli taka para ma czworo dzieci, jaka jest

funkcja rozkładu prawdopodobieństwa

liczby dzieci chorych w rodzinie?

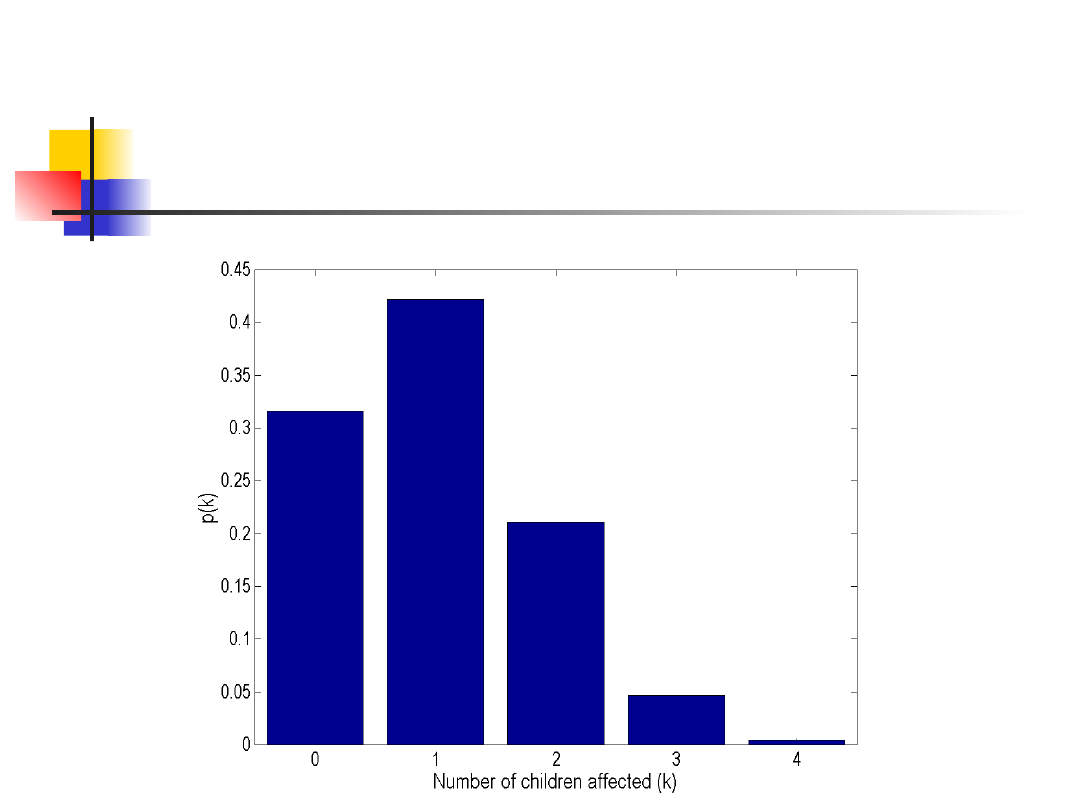
Rozkład dwumianowy

0.31
6

0.42
2

0.21
1

0.04
7

0.00
4



Rozkład geometryczny jest również
konstruowany w oparciu o próby
Bernoulliego, jednak ich liczba jest
nieskończona. W każdej próbie sukces
występuje z prawdopodobieństwem p a
zmienna losowa X określa liczbę całkowitą
prób do osiągnięcia pierwszego sukcesu –
czas oczekiwania na sukces. Aby X=k,
musi być k-1 porażek a potem sukces w k-
tej próbie. Stąd

Rozkład geometryczny

p

p

k

p

k 1

)

1

(

)

(







Rozkład geometryczny

Wartość oczekiwana:

p

X

E

1

)

(



a wariancja:

2

1

)

(

p

p

X

Var





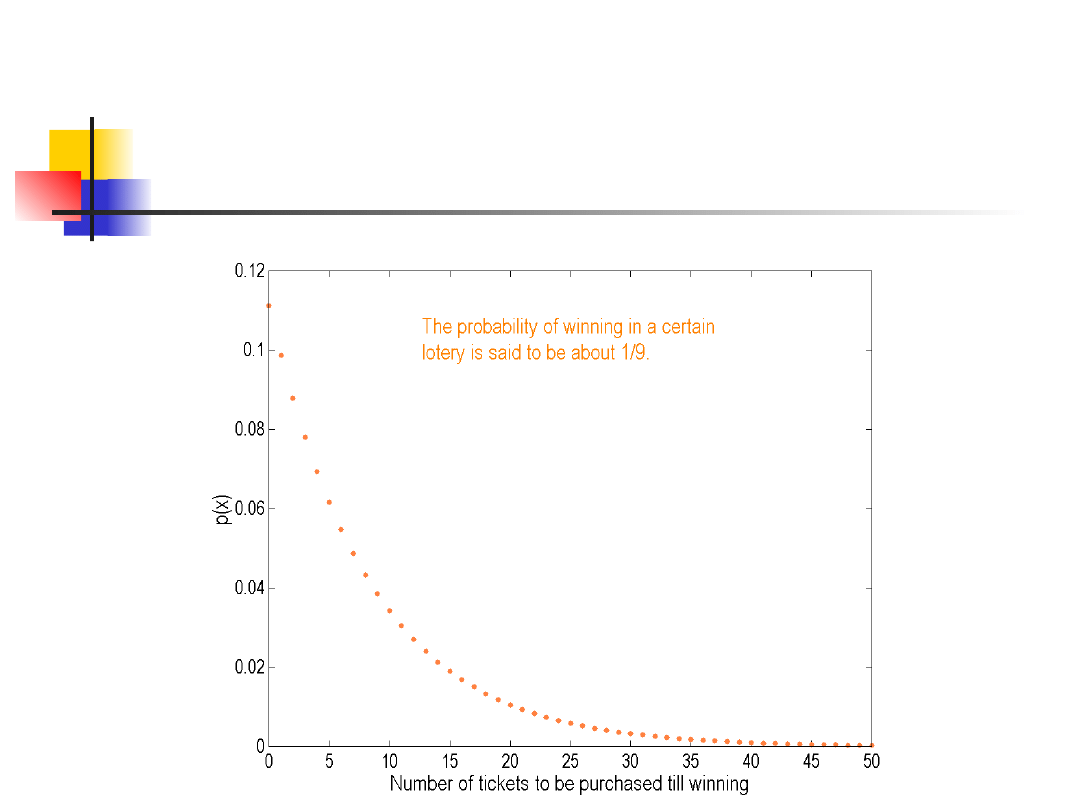
Przykład

Rozkład
hipergeometryczny



Załóżmy, że w słoju znajduje się n kul,
przy czym r jest czarnych a n-r białych.



Zmienna losowa X określa liczbę kul
czarnych spośród m wylosowanych w
jednej próbie (losowanie bez zwracania).
Zatem















































m

n

k

m

r

n

k

r

k

p

k

X

P

)

(

)

(

Rozkład
hipergeometryczny



Wybranie jednej kuli czarnej możliwe jest z
prawdopodobieństwem r/n.



Prawdopodobieństwo wybrania drugiej jest już inne i
wynosi (r-1)/(n-1). Byłoby r/n gdybyśmy losowali ze
zwracaniem.



Rozkład dwumianowy jest poprawnym modelem tylko
dla przypadków losowań ze zwracaniem i/lub
nieskończenie dużych liczności n.

Rozkład
hipergeometryczny

Wartość średnia:

mp

)

X

(

E



Wariancja:

1

n

m

n

mpq

)

X

(

Var







Przykład

Załóżmy, iż w pudle jest 100
dyskietek, z których 20 jest
uszkodzonych.
Wybieramy losowo 10 dyskietek.
Jakie jest prawdopodobieństwo, że
co najwyżej dwie będą uszkodzone?
n=100 r=20 m=10

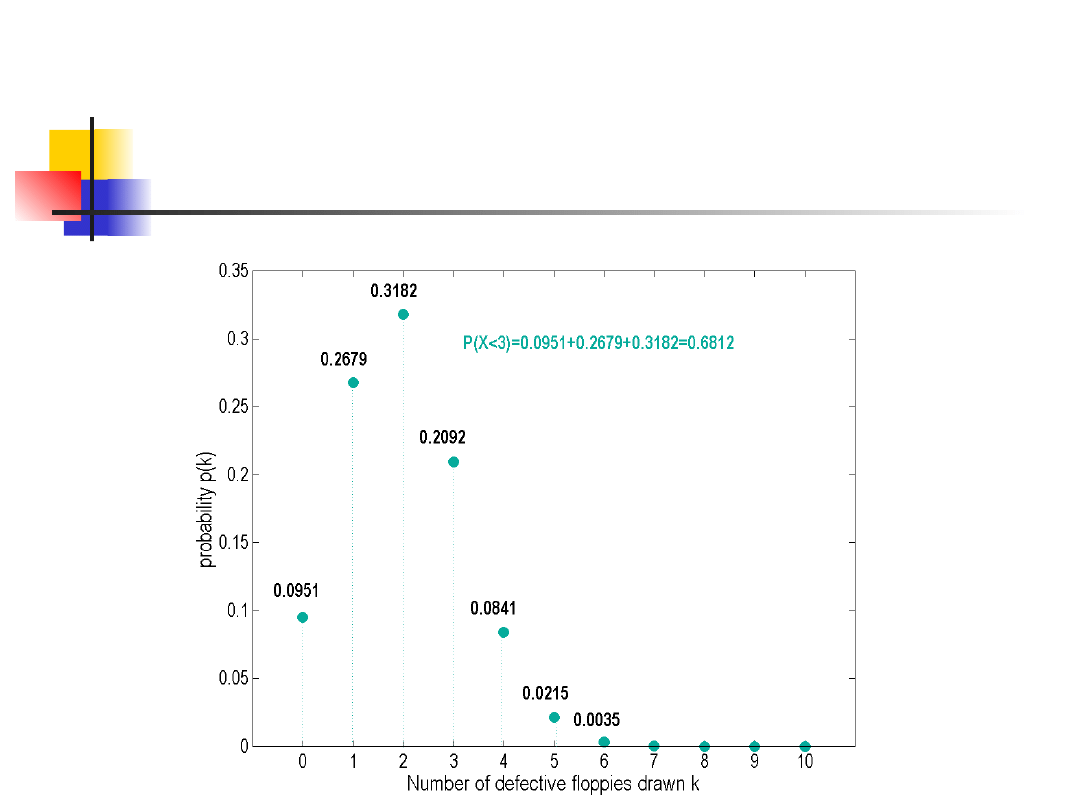
Przykład

Rozkład Poissona



Rozkład Poissona jest aproksymacją
rozkładu dwumianowego, gdy liczba
prób n jest bardzo duża oraz
prawdopodobieństwo sukcesu w każdej
próbie, oznaczone symbolem p, jest
bardzo małe. Oznaczmy np=λ, wówczas

!

)

(

k

e

k

p

k









Rozkład Poissona



Zazwyczaj uznaje się, że warunki te są spełnione
gdy p<0.1 oraz np<5.



Jeśli tak jest, zmienna będzie miała rozkład
Poissona pod warunkiem, że każde wystąpienie
‘sukcesu’ jest niezależne od pozostałych
‘sukcesów’ – dlatego sprawdzając zgodność z
rozkładem Poissona pośrednio możemy
sprawdzić niezależność prób.

Rozkład Poissona

Wartość oczekiwana:





)

(X

E

Wariancja:





)

(X

Var

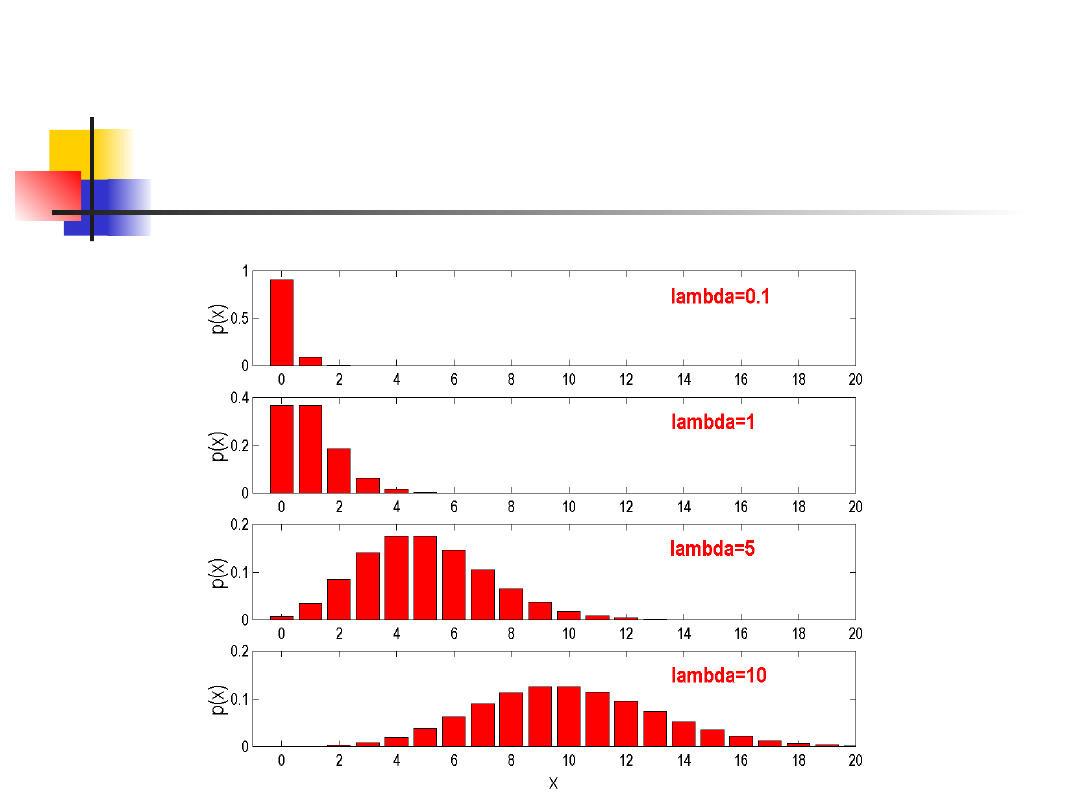
Rozkład Poissona

Przykład



Rzucamy kostką 100 razy i zliczamy liczbę
wystąpień dwóch szóstek równocześnie –
zmienna losowa X.



Zmienna losowa ma rozkład dwumianowy,
przy czym n=100 a p=1/36=0.0278.



Ponieważ n jest duże a p bardzo małe
(np<5), możemy przybliżyć rozkład
dwumianowy rozkładem Poissona z
λ=np=2.78

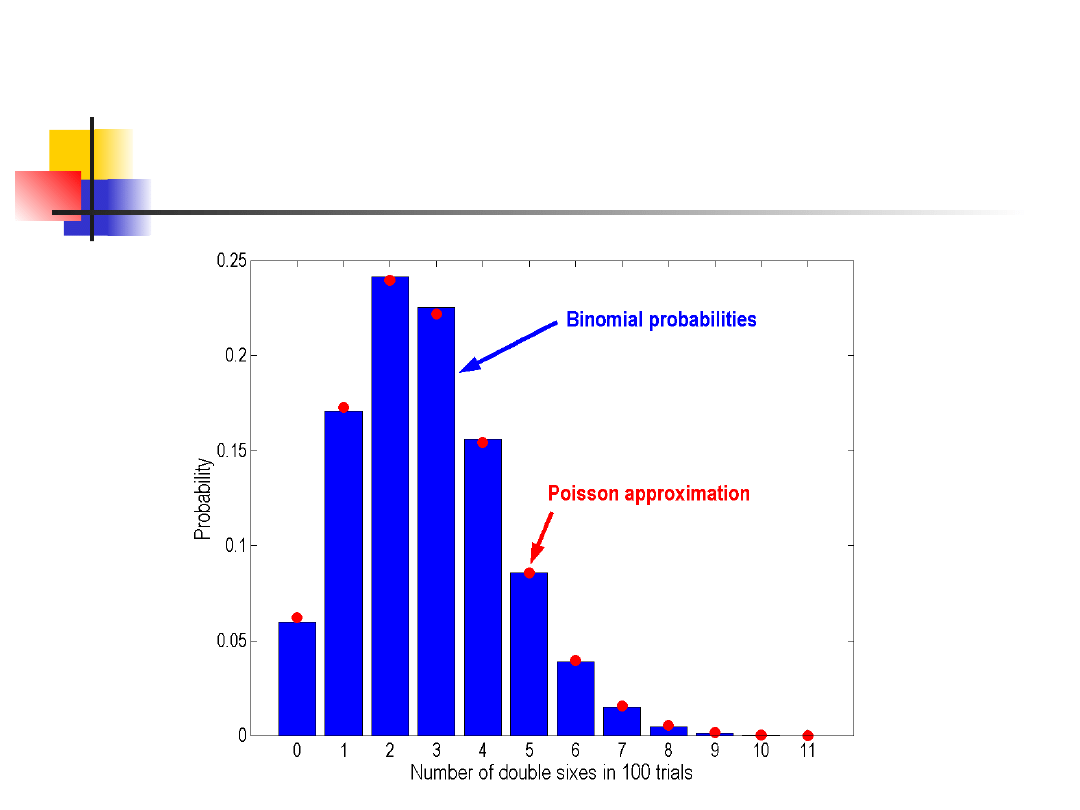
Przykład

Inny przykład



Załóżmy, iż liczba telefonicznych
zgłoszeń awarii ma rozkład Poissona o
parametrze lambda równym λ=0.5 na
godzinę.



Jakie jest prawdopodobieństwo, że nie
będzie żadnych zgłoszeń w ciągu 5
godzin?

Inny przykład



Zatem liczba zgłoszeń w przeciągu 5
godzin ma rozkład Poissona z
parametrem ω=5λ=2.5.
Prawdopodobieństwo, iż nie będzie
żadnych zgłoszeń w ciągu 5 godzin
można obliczyć jako

082

.

0

)

0

(

5

.

2









e

k

p

!

)

(

k

e

k

p

k









Rozkłady ciągłych zmiennych
losowych

W przypadku ciągłych

zmiennych losowych rolę

funkcji częstości przejmuje

funkcja gęstości f(x), która ma

następujące właściwości:













1

)

(

and

0

)

(

dx

x

f

x

f









b

a

dx

x

f

b

X

a

P

)

(

)

(

oraz

Rozkłady ciągłych zmiennych
losowych



Rozkład równomierny
(jednostajny)



Rozkład wykładniczy



Rozkład normalny

Funkcja gęstości rozkładu
równomiernego



Dystrybucja, która przyjmuje stałą wartość w
całym zakresie zmienności zmiennej losowej
jest nazywana rozkładem równomiernym.



Ma ona postać























x

b

for

b

x

a

for

a

b

a

x

for

X

P

0

1

0

)

(

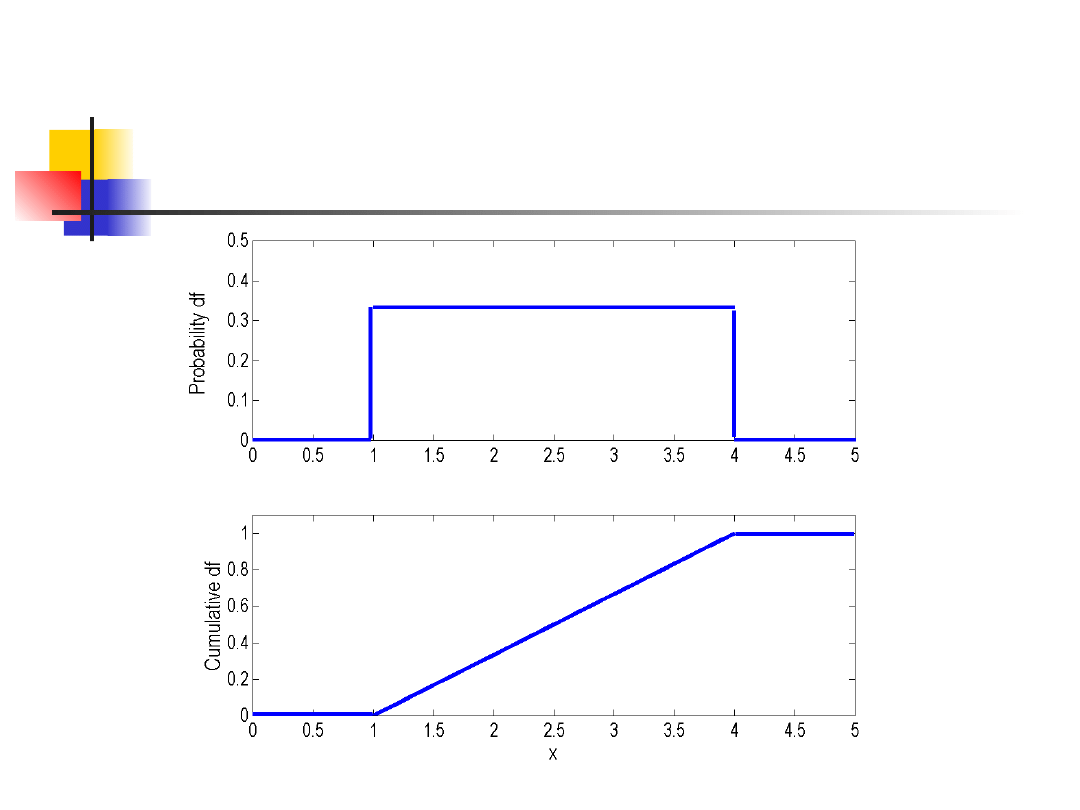
Rozkład równomierny













x

dx

x

f

x

X

P

X

F

)

(

)

(

)

(

Dystrybuant
a

Funkcja gęstości rozkładu
wykładniczego



Zmienna losowa o rozkładzie wykładniczym
używana jest najczęściej do opisu czasu
życia maszyn, części czy osób bądź innych
organizmów żywych. Używa się jej również
do opisu czasu oczekiwania do
zrealizowania zamówienia.



Funkcja gęstości prawdopodobieństwa (pdf)
dla konkretnej wartości parametru λ:

0

and

x

0

for

,

)

(

1



















x

e

x

f

Rozkład wykładniczy

Wartość oczekiwana:

wariancja:





















0

1

)

(

dx

e

x

X

E

x





2

0

2

1

)

(

























dx

e

x

X

Var

x

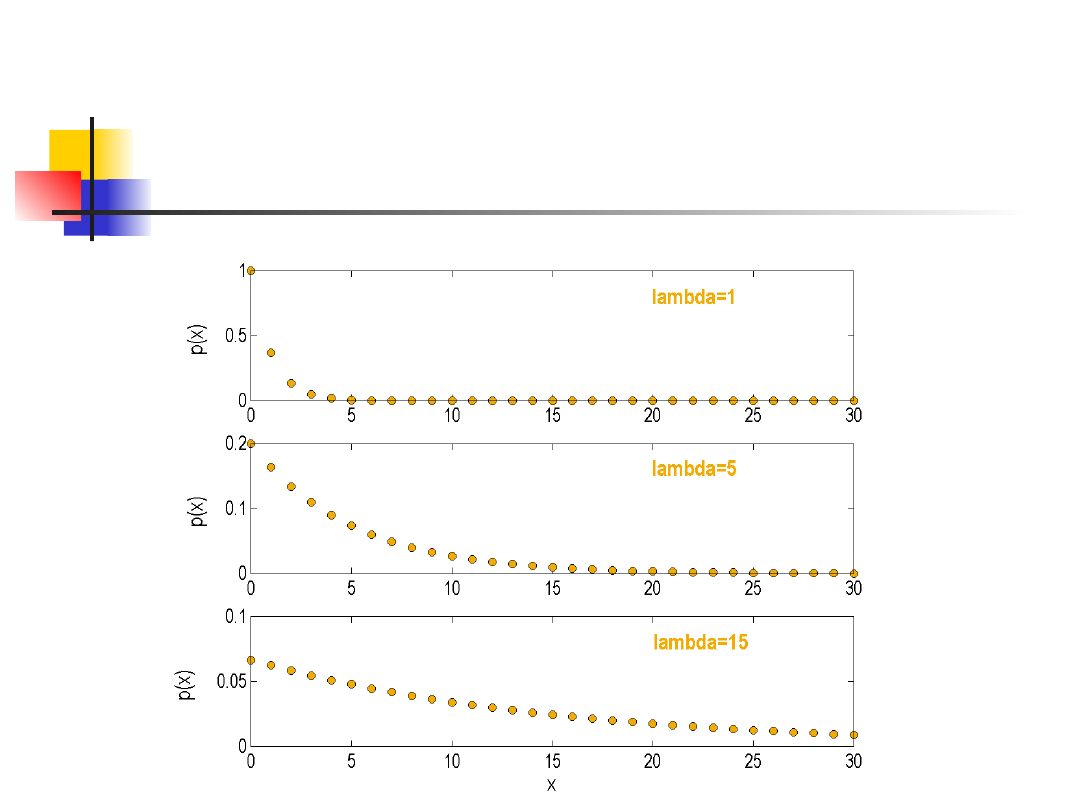
Rozkład wykładniczy

15





Rozkład wykładniczy



0

1

)

(

0

x

e

x

X

P











0

)

(

1

)

(

)

(

0

0

0

x

e

x

X

P

x

X

P

x

S















a
funkcja

nazywana jest krzywą
przeżywalności.

Możemy
wyznaczyć

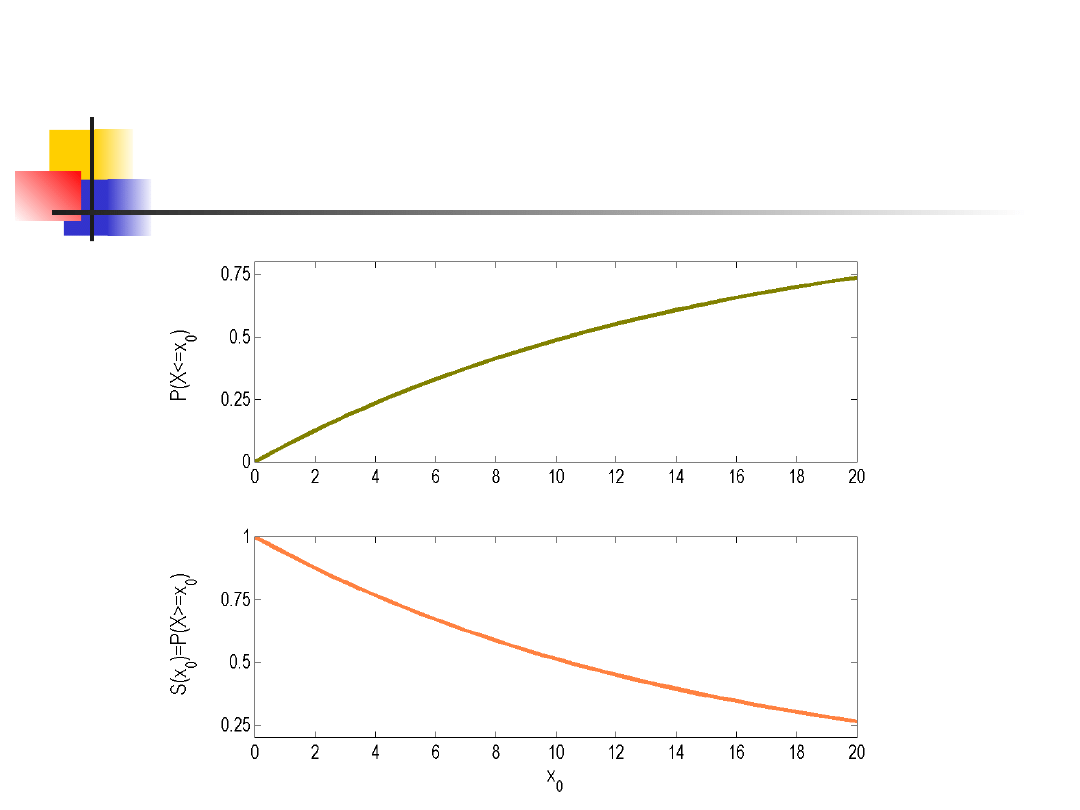
Rozkład wykładniczy

Przykład

Niech zmienna losowa X oznacza
‘czas życia’ pralki. Zgodnie z
informacjami producenta średni
użytkowania takiej pralki to 15 lat.

Jakie jest prawdopodobieństwo, że
pralka będzie mogła być używana
jedynie przez okres krótszy niż 6 lat?

Jakie jest prawdopodobieństwo, że
pralka posłuży swojemu właścicielowi
co najmniej 18 lat?

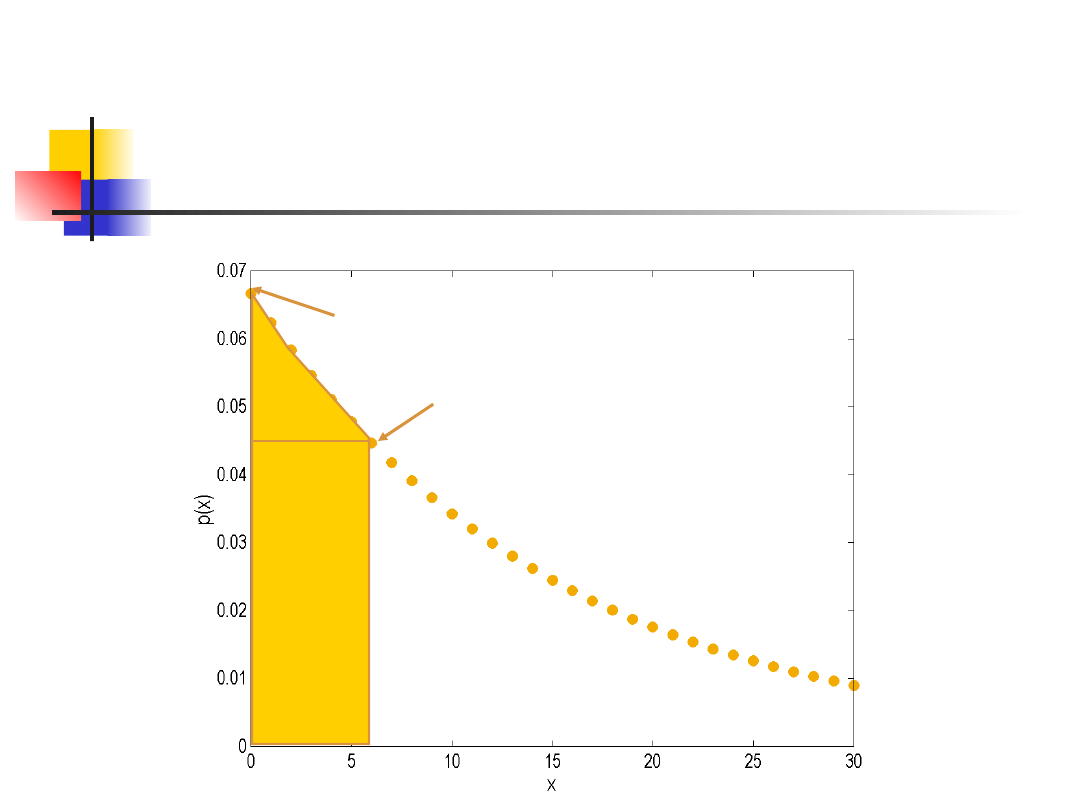
Przykład

0.0447

0.0667

P(X≤6) ≈ 0.0447·6+(0.0667-0.0447)·6/2

=

0.3342

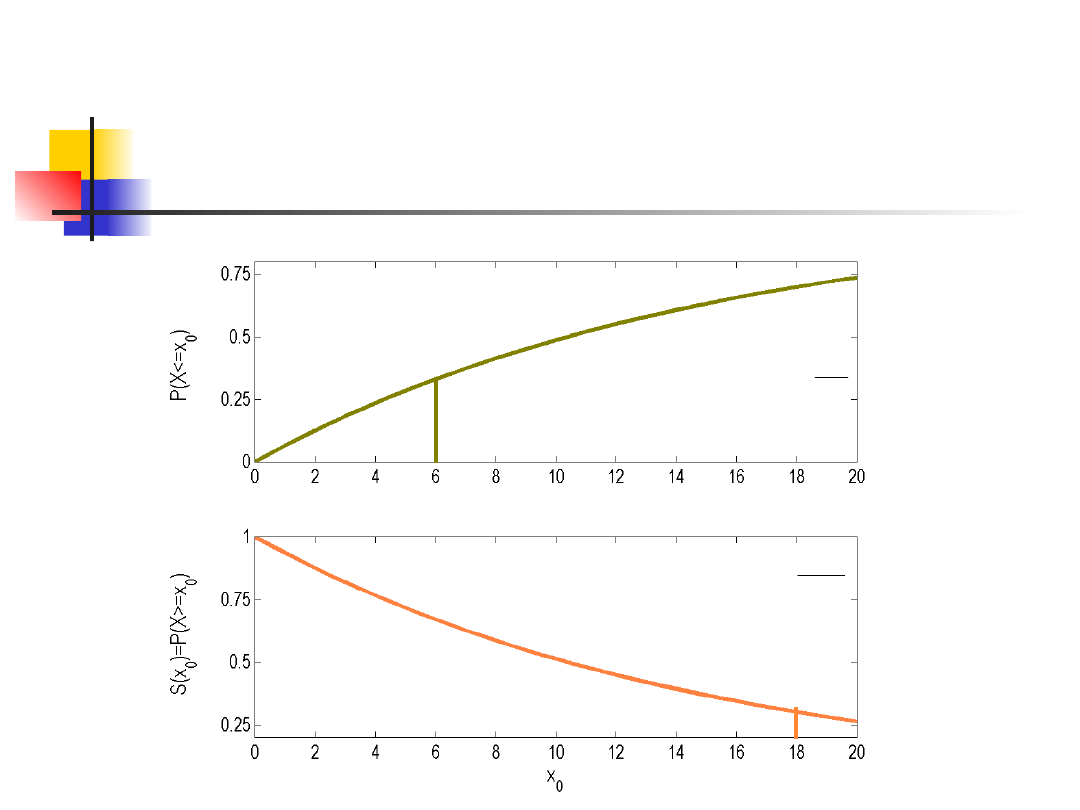
Przykład

0.3297

1

)

6

(

15

6











e

X

P

3012

.

0

)

18

(

15

18









e

X

P

Podsumowując, dla tego modelu
pralki istnieje około 30% szansa,
że pralka będzie działa zarówno
bardzo długo jak i relatywnie
krótko w stosunku do średniego
czasu pracy tych pralek.

Przykład

Niech Y będzie zmienną losową o rozkładzie
Poissona, określającą liczbę wystąpień w
jednostce czasu

gdzie μ jest średnią liczbą wystąpień w
jednostce czasu. Wtedy, jeśli X określa czas do
pierwszego wystąpienia, wówczas ta zmienna
losowa ma rozkład wykładniczy o średniej

Poisson i wykładniczy ...

,

!

)

(

k

e

k

Y

P

u

k 















1

)

(X

E

Przykład



Przeciętnie na pewnym odcinku
autostrady odnotowuje się 8
wypadków drogowych w ciągu
dwóch dni.



Jakie jest prawdopodobieństwo, że
nie będzie żadnego wypadku w
ciągu 3 dni lub więcej?

Przykład



Średnia liczba wystąpień wypadków

samochodowych w ciągu dnia to 4. Zatem

średni czas oczekiwania na wypadek to 0.25

(dnia).



Niech Y będzie zmienną losową o rozkładzie

Poissona o średniej 4, reprezentującą liczbę

wypadków na dzień.



Wtedy X będzie zmienną losową o rozkładzie

wykładniczym i średniej reprezentującej czas

oczekiwania do wystąpienia pojedynczego

wypadku.

Przykład

P(brak wypadku przez 3 lub więcej dni) =
P(czas do pierwszego wypadku ≥ 3)

0

)

3

(

12

25

.

0

3













e

e

X

P

Rozkład normalny



Funkcja gęstości rozkładu normalnego

pełni

bardzo ważną rolę w probabilistyce i
statystyce. Nazywa się ją również funkcją
gaussowską, gdyż Carl Friedrich Gauss,
zaproponował ją jako model błędów
pomiarowych (w roku 1809).



Funkcja gęstości rozkładu normalnego jest
używana jako model zmienności takich
wielkości jak wzrost osób, IQ, czy prędkość
molekuł gazu.

Rozkład normalny



Funkcja gęstości rozkładu normalnego
zależy od dwóch parametrów, μ -
średniej oraz σ – odchylenia
standardowego (przy czym -∞< μ< ∞ i σ
> 0):

2

2

2

)

(

2

1

)

(















x

e

x

f

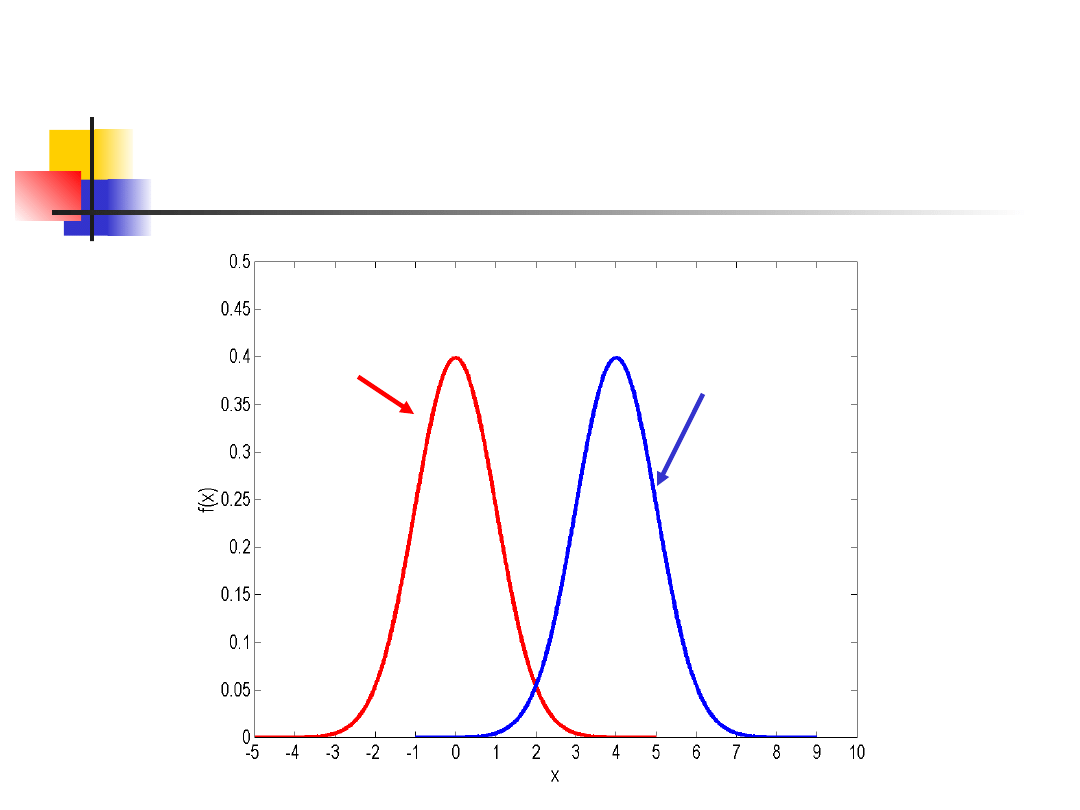
Rozkład normalny

μ=0

μ=4

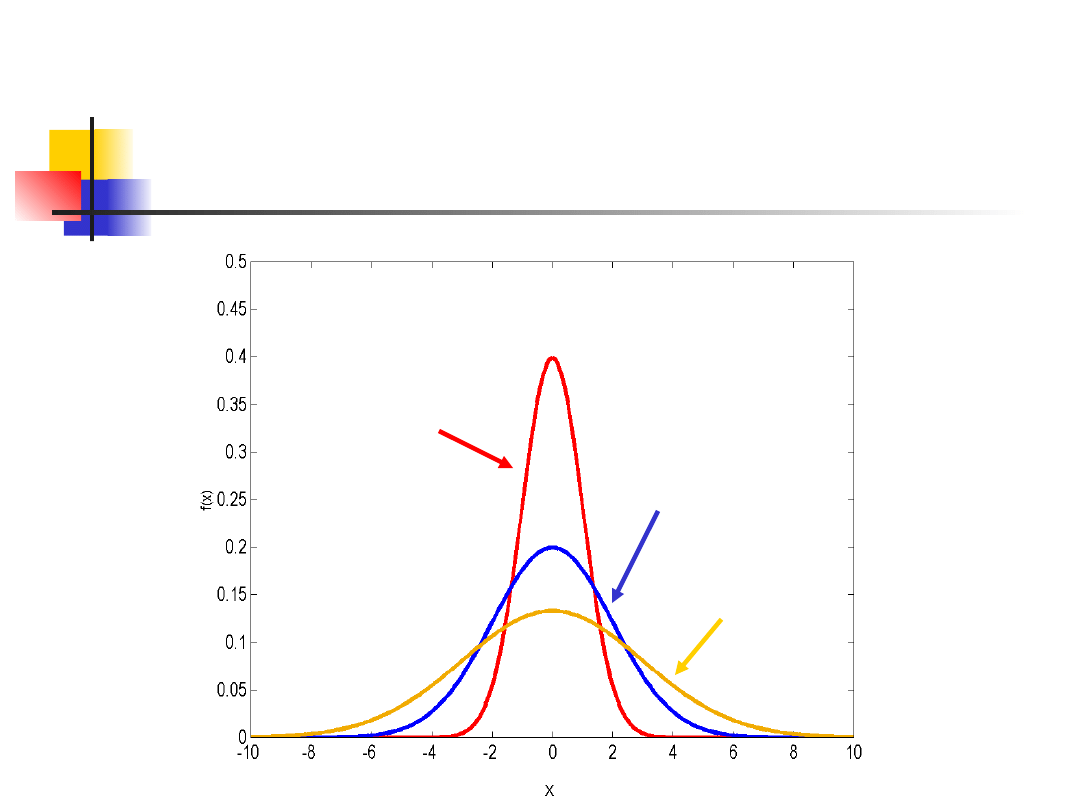
Rozkład normalny

σ=2

σ=3

σ=1

Rozkład normalny



Krzywa jest symetryczna wokół wartości

średniej. Wartość średnia, mediana i

moda są takie same.



Nastepujące części pomiarów zmiennej

o rozkładzie normalnym znajdują się

wewnatrz przedziałów:
μ ± σ zawiera 68.72 % pomiarów
μ ± 2σ zawiera 95.45 % pomiarów
μ ± 3σ zawiera 99.73% pomiarów

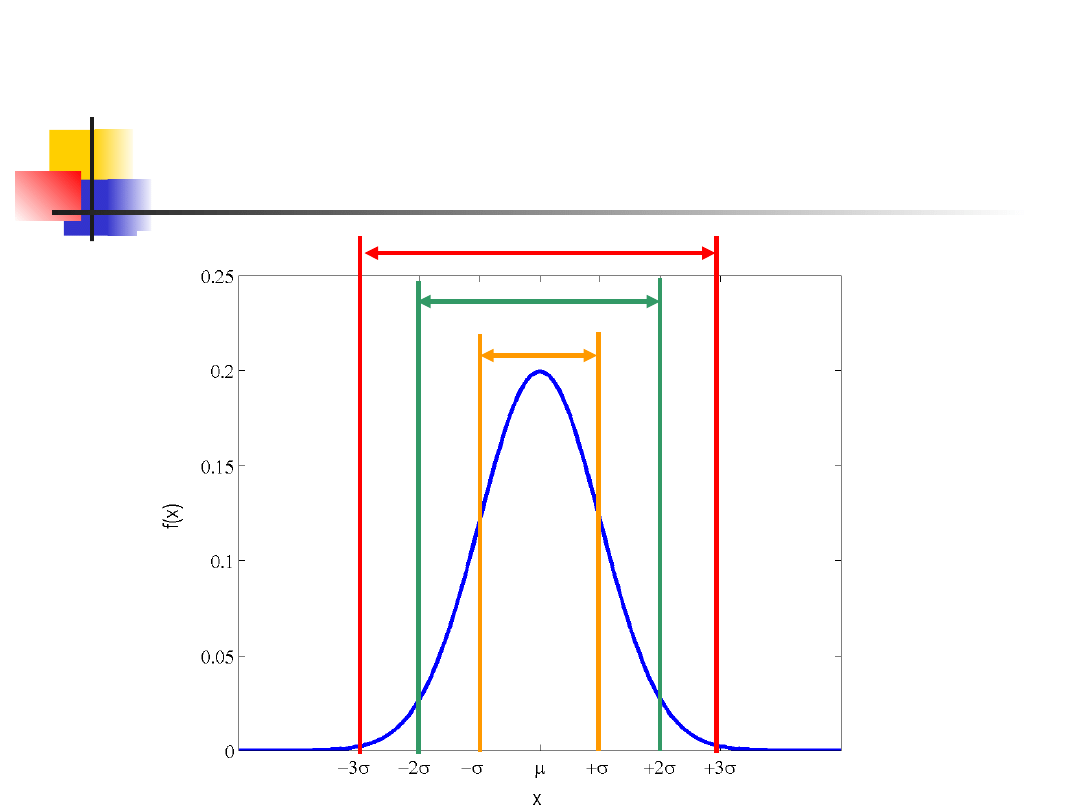
Rozkład normalny

68.27%

95.45%

99.73%

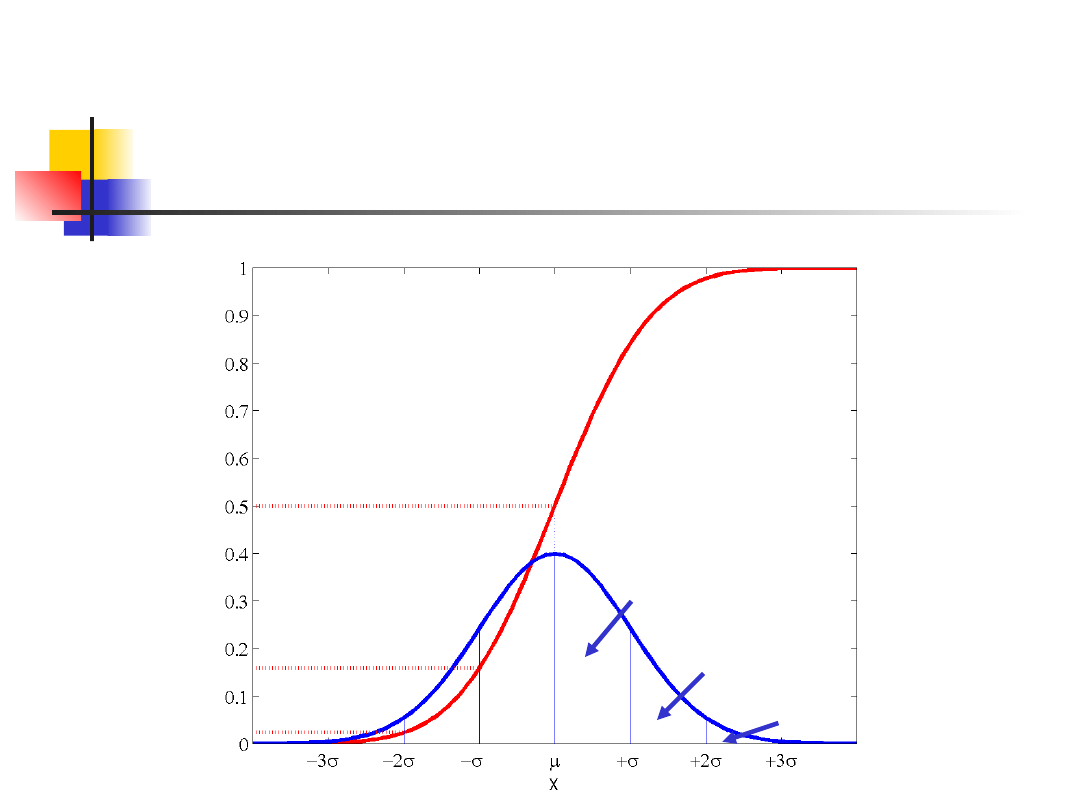
Rozkład normalny

Dystrybuanta

Funkcja gęstości
prawdopodobieństwa

2.28%

5.87%

50.00%

34.13%

13.59%

2.14%

Standardowy rozkład
normalny



Przypadek szczególny, gdy =0

oraz =1 określa tzw. standardową

normalną dystrybucję.



Dystrybuanta rozkładu
standardowego oznaczana jest
symbolem  a jego funkcja

gęstości .

Standardowy rozkład
normalny



Prawdopodobieństwo dla określonej
realizacji zmiennej losowej o dowolnym
rozkładzie normalnym może być
wyznaczone z użyciem rozkładu
standardowego.



Wykorzystuje się tutaj następującą
właściwość:

)

a

,

b

a

(

N

~

Y

then

,

b

aX

Y

and

)

,

(

N

~

X

If















Standardowy rozkład
normalny



Załóżmy, że X~N(,) a my chcemy znaleźć

prawdopodobieństwo, że P(x

0

<X<x

1

) dla

zadanych liczb x

0

i x

1

. Rozważmy

następującą zmienną losową:



















X

X

Z

gdzie a=1/ a b=-/. Wówczas

)

1

,

0

(

N

)

)

(

,

(

N

)

a

,

b

a

(

N

~

Z

1

























Standardowy rozkład
normalny



Zatem

)

(

)

(

)

(

)

(

)

(











































x

x

x

X

X

Z

P

P

x

X

P

x

F

Więc

)

(

)

(

)

(

)

(

)

(

0

1

0

1

1

0































x

x

X

X

x

F

x

F

x

X

x

P

Przykład



Wyniki standaryzowanego testu na
inteligencję, IQ, mają w przybliżeiu
rozkład normalny o średniej =100

oraz odchyleniu standardowym
=15.



Wybieramy losowo jedną osobę.
Jakie jest prawdopodobieństwo, że
uzyska ona wynik 120 < X < 130?

Przykład



Możemy wyznaczyć interesujące nas
prawdopodobieństwo dokonując
standaryzacji zmiennej losowej:

069

.

0

9082

.

0

9772

.

0

)

33

.

1

(

)

2

(

)

2

33

.

1

(

)

(

)

130

120

(

15

100

130

15

100

15

100

120









































Z

P

P

X

P

X

Symetria i kurtoza



Często obserwujemy odstępstwa
od rozkładu normalnego.
Statystyki, które pozwolą to ocenić
ilościowo bardzo użyteczne.



Zajmiemy się dwoma najczęściej
pojawiającymi się odstępstwami
rozkładów od normalności:

skośnością

i

kurtozą

.

Skośność



Skośność

, inaczej zwana asymetrią, ocenia

na ile jeden z końców krzywej rozkładu
prawdopodobieństwa jest niesymetryczny
w stosunku do drugiego końca.



W takim przypadku brak jest zgodności
wartości średniej i mediany.



W zależności od deformacji, krzywe
określa się mianem prawo- i
lewoskośności.

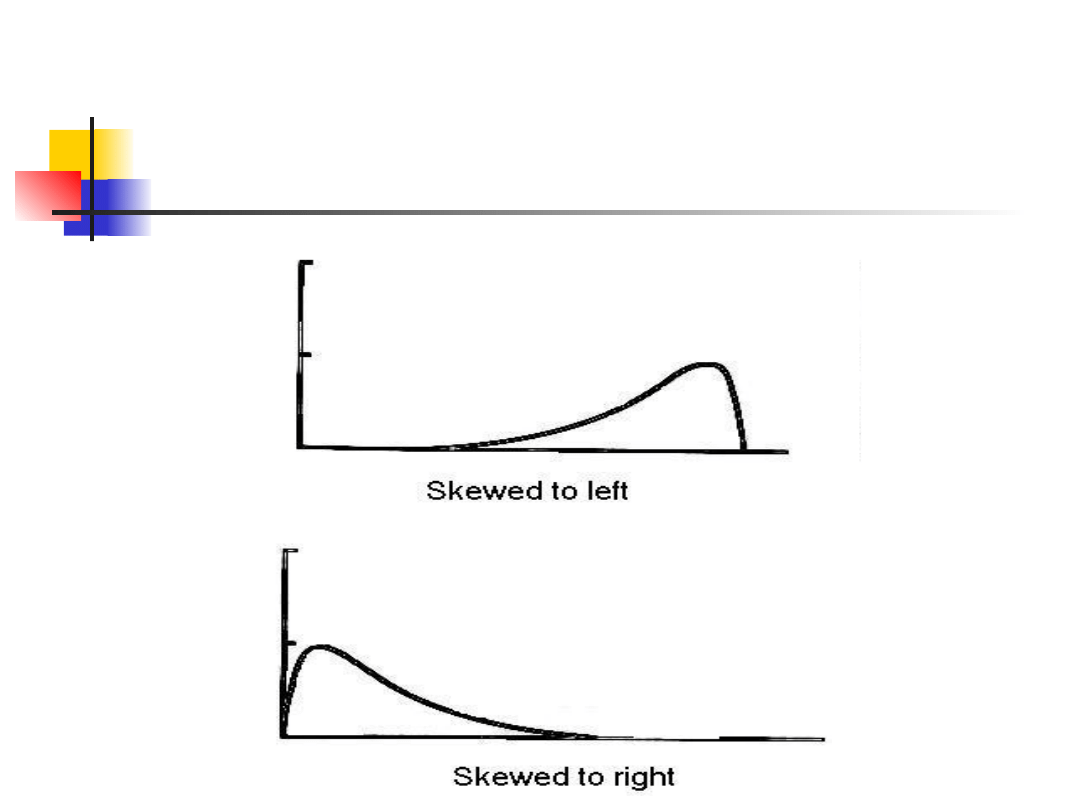
Skośność

Kurtoza



Jeśli symetryczny rozkład ma
środek, dwa ramiona i dwa końce,
kurtoza opisuje stosunek między
częścią środkową i końcami w
odniesieniu do ramion.



Definiujemy leptokurtozę
(wyostrzenie krzywej) i platykurtozę
(spłaszczenie krzywej).

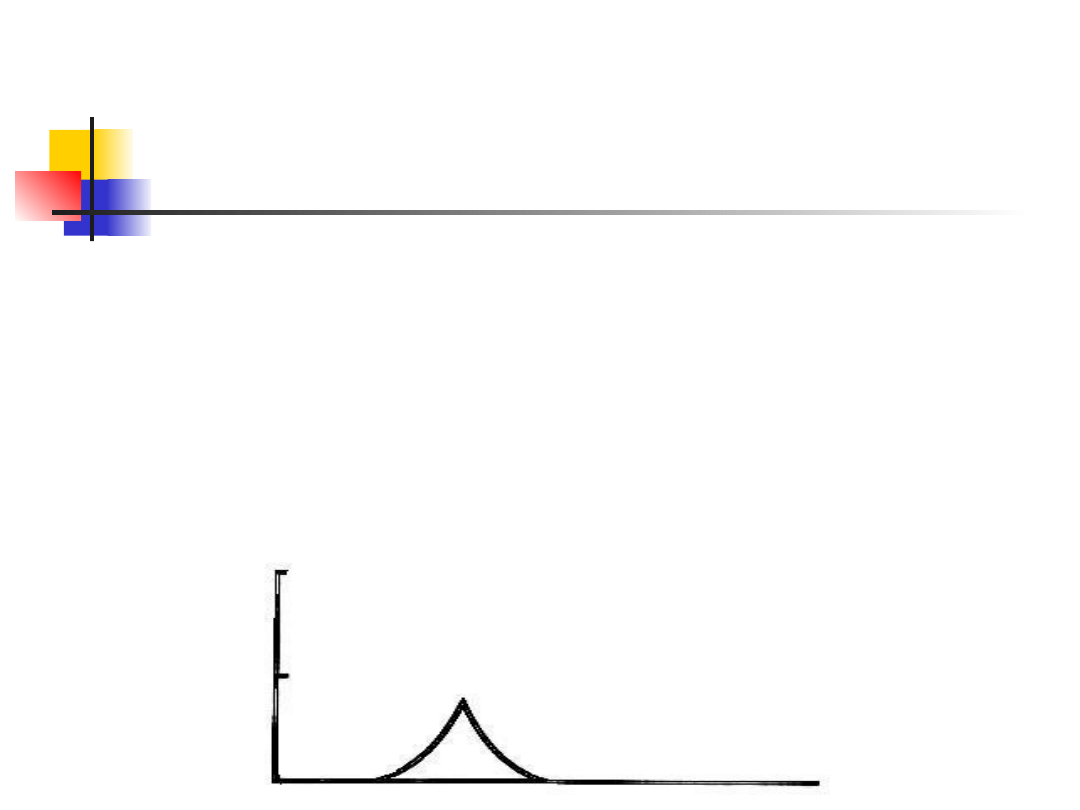
Kurtoza



O leptokurtozie (wyostrzeniu)
mówimy, gdy krzywa ma więcej
obserwacji blisko środka i na końcach a
mniej w ramionach w porównaniu do
rozkładu normalnego, z tą samą średnią i
wariancją

.

Kurtoza



O platykurtozie (spłaszczeniu)
mówimy, gdy krzywa ma mniej
elementów w środku i końcach, za to
więcej w ramionach niż krzywa
normalna.

Skośność i kurtoza



Przykładowe statystyki mierzące skośność i
kurtozę są zapisywane jako g

1

and g

2

i służą do

reprezentowania parametrów populacji γ

1

i γ

2

.

3

3

1

)

2

)(

1

(

)

(

s

n

n

X

X

n

g

i















4

2

2

4

1

)

1

(

2

)

3

)(

2

(

)

(

3

)

(

s

n

n

X

X

X

X

g

i

i

n

n

n





















Skośność i kurtoza



W normalnym rozkładzie częstości γ

1

i

γ

2

są równe zero.



Ujemne g

1

wskazuje na lewoskośność,

a dodatnie g

1

- prawoskośność.



Ujemne g

2

mówi o wyostrzeniu, zaś

dodatnie g

2

- o spłaszczeniu.



Wartości bezwzględne z g

1

and g

2

nie

mają wielkiego znaczenia.

Ocena skośności i kurtozy za
pomocą kwantyli



Oznaczając i-ty kwartyl jako Q

i

, możemy

zdefiniować współczynnik skośności
Bowley’a (Bowley, 1920):

1

3

2

1

3

2

Q

Q

Q

Q

Q

skewness









wielkość, która może przyjmować wartości od
-1 dla rozkładu ekstremalnie lewoskośnego,
przez 0 dla rozkładu symetrycznego, do 1 dla
rozkładu prawoskośnego

Ocena skośności i kurtozy za
pomocą kwantyli



Pomiar kurtozy (wyostrzenia) na podstawie
oktyli O

i

(12.5%, 25%, 37.5% itd.) został

zaproponowany przez Moors’a w 1988

1

3

1

3

5

7

)

(

)

(

Q

Q

O

O

O

O

kurtosis













Dla skrajnie spłaszczonego rozkładu ta
wartość wynosi 0; 1.233 dla normalnego;
nieskończoność dla skrajnie wyostrzonego.

Graficzny test na kształt
rozkładu



Wykresy kwantylowe (Q-Q) są
użyteczne, gdy ogólnie porównujemy
funkcje rozkładów. Na wykresach Q-
Q, rysuje się i porównuje kwantyle
obu rozkładów.

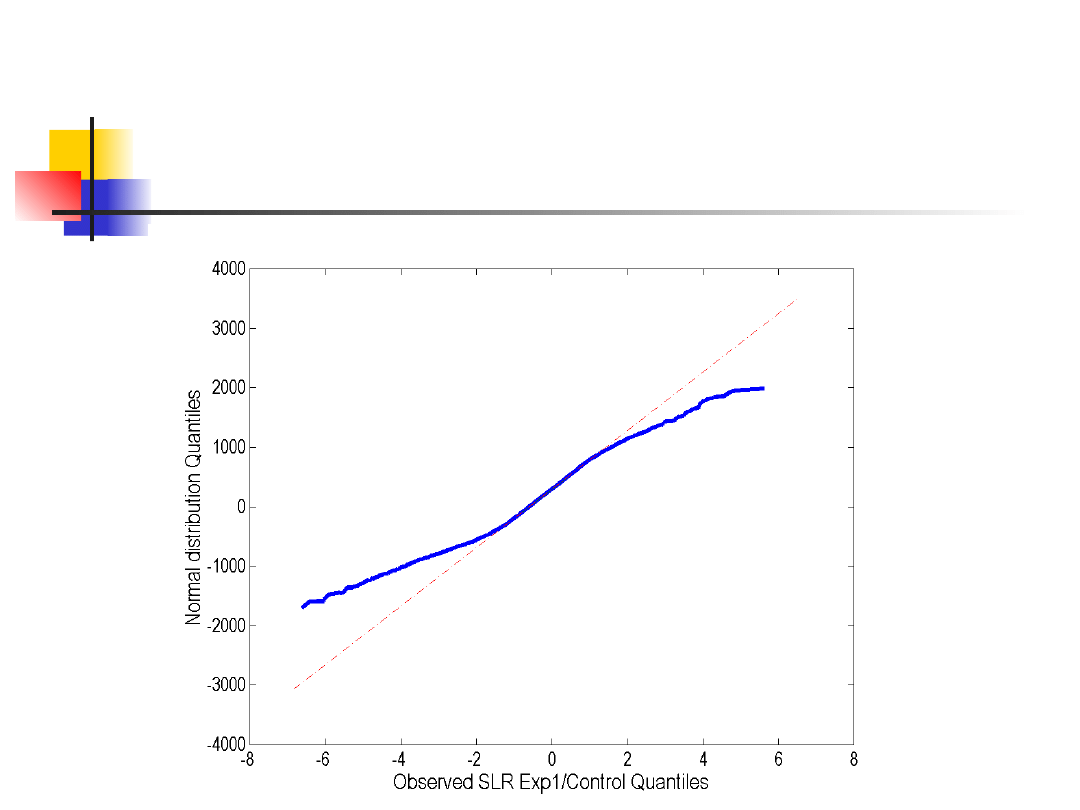
Graficzny test na kształt
rozkładu

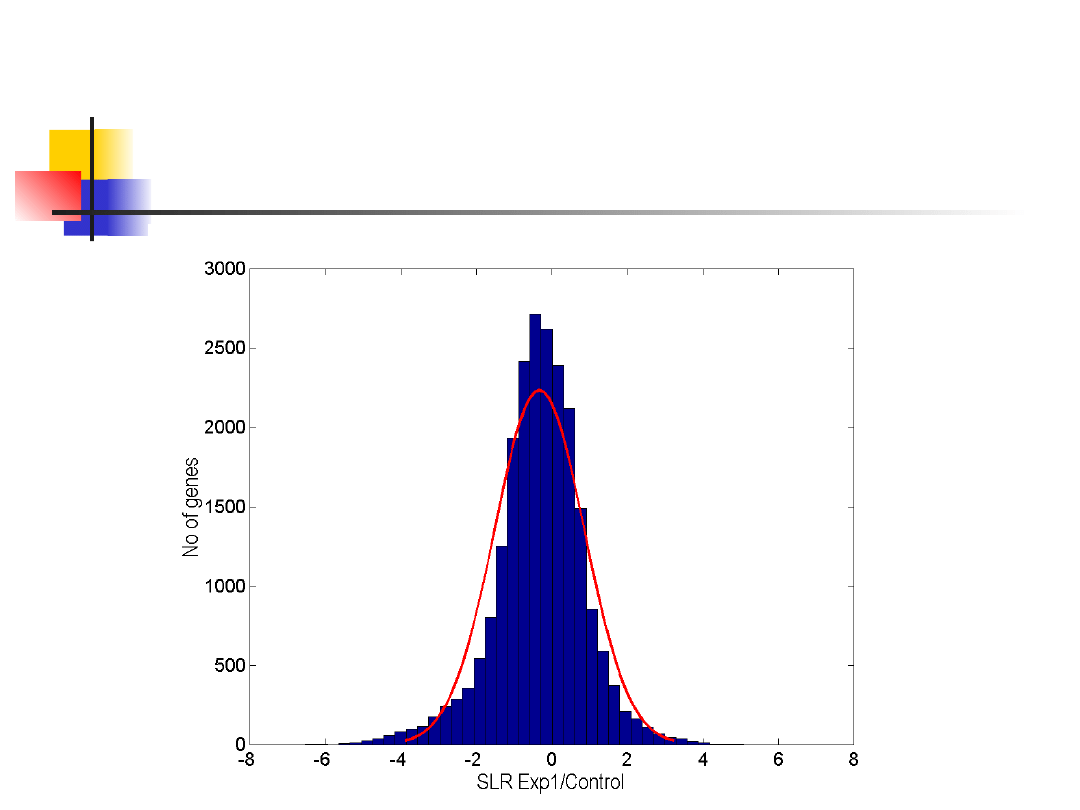
Graficzny test na kształt
rozkładu