Matematyczne techniki zarządzania - 91
Matematyczne techniki zarządzania - 91
Testowanie równości wariancji populacji
Stosuje się test Hartleya zwany też testem F
max
, który pozwala rozstrzygnąć
czy próbki pochodzą z populacji o jednakowej wariancji (czy wariancje pró-
bek są homogeniczne).
Jeśli założymy, że każda populacja ma rozkład normalny i że ich wariancje są
równe
2
i
(i = 1, 2, ..., k), to możemy zweryfikować hipotezy
H
0
:
2
1
=
2
2
= .... =
2
k
H
1
:
nie wszystkie
2
i
s
ą jednakowe
Reguła decyzyjna:
odrzucamy H
0
, jeżeli
(max)}
,
){
max(
max
.
i
k
obl
F
F
(max)}
,
){
max(
i
k
F
odczytujemy ze specjalnej tablicy, gdzie:
k — liczba czynników
i
(max) — największa liczba stopni swobody spośród próbek
Przykład 27 cd. Wariancje próbek dla poszczególnych skryptów: 114,889;
325,111; 292,000. Stąd
83
,
2
889
,
114
111
,
325
max
.
obl
F
=0,05 k=3
i
(max)=9 F
tabl
=5,34
JAKI WNIOSEK?
(min)
(max)
2
2
max
.
i
i
obl
s
s
F
Matematyczne techniki zarządzania - 92
Matematyczne techniki zarządzania - 92
ANALIZA WARIANCJI DWUCZYNNIKOWA
SSTO
CZYNNIK
BLOK
ij
j
i
ij
x
x
ij
— wartość obserwacji w i-tym poziomie bloku i j-
tym poziomie czynnika
— ogólna średnia zmiennej X
i
— odchylenie średniej i-tego poziomu bloku od
j
— odchylenie średniej j-tego poziomu czynnika od
ij
— składnik losowy (reszta) N(0;
2
)
[ — ksi]
CZYNNIK=BLOK
RANDOMIZED
BLOCK DESIGN
Założenia:
• mamy losowe próbki z n poziomów bloku i przydzielamy losowo
jednostki z każdego bloku do każdego z k poziomów czynnika
• reakcja w i-tym poziomie bloku na j-ty poziom czynnika pochodzi z
rozkładu normalnego
• wariancja każdej populacji n
k
wynosi
2
• nie ma wzajemnego oddziaływania między blokiem i czynnikiem
RESZTA
Matematyczne techniki zarządzania - 93
Matematyczne techniki zarządzania - 93
Przykład 29. Zmienną losową X jest ilość kilometrów przejechanych na 1
litrze benzyny różnej marki. Do pomiarów używamy 5 różnych samochodów:
MARKA BENZYNY
NUMER
SAMOCHODU
A
B
C
D
1
21,8
22,4
20,6
23,1
2
24,6
24,9
25,6
26,4
3
31,3
34,2
30,6
33,7
4
24,1
25,3
22,4
26,8
5
23,1
27,3
26,1
28,6
CZYNNIK
BLOK
Co można stwierdzić „gołym okiem”:
• czy marka benzyny wpływa na jej zużycie?
• czy egzemplarz użytego samochodu wpływa na zużycie paliwa?
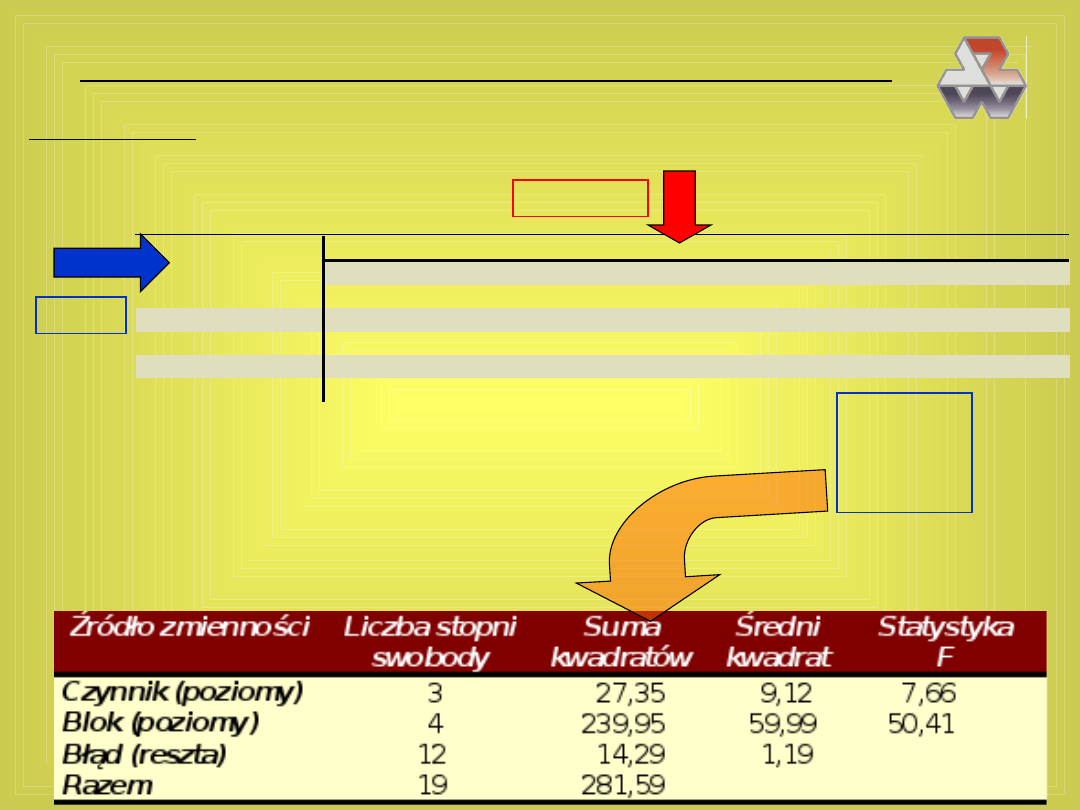
Tabelka ANOWY
%
Matematyczne techniki zarządzania - 94
Matematyczne techniki zarządzania - 94
Przyjmujemy
= 0,01 i stawiamy hipotezy:
• H
0
: czynnik nie wpływa...
H
1
: czynnik...
• H
0
: blok nie wpływa...
H
1
: blok...
JAKI JEST OFICJALNY JĘZYK TYCH HIPOTEZ?
Wartości krytyczne testu Fishera:
41
,
5
)
2
1
;
4
(
95
,
5
)
12
;
3
(
01
,
0
01
,
0
F
F
Decyzje i
wnioski.................................................................................
ANALIZA WARIANCJI DWUCZYNNIKOWA Z UWZGLĘDNIENIEM
WZAJEMNEGO ODDZIAŁYWANIA CZYNNIKÓW
j
i
j
i
ijk
x
SSA
SSB
SSAB
SSE
SSTO
SUMY KWADRATÓW
ŚREDNIE KWADRATY
1
1
b
SSB
MSB
a
SSA
MSA
ZAŁOŻENIA!
CZYNNIK A
CZYN-
NIK B
CZYNNIK A i B
RESZTA
SSTO
Matematyczne techniki zarządzania - 95
Matematyczne techniki zarządzania - 95
ab
n
SSE
MSE
b
a
SSAB
MSBA
)
1
)(
1
(
Przykład 30. W pewnym przedsiębiorstwie postanowiono przeprowadzić
badania co wpływa na sukces kierowników sklepów — wykształcenie czy
doświadczenie. Z dużej liczby sklepów wylosowano 24 kierowników i dla
każdego określono współczynnik sukcesu będący ilorazem rzeczywistej
rocznej sprzedaży do sprzedaży prognozowanej, określonej na podstawie
równania regresji
uwzględniającego lokalizację, powierzchnię, liczbę pra-
coników itd.
Wykształcenie
Staż
n = 24
1.
8
—
P
1.
6
—
<5 lat
2.
8
—
Ś
2.
6
—
5-10 lat
3.
8
—
W
3.
6
—
10-15 lat
4.
6
—
>15 lat
05
,
0
%
Matematyczne techniki zarządzania - 96
Matematyczne techniki zarządzania - 96
Można rozwiązać dwa problemy:
1.
H
0
: nie ma wzajemnego oddziaływania czynników A i B
H
1
: jest wzajemne oddziaływanie A i B
Odrzucamy H
0
, jeżeli
)}
(
);
1
)(
1
{(
ab
n
b
a
F
F
obl
2.
H
0
: czynnik A
(lub B)
nie wpływa na pracę kierownika
H
1
: czynnik A
(lub B)
wpływa na pracę kierownika
Odrzucamy H
0
, jeżeli
}
;
1
{
ab
n
a
F
F
obl
b—1
ANALIZA REGRESJI I KORELACJI
• umożliwia badanie wpływu czynników mierzalnych,
takich jak: czas nauki, zużycie materiałów, wielkość
produkcji itd.
• umożliwia ustalanie przyczyn zachowania się danego zjawiska: dlacze-
go rosną koszty, co powoduje straty w firmie itd.
• jest to bardzo popularna metoda, zgodna z naszą intuicją
• obliczenia wykonuje się
metodą najmniejszych kwadratów
• stosuje: estymację, testowanie hipotez, analizę wariancji itd.
Matematyczne techniki zarządzania - 97
Matematyczne techniki zarządzania - 97
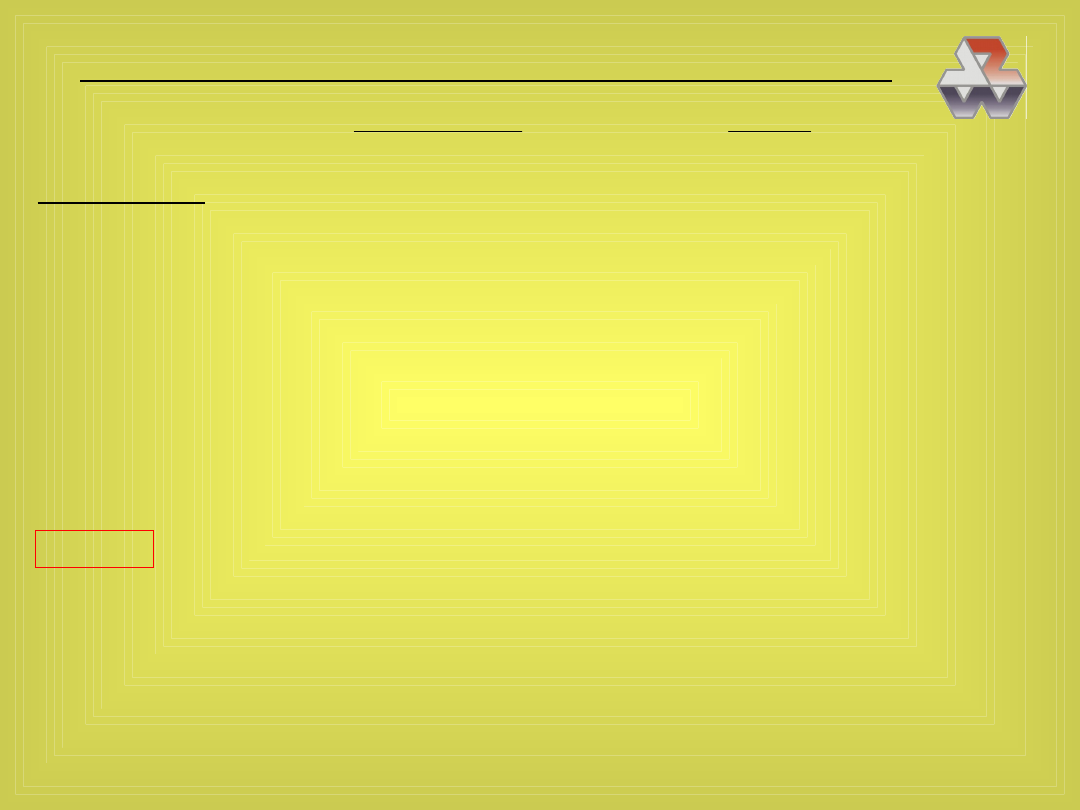
Bardzo często robimy — odruchowo — wykres zależności dwu zmiennych:
Y
X
obserwacje empiryczne
model rzeczywistości
Zapisujemy to jako:
losowy
skł
ksi
x
a
a
y
bx
a
y
i
i
i
i
.
)
(
1
0
Dla układu trójwymiarowego:
i
i
i
i
i
i
x
a
x
a
a
y
cz
bx
a
y
2
2
1
1
0
Zmienna losowa wielowymiarowa
x
ijkl
lub
x
i
, y
j
, z
k
itd.
y
1
y
2
y
i
y
m
Suma
x
1
P
11
P
12
P
1j
P
1n
P
1
x
2
P
21
P
22
P
2j
P
2n
P
2
x
i
P
i1
P
i2
P
ij
P
in
P
i
x
n
P
n1
P
n2
P
nj
P
nm
P
n
Suma
P
1
P
2
P
j
P
m
1
Tablica dwudzielna
• dwa wymiary
• P
ij
— „trzeci wymiar”
• P
i
i P
j
— rozkłady brzegowe
• suma =1
• jeśli rozkłady normalne, to
równanie liniowe
Matematyczne techniki zarządzania - 98
Matematyczne techniki zarządzania - 98
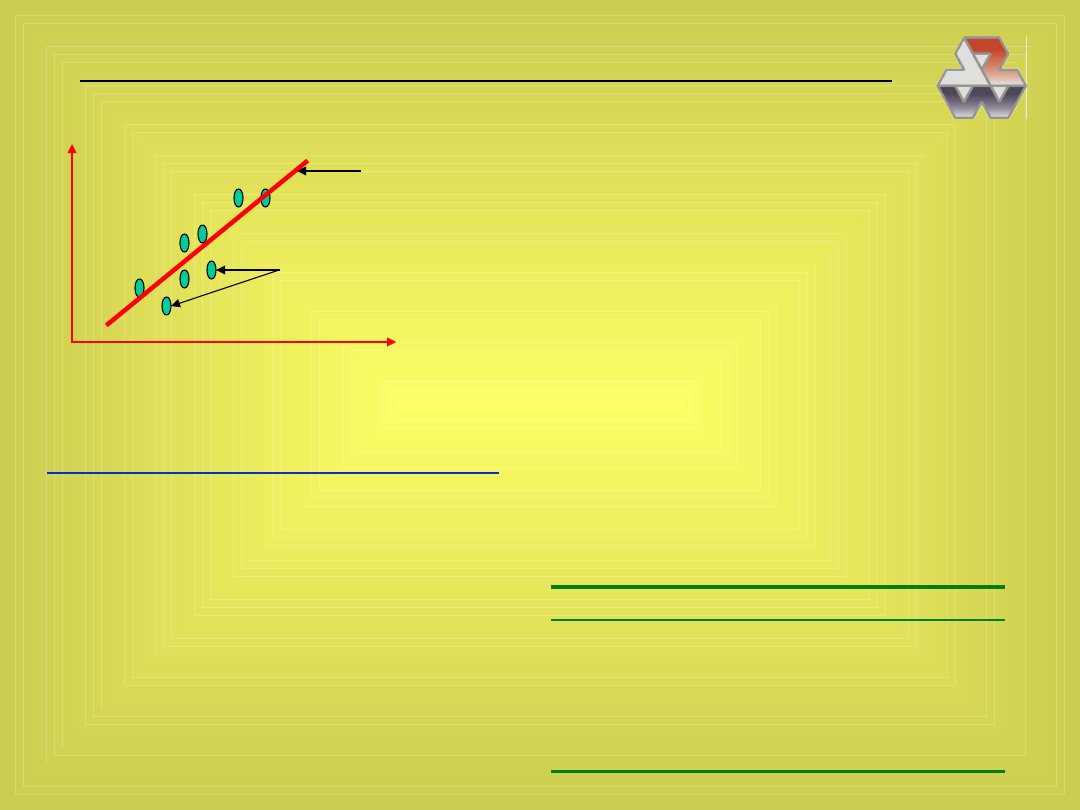
Trzy rodzaje związków pomiędzy Y i X
• związek funkcyjny (deterministyczny)
Y
X
x
i
y
i
i
i
bx
a
y
Domena — matematyka
KAŻDEJ WARTOŚCI x
i
ODPOWIADA JEDNA I
TYLKO JEDNA WARTOŚĆ y
i
• związek stochastyczny (losowy)
Domena — rzeczywistość
KAŻDEJ WARTOŚCI x
i
ODPOWIADA CAŁY ZBIÓR
WARTOŚCI y
i
TWORZACYCH OKREŚLONY
ROZKŁAD
DANE
Lp. x
i
y
i
1
x
1
y
1
2
x
2
y
2
3 x
3
y
3
............
x
i
Obserwacja
rzeczywistości
Waga i wzrost studentek
Matematyczne techniki zarządzania - 99
Matematyczne techniki zarządzania - 99
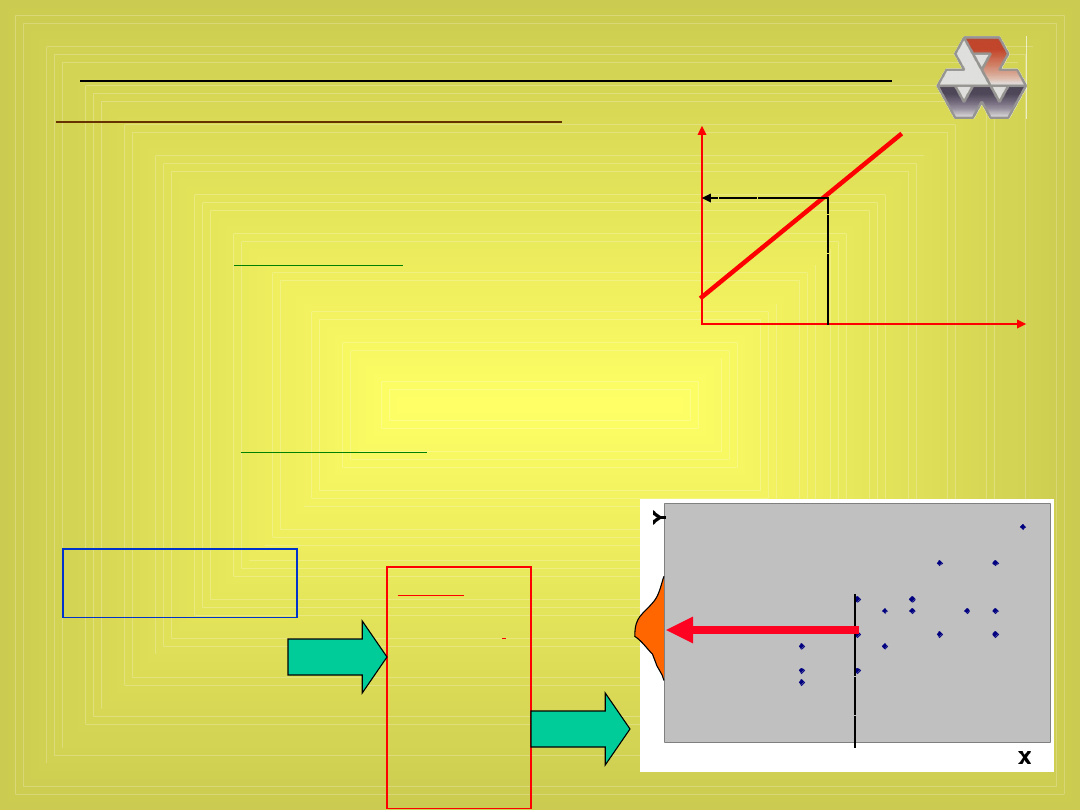
• związek statystyczny
Domena — model rzeczywistości
i
i
bx
a
y
x
i
i
yˆ
i
yˆ
—
średnia rozkładu
—
obrazuje rozrzut
y
x,
—
środek ciężkości zbioru
x
y
Dlaczego w rzeczywistości mamy do czynienia ze związkami stochastycznymi?
Podstawowe pojęcia i terminy
KORELACJA
— fakt
powiązania, współzależności, związku zmiennych ze sobą
WSPÓŁCZYNNIK KORELACJI
— liczba
określająca siłę i kierunek tego związku
• współczynnik korelacji liniowej dwu zmiennych: r lub r
xy
r
1
0
1
1
r
r
Współczynnik r niesie dwie
informacje poprzez swój
znak i moduł
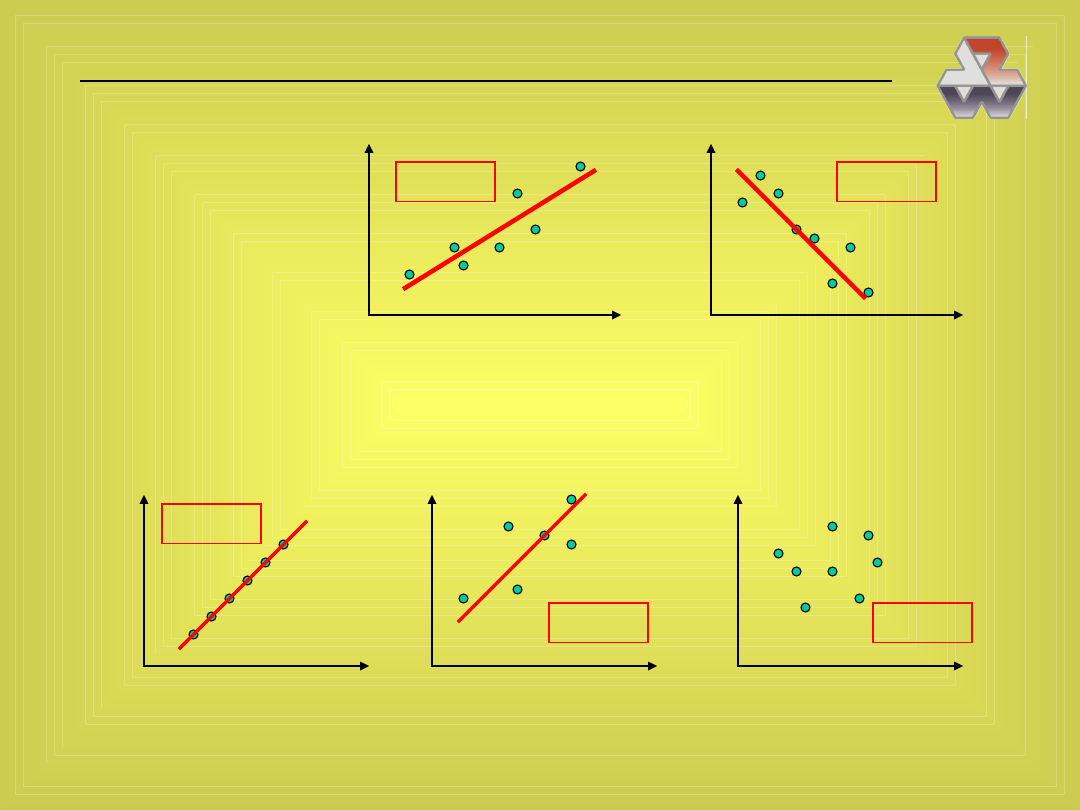
Matematyczne techniki zarządzania - 100
Matematyczne techniki zarządzania - 100
Znak
informuje o kierunku zależności
r>0
Korelacja dodatnia
r<0
Korelacja ujemna
Moduł
informuje o sile zależności
r=1
r=0,5
r=0
Który współczynnik korelacji jest korzystniejszy: —0,8 czy 0,2?
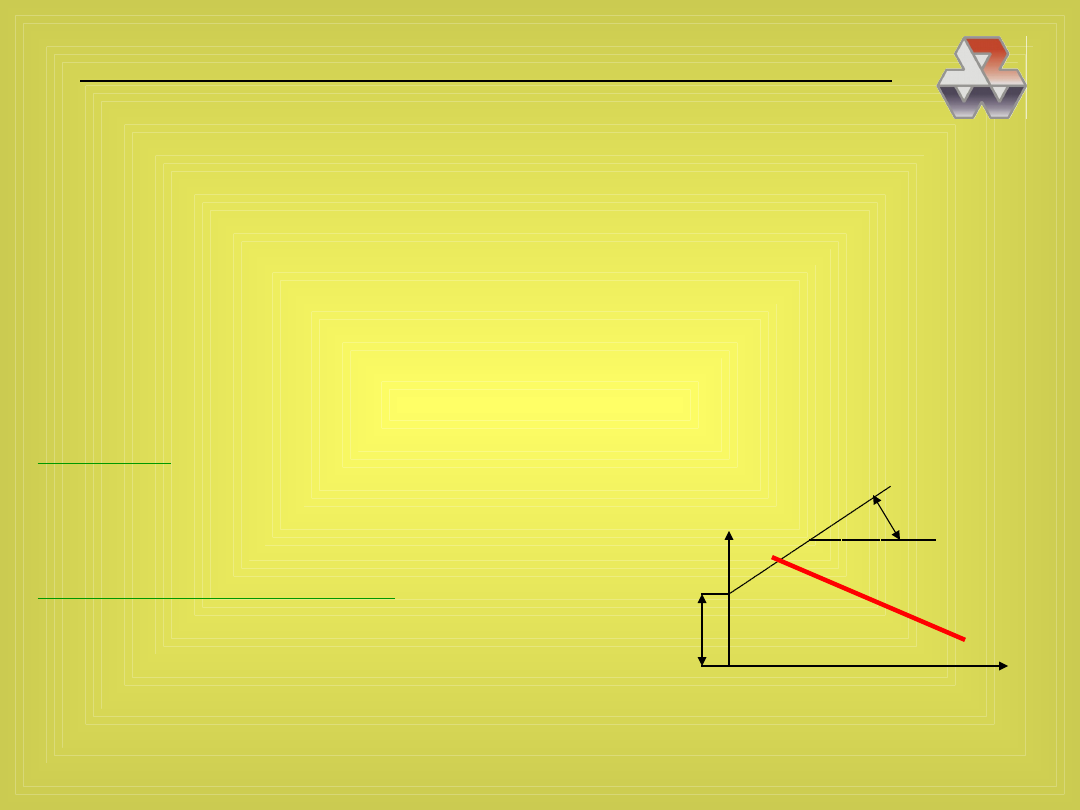
Matematyczne techniki zarządzania - 101
Matematyczne techniki zarządzania - 101
• współczynnik korelacji liniowej wielu zmiennych (korelacji wielo-krotnej
lub wielorakiej): R
R
1
0
R
Interpretacja:
• im wyższa wartość R, tym silniejsza współzależność (R=0: brak
korelacji, R=1: zależność funkcyjna, nie ma składnika losowego)
• R określa siłę powiązania zmiennej Y z wszystkimi zmiennymi X
i
, bez
względu na to jak poszczególne z nich są skorelowane z Y
• współczynnik korelacji cząstkowej dwu zmiennych
j
i
x
x
y
r
)
(
REGRESJA
— funkcja
odzwierciedlająca powiązanie zmiennych (czynników)
• w mowie potocznej regresja to cofanie się, spadek, zanik
• skąd się wzięło to słowo w statystyce?
wzrost
synów
wzrost ojców
WSPÓŁCZYNNIK REGRESJI
— liczba
stojąca
przy każdej zmiennej X, określająca jej
wpływ na zmienną Y
i
i
bx
a
y
a
— wyraz wolny (stała), współrzędna punktu przecięcia z osią Y
a
b
— współczynnik regresji, tangens kąta
nachylenia prostej
Matematyczne techniki zarządzania - 102
Matematyczne techniki zarządzania - 102
Czynności przy badaniu zależności zmiennych
• określenie co jest skutkiem (Y), a co przyczynami (X
1
, X
2,
itd.)
• zebranie danych (pobranie próbki statystycznej)
• wyznaczenie równania regresji dla próbki
• sprawdzenie (testowanie) czy równanie to może być przyjęte dla
populacji
• wnioskowanie o przyczynach na podstawie zweryfikowanego równania
Funkcja regresji I i II rodzaju
• regresja I rodzaju dotyczy populacji (jest nieznana)
...
2
2
1
1
0
X
X
Y
• regresja II rodzaju dotyczy próbki (jest znana)
...
2
2
1
1
0
x
a
x
a
a
y
Współczynniki regresji to
i
oraz a
i
; tak jak przy estymacji innych
parametrów mamy to do czynienia z estymatorami, ich odchyleniami
standardowymi (czyli błędami oszacowania) oraz z wartościami
oszacowanymi.
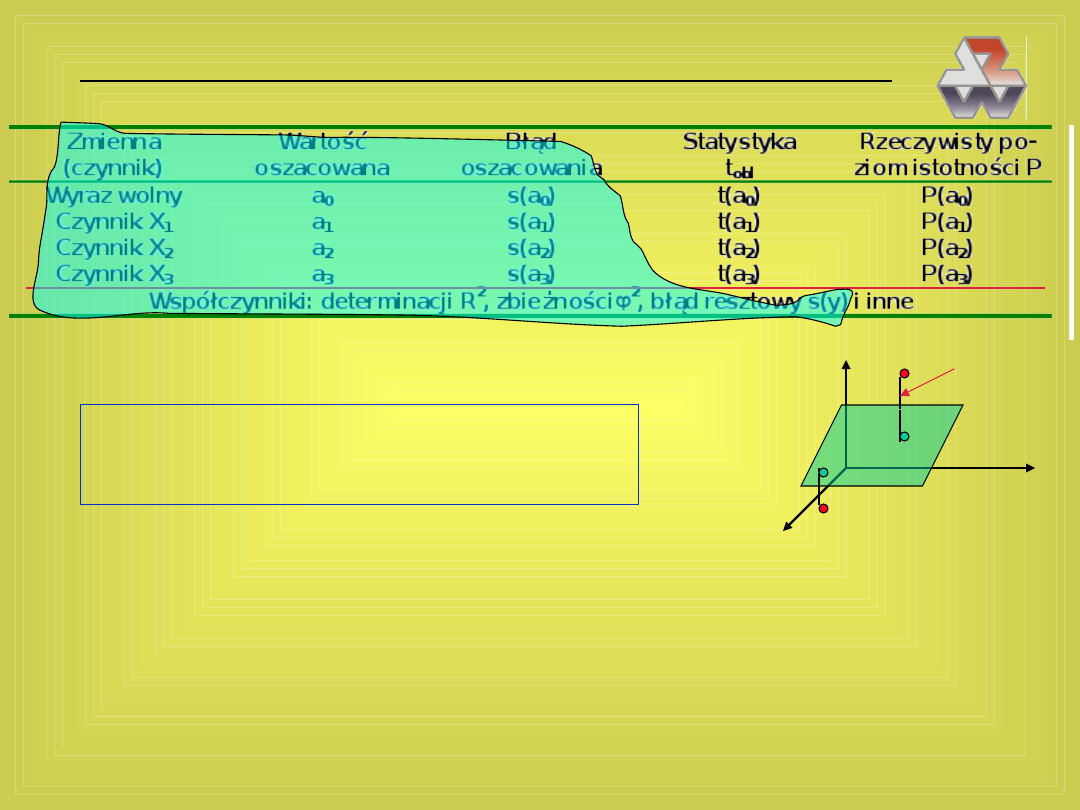
Matematyczne techniki zarządzania - 103
Matematyczne techniki zarządzania - 103
Wydruk komputerowy równania regresji
Pełny zapis równania regresji
2
3
2
1
0
2
3
3
2
2
1
1
0
)
(
)
(
)
(
)
(
)
(
)
(
y
s
a
s
a
s
a
s
a
s
R
R
x
a
x
a
x
a
a
y
i
i
i
i
Y
—
zmienna zależna, zmienna-skutek, zmienna objaśniana
y
i
— zaobserwowane wartości zmiennej zależnej dla jednostek próbki
X
k
— zmienne niezależne, zmienne-przyczyny, zmienne objaśniające
x
ki
— zaobserwowane wartości zmiennych niezależnych
a
0
— oszacowana wartość wyrazu wolnego (interpretację podano)
Y
X
1
X
2
3
3
2
2
1
1
0
ˆ
x
a
x
a
x
a
a
y
i
(wszystkie punkty czerwone)
parametry strukturalne i stochastyczne
reszta u
i
Matematyczne techniki zarządzania - 104
Matematyczne techniki zarządzania - 104
a
i
...
— oszacowane wartości współczynników regresji; określają
wpływ
poszczególnych zmiennych X
i
na zmienną Y
— składnik losowy, reprezentujący rozrzut punktów wokół płaszczyz-
ny regresji; składnik ten jest
zmienną losową;
jego wartości nazywają się
reszty
i
i
i
y
y
u
ˆ
a jego rozkład jest rozkładem normalnym o E(
)=0 i V(
)=s
2
(y)
s(a
0
)
— błąd oszacowania wyrazu wolnego; służy do budowy przedziału
ufności dla nieznanej wartości wyrazu wolnego
0
dla populacji oraz do
weryfikacji istotności
0
(H
0
:
0
=0)
s(a
i
)
— błędy oszacowania współczynników regresji; służą do budowy
przedziału ufności dla nieznanych wartości
i
współczynników regresji
dla populacji oraz do weryfikacji ich istotności (H
0
:
i
=0)
s(y)
— błąd resztowy; jest odchyleniem standardowym składnika
losowego
;
określa średnią wielkość reszty
u
i
R
2
(r
2
)
— współczynnik determinacji; określa jaka część zmienności całko-
witej
SSTO
została wyjaśniona przez równanie regresji
3
3
2
2
1
1
0
ˆ
x
a
x
a
x
a
a
y
i
2
— współczynnik zbieżności (zgodności); określa jaka część zmien-
ności całkowitej
SSTO
nie
została wyjaśniona przez równanie regresji
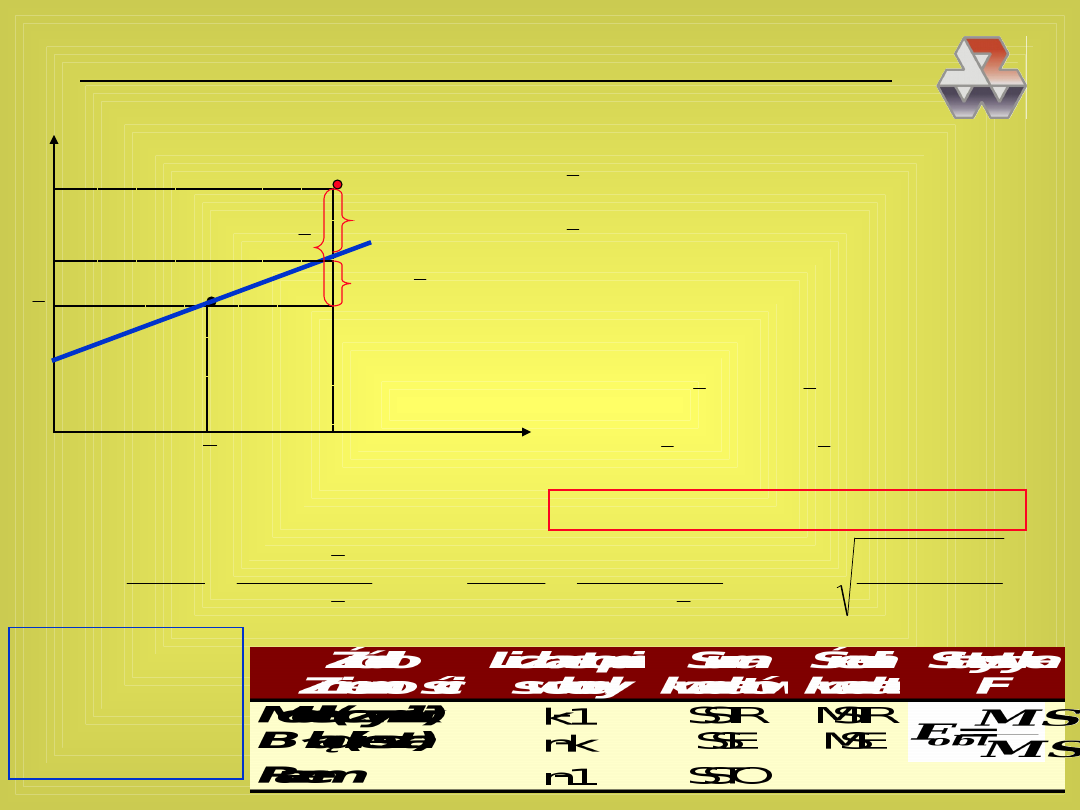
Matematyczne techniki zarządzania - 105
Matematyczne techniki zarządzania - 105
Wszystko to jest łatwiejsze do zrozumienia w układzie dwuwymiarowym
X
Y
x
y
i
x
i
y
i
yˆ
y
y
i
i
i
y
y
ˆ
y
y
i
ˆ
2
)
(
y
y
i
=
SSTO
(zmienność całkowita)
2
)
ˆ
(
y
y
i
=
SSTR
(zmienność wyjaśniona)
2
)
ˆ
(
i
i
y
y
=
SSE
(zmienność niewyjaśniona)
(SUMOWANIE OD „1” DO „n” )
)
ˆ
(
)
ˆ
(
)
(
i
i
i
i
y
y
y
y
y
y
2
2
2
)
ˆ
(
)
ˆ
(
)
(
i
i
i
i
y
y
y
y
y
y
SSTO = SSTR + SSE
2
)
ˆ
(
)
(
)
(
)
ˆ
(
)
(
)
ˆ
(
2
2
2
2
2
2
2
n
y
y
y
s
y
y
y
y
SSTO
SSE
y
y
y
y
SSTO
SSTR
R
i
i
i
i
i
i
i
RÓWNANIE REGRESJI
JEST MODELEM
RZECZYWISTOŚCI
WSZYSTKO TO JUŻ
ZNAMY Z ANALIZY
WARIANCJI
Matematyczne techniki zarządzania - 106
Matematyczne techniki zarządzania - 106
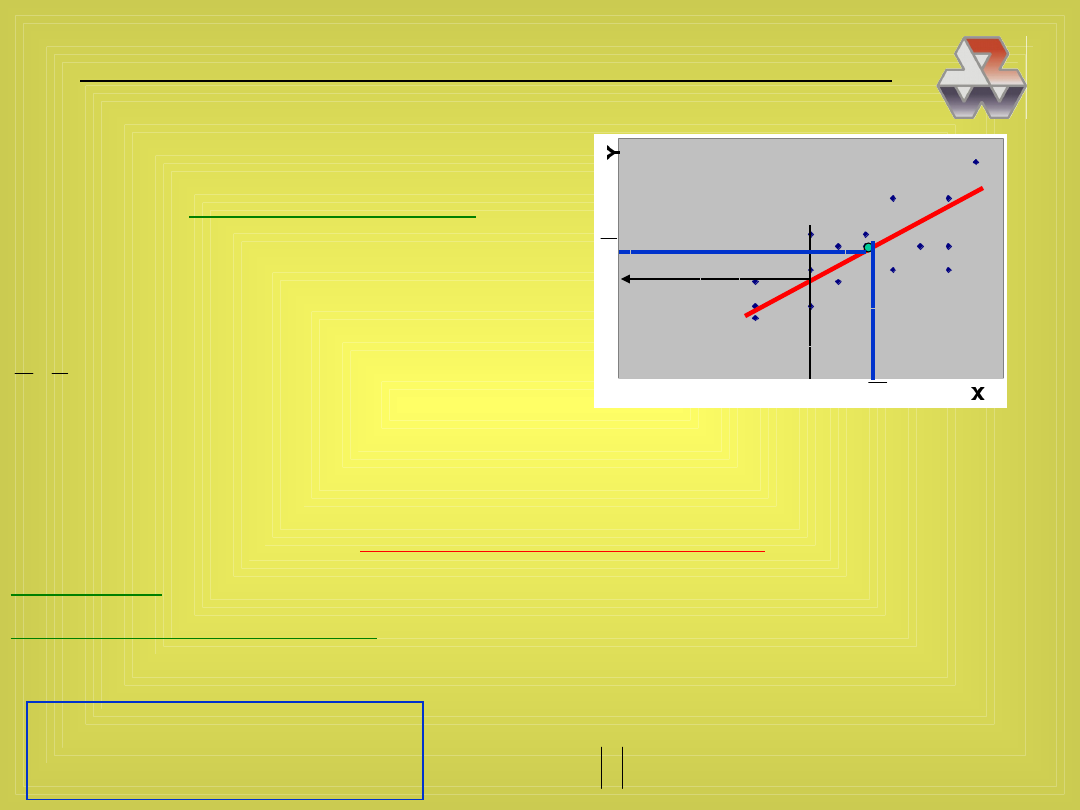
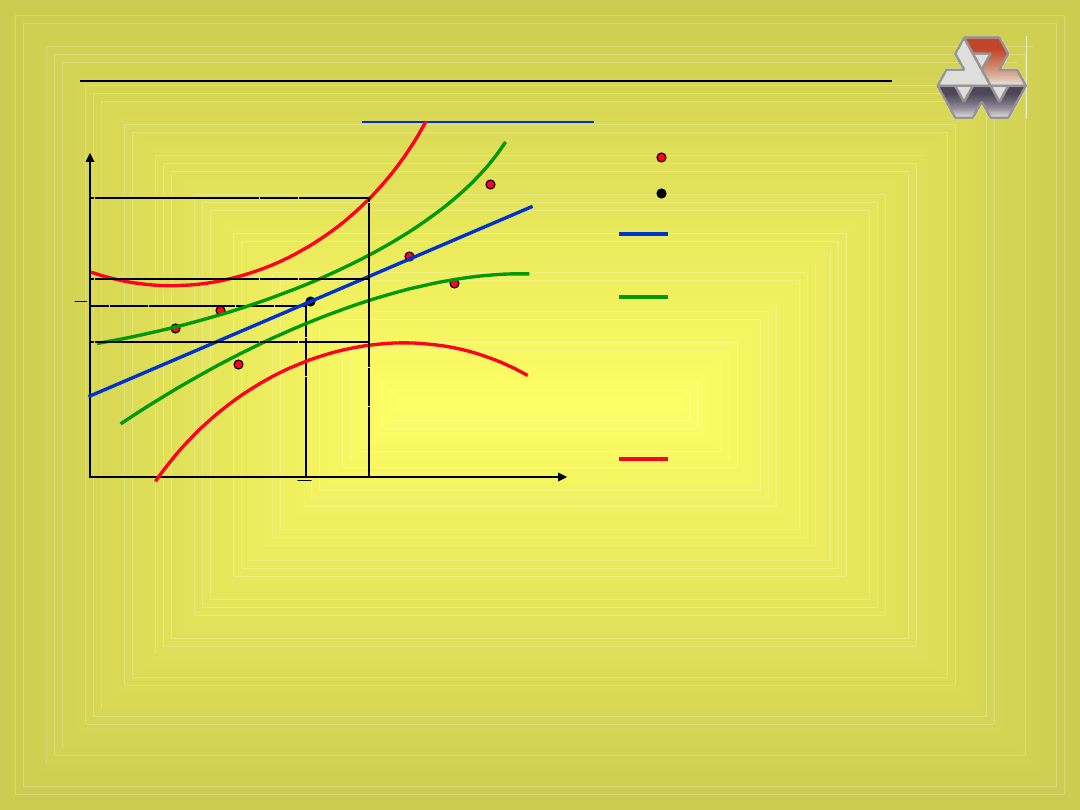
Krzywe Neymana
X
Y
x
y
obserwacje (dane empiryczne)
środek ciężkości próbki
prosta regresji II rodzaju (dla
próbki)
krzywe wyznaczające pas ufnoś-
ci, w którym z prawdopobieńst-
wem 1- znajduje się nieznana
prosta regresji I rodzaju (dla
populacji)
dlaczego taki kształt? (2 ruchy)
krzywe wyznaczające przedziało-
we prognozy wartości zmiennej Y
dla danego x
i
i
x
i
y
i
y
prognoza punktowa uzyskana przez
wstawienie x
i
do równania
gg
dg
gg,dg
przedział, w którym z szansą 1-
mieści się nieznana wartość y
i
dla i-
tej nowej jednostki spoza próbki
Przykłady:
• waga — wzrost studentek
• ocena egzaminu — zaliczenie
• koszt produkcji — wielkość produkcji
• utarg — wydatki na reklamę
• prędkość — zużycie paliwa
Matematyczne techniki zarządzania - 107
Matematyczne techniki zarządzania - 107
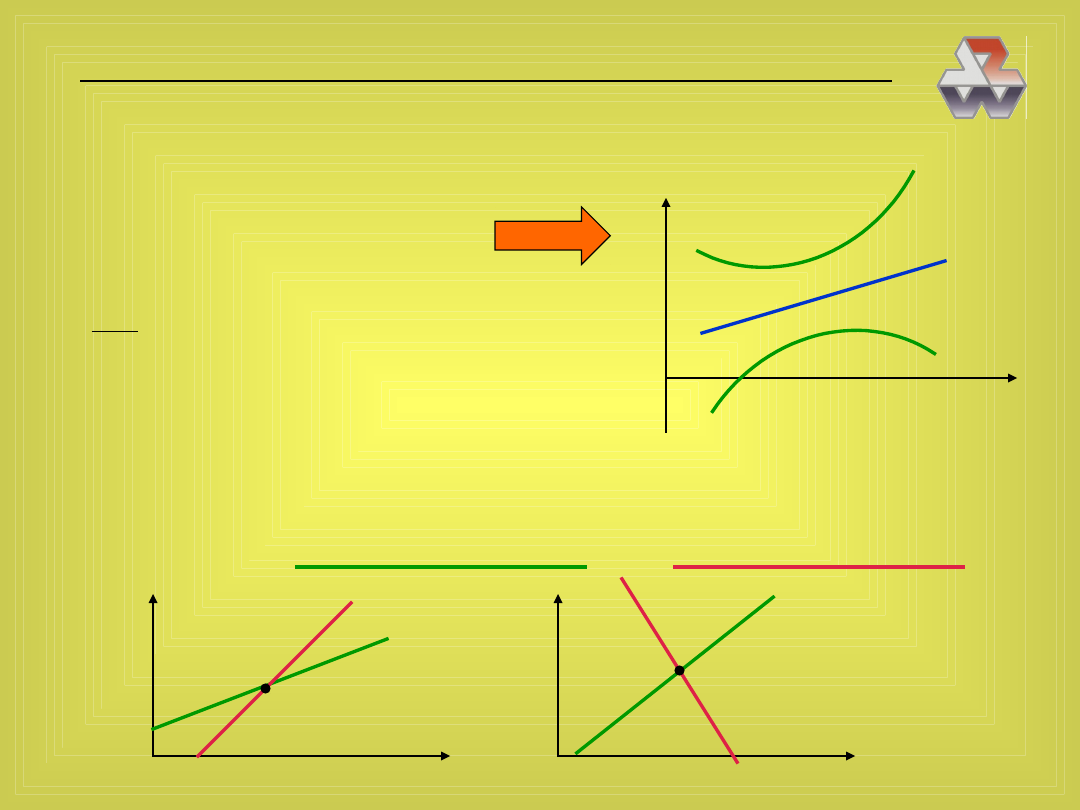
Jak patrzeć na krzywe Neymana?
• przypadek z poprzedniej planszy: niezależnie od tego, co się zdarzy,
0
>0 i
1
>0 (jak to rozumieć)
• ale może być inna sytuacja
co wtedy wiemy o
0
i
1
?
NIC — mogą być >0, =0, <0;
nie wyklu-
czymy więc, że:
• X nie wpływa na Y
• prosta I rodzaju przechodzi przez (0,0)
Te problemy można rozwiązać przez testowanie hipotez o
i
oraz o
Identyczne wnioski można wyciągnąć przy porównaniu dwu prostych II
rodzaju
y
c
c
y
g
x
x
a
a
x
f
y
1
0
1
0
)
(
)
(
mały rozrzut
duży rozrzut obserwacji
Matematyczne techniki zarządzania - 108
Matematyczne techniki zarządzania - 108
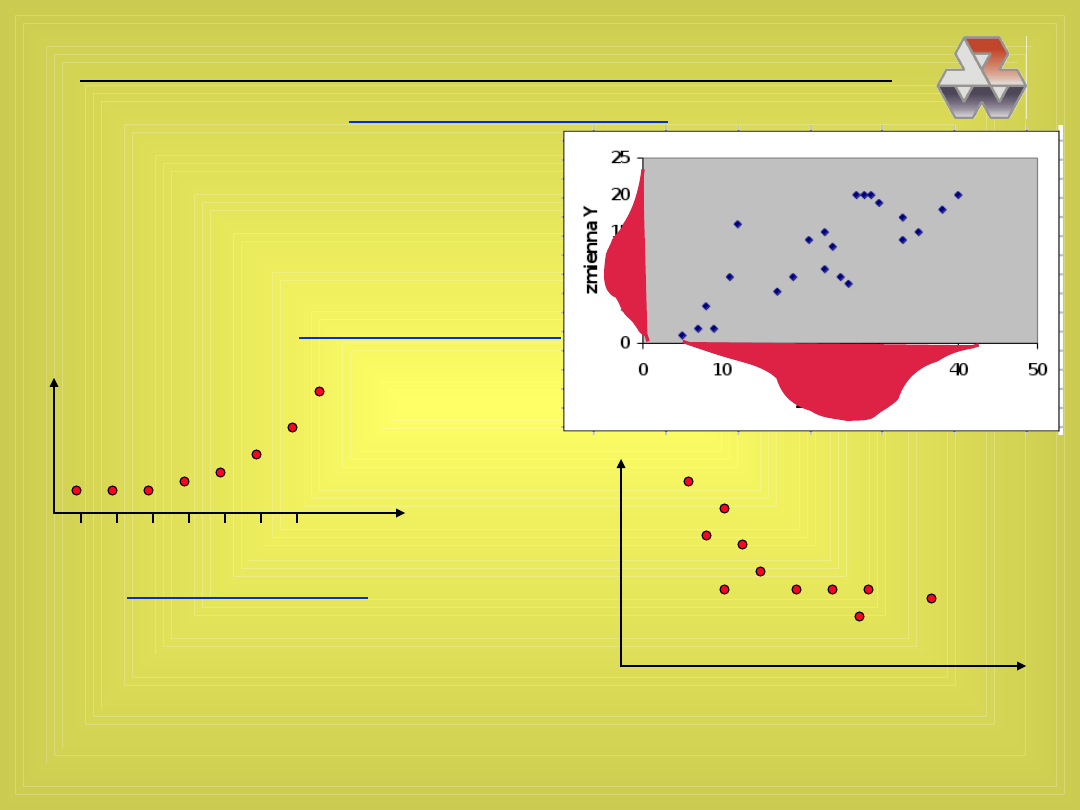
Regresja krzywoliniowa
Kiedy występuje regresja liniowa?
— gdy obie zmienne mają rozkład
normalny!
W wielu przypadkach dane układają
się w zależności nieliniowe:
• gdy mają postać szeregu czasowego
Y
)
(czas
t
• gdy dane przekrojowe układają się
w smugę nieliniową
Y
X
(na przykład — efekt skali)
• gdy krzywoliniowa funkcja wielu
zmiennych lepiej opisuje rzeczy-
wistość niż funkcja liniowa (plansza
103); tego nie widać, która lepsza
można poznać tylko po R
2
Matematyczne techniki zarządzania - 109
Matematyczne techniki zarządzania - 109
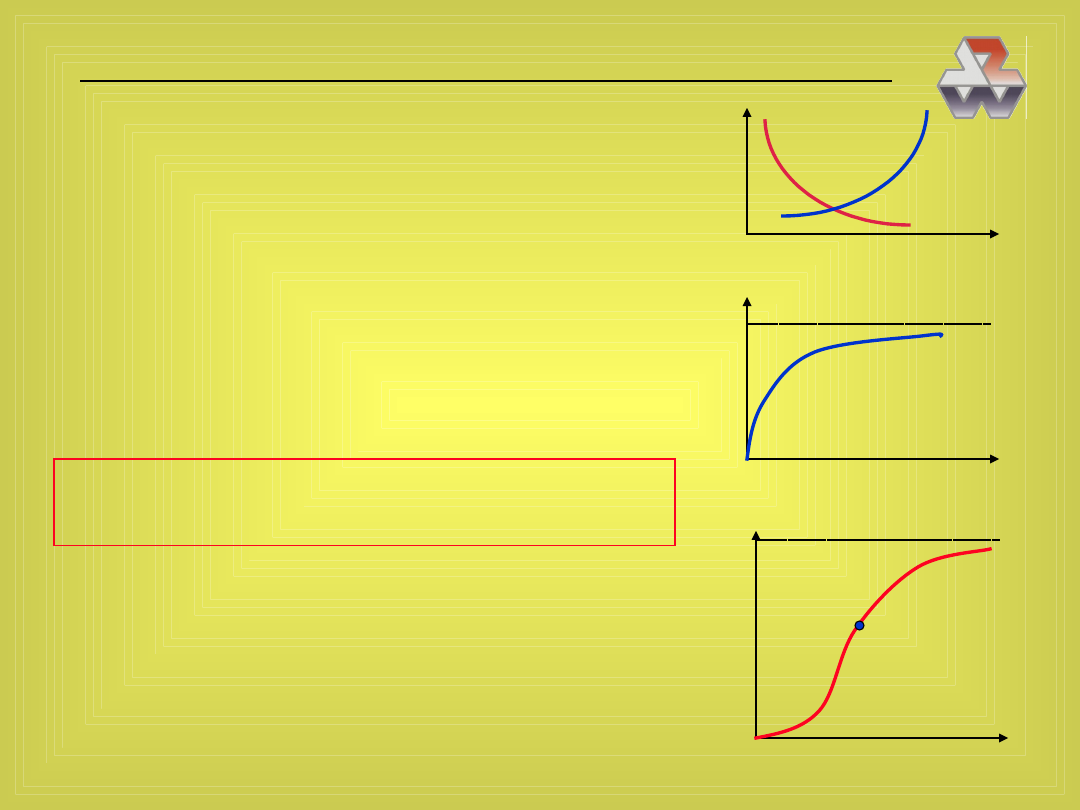
Do opisu takich zjawisk stosujemy rozmaite
funkcje krzywoliniowe:
1. proste funkcje (rosnące lub malejące) dwu
zmiennych: wykładnicze, potęgowe itp.
2. wielomiany różnego stopnia (ich fragmenty)
3. funkcje bardziej złożone: krzywe nasycenia,
krzywe logistyczne itp..
4. funkcję potęgową wielu zmiennych
...
3
2
1
3
2
1
0
a
a
a
x
x
x
a
y
ABY MOŻNA BYŁO STOSOWAĆ METODĘ NAJMNIEJ-
SZYCH KWADRATÓW, FUNKCJE TE MUSZĄ BYĆ
SPROWADZONE DO POSTACI LINIOWEJ
b
x
a
y
b
ax
y
b
x
a
y
i
i
i
i
i
i
ln
ln
ln
ln
.
1
2. Wielomiany są funkcjami liniowymi pod wzglę-
dem swych parametrów
3. Stosuje się „chwyty” (wielokrotne podstawianie)
Matematyczne techniki zarządzania - 110
Matematyczne techniki zarządzania - 110
4. Także stosujemy transformację logarytmiczną
...
ln
ln
ln
ln
2
2
1
1
0
x
a
x
a
a
y
i
Kolejność czynności przy estymacji funkcji regresji krzywoliniowej:
1. zebranie danych empirycznych
2. dobranie modelu (funkcji nieliniowej)
3. transformacja modelu do liniowego (logarytmowanie — transformata)
4. przeliczenie danych na układ liniowy (robi to komputer)
5. oszacowanie równania regresji liniowej
6. retransformacja do postaci pierwotnej (odlogarytmowanie)
Retransformacji podlegają tylko parametry strukturalne, natomiast
wszystkie parametry stochastyczne dotyczą tylko transformaty
Metody estymacji równania regresji
• klasyczna metoda najmniejszych kwadratów (KMNK) w wielu wariantach
obliczeniowych
• podwójna MNK
• regresje specjalne: grzbietowa (ridge regression), odporna (robust) itd.
• metoda największej wiarygodności
Matematyczne techniki zarządzania - 111
Matematyczne techniki zarządzania - 111
Klasyczna metoda najmniejszych kwadratów (KMNK)
n
i
i
i
y
y
1
2
)
ˆ
(
min
W książkach jest całe mnóstwo różnych wa-
riantów, wersji, metod itd. — nie należy tra-
cić głowy ani denerwować się!
PLANSZA 105
Wersja 1. Metoda równań normalnych
2
)
(
min
ˆ
b
ax
y
b
ax
y
i
i
i
i
Wyznaczamy pochodne cząstkowe względem a oraz b i przy-
równujemy je do zera, po przekształceniu otrzymujemy uk-
ład równań normalnych
i
i
i
i
i
i
y
x
x
a
x
b
y
x
a
bn
2
Niewiadome: a, b
Współczynniki: z tabelki roboczej
Z tego układu
równań wywodzą
się dziesiątki
rozmaitych
wzorów na
obliczanie
wartości a i b
Matematyczne techniki zarządzania - 112
Matematyczne techniki zarządzania - 112
Na analogicznej regule można zbudować układ równań normalnych
dla równania
c
bx
ax
y
2
1
y
x
x
b
x
x
a
x
c
y
x
x
x
b
x
a
x
c
y
x
b
x
a
cn
2
2
2
2
1
2
1
2
1
2
1
1
2
1
Wersja 2. Metoda „sigma prim”
n
y
y
y
y
y
i
i
i
2
2
2
2
)
(
)
(
uzyskuje się uproszczone równania
Wersja 3. Metoda mnożników Gaussa,
posługuje się formularzami
obliczeniowymi opartymi o wartości „sigma prim” (W. Volk, Statystyka dla
inżynierów)
Wersja 4. Metoda przekształceń Jordana
Wersja 5. Metoda macierzowa
1
1
2
2
1
1
0
...
k
k
i
i
i
x
a
x
a
x
a
a
y
y
X
X
X
a
T
T
1
)
(
1
1
0
...
k
a
a
a
a
n
k
n
k
k
x
x
x
x
x
x
X
,
1
1
2
,
1
12
1
,
1
11
.
1
...
.
...
.
.
1
.
1
n
y
y
y
y
.
2
1
X
T
X —
współczynniki układu r. n.
X
t
y —
prawe strony układu r. n.
Matematyczne techniki zarządzania - 113
Matematyczne techniki zarządzania - 113
1
2
2
2
)
(
]
)
(
[
1
X
X
s
D
a
y
X
y
y
k
n
s
T
T
T
T
na głównej przekątnej tej macierzy
znajdują się wariancje
s
2
(a
0
), s
2
(a
1
)
...
Wersja 5. Metoda uproszczona Hellwiga
Praktyczne zastosowania analizy regresji i korelacji (przykłady):
• wydajność pracy = f (liczby szkoleń i stażu)
zysk z akcji = f (ceny i dywidendy)
• cena = f (liczby asortymentów)
czas demolki = f (ilości pracy i odległości)
• zużycie prądu = f (pogody i produkcji)
produkcja = f (kapitału i robocizny)
• udział w rynku = f (ceny i liczby reklam)
płaca = f (wieku, funkcji, stażu)
• cena działki = f (obszaru i odległości od morza)
sprzedaż biletów MPK = f(pogody, dnia
• utarg = f (liczba klientów)
tygodnia, liczby mieszkańców)
• plon z ha = f (zużycie nawozów)
• czas choroby = f (temperatury i liczby bakterii)
• koszt reklamy = f (czasu)
x
y
I
II
Dzielimy zbiór na 2 podzbiory i wyzna-
czamy ich środki ciężkości
II
II
I
I
y
x
y
x
,
,
po czym budujemy prostą
przechodzącą przez te punkty
Zmienne 0-1:
3 — profesor
1 — profesor
2 — adiunkt
2 — nie-profesor
1 — asystent
Matematyczne techniki zarządzania - 114
Matematyczne techniki zarządzania - 114
E K O N O M E T R I A
TROCHĘ
GREKI I
ŁACINY
Probabilistyka
— probabilis (prawdopodobny, d. godny pochwały)
Statystyka
— status (stan, państwo); kto to jest lo statista we Włoszech? A
kto la comparsa?
Ekonomia
— oikos (dom, środowisko) + nomos (prawo, ustawa); oiko-nomos
(pan domu); oikonomia — zarządzanie gospodarstwem domowym
Metr, -metria
— metron (miara)
Ekonometria
—
nauka zajmująca się ustalaniem, za pomocą metod
matematyczno-statystycznych, ilościowych prawidłowości zachodzących w
życiu gospodarczym
Nastawienie bardziej na makroekonomię niż na mikroekonomię (ekonomikę
przedsiębiorstwa i przemysłu) — sprawdzanie teorii ekonomicznych:
• zależność eksportu krajowego od PKB,
• zależność dochodu narodowego od ilości pieniądza w obiegu,
także na badanie poziomu życia ludności:
• zależność wydatków na określone dobra od dochodów ludności,
• zależność obrotu sklepów detalicznych od odległości od dużego miasta,
• funkcje popytu i podaży
Matematyczne techniki zarządzania - 115
Matematyczne techniki zarządzania - 115
ale również na zagadnienia związane z zarządzaniem przedsiębiorstwem:
• zależność wartości dodanej na roboczo-godzinę od stawki godzinowej i
kapitałochłonności pracy,
• funkcje produkcji opisujące zależność wielkości produkcji od majątku
trwałego i robocizny.
Specyficzne warunki prowadzenia badań ekonometrycznych
• brak możliwości powtórzenia eksperymentu (nie działają prawa
statystyki matematycznej)
• zaostrzone kryteria matematyczne (n>100)
• trudności z danymi: dostępność, ilość, wiarygodność, porównywalność
NARZĘDZIEM BADAWCZYM EKONOMETRII JEST MODEL EKONOMETRYCZNY, KTÓRY
NARZĘDZIEM BADAWCZYM EKONOMETRII JEST MODEL EKONOMETRYCZNY, KTÓRY
MATEMATYCZNIE ODPOWIADA RÓWNANIU REGRESJI LUB KILKU RÓWNANIOM
MATEMATYCZNIE ODPOWIADA RÓWNANIU REGRESJI LUB KILKU RÓWNANIOM
Terminologia
•
zmienna objaśniana (Y)
—
zmienna egzogeniczna
• zmienne objaśniające (X
1
, X
2
...)
—
zmienne endogeniczne
• zmienne opóźnione w czasie: y
t
, y
t-1
, x
t
, x
t-k
; służą do analizy wpływu
czasu
Matematyczne techniki zarządzania - 116
Matematyczne techniki zarządzania - 116
Klasyfikacja modeli ekonometrycznych
I. Klasyfikacja według wnoszonej informacji:
• modele przyczynowo-skutkowe
)
,...,
,
(
1
2
1
k
x
x
x
f
y
y — skutek
X
i
— przyczyny
Przykłady zmiennej Y:
• średnia z indeksu studentów
• zużycie energii elektrycznej w firmach
• koszty produkcji różnych partii wyrobów
Modele te budujemy z danych przekrojowych
(różne obiekty w tym samym momencie)
• modele tendencji rozwojowej
)
(t
f
y
y — analizowane zjawisko
t — czas
Przykłady zmiennej Y:
• codzienne ceny cebuli
• miesięczne zużycie prądu na WZ AGH
• roczne zużycie gazu ziemnego w PL
Modele te budujemy z szeregów czasowych
(ten sam obiekt w różnych momentach)
Analiza szeregów czasowych (
Analiza szeregów czasowych (time series analysis) — odrębny dział
matematyki
interesuje nas jak zjawisko zmienia się w czasie, nie obchodzi nas co te
zmiany wywołuje
•
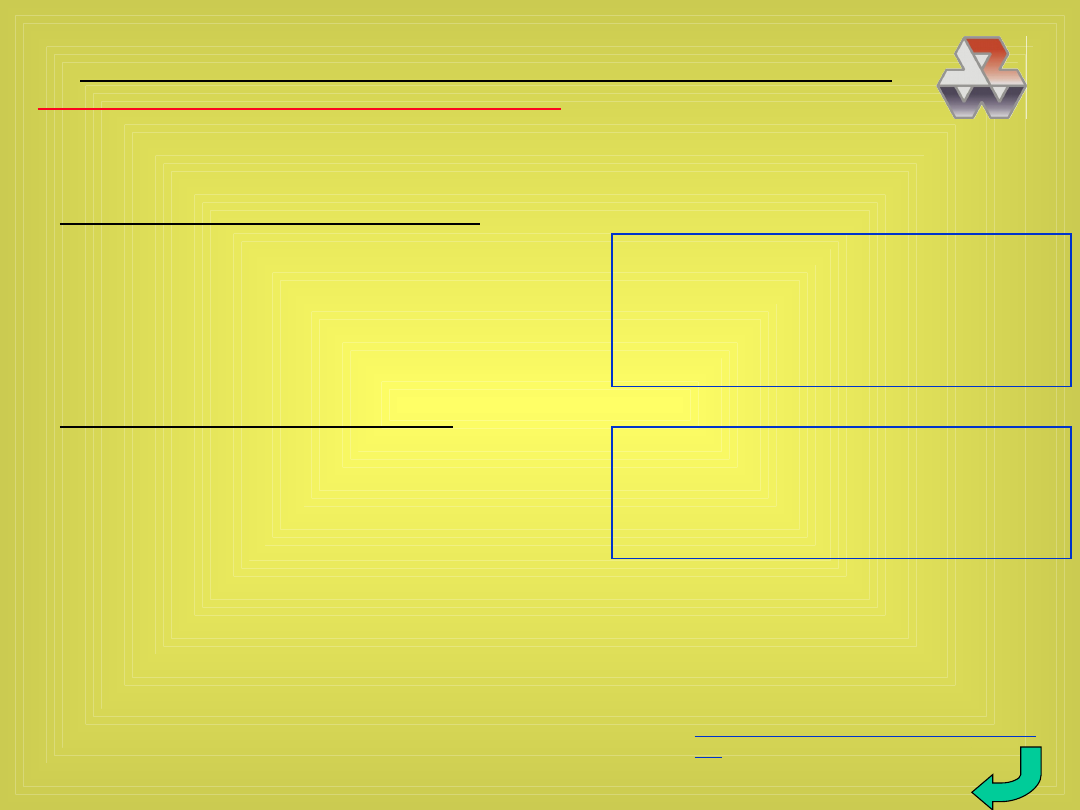
efekt długoterminowy: trend (tendencja)
efekt długoterminowy: trend (tendencja)
•
efekty krótkoterminowe: wahania okresowe, sezonowe, cykliczne
efekty krótkoterminowe: wahania okresowe, sezonowe, cykliczne
Długość: doba,....,rok, 25 lat, 500
lat
Matematyczne techniki zarządzania - 117
Matematyczne techniki zarządzania - 117
Przykład 31. Zinterpretuj wykres powstały z szeregu czasowego miesięczne-
go zużycia energii elektrycznej przez WZ AGH
y
t
1995 1996 1997 1998 1999
II. Klasyfikacja według stopnia uwzględniania czasu:
• modele statyczne
• modele dynamiczne
III. Klasyfikacja według powiązania równań:
• modele proste
• modele rekurencyjne
• modele o równaniach współzależnych
JEDNO RÓWNANIE LUB KILKA ODDZIELNYCH
)
,
,
,
,
(
)
,
,
,
(
)
,
,
,
(
3
2
1
2
1
3
3
2
1
3
2
3
2
1
2
1
x
x
x
y
y
f
y
x
x
x
y
f
y
x
x
x
y
f
y
IV. Klasyfikacja według liniowości:
• modele liniowe
• modele nieliniowe (konieczna transformacja liniowa)
Matematyczne techniki zarządzania - 118
Matematyczne techniki zarządzania - 118
ETAPY BUDOWY MODELU EKONOMETRYCZNEGO
1. Sformułowanie modelu
a. wybór zmiennych:
y, x
1
, x
2
,...
b. wybór postaci matematycznej modelu:
liniowa, potęgowa,...
2. Zebranie danych statystycznych
(różne źródła)
3. Selekcja zmiennych objaśniających
(celem podziału na dwie grupy —
nadające się do modelu i niepotrzebne w nim)
4. Estymacja parametrów modelu:
a. parametrów strukturalnych:
a
0
, a
1
, a
2
,...
b. parametrów stochastycznych:
s(a
i
), s(y), R
2
, R
5. Weryfikacja modelu
(przy użyciu hipotez i testów statystycznych)
MODEL BEZ WERYFIKACJI NIE MA ŻADNEJ WARTOŚCI
MODEL BEZ WERYFIKACJI NIE MA ŻADNEJ WARTOŚCI
NIE NALEŻY KORZYSTAĆ Z PROGRAMÓW KOMPUTEROWYCH NIE
NIE NALEŻY KORZYSTAĆ Z PROGRAMÓW KOMPUTEROWYCH NIE
DAJĄCYCH MOŻLIWOŚCI WERYFIKACJI
DAJĄCYCH MOŻLIWOŚCI WERYFIKACJI
6. Interpretacja modelu
• wyciągnięcie wniosków dla celów zarządzania
• sprzedanie go klientowi
Matematyczne techniki zarządzania - 119
Matematyczne techniki zarządzania - 119
ETAP 1a. WYBÓR ZMIENNYCH
ETAP 1a. WYBÓR ZMIENNYCH
• zmienna objaśniana Y:
według zainteresowań (na ćwiczeniach), według
polecenia szefa (w przedsiębiorstwie), według życzenia klienta (w firmie
konsultingowej)
• zmienne objaśniające X
i
(jak najwięcej dla modelu przyczynowo-
skutkowego) z następujących źródeł (w kolejności):
— teoria danej dziedziny wiedzy
— doświadczenie zleceniodawcy i statystyka
— metodą prób i błędów (intuicyjnie)
• wybrane zmienne muszą mieć dużą zmienność (W>30%)
• najczęstszy błąd — „masło maślane”
prowadzące do związku funkcyjne-
go i nie dające żadnej informacji o zmiennej objaśnianej
przykład modelu bez sensu: wynagrodzenie = f(płacy, premii i dodatku
stażowego)
i
i
x
a
y
i
i
a
i
x
a
y
x
y
i
ln
ln
ETAP 1b. WYBÓR POSTACI MATEMATYCZNEJ
ETAP 1b. WYBÓR POSTACI MATEMATYCZNEJ
• modele przyczynowo-skutkowe
—
najbardziej zalecane jest
równoczesne prowadzenie obliczeń dla dwu postaci:
— liniowej
— potęgowej
Co typujesz, gdy Y to:
• wynik studiów
• zysk firmy
Matematyczne techniki zarządzania - 120
Matematyczne techniki zarządzania - 120
— stosuje się też modele nieliniowej o narzuconej postaci
nieliniowej, których parametry ustala się przez
programowanie liniowe lub innymi metodami
• modele tendencji rozwojowej:
— funkcja liniowa
— proste funkcje nieliniowe
— wielomiany
— funkcje skomplikowane
— modele kombinowane: trend + wahania okresowe
b
x
a
y
b
ax
y
b
x
a
y
i
i
i
i
i
i
ln
ln
ln
ln
(t zamiast x)
• są to zależności dla ln, dla
układu y=f(x) mogą być
dziwne (R
2
>1)
• są to funkcje „sztywne”,
„nieposłuszne
y
t
• wielomian jest modelem liniowym!
x
x
x
x
c
bx
ax
y
2
2
1
2
• można znaleźć optymalny stopień wielomianu
(przez badanie którego rzędu wartości Δy są
sobie mniej więcej równe)
Efekt „krzywego lustra”
Document Outline