Wyrównanie 

Wyrównanie 

obserwacji GPS

obserwacji GPS

 

 

Rodzaje błędów

Rodzaje błędów

Pomyłki

B

ł

ęd

y systematyczne

B

ł

ę

d

y 

p

r

z

y

p

a

d

k

o

w

e

 

 

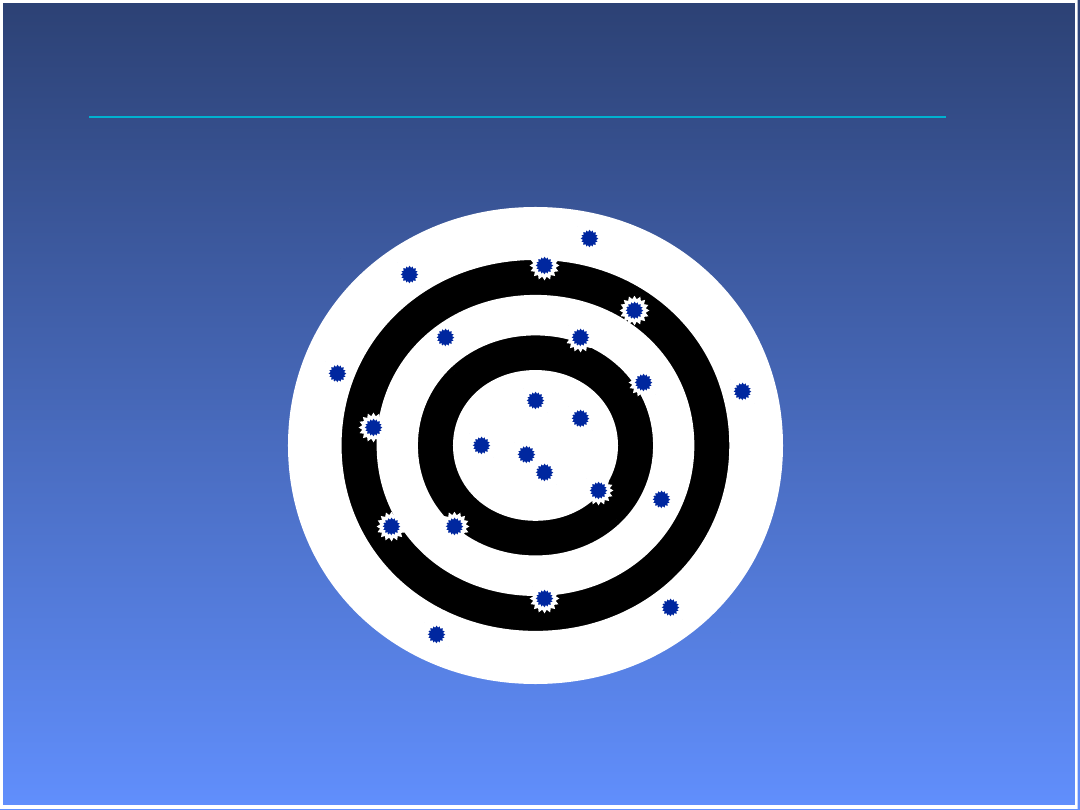
Dokładność

Dokładność

 vs. 

 vs. 

precyzja

precyzja

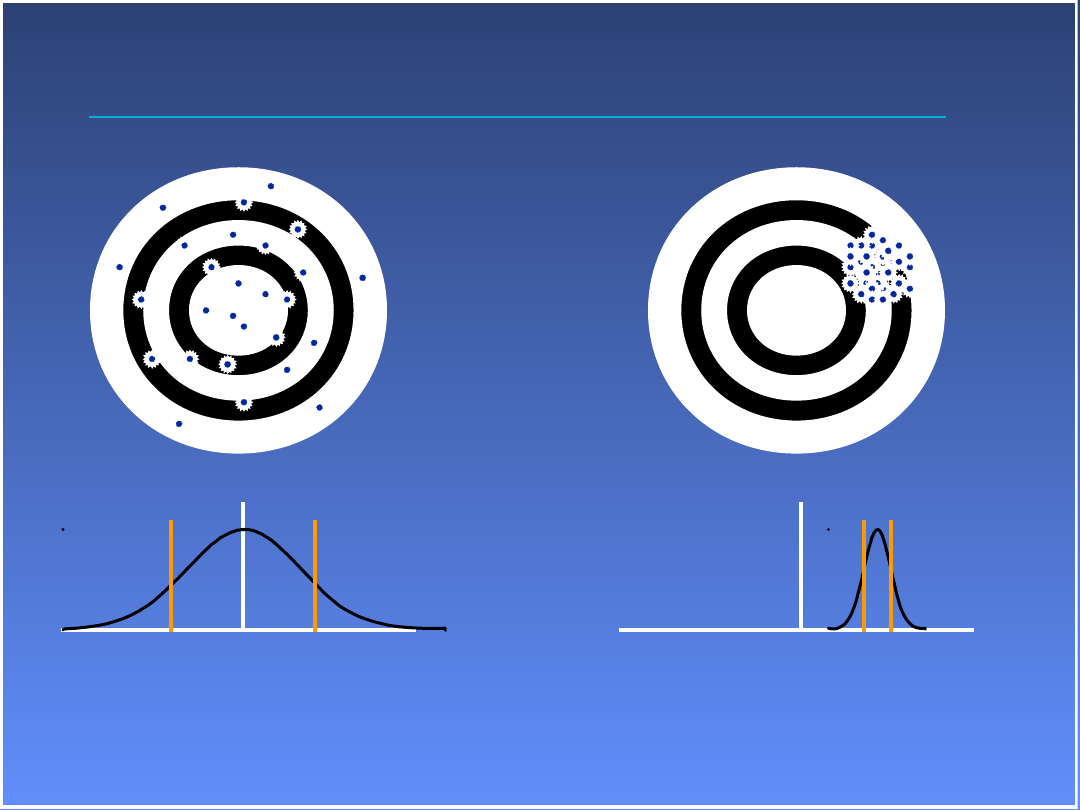
Wysoka dokładność a niska precyzja

 

 

Dokładność

Dokładność

 vs. 

 vs. 

precyzja

precyzja

Niska dokładność i wysoka 
precyzja

 

 

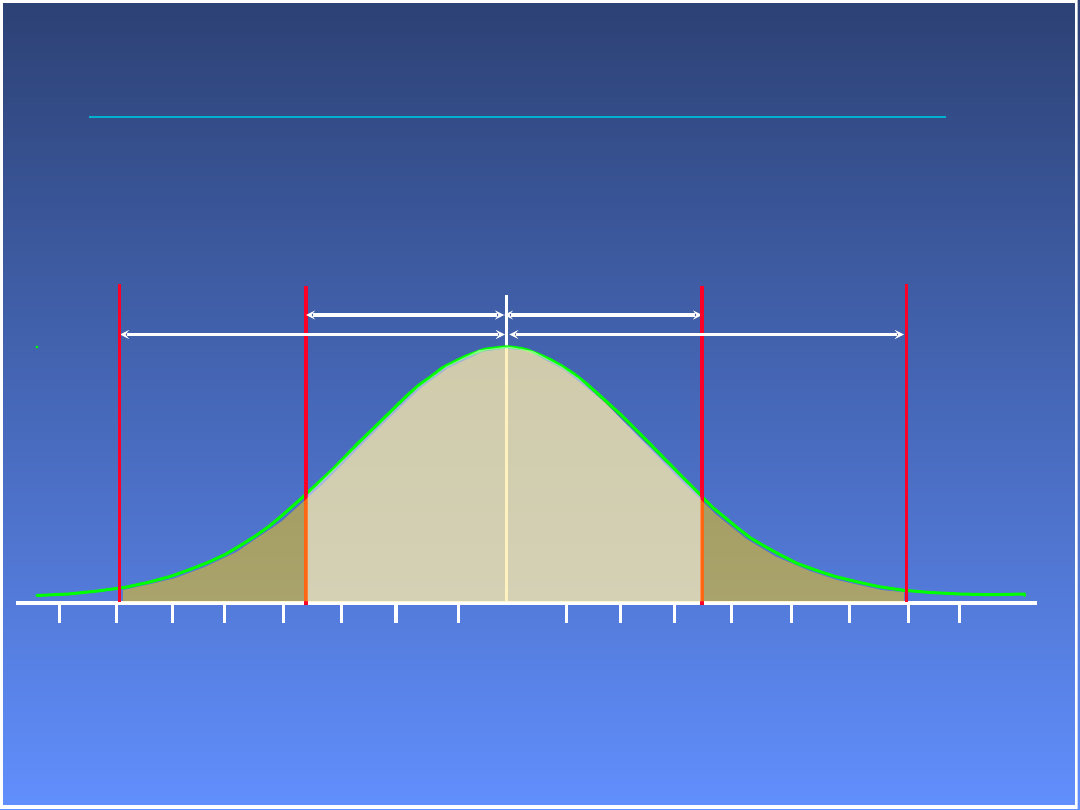
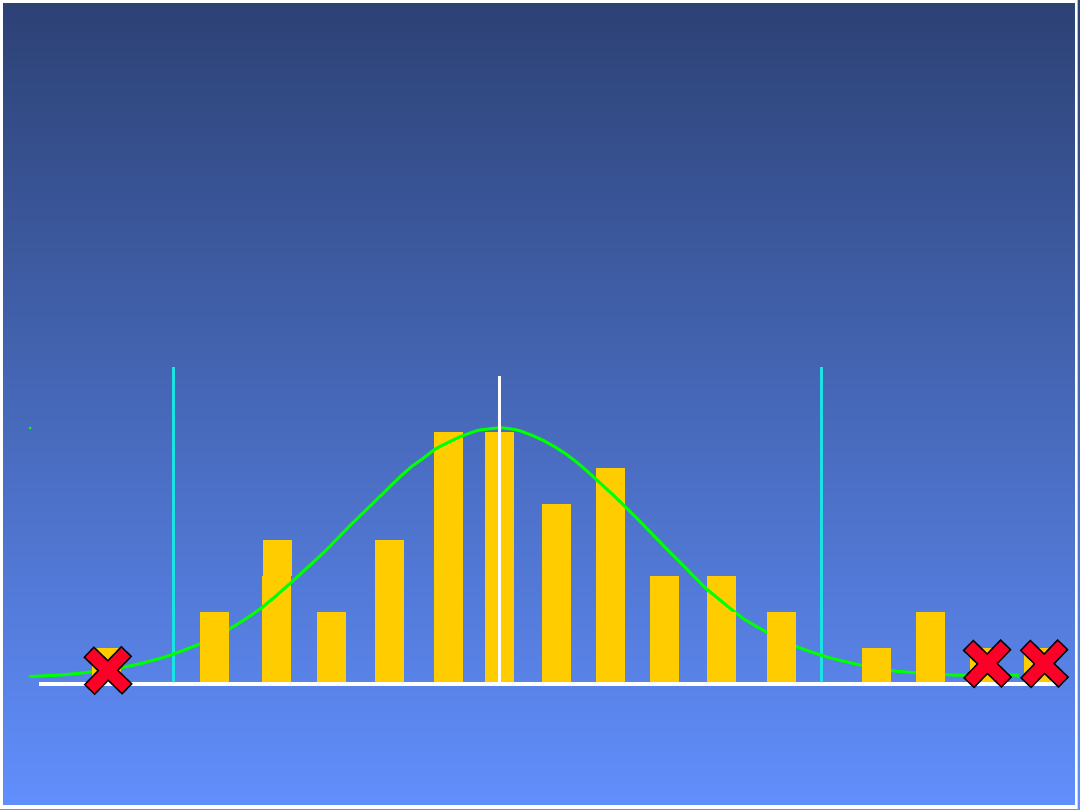
Odchylenie standardowe

Odchylenie standardowe

 

 

(

(

rozkład 

rozkład 

normalny

normalny

)

)

4.0

Ś

re

d

n

ia

 

0.5 1.0 1.5 2.0 2.5 3.0 3.5

-0.5

-1.0

-1.5

-2.0

-2.5

-3.0

-3.5

-4.0

Wartości poprawek 
(cm)

1 



1 



2 



2 



 

 



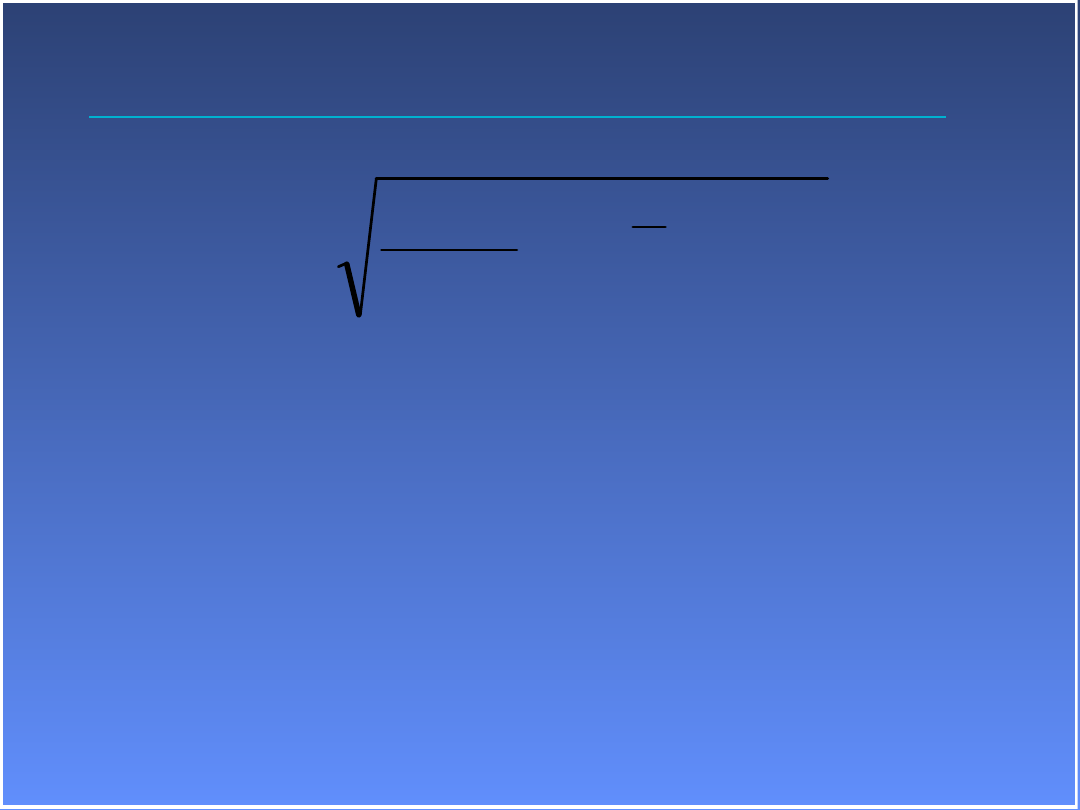
x

i 1

N

i

2

1

N 1

(x x )











Odchylenie standardowe

Odchylenie standardowe

 

 

(sigma, s)

(sigma, s)

 

 

Odchylenie standardowe - 

Odchylenie standardowe - 

przykład

przykład

 

 

 

 

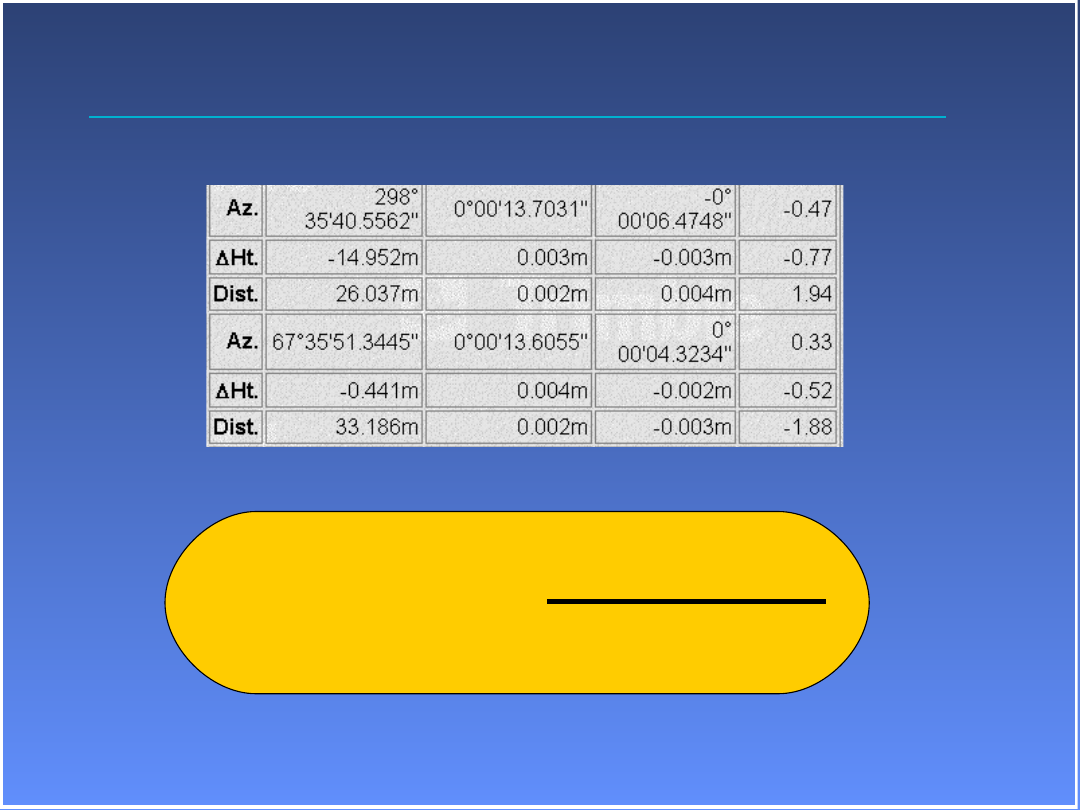
Składowe wektora (metry):                                 

dx          -7.274       

dy          81.883          

dz          84.825

Odchylenie standardowe (metry):                                 0.000392                 0.000648                   0.000883

                                                                           

dn        107.199      de         -49.608         du           -0.571

                                                                                      0.000561                0.000352                   0.000956

                                                                                                                                            

dh          -0.570

                                                                                                                                                      0.000956

Macierz wariancyjno-kowariancyjna                             1.539165E-007

                                                                                     1.168243E-007         4.202073E-007

                                                                                    -1.185407E-007        -3.448070E-007          7.789994E-007

Błędy obserwacji – a’priori

Błędy obserwacji – a’priori

•

Oszacowanie błędów obserwacji 

przed wyrównaniem

 

 

Błąd centrowania

Błąd centrowania

Określa „swobodę zaczepienia” wektora

 

 

X

+

Stała

 Macierz 

błędów
a priori

Błędy
centrowania

(

)

[ ]

Ostateczne wartości błędów 

Ostateczne wartości błędów 

obserwacji

obserwacji

 

 

Poprawka 

Poprawka 

standaryzowana

standaryzowana

Poprawka

standaryzowana

Poprawka

=



Poprawki

 

 

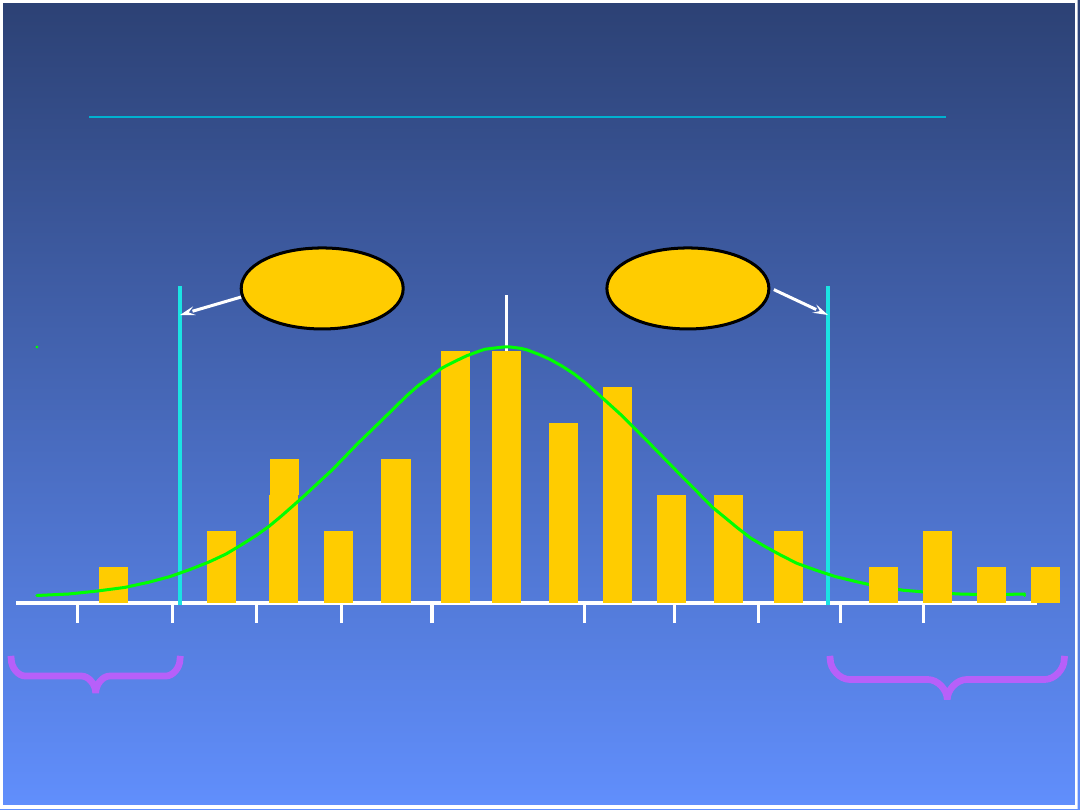
Kryterium Tau

Kryterium Tau



1

2

3

4

1

2

3

4



 



Błąd

Błąd

 

 

Wyrównanie - korzyści

Wyrównanie - korzyści

•

Możliwe przy założeniu, że obserwacje 

obarczone są błędami przypadkowymi

•

W przypadku obserwacji nadliczbowych 

pozwala uzyskać jedno rozwiązania

•

Minimalizuje wartości poprawek

•

Pozwala wykrywać błędy grube i znaczne 

błędy pomiarowe

•

Daje oszacowanie dokładności wyrównywanej 

sieci (współrzędnych i ich funkcji)

 

 

Etapy wyrównania

Etapy wyrównania

  Wyrównanie sieci wykonuje się 

zwykle w dwóch krokach:

  Wyrównanie swobodne 

(niezniekształcające)

•

Wyrównanie nawiązane

 

 

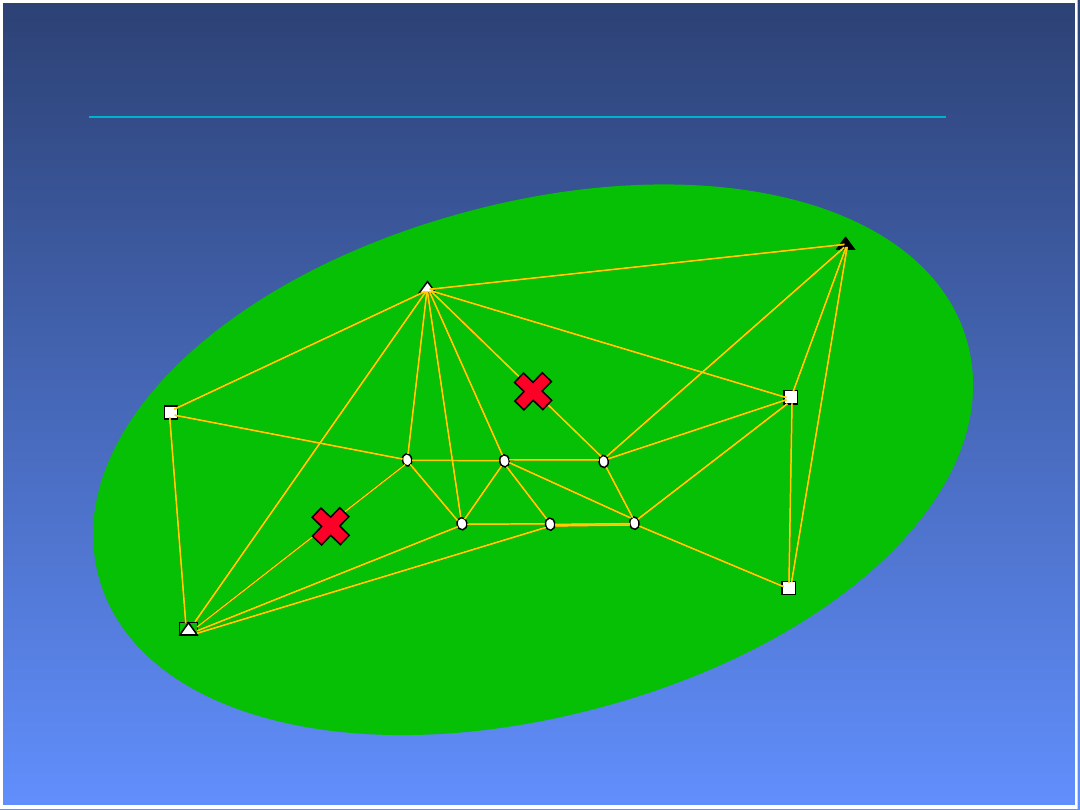
Wyrównanie niezniekształcające

Wyrównanie niezniekształcające

•

Pozwala skontrolować wewnętrzną 

spójność sieci

•

Pozwala wykryć omyłki i odstające 

obserwacje (błędy grube) 

•

Daje najlepsze oszacowanie 

rozkładu błędów w sieci

 

 

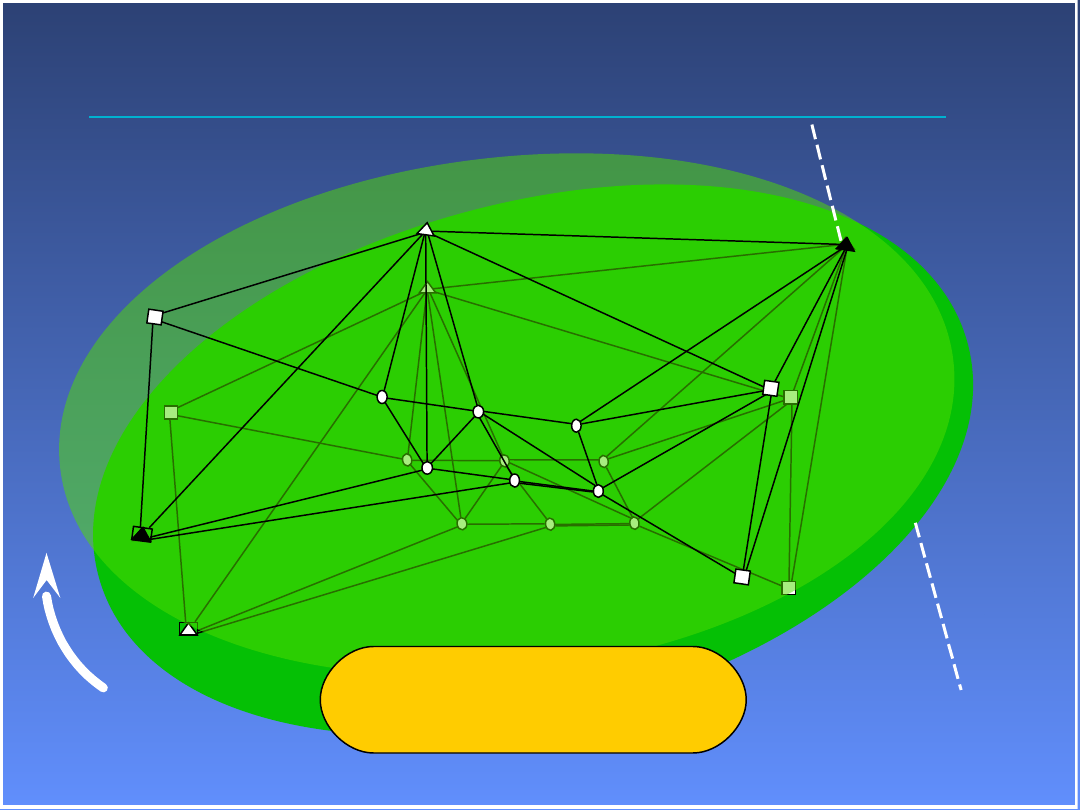
Wyrównanie 

Wyrównanie 

niezniekształcające 

niezniekształcające 

 

 

Wyrównanie niezniekształcające

Wyrównanie niezniekształcające

•

Prowadzi się iteracyjnie 

do czasu kiedy …

•

wszystkie błędne 

obserwacje zostaną 

usunięte z sieci

•

oszacowanie dokładności 

obserwacji będzie 

optymalne (np. mo=1) 

 

 

Test  (

Test  (





2

2

)

)

•

Test statystyczny badający 

zgodność obserwacji z rozkładem 

normalnym (liczony w funkcji 

błędów obserwacji, nadliczbowości 

i założonego poziomu ufności)

•

Wyrównanie zwykle nie spełnia 

testu dopóty, dopóki błąd typowy 

sieci znacznie odbiega od jedności

 

 

Wyrównanie nawiązane

Wyrównanie nawiązane

•

Nawiązuje sieć do istniejącej 

osnowy

•

Zwiększa niezawodność sieci

•

Transformuje współrzędne 

punktów sieci do układu 

zdefiniowanego poprzez punkty 

nawiązania

 

 

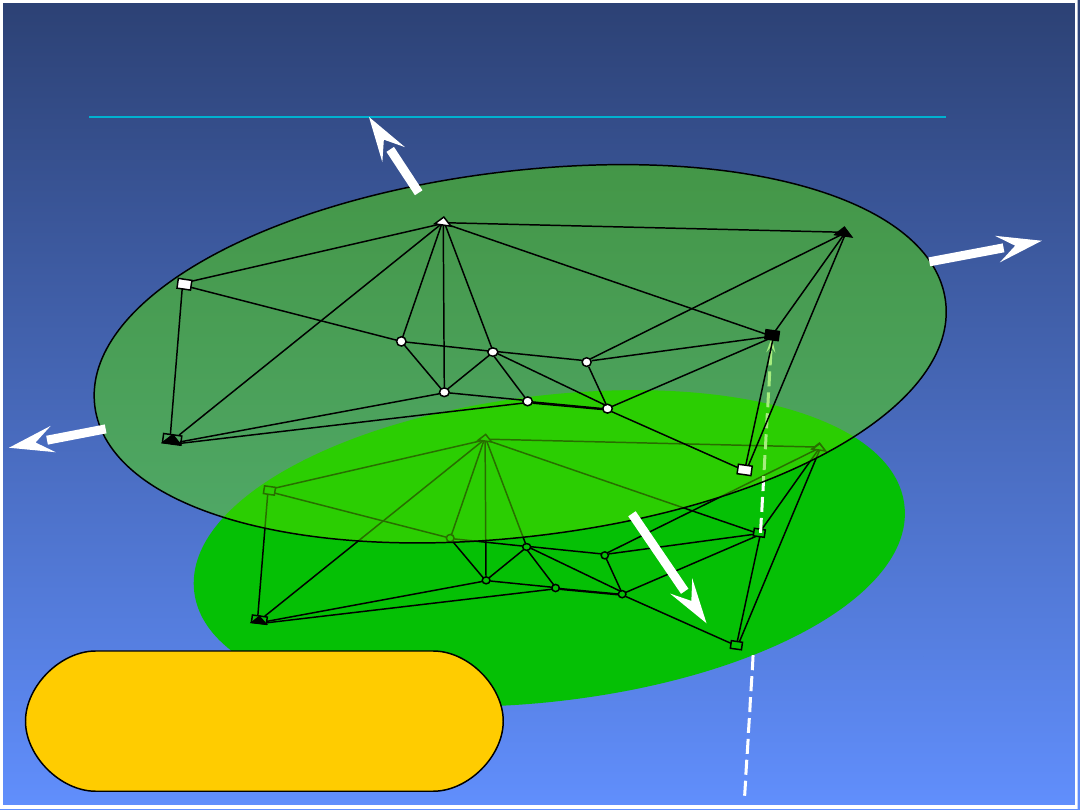
Wyrównanie nawiązane

Wyrównanie nawiązane

2 punkty (XY) określają 

kąt obrotu

 

 

Wyrównanie nawiązane

Wyrównanie nawiązane

2 punkty (XY) i

1 punkt (H)

Definiuje kąt obrotu i skalę sieci

 

 

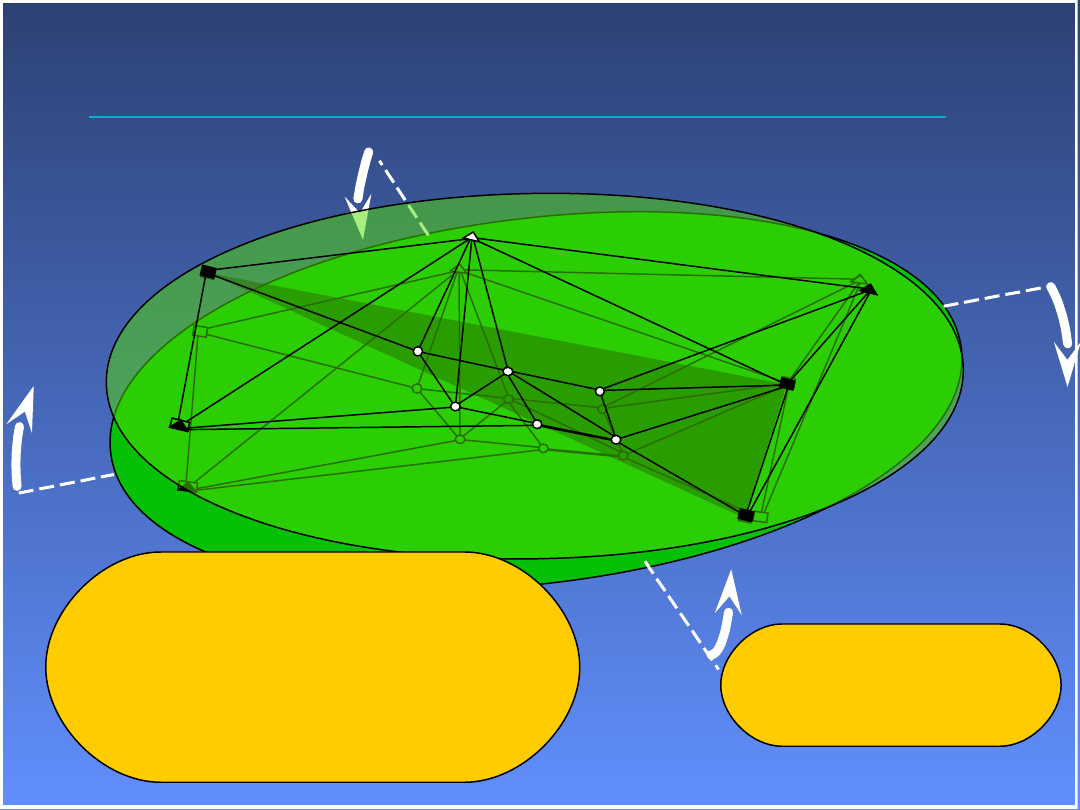
Wyrównanie nawiązane

Wyrównanie nawiązane

2 punkty (XY) i

3 punkty (H)

Definiują kąt obrotu, 

skalę sieci i odchylenie pionu

 (Transformacja 7-mio parametrowa )

Nawiązanie do większej 

liczby punktów zwiększa 

pewność rozwiązania