Wykład 3

projektowanie filtrów

cyfrowych

Lecture 3

digital filters design

Jerzy Łopatka ITK WEL WAT

Jerzy Łopatka ITK WEL WAT

PROJEKTOWANIE FILTRÓW CYFROWYCH

Filtr cyfrowy jest liniowym układem dyskretnym, niezmiennym względem

przesunięcia, zrealizowany za pomocą arytmetyki o skończonej
precyzji

etapy projektowania:
- określenie pożądanych parametrów układu
- aproksymacja tych parametrów za pomocą przyczynowego układu

dyskretnego

- realizacja za pomocą arytmetyki o skończonej precyzji
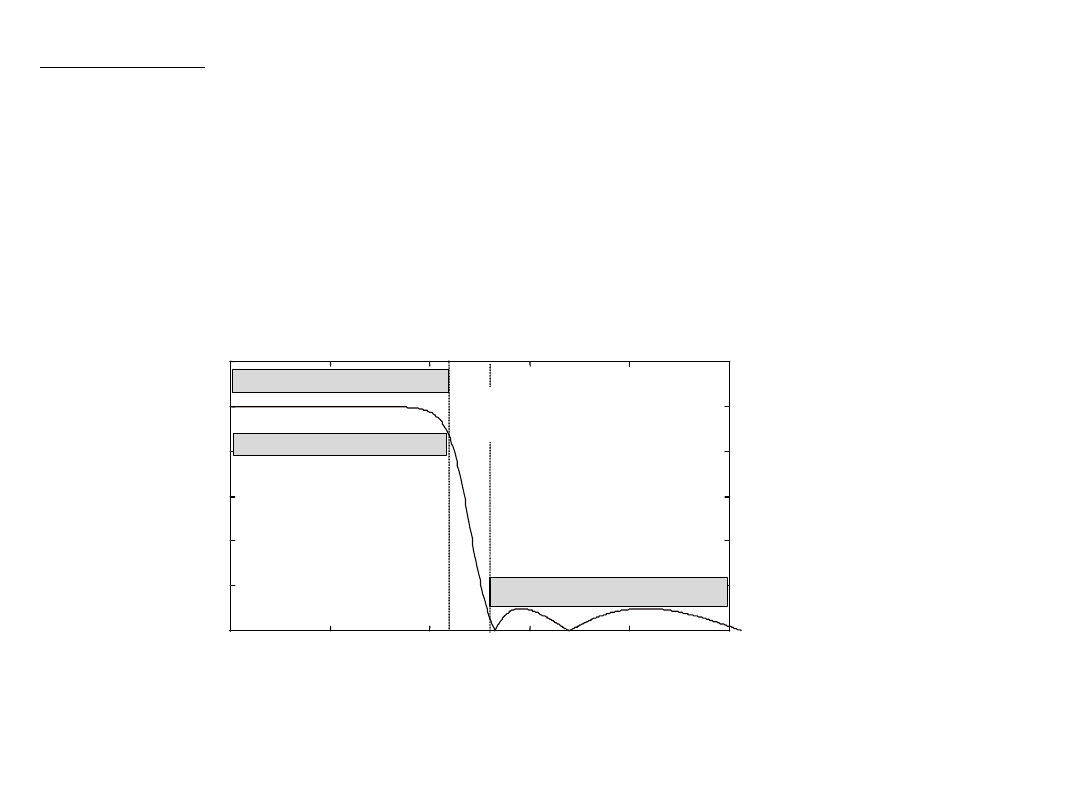
Często wymagania na filtr podawane są w postaci przedziałów tolerancji

0

100

200

300

400

500

0

0.2

0.4

0.6

0.8

1

1.2

pasmo
przepustowe

pasmo
zaporowe

pasmo
przejściowe

częstotliwość

tłumienie

przebieg charakterystyki filtru aproksymowany jest za pomocą funkcji:

- wielomianowej dla filtrów FIR,
- wymiernej dla filtrów IIR.

Jerzy Łopatka ITK WEL WAT

DIGITAL FILTER DESIGN

Digital filter is a discrete linear system, time shift independent, relizaed

by the arithmetic of finite precision
stages of design:
- Identify the desired parameters of the system
- Approximation of these parameters by means of a causal discrete
system
- Implementation using a finite precision arithmetic
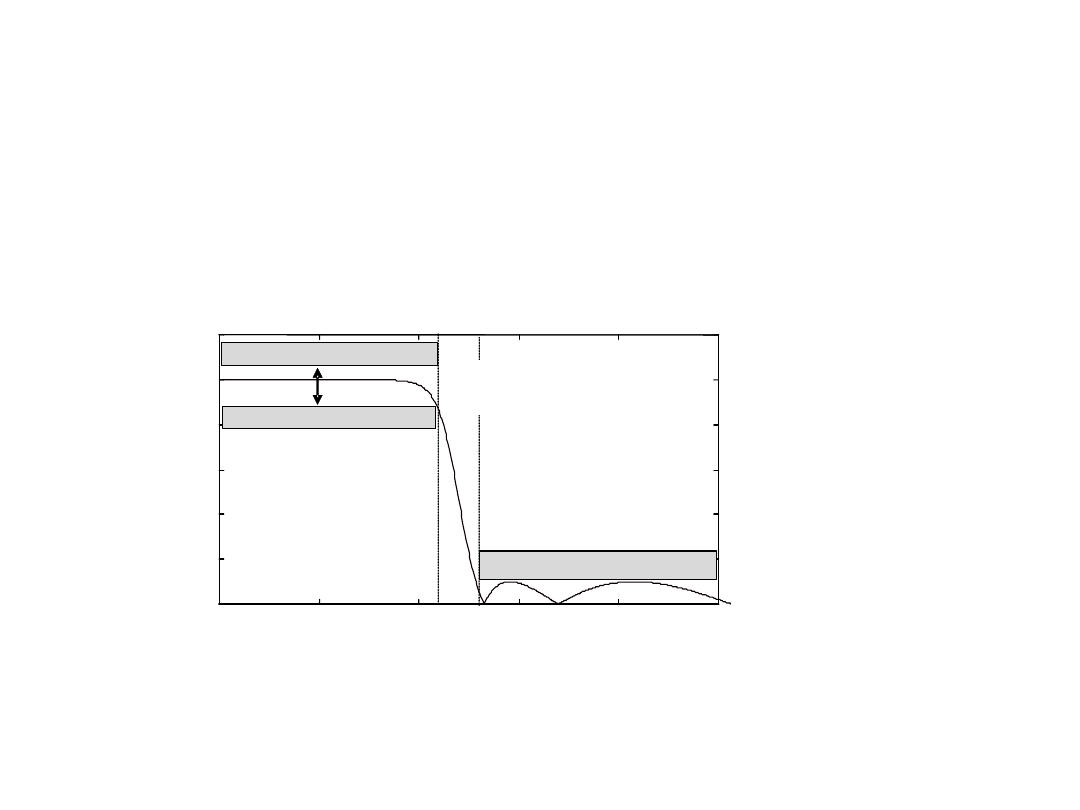
The requirements for the filter are often given as ranges of tolerances

0

100

200

300

400

500

0

0.2

0.4

0.6

0.8

1

1.2

passband

stopband

transcient
band
zejściowe

Frequency

Attenuation

ripple

filter characteristic is approximated by using:
- Polynomial function for FIR filters,
- Fractional function for IIR filters.

Jerzy Łopatka ITK WEL WAT

PROJEKTOWANIE FILTRÓW IIR W OPARCIU O CHARAKTERYSTYKI

FILTRÓW ANALOGOWYCH

Projektowanie to polega na przekształceniu filtru analogowego na filtr

cyfrowy zgodnie z założeniami.

przyczyny:

- zaawansowane metody projektowania filtrów analogowych
- prostota wielu metod analogowych
- filtry cyfrowe niejednokrotnie symulują filtry analogowe

założenia

- przekształcenie powinno zachować zasadnicze właściwości filtru

analogowego

- stabilny filtr analogowy powinien być przekształcony na stabilny filtr
cyfrowy (jeżeli filtr analogowy posiadał bieguny w lewej
półpłaszczyźnie płaszczyzny s to filtr cyfrowy powinien posiadać
bieguny wewnątrz okręgu jednostkowego na płaszczyźnie z)

Jerzy Łopatka ITK WEL WAT

IIR FILTER DESIGN BASED ON THE CHARACTERISTICS OF ANALOG

FILTERS

This design involves converting an analog filter to digital filter in

accordance with the assumptions.
reasons:
- Advanced design methods of analog filters
- Simplicity of many methods for analog filters
- Digital filters often simulate analog filters
Established
- Conversion should retain the essential characteristics of the analog
filter
- A stabile analog filter should be transformed into a stabile digital
filter (if you have an analog filter with poles in the left half-plane of
the plane S, the digital filter should have poles inside the unit circle
on the plane Z)

Jerzy Łopatka ITK WEL WAT

METODA NIEZMIENNOŚCI ODPOWIEDZI IMPULSOWEJ

Przyjmujemy że, odpowiedź impulsowa filtru cyfrowego jest ciągiem

próbek odpowiedzi impulsowej filtru analogowego, pobranych w
równych momentach czasu.

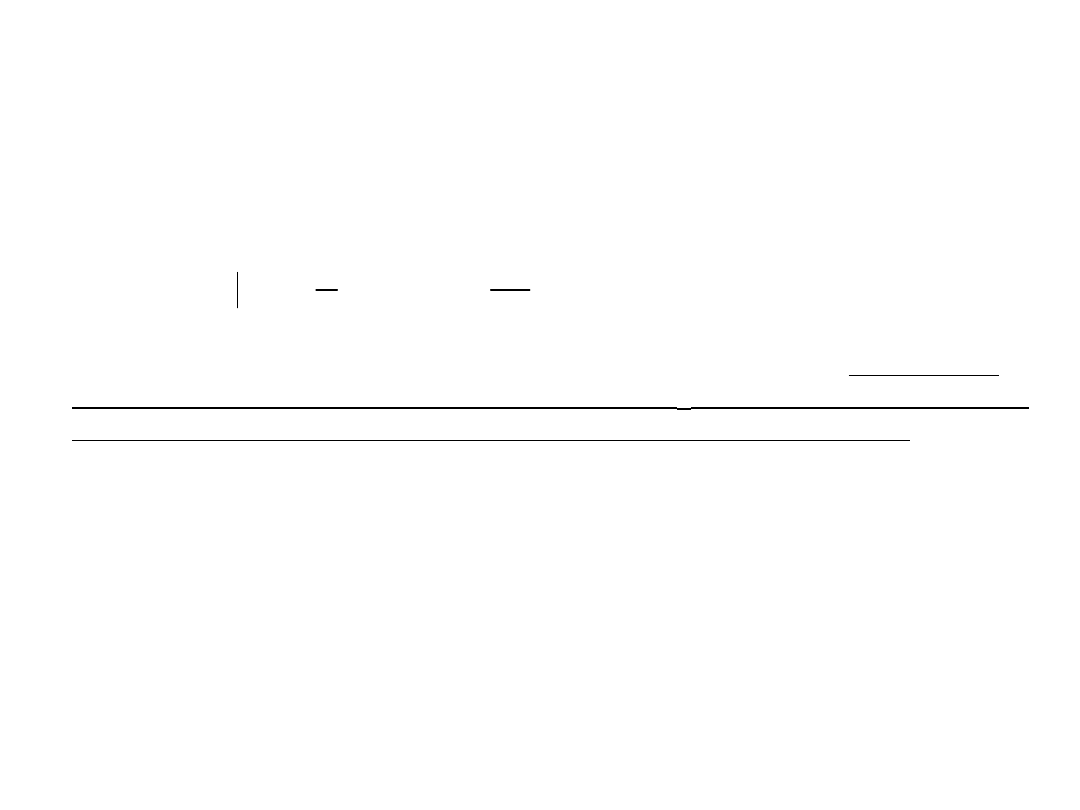
Można dowieść że, z zależności między transformatą Laplace’a funkcji

h

a

(n) a transformatą Z funkcji h(n) wynika iż, istnieje równość:

zależność pomiędzy argumentami tych funkcji wskazuje że: paski lewej

półpłaszczyzny płaszczyzny s, o szerokości 2/T transformowane są na

wnętrze okręgu jednostkowego na płaszczyźnie z i sumowane

zalety:

- prostota metody
- liniowe odwzorowanie częstotliwości analogowej na cyfrową,
- dobre odtworzenie charakterystyk częstotliwościowych filtrów

wąskopasmowych

wady:

- występuje nakładanie się charakterystyk
- mała dokładność odwzorowania
- metoda nadaje się jedynie do filtrów pasmowo-przepustowych i
dolnoprzepustowych (układów o ograniczonym paśmie przenoszenia)

h n

h nT

a

( )

( )



H z

T

H s j

T

k

z e

a

k

sT

( )



 



















1

2



Jerzy Łopatka ITK WEL WAT

METHOD OF INVARIANT IMPULSE RESPONSE

Assume that, filter impulse response is a sequence of digital samples of

the analog filter impulse response, taken in equal moments of time.
 
It can be proved that, with the relationship between the Laplace
transform of the function h

a

(n) and the transform of the function h (n)

implies that there is equality:

Relationship between the arguments of these functions indicates that:
strips of the left half-plane, havin a width of 2 / T are transformed

into the interior of the unit circle on the plane to and aggregated.
Advantages:
- Simple method
- Linear mapping of frequency analogue to digital
- Good for narrowband filters
Disadvantages:
- Overlaping characteristics
- Small precision of mapping
- The method is only suitable for passband and lowpass filters
(systems with limited transmission band)

h n

h nT

a

( )

( )



H z

T

H s j

T

k

z e

a

k

sT

( )



 



















1

2



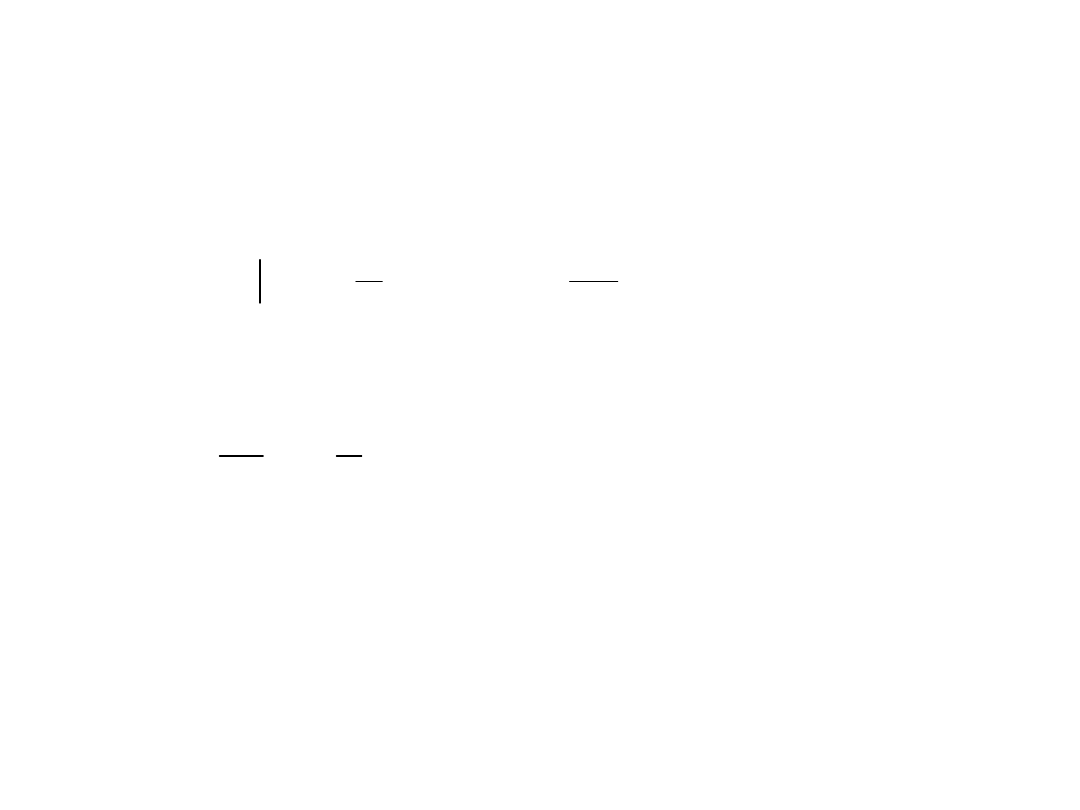
Jerzy Łopatka ITK WEL WAT

TRANSFORMACJA DWULINIOWA

To przekształcenie uzyskano stosując przybliżone wyliczane całki

(metodą trapezów) w równaniu różniczkowym opisującym filtr
analogowy (odpowiednik równania różnicowego dla filtru cyfrowego).

Otrzymano równanie:

dla wartości leżących na okręgu jednostkowym uzyskano zależność

między argumentami funkcji:

- związek pomiędzy częstotliwością analogową i cyfrową jest nieliniowy
- cała lewa półpłaszczyzna płaszczyzny s przekształcana jest na wnętrze

okręgu

jednostkowego

- oś urojona przekształcana jest na okrąg jednostkowy
- częstotliwości = na płaszczyźnie z, odpowiada nieskończona

częstotliwość

analogowa

- nie występuje zjawisko nakładania się charakterystyk.
- metodę można stosować do wszelkich filtrów.

H z

T

H s j

T

k

z e

a

k

sT

( )



 



















1

2



T

tg



2

2















Jerzy Łopatka ITK WEL WAT

BILINEAR TRANSFORMATION

This transformation was obtained using an approximate calculation of

integrals (by trapezoids) in the differential equation that describes an

analog filter (equivalent to a differential equation for the digital filter).

We received the equation:

  for the values that lie on the unit circle we obtained relationship

between the arguments of the function:

- The relationship between the analog and digital frequency is non-

linear

- The whole left half-plane of s plane is transformed into the interior of

the unit circle

- The imaginary axis is transformed to the unit circle

- Frequency = on a Z plane is equivalent to an infinite analog

frequency

- There is no overlap between the characteristics of the phenomenon.

- Method can be applied to all filters.

H z

T

H s j

T

k

z e

a

k

sT

( )



 



















1

2



T

tg



2

2













