Projektowanie filtrów cyfrowych Butterwortha i
Czebyszewa
mgr in
ż
. Grzegorz Kraszewski
Klasyczne filtry Butterwortha i Czebyszewa s
ą
to b
ą
d
ź
bierne obwody LC b
ą
d
ź
układy aktywne z
ujemnym sprz
ęż
eniem zwrotnym zbudowane na wzmacniaczach operacyjnych. Cyfrowym
odpowiednikiem takich filtrów s
ą
filtry równie
ż
z ujemnym sprz
ęż
eniem zwrotnym, zwane filtrami
rekurencyjnymi, b
ą
d
ź
te
ż
filtrami z niesko
ń
czon
ą
odpowiedzi
ą
impulsow
ą
(ang. IIR - Infinite Impulse
Response).
Najcz
ę
stszym sposobem formułowania problemu zaprojektowania filtru jest podanie jego
cz
ę
stotliwo
ś
ci granicznej, przy której wzmocnienie spada o 3 dB (71% w skali liniowej), oraz rz
ę
du
filtru. Jest to jednak sformułowanie nieprecyzyjne, bo nic nie mówi o tłumieniu w pa
ś
mie zaporowym i
zakłada z góry rz
ą
d filtru. Znacznie bardziej precyzyjnym i lepiej dostosowanym do potrzeb
praktycznych jest okre
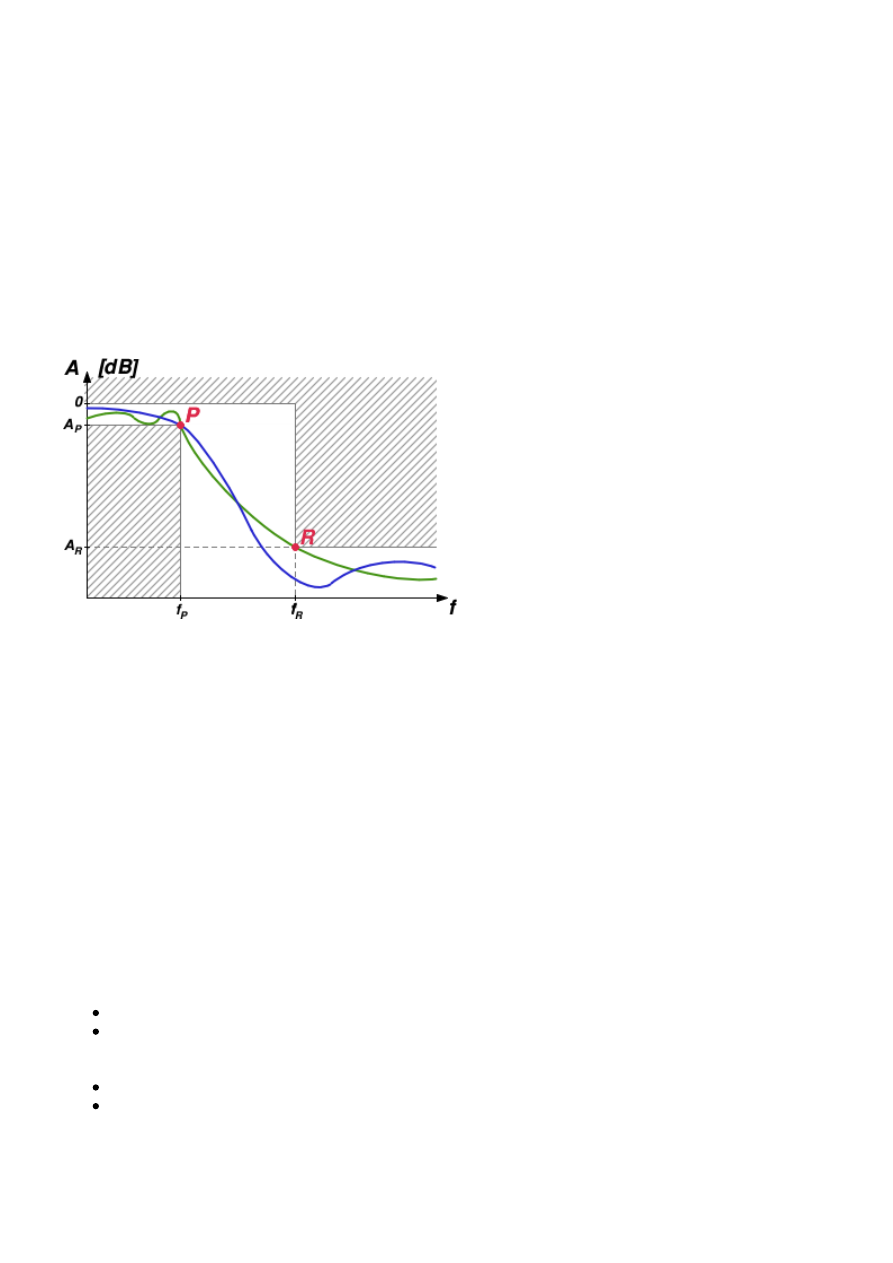
ś
lenie charakterystyki filtru przez podanie dwóch punktów: ko
ń
ca pasma
przepustowego (punkt P) i pocz
ą
tku pasma zaporowego (punkt R). Punkty te znajduj
ą
si
ę
na
charakterystyce amplitudowej filtru (wzmocnienie w funkcji cz
ę
stotliwo
ś
ci) i wyznaczaj
ą
pole, w którym
mie
ś
ci
ć
si
ę
musi charakterystyka projektowanego filtru. Na rysunku obok obie charakterystyki, zielona
i niebieska spełniaj
ą
zało
ż
one wymagania, poniewa
ż
nie przebiegaj
ą
przez zakreskowane obszary
zabronione wyznaczone punktami P i R. Warto zauwa
ż
y
ć
,
ż
e o ile charakterystyka zawsze przechodzi
przez punkt P, o tyle nie musi przechodzi
ć
przez punkt R, mo
ż
e przechodzi
ć
pod nim, wtedy mo
ż
emy
powiedzie
ć
,
ż
e filtr z zapasem spełnia wymagania projektowe. Z poło
ż
enia punktów P i R wynika rz
ą
d
filtru. Oczywi
ś
cie im bardziej stromo musi opada
ć
charakterystyka amplitudowa mi
ę
dzy punktami P i
R, tym rz
ą
d filtru b
ę
dzie wi
ę
kszy.
Tak wi
ę
c danymi pocz
ą
tkowymi do obliczenia filtru s
ą
:
Cz
ę
stotliwo
ść
ko
ń
ca pasma przepustowego (f ),
Najwi
ę
ksze dopuszczalne tłumienie w pa
ś
mie przepustowym (A ), dla filtru Czebyszewa ten
parametr okre
ś
la jednocze
ś
nie dopuszczalne zafalowanie charakterystyki amplitudowej w
pa
ś
mie przepustowym,
Cz
ę
stotliwo
ść
pocz
ą
tku pasma zaporowego (f ),
Wymagane minimalne tłumienie w pa
ś
mie zaporowym (A ).
W celu praktycznego pokazania omawianego sposobu projektowania filtrów, podaj
ą
c wzory i teori
ę
,
b
ę
d
ę
jednocze
ś
nie projektował konkretny filtr dolnoprzepustowy o nast
ę
puj
ą
cych parametrach:
P
P
R
R
Projektowanie filtrów cyfrowych Butterwortha i Czebyszewa
http://teleinfo.pb.edu.pl/krashan/articles/filtry_iir/
1 z 8
2013-09-01 22:16

A = 0,5 dB, f = 3 kHz, A = 20 dB, f = 7 kHz.
Obliczenie rz
ę
du filtru
Pierwszym krokiem jest obliczenie dwóch współczynników okre
ś
laj
ą
cych nasz filtr. S
ą
to współczynnik
selektywno
ś
ci k, oraz współczynnik dyskryminacji d. Współczynnik selektywno
ś
ci okre
ś
la jak blisko
siebie poło
ż
one s
ą
cz
ę
stotliwo
ś
ci punktów P i R, gdy punkty te zbli
ż
aj
ą
si
ę
w poziomie do siebie, to
współczynnik d
ąż
y do 1. Współczynnik ten okre
ś
lony jest wzorem:
Współczynnik dyskryminacji natomiast okre
ś
la wzajemn
ą
relacj
ę
mi
ę
dzy maksymalnym tłumieniem w
pa
ś
mie przepustowym i minimalnym tłumieniem w pa
ś
mie zaporowym. Obliczamy go ze wzoru:
Dla podanych przykładowych warto
ś
ci liczbowych po podstawieniu ich do wzoru otrzymamy: k =
0,42857 i d = 0,035107. Rz
ą
d filtru Butterwortha obliczamy ze współczynników k i d z nast
ę
puj
ą
cego
wzoru:
Rz
ą
d filtru Czebyszewa natomiast okre
ś
la si
ę
z podobnego, ale jednak nieco innego wzoru:
Po podstawieniu danych przykładowych otrzymamy dla filtru Butterwortha rz
ą
d 3,952968, dla filtru
Czebyszewa rz
ą
d 2,711062. W rzeczywisto
ś
ci rz
ą
d filtru nie mo
ż
e by
ć
ułamkowy, musi by
ć
liczb
ą
naturaln
ą
. Otrzymane liczby nale
ż
y wi
ę
c zaokr
ą
gli
ć
w gór
ę
. Zaokr
ą
glenie w dół spowodowałoby,
ż
e
charakterystyka filtru przechodziłaby ponad punktem R, a wi
ę
c filtr nie spełniałby zało
ż
e
ń
. Dlatego dla
przykładowego filtru Butterwortha przyjmujemy rz
ą
d 4, dla filtru Czebyszewa rz
ą
d 3. Rz
ą
d filtru
Czebyszewa dla tych samych danych b
ę
dzie zawsze mniejszy lub równy rz
ę
dowi filtru Butterwortha.
Cz
ę
stotliwo
ść
graniczna filtru
Cz
ę
stotliwo
ść
graniczna inaczej definiowana jest dla filtru Butterwortha i filtru Czebyszewa. W
dolnoprzepustowym filtrze Czebyszewa jest to najwy
ż
sza cz
ę
stotliwo
ść
, dla której tłumienie filtru nie
przekracza zało
ż
onych zafalowa
ń
charakterystyki. Jest to wi
ę
c dokładnie cz
ę
stotliwo
ść
punktu P na
wykresie. Dla filtru Butterwortha natomiast cz
ę
stotliwo
ść
graniczna, to taka, przy której nast
ę
puje
spadek wzmocnienia o 3 dB wzgl
ę
dem sygnału stałego (o cz
ę
stotliwo
ś
ci 0). Cz
ę
stotliwo
ść
ta jest
wi
ę
ksza od f je
ż
eli A jest mniejsze ni
ż
3 dB. Je
ż
eli tłumienie w punkcie P wynosi 3 dB, to oczywi
ś
cie
cz
ę
stotliwo
ść
graniczna jest cz
ę
stotliwo
ś
ci
ą
punktu P. Cz
ę
stotliwo
ść
graniczn
ą
filtru Butterwortha
mo
ż
na okre
ś
li
ć
ze wzoru:
P
P
R
R
P
P
f
P
f
R
ω
P
ω
R
−
=
k =
(1)
d =
10
0,1
−1
R
A
10
0,1
−1
P
A
(2)
n =
|log d|
|log k|
(3)
arc cosh −
d
1
( )
arc cosh
k
n
−
1
( )
=
(4)
f
P
=
f
g
P
10
0,1A
−1
(
)−
1
2n
(5)
Projektowanie filtrów cyfrowych Butterwortha i Czebyszewa
http://teleinfo.pb.edu.pl/krashan/articles/filtry_iir/
2 z 8
2013-09-01 22:16

Dla filtru przykładowego w wersji Czebyszewa cz
ę
stotliwo
ść
graniczna jest równa f a wi
ę
c wynosi
3000 Hz. Dla filtru Butterwortha otrzymamy po podstawieniu do wzoru (5) cz
ę
stotliwo
ść
graniczn
ą
równ
ą
3902,27 Hz.
Filtr prototypowy
Po okre
ś
leniu rz
ę
du i cz
ę
stotliwo
ś
ci granicznej obliczamy filtr prototypowy, to znaczy taki filtr
analogowy którego cz
ę
stotliwo
ść
graniczna wynosi 1 Hz. Transmitancja tego filtru to funkcja
operatora ró
ż
niczkowania s o postaci:
Mianowniki transmitancji filtrów prototypowych zostały
stablicowane
. Posta
ć
mianownika dla filtru
Butterwortha zale
ż
y wył
ą
cznie od rz
ę
du filtru, dla filtru Czebyszewa dodatkowym parametrem jest
zało
ż
one zafalowanie charakterystyki amplitudowej (równe tłumieniu A ). Dla filtru przykładowego
odczytujemy z tablic:
filtr Butterwortha
(s + 0,765366864s + 1)·(s + 1,847759065s + 1)
filtr Czebyszewa
(s + 0,62646s + 1,14245)·(s + 0,62646)
Jak wida
ć
mianownik transmitancji filtru M(s) jest wielomianem zmiennej s. Miejsca zerowe tego
mianownika s
ą
zwane biegunami filtru. Bieguny filtru s
ą
liczbami zespolonymi o ujemnej cz
ęś
ci
rzeczywistej (gdyby który
ś
biegun miał dodatni
ą
cz
ęść
rzeczywist
ą
, to filtr byłby niestabilny). Filtr ma
tyle biegunów ile wynosi jego rz
ą
d. Filtry o rz
ę
dzie parzystym maj
ą
bieguny zespolone sprz
ęż
one
parami. W filtrze o rz
ę
dzie nieparzystym jeden biegun jest ujemny rzeczywisty, reszta jest zespolona,
sprz
ęż
ona parami. Bieguny mo
ż
na bardzo prosto obliczy
ć
wyliczaj
ą
c pierwiastki trójmianów w
nawiasach. Dla przykładowego filtru Butterwortha otrzymamy dwie pary biegunów zespolonych
sprz
ęż
onych:
s = −0,382683±j0.923880
s = −0,923880±j0.382683
Dla filtru Czebyszewa otrzymamy jeden biegun rzeczywisty i par
ę
biegunów zespolonych
sprz
ęż
onych:
s = −0,62646
s = −0,31323±j1,021928
Skalowanie cz
ę
stotliwo
ś
ci i przekształcenie nieliniowe
Jak napisałem wcze
ś
niej, filtr prototypowy obliczony jest dla cz
ę
stotliwo
ś
ci granicznej 1 Hz. Nale
ż
y
teraz przeskalowa
ć
jego bieguny, tak aby odpowiadały zało
ż
onej cz
ę
stotliwo
ś
ci granicznej. Oprócz
tego nale
ż
y dokona
ć
przekształcenia nieliniowego. Polega ono na potraktowaniu przeskalowanej
cz
ę
stotliwo
ś
ci funkcj
ą
tangens rozci
ą
gni
ę
t
ą
w taki sposób,
ż
e warto
ść
π
na osi x przesuwa si
ę
do
cz
ę
stotliwo
ś
ci próbkowania sygnału. Przekształcenie nieliniowe jest elementem transformacji z
dziedziny analogowego operatora s (ró
ż
niczkowanie) do dziedziny cyfrowego operatora z (opó
ź
nienie
P
P
2
2
2
12
34
1
23
H(s)
1
M(s)
=
(6)
Projektowanie filtrów cyfrowych Butterwortha i Czebyszewa
http://teleinfo.pb.edu.pl/krashan/articles/filtry_iir/
3 z 8
2013-09-01 22:16

Filtr Butterwortha:
s = −0,218404±j0,527273
s = −0,527273±j0,218404
Filtr Butterwortha:
s = 0,706684±j0,405647
s = 0,571001±j0,135764
o 1 takt zegara). Przy projektowaniu filtrów cyfrowych ł
ą
czy si
ę
operacj
ę
skalowania i przekształcenia
nieliniowego w jedn
ą
, obliczaj
ą
c współczynnik skaluj
ą
cy W z nast
ę
puj
ą
cego wzoru:
W powy
ż
szym wzorze wyst
ę
puj
ą
ca w mianowniku warto
ść
f to cz
ę
stotliwo
ść
próbkowania
filtrowanego sygnału cyfrowego. Przy obliczeniach trzeba te
ż
pami
ę
ta
ć
o tym,
ż
e argument funkcji
tangens jest w radianach. Dla filtru Butterwortha i Czebyszewa współczynnik W liczymy oddzielnie,
poniewa
ż
z reguły filtry te maj
ą
inne cz
ę
stotliwo
ś
ci graniczne (chyba,
ż
e A wynosi 3 dB, wtedy obie
cz
ę
stotliwo
ś
ci b
ę
d
ą
równe). Dla naszego przykładowego filtru Butterwortha f wynosi 3902,27 Hz, a
współczynnik W = 0,570758. Dla filtru Czebyszewa f = 3000 Hz, W = 0,43405608.
Po obliczeniu współczynnika W transformujemy bieguny filtru prototypowego. Jest to bardzo prosta
operacja, dla filtru dolnoprzepustowego po prostu mno
ż
ymy W przez biegun. Dla filtru
górnoprzepustowego dzielimy W przez biegun. Po przemno
ż
eniu (dla filtru dolnoprzepustowego)
otrzymamy nast
ę
puj
ą
ce bieguny:
Filtr Czebyszewa:
s = −0,135959±j0,443573
s = −0,271917
Przej
ś
cie do transmitancji cyfrowej (operatora z)
Matematycznie
ś
cisłe przej
ś
cie z operatora analogowego s do cyfrowego operatora z dane jest
wzorem:
gdzie T to okres próbkowania sygnału. Wydaje si
ę
to prost
ą
zale
ż
no
ś
ci
ą
, dopóki nie zauwa
ż
ymy,
ż
e
wykładnik pot
ę
gi jest liczb
ą
zespolon
ą
, co znacznie komplikuje obliczenia. Dlatego w praktyce stosuje
si
ę
pewne przybli
ż
enie wzoru teoretycznego zwane przekształceniem dwuliniowym lub bilinearnym.
Przybli
ż
enie to wygl
ą
da nast
ę
puj
ą
co:
Gdzie s' jest to przetransformowany wcze
ś
niej biegun filtru analogowego, a z biegun filtru cyfrowego.
Takie przekształcenie jest znacznie prostsze obliczeniowo i daje dobre rezultaty praktyczne.
Przekształcenie zachowuje sprz
ęż
enie biegunów, to znaczy
ż
e para biegunów zespolonych
sprz
ęż
onych s pozostaje par
ą
biegunów zespolonych sprz
ęż
onych z. Dzi
ę
ki temu dla pary biegunów
sprz
ęż
onych mo
ż
na wykona
ć
tylko połow
ę
oblicze
ń
. Podobnie biegun rzeczywisty pozostaje po
przekształceniu biegunem rzeczywistym. Dla przykładowego filtru bieguny po przekształceniu
dwuliniowym s
ą
nast
ę
puj
ą
ce:
Filtr Czebyszewa:
s = 0,795271±j0,372823
s = 0,760628
Wyliczenie transmitancji
s
P
g
g
12
34
12
3
d
12
34
12
3
W = 2tg
π
f
g
f
s
( )
(7)
z = e
d
sT
(8)
z
2 + s′
2 − s′
=
(9)
Projektowanie filtrów cyfrowych Butterwortha i Czebyszewa
http://teleinfo.pb.edu.pl/krashan/articles/filtry_iir/
4 z 8
2013-09-01 22:16

Wyliczenie transmitancji polega na wstawieniu obliczonych biegunów do mianownika, oraz wstawieniu
odpowiednich zer (miejsc zerowych licznika) do licznika. Do oblicze
ń
w MatLabie wymna
ż
amy
wszystkie bieguny (podobnie zera) przez siebie a
ż
do uzyskania w liczniku i mianowniku wielomianów
stopnia N równego rz
ę
dowi filtru. Do praktycznej realizacji filtru korzystniej jest pozostawi
ć
licznik i
mianownik jako iloczyn wielomianów stopnia pierwszego i drugiego. Odpowiada to wykonaniu filtru
jako kaskadowego poł
ą
czenia filtrów pierwszego i drugiego rz
ę
du. Takie rozwi
ą
zanie jest korzystne
poniewa
ż
znacznie zmniejsza wra
ż
liwo
ść
filtru na zaokr
ą
glenia współczyników wzmacniaczy.
Szczególnie warto wi
ę
c je zastosowa
ć
w przypadku pracy w arytmetyce stałoprzecinkowej. Wtedy
ka
ż
dy biegun rzeczywisty odpowiada blokowi pierwszego rz
ę
du, a ka
ż
da para zespolonych biegunów
sprz
ęż
onych – blokowi drugiego rz
ę
du.
Blok I rz
ę
du
Blok taki powstaje z bieguna rzeczywistego i ma jedno zero w punkcie −1 (filtr górnoprzepustowy ma
zero w punkcie 1). Licznik transmitancji ma zatem posta
ć
z + 1
Mianownik natomiast (zakładaj
ą
c
ż
e biegun wynosi c)
z − c
Od transmitancji mo
ż
na przej
ść
do schematu blokowego, korzystaj
ą
c z definicji transmitancji, jest to
bowiem stosunek transformaty sygnału wyj
ś
ciowego Y(z) do transformaty sygnału wej
ś
ciowego X(z).
Dla bloku pierwszego stopnia mamy zatem:
Y(z) / X(z) = (z + 1) / (z − c)
Y(z)(z − c) = X(z)(z + 1)
zY(z) − cY(z) = zX(z) + X(z)
Y(z) − z cY(z) = X(z) + z X(z)
Y(z) = X(z) + z X(z) + z cY(z)
Z ostatniego wzoru bezpo
ś
rednio mo
ż
na narysowa
ć
schemat blokowy bloku filtru I rz
ę
du.
Przykładowy filtr Butterwortha nie posiada biegunów rzeczywistych, a wi
ę
c i bloków I rz
ę
du. Filtr
Czebyszewa posiada jeden biegun rzeczywisty, odpowiadaj
ą
cy mu blok ma transmitancj
ę
Blok II rz
ę
du
Blok ten powstaje z pary biegunów zespolonych sprz
ęż
onych i ma podwójne zero w punkcie -1 (filtr
górnoprzepustowy ma podwójne zero w punkcie 1). Zatem licznik transmitancji tego bloku ma posta
ć
(z + 1) = z + 2z + 1
Mianownik natomiast przyjmuje posta
ć
(przy parze biegunów a±jb)
[z − (a − jb)][z − (a + jb)] = z − 2az + (a + b )
Podobnie jak przy bloku pierwszego rz
ę
du korzystamy z definicji transmitancji, aby uzyska
ć
wzór
definiuj
ą
cy posta
ć
schematu blokowego
Y(z) / X(z) = (z + 2z + 1) / (z − 2az + a + b )
−1
−1
−1
−1
2
2
2
2
2
2
2
2
2
H(z)
z + 1
z − 0,760628
=
Projektowanie filtrów cyfrowych Butterwortha i Czebyszewa
http://teleinfo.pb.edu.pl/krashan/articles/filtry_iir/
5 z 8
2013-09-01 22:16

z Y(z) − 2azY(z) + (a + b )Y(z) = z X(z) + 2zX(z) + X(z)
Y(z) − 2az Y(z) + (a + b )z Y(z) = X + 2z X(z) + z X(z)
Y(z) = X(z) + 2z X(z) + z X(z) + 2az Y(z) − (a + b )z Y(z)
Przykładowy filtr Butterwortha posiada dwie pary biegunów zespolonych sprz
ęż
onych, b
ę
dzie zatem
miał dwa bloki drugiego rz
ę
du. Dla bieguna z transmitancja wyniesie
Dla bieguna z transmitancja wyniesie
Przykładowy filtr Czebyszewa posiada jedn
ą
par
ę
biegunów zespolonych sprz
ęż
onych. Transmitancja
odpowiadaj
ą
cego mu bloku jest nast
ę
puj
ą
ca
Do weryfikacji oblicze
ń
w MatLabie niezb
ę
dna jest kompletna transmitancja filtru jako cało
ś
ci.
Uzyskujemy j
ą
wstawiaj
ą
c wszystkie bieguny jako miejsca zerowe mianownika, oraz N-krotne zero w
punkcie -1 jako miejsce zerowe licznika, a nast
ę
pnie wymna
ż
aj
ą
c. Równowa
ż
nym sposobem jest
wymno
ż
enie przez siebie transmitancji wszystkich bloków filtru. Tramsmitancja przykładowego filtru
Butterwortha ma posta
ć
Transmitancja filrtu Czebyszewa natomiast
W programie MatLab mo
ż
na sprawdzi
ć
charakterystyk
ę
amplitudow
ą
przykładowego filtru wydaj
ą
c
nast
ę
puj
ą
ce polecenie (warto
ś
ci liczbowe dla przykładowego filtru Butterwortha):
freqz([1
4
6
4
1],[1
-2.555369
2.622493
-1.245102
0.228714],10:10:20000,44100)
Pierwszy wektor zawiera kolejne współczynniki wielomianu licznika transmitancji, drugi kolejne
współczynniki mianownika.
Charakterystyki filtru przykładowego
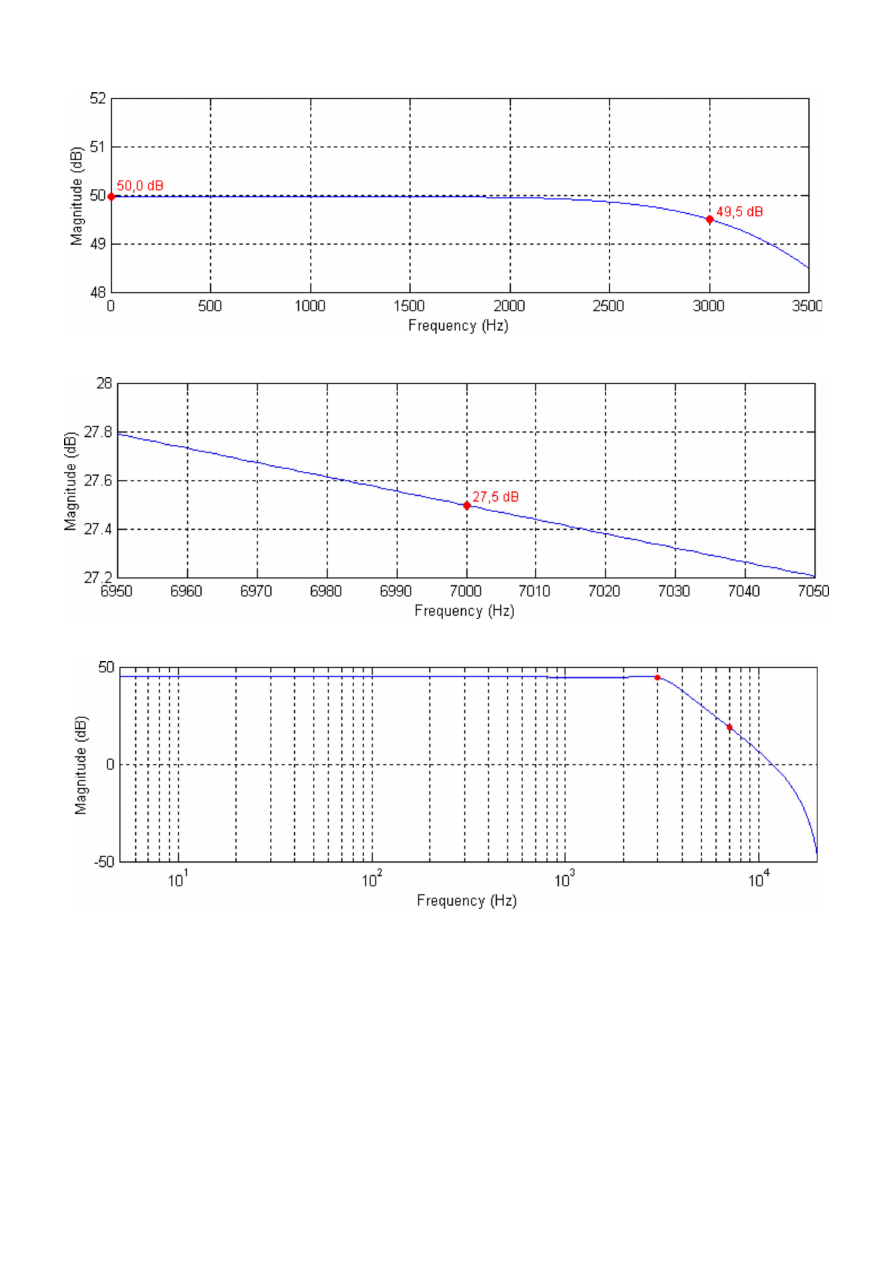
W celu weryfikacji metody projektowania sprawdziłem charakterystyki otrzymanych filtrów korzystaj
ą
c
z funkcji freqz() programu MatLab. Punkty P i R z zało
ż
e
ń
projektowych s
ą
zaznaczone kolorem
czerwonym. Pewnym zaskoczeniem mo
ż
e by
ć
fakt,
ż
e w pasmie przenoszenia wzmocnienie nie
wynosi 0 dB, to mo
ż
na jednak łatwo skorygowa
ć
umieszczaj
ą
c tłumik o odpowiednim tłumieniu (50 dB
dla filtru Butterwortha i 45,3 dB dla filtru Czebyszewa). Praktycznie realizuj
ą
c filtr w arytmetyce
stałoprzecinkowej warto podzieli
ć
tłumik na kilka tłumików rozmieszczonych przed filtrem, mi
ę
dzy jego
blokami oraz za filtrem, tak aby ich sumaryczne tłumienie było równe wymaganemu. W ten sposób
zapobiega si
ę
powstaniu przepełnienia arytmetycznego w blokach filtru, oraz pogarszaniu stosunku
2
2
2
2
−1
2
2
−2
−1
−2
−1
−2
−1
2
2
−2
12
34
H(z) =
z
2
+ 2z + 1
z
2
− 1,413368z + 0,663952
H(z) =
z
2
+ 2z + 1
z
2
− 1,412002z + 0,344474
H(z) =
z
2
+ 2z + 1
z
2
− 1,590542z + 0,771453
H(z) =
6z
2
+ 4z + 1
4z
3
+
+ 4z
3
z
4
2,622493z
2
− 1,245102z + 0,228714
2,555369z
3
+
z
4
−
H(z) =
3z
2
+ 3z + 1
z
3
+
2,351170z
2
− 1,981264z + 0,586789
z
3
−
Projektowanie filtrów cyfrowych Butterwortha i Czebyszewa
http://teleinfo.pb.edu.pl/krashan/articles/filtry_iir/
6 z 8
2013-09-01 22:16
sygnału do szumu kwantyzacji.
Charakterystyka amplitudowa przykładowego filtru Butterwortha w zakresie od 0 do 3,5 kHz.
Charakterystyka amplitudowa przykładowego filtru Butterwortha wokół cz
ę
stotliwo
ś
ci 7 kHz.
Charakterystyka amplitudowa przykładowego filtru Czebyszewa w zakresie od 0 do 20 kHz
(logarytmiczna skala cz
ę
stotliwo
ś
ci).
Projektowanie filtrów cyfrowych Butterwortha i Czebyszewa
http://teleinfo.pb.edu.pl/krashan/articles/filtry_iir/
7 z 8
2013-09-01 22:16
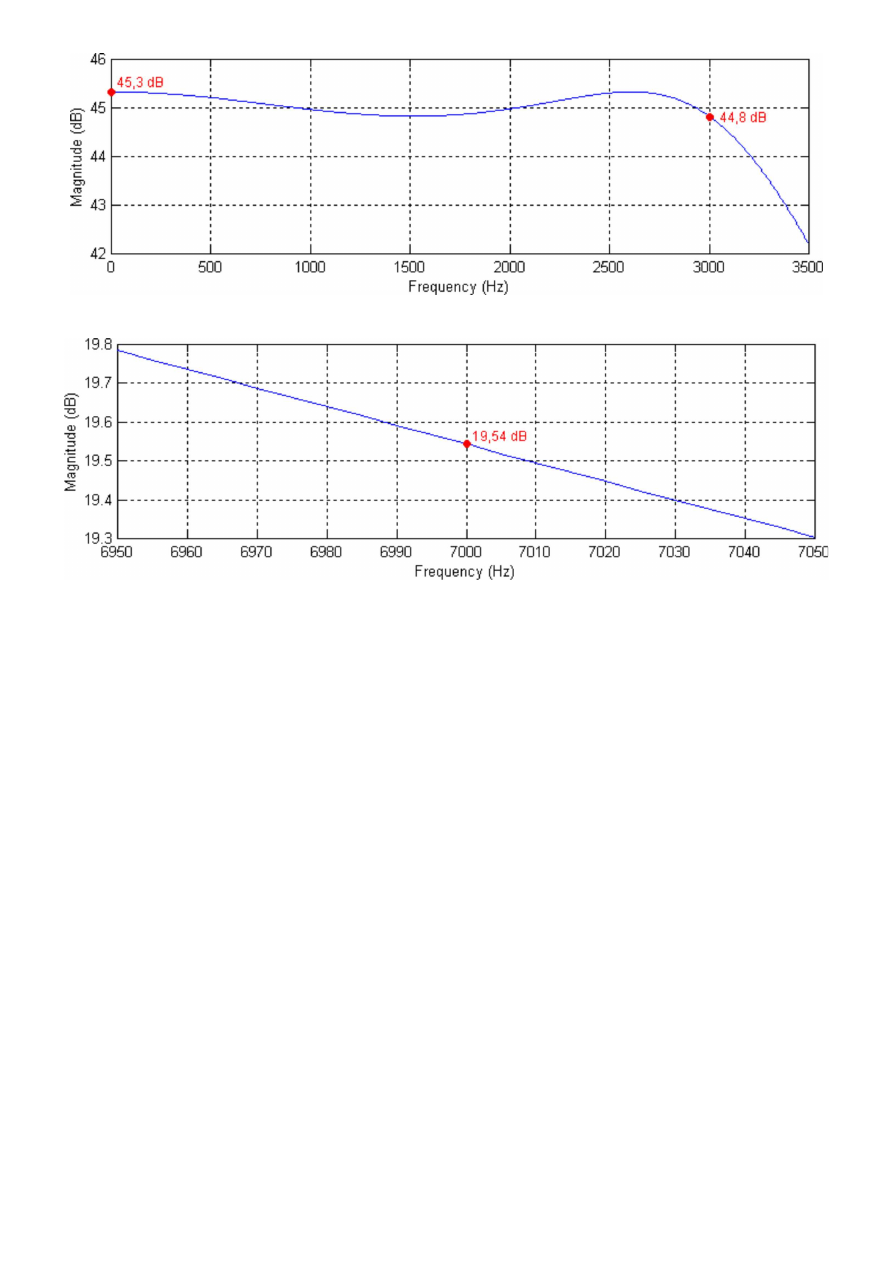
Charakterystyka amplitudowa przykładowego filtru Czebyszewa w zakresie od 0 do 3,5 kHz.
Charakterystyka amplitudowa przykładowego filtru Czebyszewa wokół cz
ę
stotliwo
ś
ci 7 kHz.
Projektowanie filtrów cyfrowych Butterwortha i Czebyszewa
http://teleinfo.pb.edu.pl/krashan/articles/filtry_iir/
8 z 8
2013-09-01 22:16
Wyszukiwarka
Podobne podstrony:
Projektowanie filtrów cyfrowych Butterwortha i Czebyszewa
Wykład 3 projektowanie filtrów cyfrowych
Projektowanie filtrów cyfrowych
Wykład 5 1 projektowanie filtrów cyfrowych
projektowanie filtrów cyfrowych metoda okien
lab 07 projektowanie filtrow II
Projektowanie filtrów typu IIR
lab 06 Projektowanie filtrow
Projektowanie filtrow FIR id 40 Nieznany
Projektowanie filtrów FIR oraz IIR1
Projektowanie filtrów typu IIR
09 Projektowanie filtrow aktywnych
,Analogowe i cyfrowe układy elektroniczne I L, Projekt filtru cyfrowego NOI (realizacja schemat bl
Stare projekty, P BRAMKI, Pawe˙ Dobro˙ gr. 3P23
Projekt lotu cyfrowe 2014
,Analogowe i cyfrowe układy elektroniczne I L, Projekt filtru cyfrowego NOI Metoda przekształcenia
więcej podobnych podstron