PROJEKTOWANIE FILTRÓW CYFROWYCH

Filtr cyfrowy jest liniowym układem dyskretnym, niezmiennym względem
przesunięcia, zrealizowany za pomocą arytmetyki o skończonej precyzji

•

etapy projektowania:

-

określenie pożądanych parametrów układu

- aproksymacja tych parametrów za pomocą przyczynowego układu

dyskretnego

- realizacja za pomocą arytmetyki o skończonej precyzji

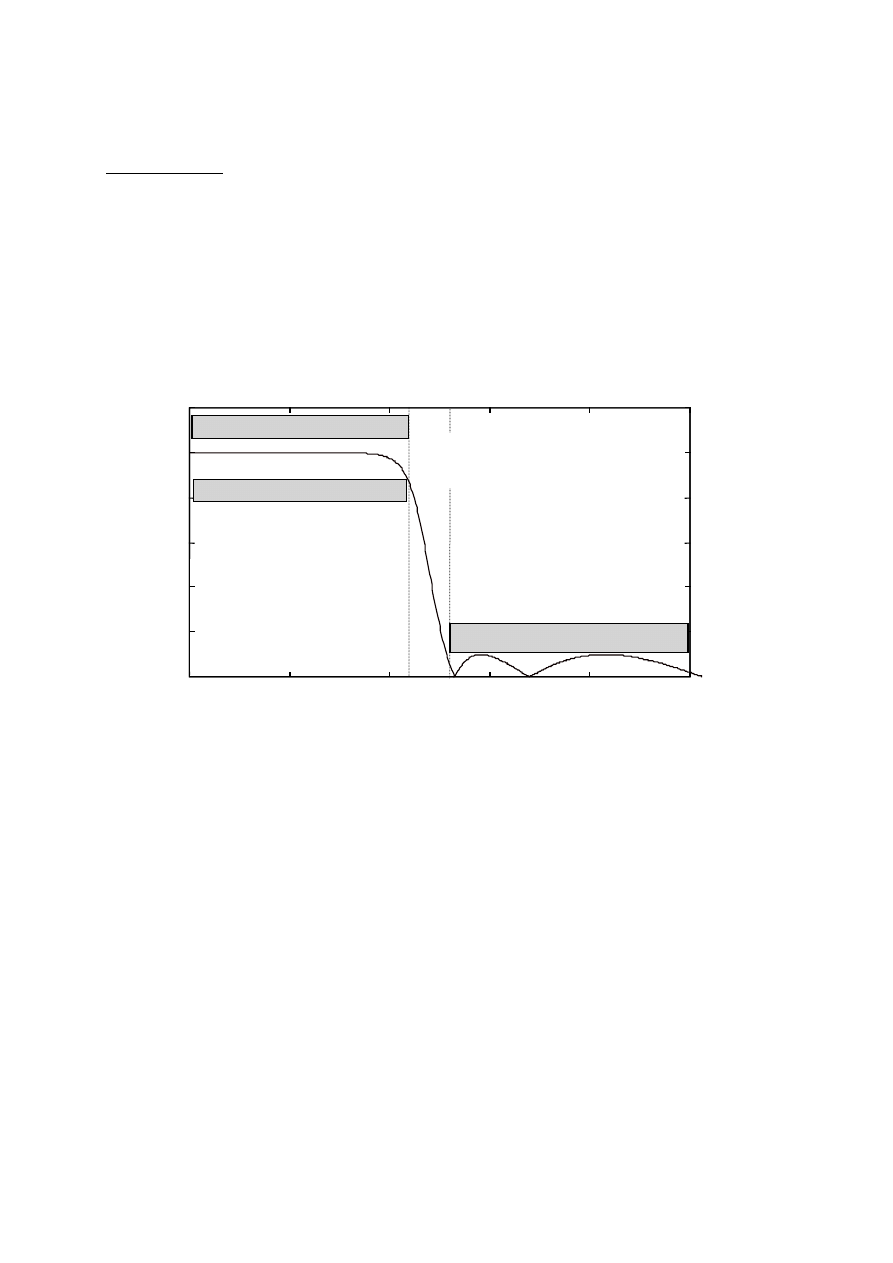
często wymagania na filtr podawane są w postaci tolerancji:

0

100

200

300

400

500

0

0.2

0.4

0.6

0.8

1

1.2

pasmo
przepustowe

pasmo
zaporowe

pasmo
przejściowe

przebieg charakterystyki filtru aproksymowany jest za pomocą funkcji:

wielomianowej dla filtrów FIR,

wymiernej dla filtrów IIR.

PROJEKTOWANIE FILTRÓW IIR W OPARCIU O CHARAKTERYSTYKI

FILTRÓW ANALOGOWYCH

Projektowanie to polega na przekształceniu filtru analogowego na filtr cyfrowy
zgodnie z założeniami.

•

przyczyny:

- zaawansowane metody projektowania filtrów analogowych

- prostota wielu metod analogowych

- filtry cyfrowe niejednokrotnie symulują filtry analogowe

•

założenia

-

przekształcenie powinno zachować zasadnicze właściwości filtru

analogowego

- stabilny filtr analogowy powinien być przekształcony na stabilny filtr cyfrowy

(jeżeli filtr analogowy posiadał bieguny w lewej półpłaszczyźnie płaszczyzny s to filtr
cyfrowy powinien posiadać bieguny wewnątrz okręgu jednostkowego na płaszczyźnie
z)

METODA NIEZMIENNOŚCI ODPOWIEDZI IMPULSOWEJ

•

Przyjmujemy że, odpowiedź impulsowa filtru cyfrowego jest ciągiem próbek
odpowiedzi impulsowej filtru analogowego, pobranych w równych momentach
czasu.

h n

h nT

a

( )

(

)

=

•

Można dowieść że, z zależności między transformatą Laplace’a funkcji h

a

(n) a

transformatą Z funkcji h(n) wynika iż, istnieje równość:

H z

T

H s

j

T

k

z e

a

k

sT

( )

=

=−∞

∞

=

+











∑

1

2

π

zależność pomiędzy argumentami tych funkcji

z

e

sT

=

wskazuje że, paski lewej półpłaszczyzny płaszczyzny s, o szerokości 2

π

/T

transformowane są na wnętrze okręgu jednostkowego na płaszczyźnie z i sumowane

Jeżeli transmitancja filtru analogowego jest niezerowa poza przedziałem częstotliwości
j

Ω

<-

π

/T do

π

/T> to występuje efekt nakładania się charakterystyk i zniekształcanie

charakterystyki filtru cyfrowego

•

częstotliwości

ω

=

π

na płaszczyźnie z, odpowiada częstotliwość analogowa

Ω

=

π

/T.

•

bieguny o położeniu s

k

transformowane są na bieguny o położeniu e

s

k

T

.

zalety:

- prostota metody

- liniowe odwzorowanie częstotliwości analogowej na cyfrową,

- dobre odtworzenie charakterystyk częstotliwościowych filtrów

wąskopasmowych

wady:
-

występuje nakładanie się charakterystyk

- mała dokładność odwzorowania

- metoda nadaje się jedynie do filtrów pasmowo-przepustowych i

dolnoprzepustowych

(układów o ograniczonym paśmie przenoszenia)

TRANSFORMACJA DWULINIOWA

To przekształcenie uzyskano stosując przybliżone wyliczane całki (metodą trapezów)
w równaniu różniczkowym opisującym filtr analogowy (odpowiednik równania
różnicowego dla filtru cyfrowego).

Otrzymano równanie:

H z

H s

a

s

T

z

z

( )

( )

=

=

−
+

−

−

2 1

1

1

1

dla wartości leżących na okręgu jednostkowym uzyskano zależność między
argumentami funkcji:

T

tg

Ω

2

2

=











ω

•

związek pomiędzy częstotliwością analogową i cyfrową jest nieliniowy

•

cała lewa półpłaszczyzna płaszczyzny s przekształcana jest na wnętrze okręgu
jednostkowego

•

oś urojona przekształcana jest na okrąg jednostkowy

•

częstotliwości

ω

=

π

na płaszczyźnie z, odpowiada nieskończona częstotliwość

analogowa

•

nie występuje zjawisko nakładania się charakterystyk.

•

metodę można stosować do wszelkich filtrów.