K ą t y
K ą t y
Beata Nowakowska
Beata Nowakowska
K ą t y
K ą t y
Beata Nowakowska
Beata Nowakowska
Wybierz lekcję
Wybierz lekcję
Kąty przyległe i wierzchołkowe
Kąty przyległe i wierzchołkowe
Kąty naprzemianległe i odpowiadaj
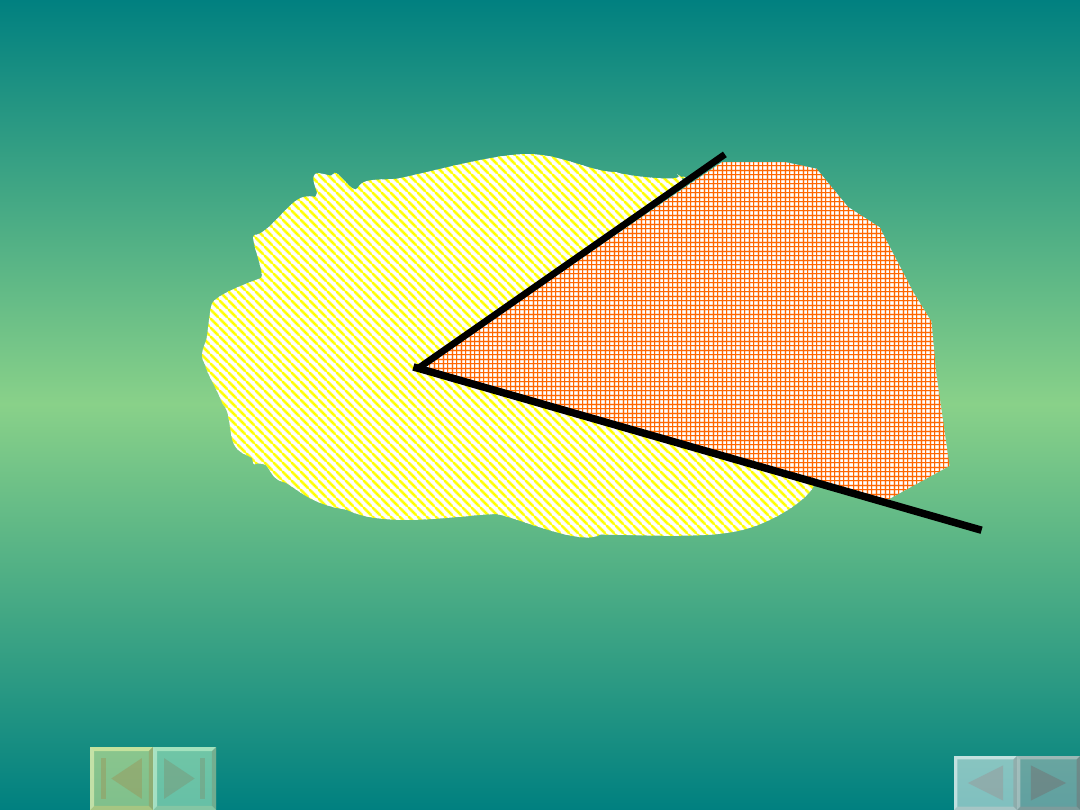
Jak powstaje
Jak powstaje
kąt ?
kąt ?
Dwie półproste o wspólnym początku
dzielą płaszczyznę na dwie części.
Każdą z tych części, wraz z półprostymi,
nazywamy kątem.
O
.
A
.
B
.
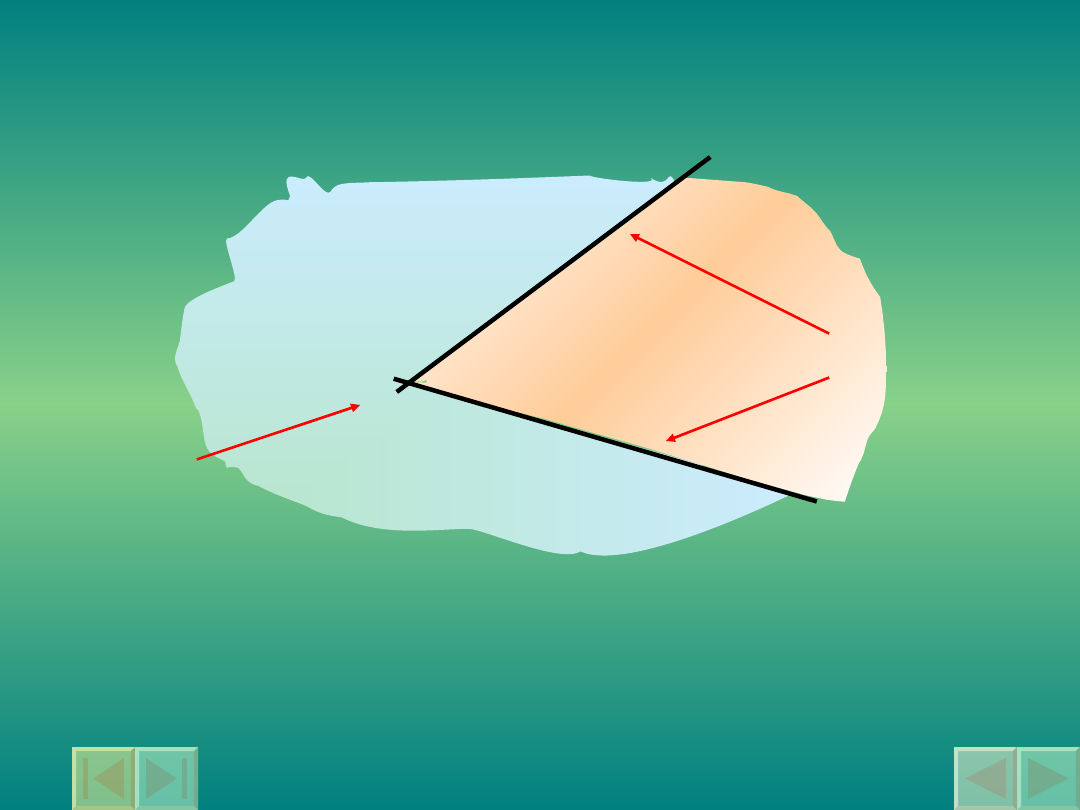
Elementy kąta
Elementy kąta
Półproste tworzące kąt
nazywamy ramionami kąta,
a ich wspólny początek wierzchołkiem
kąta.
wierzchołek
ramiona
O
.
.
Oznaczanie kątów
Oznaczanie kątów
.
A
.
B
O
.
<
AOB
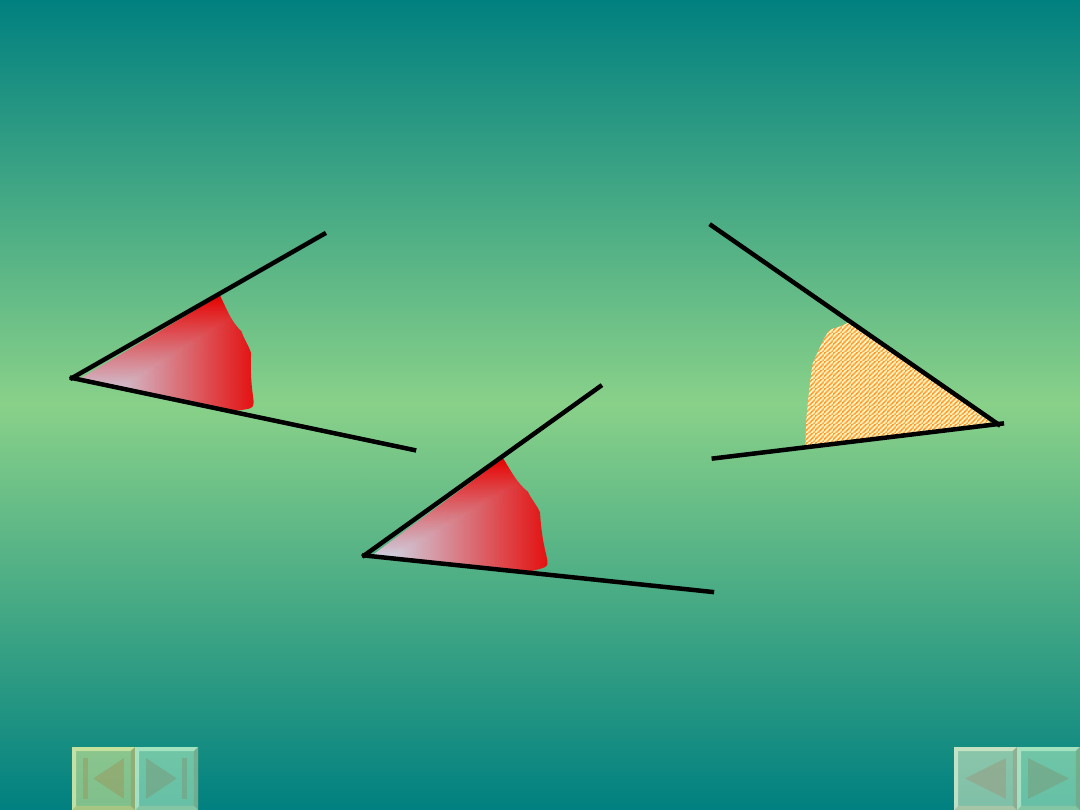
Kąty przystające
Kąty przystające
A
.
O
.
B
.
.
O
.
.
E
K
Kątami przystającymi nazywamy kąty,
które mają równe miary.
F
.
O
.
G
.
Miara kąta
Miara kąta
płaskiego
płaskiego
o
o
Miara stopniowa
1 = 60’ 1 stopień = 60
minut
1’ = 60’’ 1 minuta = 60
sekund
Miara łukowa
1 radian = 57,3
1 = 0,017
radiana
o
Zamień na minuty 42
o
37’.
42
o
37’=42
.
60’+37’ = 2520’+37’= 2557’
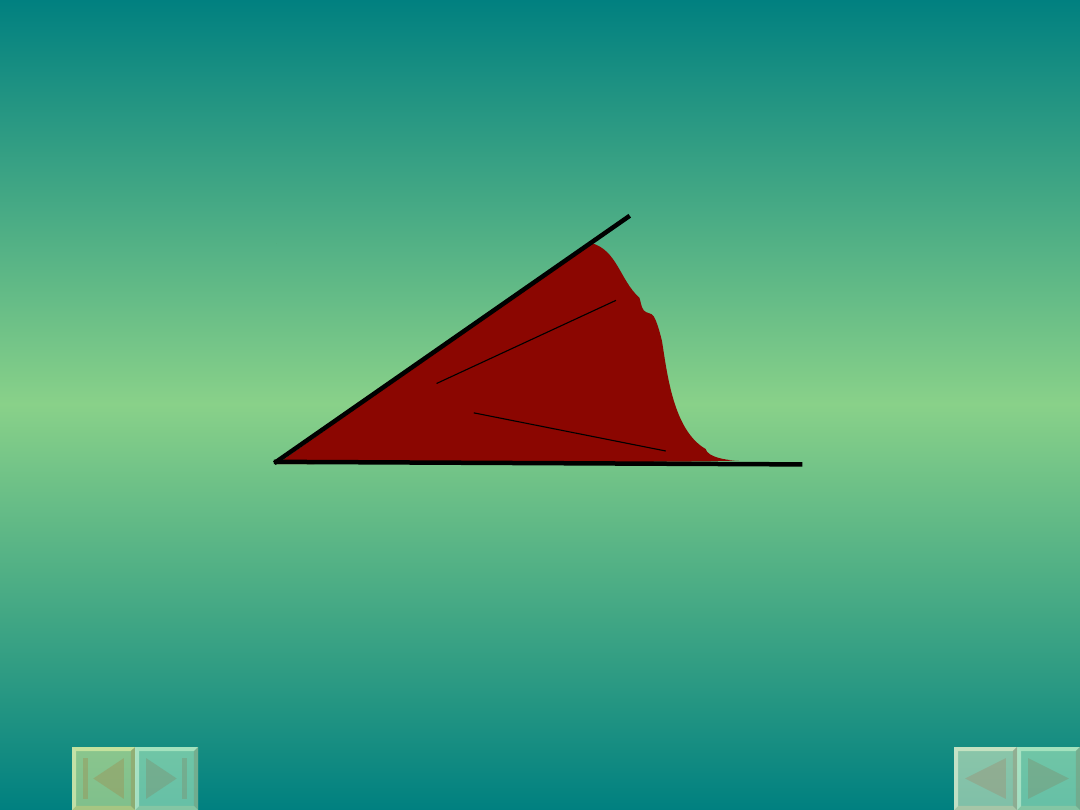
Kąt wypukły
Kąt wypukły
Kątem wypukłym nazywamy kąt,
którego każde dwa punkty
wyznaczają
0
o
< < 180
o
.
.
.
.
odcinek należący do tego
kąta.
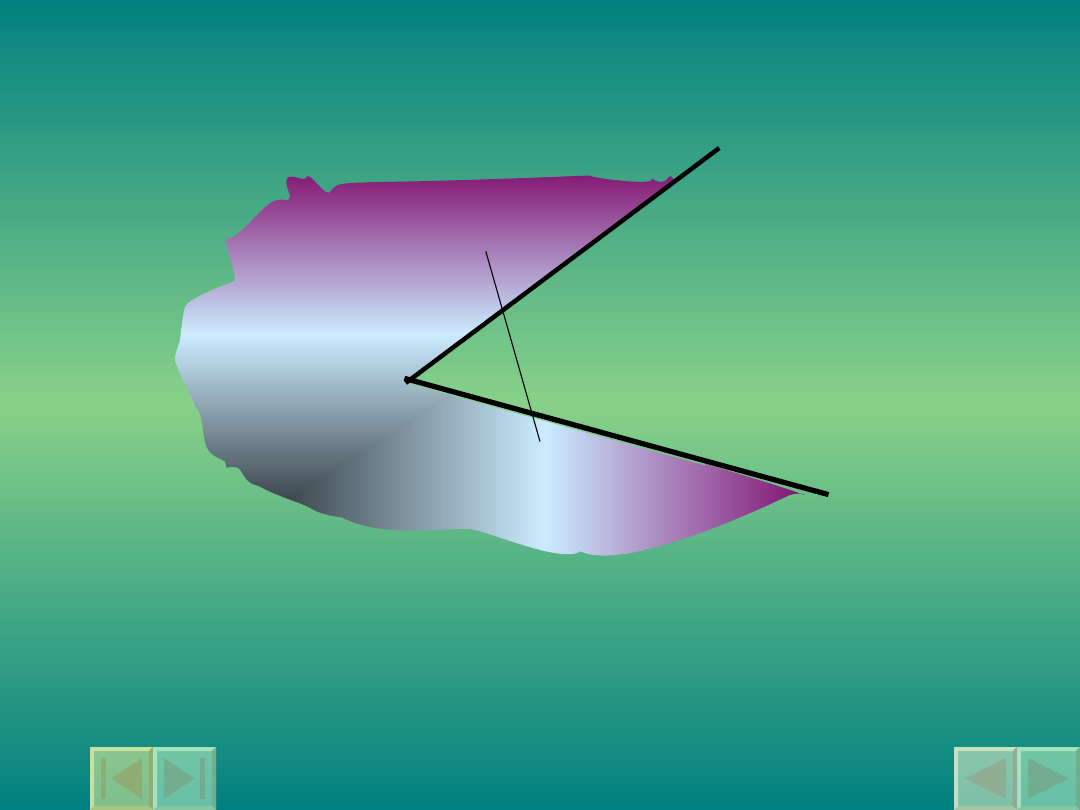
Kąt wklęsły
Kąt wklęsły
Kątem wklęsłym nazywamy kąt,
w którym istnieją punkty wyznaczające
180
o
< < 360
o
.
.
odcinek nie zawarty w tym kącie.
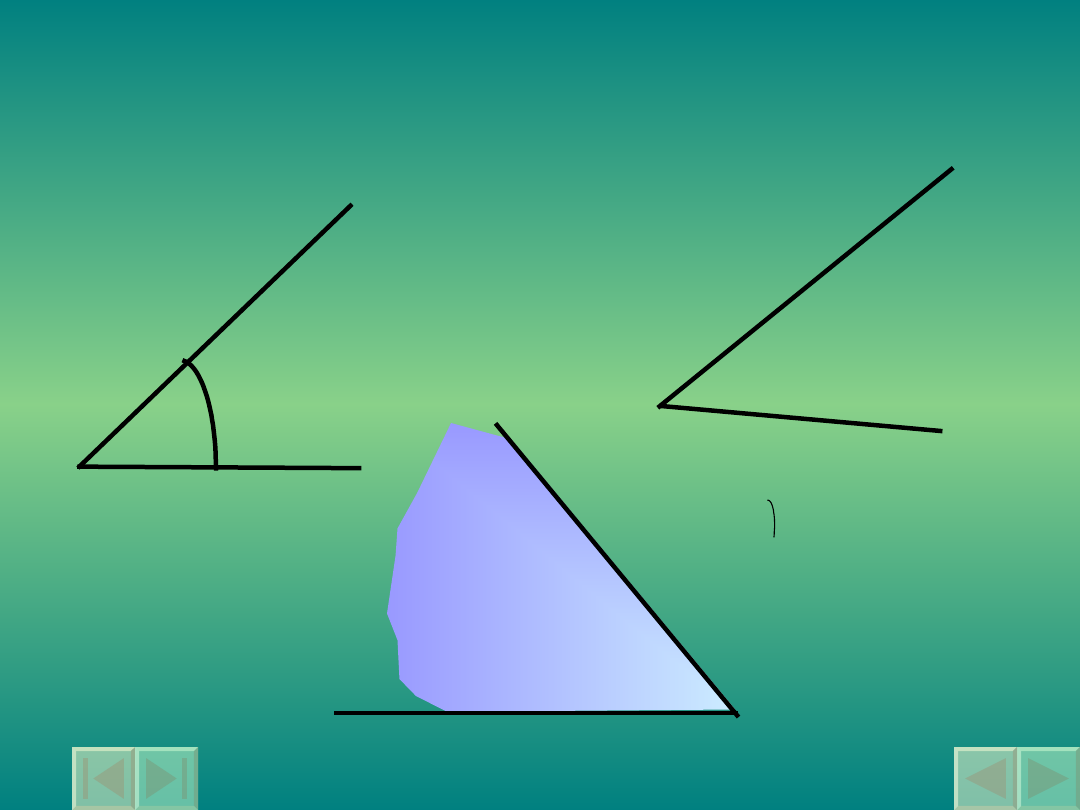
Figury wypukłe
Figury wypukłe
Figurą wypukłą nazywamy taką figurę,
której każde dwa punkty wyznaczają odcinek
zawarty w tej figurze.
Wskaż figury wypukłe
.
.
.
.
.
.
.
a
b
c
d
e
f
g
.
.
.
.
.
.
. .
..
Wybierz lekcję
Wybierz lekcję
Kąty przyległe i wierzchołkowe
Kąty przyległe i wierzchołkowe
Kąty naprzemianległe i odpowiadaj
Definicja kąta
Definicja kąta
Kątem nazywamy część płaszczyzny powstałą
przez jej rozcięcie dwiema różnymi półprostymi
o wspólnym początku, wraz z tymi półprostymi.
A
O
B
.
.
ramiona
wierzchołek
.
Rodzaje kątów
Rodzaje kątów
prosty
Kąt płaski, którego miara wynosi 90
o
.
ostry
Kąt, którego miara jest mniejsza niż 90
o
.
rozwarty
Kąt, którego miara jest
większa od 90
o
i mniejsza od 180
o
.
półpełny
Kąt, którego miara wynosi 180
o
.
pełny
Kąt, którego miara wynosi 360
o
.
wypukły
Kąt, którego miara jest mniejsza niż 180
o
.
wklęsły
Kąt, którego miara jest
większa od 180
o
i mniejsza od 360
o
.
Półproste
Półproste
dopełniające się
dopełniające się
Dwie różne półproste leżące na jednej prostej
i mające wspólny początek nazywamy
półprostymi dopełniającymi się.
< BOA =
180
o
.
A
B
.
O
Kąty przyległe
Kąty przyległe
Kątami przyległymi nazywamy takie dwa kąty,
które mają jedno ramię wspólne,
= 180
o
półprostymi dopełniającymi się.
AOB +
<
COB
<
O
B
.
C
.
.
a pozostałe ramiona są
.
A
Kąty
Kąty
wierzchołkowe
wierzchołkowe
Kąty wypukłe, których ramiona wzajemnie się
przedłużają, nazywamy kątami wierzchołkowymi.
Kąty wierzchołkowe mają równe miary.
O
B
.
.
A
D
.
C
.
AOB =
<
COD
<
Budowa
Budowa
twierdzenia
twierdzenia
W matematyce używamy zdań opisujących własności
(aksjomaty i twierdzenia) i zdań określających nowe
pojęcia (definicje). Oto najczęściej stosowany sposób
formułowania twierdzeń.
Jeżeli
, to
.
założenie
teza
Każde twierdzenie matematyczne musi mieć dowód,
czyli logiczne uzasadnienie.
Aksjomaty są też zdaniami opisującymi
pewne pojęcia i własności, ale przyjmujemy je za
prawdziwe bez dowodu.
Dowód
Dowód
twierdzenia
twierdzenia
Jeżeli kąty są wierzchołkowe
,
to
Twierdzenie:
Dowó
d:
mają równe miary.
BOA =
<
KOT
<
Niech kąty BOA i KOT
będą kątami
wierzchołkowymi.
Wtedy kąt BOA i kąt KOA
są kątami przyległymi
ora
z
kąt KOT i kąt KOA są kątami przyległymi.
Zate
m
BOA +
<
KOA
<
KOT +
<
KOA
<
=
180
o
=
180
o
i
Z równości tych wynika, że
BOA +
<
KOA
<
KOT +
<
KOA
<
=
czyli
.
.
K
T
O
A
.
B
.
co kończy dowód.
Wybierz lekcję
Wybierz lekcję
Kąty przyległe i wierzchołkowe
Kąty przyległe i wierzchołkowe
Kąty naprzemianległe i odpowiadaj
Kąty
Kąty
odpowiadające
odpowiadające
1
1
1
1
Dwie różne proste przecięte trzecią
prostą
tworzą m.in. kąty odpowiadające.
Wskaż kąty
Wskaż kąty
odpowiadające
odpowiadające
1
2
3
4
5
6
8
1 i
5
2 i 6
3 i
7
4 i 8
7
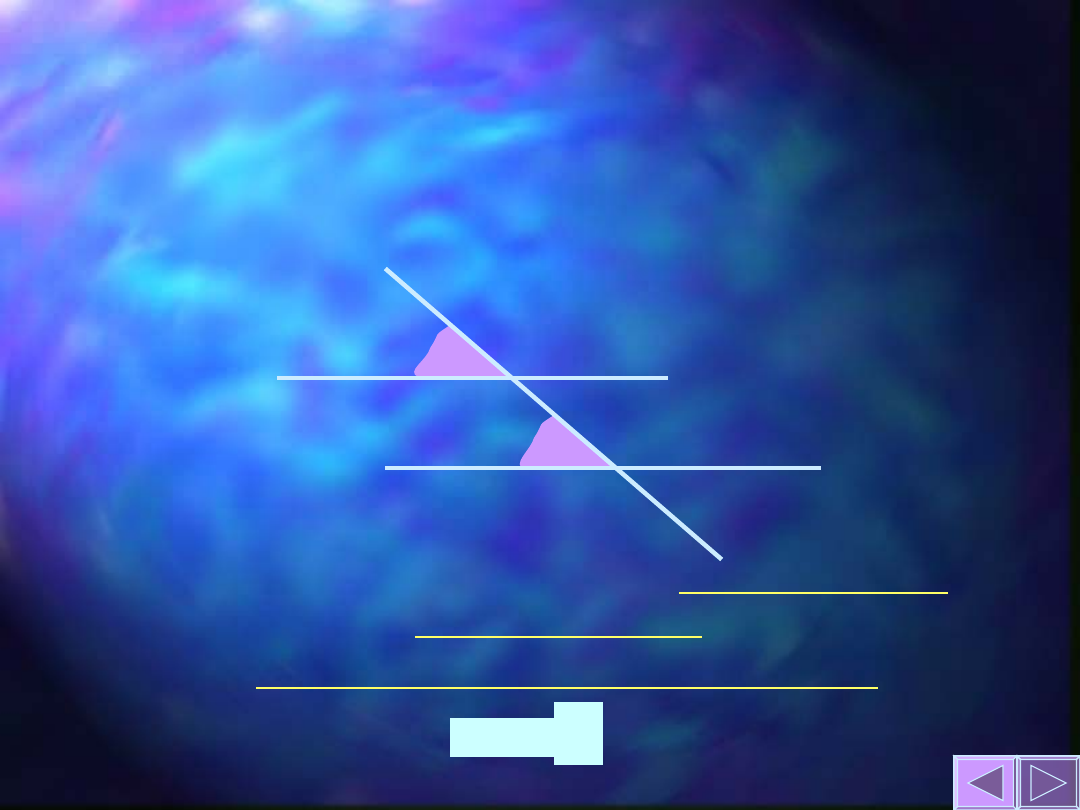
Twierdzenie o kątach
Twierdzenie o kątach
odpowiadających
odpowiadających
k ll m
Jeżeli dwie proste równoległe są
przecięte trzecią prostą, to utworzone
przez nie kąty
k
m
odpowiadające są przystające.
Twierdzenie odwrotne
Twierdzenie odwrotne
o kątach
o kątach
odpowiadających
odpowiadających
Jeżeli dwie proste k i m są przecięte trzecią
prostą
i utworzone przez nie kąty odpowiadające
są przystające,
k ll m
to proste k i m są równoległe.
k
m
Kąty naprzemianległe
Kąty naprzemianległe
wewnętrzne
wewnętrzne
zewnętrzne
zewnętrzne
k
m
c
k
m
c
Dwie różne proste przecięte trzecią prostą
tworzą m.in. kąty naprzemianległe
wewnętrzne i zewnętrzne.
Twierdzenie o kątach
Twierdzenie o kątach
naprzemianległych
naprzemianległych
wewnętrznych
wewnętrznych
k ll m
Jeżeli dwie proste równoległe są
przecięte
trzecią prostą, to utworzone przez nie
kąty
k
m
naprzemianległe wewnętrzne są przystające.
Twierdzenie odwrotne
Twierdzenie odwrotne
o kątach naprzemianległych
o kątach naprzemianległych
wewnętrznych
wewnętrznych
Jeżeli dwie proste k i m są przecięte trzecią prostą
i utworzone przez nie kąty naprzemianległe
wewnętrzne
są przystające,
k ll m
k
m
to proste k i m są równoległe.
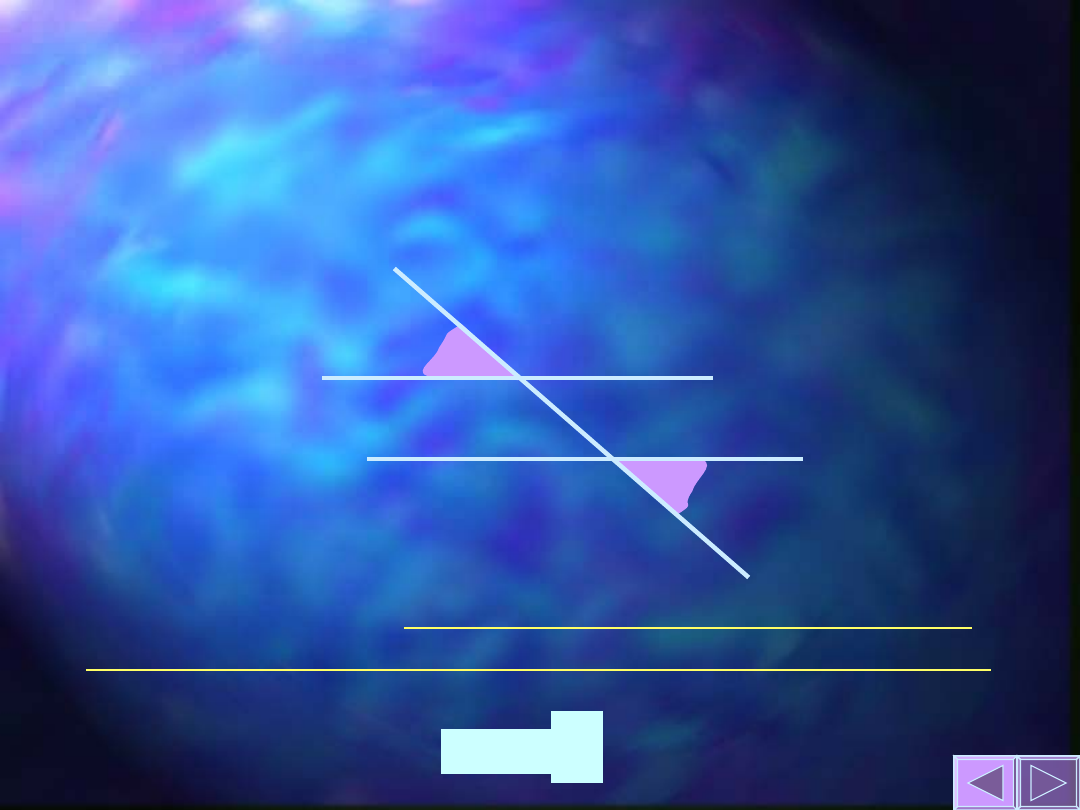
Twierdzenie o kątach
Twierdzenie o kątach
naprzemianległych
naprzemianległych
zewnętrznych
zewnętrznych
k ll m
Jeżeli dwie proste równoległe są przecięte
trzecią prostą, to utworzone przez nie kąty
k
m
naprzemianległe zewnętrzne są przystające.
Twierdzenie odwrotne
Twierdzenie odwrotne
o kątach naprzemianległych
o kątach naprzemianległych
zewnętrznych
zewnętrznych
Jeżeli dwie proste k i m są przecięte trzecią prostą
i utworzone przez nie kąty naprzemianległe
zewnętrzne
k ll m
m
k
są przystające, to proste k i m są równoległe.
Wybierz lekcję
Wybierz lekcję
Kąty przyległe i wierzchołkowe
Kąty przyległe i wierzchołkowe
Kąty naprzemianległe i odpowiadaj