
Image zoom
Professor
Valery Starovoitov
Digital Image Processing
Cyfrowe Przetwarzanie Obrazów

2
Zoom 0
-o
rder
W
e
f
rs
t
d
e
sc
ri
b
e
a
s
im
p
le
m
e
th
o
d
f
o
r
x
2
z
o
o
m
in
g
o
n
a
n
n
x
n
im
a
g
e
u
si
n
g
s
p
a
ti
a
l
lin
e
a
r
f
lt
e
rs
.
T
h
e
f
rs
t
st
e
p
i
s
to
c
re
a
te
a
n
e
w
(
2
n
)
x
(
2
n
)
im
a
g
e
s
u
ch
t
h
a
t:
T
h
e
n
e
w
i
m
a
g
e
h
a
s
th
e
o
ri
g
in
a
l
im
a
g
e
c
o
p
ie
d
o
n
i
ts
p
ix
e
ls
w
it
h
b
o
th
c
o
o
rd
in
a
te
s
e
v
e
n
,
a
n
d
z
e
ro
s
e
v
e
ry
w
h
e
re
e
ls
e
.
0
0
0
0
0
0
0
3
0
7
0
8
0
0
0
0
0
0
3
7
8
0
7
0
5
0
4
7
5
4
0
0
0
0
0
0
4
3
1
0
4
0
3
0
1

3
Zoom 0-order
The second step is to apply the 2x2 flter on the (2n) x (2n)
image
0 0 0 0 0 0
1 1 7 7 8 8
0
3
0
7
0
8
1
3
7
7
8
8
0 0 0 0 0 0
7 7 5 5 4 4
3 7 8
0
7
0
5
0
4
7
7
5
5
4
4
7 5 4
0 0 0 0 0 0
4 4 3 3 1 1
4 3 1
0
4
0
3
0
1
4
4
3
3
1
1
The pixels of the original image have been replicated into 2x2
blocks.
This is called 0-order interpolation.
1
1
1
1
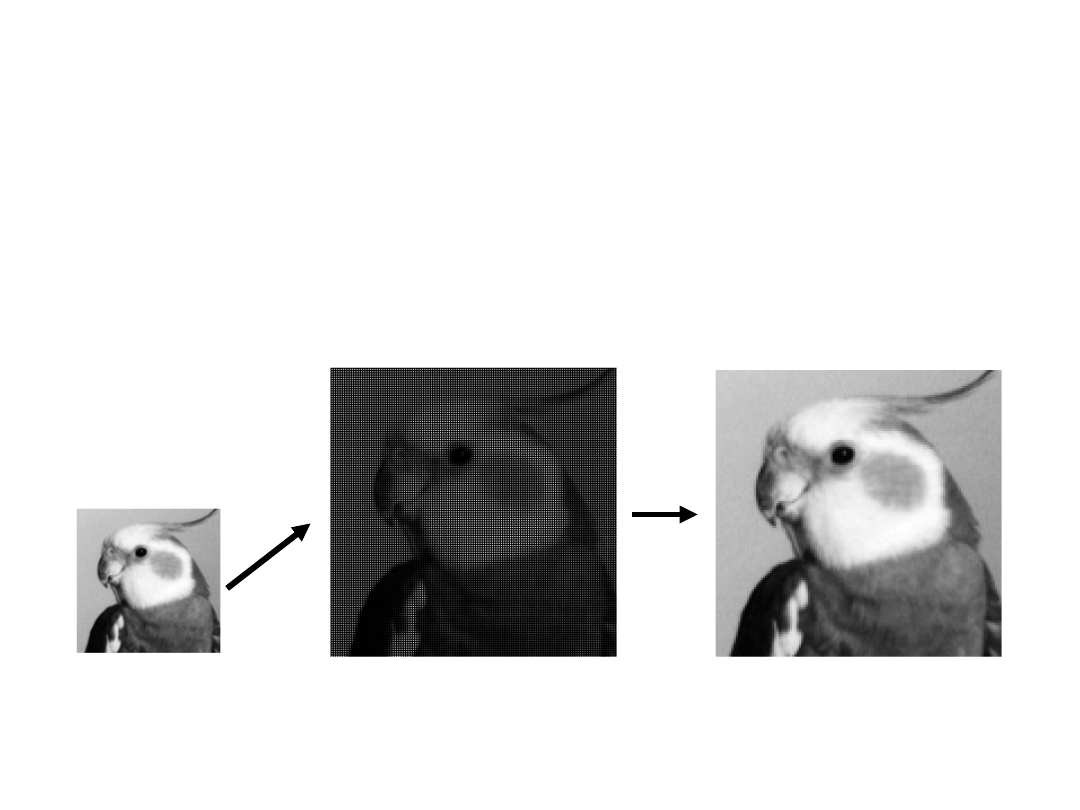
4
Zoom 0-order
The 0-order x2 zooming method described in the previous
slides.

5
Zoom 1-order
Because of the pixel replication the previous method creates
blocky
images.
To address this problem, instead of the 2x2 flter
we can apply the 3x3 flter
This method is called 1-order or linear interpolation.
4
/
1
2
/
1
4
/
1
2
/
1
1
2
/
1
4
/
1
2
/
1
4
/
1
1
1
1
1

6
Zoom 1-order
Linear interpolation also preserves the original pixels:
0 0 0 0 0 0
(1/4)·0 + (1/2)·0 + (1/4)·0 +
0
3
0
7
0
8
+ (1/2)·0 + (1)·
7
+ (1/2)·0 +
0 0 0 0 0 0
+ (1/4)·0 + (1/2)·0 + (1/4)·0 = 7
0
7
0
5
0
4
0 0 0 0 0 0
0
4
0
3
0
1

7
Zoom 1-order
Assuming zeros on the boundary, a new pixel between two old
ones is
the average of them:
0 0 0 0 0 0
(1/4)·0 + (1/2)·0 + (1/4)·0 +
0
3
0
7
0
8
+ (1/2)·
7
+ (1)·0 + (1/2)·
5
+
0 0 0 0 0 0
+ (1/4)·0 + (1/2)·0 + (1/4)·0 = 6
0
7
0
5
0
4
0 0 0 0 0 0
0
4
0
3
0
1

8
Zoom 1-order
A new pixel between four old ones is again the average of
them:
0 0 0 0 0 0
(1/4)·
7
+ (1/2)·0 + (1/4)·
5
+
0
3
0
7
0
8
+ (1/2)·0 + (1)·0 + (1/2)·0 +
0 0 0 0 0 0
+ (1/4)·
4
+ (1/2)·0 + (1/4)·
3
=
19/4
0
7
0
5
0
4
0 0 0 0 0 0
0
4
0
3
0
1

9
Zoom 1-order
The 1-order x2 zoom described in the previous slides.

10
Zoom
x1
x2
x4
We can repeat the process to obtain x4, x8, x16, … , zooms of
the
original.

11
Other zooming methods
Other more sophisticated algorithms use:
Higher order interpolation, e.g. cubic interpolation.
Assume that the original pixels are on a cubic B-spline.
Compute the pixels in between so that they also lie on the
same spline.
Nonlinear diffusion.
Assume that the values of the original pixels correspond to a
natural property of them, e.g. temperature.
Solve a differential equation to compute the flow of the heat in
the image and thus fnd the values of the pixels in between.

12
Summary of zoom methods
0-order and 1-order linear interpolation can be used to obtain zooms of
an image.
The results are generally poor, but the method is very fast and simple.
Implementing these algorithms with spatial linear flters is better than
a
direct implementation:
It is always good to use general tools; spatial linear flters have
other uses than zooming.
Spatial linear flters are very fast because they are supported by the
GPU (Graphics Processing Unit).
Document Outline
Wyszukiwarka
Podobne podstrony:
wykład 12 pamięć
Figures for chapter 12
Mechanika techniczna(12)
Socjologia wyklad 12 Organizacja i zarzadzanie
CALC1 L 11 12 Differenial Equations
zaaw wyk ad5a 11 12
budzet ue 11 12
zapotrzebowanie ustroju na skladniki odzywcze 12 01 2009 kurs dla pielegniarek (2)
Stomatologia czesc wykl 12
Etyka 12
RI 12 2010 wspolczesne koncepcje
podst gospod grunt s 6 w 12
Wykład 12(3)
Wykład 12
więcej podobnych podstron