
Metoda
potencjałów węzłowych
R
1
R
2
R
3
R
4
R
5
j
7
j
6
i
1
i
2
i
4
i
3
i
5
1
3
2
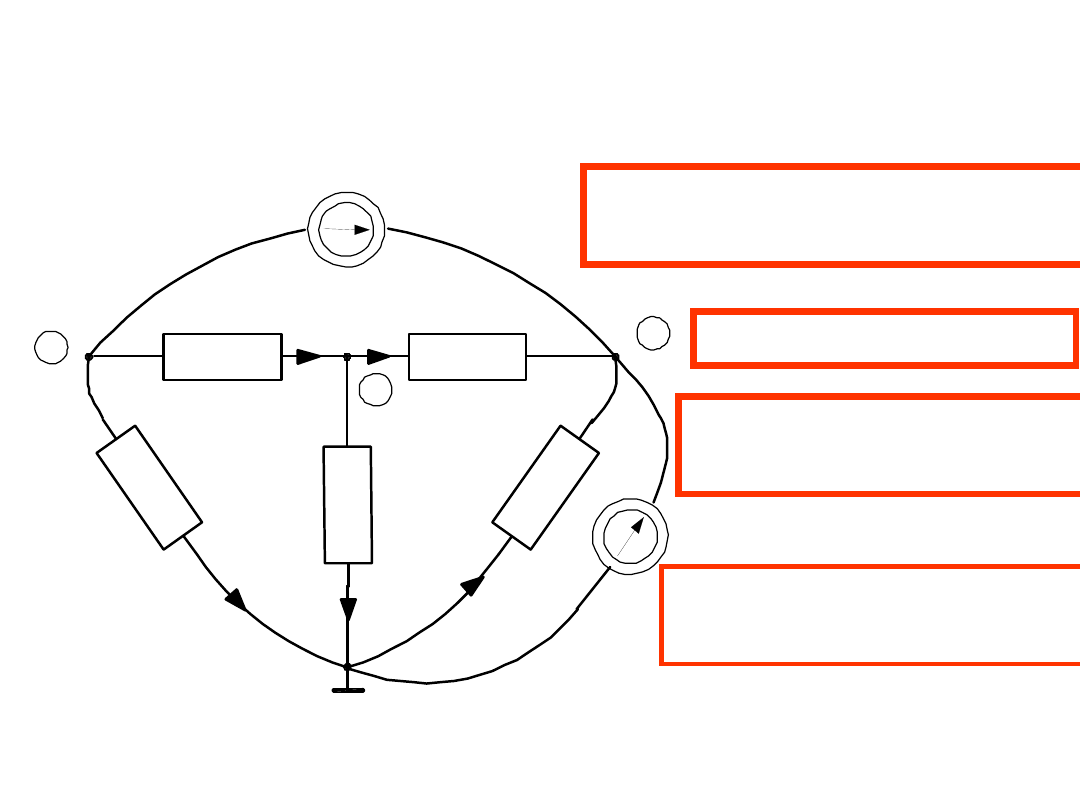
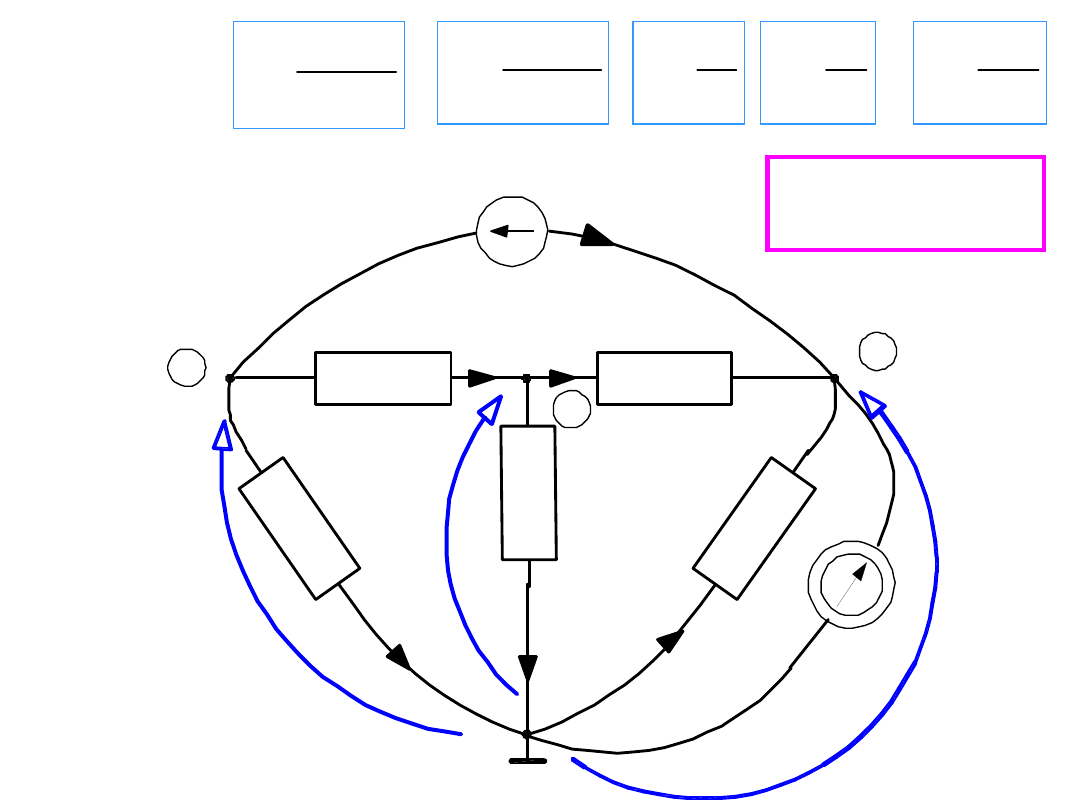
W obwodzie są 4 węzły i 7 gałęzi. Jeśli prądy źródeł są znane –
mamy 5 niewiadomych prądów.
Ile można napisać równań
liniowo niezależnych?
Z PPK 3 równania
Z NPK potrzebne są
2 równania
Mamy do rozwiązania
układ 5 równań
R
1
R
2
R
3
R
4
R
5
j
7
j
6
i
1
i
2
i
4
i
3
i
5
1
3
2
v
1
v
3
v
2
1
2
1
1
R
V
V
i
2
3
2
2
R
V
V
i
3
2
3
R
V
i
4
1
4
R
V
i
5
3
5
R
V
i
0
.
1
6
4
1
j
i
i
dla
0
.
2
2
3
1
i
i
i
dla
0
.
3
7
6
5
2
j
j
i
i
dla
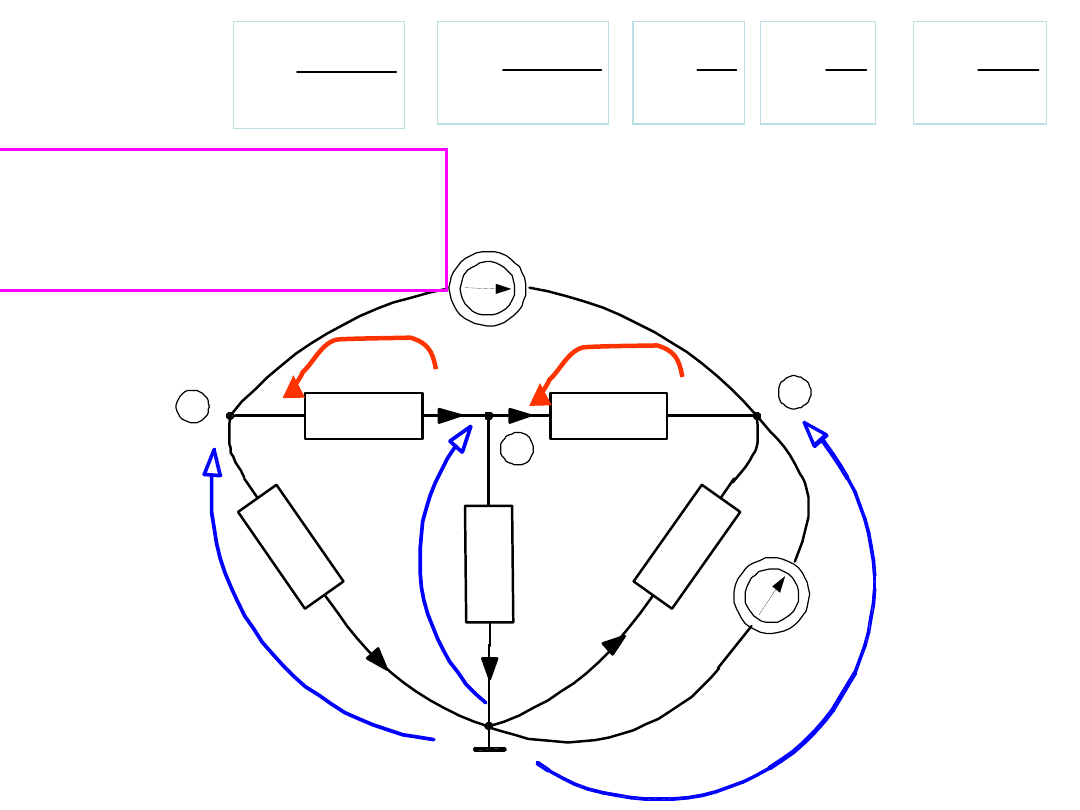
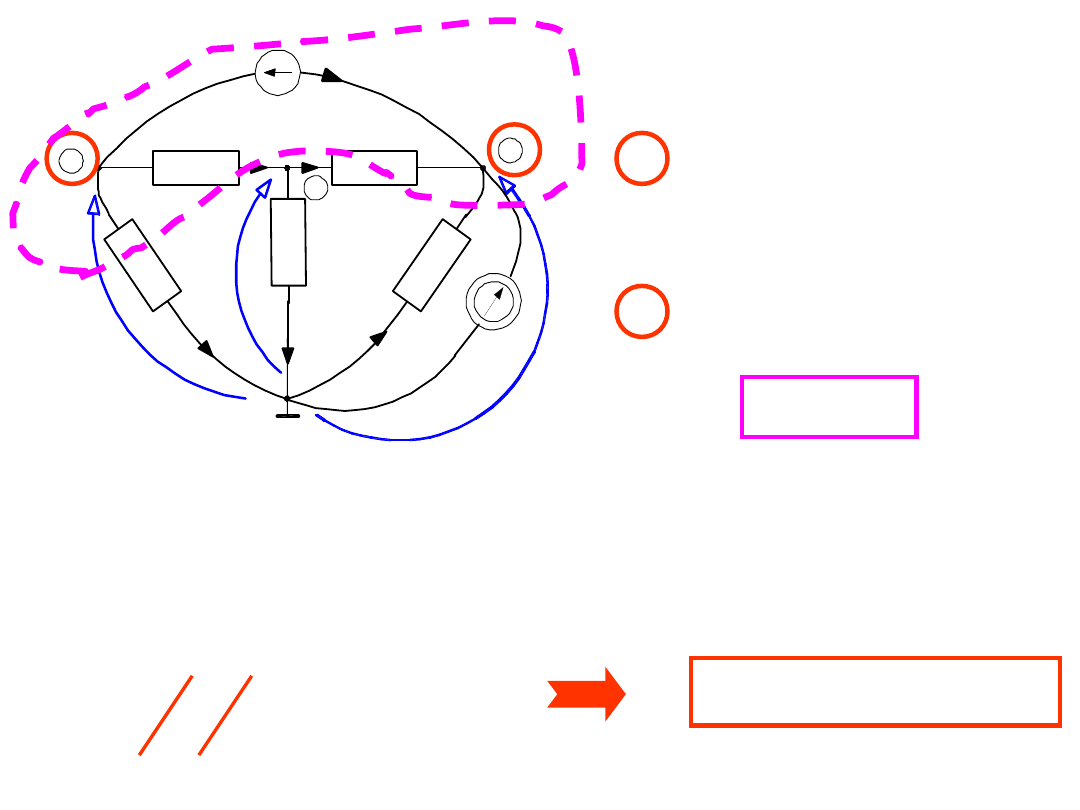
Pokażemy, że
wystarczy znajomość
trzech potencjałów węzłowych
tzn. układ trzech równań
0
6
4
1
1
2
1
j
R
V
R
V
V
0
2
3
2
3
2
1
2
1
R
V
V
R
V
R
V
V
0
7
6
5
3
2
3
2
j
j
R
V
R
V
V
Po uporządkowaniu
otrzymamy:
6
1
2
4
1
1
1
1
1
j
R
V
R
R
V
0
1
1
1
1
1
2
3
3
2
1
2
1
1
R
V
R
R
R
V
R
V
7
6
5
2
3
2
2
1
1
1
j
j
R
R
V
R
V
Są 3 niewiadome
potencjały: V
1
, V
2
, V
3
.
R
1
R
2
e
3
R
4
R
5
j
7
j
6
i
1
i
2
i
4
i
3
i
5
1
3
2
v
1
v
3
v
2
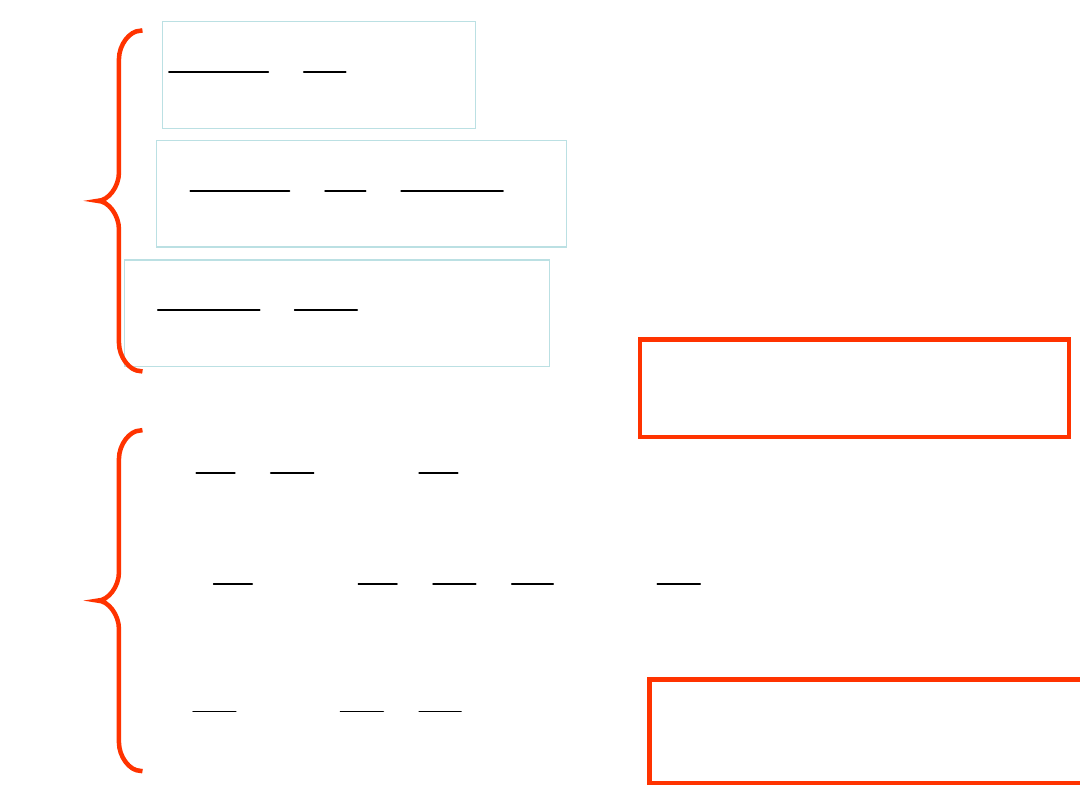
Przykład 2
Przykład 2
Teraz V
2
=e
3
!!!
Są 2 niewiadome !!!

0
6
4
1
1
2
1
j
R
V
R
V
V
0
2
3
2
3
2
1
2
1
R
V
V
R
V
R
V
V
0
7
6
5
3
2
3
2
j
j
R
V
R
V
V
3
2
e
V
Zamiast drugiego równania jest:
0
6
4
1
1
2
1
j
R
V
R
V
V
0
7
6
5
3
2
3
2
j
j
R
V
R
V
V
3
2
e
V
2
3
7
6
5
2
3
6
1
3
4
1
1
1
1
1
1
R
e
j
j
R
R
V
j
R
e
R
R
V
R
1
R
2
R
3
R
4
R
5
j
7
e
6
i
1
i
2
i
4
i
3
i
5
1
3
2
i
2
6
v
1
v
3
v
2
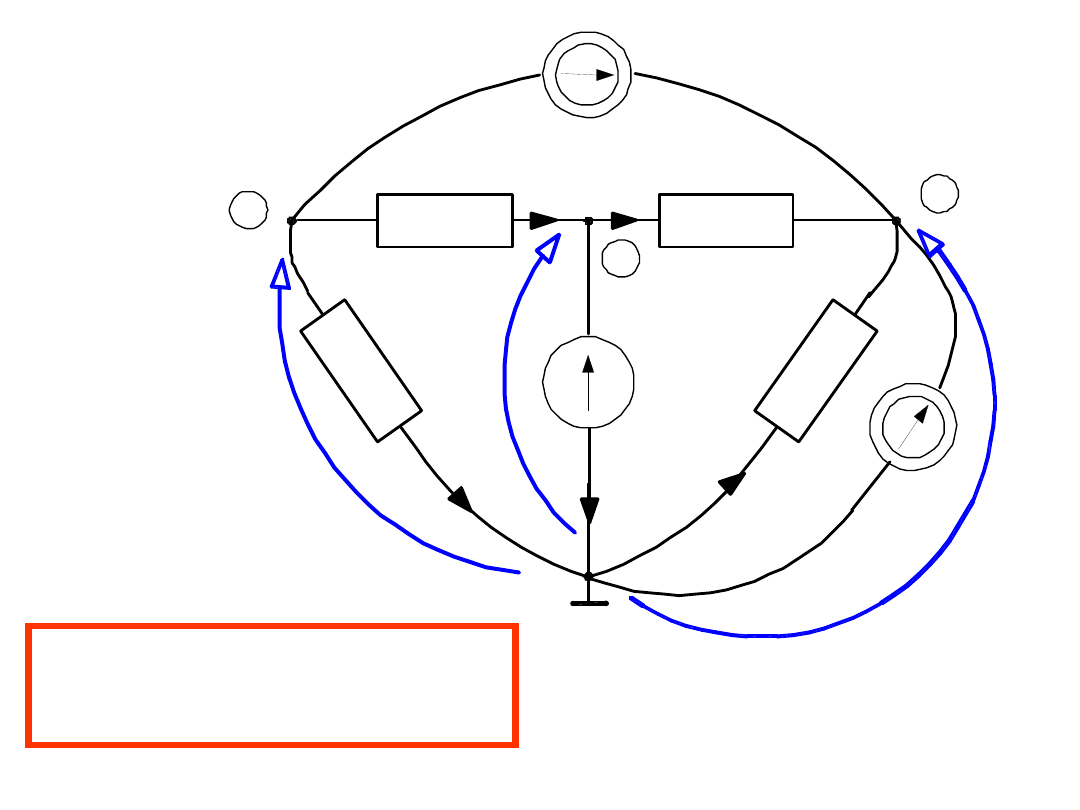
Przykład 3
Przykład 3
1
2
1
1
R
V
V
i
2
3
2
2
R
V
V
i
3
2
3
R
V
i
4
1
4
R
V
i
5
3
5
R
V
i
6
3
1
e
V
V
R
1
R
2
R
3
R
4
R
5
j
7
e
6
i
1
i
2
i
4
i
3
i
5
1
3
2
i
2
6
v
1
v
2
v
3
0
.
3
0
.
2
0
.
1
7
5
2
6
2
3
1
6
1
4
j
i
i
i
i
i
i
i
i
i
PPK:
W równaniach pojawiła się dodatkowa niewiadoma – prąd i
6
.
Możemy ją usunąć z równań.
Dodajmy stronami równania 1. i 3.
0
7
5
2
6
6
1
4
j
i
i
i
i
i
i
0
7
5
2
1
4
j
i
i
i
i
To równanie można napisać dla przekroju przez gałęzie 4-1-2-5-7.
6
3
1
e
V
V

Twierdzenie Thevenina-
Twierdzenie Thevenina-
Nortona
Nortona
Twierdzenie Thevenina-
Twierdzenie Thevenina-
Nortona
Nortona
u
i
A
B
G
z
i
z
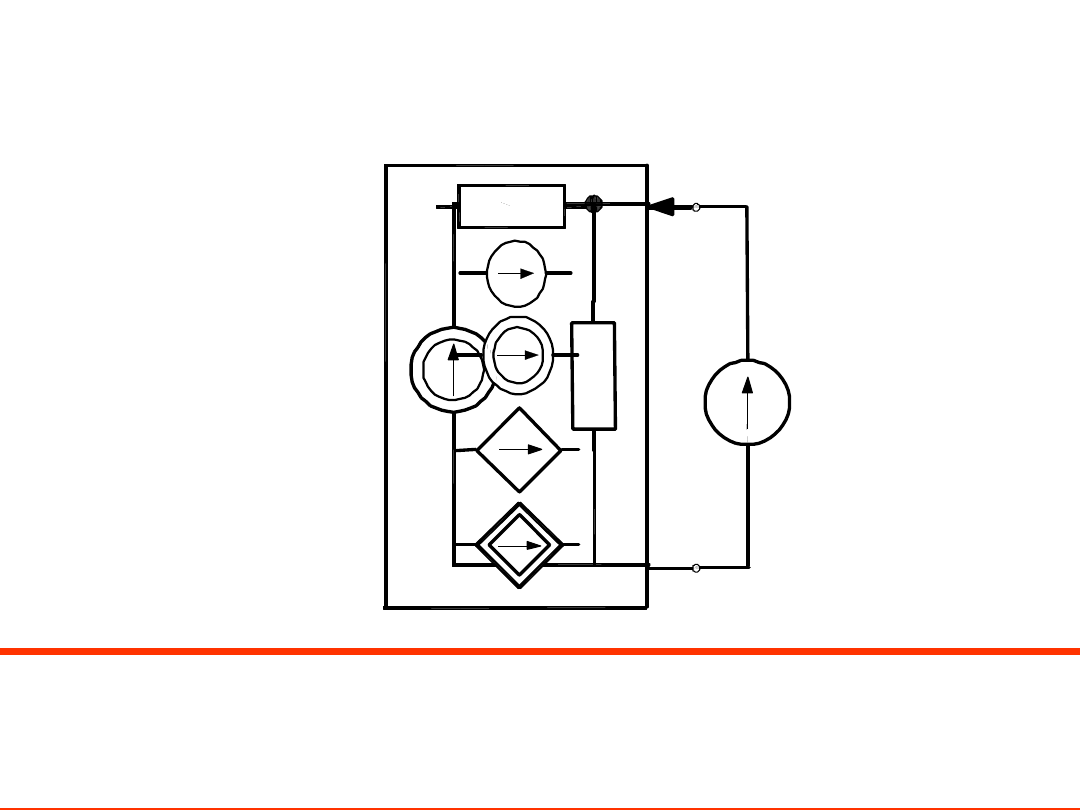
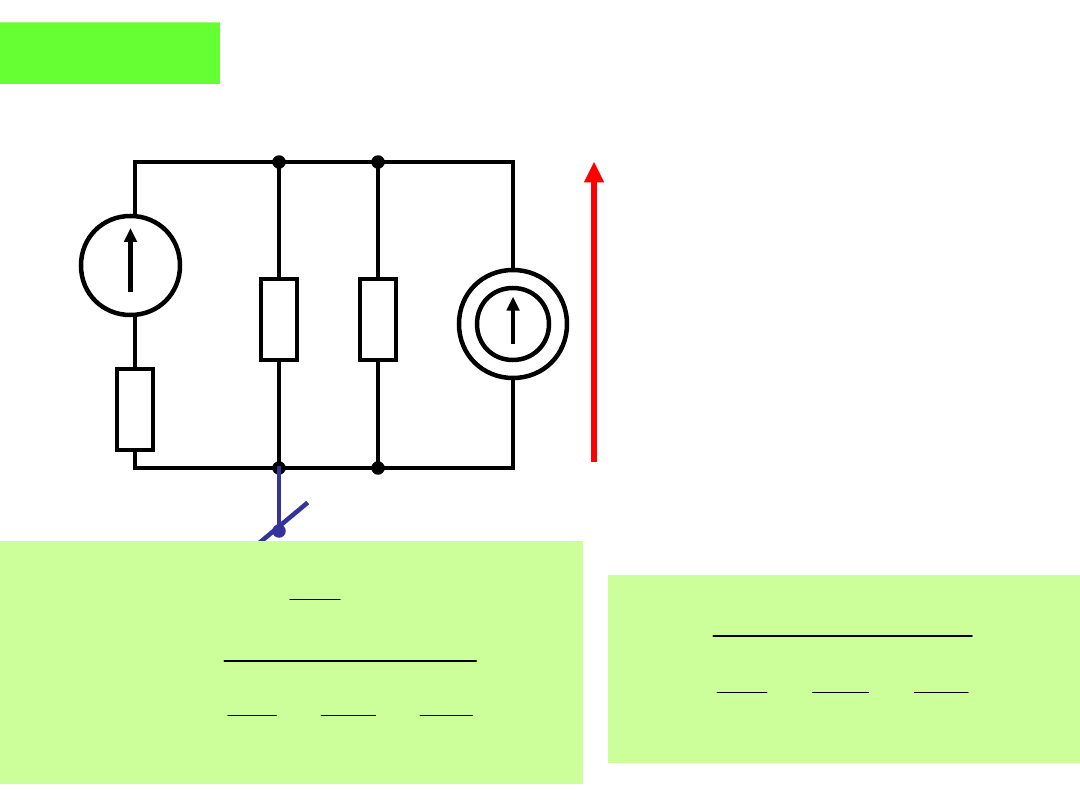
A. Twierdzenie Nortona
Każdy liniowy dwójnik aktywny można zastąpić z wybranej pary zacisków AB
rzeczywistym źródłem prądu o parametrach i
z
i G
z.
Prąd jest prądem zwarciowym, a konduktancję liczymy z zacisków AB
po usunięciu wszystkich źródeł niezależnych.
u
i
A
B
u
z
R
z
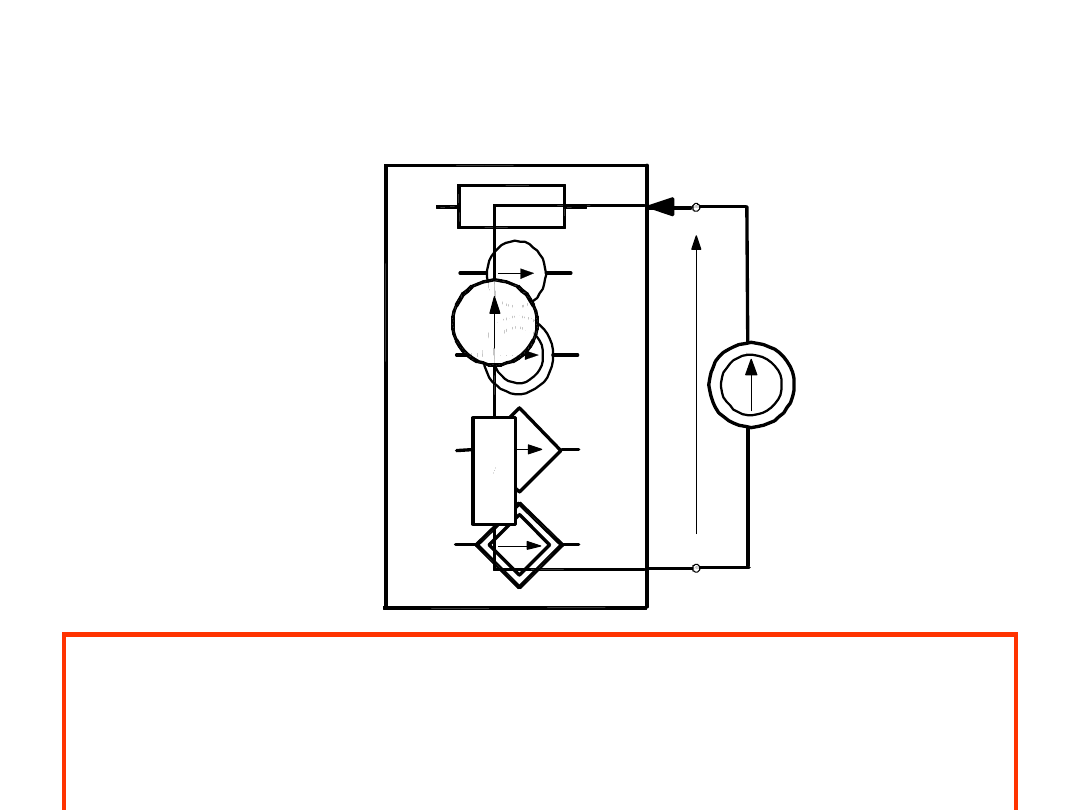
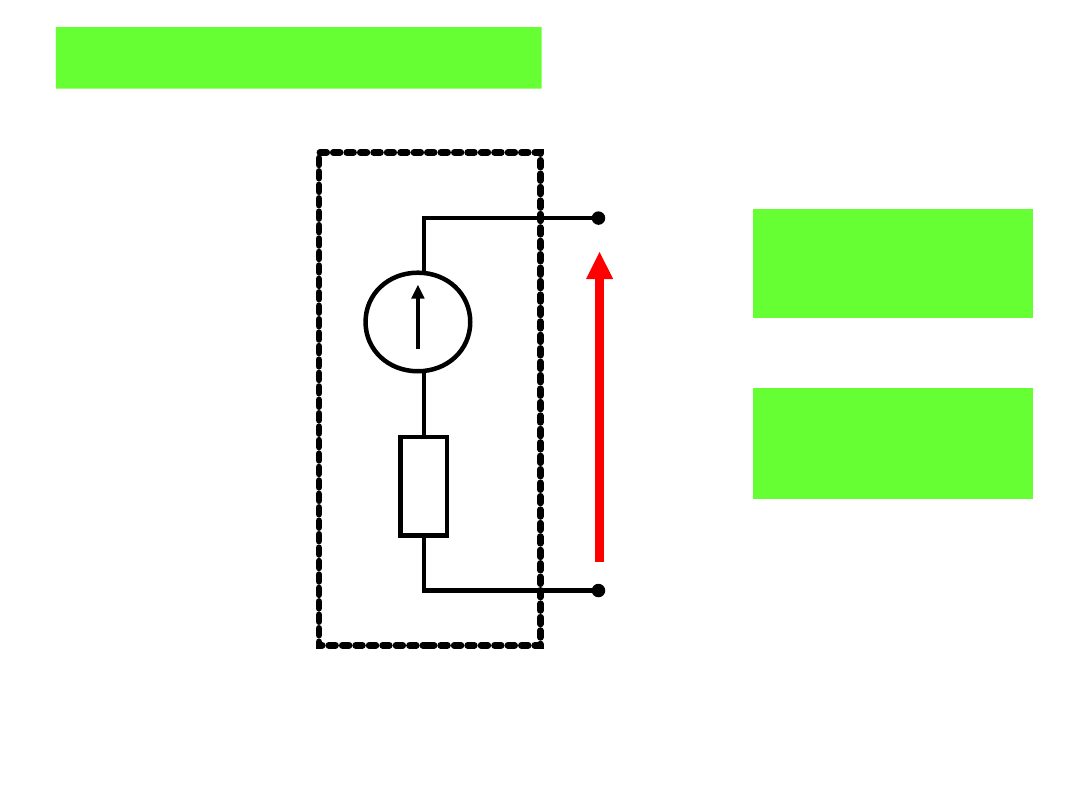
A. Twierdzenie Thevenina
Każdy liniowy dwójnik aktywny można zastąpić z
wybranej pary zacisków AB rzeczywistym źródłem
napięcia o parametrach u
z
i R
z
.
Napięcie u
z
występuje na rozwartych zaciskach AB, a
rezystancję liczymy z zacisków AB po usunięciu
wszystkich źródeł niezależnych.
Przykład:
E
1
J
R
1
R
2
R
3
Wyznaczymy parametry dwójnika Thevenina (E
z
i R
z
)
widzianego z zacisków AB.
Dane:
A
J
V
E
R
R
R
2
4
3
6
2
1
3
2
1
A
B
U
AB
V
R
R
R
J
R
E
V
u
A
AB
4
1
1
1
3
2
1
1
1
1
1
1
1
1
3
2
1
R
R
R
R
z
A
B
E
z
R
z
V
E
Z
4
1
Z
R
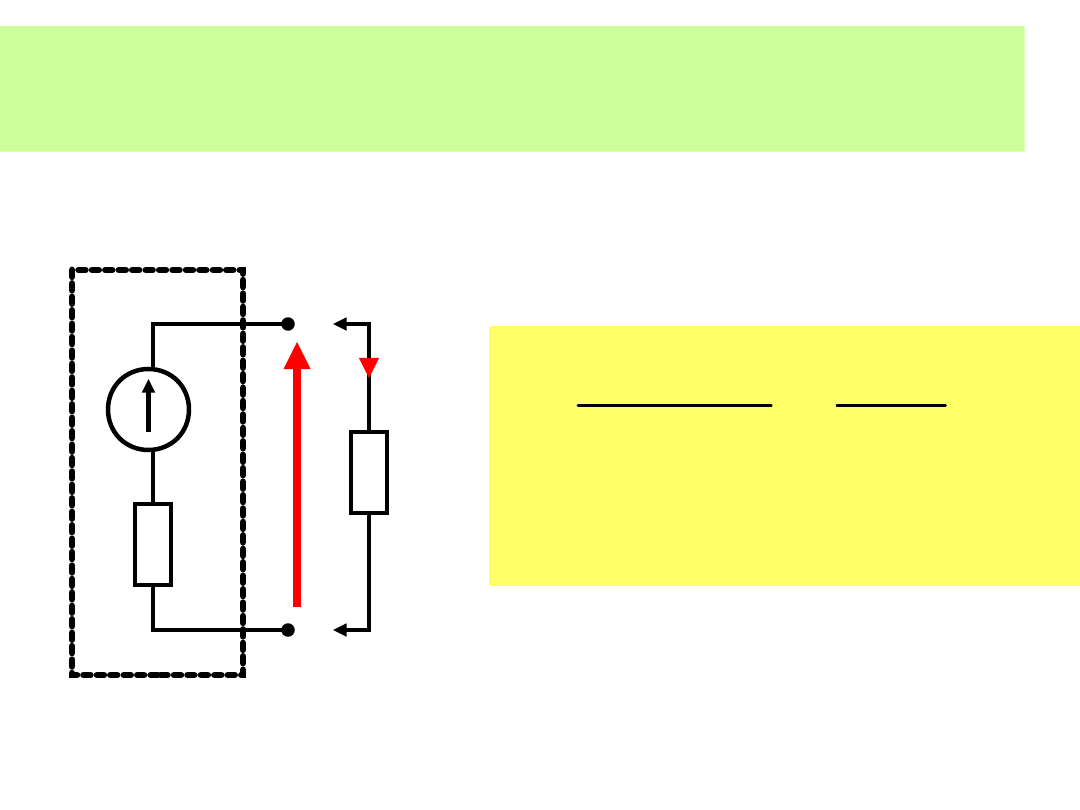
Dwójnik Thevenina:
u
AB
R
0
A
B
E
z
R
z
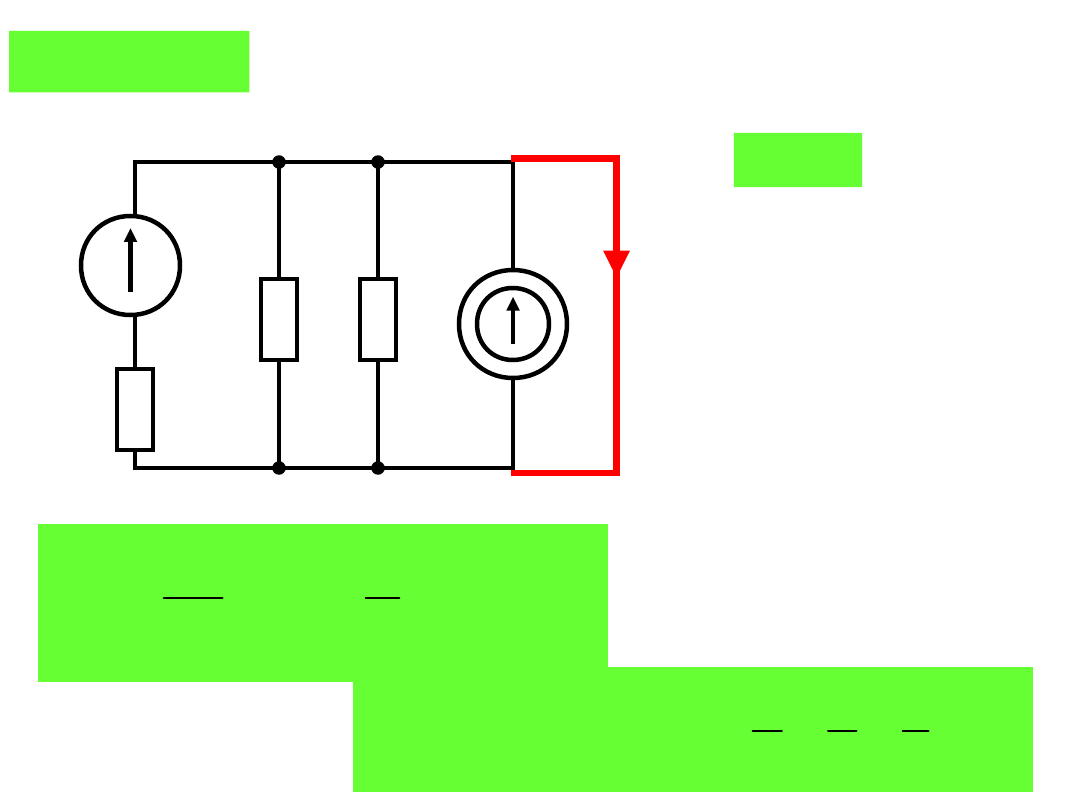
Jak zmieni się napięcie u
AB,
gdy do dwójnika dołączymy rezystor R
0
=3Ω?
V
iR
u
A
R
R
E
i
AB
z
z
3
3
1
1
3
1
4
0
0
i
E
1
J
R
1
R
2
R
3
Wyznaczymy parametry dwójnika Nortona (J
z
i G
z
)
widzianego z zacisków AB.
Przykład:
A
J
V
E
R
R
R
2
4
3
6
2
1
3
2
1
Dane:
A
B
J
Z
A
J
R
E
J
Z
4
2
2
4
1
1
S
G
G
G
G
Z
1
3
1
6
1
2
1
3
2
1
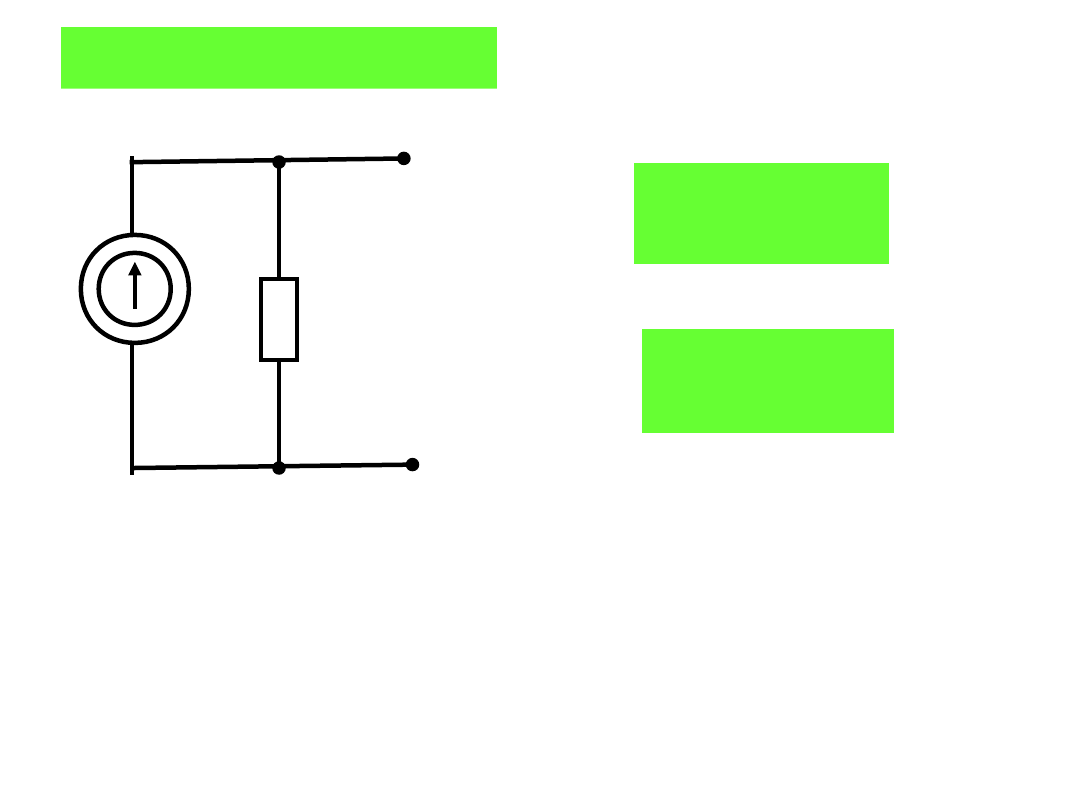
J
G
Z
A
B
Dwójnik Nortona:
A
J
Z
4
S
G
Z
1
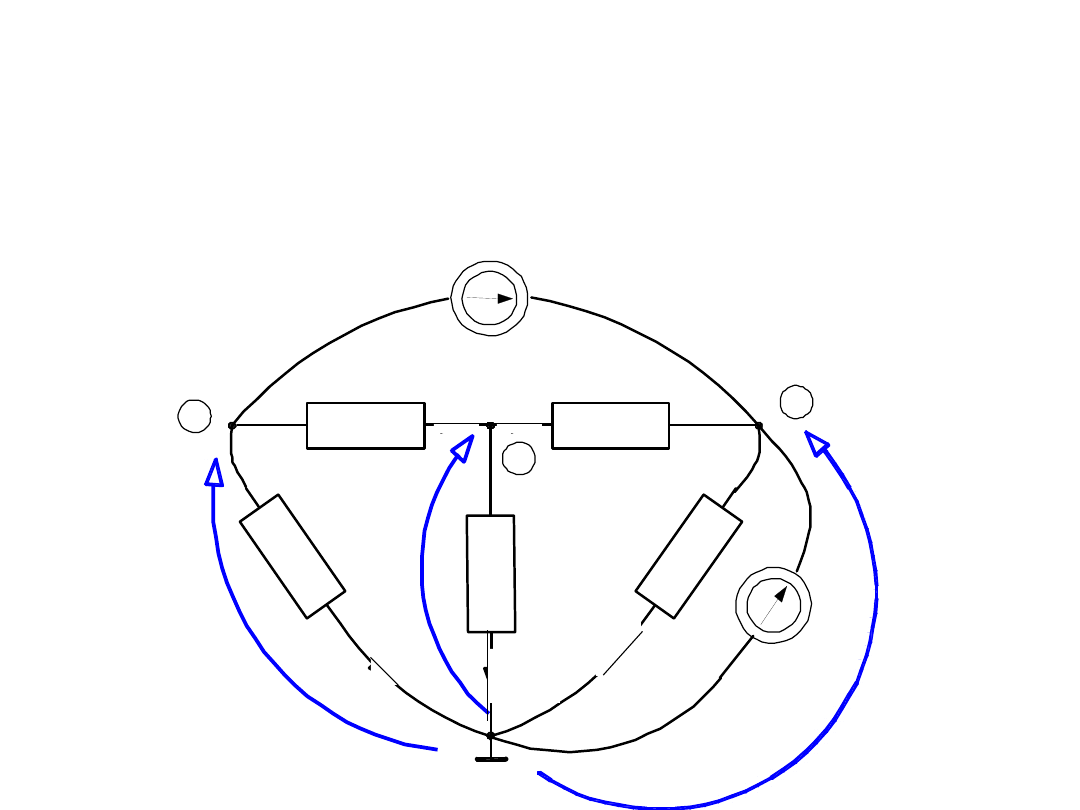
Przykład 1 -inaczej
Przykład 1 -inaczej
R
1
R
2
R
3
R
4
R
5
j
7
j
6
i
1
i
2
i
4
i
3
i
5
1
3
2
v
1
v
3
v
2
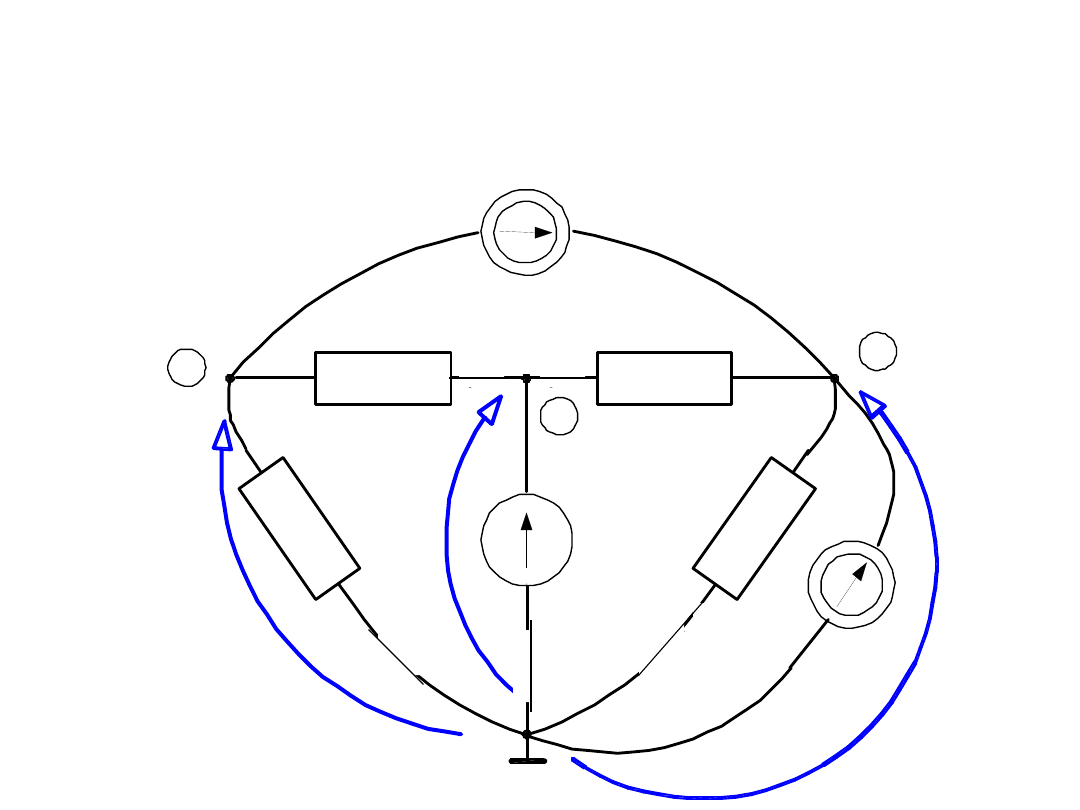
Przykład 2 - inaczej
Przykład 2 - inaczej
R
1
R
2
e
3
R
4
R
5
j
7
j
6
i
1
i
2
i
4
i
3
i
5
1
3
2
v
1
v
3
v
2
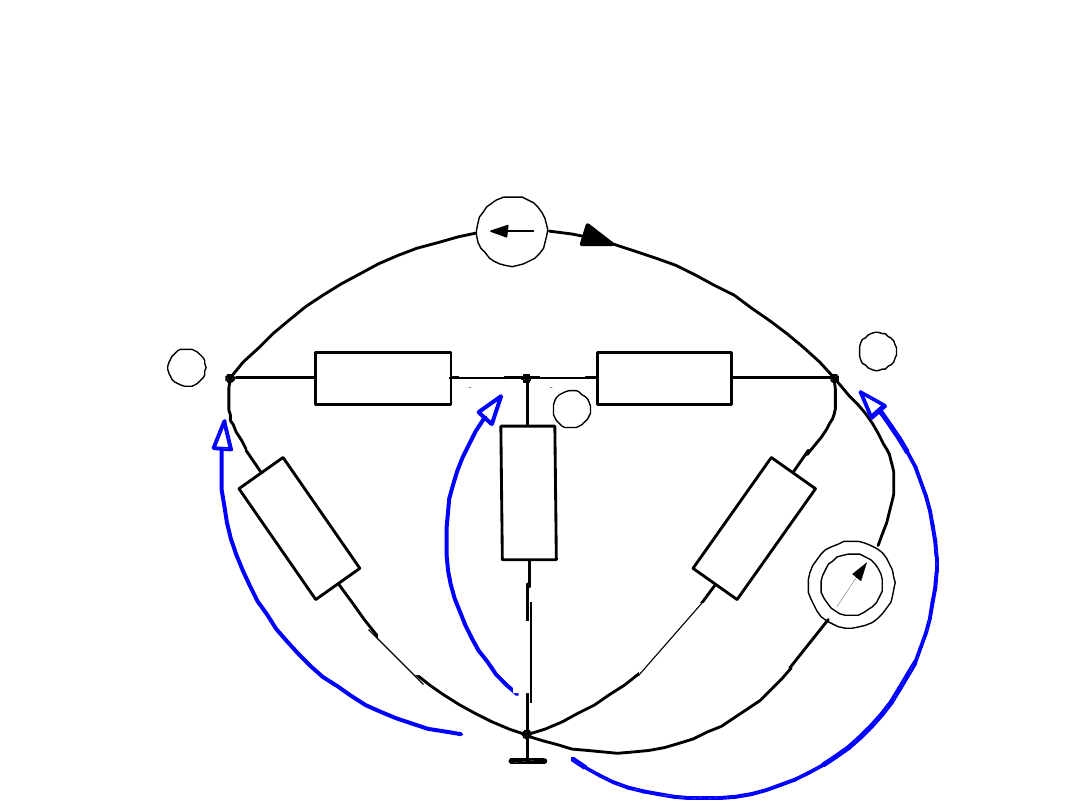
Przykład 3 - inaczej
Przykład 3 - inaczej
R
1
R
2
R
3
R
4
R
5
j
7
e
6
i
1
i
2
i
4
i
3
i
5
1
3
2
i
2
6
v
1
v
3
v
2
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
Wyszukiwarka
Podobne podstrony:
Nauka, przykład + Matlab, Matoda potencjałów węzłowych, Matoda potencjałów węzłowych
Nauka, przykład + Matlab, Matoda potencjałów węzłowych, Matoda potencjałów węzłowych
Metoda potencjalow wezlowych
Metoda potencjałów węzłowych, Automatyka i robotyka air pwr, I SEMESTR, elektrotechnika, kolokwium
potencjal wezlowy id 378783 Nieznany
cw4 Potencjały węzłowe
Wykład Ch F potencjometria
2015 wyklad VIII POTENCJOMETRIA Nieznany
potencjalne pytania, Automatyka i Robotyka, Semestr II, Zasady doboru materiałów inżynierskich, wykl
Wykład 06 - Zapalenie węzłów chłonnych, OML, III rok, Patomorfologia
Wykład 21 potencjał pola el
Napęd Elektryczny wykład
wykład5
więcej podobnych podstron