SPEKTROSKOPIA

  jest  nauką,  która  bada  i 

wyjaśnia  oddziaływania  pomiędzy  materią 
będącą  zbiorowiskiem  atomów  i  cząsteczek  a 
promieniowaniem elektromagnetycznym. 

Promieniowanie 

elektromagnetyczne 

jest 

falowym 

zaburzeniem 

pola 

elektromagnetycznego  rozchodzącym  się  w 
próżni  z  prędkością  światła.  W  fizycznym 
opisie  promieniowania  zakłada  się  jego 

dualistyczną 

naturę

. 

Z 

jednej 

strony 

uwzględnia  się  jego 

charakter  falowy

,  a  z 

drugiej  strony  traktuje  się  je  jako  wiązkę 
cząstek 

– 

fotonów, 

mających 

określoną 

energię

.

Do  badania  budowy  związków  organicznych 
metodami 

spektroskopowymi 

stosuje 

się 

promieniowanie 

elektromagnetyczne 

o 

różnych zakresach długości fali, od ultrafioletu 
aż do fal radiowych.

 

 

czas

(1 cykl/sek = 1 

Hz)

odległość

(1 cykl/cm = 1 

cm

-1

)

PROMIENIOWANIE ELEKTROMAGNETYCZNE

 

gdzie  (c)    -      prędkość  rozchodzenia  się  fali 
elektromagnetycznej  w  próżni,  tzw.  prędkość  światła, 
jest wielkością stałą i wynosi, c =  2.9979   10

8

 ms

-1

 

= 2.9979  10

10

 cms

-1

. 



λ

 

 

c

Fali promieniowania elektromagnetycznego można przypisać 

długość () i/lub częstość (). Obydwie wielkości są ze sobą 

związane zależnością:

 

 

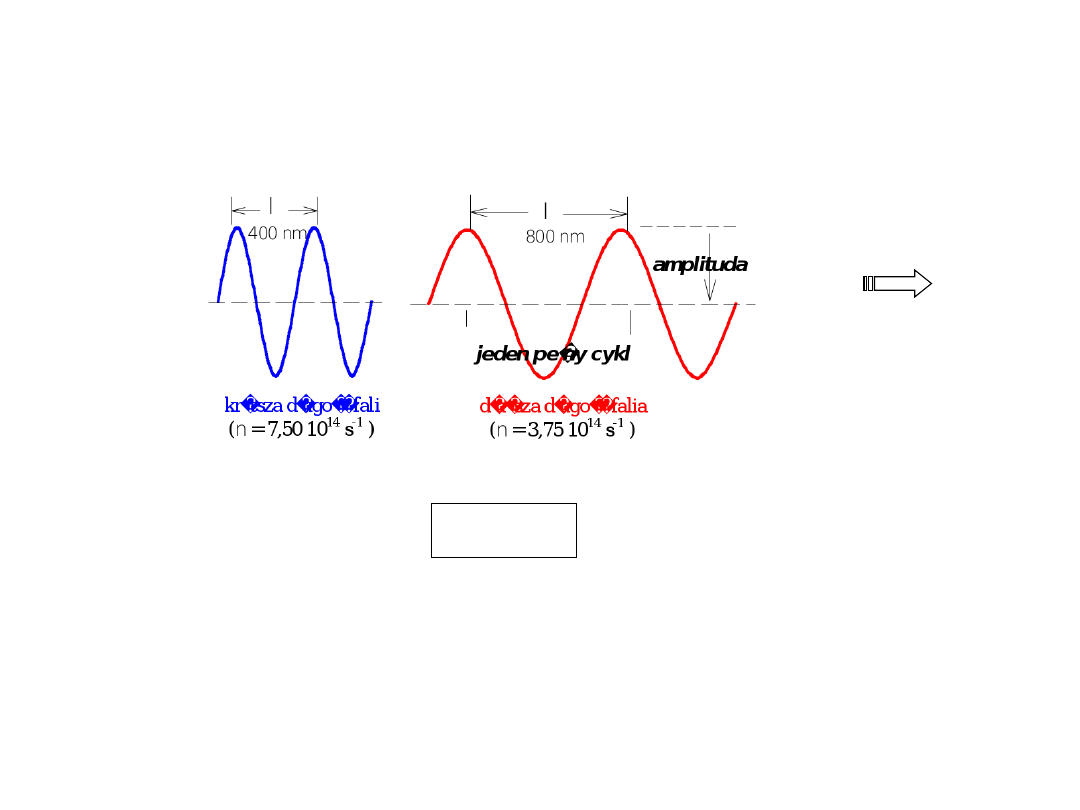
Częstość  ()

  – 

liczbę  pełnych  cykli  fali  przechodzących   

przez  dany  punkt  w  każdej  sekundzie,  w  miarę  jak  fala 
przesuwa się w przestrzeni, mierzy się w cyklach na sekundę 
(cps – cycles per second)  lub w hercach (Hz- hertz)

Liczba falowa (      = 1/ = /c )

 

– liczba pełnych cykli fali 

na cm

 (cm 

-1

) 

Długość fali ()

 

– długość jednego pełnego cyklu fali, 

wyraża się w: 

metrach (m) lub centymetrach (1 cm = 10

-2

 m)

mikrometrach (1 m = 10

-6

 m) [ starsza nazwa 

mikron,  ]

nanometrach   (1 nm = 10

-9

 m) [ starsza nazwa 

milimikron, m ]

_



podwielokrotności

decy, centy
mili = 10

-3

mikro = 10

-6

nano = 10

-9

piko = 10

-12

femto = 10

-15

atto = 10

-18

wielokrotności

deka, hekto
kilo (k) = 10

3

mega (M) = 10

6

giga (G) = 10

9

tera (T) = 10

12

peta (P) = 10

15

eksa (E) = 10

18

Angstrem (Å) 
= 10

-10 

m 

(1868 r)
1 Å = 0,1 nm
1 Å = 100 pm

 

 



_

hc

  

  

λ

c

 

h

 

  

ν

 

h

  

 

E







prędkość światła 
(m s 

-1

)

częstość 
(Hz)

stała 
Plancka

energia 

kwantu

(J mol 

-1

)

liczba falowa 
(m

-1

)

stała Plancka (h) =  6,626  10

 –34 

 J s   = 1,584  10

-34 

 cal 

s       

[1 cal = 4,184 J]

 

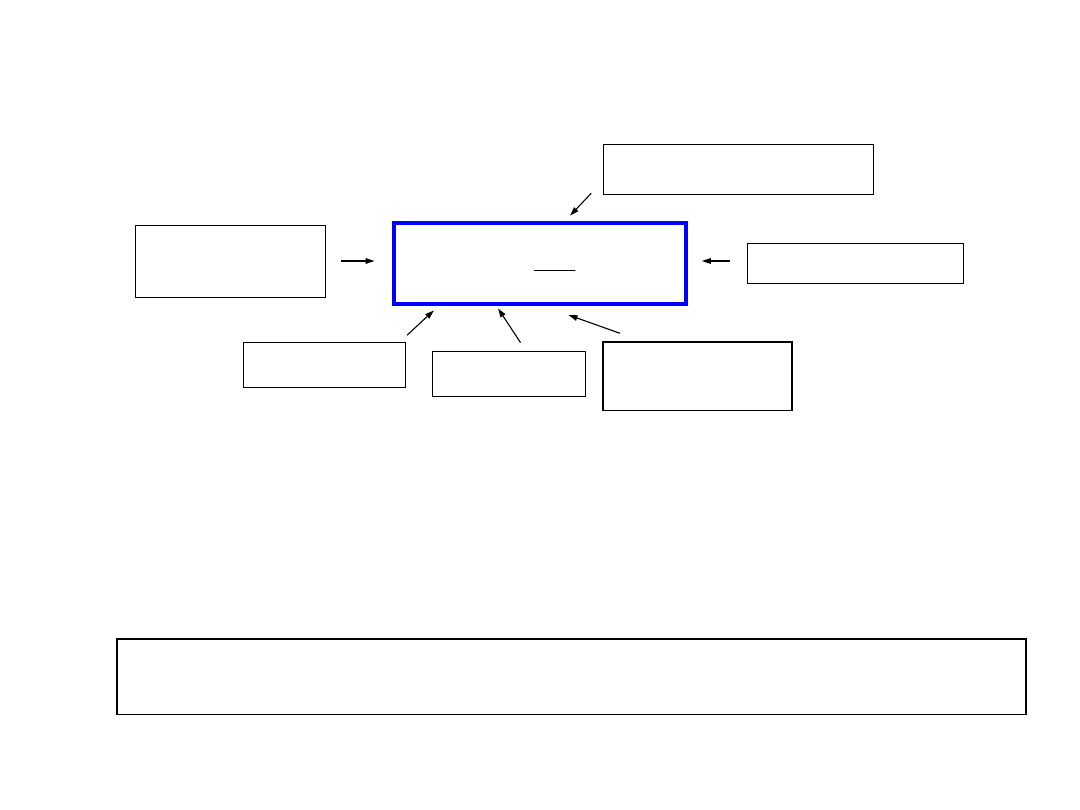
Równanie 
Plancka:

 

długość fali 
(m)

PROMIENIOWANIE ELEKTROMAGNETYCZNE

  

jako wiązka cząstek – FOTONÓW mających określoną 

energię E

Energia  promieniowania  elektromagnetycznego  jest 
przenoszona  jedynie  przez  ściśle  określone  porcje 
energii zwane kwantami (lub fotonami).

 Zależność 

energii 

przenoszonej 

przez 

kwanty 

promieniowania  z  wielkościami  charakteryzującymi 
promieniowanie  jako  falę  jest  opisana  równaniem 
Plancka.

Im wyższa 

częstość

 () i większa 

liczba falowa

 (   ), tym wyższa 

energia

 ( 





 ). ( 





 )

Im większa 

długość fali

 ( = c / ), tym niższa 

energia

  ( 





 )

_



 

 

nm

 

w

mol

kcal

  

10

2,86

nm

 

w

mol

kJ

10

1,2

 

 

c

h

N

  

E

1

4

-1

5

A



























        

 (m)

E = 1,2  10

-4

 ; 2,86 

 10

-5

    

     (cm)

E = 1,2  10

-2

 ; 2,86 

 10

-3

    

      (m)

E = 1,2  10

2 

 ; 2,86 

 10

1

Energia 1 mola 
fotonów

liczba Avogadro (N

A

) = 6,02 x 

10

23

stała Plancka (h) = 6,62 x 10

-31 

kJ m

prędkość światła (c) = 3 x 10

8

 

m/ s

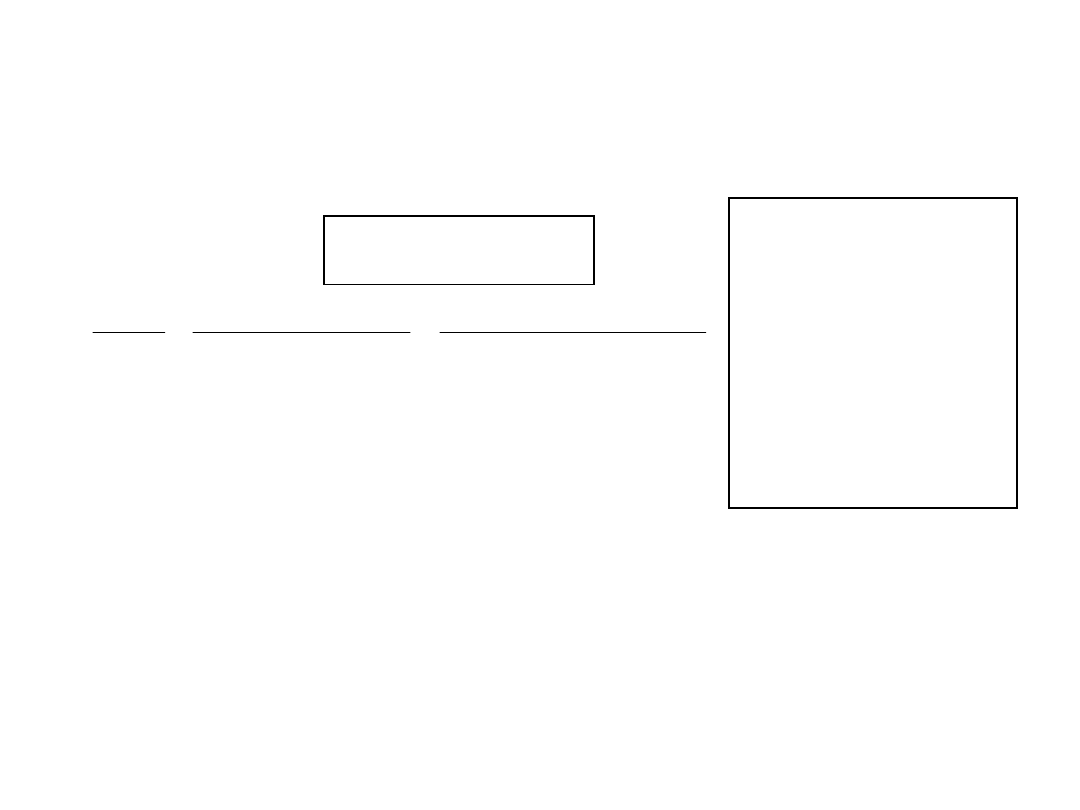
Dogodną  relacją  wiążącą  długość  fali  (,  w  nm)  z 

energią  promieniowania  elektromagnetycznego  (energią  1  mola 
fotonów o długości fali ) jest zależność:

200 nm = 600 kJ/mol = 143 
kcal/mol; 
400 nm = 300 kJ/mol = 71,5 
kcal/mol
800 nm = 150 kJ/mol =  35,7 
kcal/mol;

2,5 m = 48 kJ/mol = 11,44 

kcal/mol;
10 m  = 12 kJ/mol =   2,86 

kcal/mol;
25 m  = 4,8 kJ/mol =  1,14 

kcal/mol

N

A 

· h · c = 1,2 x 10

-4

 kJ · m / 

mol
               = 2,86 x 10

-5

 kcal · 

m / mol

1 m = 0,00012 
kJ/mol
5 m = 0,00002 
kJ/mol

UV/vis

IR

NMR

 

 

_



nm

 

w

m

 

w

000

 

10

cm

 

w

7

10

1

 

















Dogodną  relacją  wiążącą  długość  fali  ()  z  liczbą  falową  (w 

cm 

-1

) jest zależność:

m () = 10

-6 

m

nm = 10

-9

 m

(cm

-1

) 

=

4000 cm

-1

 = 10 000 / 2,5 m;      

1000 cm

-1

 = 10 

000 / 10 m;     
  666 cm

-1

 = 10 000 / 15 m; 

  400 cm

-1

 = 10 

000 / 25 m;

12 500 cm

-1 

= 10

7

 / 800 nm; 

25 000 cm

-1

 = 10

7

 / 

400 nm;

50 000 cm

-1

 = 10

7

 / 200 nm

 

 

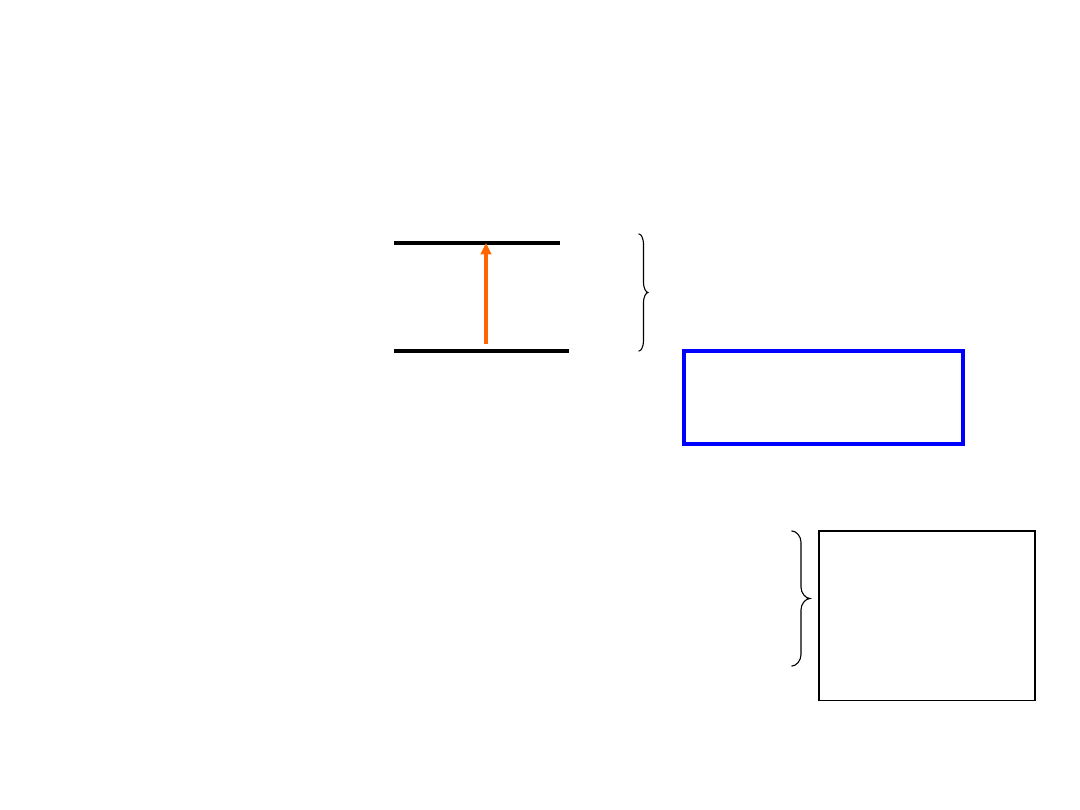
Energia

promieniowania

elektromagnetyc

znego

 

Różnica 
poziomów 
energetycznych 
cząsteczki

 

E

2

E

1

h   =  E = E

2

 

– E

1

 

h


ABSORPCJA ENERGII JEST KWANTOWANA

Cząsteczka może absorbować tylko takie kwanty 

promieniowania elektromagnetycznego, których energia 

ściśle odpowiada różnicy poziomów energetycznych 

cząsteczki

Absorpcja energii może:

 powodować przejście elektronów z orbitali o niższej 
energii (w stanie podstawowym) na orbitale o wyższej 
energii (w stanie wzbudzonym)
 zmieniać energię drgań oscylacyjnych cząsteczki
 zmieniać energię rotacyjną ruchu obrotowego 
cząsteczki
 zmieniać energię ruchów translacyjnych cząsteczki
 energię związaną z ukierunkowaniem spinu 
niesparowanych elektronów – (spektroskopia EPR) lub 
spinu niektórych jąder w stosunku do wektora indukcji 
pola magnetycznego – (spektroskopia NMR) 

3N stanów 
swobody

N – liczba 
atomów w 
cząsteczce

 

 

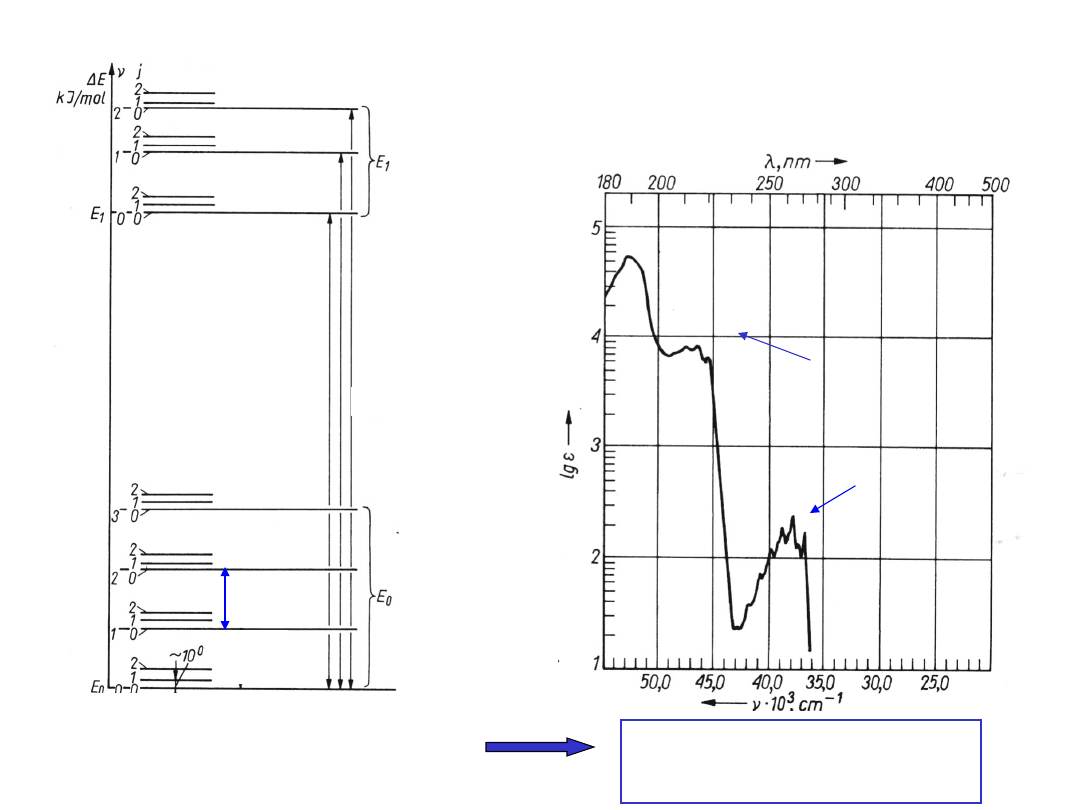
PRZEJŚCIA ELEKTRONOWE 

               Przejściom elektronowym 

towarzyszą zmiany

          energii oscylacyjnej i rotacyjnej 

cząsteczki

wzbudzo
ne stany 
elektrono
we

podstawo
we stany 
elektrono
we

~10

3 

kJ/m
ol

~10 
kJ/m
ol

~1 
kJ/mol

Widmo 

elektronowe 

chlorobenzenu

Szerokie pasma 
absorpcji

Struktura 
subtelna 
przejść 
oscylacyjny
ch

 energia         energia          
energia
rotacyjna   oscylacyjna   
elektronowa  

 

 

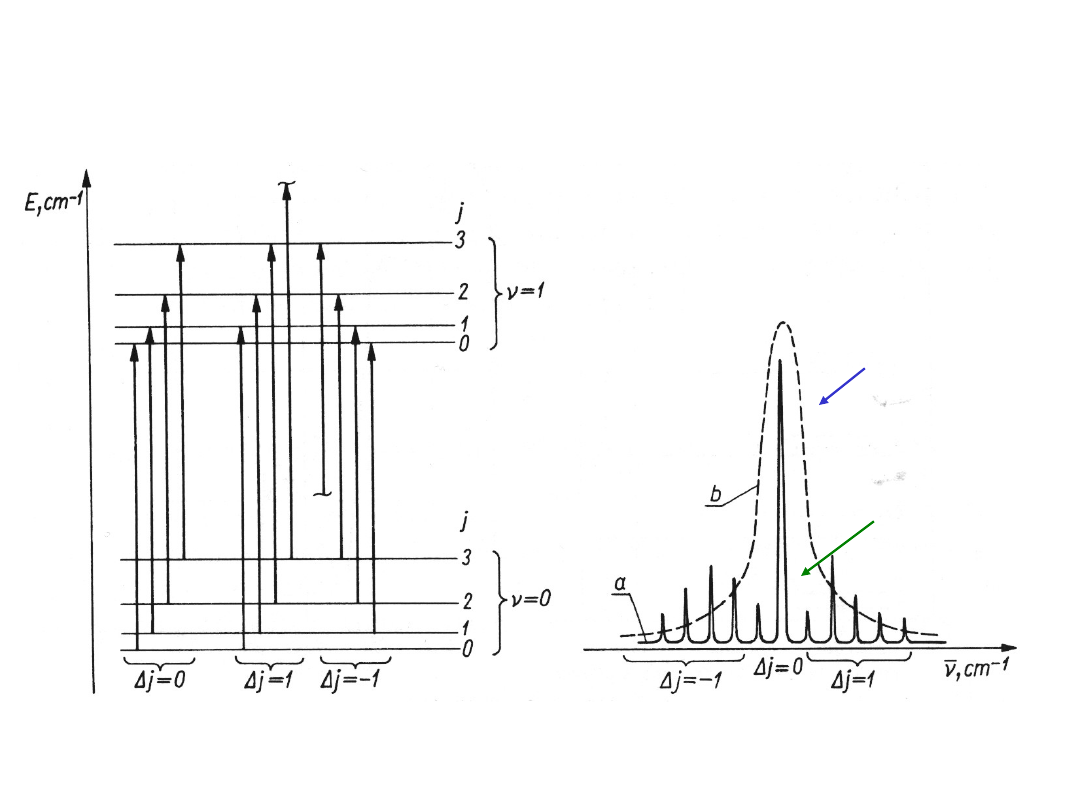
PRZEJŚCIA OSCYLACYJNO - 
ROTACYJNE

~10 
kJ/m
ol

Widmo 

oscylacyjno-

rotacyjne

w fazie 
skondensow
anej

w fazie 
gazowe
j

 

 

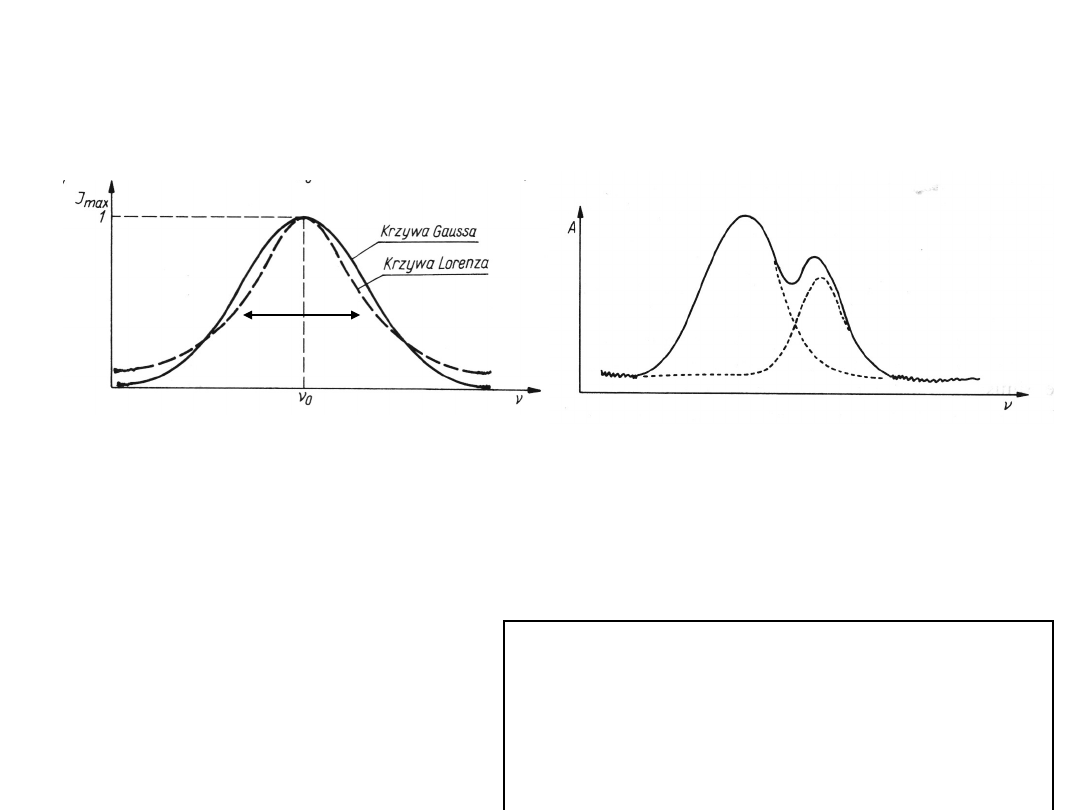
CHARAKTERYSTYKA PASM 
ABSORPCYJNYCH

Kształt pasma absorpcji można w przybliżeniu opisać funkcją 

Gaussa lub Lorenza 

Parametry charakteryzujące absorpcję:

 intensywność w maksimum absorpcji I

max

 szerokość połówkowa 

½

 - w połowie wysokości pasma

 intensywność integralna I

i

 – powierzchnia pod linią pasma 

absorpcyjnego

I

ma

x



½





d

I )

(

2

1

ν

ν

i

I





Oddziaływania międzycząsteczkowe

 

(np. wiązanie wodorowe, oddziaływania 
dipolowe) - powodują poszerzenie i 
wzrost intensywności pasma. Kształt 
pasm absorpcyjnych informuje o 
oddziaływaniach 
międzycząsteczkowych. 

Matematyc
zny rozkład 
nakładając
ych się 
pasm 
absorpcyjn
ych



1



2

 

 

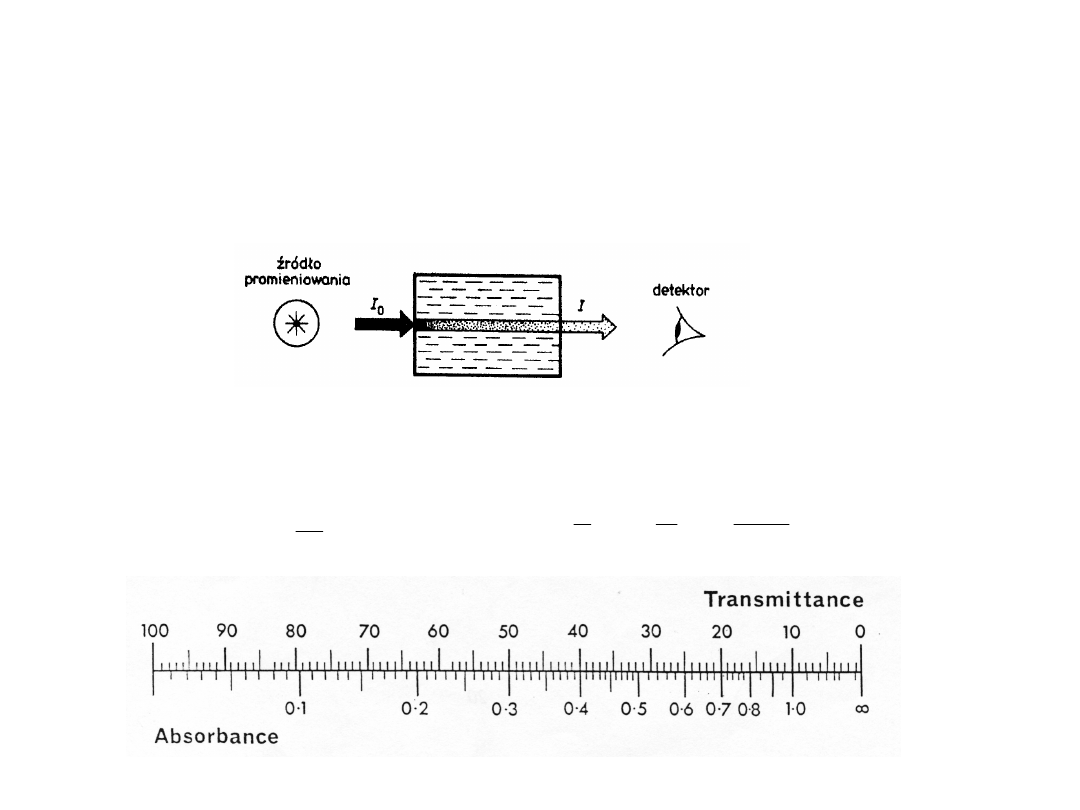
Pomiar  spektrometryczny

  –sygnał  detektora,  (I

S

)  – 

widma NMR i EPR

Pomiar 

spektrofotometryczny

 

– 

porównanie 

intensywności 

promieniowania padającego (I

0

)

                                                              i przechodzącego (I) przez próbkę 

– widma UV/VIS i IR

ILOŚCIOWA OCENA ZJAWISKA 

ABSORPCJI

(określenie ilości zaabsorbowanej energii)

 

Transmitancja

 

T

 (przepuszczalność), 

– jest to stosunek intensywności 

promieniowania
                                  przechodzącego przez próbkę (I) do jego 
intensywności początkowej (I

0

)

Absorbancja A

 

– jest to logarytm z odwrotności transmitancji

100





0

I

 

I

 

 

T[%]

T[%]

100

log

 

I

I

log

T

1

log

 

 

A

0







 

 

ILOŚCIOWA ANALIZA 

SPEKTROSKOPOWA

PRAWO LAMBERTA - BEERA

Absorbancja A jest wprost proporcjonalna do stężenia 
(c) i grubości warstwy roztworu (l) 

A = 



 



 

c



 l

 



  = A / 

c



 l 

(c) – stężenie w mol dm

-3

 

(l) – długość drogi optycznej (grubość 
kuwety) w cm
(

 ) – molowy współczynnik absorpcji (dm

3

 

mol

-1

 cm

-1

) 

        ( molowy współczynnik ekstynkcji ) 

Absorbancja  jest  wprost  proporcjonalna  do  ilości  cząsteczek 
absorbujących dane promieniowanie, dlatego łatwo ją powiązać 
z  chemicznym  sposobem  (stężeniem)  wyrażania  ilości 
cząsteczek  znajdujących  się  na  drodze  promieniowania, 
zwłaszcza w roztworach.