Uproszczone metody rozwiązywania

zagadnień przewodzenia ciepła

Opory cieplne, współczynniki kształtu

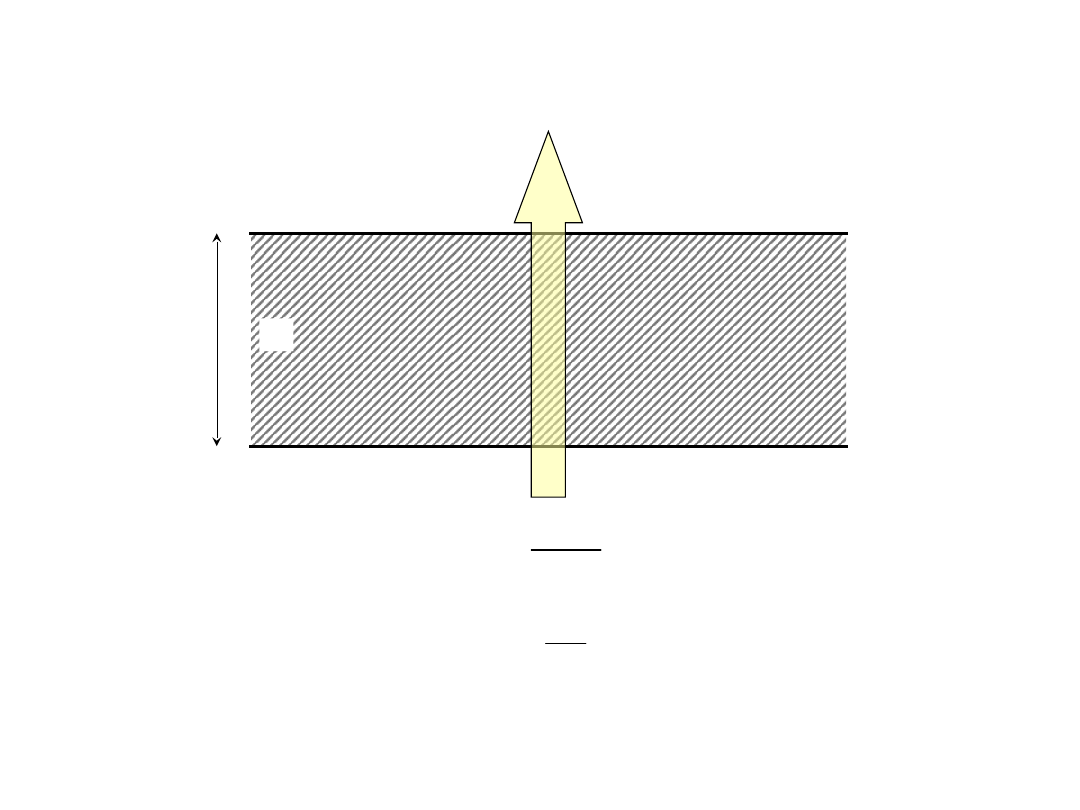
Opory cieplne

R

T

T

Q

1

2







T

2

T

1









A

R

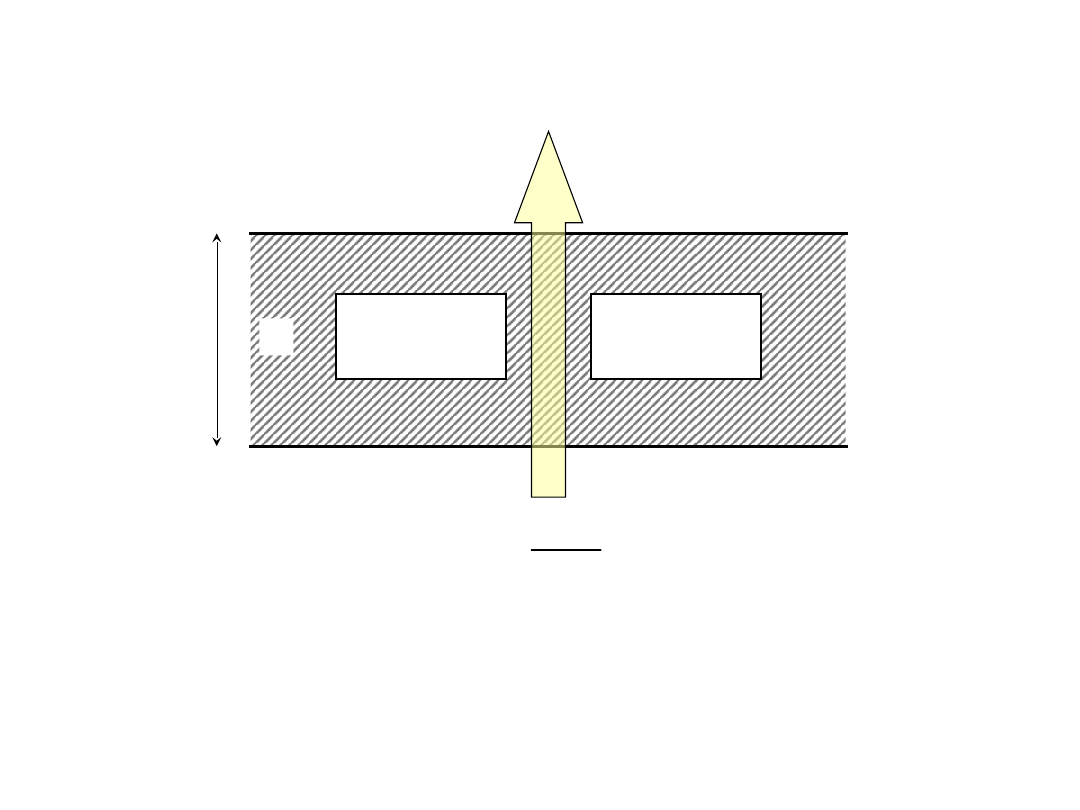
Opory cieplne

R

T

T

Q

1

2







T

2

T

1



1



???



R



2



2

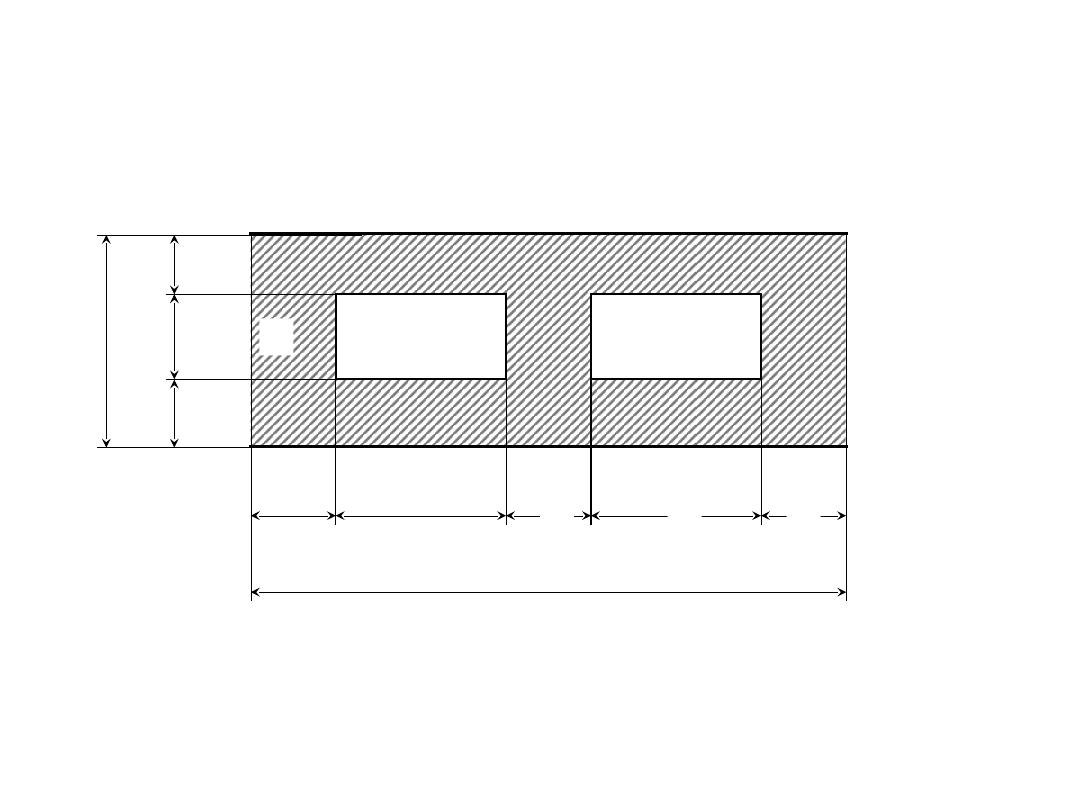
Opory cieplne



1



2



2

a

1

a

2

a

1

a

1

a

2

b

1

b

2

b

1

a

b

a = 0,25; a

1

= 0,03; a

2

= 0,08 [m]

b = 0,12; b

1

= 0,03; b

2

= 0,06 [m]



1

= 0,70;



2

= 0,12 W/(mK)

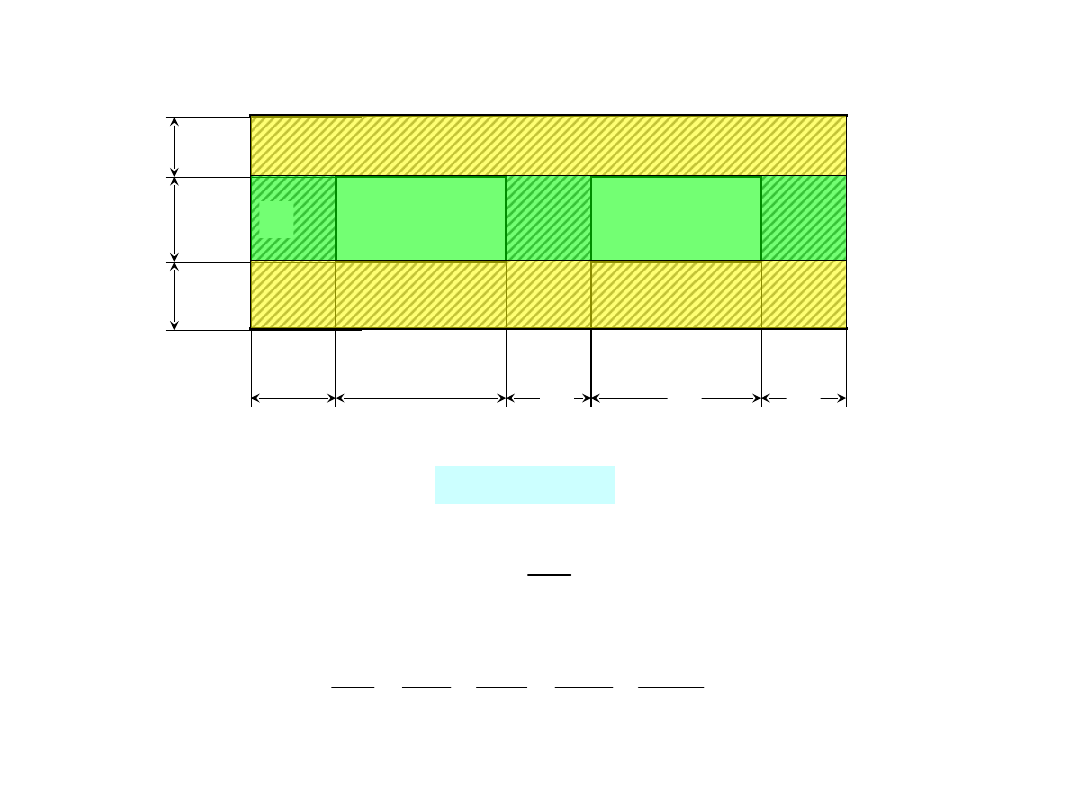
Podział prostopadły (do kierunku strumienia ciepła)

2

1

2











R

R

R

1

1

1



a

b

R 





1



2



2

a

1

a

2

a

1

a

1

a

2

b

1

b

2

b

1

R

1

R

2

R

1

2

2

2

2

1

1

22

21

2

2

3

2

3

1

b

a

b

a

R

R

R



















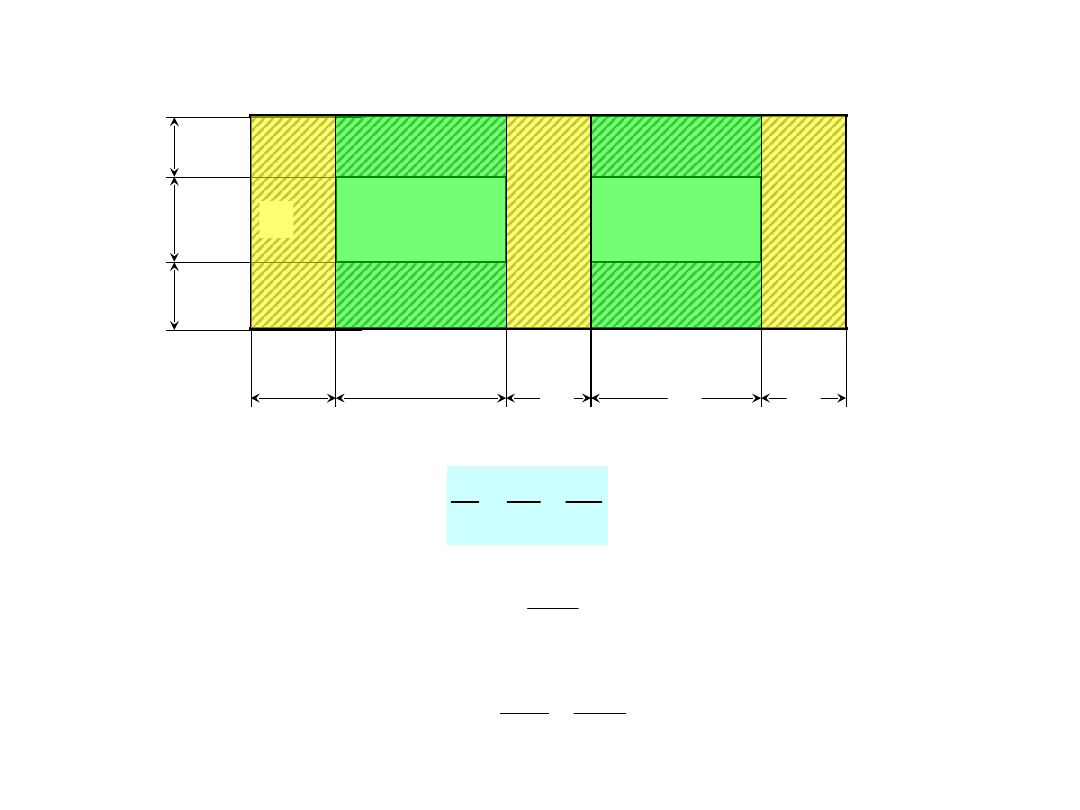
Podział równoległy (do kierunku strumienia ciepła)



1



2



2

a

1

a

2

a

1

a

1

a

2

b

1

b

2

b

1

R

||1

R

||2

R

||1

R

||1

R

||2

2

||

1

||

||

2

3

1

R

R

R





1

1

1

||



a

b

R 

2

2

2

1

2

1

2

||

2





a

b

a

b

R





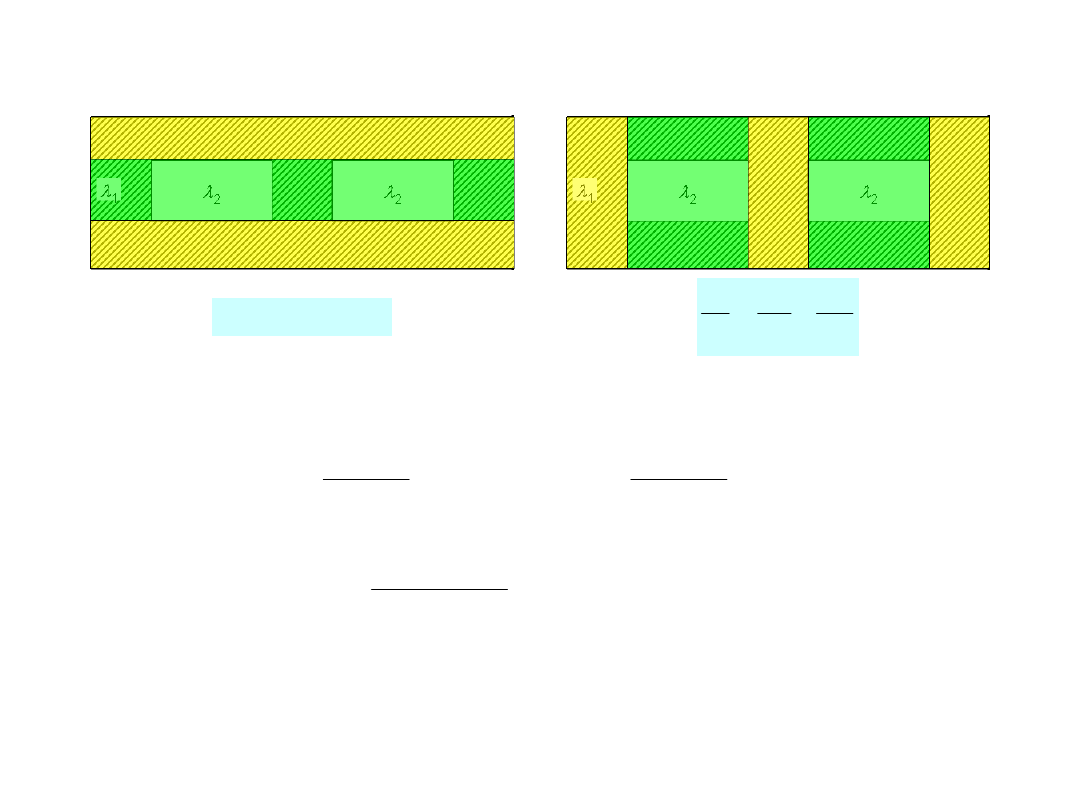
Wyniki obliczeń

2

1

2











R

R

R

2

||

1

||

||

2

3

1

R

R

R





K/W

m

073

,

1







R

K/W

m

253

,

1

||





R

3

2

%

25

R

||

||

















R

R

R

R

R

K/W

m

133

,

1

%

8

,

16

168

,

0

073

,

1

073

,

1

253

,

1











R

Jeżeli różnica między R

||

a R



jest większa niż 25%,

to należy zastosować inne metody szacowania oporu

cieplnego

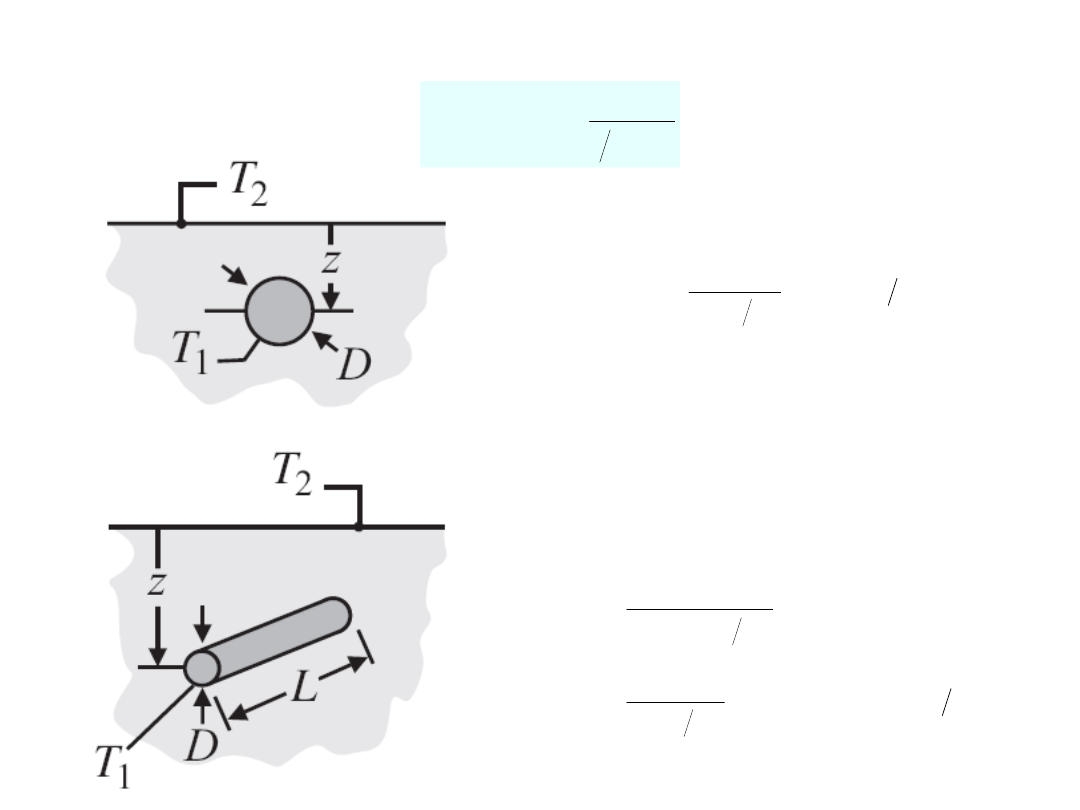
Współczynniki kształtu

Kula w półprzestrzeni (zakopana kula)

2

;

4

2

D

z

z

D

D

S





1





Zakopana rura o długości L









2

3

,

;

4

ln

2

;

2

cosh

2

1

D

z

D

L

D

z

L

S

D

L

D

z

L

S

















)

(

1





S

T

T

S

q









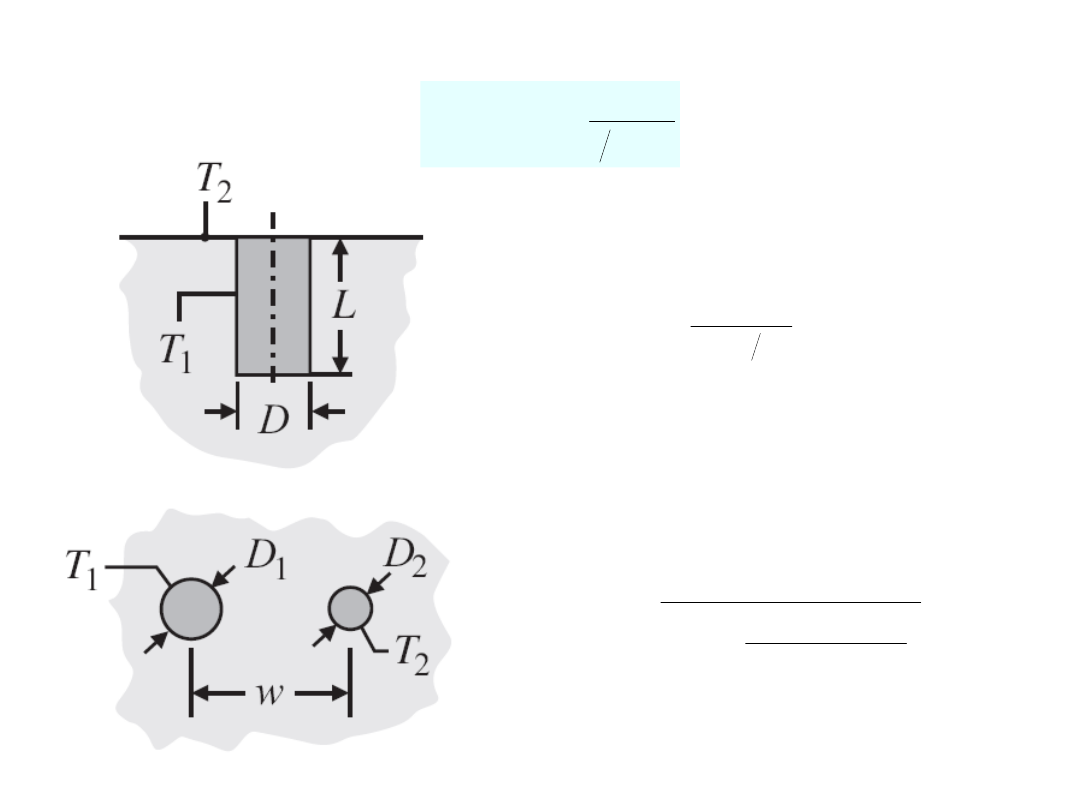
Współczynniki kształtu

Walec w półprzestrzeni





D

L

D

L

L

S







;

4

ln

2

Przepływ ciepła między dwiema rurami

o długości L

w

L

D

D

L

D

D

D

D

w

L

S



























;

,

;

2

4

cosh

2

2

1

2

1

2

2

2

1

2

1

)

(

1





S

T

T

S

q









Współczynniki kształtu

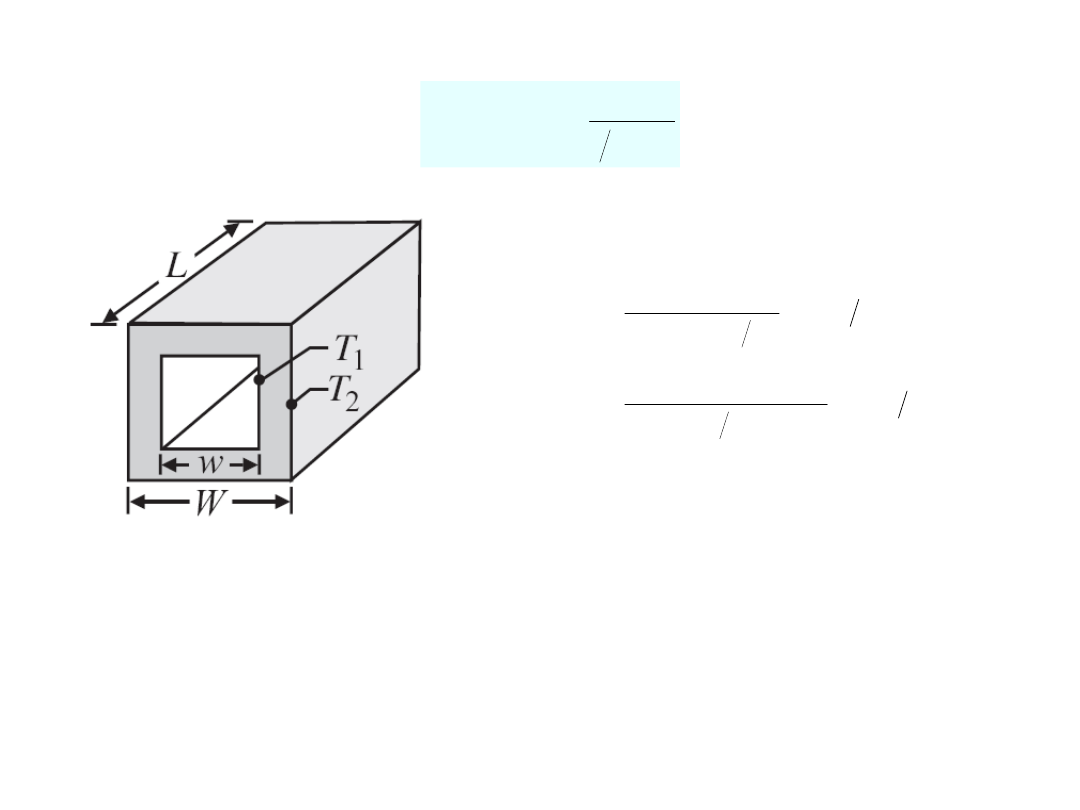
Kanał o przekroju kwadratowym









4

,

1

;

05

,

0

930

,

0

2

4

,

1

;

ln

785

,

0

2















w

W

w

W

L

S

w

W

w

W

L

S

)

(

1





S

T

T

S

q









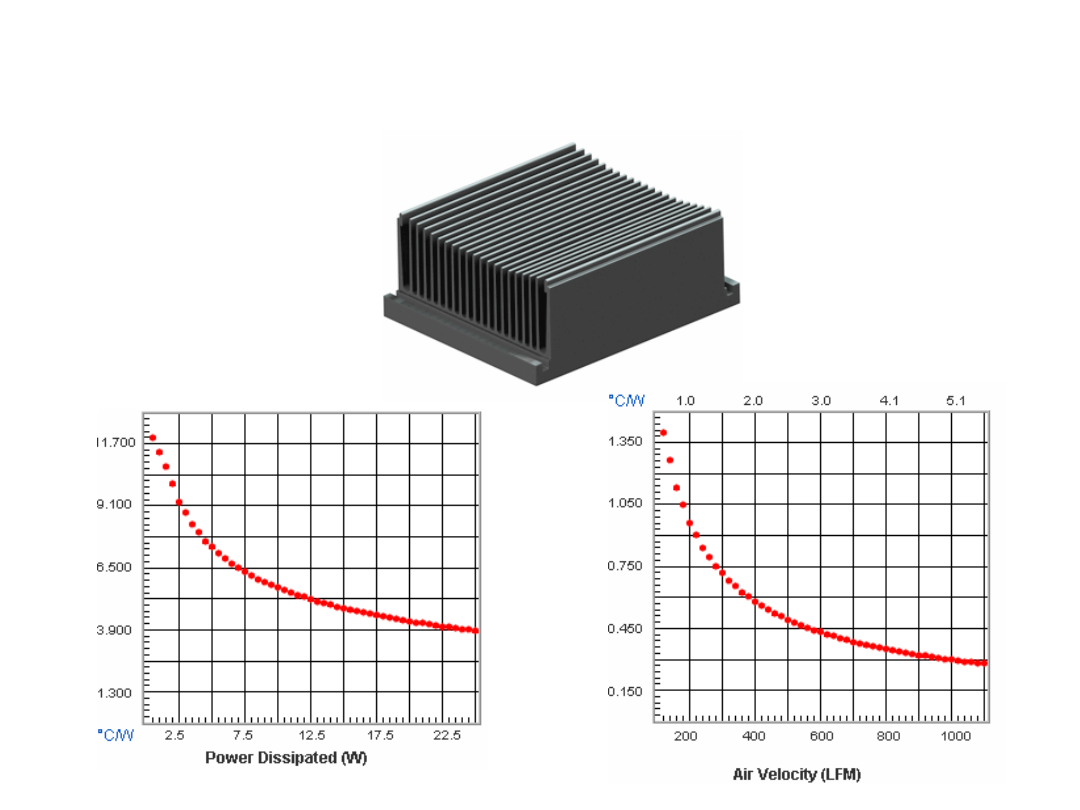
Radiator do chłodzenia procesorów

Opory cieplne w warunkach

konwekcji naturalnej i wymuszonej

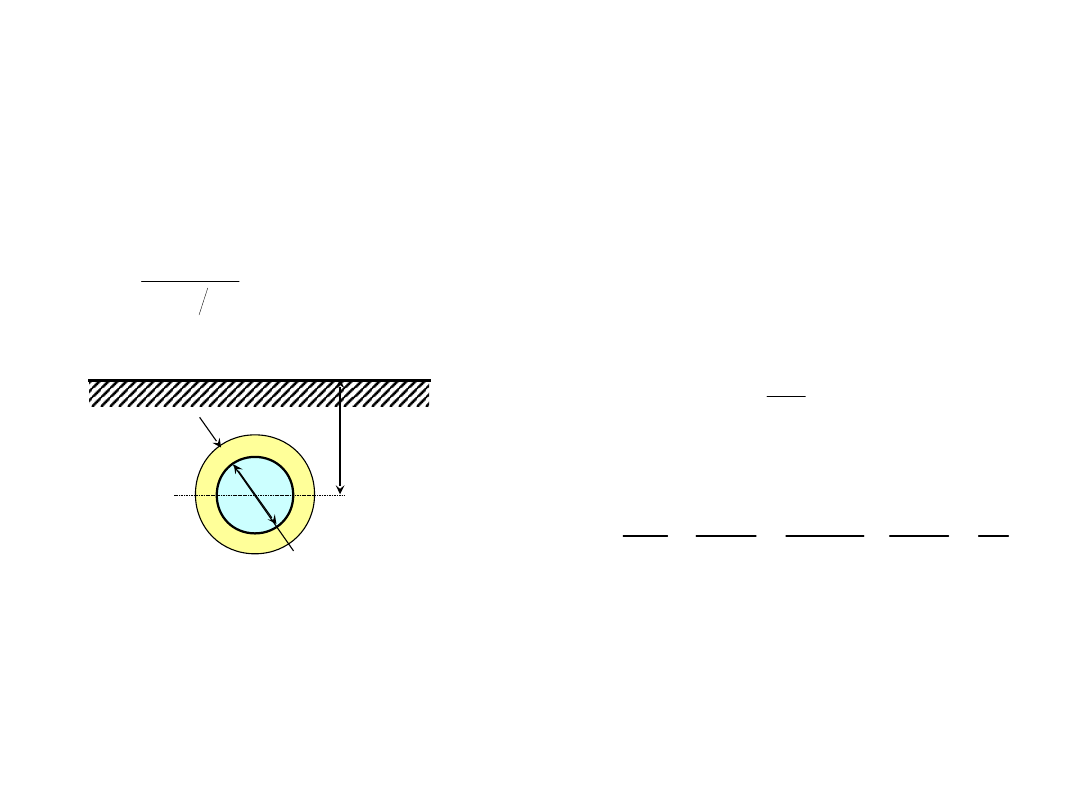
Zadanie

Rurociąg do transportu gorącego oleju (T

1

= 120°C) jest zakopany na

głębokości
z = 1,5 m pod powierzchnią. Średnica rurociągu D = 0,5 m, grubość izolacji 

= 100 mm (



iż

= 0,06 W/(mK)). Jakie są straty ciepła z rurociągu przy

temperaturze powierzchni T

2

= 0°C? Przewodność cieplna gruntu



g

= 0,52

W/(mK).

D

z

D

D

S

R

R

iz

s

iz

4

ln

2

2

ln

2

1

1





1

























D

z

S

4

ln

2



Współczynnik kształtu dla jednostki długości rurociągu

T

1

T

2

z

D



Przepływ ciepła między powierzchnią rury a
powierz-chnią ziemi. Gęstość strumienia ciepła
(na jednostkę długości):

R

T

q 



Opór cieplny

m/W

K

551

,

1



R

W/m

4

,

77



q

Metody numeryczne

w zagadnieniach wymiany ciepła

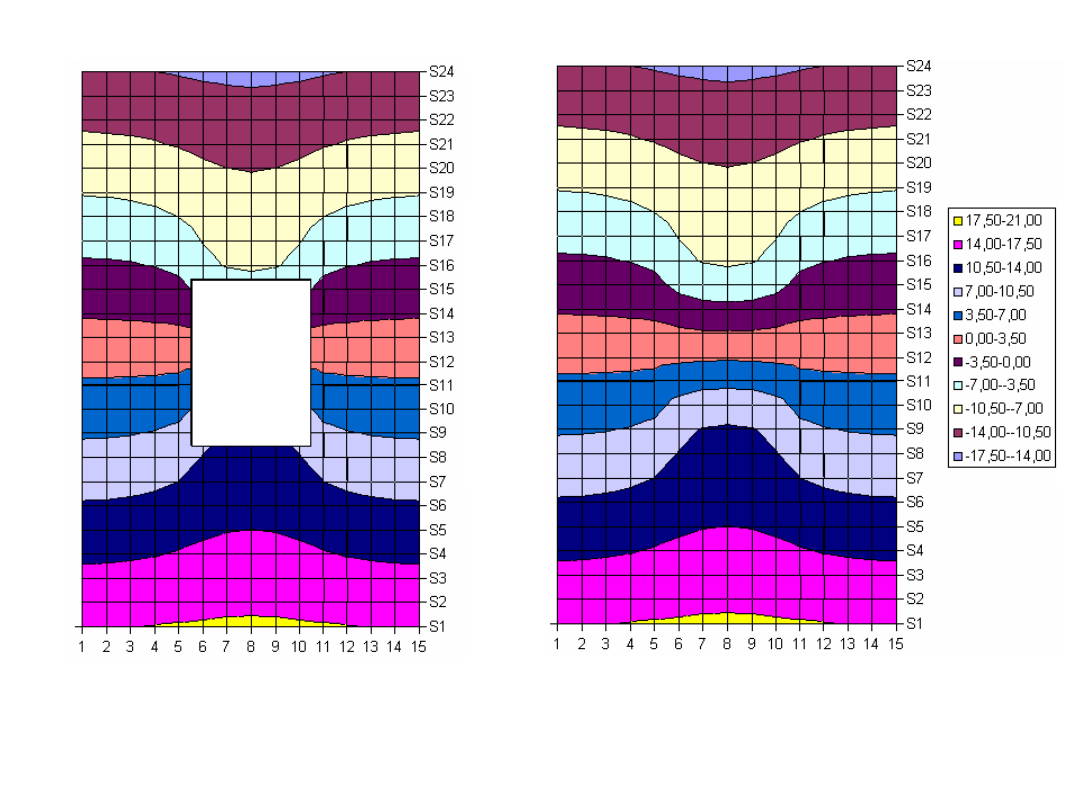
W zagadnieniach wymiany ciepła zasadniczym celem analizy jest ciągła
funkcja określająca pole temperatury w przestrzeni i czasie:

)

,

,

,

(



z

y

x

T

T 

Przy podejściu numerycznym do rozwiązania tego zagadnienia zamiast
funkcji ciągłej poszukuje się

wektora obejmującego skończoną liczbę

wartości temperatury w określonych punktach przestrzeni i
określonych momentach czasu

.

Dyskretyzacja przestrzeni:
– wydzielenie objętości kontrolnych,
– ustalenie punktu reprezentującego każdą objętość (węzeł, grid point),

Dyskretyzacja równania:
– zastąpienie ciągłej funkcji polowej wektorem (skończony zbiór wartości w
punktach węzłowych)
– zastąpienie równania różniczkowego (całkowego) układem równań
algebraicznych,

Metoda różnic skończonych

Dyskretyzacja równania przewodzenia ciepła

0

2

2

2

2













y

T

x

T

v

p

q

y

T

x

T

T

c































2

2

2

2







Stan ustalony bez wewnętrznych źródeł ciepła – równania

Laplace’a

Pochodne należy zastąpić wyrażeniami różnicowymi

Rozwinięcie funkcji w szereg Taylora:

...

2

)

(

)

(

)

(

)

(

)

(

2























x

x

f

x

x

f

x

f

x

x

f

...

2

)

(

)

(

)

(

)

(























x

x

f

x

x

f

x

x

f

x

f

x

x

f

x

x

f

x

f













)

(

)

(

)

(

x

x

x

f

x

x

f

x

f

















2

)

(

)

(

)

(

2

)

(

)

(

)

(

2

)

(

)

(

x

x

x

f

x

f

x

x

f

x

f





















Pierwsza pochodna:

Aproksymacja pierwszej pochodnej (iloraz różnicowy przedni)

Błąd aproksymacji jest proporcjonalny do x. Dokładność zależy od gęstości węzłów siatki różnicowej.

Przy zastosowaniu ilorazu różnicowego środkowego:

błąd aproksymacji jest rzędu (x)

2

.

i jest obarczona błędem proporcjonalnym do (x)

2

.

Aproksymacja drugiej pochodnej jest oparta na ilorazie różnicowym środkowym

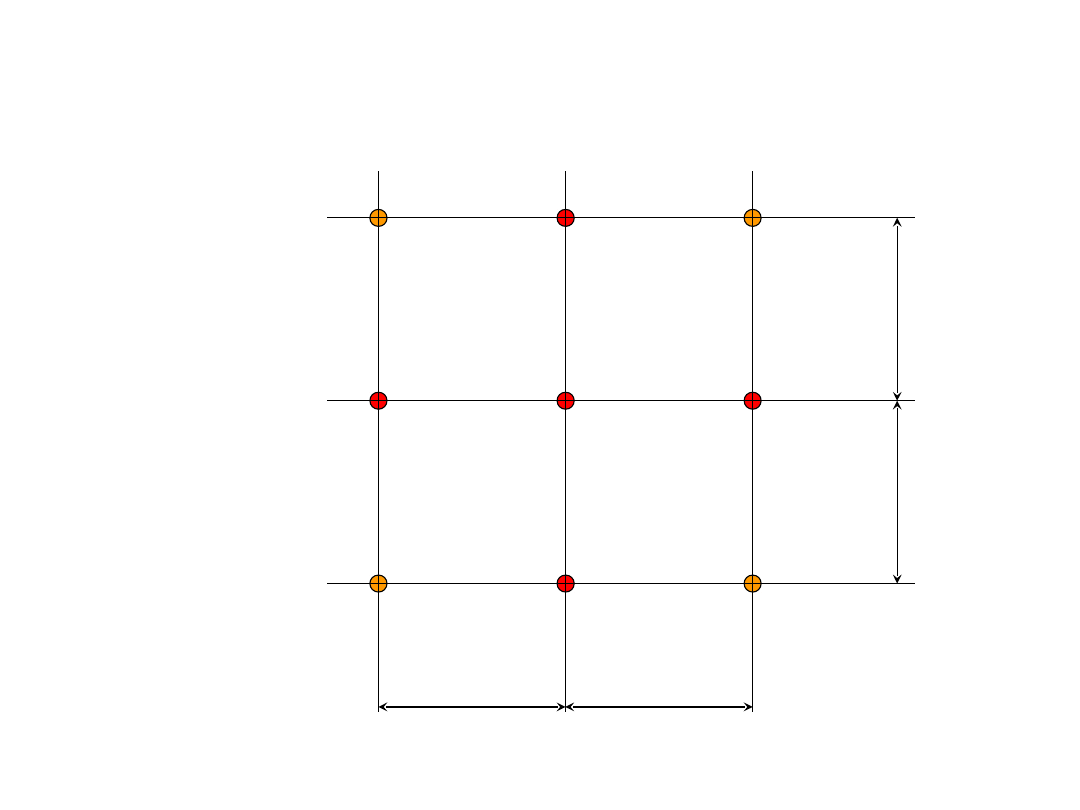
Dyskretyzacja przestrzenna – przypadek dwuwymiarowy

P

W

E

N

S

y

x

y

x

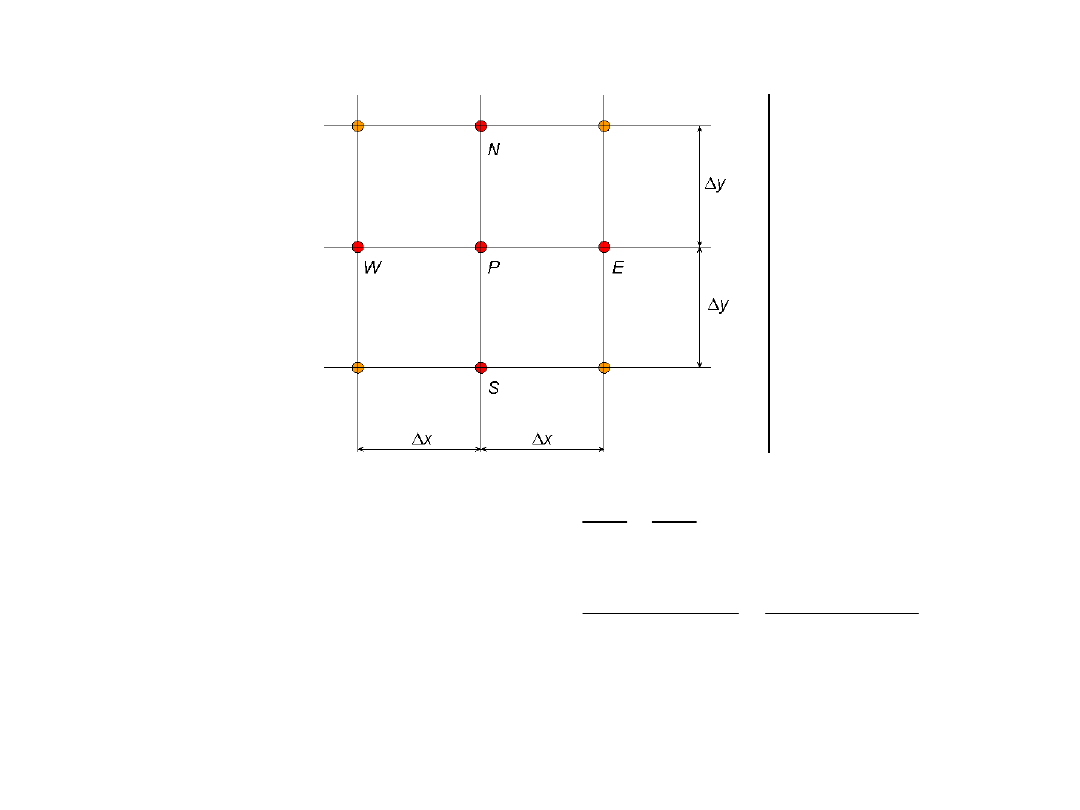
Dyskretyzacja przestrzenna – przypadek dwuwymiarowy

0

)

(

2

)

(

2

2

2

















y

T

T

T

x

T

T

T

S

P

N

W

P

E

0

2

2

2

2













y

T

x

T

Równanie różniczkowe

Równanie różnicowe

Układ równań liniowych – równania różnicowe dla wszystkich

punktów

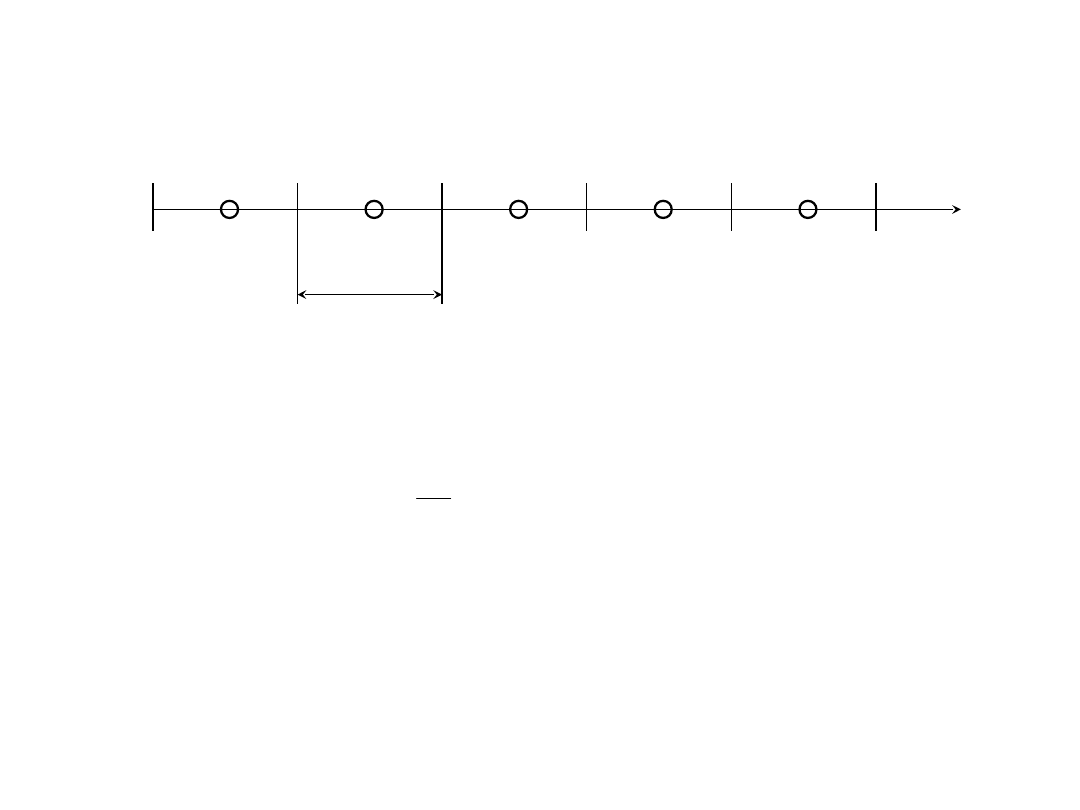
Metoda objętości kontrolnych

Stan ustalony, przypadek jednowymiarowy

i = 1

2

3

4

5

…

x

Element kontrolny – objętość kontrolna: x11; węzeł – w środku masy

(objętości)

Podstawą jest całkowa postać równania transportu energii





























V

v

S

V

p

V

q

S

n

q

V

T

c

d

d

d





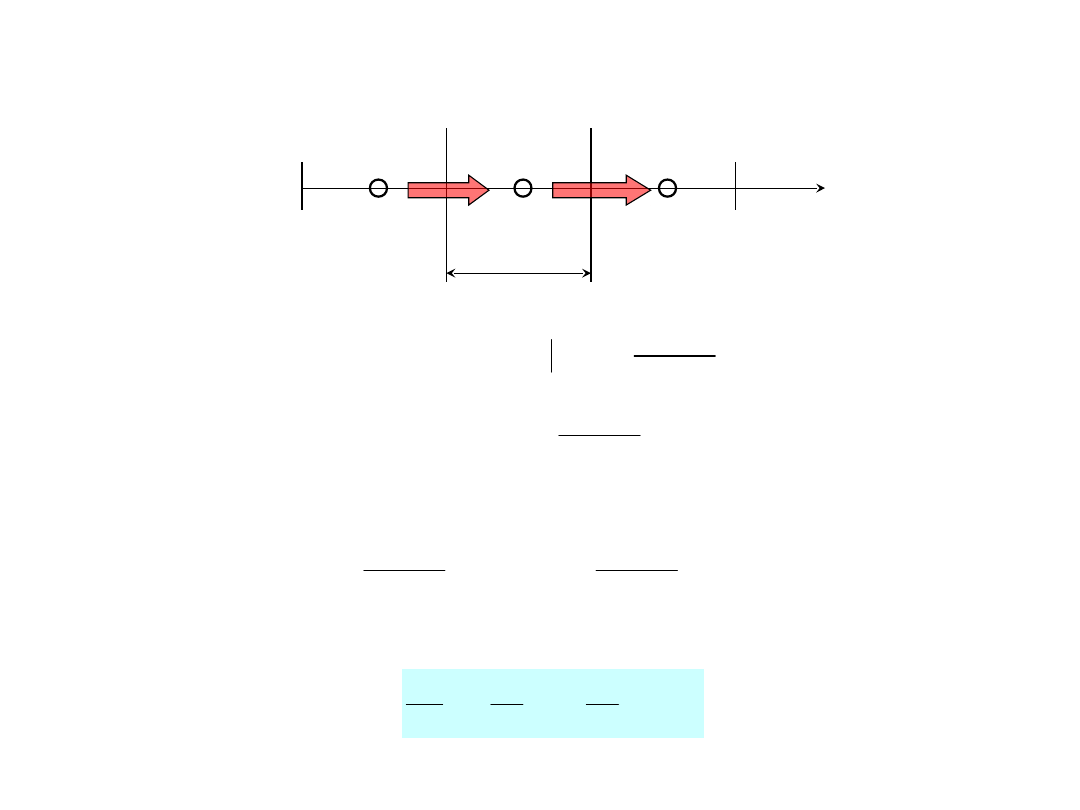
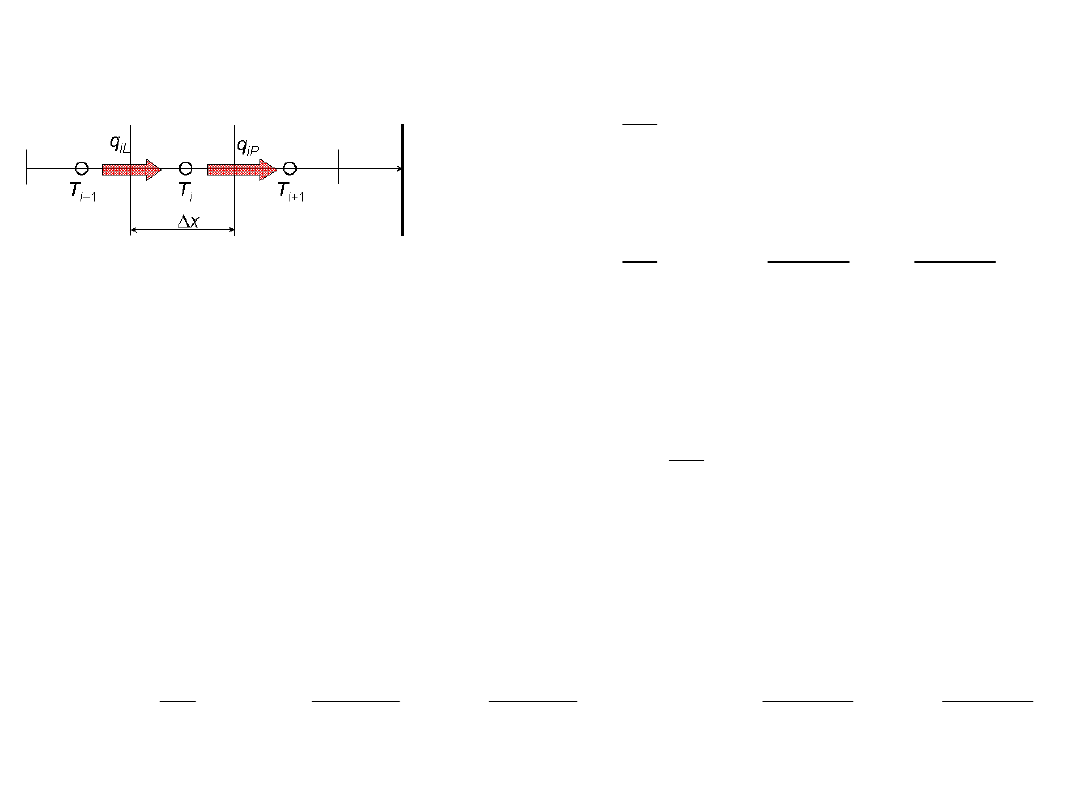
Stan ustalony, przypadek jednowymiarowy

x

T

T

T

q

i

i

iL

iL













 1

grad





x

T

T

q

i

i

iP









1



T

i

T

i+1

x

Bilans strumieni ciepła dla elementu kontrolnego (przewodzenie)

T

i–1

q

iP

q

iL

W stanie ustalonym:

0

2

1

1

















i

i

i

T

x

T

x

T

x







Stąd równanie algebraiczne dla węzła i-tego

0

)

1

1

(

)

1

1

(

1

1





















































x

T

T

x

T

T

i

i

i

i





Analogicznie dla pozostałych węzłów brzegowych

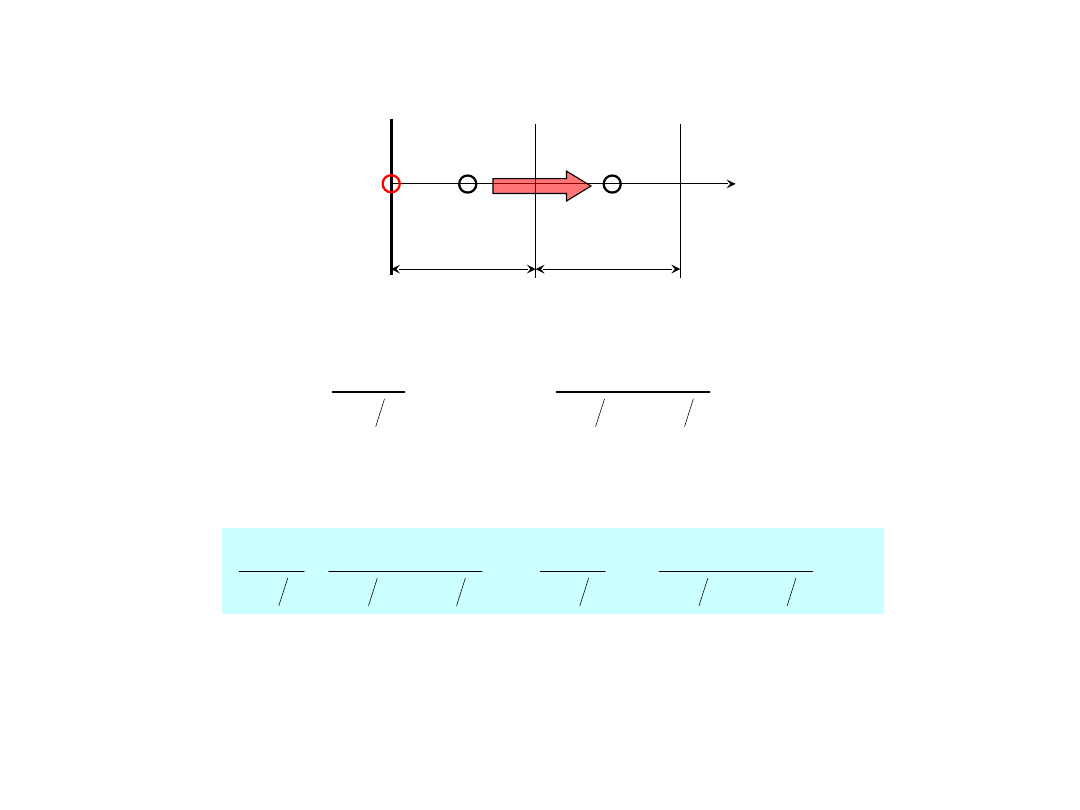
Warunki brzegowe – warunek I rodzaju – T

B

T

2

x

2

Bilans strumieni ciepła dla pierwszego elementu

T

1

q

1P

0

2

2

2

2

2

2

2

2

1

1

1

2

1

1





































T

x

x

T

x

T

x

x

x

B









Stąd równanie algebraiczne dla pierwszego (1)

0

)

1

1

(

2

2

)

1

1

(

2

2

1

1

2

1

1





















































x

x

T

T

x

T

T

B





x

1

T

B

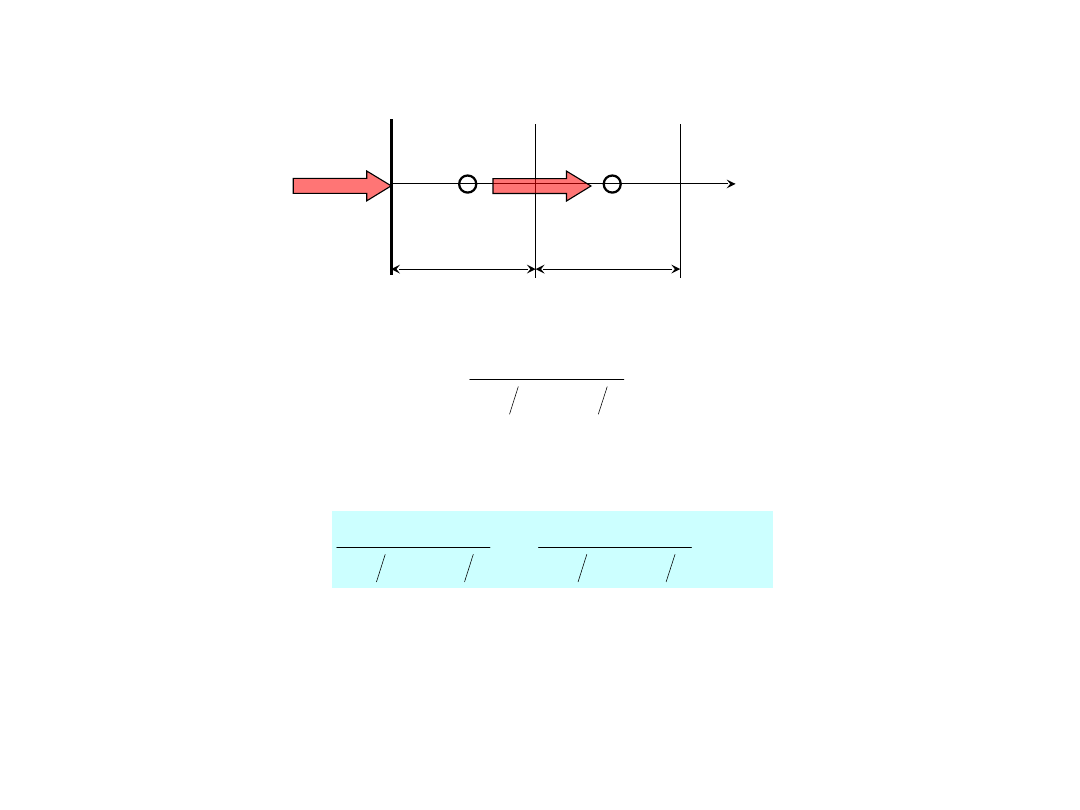
Warunki brzegowe – warunek II rodzaju – strumień q

B

T

2

x

2

Bilans strumieni ciepła dla pierwszego elementu

T

1

q

1P

b

q

T

x

x

T

x

x

















2

2

1

1

2

1

2

2

2

2





Stąd równanie algebraiczne dla pierwszego (1)

0

)

1

1

(

2

2

2

1

1

2































x

x

T

T

q

B



x

1

q

B

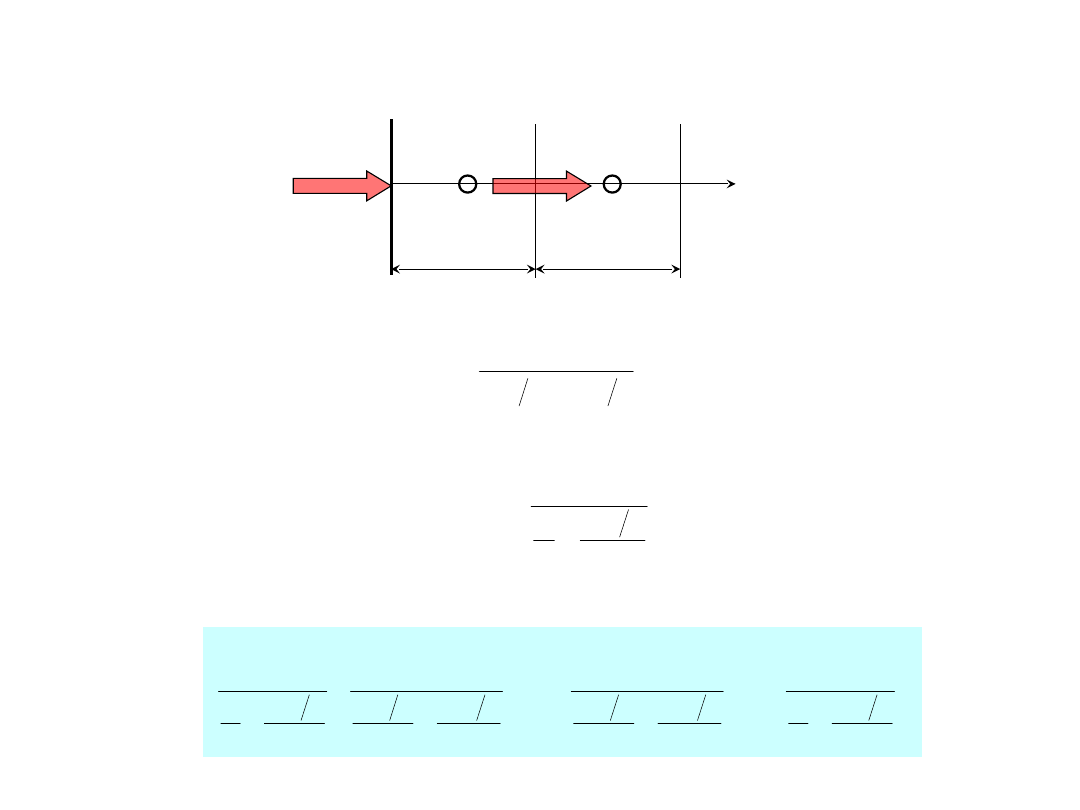
Warunki brzegowe – warunek III rodzaju – (T

0

,

)

0

1

2

2

1

1

2

1

1

2

1

1

2

2

1

2

2

1

2

1

1

T

x

T

x

x

T

x

x

x



















































































T

2

x

2

Bilans strumieni ciepła dla pierwszego elementu

T

1

q

1P

Stąd równanie algebraiczne dla pierwszego (1)

0

)

1

1

(

2

2

2

1

1

2































x

x

T

T

q

B



x

1

q

B

Strumień na brzegu z warunku brzegowego III rodzaju





2

1

1

1

0

x

T

T

q

B









T

0

, 

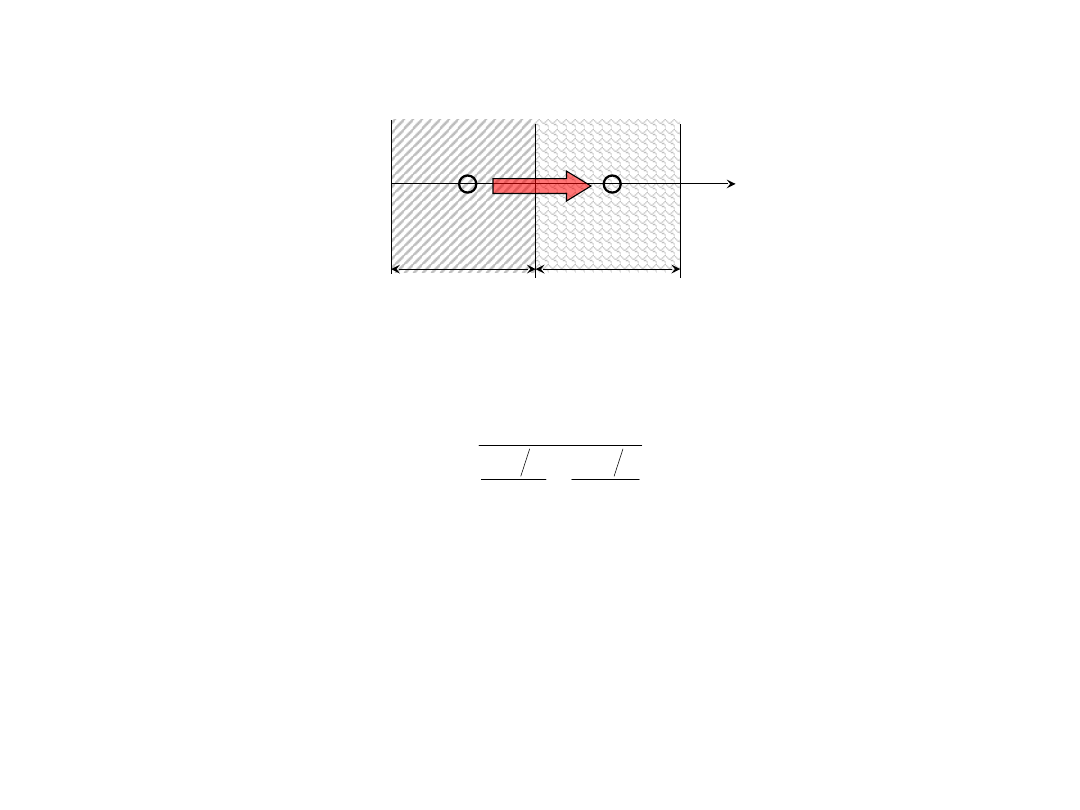
Warunki brzegowe – warunek IV rodzaju – granica różnych

materiałów

T

2

x

2

Bilans strumieni ciepła – tak jak dla węzłów wewnętrznych

T

1

q

B

x

1

Strumień ciepła na granicy materiałów

2

2

1

1

1

2

2

2





x

x

T

T

q

B













1



2

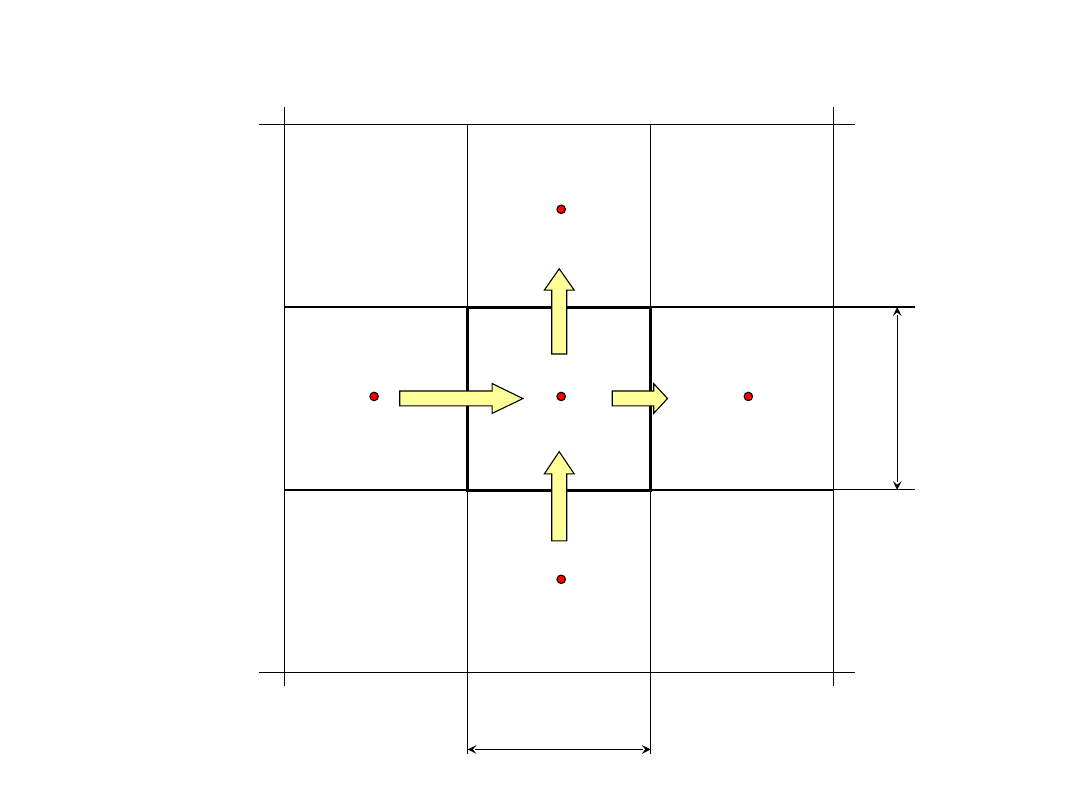
Przypadek dwuwymiarowy

T

i,j

T

i-1,j

T

i+1,j

T

i,j+1

T

i,j-1

y

x

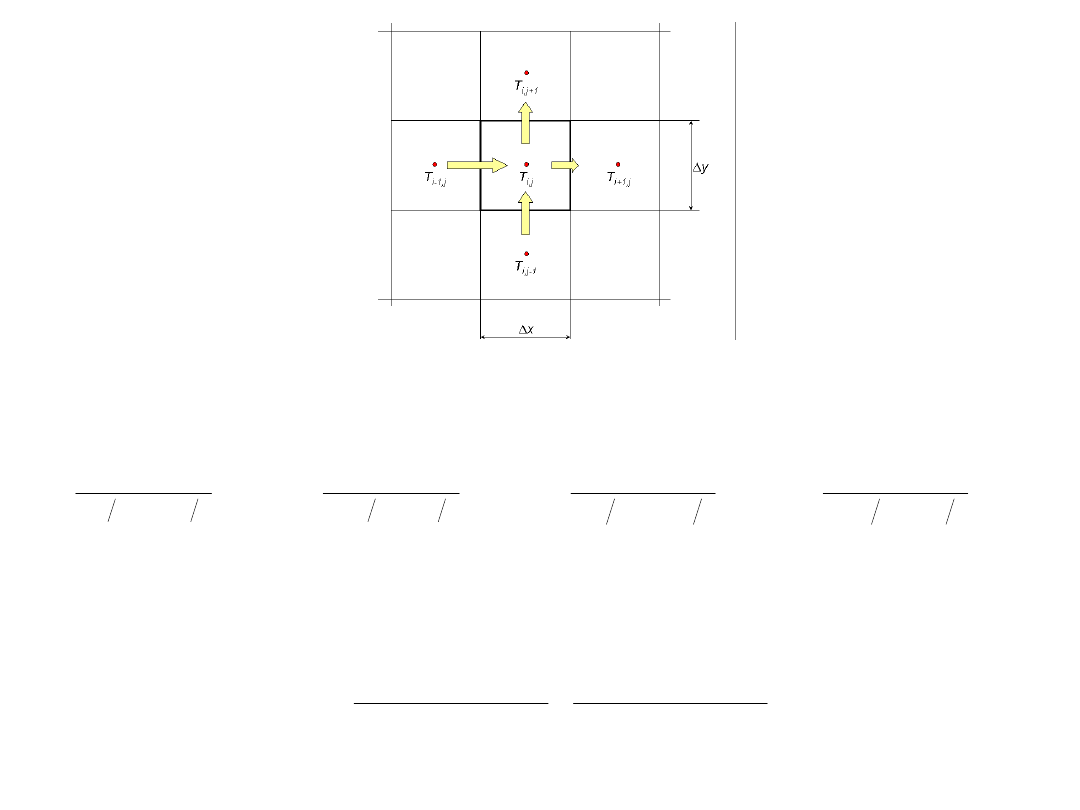
Równanie bilansowe:

0

2

2

2

2

2

2

2

2

1

,

1

,

1

1

,

,

1

,

,

1

1

,

1

,





























































































































i

j

j

j

i

j

i

i

j

j

j

i

j

i

j

i

i

j

i

j

i

j

i

i

j

i

j

i

x

y

y

T

T

x

y

y

T

T

y

x

x

T

T

y

x

x

T

T









Dla

 = const, x = cosnt, y = const; po uporządkowaniu

0

)

(

2

)

(

2

2

1

,

,

1

,

2

,

1

,

,

1

























y

T

T

T

x

T

T

T

j

i

j

i

j

i

j

i

j

i

j

i

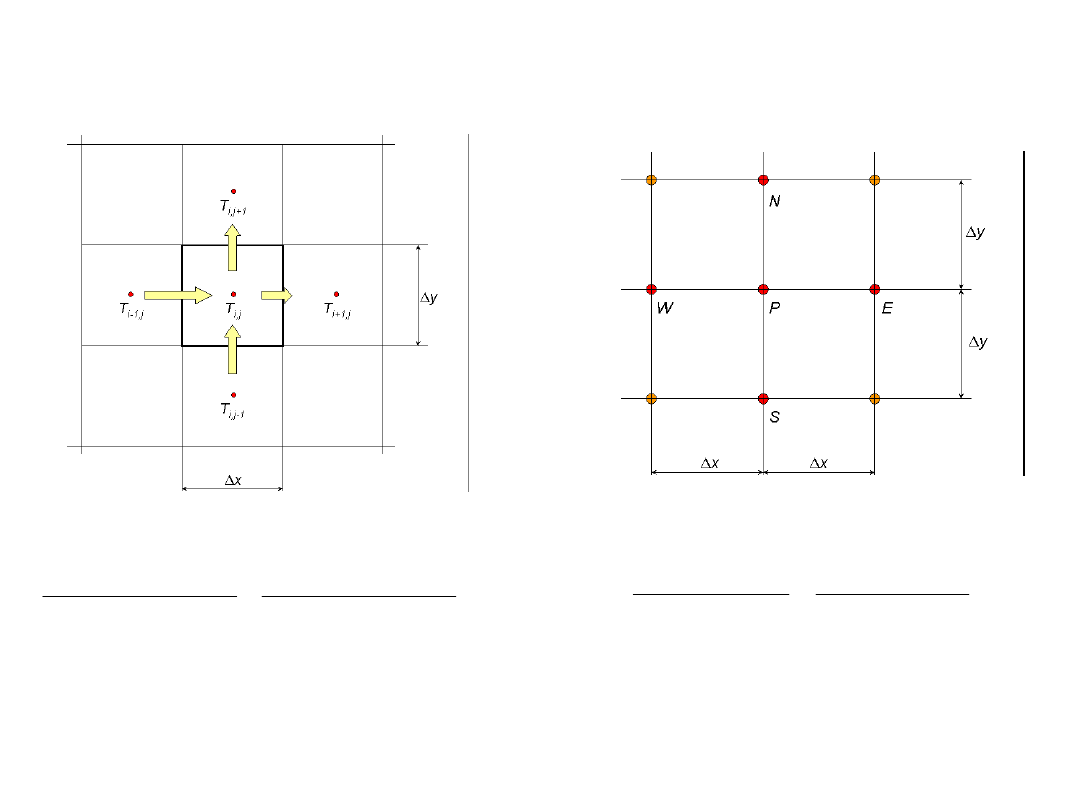
0

)

(

2

)

(

2

2

1

,

,

1

,

2

,

1

,

,

1

























y

T

T

T

x

T

T

T

j

i

j

i

j

i

j

i

j

i

j

i

0

)

(

2

)

(

2

2

2

















y

T

T

T

x

T

T

T

S

P

N

W

P

E

Metoda objętości kontrolnych

Metoda różnic skończonych

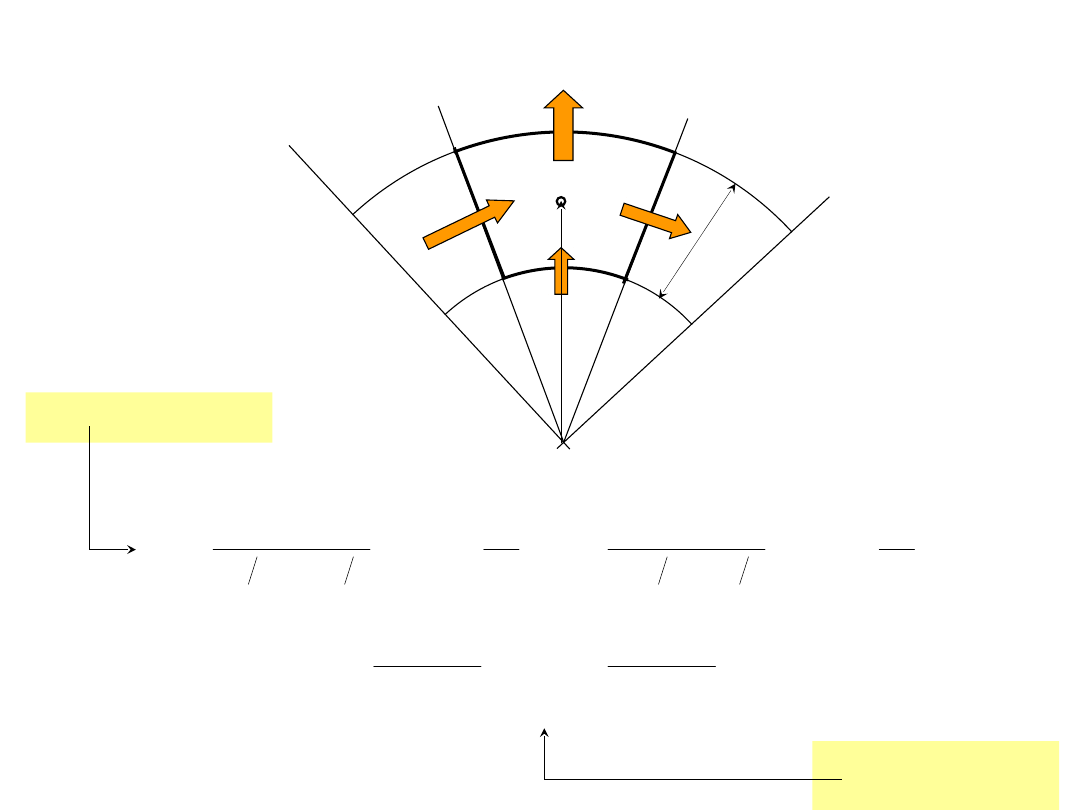
Przypadek dwuwymiarowy – współrzędne walcowe





j

r

i

r

i

Bilans strumieni ciepła:

0

2

2

2

2

2

2

,

1

,

1

,

,

1

,

,

1

1

,

1

,



















































































































































i

i

j

j

i

j

i

i

i

j

j

i

j

i

i

i

j

i

i

j

i

j

i

i

i

j

i

i

j

i

j

i

r

r

T

T

r

r

T

T

r

r

r

r

T

T

r

r

r

r

T

T

















Strumienie w

kierunku promienia

Strumienie w

kierunku

obwodowym





x

T

T

c

V

T

c

i

i

p

V

p























 





0

1

d

d















Zapis różnicowy:

Dyskretyzacja członu nieustalonego w równaniu przewodzenia

ciepła

























S

V

p

S

n

q

V

T

c

d

d

































0

1

)

1

(

d

i

i

i

T

f

T

f

T

































































































































x

T

T

x

T

T

f

x

T

T

x

T

T

f

x

T

T

c

i

i

i

i

i

i

i

i

i

i

p

0

0

1

0

1

0

1

1

1

1

1

1

0

1

1













x

T

T

x

T

T

V

T

c

i

i

i

i

i

i

V

p







































1

1

1

1

d









Kroczenie po czasie –

człon nieustalony

:

Kroczenie po czasie –

człon dyfuzyjny

,

symbolicznie całka po czasie temperatury
w węźle:

Kroczenie po czasie – całka po czasie w zakresie od 

(indeks 0)

do +

(indeks 1)







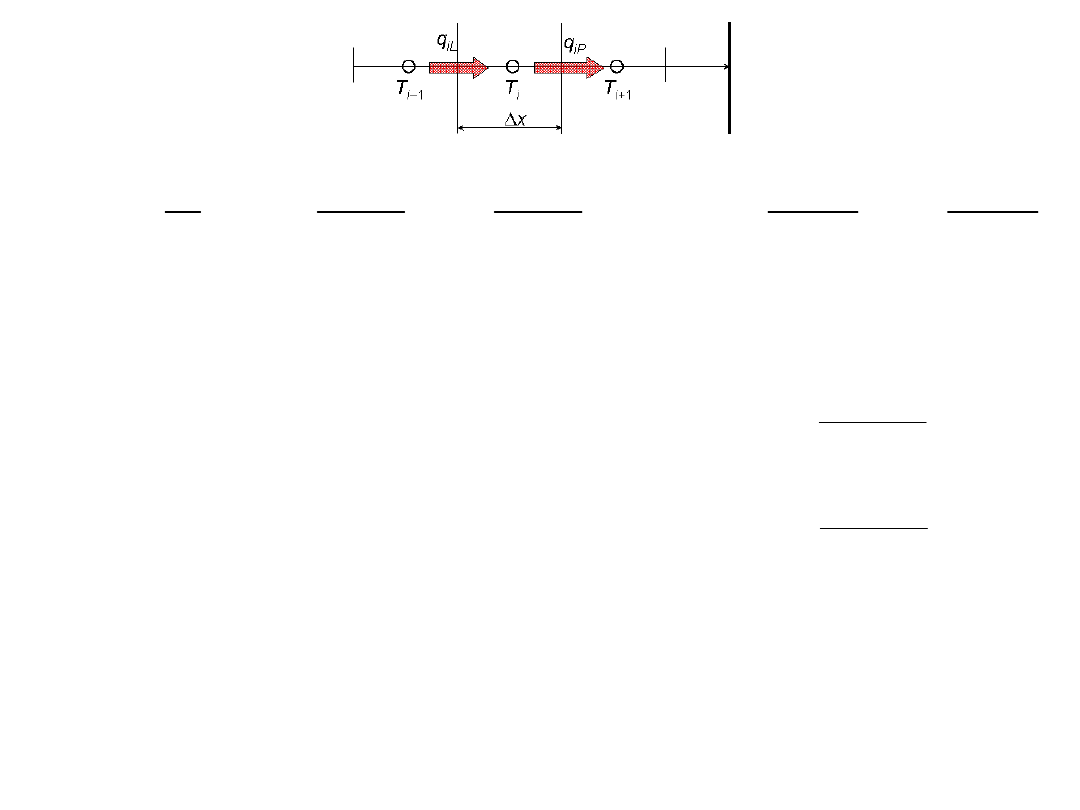
2

)

(

2

x

c

p













2

)

( x

c

p







f = 0: metoda jawna (explicit); warunkowo stabilna

f = 0,5: schemat Crancka-Nicholsona; warunkowo stabilna

f = 1: metoda niejawna (implicit); bezwarunkowo stabilna

































































































































x

T

T

x

T

T

f

x

T

T

x

T

T

f

x

T

T

c

i

i

i

i

i

i

i

i

i

i

p

0

0

1

0

1

0

1

1

1

1

1

1

0

1

1















+



+



+

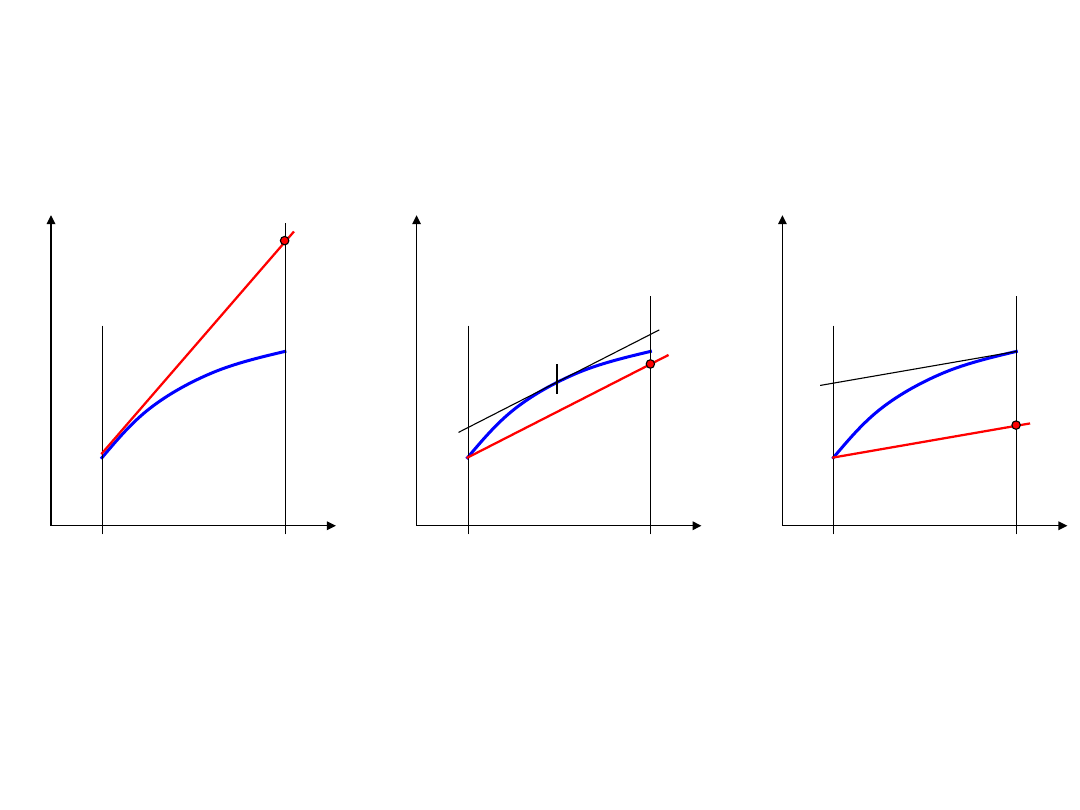
Schemat jawny

kierunek zmian na

podstawie informacji z

początku kroku

całkowania

Schemat Crancka-

-Nicholsona

kierunek zmian na

podstawie informacji z

całego kroku

całkowania

Schemat niejawny

kierunek zmian na

podstawie informacji z

końca kroku całkowania

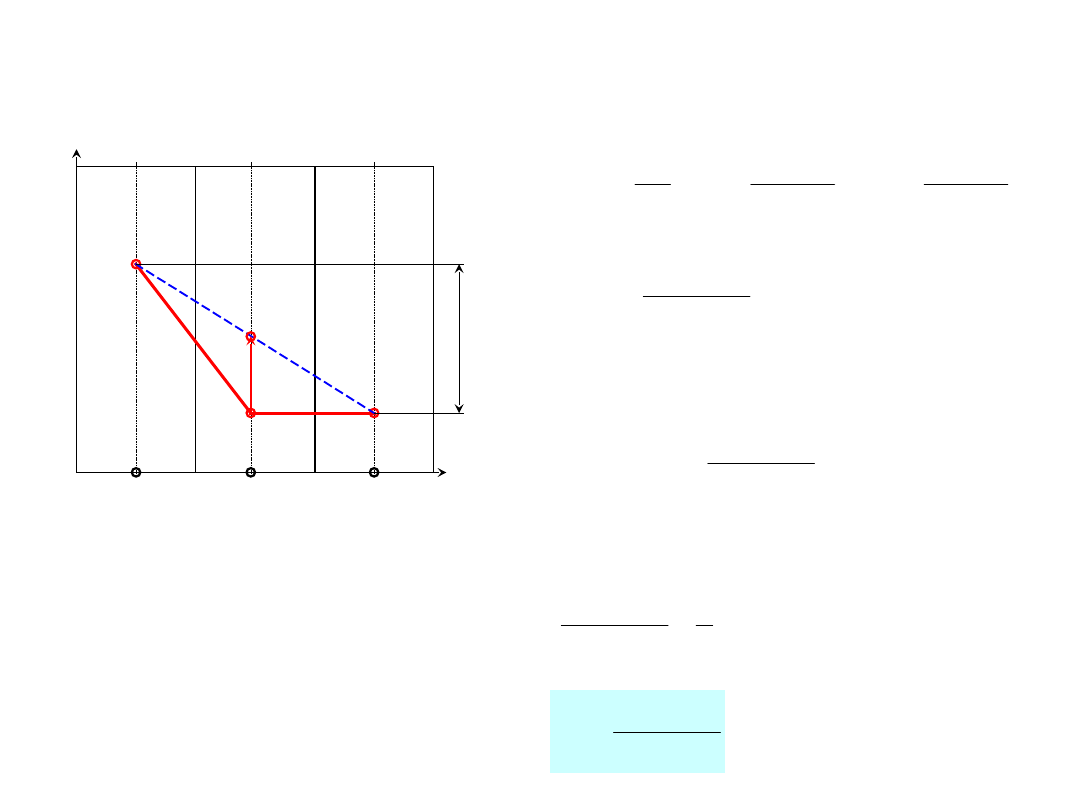
Niestabilność całkowania po czasie

przykład dla schematu jawnego



















































x

T

T

x

T

T

x

T

T

c

p

0

2

0

3

0

1

0

2

0

2

1

2











 







0

2

0

3

0

1

0

2

2

0

2

1

2

)

(

T

T

T

T

x

c

T

T

p

























0

2

0

1

2

0

2

1

2

)

(

T

T

x

c

T

T

p

















T

2

1

3

Szczególny przypadek: T

2

= T

3

T

1

– T

2

Fizycznie dopuszczalna zmiana temperatury w
punkcie 2

1

2

T

2

1

)

(

2







x

c

p













2

)

(

2

x

c

p







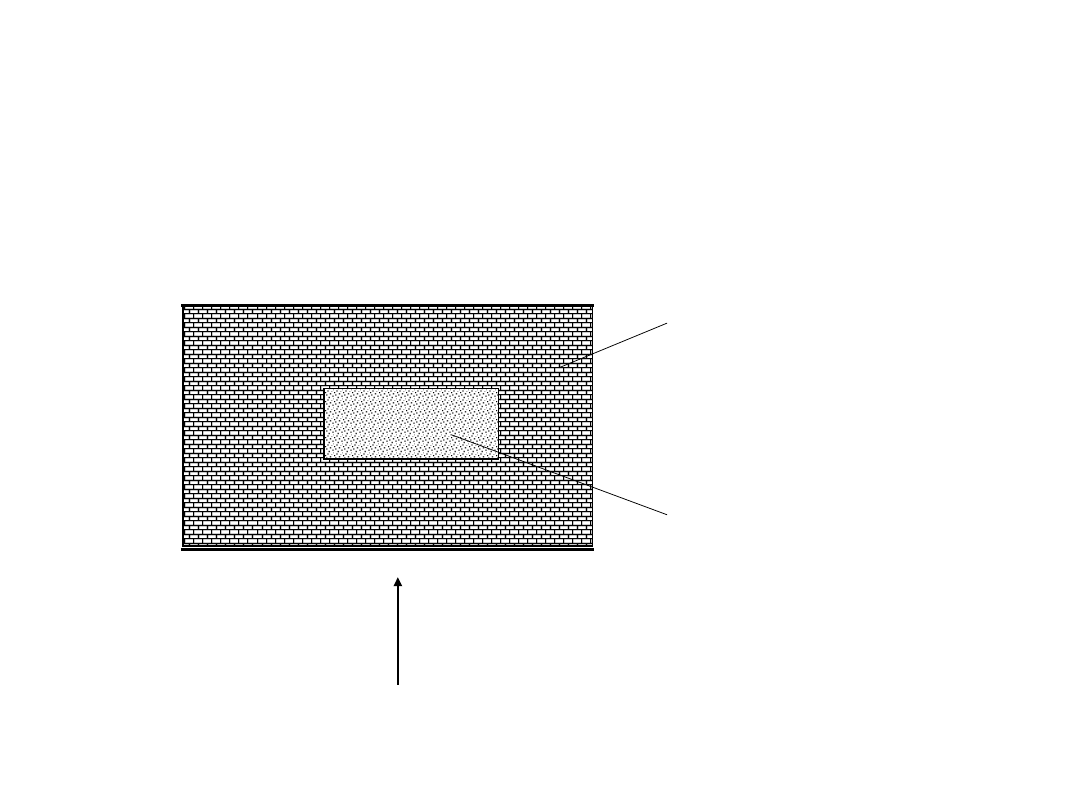
Zadanie domowe

Kierunek przepływu ciepła

temperatura t

2

temperatura t

1

Materiał o przewodności



1

Materiał o przewodności



2

Należy oszacować opór przewodzenia ciepła (lub efektywną przewodność

cieplną) dla układu dwuwymiarowego, którego schemat pokazano na

rysunku.