RACHUNEK CAŁKOWY

RACHUNEK CAŁKOWY

FUNKCJI DWÓCH

FUNKCJI DWÓCH

ZMIENNYCH

ZMIENNYCH

0

X

Y

0

X

Y

Obsz
ar

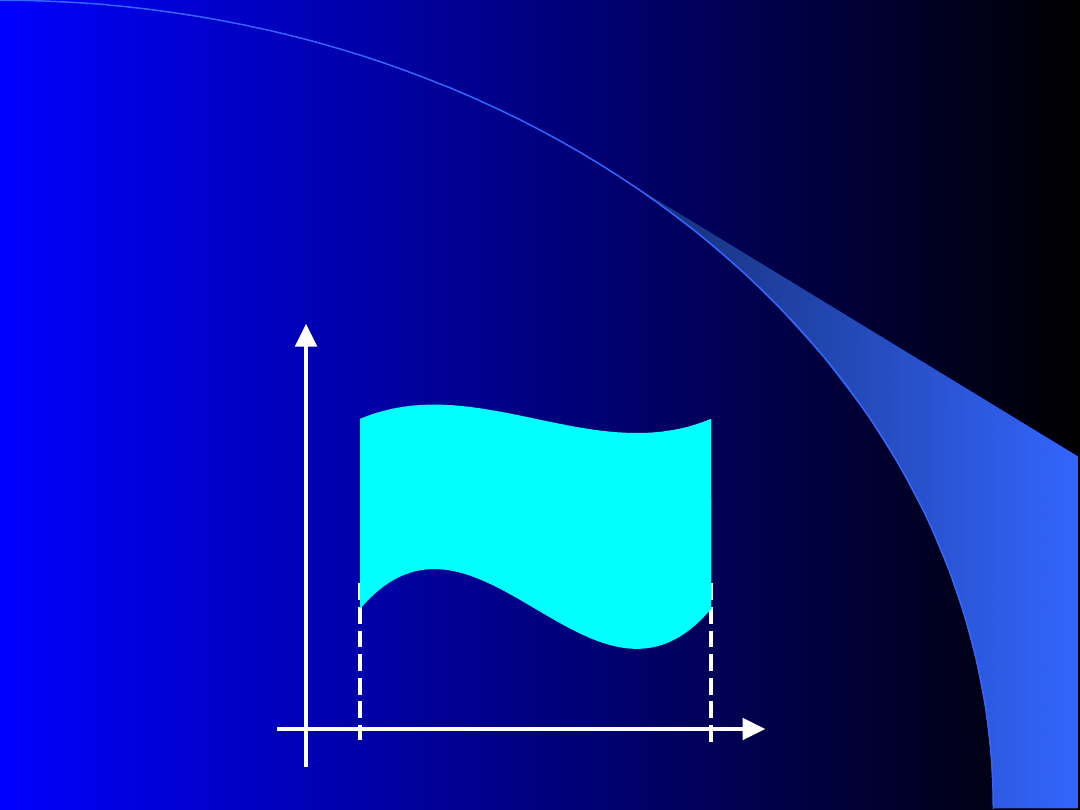
Obszar
domknięty

0

X

Y

Obszar domknięty D określony nierównościami

)

x

(

h

,

b

x

a









y

g(x)

gdzie g(x) i h(x) są funkcjami ciągłymi dla każdego x
<a,b> nazywamy

obszarem normalnym

względem

osi OX.

y=h(x)

y=g(x)

a

b

0

X

Y

Obszar domknięty D określony nierównościami

)

y

(

q

,

d

y

c









x

p(y)

gdzie p(y) i q(y) są funkcjami ciągłymi dla każdego y
 <c,d>

nazywamy obszarem normalnym względem

osi OY

.

x=p(y)

x=q(y)

c

d

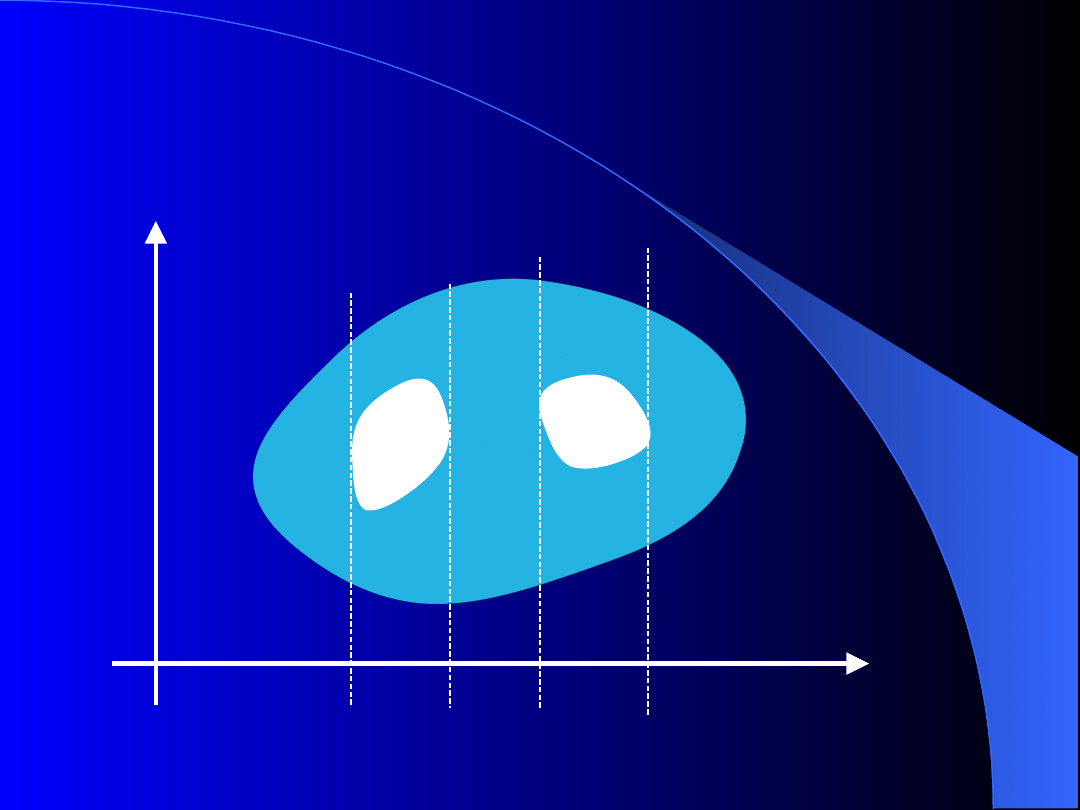
Mówimy, że obszar domknięty D

jest obszarem

regularnym względem osi OX (osi OY)

, jeżeli obszar

ten można podzielić prostymi równoległymi do osi OY
(osi OX) na obszary normalne względem osi OX (osi
OY).

0

X

Y

D

1

D

2

D

3

D

4

D

5

D

6

D

7

Obszary w przestrzeni R

2

nazywamy

obszarami

płaskimi

i oznaczamy literą D. Obszary w przestrzeni R

3

nazywamy

obszarami przestrzennymi

i oznaczamy

literą .
Obszar w przestrzeni R

3

o podstawie D ograniczony

powierzchnią będącą wykresem funkcji z=f(x,y) oraz
powierzchnią utworzoną
z prostych równoległych do osi OZ i przechodzących
przez brzeg obszaru D nazywamy

bryłą cylindryczną

.

Y

X

Z

z=f(x,y)

D

Średnicą obszaru

nazywamy kres górny zbioru

odległości dwóch dowolnych punktów tego obszaru.

Przykład: Średnicą prostokąta jest jego przekątna.
Średnicą trójkąta jest jego najdłuższy bok.

Niech f(x,y) będzie funkcją dwóch zmiennych
określoną w obszarze domkniętym i ograniczonym D w
polu S. Obszar D dzielimy
w dowolny sposób na n podobszarów D

i

odpowiednio o

polach  s

i

(i=1,2,...,n). Podział ten oznaczamy

symbolem 

n

. W każdym

podobszarze D

i

obieramy

dowolny punkt P

i

= (

i

, 

i

).





i

n

1

i

i

i

n

s

,

f















Tworzymy sumę.

Sumę tę nazywamy

sumą

całkową funkcji

f(x,y) w

obszarze D.

Przez d

i

(i=1,2,...,n) oznaczamy średnicę podobszaru D

i

.

 

i

n

i

1

n

d

max









Liczbę

nazywamy

średnicą

podziału



n

.

0

X

Y

a

b

P

i

D

i

Ciąg {

n

} podziałów obszaru D na podobszary nazywamy

ciągiem normalnym podziałów

, jeżeli odpowiadający mu

ciąg średnic {

n

} dąży do 0, tj.

.

0

lim

n

n









Jeżeli dla każdego normalnego ciągu podziałów obszaru
D ciąg sum całkowych {

n

} dąży do tej samej granicy

właściwej, niezależnej od wyboru punktów P

i

, to tę

granicę nazywamy

całką podwójną

funkcji f(x,y) w

obszarze D i oznaczamy symbolem



D

ds

)

y

,

x

(

f

Definicję powyższą można zapisać następująco:

i

n

1

i

i

i

n

D

s

)

,

(

f

lim

ds

)

y

,

x

(

f



















Jeżeli całka istnieje, to mówimy, że funkcja dwóch
zmiennych f(x,y) jest całkowalna w sensie Riemanna w
obszarze D lub krótko, że jest całkowalna w obszarze D.

Zamiast ds piszemy też dxdy. Czyli:







D

D

dxdy

)

y

,

x

(

f

ds

)

y

,

x

(

f

• wyrażenie f(x,y)ds lub f(x,y)dxdy nazywamy

wyrażeniem podcałkowym

,

• f(x,y) nazywamy

funkcją podcałkową

,

• D nazywamy

obszarem całkowania

,

• zmienne x i y nazywamy

zmiennymi całkowania

.

Twierdzenie o całkowalności funkcji dwóch
zmiennych
Jeżeli funkcja f(x,y) jest ciągła w obszarze domkniętym i
ograniczonym D, to jest całkowalna w tym obszarze.

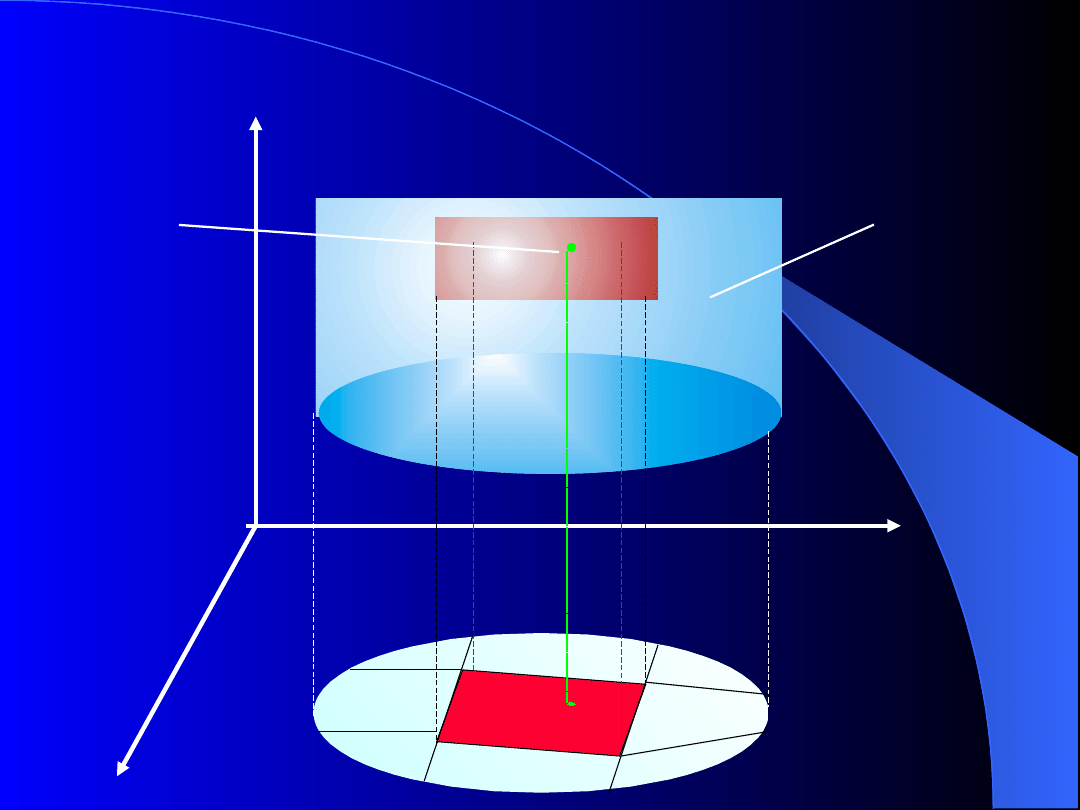
Interpretacja geometryczna całki

podwójnej

D

i

P

i

Y

X

Z

D

z=f(x,y)

)

,

(

f

i

i





Jeżeli

oraz istnieje całka



D

)

y

,

x

(

0

)

y

,

x

(

f





D

dxdy

)

y

,

x

(

f

to jest ona równa objętości V bryły cylindrycznej o
podstawie D
i ograniczonej powierzchnią będącą wykresem funkcji
z=f(x,y).

Więc:





D

dxdy

)

y

,

x

(

f

V

Z definicji całki wynika, że







D

D

dxdy

dxdy

1

jest równa polu S obszaru D.

Jeżeli

to z definicji wynika, że całka

podwójna jest równa objętości bryły ze znakiem
ujemnym.



D

)

y

,

x

(

,

0

)

y

,

x

(

f



W szczególności, jeżeli funkcja (f(x,y) jest stała w
prostokącie

 



 







,

d

y

c

b

x

a

:

R

y

,

x

D

2















przy czym

f(x,y) = k (k>0), to



D

)

y

,

x

(

)

c

d

)(

a

b

(

k

ds

)

y

,

x

(

f

D









(*)

Całka podwójna (*) jest więc równa objętości
prostopadłościanu, którego podstawą jest prostokąt D,
a wysokość jest równa k.

WŁASNOŚCI CAŁKI PODWÓJNEJ

1. Jeżeli funkcja f(x,y) jest całkowalna w obszarze D, a
c jest dowolną stałą to:











D

D

dxdy

)

y

,

x

(

f

c

dxdy

)

y

,

x

(

f

c

2. Jeżeli funkcje f(x,y) oraz g(x,y) są całkowalne w
obszarze D, to:

















D

D

D

dxdy

)

y

,

x

(

g

dxdy

)

y

,

x

(

f

dxdy

)

y

,

x

(

g

)

y

,

x

(

f

3. Jeżeli obszar D podzielimy na dwa obszary D

1

i D

2

,

gdzie D

1

i D

2

są obszarami mającymi tylko wspólny

brzeg, to:











2

1

D

D

D

dxdy

)

y

,

x

(

f

dxdy

)

y

,

x

(

f

dxdy

)

y

,

x

(

f

WŁASNOŚCI CAŁKI PODWÓJNEJ

4. Jeżeli

f(x,y) g(x,y), to:







D

D

dxdy

)

y

,

x

(

g

dxdy

)

y

,

x

(

f



D

)

y

,

x

(

5. Jeżeli f(x,y) jest funkcją całkowalną w obszarze D,
to:

,

S

M

dxdy

)

y

,

x

(

f

S

m

D











gdzie:
S jest polem obszaru D,

),

y

,

x

(

f

inf

m

D

)

y

,

x

(





).

y

,

x

(

f

sup

M

D

)

y

,

x

(





Ostatnią nierówność można zapisać następująco:

M

m

S

dxdy

)

y

,

x

(

f

D







Liczbę

nazywamy wartością

średnią funkcji z = f(x,y) w obszarze D.

S

dxdy

)

y

,

x

(

f

śr

D

z





TWIERDZENIE O WARTOŚCI ŚREDNIEJ

DLA CAŁKI PODWÓJNEJ

Jeżeli funkcja f(x,y) jest ciągła w obszarze domkniętym
D, to
w obszarze tym istnieje taki punkt P

0

należący do D, że

S

)

P

(

f

dxdy

)

y

,

x

(

f

0

D







OBLICZANIE CAŁKI PODWÓJNEJ

W OBSZARZE NORMALNYM

ZA POMOCĄ CAŁKI ITEROWANEJ

Całkę postaci

dx

y)dy

f(x,

b

a

h(x)

g(x)

 















nazywamy całką iterowaną w obszarze

 





 

 









x

h

y

x

g

b

x

a

:

R

y

x,

D

2















normalnym względem osi OX.

Całkę postaci

dy

y)dx

f(x,

d

c

q(y)

p(y)

 















OBLICZANIE CAŁKI PODWÓJNEJ

W OBSZARZE NORMALNYM

ZA POMOCĄ CAŁKI ITEROWANEJ

nazywamy całką iterowaną w obszarze

normalnym względem osi OY.

 



 







d

y

c

q(y)

x

p(y)

:

R

y

x,

D

2















TWIERDZENIE O ZAMIANIE CAŁKI PODWÓJNEJ

NA CAŁKĘ ITEROWANĄ

Jeżeli funkcja f(x,y) jest ciągła i ograniczona w
obszarze normalnym względem osi OX:

 





 

 









x

h

y

x

g

b

x

a

:

R

y

x,

D

2















to:

dy

y)dx

f(x,

y)dxdy

f(x,

d

c

q(y)

p(y)

D

 



















to:

dx

y)dy

f(x,

y)dxdy

f(x,

b

a

h(x)

g(x)

D

 



















Jeżeli funkcja f(x,y) jest ciągła i ograniczona w
obszarze normalnym względem osi OY:

 



 







d

y

c

q(y)

x

p(y)

:

R

y

x,

D

2















Z twierdzenia tego wynika, że jeżeli obszar D jest
normalny względem obu osi układu
współrzędnych OX i OY, to wartość całki
podwójnej nie zależy od kolejności całkowania.

to:

dy

dx

)

y

,

x

(

f

dx

dy

)

y

,

x

(

f

dxdy

)

y

,

x

(

f

d

c

b

a

b

a

d

c

D

 

 































 



 







,

d

y

c

b

x

a

:

R

y

,

x

D

2















W szczególności, jeżeli obszar normalny D jest prostokątem

dy

dx

)

y

,

x

(

f

dx

dy

)

y

,

x

(

f

dxdy

)

y

,

x

(

f

d

c

)

y

(

q

)

y

(

p

b

a

)

x

(

h

)

x

(

g

D

 

 





































