3. Elementy teorii liczb

Liczby pierwsze i liczby doskonałe. Podzielność liczb naturalnych,
operatory NWP, NWW, MOD, DIV. Równania diofantyczne i
rozstrzygalność problemów decyzyjnych. Wykorzystanie w
projektowaniu systemów kryptograficznych

1

Wiara w magiczne znaczenie liczb jest powszechna i niewątpliwie bardzo
stara.
W starożytności nauka szła w parze z magią; pierwsza starała się poznać
świat, druga zapanować nad nim. Nic więc dziwnego, że adepci nauk
tajemnych skwapliwie skorzystali z zastanawiających prawidłowości i
współzależności liczb i miar, odkrytych przez poszukiwaczy wiedzy. Wcześnie
zainteresowano się siódemką. Świadczy o tym choćby liczba dni tygodnia.
Spośród wszystkich ciał niebieskich największy wpływ na życie na Ziemi
wywiera Księżyc. Pełny cykl jego przemian, zwany miesiącem księżycowym,
dokonuje się w ciągu 28 dni, w czterech, wyraźnie zróżnicowanych,
siedmiodniowych etapach. Siódemkę uznano więc za liczbę rządzącą
procesami życiowymi, a także za symbol pełni. Siedem barw składa się na
widmo świetlne, siedem tonów na gamę.

W starożytności wierzono, że przebiegiem wydarzeń na Ziemi rządzi siedem
planet połączonych systemem korespondencji z tylu właśnie dniami
tygodnia Równie wiele można powiedzieć praktycznie o każdej liczbie
naturalnej.

2

Fakt ten znajduje swoje odzwierciedlenie w numerologii zajmującej się
badaniem wpływu dnia, godziny, miejsca urodzenia na nasze życie, oraz bada
wibracje naszych imion, nazwiska, przezwisk i pseudonimów, które razem
tworzą portret, czy też horoskop numerologiczny. W numerologii zakłada się,
że całą rzeczywistość można wyrazić w liczbach pojedynczych od 1 do 9. Zero
jest pustką i nicością i samo w sobie nie jest dla numerologii istotne. Każdą
liczbę można wyrazić w zredukowanej formie. Czyli dla numerologa liczba 25
będzie siódemką (2+5=7) . 126 to dziewiątka (1+2+6=9) itd. Obok liczb
zwykłych (od 1 do 9) w numerologii wyróżnia się także tzw. liczby
mistrzowskie. Są to: 11, 22, 33 i 44. Liczby te jeśli pojawią się w portrecie
numerologicznym znamionują wysoki poziom świadomości, duchowość,
mądrość i wiedzę. Istnieje także zasada, że nie redukuje się tzw. liczb
mistrzowskich, to znaczy 11 i 22. Są one doskonałe i nie można ich
redukować, choć w domyśle są dwójką i czwórką.

Oprócz wspomnianej, wątpliwie wpływającej na nasze życie roli liczb, warto

więcej uwagi poświęcić niektórym klasom liczb, a właściwie ich

właściwościom, dzięki którym znajdują one swoje praktyczne wykorzystanie.

Tak ma się rzecz np. z liczbami pierwszymi (zastosowania w kryptografii) czy

też liczbami Fibonacciego (zastosowania w modelowaniu struktur fraktalnych,

np. ilustrujących plenność gryzoni, rozrastanie się roślin, itp.).

NAJWIĘKSZY WSPÓLNY DZIELNIK DWÓCH LICZB NWD(m,n)

Liczba k jest największym wspólnym dzielnikiem m i n, tzn.
NWD(m,n), jeśli dzieli m oraz n i jest największą liczba o tej
właściwości.

NWD(n,m) = max{kN : k dzieli n  k dzieli m }

NWD(48,6) = 6 , NWD(26,15) = 1

i sprowadza się do iteracyjnego wyznaczania prawej strony
wyrażenia:
NWD(n,m) = NWD(m,r). Warunek stopu: r=0.
gdzie: n  m, n/m = q + r ; n = q m + r ; r = n - q m ;
0  r  m-1

Przykład 1

NWD(24,12) = NWD(12,0)

NWD(37,35) = NWD(35,2) = NWD(17,1) = NWD(1,0)

3

Algorytm Euklidesa znajduje NWD(m,n)

Algorytm wyznaczania NWD(n,m) raz jeszcze:

NWD(721,448)

n = q x m

+ r

721

= 1 x 448

+ 273

448

= 1 x 273

+ 175

273

= 1 x 175

+ 98

175

= 1 x 98 + 77

98 = 1 x 77+ 21

77 = 3 x 21+ 14

21 = 1 x 14+ 7

14 = 2 x 7 + 0

NWD(721,448) = 7

4

5

, to sprowadzamy go do postaci
zwykłej

q

p

q

p,

Obliczanie NWD dwóch liczb ma zastosowanie w obliczeniach, w których

posługujemy się ułamkami zwykłymi postaci (

-liczby względnie

pierwsze).

Np. liczby 13 i 15 są względnie pierwsze
ponieważ





1

15

,

13



NWD

Jeśli ułamek nie jest zwykły np.

16

8

dzieląc licznik i mianownik przez ich największy wspólny dzielnik
(skracanie ułamków). Dzięki temu w obliczeniach nie pojawiają się
niepotrzebnie zbyt duże liczby.





8

16

,

8

NWD



16

8

2

1

=

Stąd

Równania diofantyczne

A

2

+ B

2

= C

2

3

2

+ 4

2

= 5

2

trójkąty pitagorejskie

A

n

+ B

n

= C

n

Przykład
Dane są naczynia o pojemności m i n. Czy korzystając z
nich można napełnić zbiornik o pojemności k ? Jeżeli tak to
w jaki sposób?

Niech m, n  N , x, y  Z;

k = x m + y n

m =5, n=7

m =4, n=10 m =6, n=18

5 x + 7 y = 3 ;

15 = 4 x + 10 y ;

3 = 6 x + 18 y

NWD(7,5) = 1

NWD(10,4) = 2

NWD(18,6) =6

Rozwiązanie istnieje gdy k jest wielokrotnością
NWD(m,n).

15 = 4 x + 10 y

nie ma rozwiązania, bo 2 = NWD(4,10),

3 = 5 x + 7 y

rozwiązanie istnieje, bo 1 = NWD(5,7).

6

NAJMNIEJSZA WSPÓLNA WIELOKROTNOŚĆ

NWW(m,n)

Najmniejszą wspólną wielokrotnością liczb naturalnych jest najmniejsza

liczba naturalna która dzieli się przez m i n .

NWW(m,n) = min{k: k jest podzielne przez m  k jest

podzielne przez m}

Dodając ułamki zwykłe za wspólny mianownik obieramy zawsze najmniejszą

wspólną wielokrotność mianowników.

NWW(12,9) = 36 bo 12 = 2*2*3 ;

9 = 3*3 stąd 2*2*3*3

m * n 12 * 9

NWW(12,9) = ---------------- = --------- = 36
NWD(12,9) 3

Liczby pierwsze

nN jest liczbą pierwszą jeśli n jest podzielne tylko przez 1 i n. 1 –

nie jest liczbą pierwszą.

Liczb pierwszych jest nieskończenie wiele.

7

8

Tak naprawdę nikt nie wie, czy istnieje jakikolwiek wzór generujący
duże liczby pierwsze i tylko pierwsze.

Liczby pierwsze Mersena (Mersenn’a XVII w.)
Najczęściej stosowanym wzorem na liczby pierwsze jest

1

2 

p

gdzi
e

p

- liczba pierwsza

Łatwo zauważyć, że liczba

nie zawsze jest pierwszą, np. dla

1

2 

p

11



p

89

*

23

2047

1

2

11







ale dla p=2, 3, 5, 7, 19, 31, 61, 89 liczby tej postaci są
pierwsze.

Liczby pierwsze Fermat’a

L

k

= 2 + 1

k = 1, 2 , 3 , 4 - liczba pierwsza

ale dla k = 5 nie jest liczbą pierwszą

2

k

9

H = 2

l1

3

l3

5

l5

7

l7

11

l11

13

l13

....

.....

l

1

, l

3

, l

5

, . .. – nieujemne liczby całkowite

Liczby pierwsze Euklidesa

E

n

= E

1

E

2

... E

n-1

+1 gdy n  1

E

1

= 1 + 1=2

E

2

= 2 +1 = 3

E

3

= 2 *3 +1 = 7

E

4

= 2 *3 *5 + 1 = 43

Są to wszystkie liczby pierwsze, ale kolejna E

5

nie jest liczbą pierwszą

E

5

= 2 *3* 5* 43 + 1 = 1807 = 13 *139

Niemniej jednak liczby Euklidesa są parami względnie pierwsze
czyli
NWD(E

m

, E

n

)=1 gdy n  m

Każda liczba naturalna może być przedstawiona jako iloczyn liczb
pierwszych, tzn. każdą liczbę naturalną można przedstawić w postaci

Liczba doskonała

Liczba doskonała jest liczbą naturalną gdy jest równa sumie
wszystkich swoich dzielników właściwych, tzn. takich które są od niej
mniejsze.

6 = 1 + 2 + 3

28 = 1 + 2 + 4 + 7 + 14

10

Rozważmy oznaczenia operatorów MOD i DIV:
nMODm lub MOD(n,m)

- reszta z dzielenia n przez m

nDIVm

lub DIV(n,m) - iloraz całkowity z dzielenia n

przez m

nDIVm =









m

n

nMODm =













 nDIVm

m

n

m

3

7

MOD

31







3

7

31







MOD

4

7

DIV

31







4

7

31







DIV

Przykład 2
7 MOD 3 = 1 ;

1 MOD 7 = 1 ;

7 MOD 7 = 0

7 DIV 3 = 2

,

1 DIV 7 = 0

;

7 DIV 7 = 1

;

11

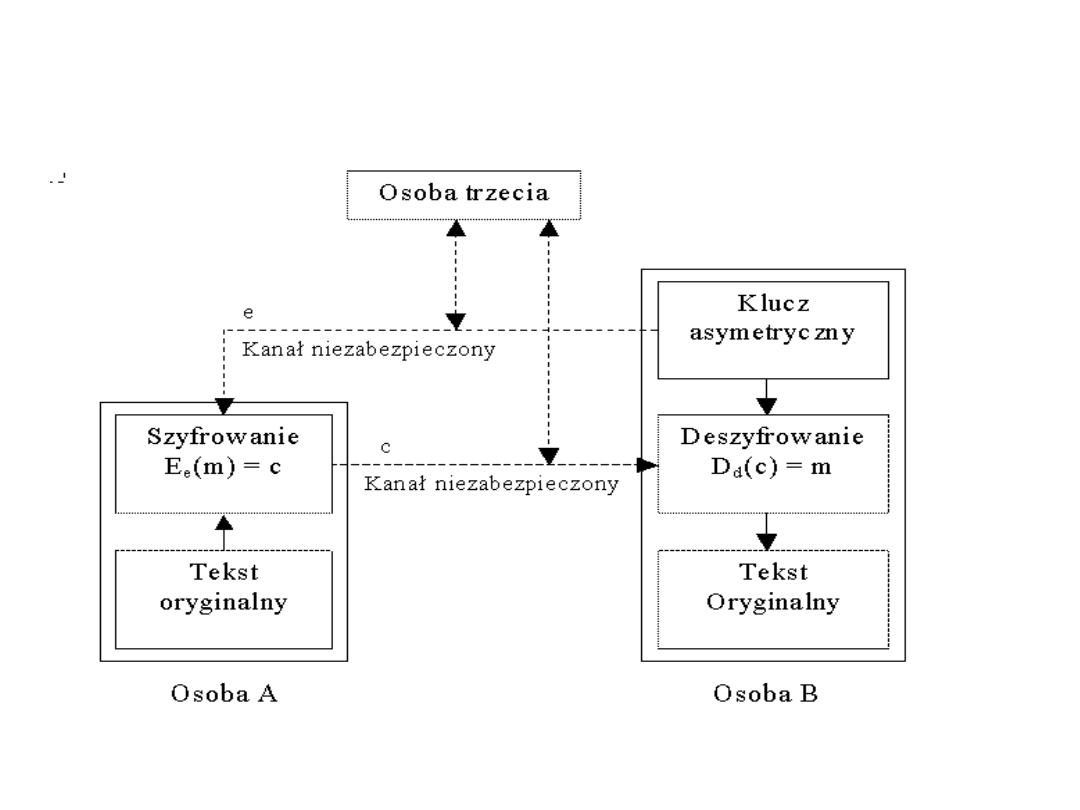
Schemat dwustronnej komunikacji przy użyciu klucza
asymetrycznego e- klucz publiczny, d – klucz prywatny

Liczby pierwsze są obecnie wykorzystywane w kryptografii do
kodowania wiadomości przesyłanych w sieciach komputerowych. W
tym celu właśnie są poszukiwane bardzo duże liczby pierwsze.

12

Wiadomość pozostaje poufna nawet w przypadku przechwycenia szyfrogramu oraz
klucza szyfrującego przez osobę trzecią. Komunikacja w drugą stronę wymaga
wygenerowania przez osobę A klucza publicznego i przekazania go osobie B.
Dalsze postępowanie wygląda analogicznie

RSA jest najbardziej rozpowszechnionym algorytmem klucza publicznego
używanym zarówno do szyfrowania danych, jak i do generowania podpisu
elektronicznego.
Klucze w kryptosystemie RSA generuje się według następującego
algorytmu:

•Wyznacza się losowo dwie odpowiednio duże liczby pierwsze p i q

•Oblicza się n = p*q i  = (p – 1)*(q – 1)

•Wybiera się losowo liczbę całkowitą e spełniającą warunki

1< e<  i NWD(e, ) = 1

•Oblicza się liczbę całkowitą d taką, że 1<d<  i e*d ≡ 1 (MOD )

•Otrzymuje się klucz publiczny – (n,e) oraz klucz prywatny – d.

Szyfrogram c odpowiadający wiadomości wyrażonej liczbą
całkowitą m otrzymuje się obliczając:

c = m

e

MOD n

Wiadomość odszyfrowuje się za pomocą wzoru:

m = c

d

MOD n

13

Przykład 3

Niech p= 3 i q=5

n=p*q = 15
 = (p – 1)*(q – 1) = 2*4 = 8

Wyznaczanie „e”

1< e<  ; 1< e< 8
NWD(e, ) = NWD(e, 8) = 3
e=3

Wyznaczanie „d“

1<d<  i e*d ≡ 1 (MOD )
1<d< 8 i 3*d ≡ 1 (MOD 8)
d=3

Zatem n=15, e=3 , d=3

Chcemy zaszyfrować m =3 zgodnie z c = m

e

MOD n odpowiada

temu
c = 3

3

MOD 15 = 27 MOD 15 = 12 MOD 15 = 12

Wiadomość odszyfrowana m = c

d

MOD n = 12

3

MOD 15 = 1728

MOD 15 = 3
bo 115 15 = 1725

14

Przykład 4

Niech p= 5 i q=7

n=p*q = 35
 = (p – 1)*(q – 1) = 4*6 = 24

Wyznaczanie „e”

1< e<  ; 1< e< 24
NWD(e, ) = NWD(e, 24) = 1
e=11

Wyznaczanie „d“

1<d<  i e*d ≡ 1 (MOD )
1<d< 24 i 11*d ≡ 1 (MOD 24)
d=11

Zatem n=35, e=11 , d=11

Chcemy zaszyfrować m =8 zgodnie z c = m

e

MOD n

odpowiada temu
c = 8

11

MOD 35 = 22 MOD 35 = 22

Wiadomość odszyfrowana m = c

d

MOD n = 22

11

MOD 35 = 8

MOD 35 = 8

ZADANIA

7. Oblicz liczby całkowite x i y spełniające równość 5 x + 7 y = 1

.

1. Wyznacz:

7 MOD 7 =

;

0 MOD 7 =

;

17 MOD 7 =

0 DIV 3 = ,

7 DIV 7 = ;

-17 DIV 7 =

2. Zastosuj algorytm Euklidesa do dwóch liczb: 55 i 34.

3. Przedstaw liczbę n = 29529 w postaci iloczynu liczb pierwszych.

4. Wyznacz NWD i NWW dla dwóch liczb: 448 i 721.

5. Na ilu bitach można zapisać liczbę 63788?

6. Oblicz:

MAX{3,NWW(5,9), NWD(5,9),[MOD(4,DIV(10,3))]} =
MIN{3,2,[MOD(4,MOD(10,3))]} =

8. Dla jakich m i n równość ta NWW(m,n) = NWD(m.n) jest
prawdziwa?

9. Dla jakich m i n równość ta MOD(m,n) = DIV(m.n) jest
prawdziwa?

n

10. Oblic  2

k

dla n = 1, 2, 3, 4, 5. Podaj wzór ogólny dla tej sumy.

k=0