KRAWĘDZIE, ŁUKI, WIERZCHOŁKI, DROGI, ŚCIEŻKI, PĘTLE, KONTURY,

OBWODY, CYKLE, DROGI ZAMKNIĘTE.

Ścieżka (droga) – sekwencja łuków (krawędzi), np.. …(a,b),(b,d),(d,c)…

Ścieżka (droga) elementarna - nie przecina samej siebie.
Graf spójny G - jeżeli istnieje przynajmniej jedna ścieżka (droga) miedzy

każdą para wierzchołków w G.

Podgraf

G’  G = (X,R) ,

G’ = (X’,R’); X’  X ; R’  R

Długość drogi – liczba krawędzi drogi.

Stopień wierzchołka - liczba krawędzi z nim incydentnych.

Graf regularny

– wszystkie wierzchołki są tego samego stopnia

Krawędź (a,b) – relacja symetryczna łącząca a i b

Łuk (a,b) – relacja niesymetryczna łącząca a i b , np., a poprzedza b

Pętla (a,a) – relacja zwrotna symetryczna łącząca a i a

1

9. Elementy teorii grafów (Grafy i ich właściwości)

Grafy symetryczne i skierowane. Charakterystyki: drogi, cykle, pętle, itd. właściwości

i

klasyfikacje grafów: drzewa, grafy dwudzielne, grafy pełne, grafy planarne, itp.
Izomorfizm grafów. Wykorzystanie w algorytmach analizy związków chemicznych,
kolorowaniu map, trasowaniu ścieżek obwodów drukowanych

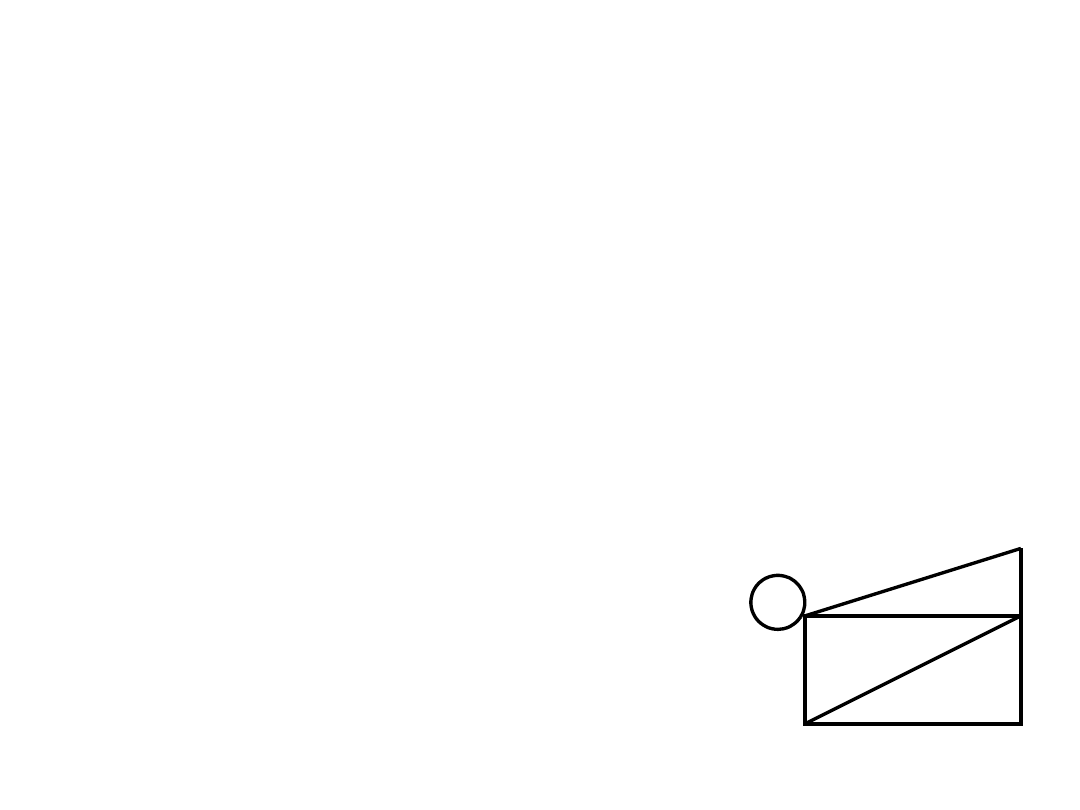
Charakterystyki grafu

n - liczba wierzchołków

e - liczba krawędzi

k - liczba składowych (spójności)

e  n – k

r - rząd grafu

r = n – k

 - zerowość grafu

 = e – n + k

Przykład 1

Rząd grafu = liczba gałęzi w każdym dendrycie

grafu

Zerowość grafu = liczba cięciw w grafie

rząd + zerowość = liczba krawędzi w grafie

2

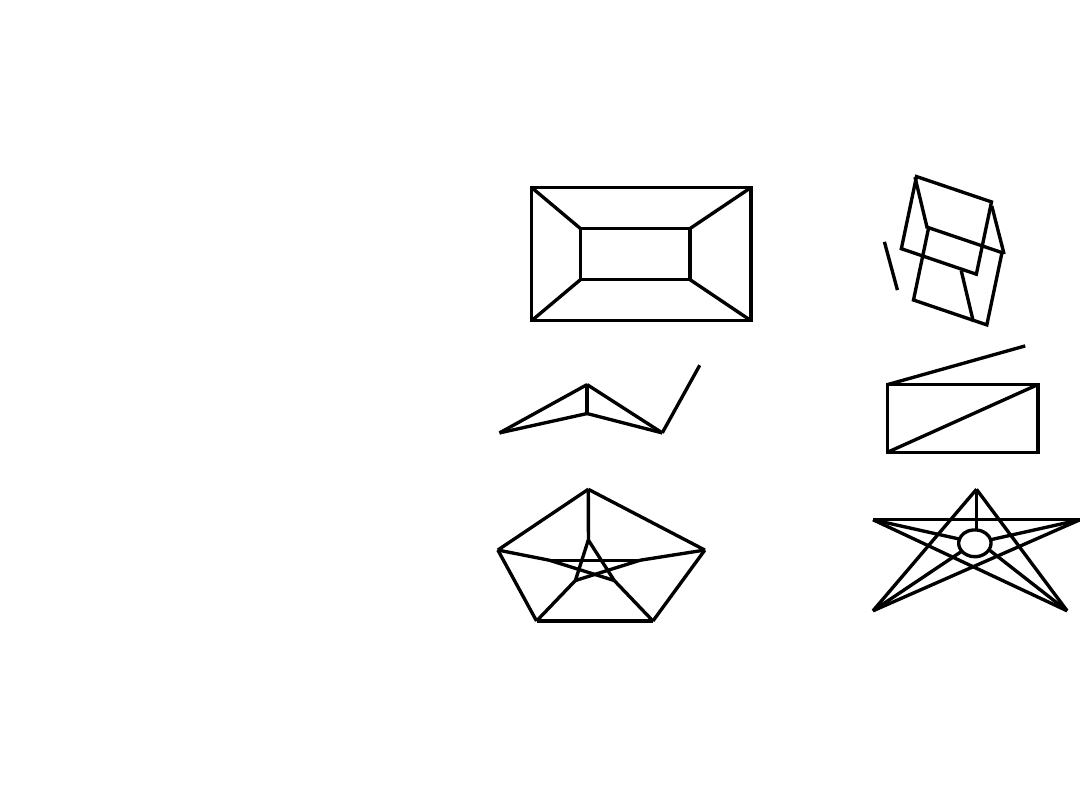
Izomorfizm grafów

Dwa grafy są izomorficzne jeśli zachodzi wzajemnie jednoznaczna
odpowiedniość między ich wierzchołkami oraz ich krawędziami przy
zachowaniu relacji incydencji.

Grafy izomorficzne muszą mieć:

•tę samą liczbę wierzchołków

•tę samą liczbę krawędzi

•równa liczbę wierzchołków o
danym stopniu

  

I nikt tak naprawdę nie wie ile i
jakich
jeszcze cech zagwarantuje, że ich
sprawdzenie wystarczy dla
stwierdzenia podobieństwa

Poszukiwane jest kryterium
efektywnego obliczeniowo
wykrywania izomorfizmu!

3

Przykłady grafów izomorficznych

Grafy nie izomorficzne

N o m e n k l a t u r a

O Izomorfizmie (podobieństwie) raz jeszcze - Dwa grafy G

1

i G

2

są

izomorficzne, jeżeli istnieje wzajemna jednoznaczna odpowiedniość między
wierzchołkami grafu G

1

i wierzchołkami grafu G

2

, taka że liczba krawędzi

łącząca dwa dowolne wierzchołki w G

1

jest równa liczbie krawędzi łączących

odpowiadające im wierzchołki w G

2

.

4

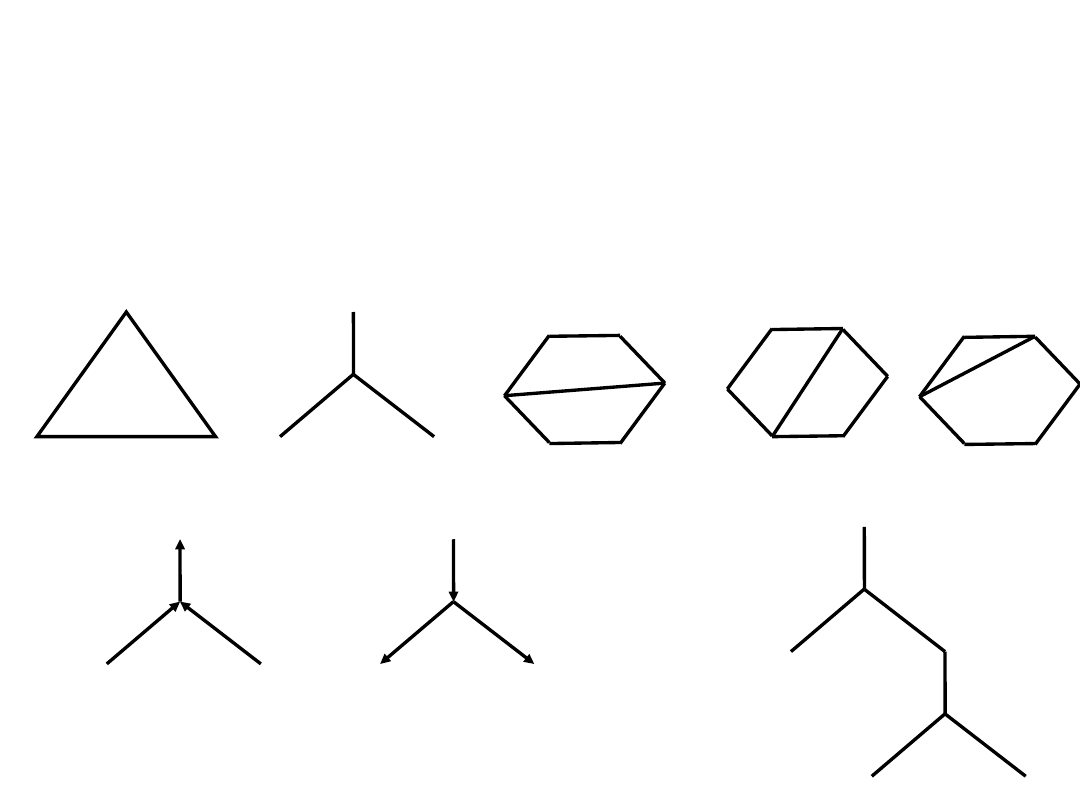
Krzak

Drzewo

Grafy dwudzielne, grafy pełne, drzewa

Graf dwudzielny

Graf pełny

Drzewo

Graf dwudzielny – wierzchołki którego można pokolorować dwoma

barwami.

Graf pełny

– każdy wierzchołek którego jest połączony

(krawędzią lub łukiem) z

pozostałymi wierzchołkami

Drzewo

– graf spójny bez obwodów (drzewo genealogiczne,

rzeka,

drzewo decyzyjne, itp.)

Właściwości drzewa:

•między każdą parą wierzchołków istnieje tylko jedna

droga

•drzewo o n wierzchołkach ma n-1 krawędzi

5

Drzewo binarne - dokładnie jeden wierzchołek jest stopnia drugiego a

pozostałe stopnia trzeciego lub pierwszego.

poziom 0

poziom 1

poziom 3
poziom 4

Właściwości drzew binarnych:

- liczba wierzchołków n w drzewie binarnym jest zawsze

nieparzysta.

- liczba krawędzi w drzewie jest równa p = (n+1)/2,

- p – liczba wierzchołków wiszących

1/2(p + 3(n-p-1)+2) = n-1 - liczba krawędzi w drzewie

6

Własności drzew (dla grafu T mającego n-wierzchołków):
• T nie zawiera cykli, ilość krawędzi = n-1
• T jest grafem spójnym, każda krawędź jest mostem.
• Każde dwa wierzchołki T połączone są dokładnie jedną drogą.

• T nie zawiera cykli, ale po dodaniu dowolnej nowej krawędzi otrzymujemy
graf z

dokładnie jednym cyklem.

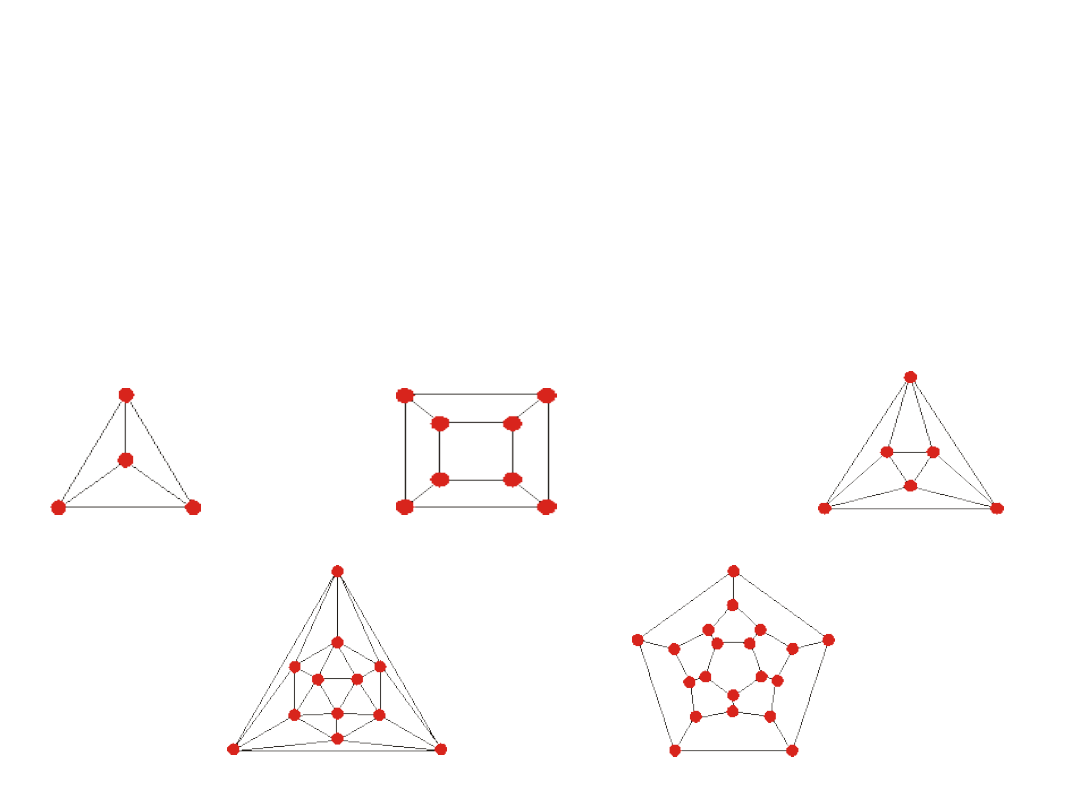
Grafy platońskie

7

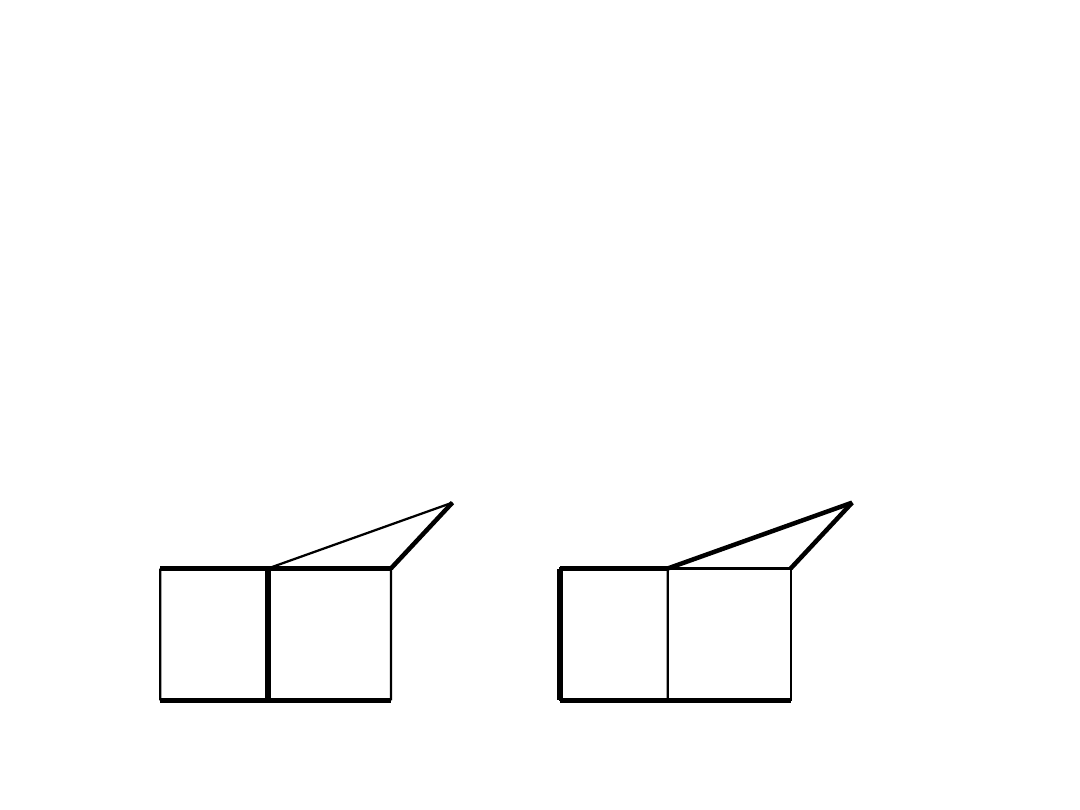
Łatwo zauważyć, że liczba drzew niezaetykietowanych o czterech
wierzchołkach wynosi 2.

Dendrytem grafu spójnego G nazywamy drzewo będące jego podgrafem i
zawierającym wszystkie wierzchołki grafu G.

Graf niespójny o k składowych ma las dendrytów składający się z k
drzew.

Każdy graf spójny ma przynajmniej jeden dendryt.

Cięciwą nazywamy krawędź grafu G która nie należy do danego dendrytu.

Przykład 2

Przykładowe dendryty (rozpinające) grafu

8

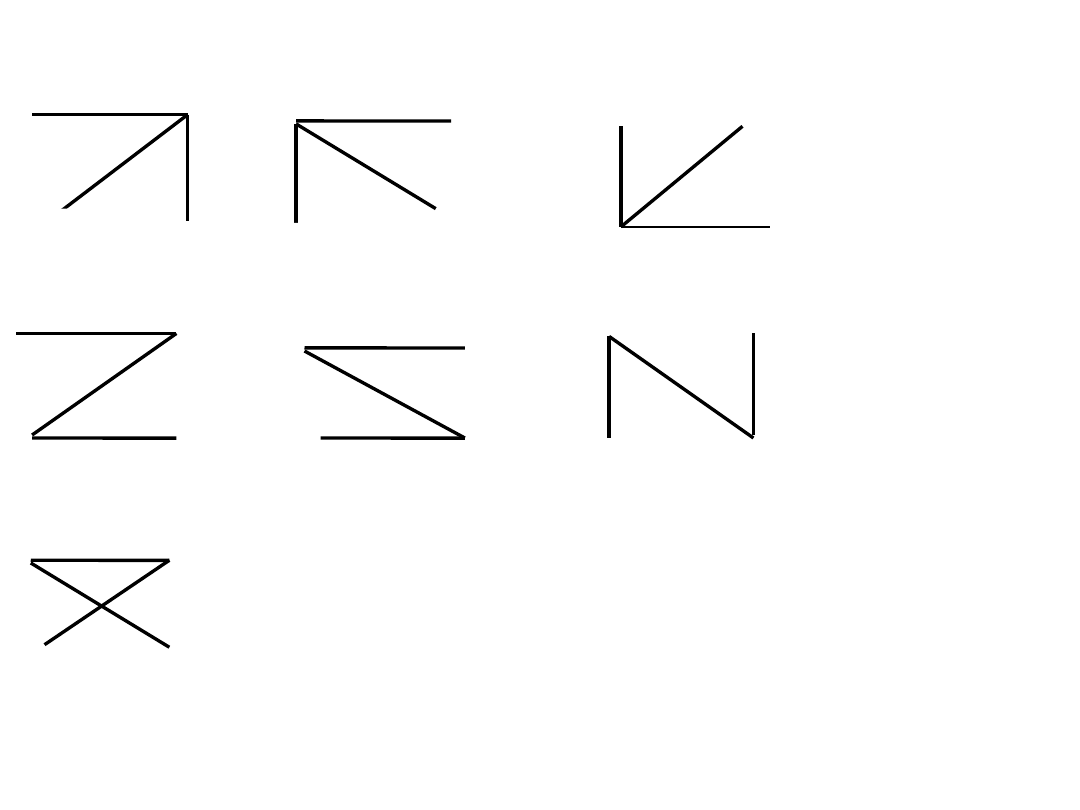
A

A

A

A

B

D

C

B

D

C

B

D

C

B

D

C

Drzewa o wierzchołkach zaetykietowanych

Liczba drzew zaetykietowanych o n wierzchołkach (n2)
wynosi n

n-2

.

Uzupełnij przedstawione przykłady o pozostałe

brakujace.

A

A

B

D

C

B

D

C

C

A

B

D

9

10

a)

b)

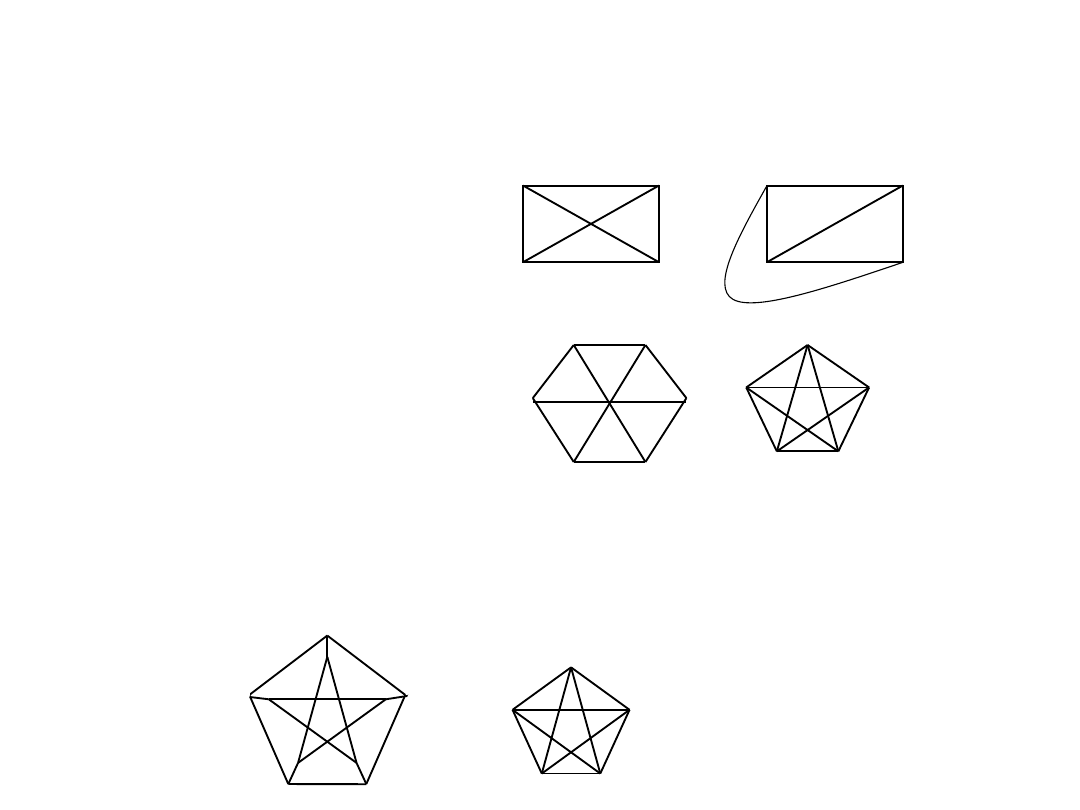
GRAFY PLANARNE

Graf planarny to graf który można narysować na płaszczyźnie bez przecięć –
to znaczy tak aby, żadne dwie krawędzie nie przecinały się na rysunku poza
wierzchołkiem z którym są incydentne.

Grafy planarne
Grafy K

3,3

i K

5

są nieplanarne

.

Grafy a) K

3,3

, b) K

5

Dany graf G jest planarny wtedy i tylko wtedy gdy nie zawiera podgrafu
homeomorficznego z grafem K

3,3

i K

5

. Dany graf G nie jest planarny wtedy i

tylko wtedy gdy jest ściągalny do podgrafu K

3,3

lub do podgrafu K

5

.

Rys. 5.23

Grafy nieplanarne

11

ZADANIA

1. Ile jest drzew nieoznakowanych mających 5 wierzchołków?

3. Dla poniższego grafu wyznacz wszystkie dendryty (grafy rozpinające).

2. Podaj przykład grafu skierowanego o wierzchołkach x, y, z, w którym jest
cykl

z wierzchołkami x i y i inny cykl z wierzchołkami y i z ale nie ma cyklu

mającego

wierzchołki x i z.

4.

Czy poniższe grafy są izomorficzne? Odpowiedź uzasadnij.

5. Znajdź wszystkie nieizomorficzne drzewa spinające grafu K

5

(K

3,3

).

Ile cykli Hamiltona ma ten graf? Ile dróg Hamiltona ma graf K

n,n-1

?

12

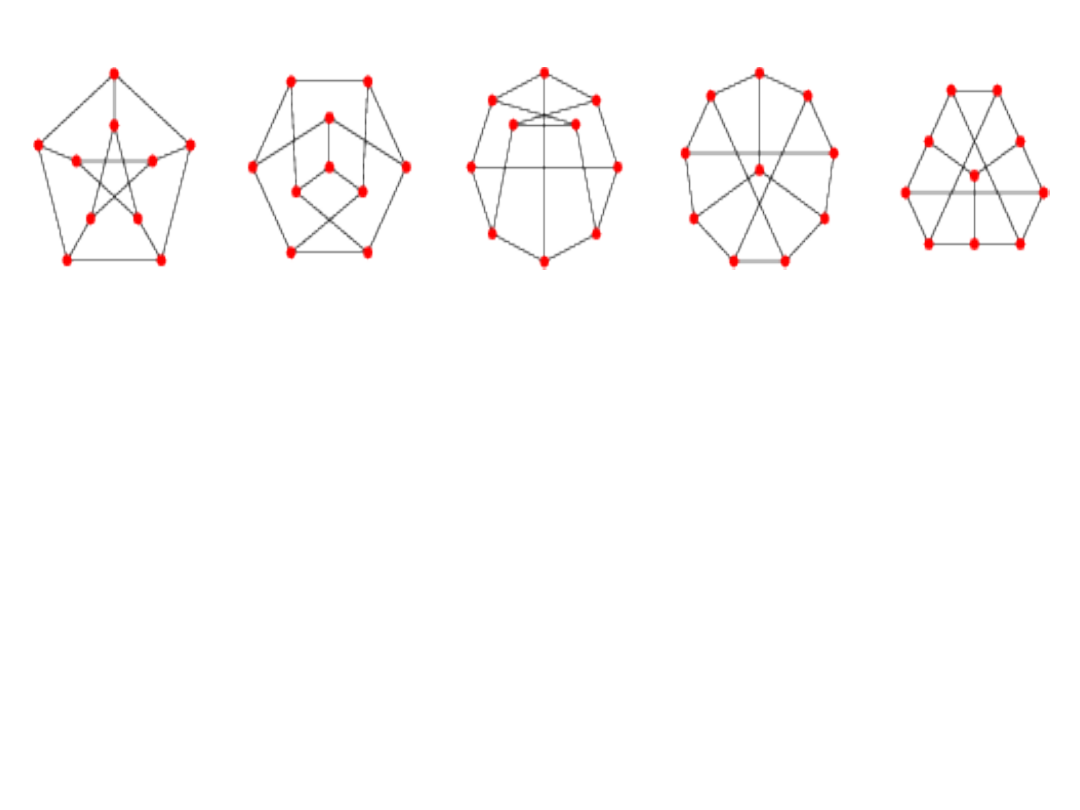
6. Udowodnij, że wszystkie grafy na rysunku poniżej są izomorficzne:

7.Czy istnieje spójny graf kubiczny o 10 wierzchołkach, który nie jest izomorficzny z
powyższym grafem?

8. Z dokładnością do izomorfizmu, wyznacz wszystkie drzewa siedmio-wierzchołkowe

.

9. Jaka jest minimalna liczba liści (wierzchołków stp. 1) w drzewie?

10 Indiana Jones znalazł się nad labiryntem, w którym jest 6 podziemnych
jaskiń. Każda z jaskiń połączona jest z każdą inną osobnym korytarzem, który
nie przecina innego korytarza i ma zapadnię pozwalającą przejść tym
korytarzem tylko jeden raz. W każdym korytarzu znajduje się skarb. Tylko
dwie z jaskiń są połączone bezpiecznym przejściem z powierzchnia. Indiana
może tylko raz zejść pod powierzchnię. Ile skarbów ma szanse zebrać?

13

11. Iloma ciągłymi pociągnięciami ołówka można narysować figurę pokazaną na rysunku
poniżej tak, aby nie rysować żadnej linii dwukrotnie?