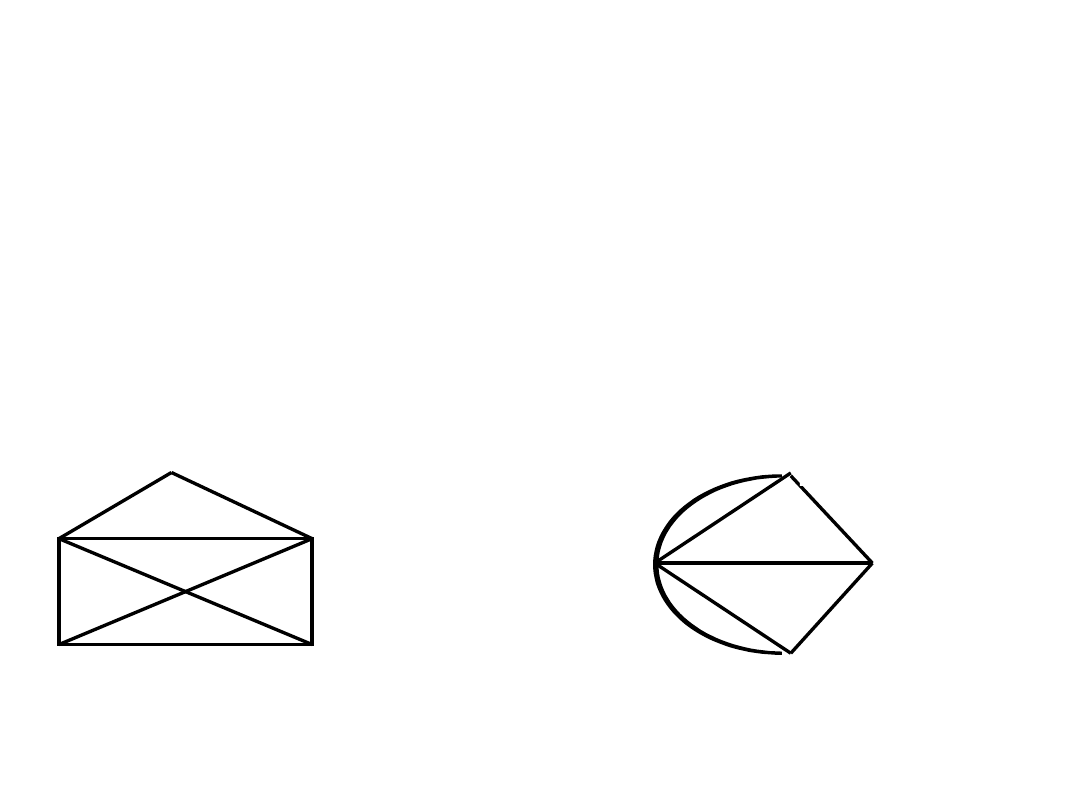
Grafy Eulera

(przechodzenie przez krawędzie)

Grafem Eulera nazywamy graf składający się z drogi Eulera.

Drogą Eulera nazywamy drogę zamknięta przechodzącą dokładnie
jeden raz przez każdą krawędź z grafu G.

Graf jest grafem Eulera wtedy i tylko wtedy gdy wszystkie
wierzchołki G są stopnia parzystego

.

A

D

C

B

Graf spójny mający dokładnie dwa wierzchołki stopnia
nieparzystego, ma drogę Eulera

.

1

10. Elementy teorii grafów (Algorytmy na grafach)

Drzewa rozpinające. Grafy Eulera i Hamiltona. Grafy AND/OR. Wykorzystanie w
algorytmach wyznaczania sieci instalacji elektrycznej, najkrótszych połączeń,
planowaniu działań (np. montażu).

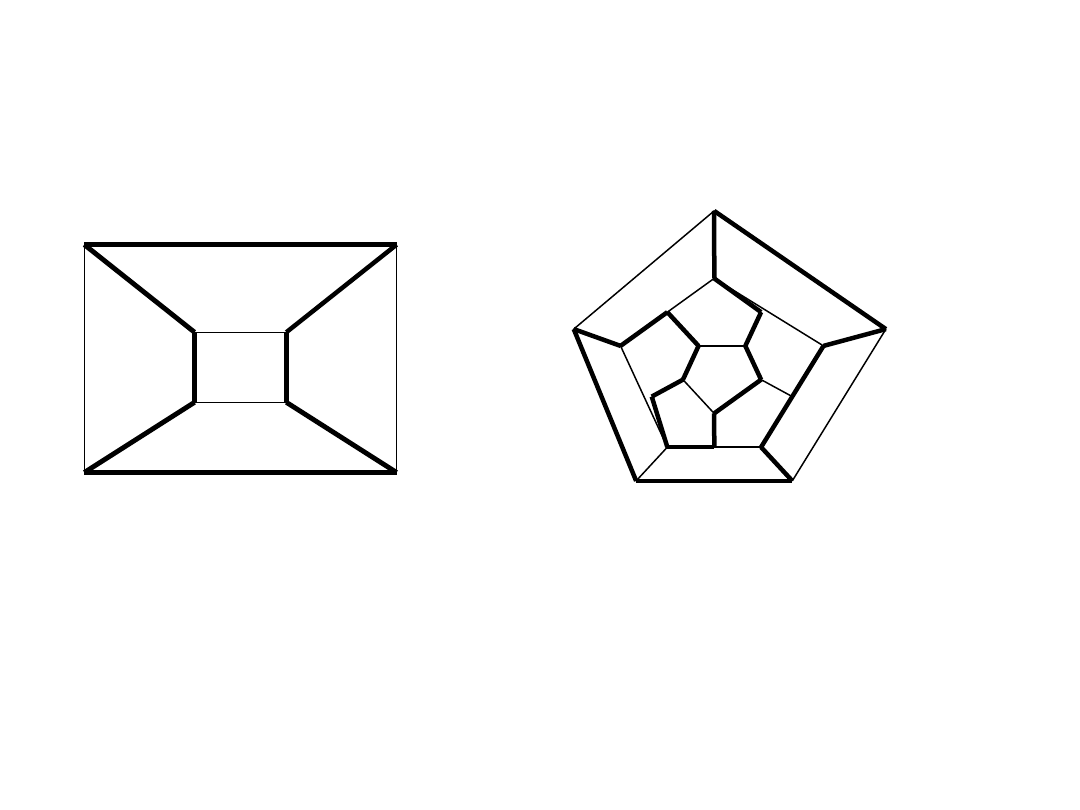
Obwód Hamiltona

(przechodzenie przez wierzchołki)

Obwodem Hamiltona w grafie spójnym jest droga zamknięta. Która

przechodzi przez każdy wierzchołek grafu G dokładnie jeden raz.

Obwód Hamiltona w grafie o n wierzchołkach składa się z n
krawędzi.

Problem komiwojażera.

Całkowita liczba różnych obwodów Hamiltona w grafie pełnym
o
n wierzchołkach: (n-1)/2!

2

Problem kolorowania

Shell

Esso

Gulf

BP

Shell

lub

Gulf

Graf jest k - kolorowalny jeżeli każdemu wierzchołkowi można przypisać

jeden z k kolorów, w taki sposób że żadne dwa wierzchołki sąsiednie nie

mają tego samego koloru.

3

Graf rozmieszczenia stacji benzynowych

Problem wyznaczania najkrótszej trasy: znaleźć taka ścieżkę, prowadzącą
od węzła i do węzła j, by suma wartości przebywanych połączeń była jak
najmniejsza. Wyznacz najkrótsza ścieżkę łączącą węzły A i J.

PRZESZUKIWANIE GRAFÓW (metoda podziału i ograniczeń)

4

A

B

G

C

D

I

J

F

E

12

15

8

11

6

5

5

7

5

3

12

10

7

9

6

4

9

10

11

12

12

13

10

12

8

10

8

6

8

5

4

6

4

10

12

10

8

D(12)

C(10)

B(15)

I(25) F(24)

F(20) E(19)

B(16)

C(20) E(22)

G(26)

A(0)

D(12)

C(10)

B(15)

I(25) F(24)

F(20) E(19)

B(16)

C(20) E(22)

G(26)

A(0)

D(12)

C(10)

B(15)

I(25) F(24)

F(20) E(19)

B(16)

C(20) E(22)

G(26)

F(25)

G(24)

B(24)

H(23)

A(0)

D(12)

C(10)

B(15)

I(25) F(24)

F(20) E(19)

B(16)

C(20) E(22)

G(26)

F(25)

G(24)

B(24)

H(23)

A(0)

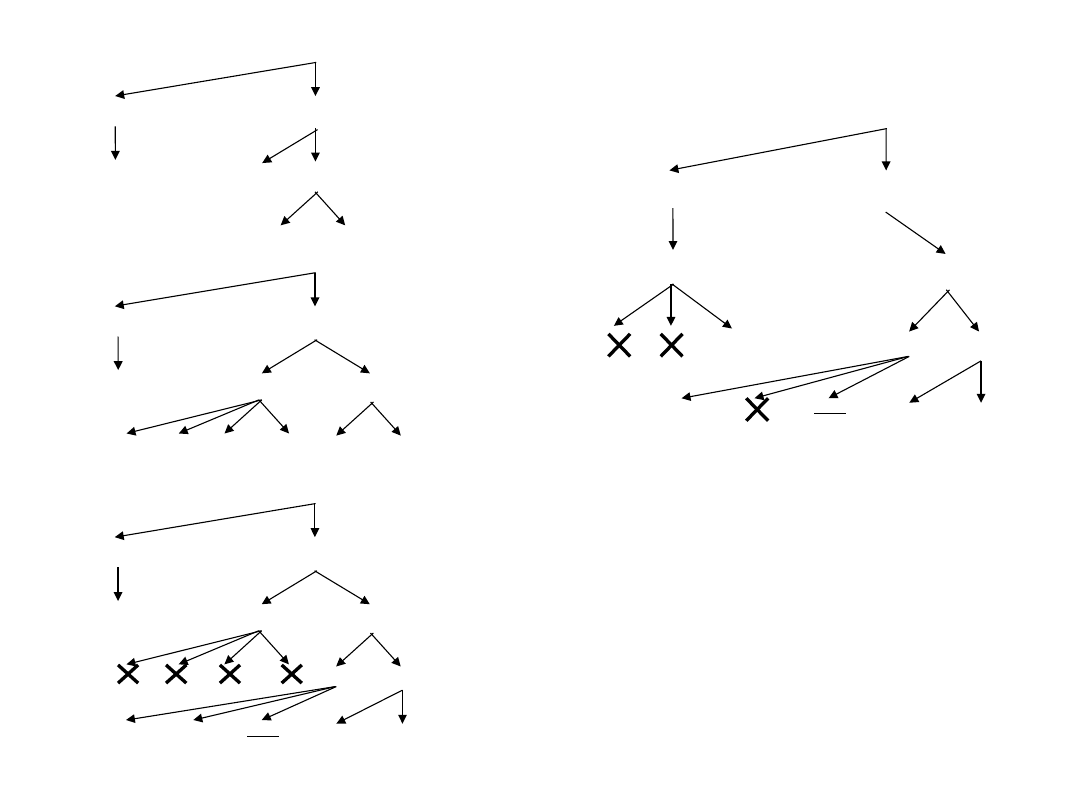
Drzew kolejnych etapów przeszukiwania

5

D(12)

C(10)

I(25)

F(20)

E(19)

G(24)

H(23)

A(0)

D(12)

C(10)

I(25)

F(20)

E(19)

G(24)

H(23)

A(0)

E(24)

H(25)

I(26)

D(30)

D(12)

C(10)

I(25)

F(20)

E(19)

G(24)

H(23)

A(0)

E(24)

H(25)

I(26)

D(30)

J(36)

J(31)

I(27)

F(31)

B(32)

D(12)

C(10)

I(25)

E(19)

G(24)

H(23)

A(0)

J(35)

H(28)

F(33)

J(36)

J(31)

I(27)

F(31)

B(32)

Drzewa kolejnych etapów przeszukiwania

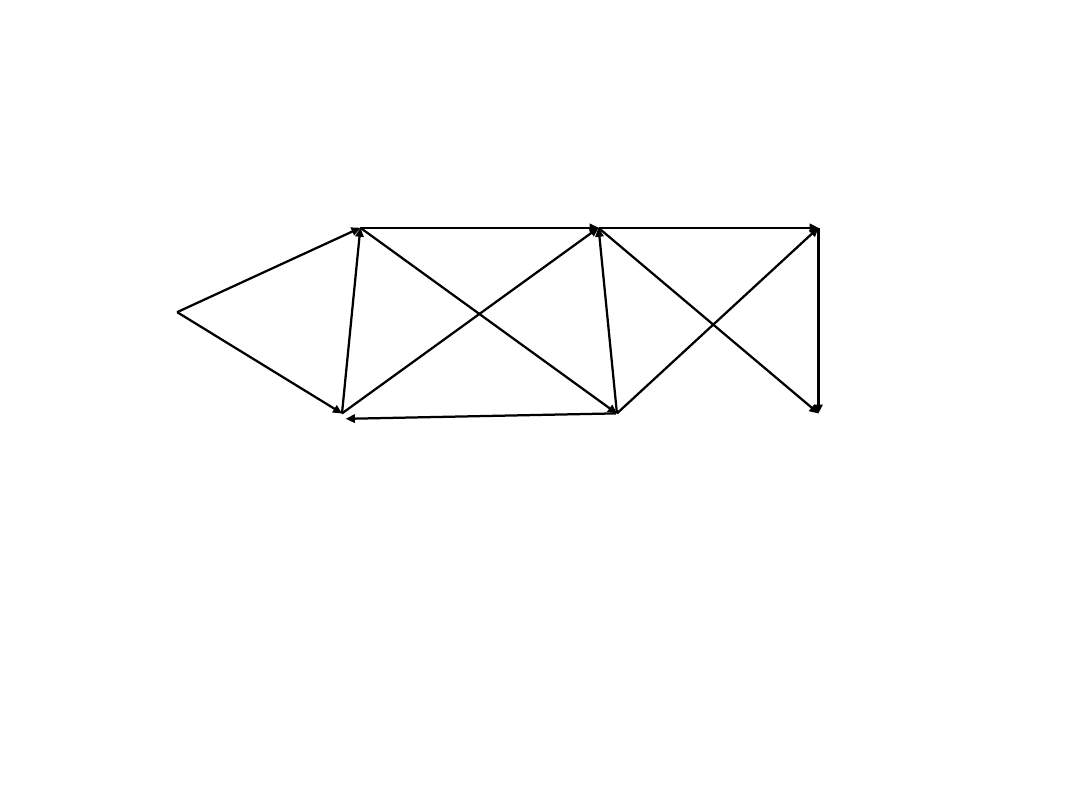
Korzystając z przedstawionej wyżej metody wyznacz:

Długość najkrótszej drogi łączącej dwa wierzchołki w danym grafie

skierowanym?

Jeśli graf skierowany ma wagi, to jaka jest waga minimalna lub

maksymalna takiej drogi?

3 7 9

v

1

2 5 4

9

1 8

v

3

4 v

5

v

7

6

ALGORYTMY NA GRAFACH

Algorytm Fleury’go

(wyznaczanie drogi Eulera)

Niech ES – ciąg krawędzi drogi lub cyklu Eulera, VS – ciąg wierzchołków

tej drogi lub cyklu. Niech V(G) – zbiór wierzchołków, a E(G) – zbiór

krawędzi grafu G

1. Wybierz dowolny wierzchołek v nieparzystego stopnia, jeśli taki

istnieje. W przeciwnym przypadku wybierz dowolny wierzchołek v. Niech

VS = v i niech ES = .

2. Jeśli z wierzchołka v nie wychodzi już żadna krawędź, zatrzymaj się.

3. Jeśli pozostała dokładnie jedna krawędź wychodząca z wierzchołka v ,

powiedzmy krawędź e z wierzchołka v do w, to usuń e z E(G) oraz

v z V(G) i przejdź do kroku 5.

4. Jeśli została więcej niż jedna krawędź wychodząca z wierzchołka v ,

wybierz krawędź, powiedzmy e z v do w , po usunięciu której graf

pozostanie spójny, następnie usuń e z E(G).

5. Dołącz w na końcu ciągu VS, dołącz e na końcu ciągu ES, zastąp v

wierzchołkiem w i przejdź do kroku 2.

7

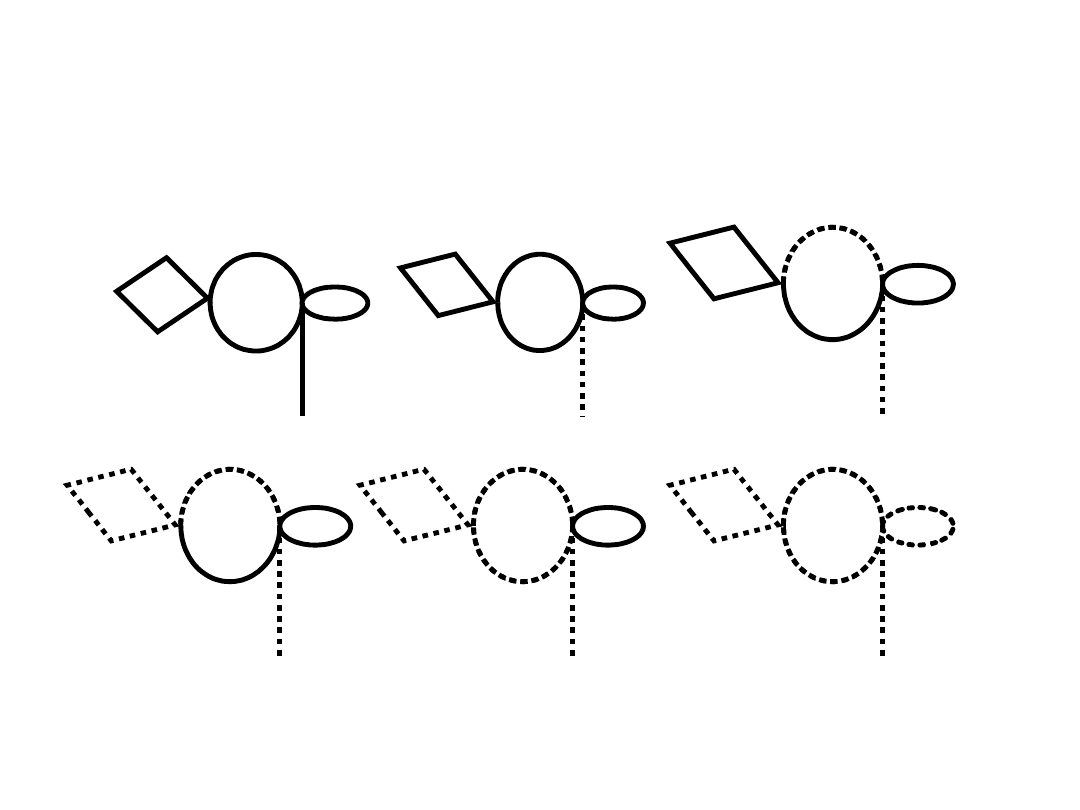
Algorytm Fleury’go

(wyznaczanie drogi Eulera)

8

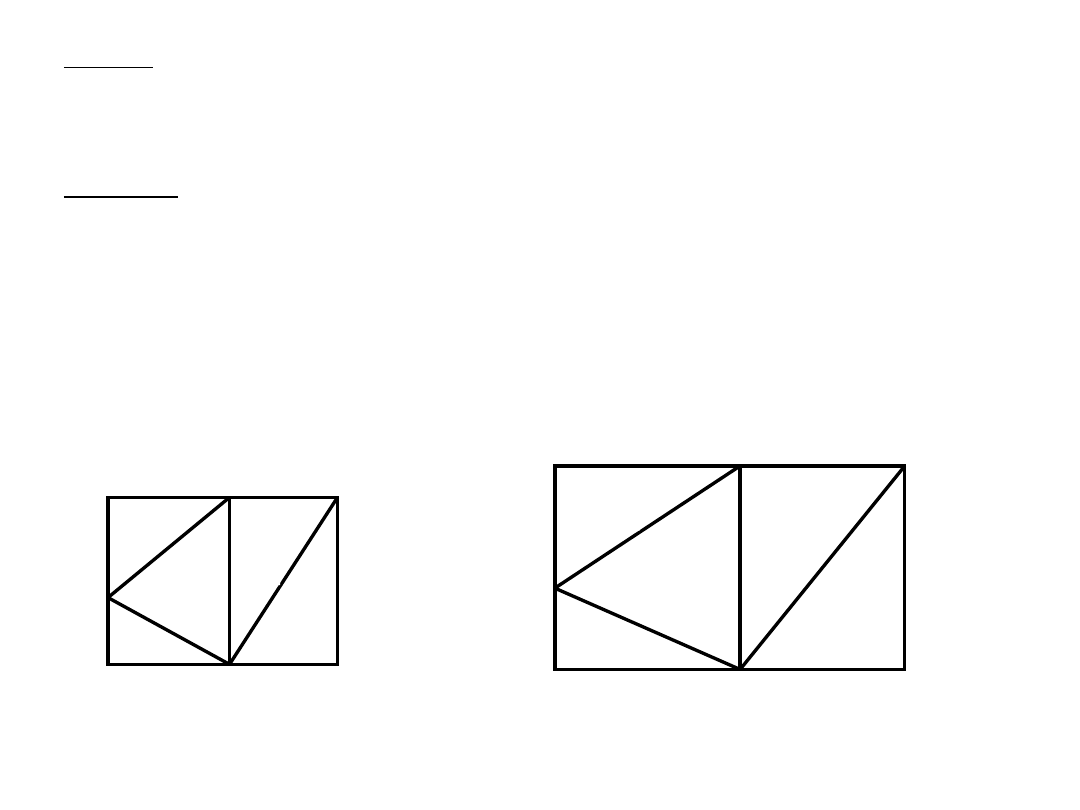
Algorytm Kruskala

(minimalne drzewo spinające)

Dane: skończony graf spójny G z wagami, którego krawędzie są

uporządkowane według

wzrastających wag.

Wyniki: zbiór E krawędzi minimalnego drzewa spinającego grafu

G

Niech E:= .

Dla j = 1 do |E(G)|

Jeśli graf E  {e

j

} jest acykliczny, to dołącz e

j

do E.

Przykład

2

5

3

3

5

5

5

3

4

1

5

2

e

8

e

9

e

7

e

8

e

4

e

5

e

6

e

2

e

1

e

10

e

3

e

11

9

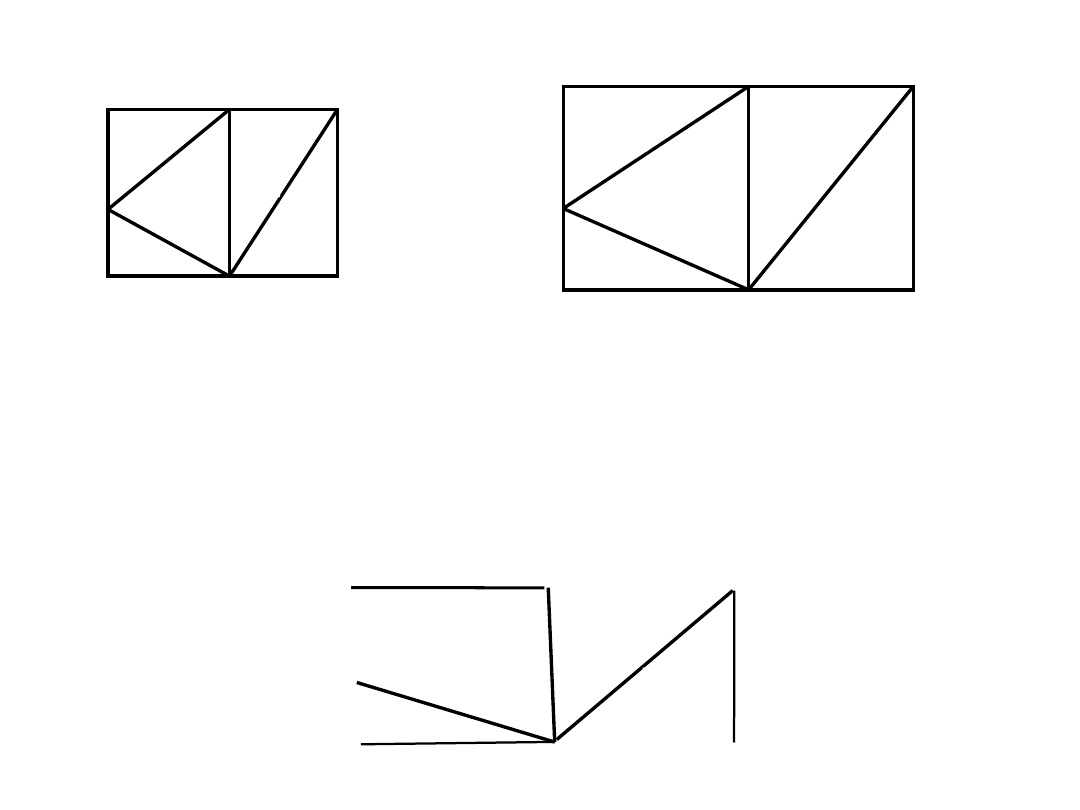
Wagi krawędzi W(e

i

) mają tworzyć ciąg niemalejący, tzn. W(e

i

) <

W(e

j

) dla i < j , zatem:

e

1

2

5

3

3

5

5

5

3

4

1

5

2

e

8

e

9

e

7

e

8

e

4

e

5

e

6

e

2

e

1

e

10

e

3

e

11

e

1

e

2

e

3

e

4

e

5

e

6

e

7

e

8

e

9

e

10

e

11

1 2 2 3 3 4 5 5 5 5 5

e

7

e

3

e

5

e

6

e

2

10

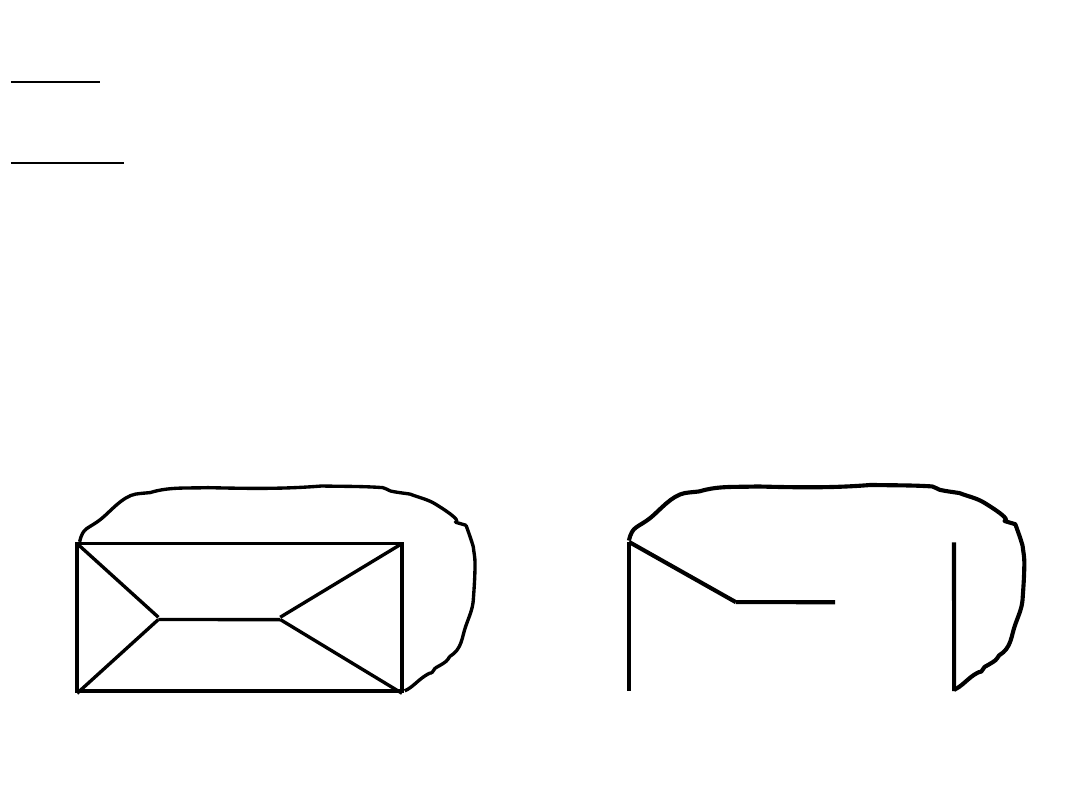
Algorytm Prima

(minimalne drzewo spinające)

Dane: skończony graf spójny G z wagami (z krawędziami wypisanymi w
dowolnym porządku)

Wyniki: zbiór E krawędzi minimalnego drzewa spinającego grafu G

Niech E:= .

Wybierz w ze zbioru V(G) i niech V := {w}

Dopóki V  V(G), wykonuj wybierz w zbiorze E(G) krawędź (u,v) o

najmniejszej możliwej wadze, taką że u  V i v  V(G) \ V dołącz krawędź

(u,v) do zbioru E i wierzchołek v do zbioru V.

2

b

3 1

d e

1

c

2

1

4

5

4

3

a

Algorytmy Prima i Kruskala są algorytmami zachłannymi, tzn.
algorytmami wybierającymi zawsze najmniejszą krawędź, która
należy dodać lub największą krawędź, którą należy odrzucić.

Przykład

11

12

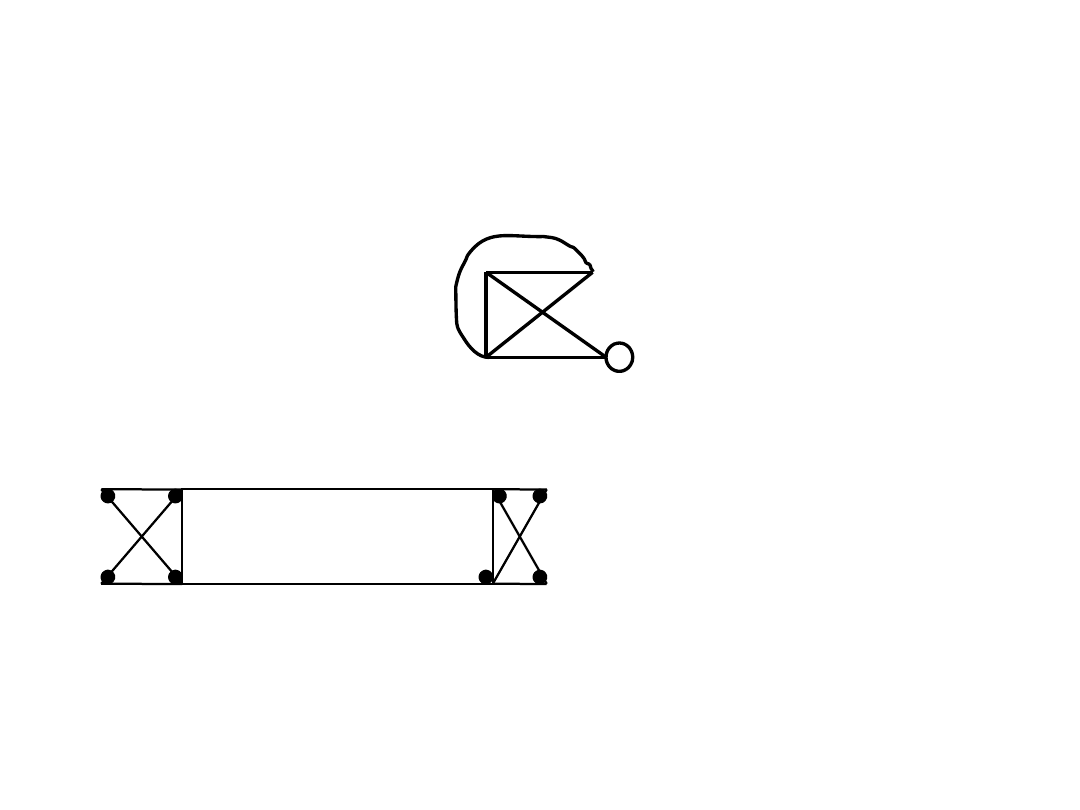
ZADANIA

1. Czy jest możliwe, aby owad poruszający się wzdłuż krawędzi sześcianu przeszedł
każdą krawędź dokładnie raz? Odpowiedź uzasadnij.

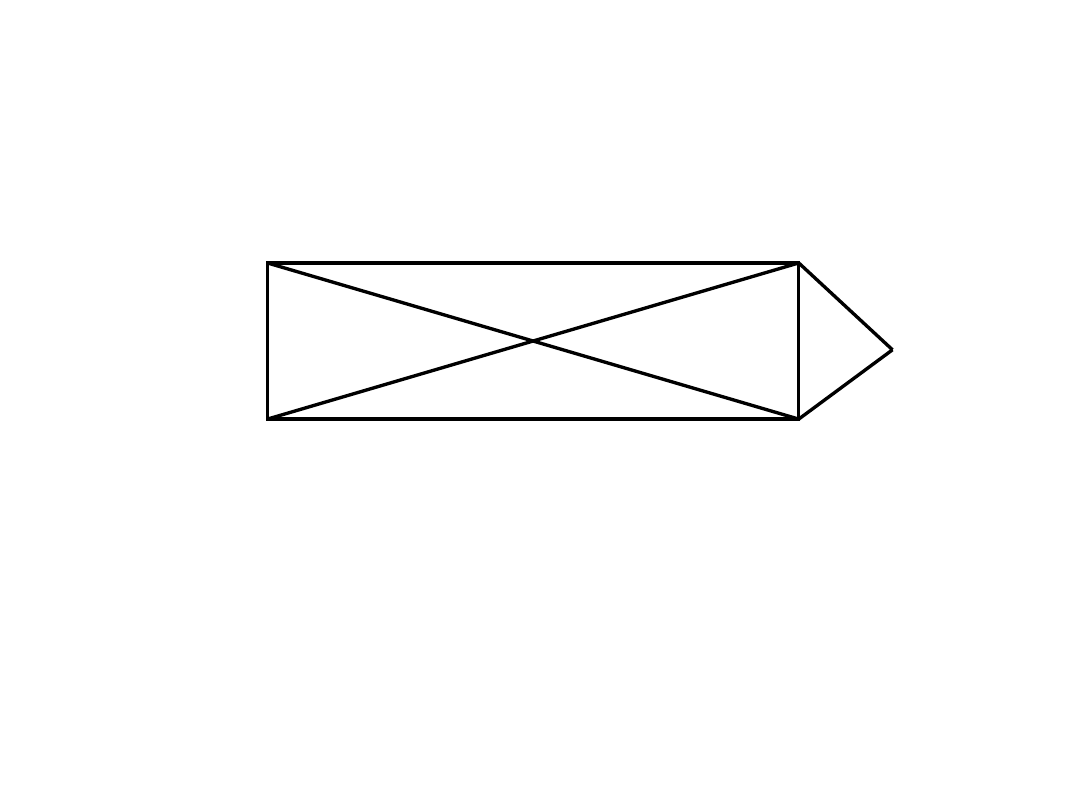
2. Zastosuj algorytm Fleury’ego aby otrzymać drogę Eulera w poniższym grafie

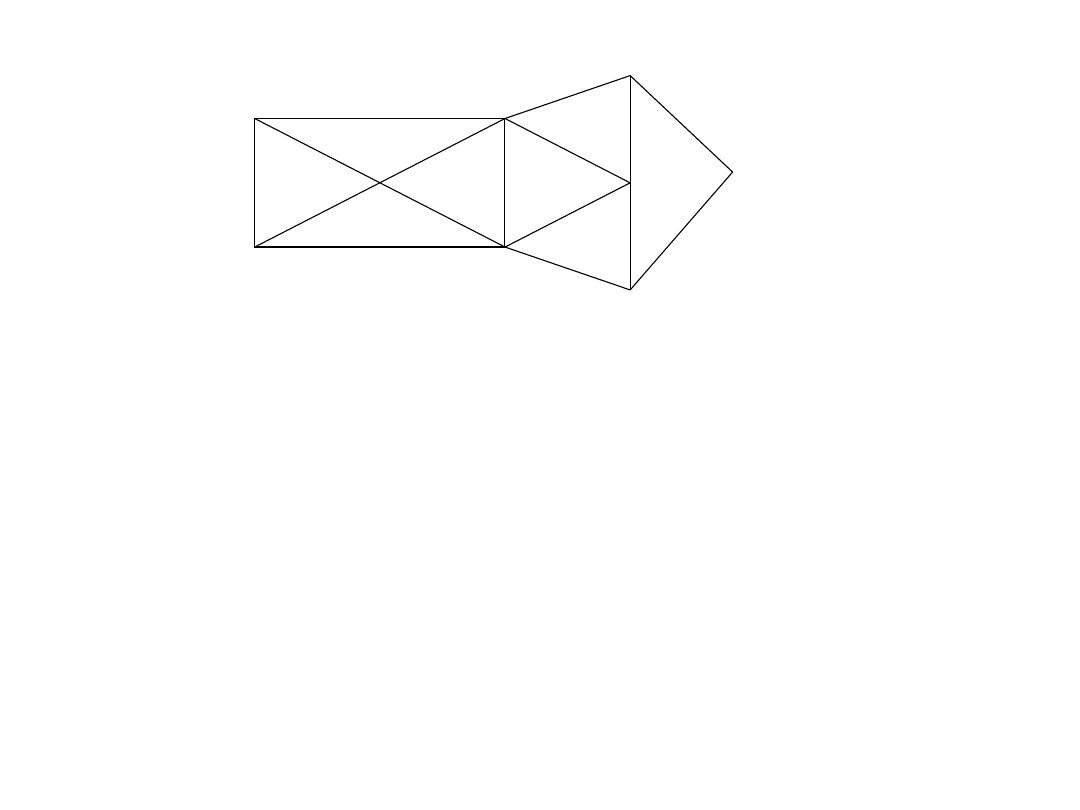
4. Wyznacz w podanym grafie cykl Eulera i cykl Hamiltona

3. Dla poniższego grafu wyznacz

5. Czy w grafie Hamiltona istnieje obwód Eulera?

13

180

240

320

270

200

280

330

240

350

220

280

90

120

300

6. Zastosuj algorytm Prima, aby znaleźć minimalne drzewo rozpinające w
poniższym grafie.

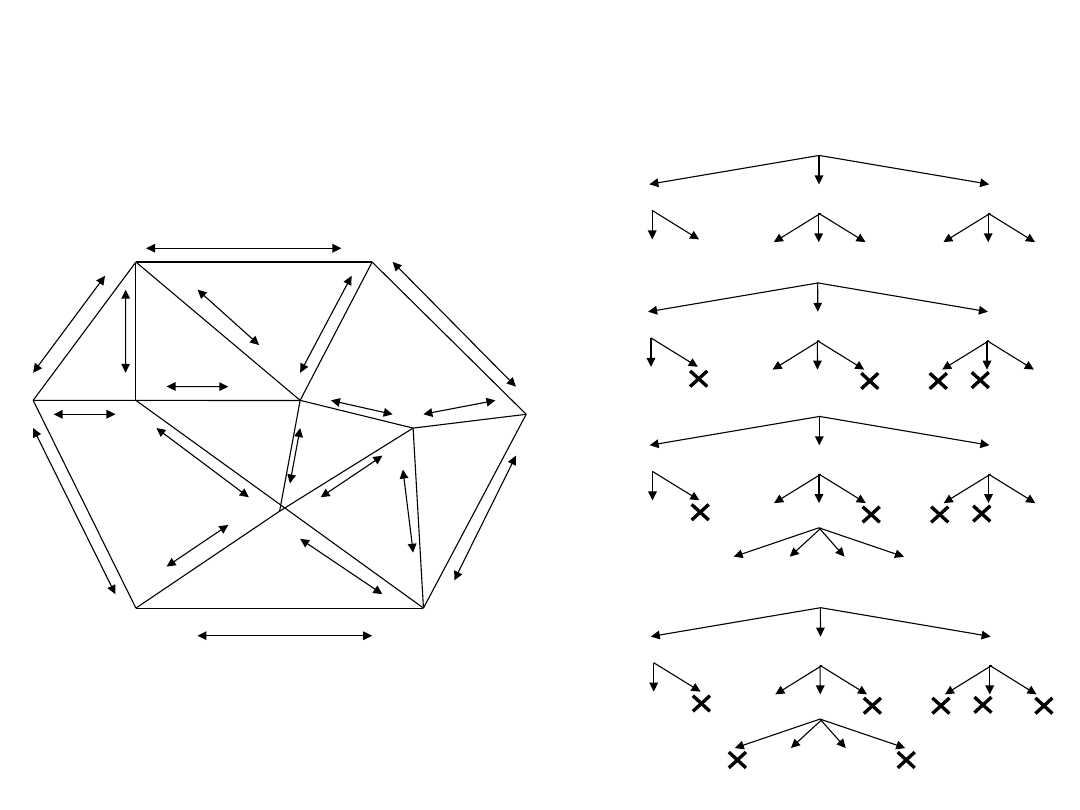
7. Danych jest n kul, z których każda waży 10 g., za wyjątkiem jednej, która
waży 9 g. lub 11 g. Za pomocą k ważeń (na wadze szalkowej) należy
rozstrzygnąć, która kula ma inną masę oraz czy jest ona lżejsza czy cięższa
od pozostałych. Wyznacz, jaką maksymalną wartość może przyjmować n przy
zadanym k jako funkcję f(k). Przedstaw algorytm ważenia dla dowolnego k i n
= f(k).

8. Rozwiąż zadanie 7) dla k = 3. Tzn. wyznacz maksymalną liczbę kul, dla
których w 3 ważeniach zawsze można rozstrzygnąć, która z kul jest inna oraz
czy jest cięższa czy lżejsza od pozostałych.

9. Rozwiąż zadanie 7) przy założeniu, że nie trzeba odpowiedzieć czy
wyjątkowa kula jest cięższa czy lżejsza, a jedynie odpowiedzieć, która z kul
jest inna.

Rozwiąż zadanie 7)przy założeniu, że wiadomo, że wyjątkowa kula jest
cięższa.