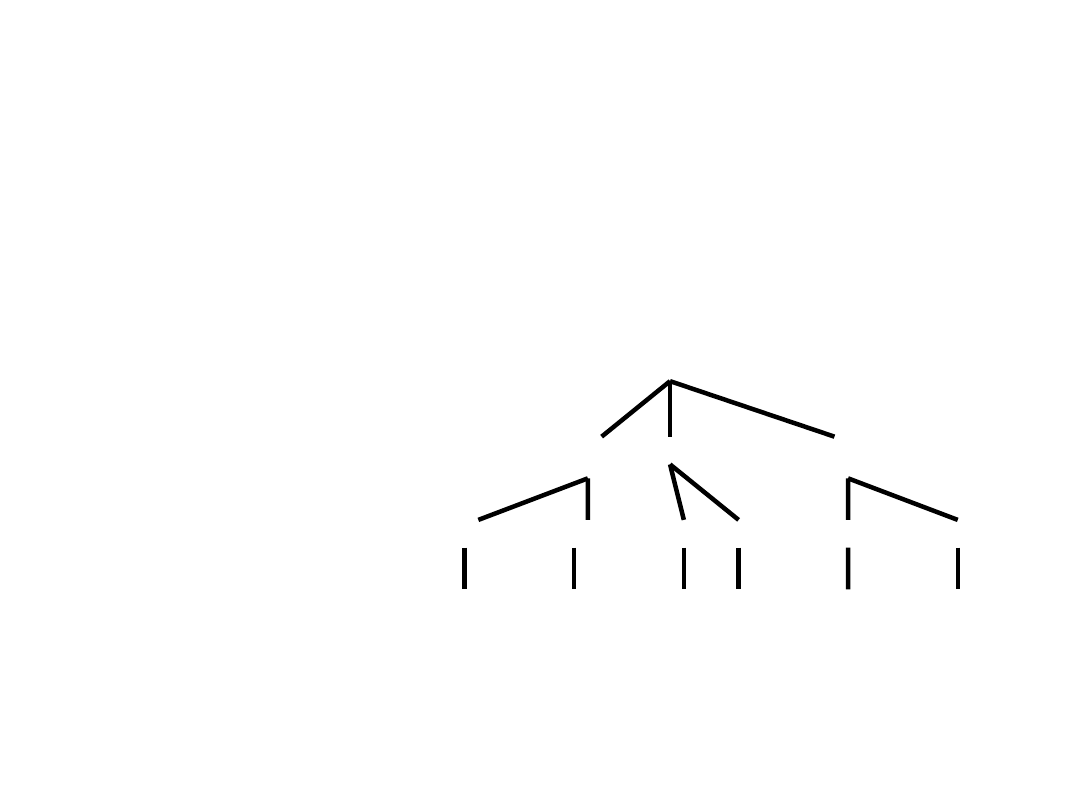
PERMUTACJE

- funkcje na zbiorze liczb naturalnych

{a

1

,a

2

, ...,a

n

}

Liczba permutacji

P

n

= n! = n (n-1) (n-2) ...1 = 1 2 3 ...n ;

0! = 1

U = {A , B , C}

A B
C

B C A C
A B

C B C A
B A

Urzędnik zapomniał hasła do swoje aktówki. Hasło jest liczbą 7 cyfrową

złożoną z cyfr od 1 do 7. Cyfry w haśle nie powtarzają się. (Ostatnie 3

cyfry wybierane są ze zbioru {3,4,7}). Ile możliwości w najgorszym

przypadku trzeba sprawdzić aby otworzyć zamek?

{3,4,7} -

(3,4,7) , (4,7,3) , (7,4,3) , (3,7,4) , (4,3,7) , (7,3,4)

1

Przykład 1

5 Elementy kombinatoryki

Permutacje, kombinacje, wariacje. Wykorzystanie w procedurach

szacowana złożoności obliczeniowej problemów decyzyjnych i/lub
optymalizacyjnych oraz rozwiązywaniu problemów z rachunku
prawdopodobieństwa.

Permutacja to n-
elementowy ciąg nie
powtarzających się
obiektów zbioru U.

WARIACJE

-bez powtórzeń
-Dany zbiór A = {a

1

,a

2

, ...,a

n

}. Wariacja – k-elementowy ciąg

nie

powtarzających się obiektów zbioru A.

Liczba k-elementowych wariacji zbioru A, n = |A| .

V

n

k

= n (n-1) (n-2) ... (n – k+1))

n!

n (n-1) (n-2)*...*(n-k+1) (n- k)*(n-k-1)*…*2*1

V

n

k

=

= * *

*

(n-k)!

(n-k) (n-k-1) ...2 1

= n(n-1)...(n-k+1)

A = {a,b,c} ; k = 2 ; (a,b) , (a,c) , (b,c) , (b,a) , (c,a) ,
(c,b)

W urnie jest 10 kul ponumerowanych od 1 do 10. Losujemy kolejno i bez

zwrotu 5 kul. Po każdym losowaniu zapisujemy jej numer. Ile jest

wszystkich możliwych wyników losowania?

V

n

k

= n (n-1) (n-2) ... (n – (k-1)) ; V

10

5

= 10 9 8 7 6

2

Przykład 2

WARIACJE ciag dalszy

-z powtórzeniami
Rzucamy 10 razy monetą. Ile jest możliwych wyników

tego

doświadczenia?

Liczba k- elementowych wariacji z powtórzeniami

W

n

k

= n*n*n*n*...*n = n

k

k

{O,R} , {O,R},..., {O,R} ;

2

n

Na ile sposobów można rozmieścić 2 kule (czarną i białą) w 3
szufladach?

I

II

III

0

b

c

0

c

b

0

c-b 0

0

0

c-b

b

c

0

c

b

0

c-b 0

0

b

0

c

c

0

b

3

Przykład 3

KOMBINACJE

Dany zbiór A = {a

1

,a

2

, ...,a

n

}.

Kombinacja – k-elementowy podzbiór zbioru A.

Liczba k-elementowych kombinacji ze zbioru A, n = |

A| .

3 3!

=

= 3 , {3,2,1} , k = 2 ; (1,2) , (1,3) ,

(2,3)
2

2! 1!

Łatwo zauważyć, że:

4





!

!

!

k

n

k

n

k

n

C

k

n



















k

n

k

n

C

k

k

n

n

V

!

)!

-

(

!





5





































13

26

*

13

39

*

13

52







































!

3

*

2

5

*

3

8

*

2

10

!

3

*

!

3

!

2

!

5

*

!

5

!

3

!

8

*

!

8

!

2

!

10

!

2

!

3

!

2

!

10



Przykład 3

Na ile sposobów można 52 karty rozdać pomiędzy 4 graczy tak aby każdy z nich dostał
13 kart.

Ile słów można utworzyć ze słowa MATEMATYKA przestawiając litery? Słowo
oznacza dowolny skończony ciąg liter.

Na ile sposobów można wybrać 8 kart z talii 24 kart jeżeli kolejność nie
jest ważna?

Ile z tych układów 8- kartowych zawiera 2 asy?

Na ile sposobów można rozmieścić

6

osób w

3

różnych pokojach

2

osobowych?

C

6

2

C

4

2

C

2

2

C

20

6

C

4

2

C

20

8

c)

n

n

=

1

n - 1

Własności kombinacji

a)

n

n

=

k

n - k

b)

n

n

=

0

n

 

 

0

1

1

2

1

0















































































n

n

k

n

n

n

n

n

k





 





0

1

1







n

Przykład 4

Udowodnij, że

Korzystając ze wzoru Newtona dla a = 1, b =--1 , to

7

Przykład 5

Wykaż, że

n

n

=

k

n-k

n! = n!

(n-k)!k! (n-(n-k))! (n-k)!

n! = n!

(n-k)!k! (n-n+k)! (n-k)!

n! = n!

(n-k)!k! (k)! (n-k)!

Dwumian Newton’a

n

n

n

n

(a + b)

n

=

a

n

+ a

n-1

b + ... + a b

n-1

+ b

n

0

1

n-1

n

8

Od dwumianu Newtona do trójkąta Pascal’a

(a+b)

0

= 1

1

(a+b)

1

= a + b

1 1

(a+b)

2

= a

2

+ 2ab + b

2

1 2 1

(a+b)

3

= a

3

+ 3a

2

b +3ab

2

+ b

3

1 3 3

1

. . . . . . . . . . . . . . . . . . . . . . . . . . .. .

. . . . . . . . . . . . . . . . . . .

. . . . . . . .. .

n

n

(a +b)

n

=



a

n-i

b

i

i=0

i

n n

,

 =

2

n

i=0 i

a = b =
1

n

n

n

n n

2

n

=

+ + ... + +

= (a + b)

0

1

n-1

n

,

9

ZADANIA

1.Dany jest zbiór 20-cio elementowy. Ile sekwencji 4-o elementowych (nie
zawierających
tych samych liczb) można utworzyć z elementów tego zbioru? Ile
podzbiorów 5-o
elementowych można utworzyć z elementów tego zbioru?

2. Ile różnych sekwencji można wyrzucić rzucając kostką 6 razy po rząd?

3. Dany jest zbiór {a,b,c,d}. Wypisz wszystkie sekwencje odpowiadające:
V

3

4

oraz

wszystkie podzbiory odpowiadające C

2

4

.

5. Czy zależność ta jest prawdziwa

n

n

+

= 2

1

n-1

4 4
4. Oblicz:  =
i =0 i

10

6. Ile różnych liczb cztero cyfrowych można ułożyć z czterech
klocków ponumerowanych 6, 7, 8, 9?

7. Rozważmy 15 osobową grupę studencką. Na ile sposobów
możemy z tej grupy wybrać trzy osoby na wycieczkę?

8. Ile liczb 3-cyfrowych można ułożyć używając cyfr ze zbiory {1,
2, 3, 4, 5}?

9. Zosia ma 5 spódnic, 7 bluzek i 3 kapelusze. Na ile sposobów
może skompletować swój strój?

10. Wykaż, że:

n +1

n n

=

+

k

k-1 k