1

4.

Zliczanie zbiorów i funkcji

Funkcje całkowitoliczbowe: powała i podłoga. Zasada gołębnika.
Zasada
włączania

i

wyłączania.

Asymptotyka

funkcji

liczbowych.

Wykorzystanie przy szacowaniu złożoności obliczeniowej problemów
decyzyjnych i/lub optymalizacyjnych.

FUNKCJE CAŁKOWITOLICZBOWE
Liczby całkowite są duszą matematyki dyskretnej. Często jesteśmy
zmuszeni przekształcać liczby wymierne lub rzeczywiste na całkowite.
Jednymi z takich przekształceń są funkcje całkowitoliczbowe:
podłoga i sufit (powała).

f : R  Z

Przykłady funkcji całkowitoliczbowych:
Należą do nich wcześniej omawiane NWD(m,n) = k czy NWW(m,n) = d
będące dwuargumentowymi funkcjami całkowitoliczbowymi F(m,n)
określonymi na na zbiorze liczb naturalnych, podobnie jak (n) = n!, a także
operatory dwuargumentowe MOD(m,n) i DOV(m.n) określone na zbiorze liczb
całkowitych.
Czy też typu:

A dla x  13

(x) = B dla 13 < x < 15 gdzie: xR ; A,B,CZ

C dla x  15

Żeby nie wspomnieć o ciągach, np. (n) = 2n, nN

2

FUNKCJE CAŁKOWITOLICZBOWE
Liczby całkowite są duszą matematyki dyskretnej. Często jesteśmy
zmuszeni przekształcać liczby wymierne lub rzeczywiste na całkowite.
Jednymi z takich przekształceń są funkcje całkowitoliczbowe:
podłoga i sufit (powała).

f : R 
Z

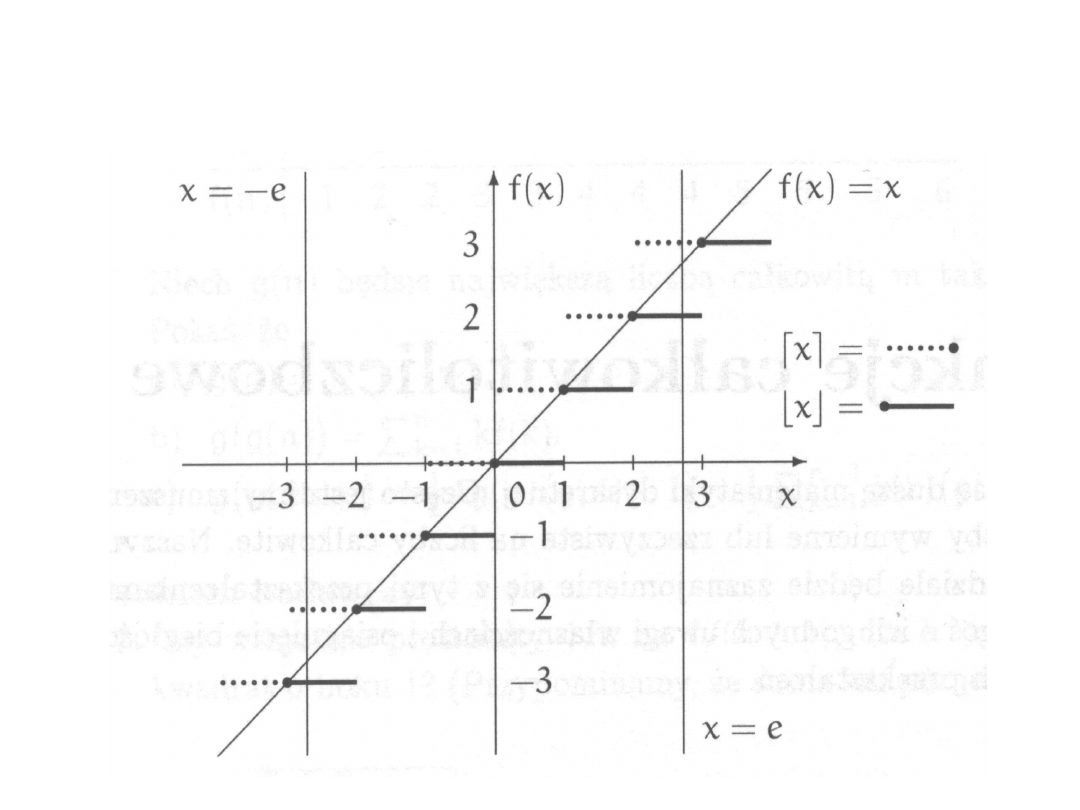
Funkcje całkowitoliczbowe

Podłoga   - dolne zaokrąglenie całkowitoliczbowe

xR

, x = max{nC : n x}

 = 3 ;

- = -4

Powała   - górne zaokrąglenie całkowitoliczbowe

xR

, x = min{nC : n x}

 = 4 ;

- = -3

-

-





0

-3

-4

-

3

4



3

2 = 2 ; -3.5 = -
4

1 x = x  x = x  xC

;

x  x 

x

2 x - x = 1  xR

3 - x = - x

;

x = - - x

4 x = n  n  x < n+1

5 x = n  x – 1 < n  x

6 x = n  n – 1 < x  n

7 x = n  x  n < x+1

4

 

2

e 

 

3

e







;

 

3

e 

 

2

e







;

-3.5  = - 3 ; 1.7 = 2

Własności funkcji podłoga i powała

Przykład 1

5

Przykład 2
Jaką największa liczbę można zapisać na n bitach? Liczba taka
ma wszystkie bity równe 1 w swoim rozwinięciu binarnym (111...1),
więc jej wartość jest równa 2

n-1

+2

n-2

+...+2

1

+2

0

=2

n

-1. Tę równość

można uzasadnić obliczając sumę

1

2

1

2







n

S

Ile bitów zajmuje napisanie liczby naturalnej  w postaci
binarnej?

ciągu geometrycznego o ilorazie q = 2 i a

1

=

1, tzn.





 1

2

n

1

2

n







2

log





1

log

2







n

Aby była to najmniejsza liczba bitów korzystamy z funkcji sufit,
czyli

Stąd

/









1

log

2







n

A inaczej mówiąc: Ile potrzeba zarezerwować bitów pamięci
dla zapisania liczby nN w komputerze?

Zauważmy, że:

W systemie dziesiętnym mamy (2002)

10

= 2 10

3

+ 0 10

2

+ 0

10

1

+ 2 10

0

I podobnie w dwójkowym (101001)

2

= 1 2

5

+ 0 2

4

+ 1 2

3

+ 0 2

2

+ 0 2

1

+ 1 2

0

32 8

1

2

5

= 32  41 < 64 = 2

6

; dla liczby n=41 w obu systemach (41)

10

~ (101001)

2

Zatem liczba n zapisana na m bitach spełnia nierówność

2

m-1

 n < 2

m

2

m-1

 n < 2

m

/ log

2

x = n  n  x < n+1

m-1  log

2

n < m

log

2

n = m-1 a zatemm = log

2

n +1

Przykład

n = 7 ;

log

2

7 = 2 (bo 2

2

= 4 a 2

3

= 8 ) zatem m = 2

+ 1 = 3

Właściwość: 3 x = n  n  x <n+1

m-1  log

2

n < m

6

Zasada Gołębnika

(Zasada szufladkowa DIRICHLET’A

)

Niech:

m obiektów oraz n pudełek

jeżeli n < m, to przynajmniej dwa obiekty są w jednym

pudełku

Niech |A| - moc zbioru A ; np. A = {a,b,c,d,e} ; |A| = 5

Jeżeli skończony zbiór S jest podzielony na k zbiorów, to

co najmniej jeden z tych zbiorów ma |S|/k lub więcej

elementów.
Przykład zastosowania:

W każdej grupie n osób są przynajmniej 2 osoby, które
znają tę samą liczbę osób.

7

Dany jest zbiór A = {a

1

, a

2

,...,a

9

} taki, że suma jego

elementów = 90.

Wykaż, że w obu przypadkach istnieją rozwiązania.

a)  trzy takie elementy zbioru A, że ich suma  30.

b)  cztery takie elementy zbioru A, że ich suma  40.

(a

1

+ a

2

+ a

3

) + (a

4

+ a

5

+ a

6

) + (a

7

+ a

8

+ a

9

) =

90

 < 30

 < 30

 > 30

 < 30

 = 30

 > 30

b

)

a

1

a

2

a

3

a

4

a

5

a

6

a

7

a

8

a

9

a

2

a

3

a

4

a

5

a

6

a

7

a

8

a

9

a

1

a

3

a

4

a

5

a

6

a

7

a

8

a

9

a

1

a

2

a

4

a

5

a

6

a

7

a

8

a

9

a

1

a

2

a

3

4 x 90 = 360 zatem 360/9 = 40

a

1

+ a

2

+ a

3

+ a

4

lub a

2

+ a

3

+ a

4

+ a

5

lub

.......  40

8

Przykład 3

a

)

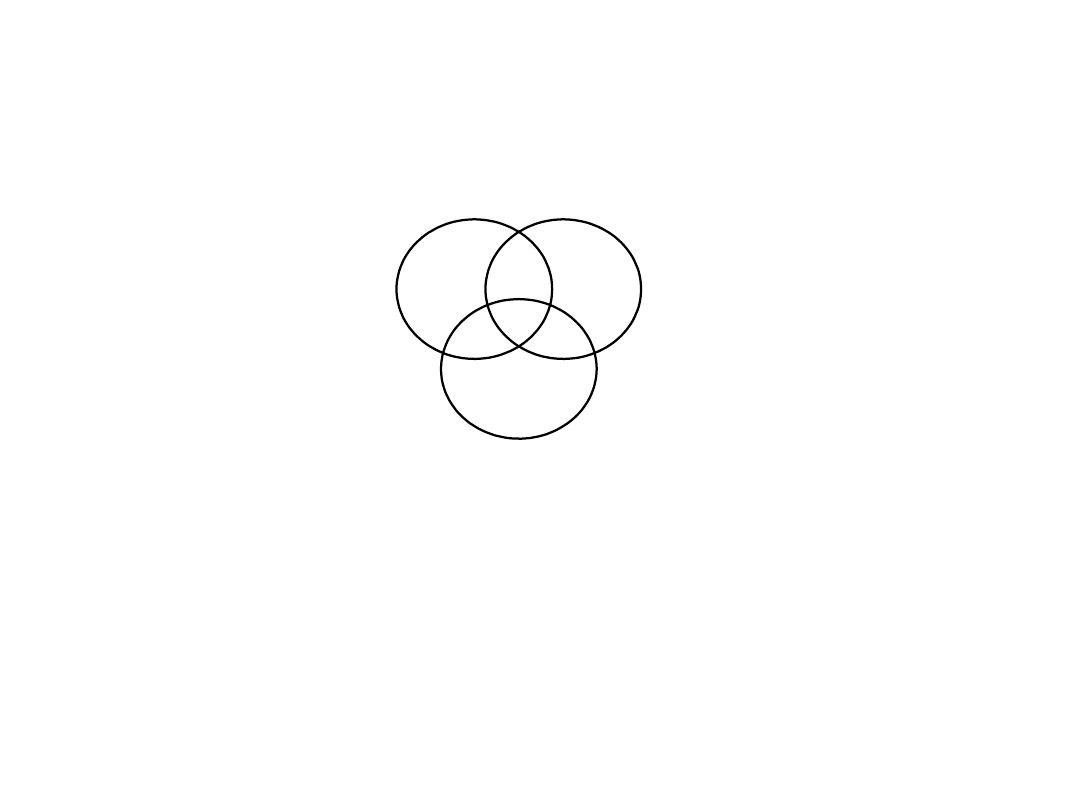
Zasada włączania i wyłączania

Należy „włączyć” (dodać do siebie liczności poszczególnych
zbiorów), następnie „wyłączyć” (odjąć liczność przecięć po
dwa zbiory), potem „włączyć” (dodać liczności wszystkich
przecięć po trzy zbiory), itd.

| A  B  C | = |A| + |B| + |C| - |A  B| - |A  C| - |B  C| + |A
 B  B|

Przykład

A = {a,b};

B = {1,2}

;

C = {x,y}

|A  B  C | = 6 = 2 + 2 + 2 – 0 – 0 – 0 + 0 = 6

A

B

C

9

Ilustracja

Ile liczb naturalnych ze zbioru S = {1,2,3,...,1000} dzieli się

przez 3 lub

5 lub przez obie te liczby jednocześnie?

Niech D

3

= {nS : n dzieli się przez 3}

D

5

= {nS : n dzieli się przez 5}

D

3



D

5

= {nS : n dzieli się przez 15}

D

3

= {3mS : 1 m  333}

| D

3

| =  1000/3  = 333

D

5

= {5mS : 1 m  200}

| D

5

| =  1000/5  = 200

| D

3



D

5

| =  1000/15  = 66

Zatem

| D

3

 D

5

| = | D

3

| + | D

5

| - | D

3



D

5

| = 333 + 200 – 66 = 467

10

Przykład zastosowania

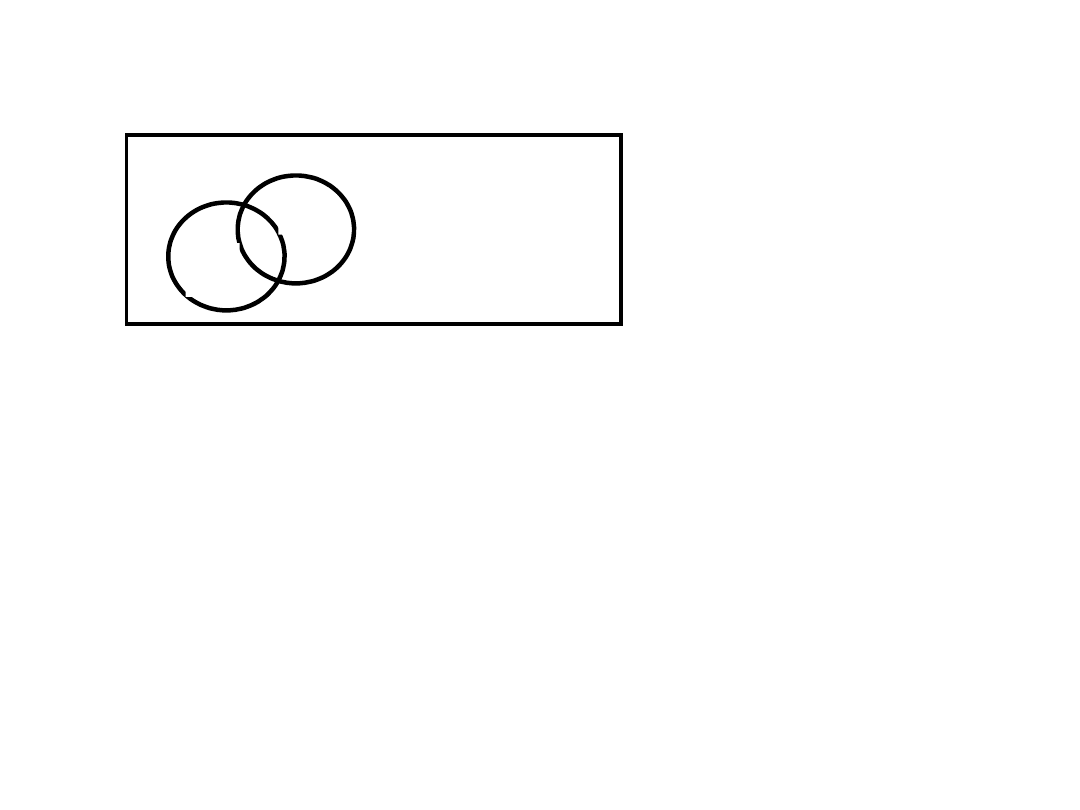
Przykład zastosowania - raz jeszcze

Ile jest liczb między 1 a 999 niepodzielnych, ani przez 5,

ani przez 7?

/7

/5

1, 2, ... ,
999

999 - „/5” - „/7” + „/5 7” = 999 -  999/5  -  999/7
 +  999/(5*7) =

= 999 -  999/5  -  999/7  +  999/35 = 999 - 199
- 142 + 28 = 686

11

A dokładniej:

999 -  999/5  -  999/7  + 999/NWW(3,5)

lub też

999 – DIV(999,5) – DIV(999,7) + DIV(999,NWW(3,5))

12

W zależności od asymptotycznego tempa wzrostu, funkcje dzieli się na rzędy
złożoności obliczeniowej. Najczęściej wyróżnia się:

stała
logarytmiczna
liniowa
liniowo-logarytmiczna (lub

quasi-liniowa)
kwadratowa
wielomianowa
wykładnicza

Najczęstszym zastosowaniem asymptotycznego tempa wzrostu jest
szacowanie złożoność problemów obliczeniowych, w szczególności
algorytmów.
Oszacowanie rzędów złożoności obliczeniowej funkcji pozwala na
porównywanie ilości zasobów (np. czasu, pamięci), jakich wymagają
do rozwiązania problemu opisanego określoną ilością danych
wejściowych.

W dużym uproszczeniu można powiedzieć, że im niższy rząd
złożoności obliczeniowej algorytmu, tym będzie on wydajniejszy przy
coraz większym rozmiarze problemu (np. ilości danych do algorytmu).

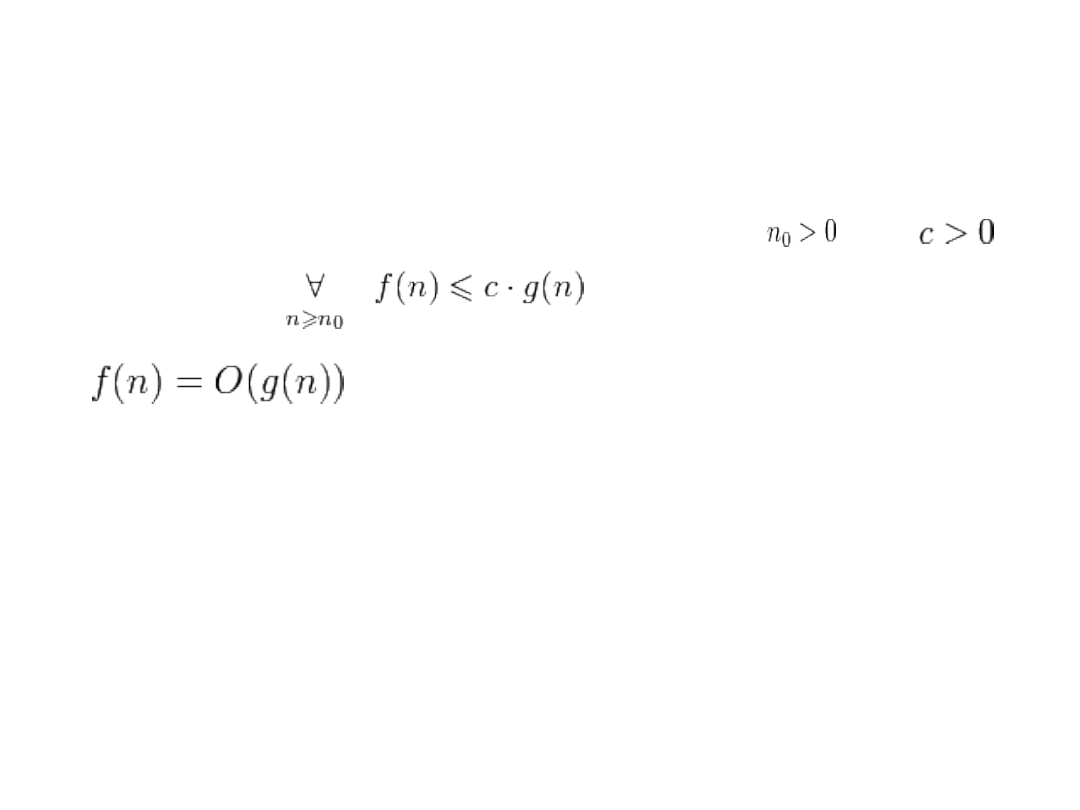
13

Asymptotyczne tempo wzrostu jest miarą określającą zachowanie
wartości funkcji wraz ze wzrostem jej argumentów. Stosowane jest w teorii
obliczeń, w celu opisu złożoności obliczeniowej, czyli zależności ilości
potrzebnych zasobów (np. czasu i) od rozmiaru danych wejściowych
algorytmu. Asymptotyczne tempo wzrostu opisuje jak szybko dana funkcja
rośnie lub maleje, abstrahując od konkretnej postaci tych zmian.
 

Notacja "duże O"
Mówimy, że f jest co najwyżej rzędu g, gdy istnieją takie stałe , oraz

,
że:

Zapis:

Określenia "złożoność co najwyżej O(f(n))" i "złożoność O(f(n))" są
matematycznie równoważne

.

Oznacza to, że funkcje O(n), O(n

c

) , O(c

n

) , O(n!) są funkcjami

asymptotycznie zdominowanymi przez funkcje: F(n) = n, F(n) = n

c

, F(n) =

c

n

, F(n) = n!

Problemy o złożoności obliczeniowej O(c

n

) i O(n!) zaliczane są do klasy

problemów trudnych, a problemy charakteryzujące się złożonością O(n

c

)

zaliczane
są do klasy problemów łatwych.

14

2

)

1

( 

n

n

Przykład ilustrujący szacowanie złożoności obliczeniowej
algorytmu bąbelkowego

Wykaż, że 1 + 2 + 3 + ...+ n =

to dla n = k + 1

1 + 2 + 3 + ...+ k + (k + 1) =

Dowód indukcyjny:

1

o

n=1 wówczas

1 =

2

1)

1(1

2

)

1

( 

k

k

2

)

2

)(

1

(



 k

k

2

)

1

( 

k

k

2

)

2

)(

1

(



 k

k

2

o

n=k wówczas 1 + 2 + 3

+ ...+ k =

(teza indukcyjna)
stąd

+ (k+1)

=

cnd.

(założenie indukcyjne)

15

Problem sortowania

Dany jest zbiór: {7,5,6,1,3,4,2,9,8,10}. Zbiór ten należy uporządkować
(posortować)

od

najmniejszego

do

największego

elementu,

tzn.

{1,2,3,4,5,6,7,8,9, 0}. Ile, w najgorszym przypadku, należy dokonać
elementarnych porównań i przestawień elementów zbioru, aby go
uporządkować? Wg. algorytmu „bąbelkowego” (patrz poniższy przykład)
liczba ta nie przekracza

2

2

2

n

n



Złożoności obliczeniową tego problemu określa funkcja O(n

2

).

Algorytm bąbelkowy
Ciąg wejściowy (4,2,5,1,7) należy posortować od najmniejszego do
największego elementu. Porównywanie parami kolejnych elementów ciągu
powoduje „wypłynięcie największego bąbelka". Liczba porównań w każdy
wierszu jest o jeden mniejsza od ilości elementów wymagających
posortowania – w rozważanym przypadku liczby te składają się na sumę 4 +
3 + 2 + 1. Oznacza to, ze dla posortowania ciagu n elementowego potrzeba
1 + 2 +…+ n-1 operacji.

gdzie n – liczność porządkowanego zbioru

16

Problem plecakowy

Dany jest zbiór A = {a

i

: i = 1, ..., n} różnych typów towarów. Każda

jednostka danego typu towaru ma tę sama objętość g

i

(wagę w

i

) oraz cenę c

i

.

Dysponujemy plecakiem o pojemności G (możemy udźwignąć W). Ile, jakich

towarów należy załadować do plecaka aby wyjść z maksymalnym zyskiem?

Przyjmując, że jednostek każdego towaru jest ta sama ilość m, liczba

wszystkich wariantów nie przekracza m

n

. Złożoności obliczeniową tego

problemu określa funkcja O(m

n

).

Problem komiwojażera

Komiwojażer, każdego dnia odwiedza n – miast. Dane są odległości d

i,j

pomiędzy każdą para miast i i j. Startując z wybranego miasta, należy

powrócić do niego przejeżdżając przez każde z pozostałych miast tylko jeden

raz. Która z tras jest najkrótsza? Liczba wszystkich tras, które trzeba

sprawdzić nie przekracza (n-1)! Złożoności obliczeniową tego problemu

określa funkcja O(n!).

Niech funkcja g(n) asymptotycznie dominuje nad funkcją f(n) wtedy i tylko

wtedy gdy k  0 n  k : |f(n)|  |g(n)|.

17

3. Uporządkuj podane funkcje w porządku rosnącego tempa wzrostu:

• x + logx + x

2

• (0,5)

x

+ x/logx

• 2002logx + x

• xlogx + log

4

x

• 2002x

1/2

Zadania

1. Uporządkuj następujące funkcje tak, aby każda poprzednia funkcja była
funkcją wolniej rosnącą niż funkcja po niej następująca (wszystkie logarytmy
są przy takiej samej podstawie 2): log n , (log n)

n

,

n

log n

, log(n

n

) , 2

log n

, n

, n

3

, (1 + 1/n)

n

2. Wykaż, że 2

n

< 10n! < 6n

n

, dla n >2

4. Dany jest zbiór {1,2,3,…,500}. Ile w tym zbiorze jest liczb podzielnych
przez 4 lub 6
i niepodzielnych przez 7.

5. Dany jest zbiór {1,2,3,…,400}. Ile w tym zbiorze jest liczb podzielnych
przez 4 lub 5
i niepodzielnych przez 6.

6. Podaj dziedzinę D do której muszą należeć x i y aby poniższa zależność
była
prawdziwa:  x + y  x + y

7. Podaj dziedzinę D do której muszą należeć x i y aby poniższa zależność
była
prawdziwa: x + y = x + y

18

8.Podaj przykład, że równość nx = n x, gdzie n jest liczbą naturalna,
nie
zawsze jest spełniona.

9. Wykaż, że - x = - x ; - x = - - x ;

x + y = x + y

10. Stosując zasadę gołębnika uzasadnij, że wśród dowolnych 5 punktów, umieszczonych
w polu trójkąta równobocznego o boku 1, zawsze można znaleźć 2 punkty, które są
oddalone od siebie o nie więcej niż ½.

11. Potrafisz bez większego problemu porządkować trzy dowolne liczny,
wykonując
trzy porównania. Podaj algorytm porządkowania dowolnych czterech
liczb, w
którym jest wykonywanych nie więcej niż pięć porównań.

12. Wykaż, że każdy wielościan wypukły zawiera dwie ściany o tej samej
liczbie
krawędzi.

13. Wykaż, że wśród dowolnych trzech liczb całkowitych muszą być dwie
takie, których
suma jest parzysta.