8. Elementy teorii grafów (Relacje i ich reprezentacje)

Klasyfikacja, reprezentacja, modele. Macierzowe reprezentacje grafów:
macierz incydencji, macierz stowarzyszona. Wykorzystanie do
modelowania dziedzin problemów decyzyjnych i/lub optymalizacyjnych

Przykład

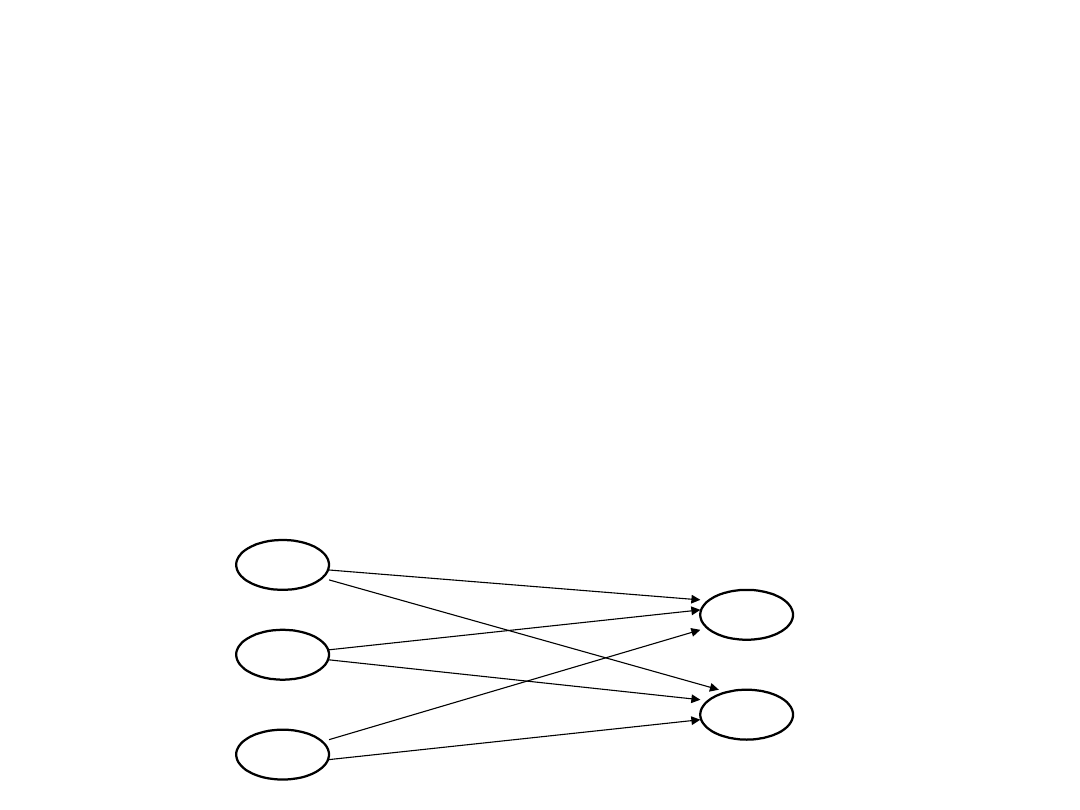
S = {1,2,3}, T = {a, b} ,S x T = {(1,a), (1,b), (2,a), (2,b),

(3,a), (3,b)}

R = S x T = {(1,a), (1,b), (2,a), (2,b), (3,a), (3,b)}

1

2

3

a

b

1

RELACJE
R - relacja dwuargumentowa na zbiorze S x T
Relacja na zbiorze S x T jest to każdy podzbiór tego zbioru.
Elementy relacji R  S x T wyróżniają się spośród elementów zbioru S x T
tym,
że mają pewną wspólną własność.
Mówimy, x jest w relacji z y  (x,y)R

1

2

3

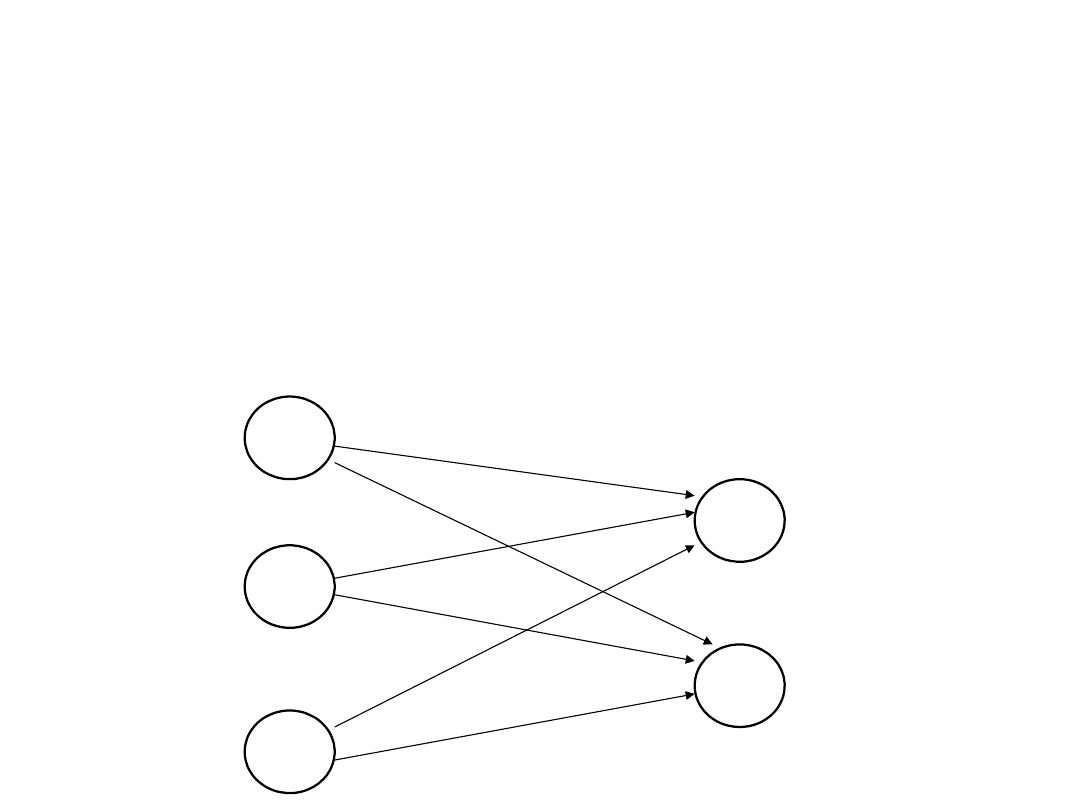
Przykład 1

Dane są zbiory: S = {1,2,3}, T = {1,2,3} ,

Relacja określona na tych zbiorach:

def

R = S x T = {(1,1), (1,2), (1,3), (2,1), (2,2), (2,3),(3,1), (3,2),

(3,3)}

Jej reprezentacja graficzna: parze (x,y) odpowiada łuk x y

2

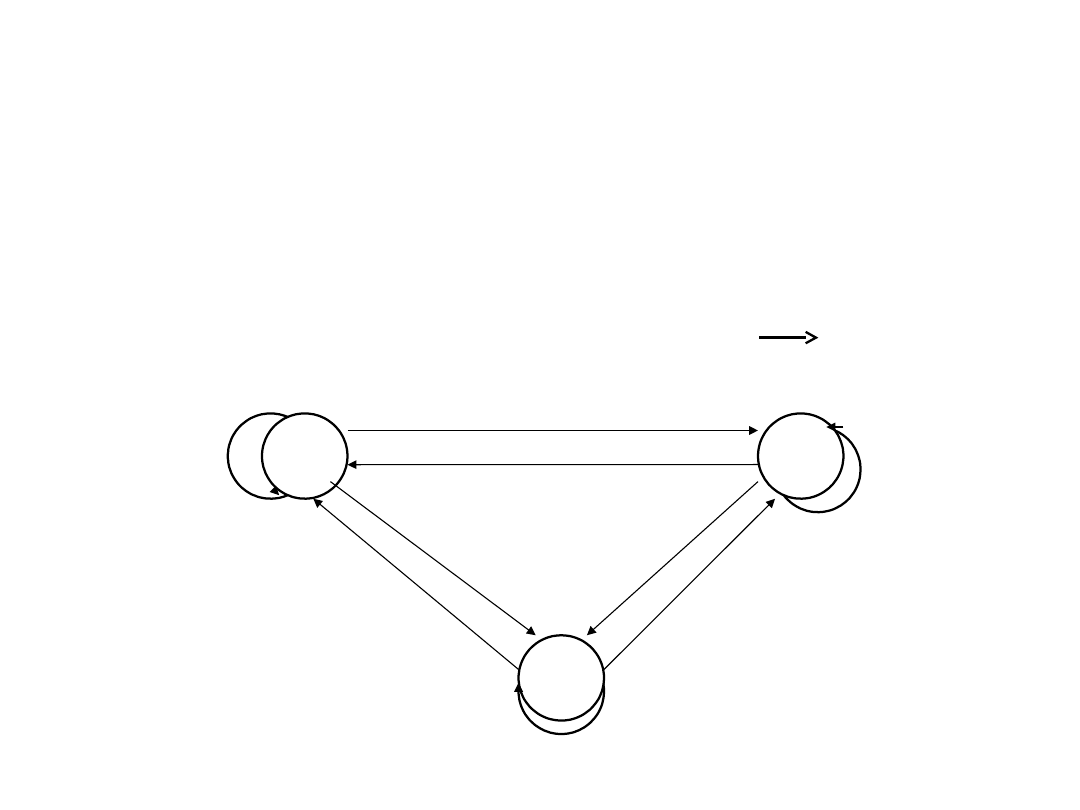
Przykłady relacji R’, R”, R”’  R

R’ = {(1,2),(1,3),(2,3)}  S x T;

a R’ b  a < b dla a S, bT

R” = {(1,1),(2,2),(3,3)}  S x T

;

a R” b  a = b

dla a S,

bT

R’’’ = { }  S x T ;

a R’’’ b  a mod 5 = b mod 5 = 4 mod 5

dla a S, bT

1

2

3

a

b

3

Jest zwrotna

(x,x)  R

, x  S

Jest przeciwzwrotna

(x,x)  R

, x S

Jest symetryczna

(x,y)  R  (y,x)  R, x,y S

Jest antysymetryczna

(x,y)  R & (y,x)  R  x = y

Jest przechodnia

(x,y)  R & (y,z)  R  (x,z)  R

4

Własności relacji

Niech R  S x S oznacza relację R w zbiorze S

Jeżeli R  S x T to R^  T x S

jest relacja odwrotną

Niech będzie dany zbiór X = {a, b, c, d}. Zdefiniujmy relację R =

{(a,a), (b,b),

(c,c), (d,d), (a,b)}. Czy relacja ta jest zwrotna (tzn. czy x  S (x,x)

 R )?

Niech będzie dany zbiór X = {a, b, c, d}. Zdefiniujmy relację R = {(a,a),

(b,b),(c,c), (d,d)}. Czy relacja ta jest przechodnia (tzn czy (x,y)  R &

(y,z)  R  (x,z)  R )?

Niech będzie dany zbiór X = {a, b, c, d}. Zdefiniujmy relację R =

{(a,b), (b,c),

(a,a)}. Czy relacja ta jest przeciwzwrotna (tzn. czy x S (x,x)  R )?

Przykład 2

Niech będzie dany zbiór X = {a, b, c, d}. Zdefiniujmy relację R = {(a,b),

(b,a),(c,c), (d,c), (c,d)}. Czy relacja ta jest symetryczna x,y S ((x,y)  R

 (y,x)  R)?

5

Niech będzie dany zbiór X = {a, b, c, d}. Zdefiniujmy relację R = {(a,b), (b,c),

(c,d), (d,a)}. Czy relacja ta jest przeciwsymetryczna (tzn. czy

)?

.

Niech będzie dany zbiór X = {a, b, c, d}. Zdefiniujmy relację R = {(a,b),

(a,c), (b,a)}.

Czy relacja ta jest spójna?

Niech będzie dany zbiór X = {a, b, c, d}. Zdefiniujmy relację R = {(a,b),

(b,a),(c,c)}. Czy relacja ta jest symetryczna?

Relacja jest spójna, jeżelix,y S, x ≠ y  (y,x)  R  (x,y)  R

Relacje < i ≤ są relacjami spójnymi w zbiorze liczb rzeczywistych

6

Jeżeli dana relacja jest symetryczna, zwrotnia i przechodnia, to jest

relacją

równoważności, na której definiujemy klasy abstrakcji.

Przykład 3

Relacja   N x N a R b  a mod T = b mod T , jest relacją równoważności
generującą w zbiorze liczb naturalnych N klasę abstrakcji klasę – zbiór liczb
przystających modulo T (podzielnych przez T be z reszty).

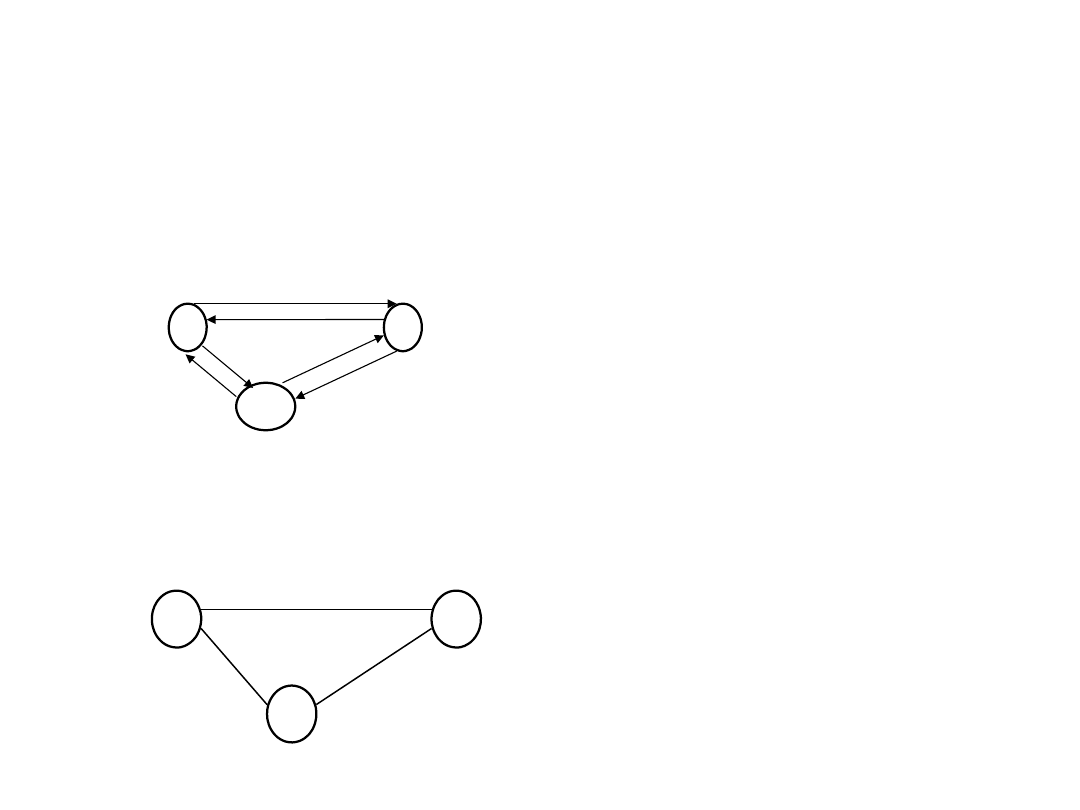
a

b

c

a

b

c

S = {a,b,c} ; R’ = {(a,b),(c.b),
(a,c)}

G R A F Y - graficzne reprezentacje relacji.

Graf: G = (S, R

),

gdzie

S

– zbiór wierzchołków,

R

– relacja łącząca

elementy

S

Przykład 4

G = (S, R

) ;

S = {a,b,c} ;R = {(a,b),(b,a),(b,c),(c.b),(c,a),(a,c)}

G = (S, R’) ;

7

Graf skierowany

Graf nieskierowany – krawędzie
odwzorowują
relację
symetryczną.

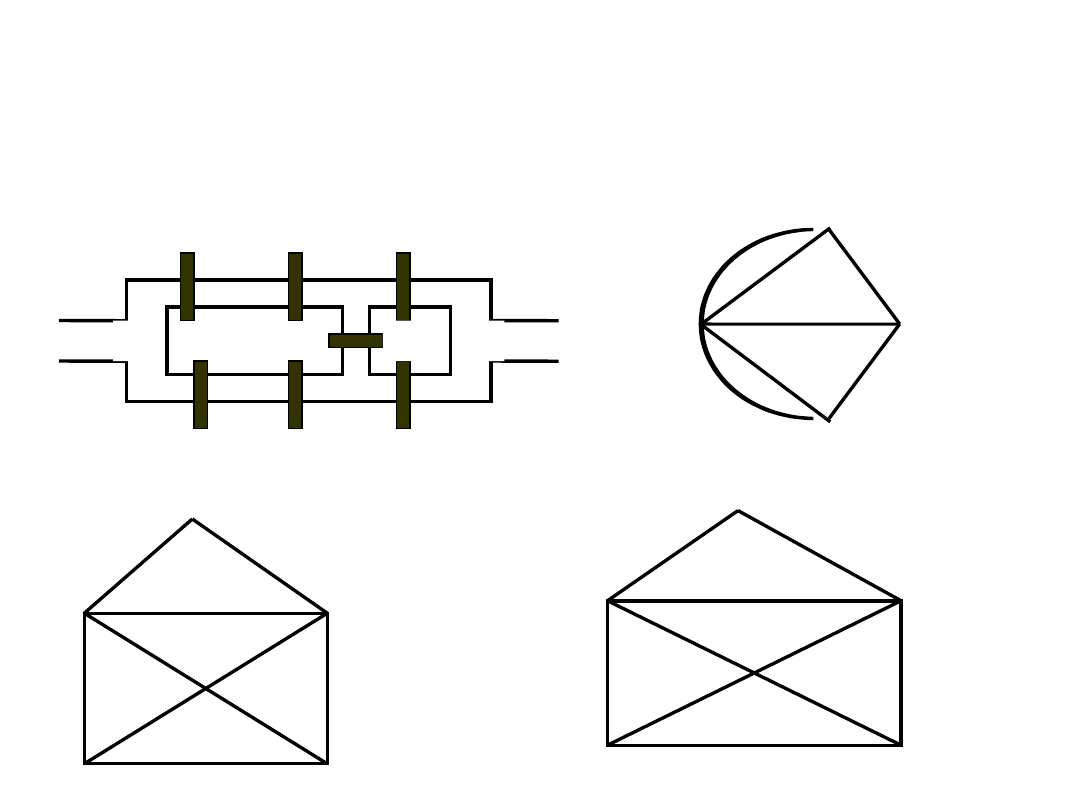
REPREZENTACJE MACIERZOWE

Macierz sąsiedztwa A

(n x n)

,

Macierz incydencji

M

(n x m)

grafu o n wierzchołkach i m krawędziach

a

i,j

- liczba krawędzi łączących wierzchołek „i” z wierzchołkiem

„j”

m

i,j

= 1 jeśli i-ty wierzchołek jest incydenty z j-tą krawędzią

3 b
4

1 a
2

c d
e

m

i,j

= 0 w przeciwnym wypadku

1 2 3

4

1

0 1

1 0

2

1 0

1 1

A =

3

1 1 0 1

4

0 1 1 0

a b

c d e

1

1 0 1 0 0

2

1 0 0 1 1

M =

3

1 1 1 0 0

4

0 1 0 0 1

8

Modelowanie

Problem mostów królewieckich (1736) Leonard Euler

Przejść przez każdy z mostów dokładnie jeden raz i powrócić do
punktu wyjściowego.

6

7

2

3

1 8

3 5

4

A

D

C

B

C

D

B

A

9

Inny problem tej samej klasy:

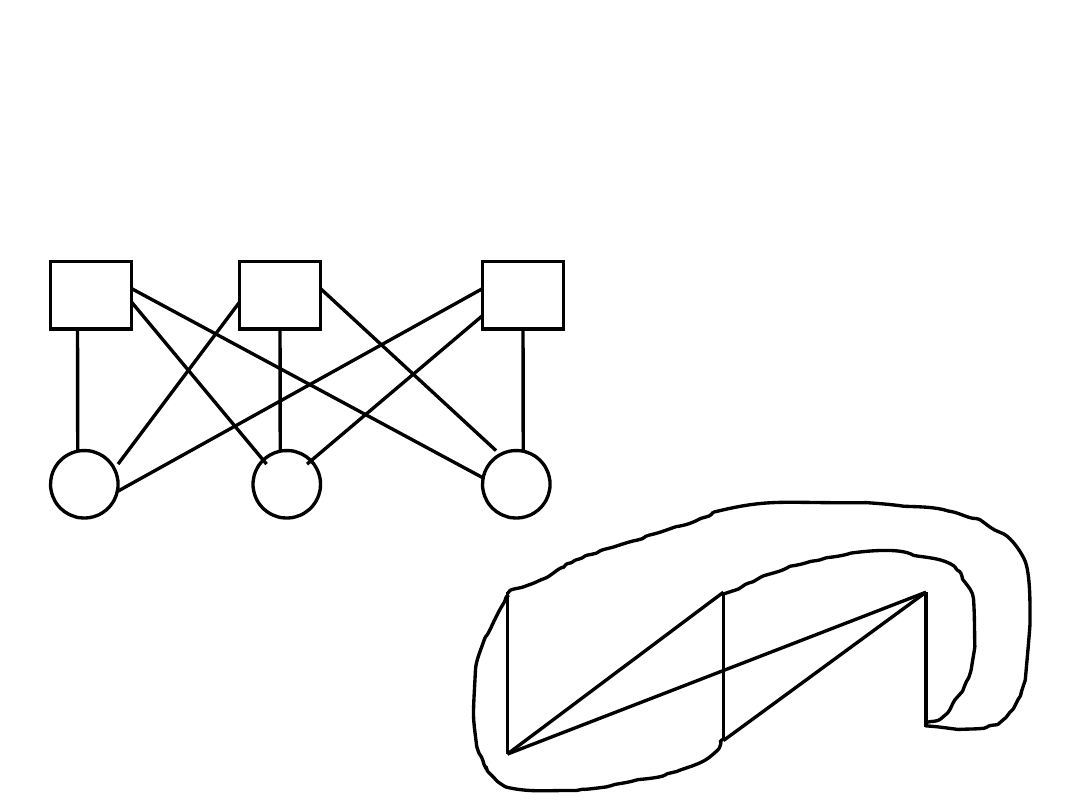
Jeszcze jedno zastosowanie

.

Problem sieci wodnej (W), gazowej (G) i elektrycznej (E). Są trzy

domy H

1

, H

2

i H

3

, z których każdy musi być podłączony przewodami

do każdej z trzech sieci. Czy jest możliwe dokonanie takich

połączeń bez skrzyżowania przewodów?

H

1

H

2

H

3

W

G

E

10

11

3. Narysuj rysunek grafu G = (X,R), gdzie X = {x,y,z,w} ,
R={(x,y),(w,x),(w,y),(y,z),(y,z),(w,z)}.
Wyznacz macierze incydencji i sąsiedztwa tego grafu. Wyznacz rząd i

zerowość grafu.

4. Wyznacz macierz incydencji grafu zadanego poniższą macierzą sąsiedztwa

.

0

1

1

1

0

1

1

0

0

ZADANIA

1. Zapisz relację dwuargumentową w zbiorze N określona wzorem:

m+n=5 , max{m,n} = 2

2. Podaj przykład relacji która jest:: antysymetryczna i przechodnia ale nie
jest zwrotna;
symetryczna ale nie jest zwrotna ani przechodnia

5. Czy graf może mieć nieparzystą liczbę wierzchołków nieparzystego
stopnia?
6. Dana jest społeczność X w której istnieją relacje S, S’, S”, S”’  X x
X . Która z tych relacji
jest relacja równoważności?
xSy <=> x jest szefem y ; xS’y <=> x jest przyjacielem
y
xS”y <=> x jest synem y ; xS”’y <=> x ma taki sam
wiek jak y