1
Metody rozwiązywania
problemów decyzyjnych
Metody rozwiązywania
problemów decyzyjnych
Piotr Sawicki
Piotr Sawicki
Wydział Maszyn Roboczych i Transportu
pok. 719, tel. 665 22 30, 665 21 29
E-mail: piotr.sawicki@put.poznan.pl
URL: http://www.put.poznan.pl/~piotrs
Wydział Maszyn Roboczych i Transportu
pok. 719, tel. 665 22 30, 665 21 29
E-mail: piotr.sawicki@put.poznan.pl
URL: http://www.put.poznan.pl/~piotrs
Harmonogramowanie pracy
Zastosowanie wielokryterialnej
metody przydziału
Harmonogramowanie pracy
Zastosowanie wielokryterialnej
metody przydziału
25
2
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Harmonogramowanie pracy
Plan prezentacji
Wprowadzenie
•
harmonogramowanie a problem przydziału
•
jedno vs. wiele kryteriów przydziału
•
rozwiązanie wielokryterialne
– charakterystyczne pojęcia
Metoda rozwiązywania problemu
•
algorytm wielokryterialnej metody przydziału
•
ustalanie kompromisu kryteriów
Analiza przypadku
•
istota problemu
•
kryteria oceny rozwiązań
•
rozwiązanie problemu / ustalenie kompromisu
Podsumowanie
•
wnioski
•
przypomnienie pojęć
2
25
3
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Wprowadzenie
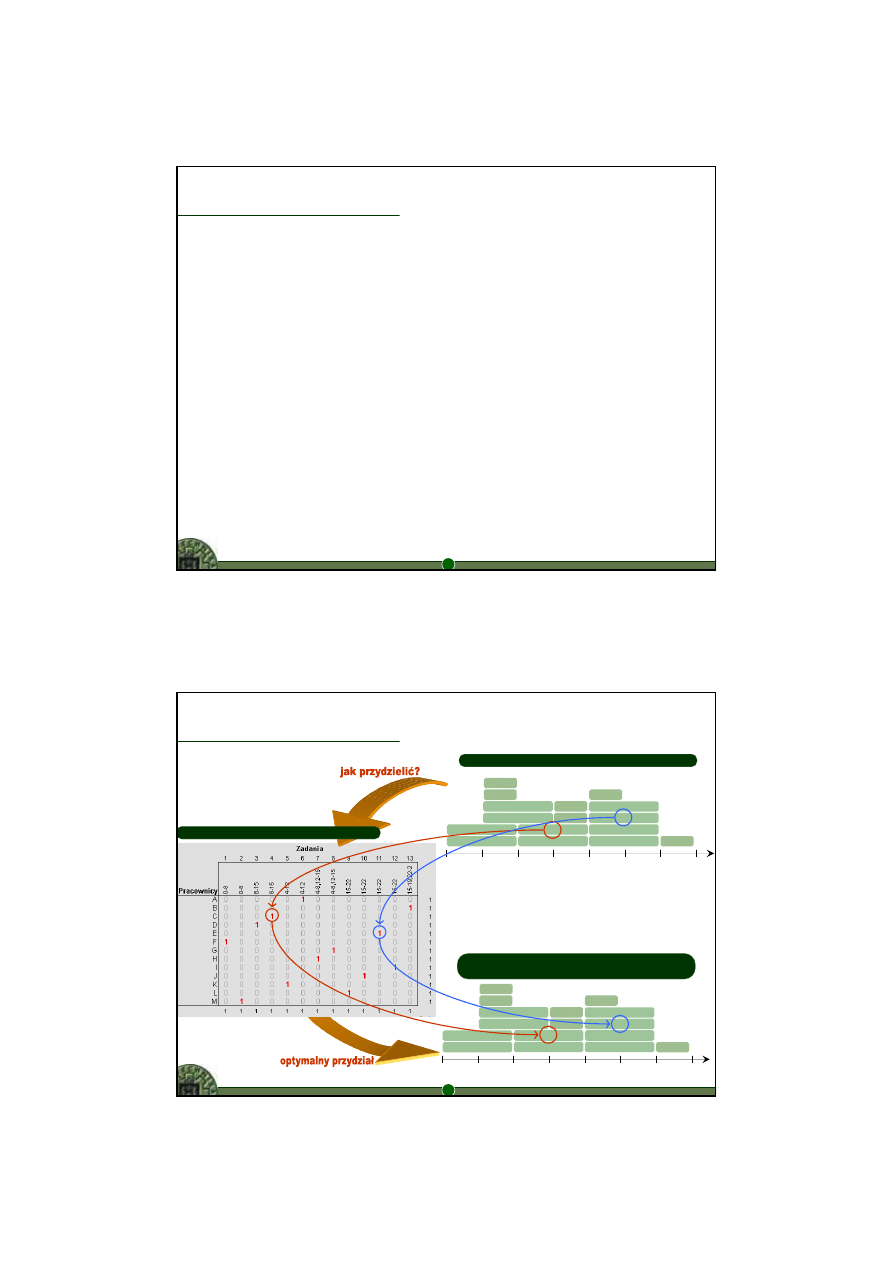
Harmonogramowanie a problem przydziału
Harmonogramowanie
•
znane
– lista zadań/prac do wykonania
•
problem polega na zaplanowaniu kolejności wykonywania zadań/prac
– na poszczególnych stanowiskach
– w oparciu o dostępne zasoby (ludzkie i techniczne)
Problem przydziału
•
znane
– kolejność wykonywania zadań
– dostępne zasoby
{
ludzie: kierowcy, operatorzy, ...
{
środki techniczne: pojazdy, urządzenia przeładunkowe,...
•
problem polega na optymalnym przydziale zasobów do realizacji zadań
– pracowników do zadań
– pojazdów do zadań
– ....
25
4
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Wprowadzenie
Harmonogramowanie a problem przydziału
F
0:00 4:00 8:00 12:00 15:00 19:00 22:00 2:00
M
D
C
K
A
H
H
G
G
L
J
E
I
B
B
1
0:00 4:00 8:00 12:00 15:00 19:00 22:00 2:00
2
3
4
5
6
7
7
8
8
9
10
11
12
13
13
Zestaw 13 zada
ń (1, 2, ..., 13) do realizacji
Przydzia
ł 13 pracowników (A, B, ...M) do zadań
HARMONOGRAM PRACY KIEROWCÓW
Rozwi
ązanie problemu przydziału
3
25
5
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Wprowadzenie
Jedno vs. wiele kryteriów przydziału
Potencjalne kryteria przydziału
Poziom skomplikowania problemu
•
rozwiązanie problemu jednokryterialnego przysparza trudności
– np.: 20 pracowników i 20 zadań Æ 400 zmiennych decyzyjnych
•
rozwiązanie problemu wielokryterialnego powoduje dodatkową trudność
– konieczność podjęcia decyzji jednocześnie w wielu wymiarach
9
9
9
Jakość realizacji zadań
6
Marketingowe
9
9
9
9
Liczba nadgodzin
5
Inne
7
Charakter kryteriów
9
9
Równomierny rozkład dni wolnych
4
9
9
Atrakcyjność zadań
3
9
9
9
Efektywność realizacji zadań
2
9
9
9
Koszt realizacji zadań
1
Społeczne
Techniczne
Ekonomiczne
Kryteria
25
6
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Wprowadzenie
Rozwiązanie wielokryterialne / Charakterystyczne pojęcia
Charakterystyczne pojęcia
•
rozwiązanie niezdominowane
•
punkt nadir
•
punkt ideal
4
25
7
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Wprowadzenie
Rozwiązanie wielokryterialne / Charakterystyczne pojęcia
Rozwiązanie niezdominowane (sprawne)
(B.Roy, 1990)
•
rozwiązanie dla którego nie można znaleźć innych rozwiązań w przestrzeni
kryterialnej, które byłyby lepsze względem jednego kryterium i nie gorsze względem
pozostałych
Przykład
– ocena 5 firm kurierskich (A, B, C, D, E)
– 4 kryteria oceny (2 minimalizowane, 2 maksymalizowane)
– znajdź rozwiązania niezdominowane
2100
2100
2000
2000
1300
1300
1000
1000
1000
1000
Zasięg
(max)
,46
,46
542
542
12
12
Firma E
5
Kryteria oceny
,51
,51
1204
1204
12
12
Firma D
4
,57
,57
2437
2437
12
12
Firma C
3
,65
,65
4850
4850
12
12
Firma B
2
,76
,76
4634
4634
12
12
Firma A
1
Jakość
(max)
Koszt
(min)
Czas
(min)
Firmy kurierskie
(warianty)
Niezdominowane
Niezdominowane
Niezdominowane
Zdominowane
Zdominowane
Zdominowane
Niezdominowane
Niezdominowane
Niezdominowane
Niezdominowane
Niezdominowane
Niezdominowane
Niezdominowane
Niezdominowane
Niezdominowane
25
8
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Wprowadzenie
Rozwiązanie wielokryterialne / Charakterystyczne pojęcia
Punkt nadir
(P.Vincke, 1992)
•
rozwiązanie złożone z najgorszych ocen w przestrzeni kryterialnej
– max dla kryteriów minimalizowanych
– min dla kryteriów maksymalizowanych
•
rozwiązanie nie istnieje w rzeczywistości
Przykład
– parametry jak wcześniej
– znajdź punkt nadir
2100
2100
2000
2000
1300
1300
1000
1000
1000
Zasięg
(max)
,46
,46
542
542
12
12
Firma E
5
Kryteria oceny
,51
,51
1204
1204
12
12
Firma D
4
,57
,57
2437
2437
12
12
Firma C
3
,65
4850
12
Firma B
2
,76
,76
4634
4634
12
12
Firma A
1
Jakość
(max)
Koszt
(min)
Czas
(min)
Firmy kurierskie
(warianty)
― punkt nadir: 12; 4634; 0,46; 1000
Zdominowane
Zdominowane
Zdominowane
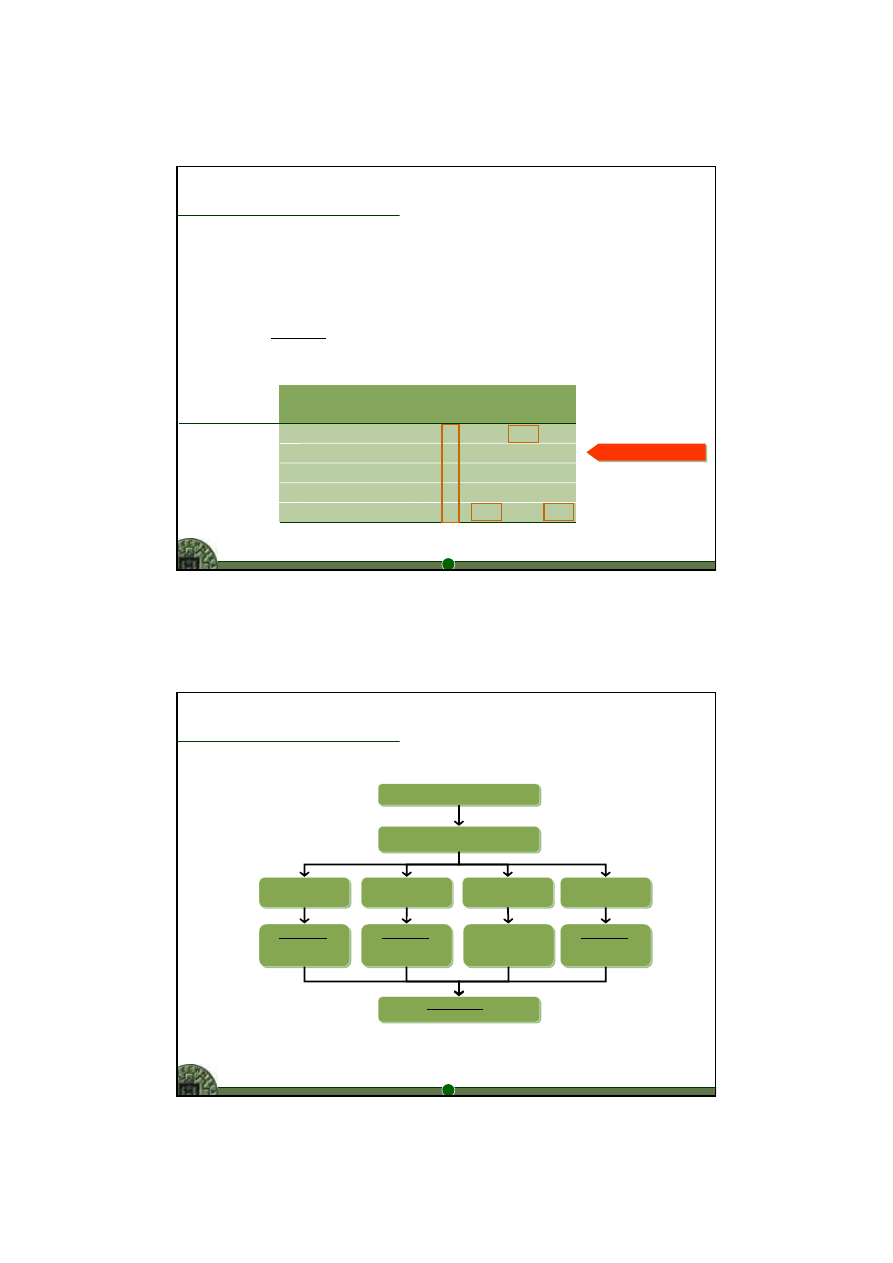
5
25
9
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Wprowadzenie
Rozwiązanie wielokryterialne / Charakterystyczne pojęcia
Punkt ideal
(P.Vincke, 1992)
•
rozwiązanie złożone z najlepszych ocen w przestrzeni kryterialnej
– min dla kryteriów minimalizowanych
– max dla kryteriów maksymalizowanych
•
rozwiązanie nie istnieje w rzeczywistości
Przykład
– parametry jak wcześniej
– znajdź punkt ideal
2100
2100
2000
2000
1300
1300
1000
1000
1000
Zasięg
(max)
,46
,46
542
542
12
12
Firma E
5
Kryteria oceny
,51
,51
1204
1204
12
12
Firma D
4
,57
,57
2437
2437
12
12
Firma C
3
,65
4850
12
Firma B
2
,76
,76
4634
4634
12
12
Firma A
1
Jakość
(max)
Koszt
(min)
Czas
(min)
Firmy kurierskie
(warianty)
― punkt ideal: 12; 542; 0,76; 2100
Zdominowane
Zdominowane
Zdominowane
25
10
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Metoda rozwi
ązywania problemu
Algorytm wielokryterialnej metody przydziału
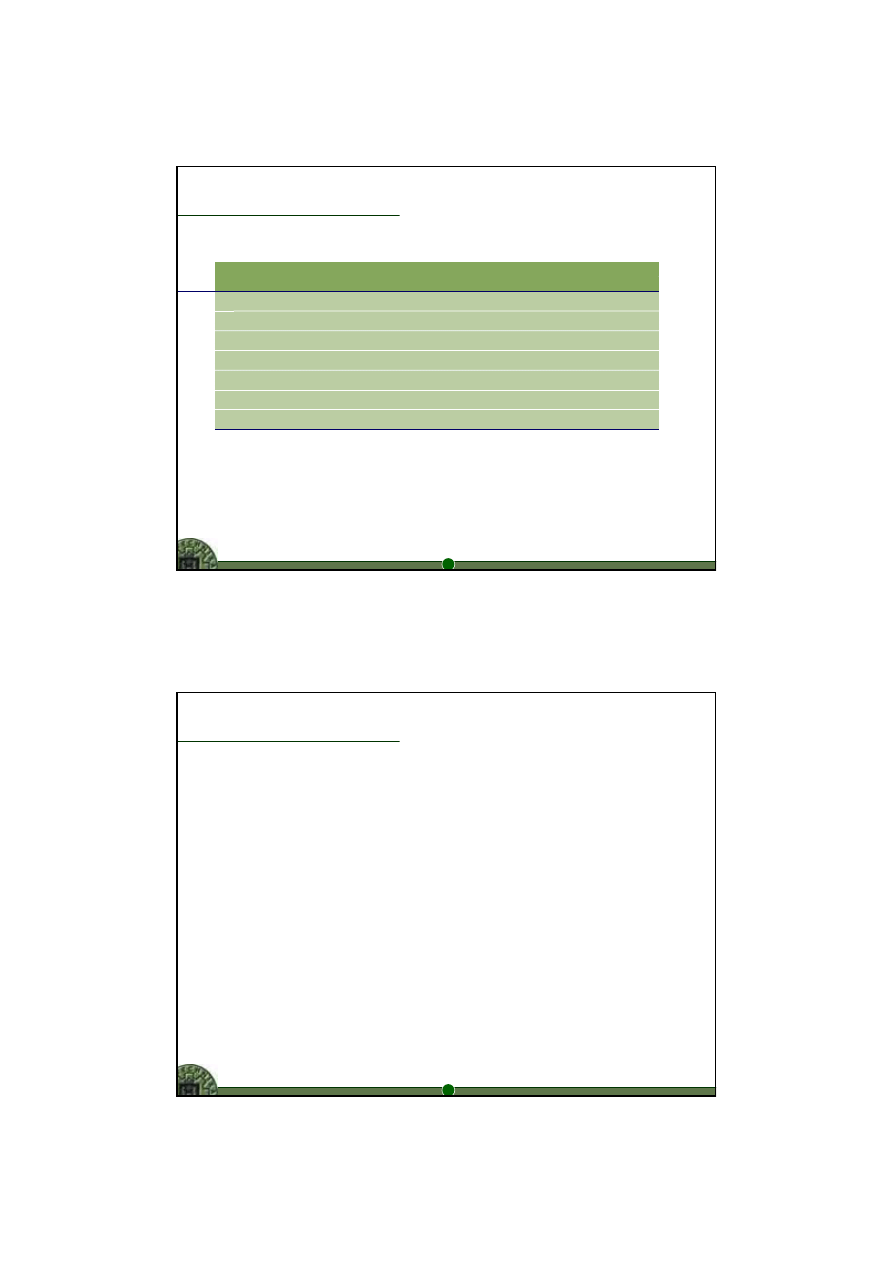
Ogólny schemat postępowania
Rozpoznaj specyfik
ę problemu
Rozpoznaj specyfik
ę problemu
Zdefiniuj k-kryteriów przydzia
łu
(k = 1, 2, ..., n)
Zdefiniuj k-kryteriów przydzia
łu
(k = 1, 2, ..., n)
Rozwi
ąż problem
dla kryterium 1
Rozwi
ąż problem
dla kryterium 1
Rozwi
ąż problem
dla kryterium 2
Rozwi
ąż problem
dla kryterium 2
...
...
Rozwi
ąż problem
dla kryterium n
Rozwi
ąż problem
dla kryterium n
Optymalne
rozwi
ązanie
dla kryterium 1
Optymalne
rozwi
ązanie
dla kryterium 1
Optymalne
rozwi
ązanie
dla kryterium 2
Optymalne
rozwi
ązanie
dla kryterium 2
...
...
Optymalne
rozwi
ązanie
dla kryterium n
Optymalne
rozwi
ązanie
dla kryterium n
Poszukaj kompromisu k-kryteriów
(k = 1, 2, ..., n)
Poszukaj kompromisu k-kryteriów
(k = 1, 2, ..., n)
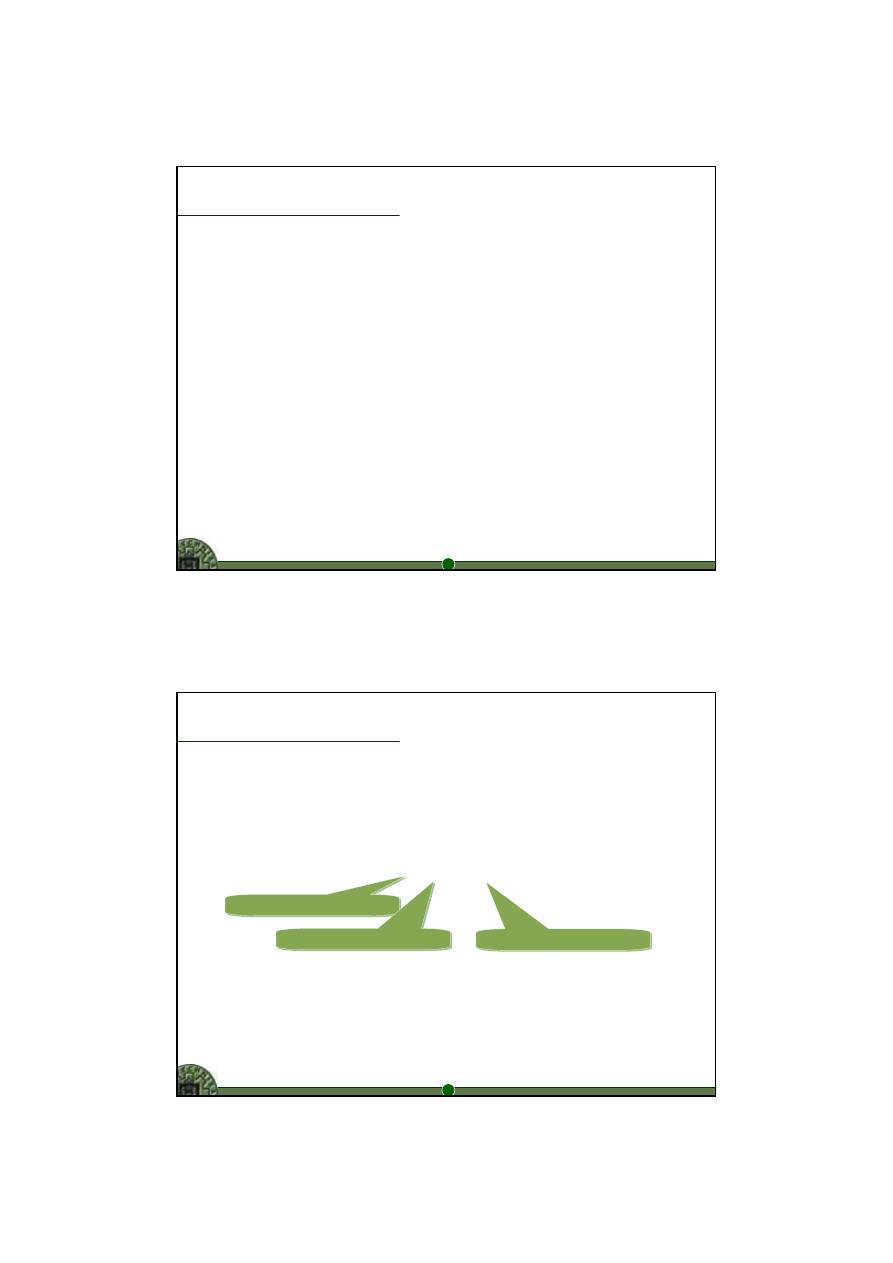
6
25
11
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Metoda rozwi
ązywania problemu
Algorytm wielokryterialnej metody przydziału
Sformułowanie matematyczne wielokryterialnego problemu przydziału
•
zmienna decyzyjna (zmienna binarna)
x
ij
- przydział i-tego pracownika do realizacji j-tego zadania
•
funkcja celu
gdzie:
- element tablicy przydziału dla k-tego kryterium przydziału
•
ograniczenia
oraz
∑∑
=
=
→
m
i
m
j
ij
k
ij
min
max
x
w
1
1
lub
k
ij
w
∑
=
=
=
m
i
ij
m
j
x
1
...,
,
2
,
1
dla
1
∑
=
=
=
m
j
ij
m
i
x
1
...,
,
2
,
1
dla
1
25
12
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Metoda rozwi
ązywania problemu
Algorytm wielokryterialnej metody przydziału
Sformułowanie matematyczne wielokryterialnego problemu przydziału
•
zbiór rozwiązań optymalnych
– zbiór zawiera tyle rozwiązań ile jest kryteriów
(
)
∗
∗
∗
∗
=
n
k
f
f
f
f
...,
,
,
2
1
(
)
∗
∗
∗
∗
=
n
k
f
f
f
f
...,
,
,
2
1
Optymalna warto
ść kryterium 1
Optymalna warto
ść kryterium 1
Optymalna warto
ść kryterium 2
Optymalna warto
ść kryterium 2
Optymalna warto
ść kryterium n
Optymalna warto
ść kryterium n
7
25
13
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Metoda rozwi
ązywania problemu
Algorytm wielokryterialnej metody przydziału
Sformułowanie matematyczne wielokryterialnego problemu przydziału
•
kompromis
– uzyskiwany dla takich zmiennych decyzyjnych x
ij
, które minimalizują wartość funkcji d
1
i d
2
∑∑
∑
=
=
=
∗
=
m
i
m
j
ij
k
ij
n
k
k
x
w
f
d
1
1
1
1
1
2
1
1
1
2
1
1
∑ ∑∑
=
=
=
∗
⎥
⎦
⎤
⎢
⎣
⎡
−
=
n
k
m
i
m
j
ij
k
ij
k
x
w
f
d
25
14
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Analiza przypadku
Istota problemu
Rozważany problem
•
przydział kierowców do realizacji zadań
– 13 kierowców
– 13 zadań (tras realizowanych według rozkładu)
•
kryteria przydziału
– koszt realizacji [zł]
– efektywność pracy [%]
– jakość obsługi pasażerów [pkt]
•
poszukiwane rozwiązanie kompromisowe
8
25
15
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Analiza przypadku
Kryteria oceny rozwiązania
Kryterium kosztu realizacji zadań (kosztu obsługi rozkładu)
•
kryterium wyrażone w [zł]
•
minimalizowane
Kryterium 1:
Koszt realizacji
[z
ł]
Zadania
1
2
3
4
5
6
7
8
9
10
11
12
13
Pracownicy
0-8
0-8
8-1
5
8-1
5
4-1
2
4-1
2
4-8
,12-
15
4-8
,12-
15
15-
2
2
15-
2
2
15-
2
2
15-
2
2
1
5
-1
9;
22
-2
A
87
84
86
85
87
84
96
94
94
88
95
96
94
B
85
85
83
87
87
87
96
95
96
89
89
105
94
C
83
84
83
82
96
87
92
97
94
88
89
96
100
D
87
83
82
83
92
89
89
93
97
94
90
95
96
E
84
83
83
87
90
87
87
91
96
97
88
91
97
F
82
83
84
87
90
88
88
87
95
96
89
94
98
G
85
85
86
92
94
88
86
84
96
95
96
98
95
H
85
84
85
92
91
87
84
85
90
96
97
99
97
I
84
85
94
94
90
94
87
91
90
96
98
90
97
J
84
86
86
94
89
95
86
94
89
87
98
94
96
K
85
87
87
83
86
94
85
87
89
89
94
91
100
L
86
85
85
83
90
96
89
85
88
94
94
91
104
M
87
82
85
84
90
97
94
86
89
94
89
93
95
Koszt realizacji zadania 4 przez pracownika L
25
16
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Kryterium 2:
Efektywno
ść pracy
[%]
Zadania
1
2
3
4
5
6
7
8
9
10
11
12
13
Pracownicy
0-
8
0-
8
8-
15
8-
15
4-
12
4-
12
4-
8,
12
-1
5
4-
8,
12
-1
5
15
-2
2
15
-2
2
15
-2
2
15
-2
2
15
-1
9
;22
-2
A
51
56
53
56
49
71
76
71
71
58
73
76
71
B
56
56
47
51
51
71
76
73
76
60
60
96
71
C
44
76
47
47
49
84
67
78
71
58
60
76
84
D
47
67
44
56
47
76
60
69
78
71
62
73
76
E
56
62
47
49
47
78
56
64
76
78
58
64
78
F
56
62
49
44
47
80
58
56
73
76
60
71
80
G
67
71
53
51
51
73
53
49
76
73
76
80
73
H
67
64
51
51
49
78
49
51
62
76
78
82
78
I
71
62
71
49
51
78
56
64
62
76
80
62
78
J
71
60
53
49
53
76
53
71
60
56
80
71
76
K
47
53
56
51
56
84
51
56
60
60
71
64
84
L
47
62
51
53
51
93
60
51
58
71
71
64
93
M
49
62
51
56
44
73
71
53
60
71
60
69
73
Analiza przypadku
Kryteria oceny rozwiązania
Kryterium efektywności pracy
•
kryterium wyrażone w [%]
•
przedział zmienności: <0, 100>
•
maksymalizowane
Efektywno
ść realizacji zadania 4 przez pracownika L
9
25
17
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Kryterium 3:
Jako
śc obsługi pasażerów
[pkt]
Zadania
1
2
3
4
5
6
7
8
9
10
11
12
13
Pracownicy
0-8
0-8
8-1
5
8-1
5
4-1
2
4-1
2
4-8
,12-
15
4-8
,12-
15
15-
22
15-
22
15-
22
15-
22
15-
19
;2
2-
2
A
77
68
66
78
77
78
80
74
76
70
67
67
68
B
79
66
67
72
78
79
81
74
73
69
67
66
67
C
79
69
73
72
78
80
72
76
72
76
66
67
76
D
78
71
75
79
76
72
77
65
74
71
69
65
64
E
79
69
73
78
79
70
73
69
72
69
66
65
65
F
86
71
67
70
76
76
73
65
72
78
68
67
67
G
76
78
76
76
70
77
78
67
69
66
69
66
68
H
76
78
77
78
71
71
87
69
69
69
67
67
65
I
82
74
79
76
70
71
78
64
78
69
65
66
65
J
78
68
76
71
69
80
76
76
71
77
66
68
68
K
82
67
69
71
71
76
73
65
68
76
67
69
69
L
80
70
69
77
78
71
76
69
72
70
64
65
66
M
77
76
68
71
76
71
75
66
72
79
69
64
67
Analiza przypadku
Kryteria oceny rozwiązania
Kryterium jakości obsługi
•
kryterium wyrażone w [pkt]
•
przedział zmienności: <0, 100>
•
maksymalizowane
Jako
ść obsługi pasażerów w ramach zad. 4 przez pracownika L
25
18
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Analiza przypadku
Rozwiązanie problemu
Optymalizacja jednokryterialna
(Kryterium 1)
Optymalizacja jednokryterialna
(Kryterium 2)
Optymalizacja jednokryterialna
(Kryterium 3)
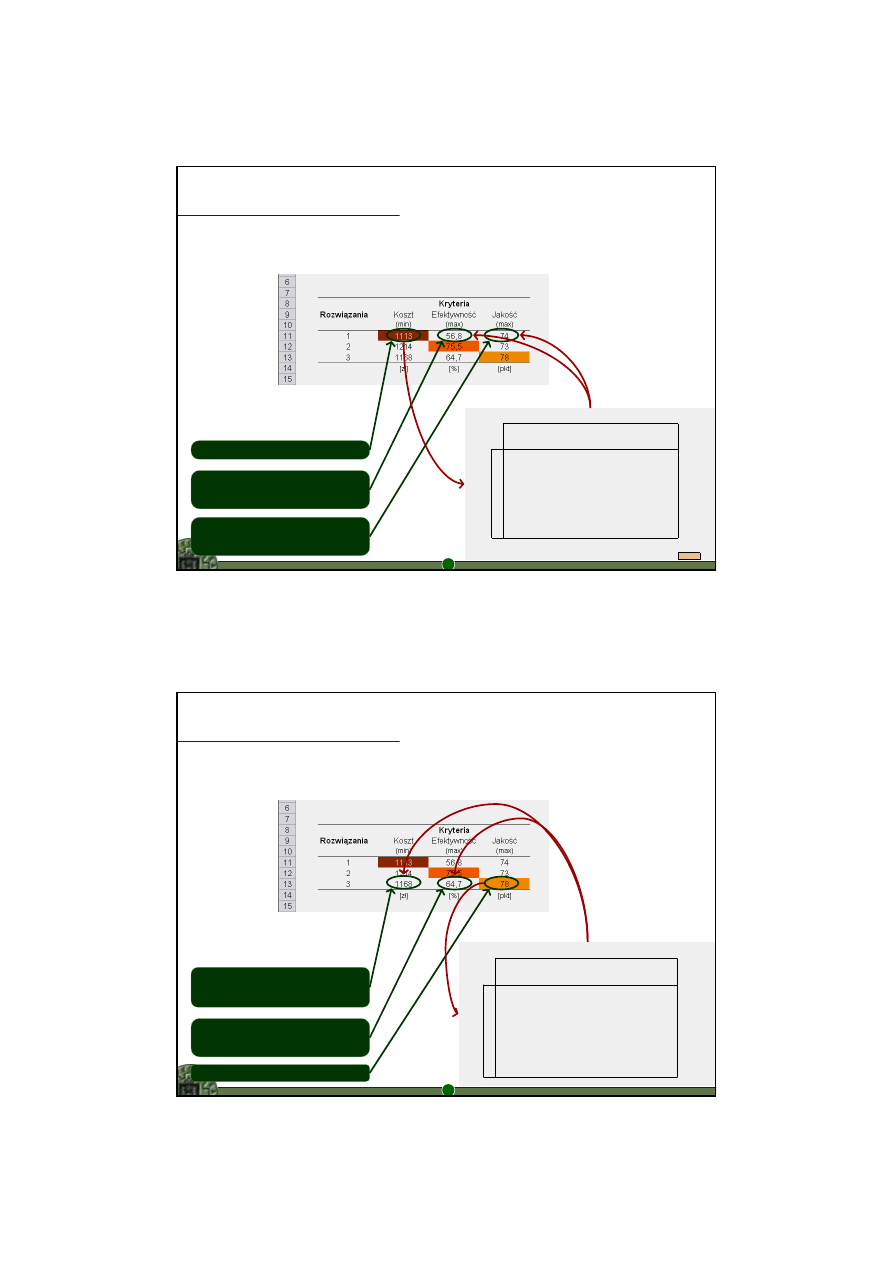
10
25
19
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Analiza przypadku
Rozwiązanie problemu
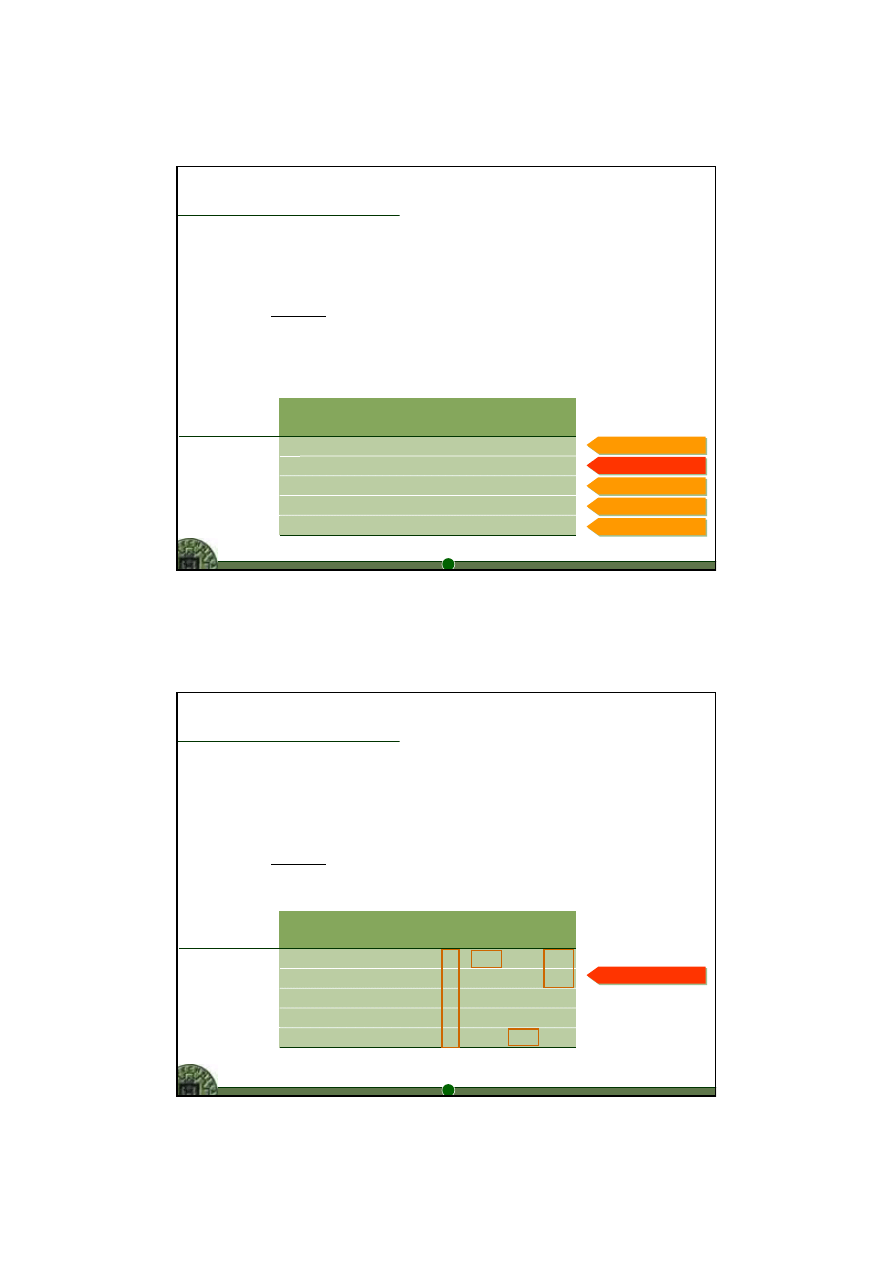
Jak ustalić wartości kryteriów dla danego rozwiązania?
•
rozwiązanie 1
Optimum dla kryterium 1
Optimum dla kryterium 1
Warto
ść kryterium 2
przyjmuj
ąc rozwiązanie
dla optymalnej warto
ści kryterium 1
Warto
ść kryterium 3
przyjmuj
ąc rozwiązanie
dla optymalnej warto
ści kryterium 1
Zadania
1
2
3
4
5
6
7
8
9
10
11
12
13
Pracownicy
0-
8
0-
8
8-
15
8-
15
4-
12
4-
12
4-
8,
12-
15
4-
8,
12-
15
15-
22
15-
22
15-
22
15-
22
15-
19;
22-
2
A
0
0
0
0
0
1
0
0
0
0
0
0
0
1
B
0
0
0
0
0
0
0
0
0
0
0
0
1
1
C
0
0
0
1
0
0
0
0
0
0
0
0
0
1
D
0
0
1
0
0
0
0
0
0
0
0
0
0
1
E
0
0
0
0
0
0
0
0
0
0
1
0
0
1
F
1
0
0
0
0
0
0
0
0
0
0
0
0
1
G
0
0
0
0
0
0
0
1
0
0
0
0
0
1
H
0
0
0
0
0
0
1
0
0
0
0
0
0
1
I
0
0
0
0
0
0
0
0
0
0
0
1
0
1
J
0
0
0
0
0
0
0
0
0
1
0
0
0
1
K
0
0
0
0
1
0
0
0
0
0
0
0
0
1
L
0
0
0
0
0
0
0
0
1
0
0
0
0
1
M
0
1
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
funkcja celu:
1113
[z
ł]
25
20
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Analiza przypadku
Rozwiązanie problemu
Jak ustalić wartości kryteriów dla danego rozwiązania?
•
rozwiązanie 3
Warto
ść kryterium 1
przyjmuj
ąc rozwiązanie
dla optymalnej warto
ści kryterium 3
Warto
ść kryterium 2
przyjmuj
ąc rozwiązanie
dla optymalnej warto
ści kryterium 3
Optimum dla kryterium 3
Zadania
1
2
3
4
5
6
7
8
9
10
11
12
13
Pracownicy
0-8
0-8
8-15
8-15
4-12
4-12
4-8,12-15
4-8,12-15
15-22
15-22
15-22
15-22
15-19;22-2
A
0
0
0
0
0
0
0
0
1
0
0
0
0
1
B
0
0
0
0
0
1
0
0
0
0
0
0
0
1
C
0
0
0
0
0
0
0
0
0
0
0
0
1
1
D
0
0
0
0
0
0
0
0
0
0
1
0
0
1
E
0
0
0
1
0
0
0
0
0
0
0
0
0
1
F
1
0
0
0
0
0
0
0
0
0
0
0
0
1
G
0
1
0
0
0
0
0
0
0
0
0
0
0
1
H
0
0
0
0
0
0
1
0
0
0
0
0
0
1
I
0
0
1
0
0
0
0
0
0
0
0
0
0
1
J
0
0
0
0
0
0
0
1
0
0
0
0
0
1
K
0
0
0
0
0
0
0
0
0
0
0
1
0
1
L
0
0
0
0
1
0
0
0
0
0
0
0
0
1
M
0
0
0
0
0
0
0
0
0
1
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
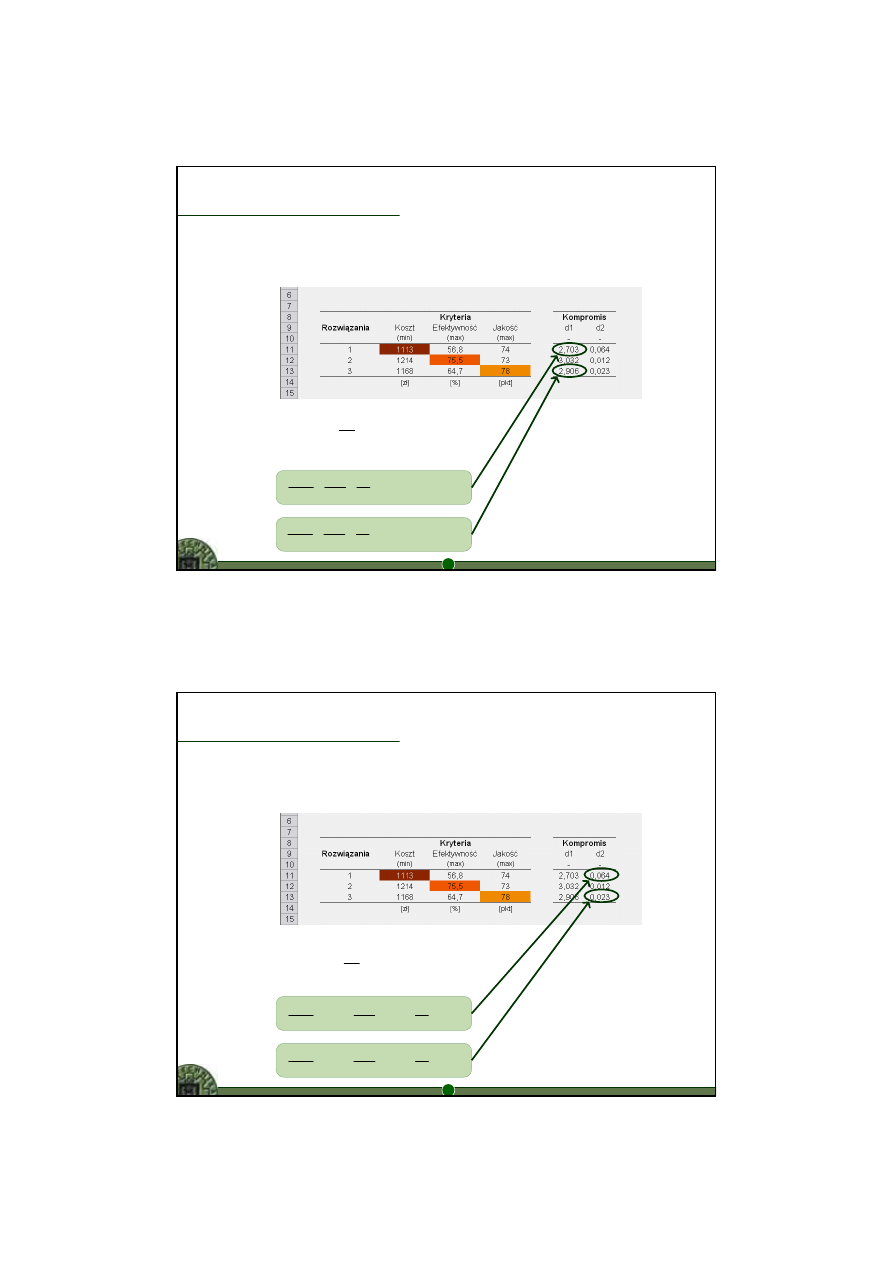
11
25
21
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Analiza przypadku
Rozwiązanie problemu
Jak wyznaczyć kompromis?
•
poszukiwanie takich zmiennych decyzyjnych x
ij
, które minimalizują wartość
funkcji d
1
i d
2
∑∑
∑
=
=
=
∗
=
m
i
m
j
ij
k
ij
n
k
k
x
w
f
d
1
1
1
1
1
78
74
5
,
75
8
,
56
1113
1113
+
+
78
78
5
,
75
7
,
64
1113
1168
+
+
25
22
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Analiza przypadku
Rozwiązanie problemu
Jak wyznaczyć kompromis?
•
poszukiwanie takich zmiennych decyzyjnych x
ij
, które minimalizują wartość
funkcji d
1
i d
2
2
2
2
1
78
74
1
5
,
75
8
,
56
1
1113
1113
⎟
⎠
⎞
⎜
⎝
⎛
−
+
⎟
⎠
⎞
⎜
⎝
⎛
−
+
⎟
⎠
⎞
⎜
⎝
⎛
−
2
2
2
1
78
78
1
5
,
75
7
,
64
1
1113
1168
⎟
⎠
⎞
⎜
⎝
⎛
−
+
⎟
⎠
⎞
⎜
⎝
⎛
−
+
⎟
⎠
⎞
⎜
⎝
⎛
−
2
1
1
1
2
1
1
∑ ∑∑
=
=
=
∗
⎥
⎦
⎤
⎢
⎣
⎡
−
=
n
k
m
i
m
j
ij
k
ij
k
x
w
f
d
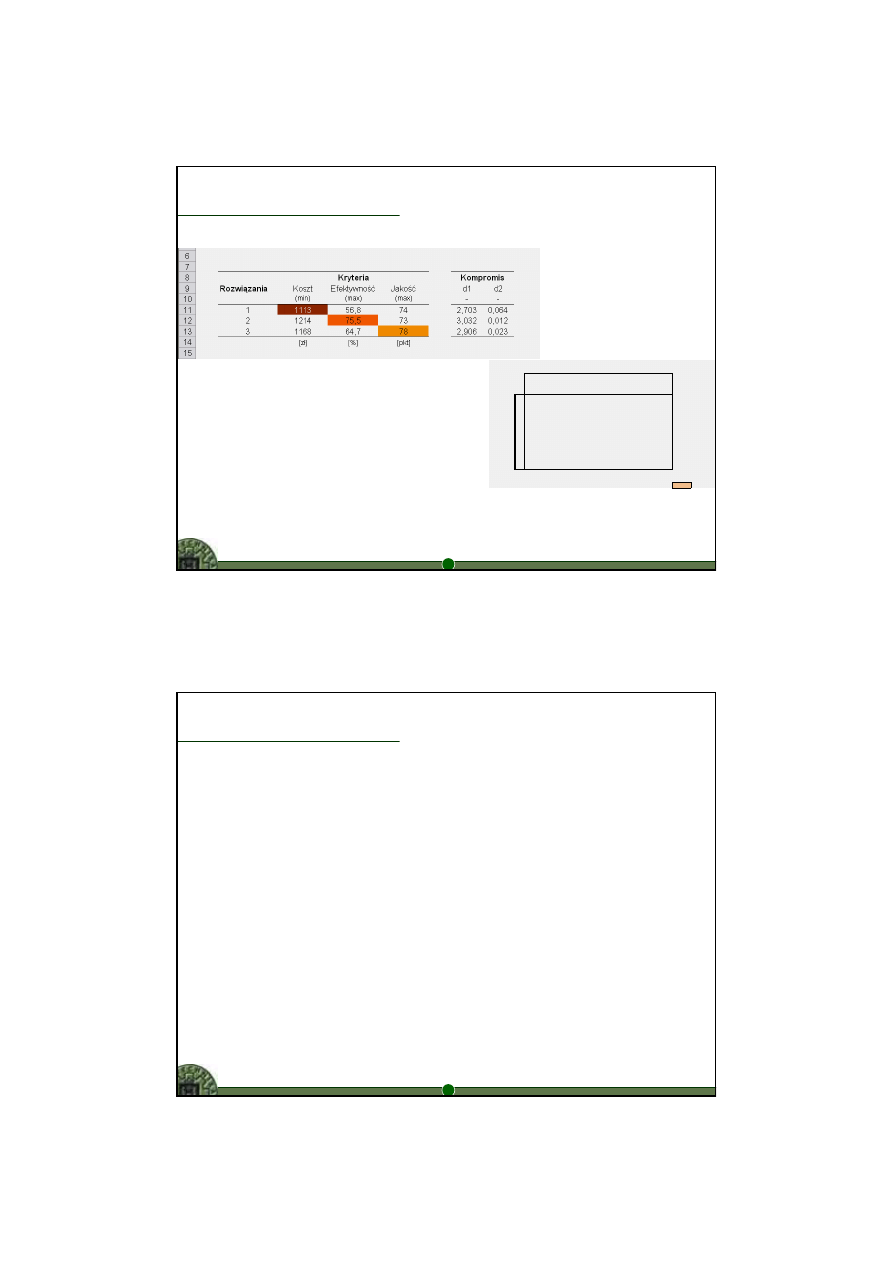
12
25
23
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Analiza przypadku
Rozwiązanie problemu
Interpretacja rozwiązania
•
wszystkie 3 rozwiązania są
niezdominowane
•
rozwiązanie idealne: (1113; 75,5; 78)
•
rozwiązanie nadir: (1214; 56,8; 73)
•
rozwiązanie 3 jest rozwiązaniem
kompromisowym
•
d
1
i d
2
uzyskują najniższe wartości
– „odległość” od rozwiązania idealnego jest
relatywnie najmniejsza
Zadania
1
2
3
4
5
6
7
8
9
10
11
12
13
Pracownicy
0-
8
0-
8
8-
15
8-
15
4-
12
4-
12
4-
8,
12
-1
5
4-
8,
12
-1
5
15
-2
2
15
-2
2
15
-2
2
15
-2
2
15
-1
9;
2
2
-2
A
0
0
0
0
0
0
0
0
1
0
0
0
0
1
B
0
0
0
0
0
1
0
0
0
0
0
0
0
1
C
0
0
0
0
0
0
0
0
0
0
0
0
1
1
D
0
0
0
0
0
0
0
0
0
0
1
0
0
1
E
0
0
0
1
0
0
0
0
0
0
0
0
0
1
F
1
0
0
0
0
0
0
0
0
0
0
0
0
1
G
0
1
0
0
0
0
0
0
0
0
0
0
0
1
H
0
0
0
0
0
0
1
0
0
0
0
0
0
1
I
0
0
1
0
0
0
0
0
0
0
0
0
0
1
J
0
0
0
0
0
0
0
1
0
0
0
0
0
1
K
0
0
0
0
0
0
0
0
0
0
0
1
0
1
L
0
0
0
0
1
0
0
0
0
0
0
0
0
1
M
0
0
0
0
0
0
0
0
0
1
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
funkcja celu:
1010
[pkt]
25
24
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Podsumowanie
Literatura uzupełniająca
•
Roy B.,: Wielokryterialne wspomaganie decyzji.
Wydawnictwo Naukowo Techniczne, Warszawa, 1990
•
Vincke P., Multicriteria Decision-Aid.
John Wiley & Sons, Chichester, 1992
Wnioski
•
przedstawiona procedura pozwala rozwiązać wielokryterialny problem przydziału
•
uzyskane rozwiązanie charakteryzuje się
– kompromisem uwzględnionych kryteriów
– uwzględnieniem szeregu aspektów podejmowania decyzji (ekonomicznych, społecznych,
marketingowych)
– możliwe jest do uzyskania dzięki ogólnodostępnym narzędziom obliczeniowym
(Solver dla MS Excel)
13
25
25
Piotr Sawicki / Metody rozwi
ązywania problemów decyzyjnych
Podsumowanie
Przypomnienie pojęć
•
harmonogramowanie a problem przydziału
•
jedno vs. wiele kryteriów przydziału
•
rozwiązanie wielokryterialne
•
rozwiązanie niezdominowane (sprawne)
•
punkt nadir
•
punkt ideal
•
algorytm wielokryterialnej metody przydziału
•
kompromis kryteriów (d
1
i d
2
)
Metody rozwiązywania
problemów decyzyjnych
Metody rozwiązywania
problemów decyzyjnych
Piotr Sawicki
Piotr Sawicki
Wydział Maszyn Roboczych i Transportu
pok. 719, tel. 665 22 30, 665 21 29
E-mail: piotr.sawicki@put.poznan.pl
URL: http://www.put.poznan.pl/~piotrs
Harmonogramowanie pracy
Zastosowanie wielokryterialnej
metody przydziału
Harmonogramowanie pracy
Zastosowanie wielokryterialnej
metody przydziału