1.

Wielkości w ruchu obrotowym

2.    Moment pędu i moment siły

3.

Zasada zachowania momentu pędu

4.    Ruch obrotowy bryły sztywnej względem ustalonej osi

-II zasada dynamiki dla ruchu obrotowego
-moment bezwładności
-energia kinetyczna ruchu obrotowego

5.    Precesja

ZASADA ZACHOWANIA 

MOMENTU PĘDU: PODSTAWY 

DYNAMIKI BRYŁY SZTYWNEJ

WSTĘP

Dotychczas opisywaliśmy ruch (kinematykę) i przyczyny ruchu 
(dynamikę) tylko dla punktu materialnego

Ale rzeczywiste obiekty są znacznie bardziej skomplikowane: 
składają się z wielu punktów materialnych, czasem zupełnie ze 
sobą nie powiązanych.

Jeśli wzajemne położenie punktów materialnych w ciele jest stałe, to 

ciało takie nazywa się bryłą sztywną , a jego ruch jest szczególnie 

prosty: da się opisać jako złożenie ruchu postępowego i ruchu 

obrotowego. 

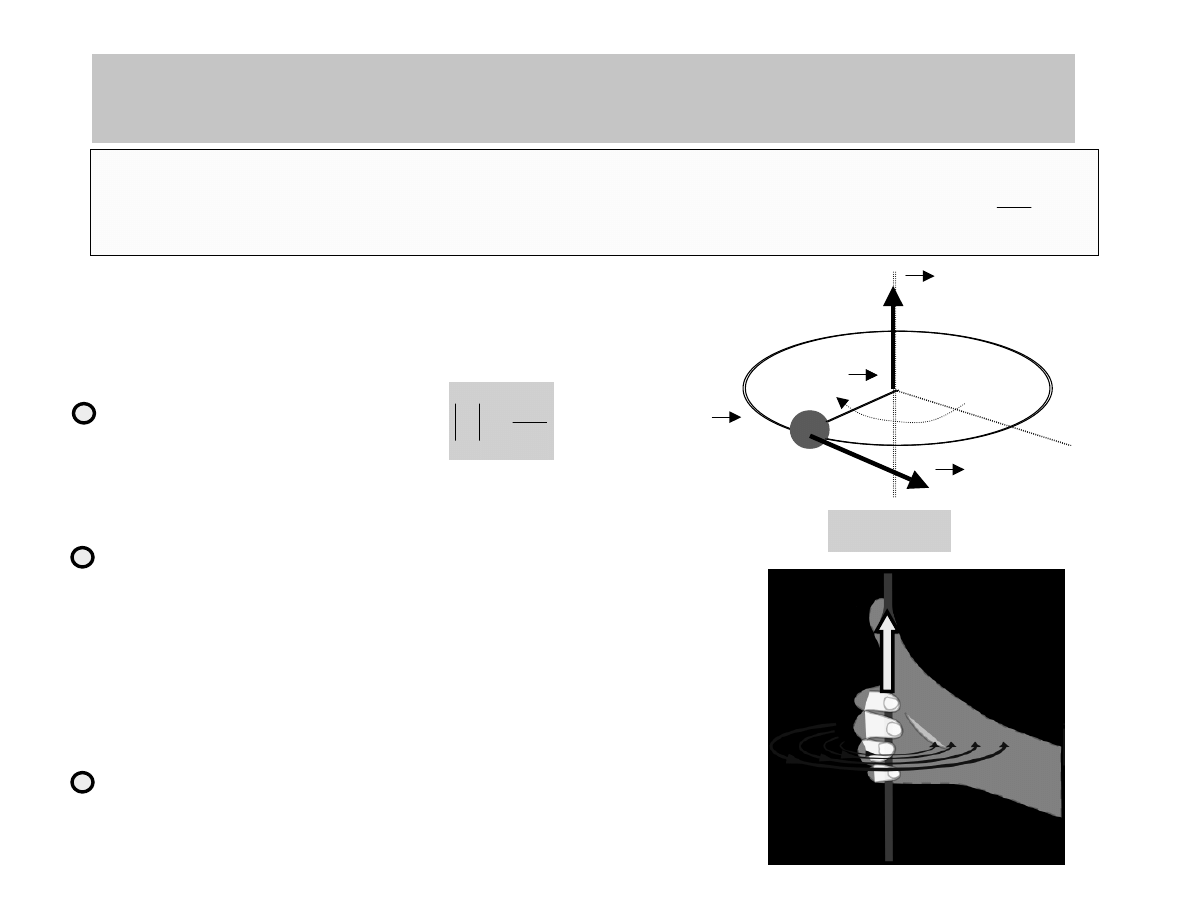
WIELKOŚCI W RUCHU OBROTOWYM: PRĘDKOŚĆ 

KĄTOWA

Kierunek wektora prędkości 
kątowej określony jest regułą 
prawej dłoni

Ruch ciała obracającego się względem stałej osi można opisać 
szybkością zmian kąta θ zakreślonego przez wektor wodzący 
dowolnego punktu

dt

dθ

=

ω

r

θ

V

dt

dθ

=

ω

r

Prędkość kątowa jest 
wektorem

r

θ

Kierunek wektora 
prędkości kątowej zależy 
od kierunku obrotu

r

V

r

v

r

×

ω

=

V

ω

ω

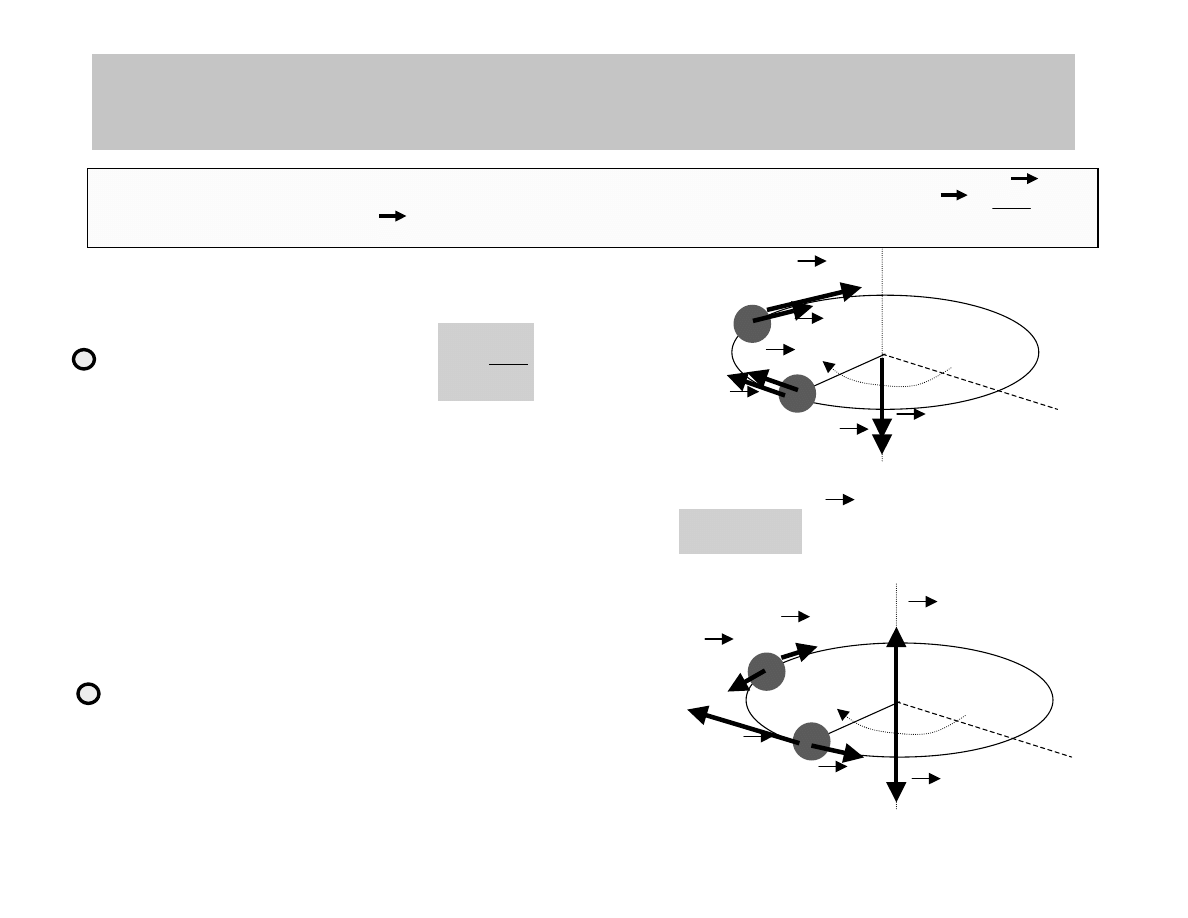
WIELKOŚCI W RUCHU OBROTOWYM: 

PRZYŚPIESZENIE KĄTOWE

ω

ω

ω

ω

θ

V

ε

ε

ε

ε

dt

dω

=

ε

r

r

Przyśpieszenie kątowe 
jest wektorem

Przyśpieszenie ciała w ruchu obrotowym można opisać szybkością 
zmian prędkości kątowej ω

dt

dω

=

ε

V’

a

s

a’

s

Kierunek wektora 
przyśpieszenia kątowego 
zależy od kierunku zmian ω

ω

ω

ω

r

a

s

r

r

r

×

ε

=

a

s

- przyśpieszenie 

styczne do toru

θ

V

ε

ε

ε

ε

a

s

’

a

s

ω

ω

ω

ω

V’

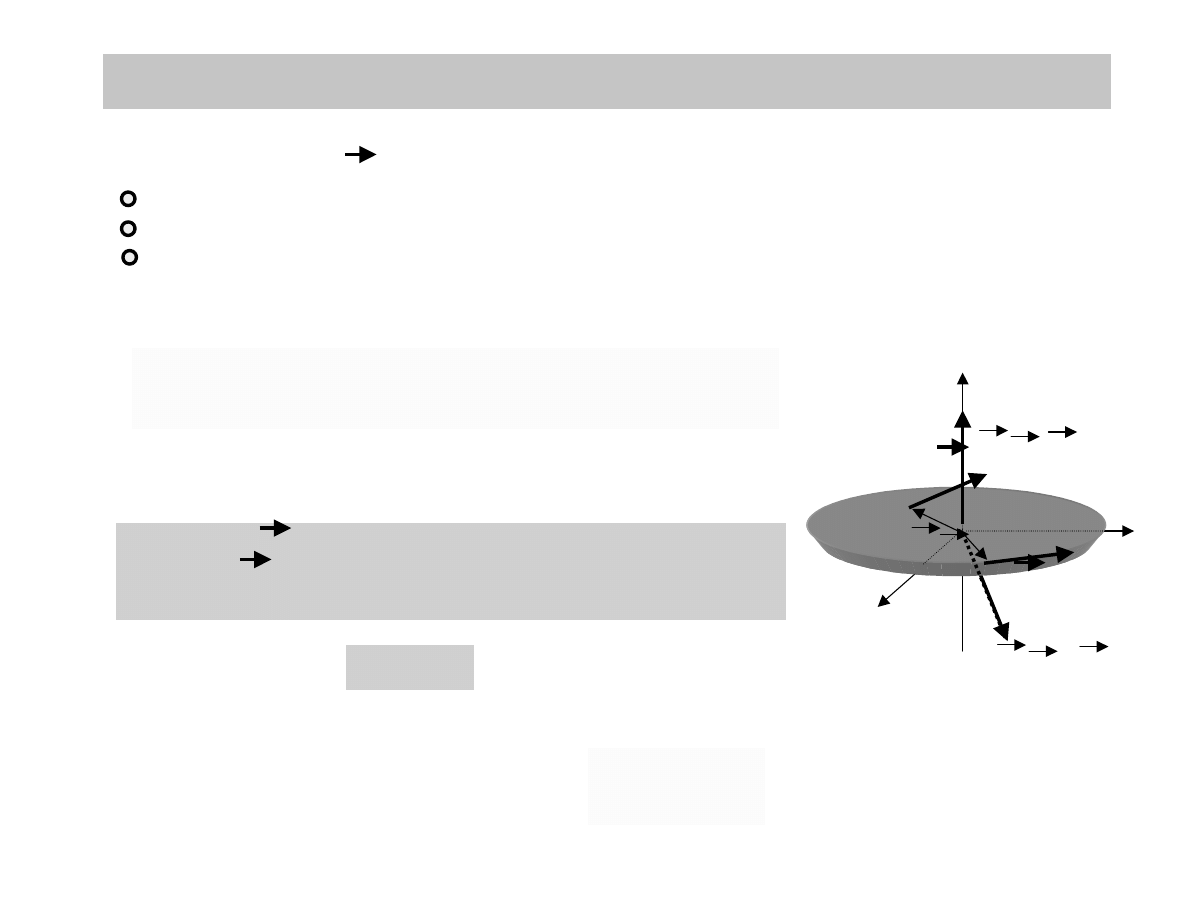
MOMENT SIŁY

Moment siły F przyłożonej do bryły w punkcie o wektorze 
wodzącym r, w stosunku do początku inercjalnego układu 
odniesienia wynosi

F

r

N

r

r

r

×

≡

Ruch obracającego się ciała można zmienić przykładając 

do niego moment siły

x

y

z

F

r

N=r × F

Jeśli sił jest więcej, to całkowity 
moment jest sumą wektorową 
wszystkich momentów

r

1

F

1

N

1

=r

1

×

F

1

∑

×

=

i

i

i

F

r

N

r

r

r

Efekt przyłożenie siły F do ciała, które może się obracać zależy od:

wielkości siły 
odległości punktu przyłożenia od osi obrotu
kąta przyłożenia siły w stosunku do prędkości punktu przyłożenia

MOMENT PĘDU

Efektem przyłożenie momentu siły N do ciała, jest nadanie mu ruchu obrotowego

Moment pędu bryły w stosunku do początku 
inercjalnego układu odniesienia wynosi

∑

×

≡

i

i

i

p

r

L

r

r

r

Moment pędu i moment siły to pojęcia, które można stosować do dowolnego ruchu, 
nie tylko obrotowego

Jeśli do ciała przyłożony jest moment siły, to zmienia się 
moment pędu ciała

x

y

z

r

i

p

1

L=

Σ

r

i

×

p

i

ω

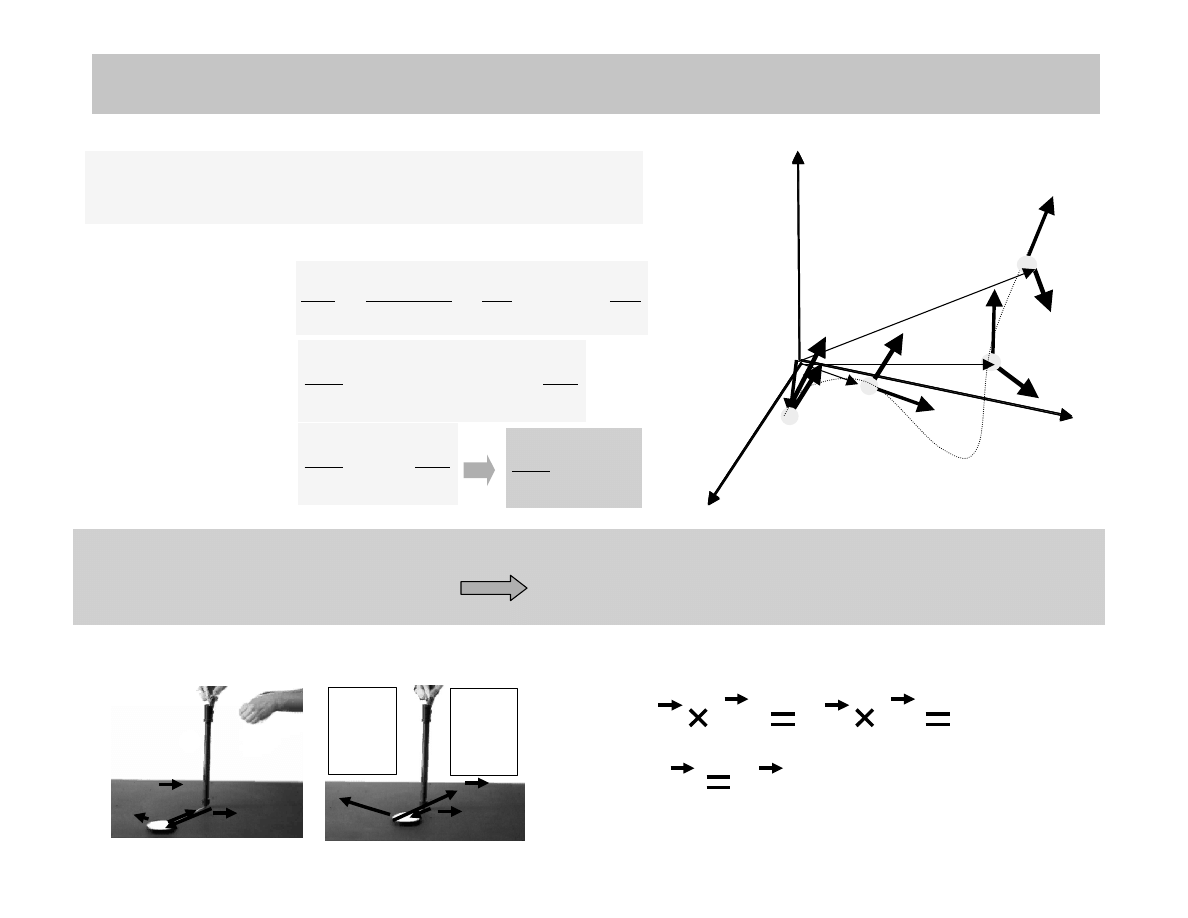
W jakich okolicznościach moment pędu może się 
zmienić?

ZASADA ZACHOWANIA MOMENTU PĘDU

dt

p

d

r

p

dt

r

d

dt

)

p

r

(

d

dt

L

d

r

r

r

r

r

r

r

×

+

×

=

×

=

dt

p

d

r

)

v

m

v

(

dt

L

d

r

r

r

r

r

×

+

×

=

dt

p

d

r

dt

L

d

r

r

r

×

=

Szybkość zmiany 
momentu pędu 
wynosi:

x

z

F

y

r

p

Jeśli brak jest zewnętrznego momentu siły to moment pędu układu mas jest zachowany

0

N

zewn

=

r

=

L

r

const

F

r

dt

L

d

r

r

r

×

=

F

x

z

x

y

p

p

x

z

x

y

F

x

F

p

z

x

y

r

F

i

ale

r

i

F

f

r

f

r

i

F

i

r

f

F

f

stąd

0

L

i

L

f

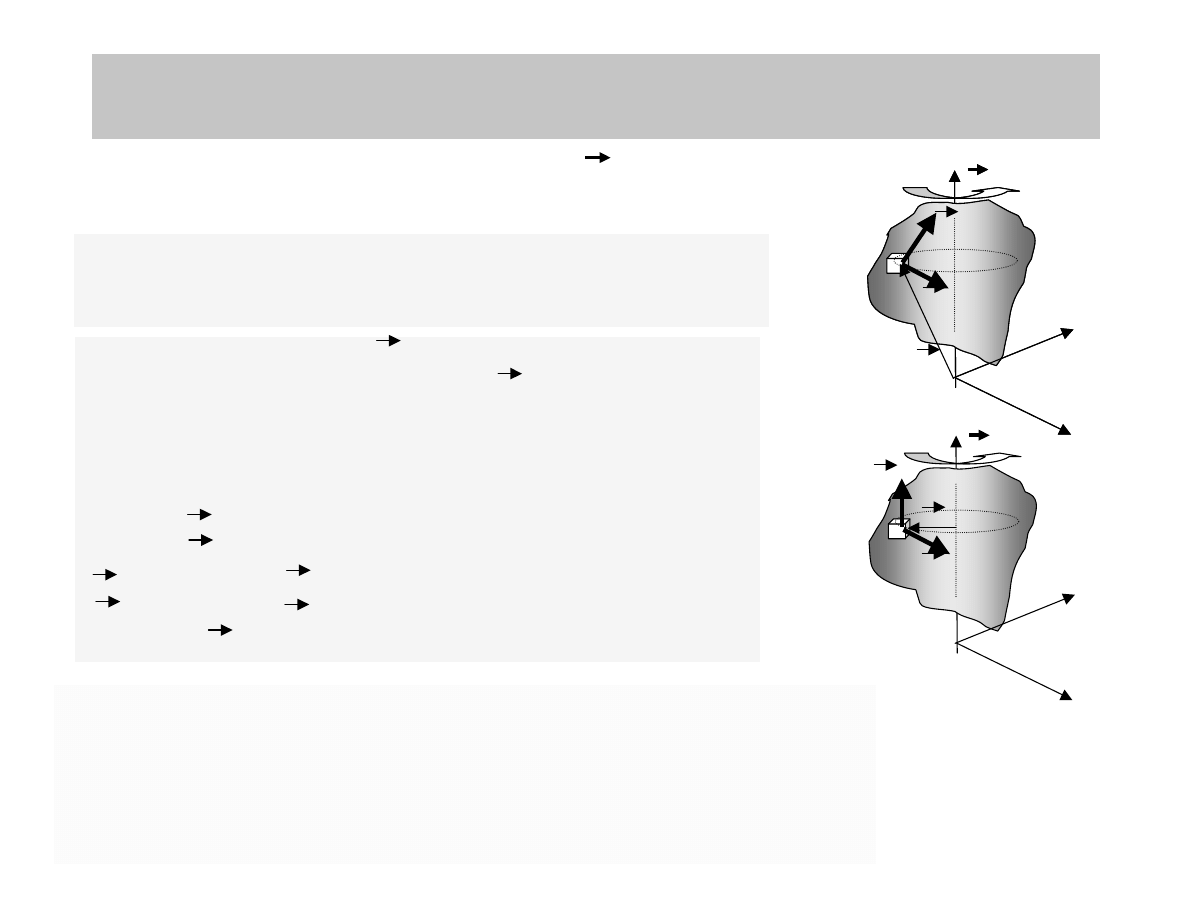
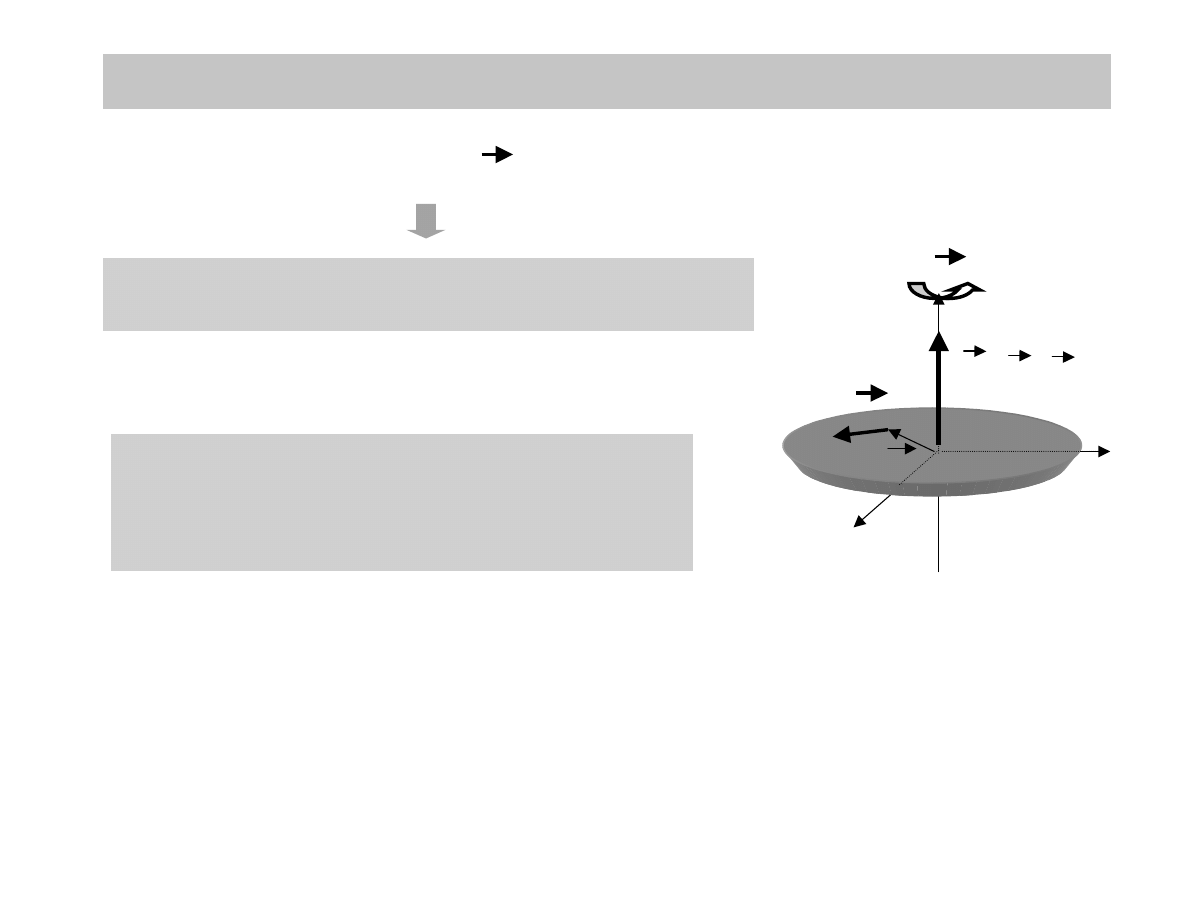
RUCH OBROTOWY BRYŁY SZTYWNEJ WZGLĘDEM 

NIERUCHOMEJ OSI

Bryła obraca się ze stałą prędkością kątową ω

ω

ω

ω

wokół stałej osi z

obrót bryły względem 
stałej osi w kierunku z

Jaki jest moment pędu bryły? 

W ogólności jest to skomplikowane zagadnienie: trzeba 
zsumować iloczyny

, w wyniku czego moment 

pędu będzie zależał od rozłożenia masy w bryle.

i

i

i

m

V

r

∆

×

r

r

Ponieważ jednak prędkość V

i

każdego punktu bryły leży w 

płaszczyźnie xy dlatego wyrażenie na L rozpada się na dwie 
części:

ponieważ V

i

leży w płaszczyźnie xy. Tutaj: 

L

xy

jest składową L w płaszczyźnie xy, a

L

z

jest składową L wzdłuż osi z

Obliczenie L

z

jest proste: 

z

xy

i

i

i

i

i

i

i

i

i

i

i

i

i

L

L

∆

m

V

r

∆

m

V

r

∆

m

V

)

r

r

(

∆

m

V

r

L

r

r

r

r

r

r

r

r

r

r

r

r

+

=

×

+

×

=

=

×

+

=

×

=

∑

∑

∑

⊥

⊥

ll

ll

ponieważ prędkość elementu ∆m

i

masy w położeniu r

i

wynosi V

i

= r

i

ω

.

I-moment bezwładności

,

m

r

zˆ

m

r

r

zˆ

m

V

r

zˆ

m

V

r

L

i

2

i

i

i

i

i

i

i

i

i

z

i

∑

∑

∑

∑

∆

ω

=

∆

ω

=

∆

=

∆

×

=

⊥

⊥

⊥

⊥

⊥

r

r

r

∑

∆

=

⊥

i

2

m

r

I

i

ω

z

y

x

V

i

r

i⊥

L

z

ω

z

y

x

ω

z

y

x

V

i

r

i

L

i

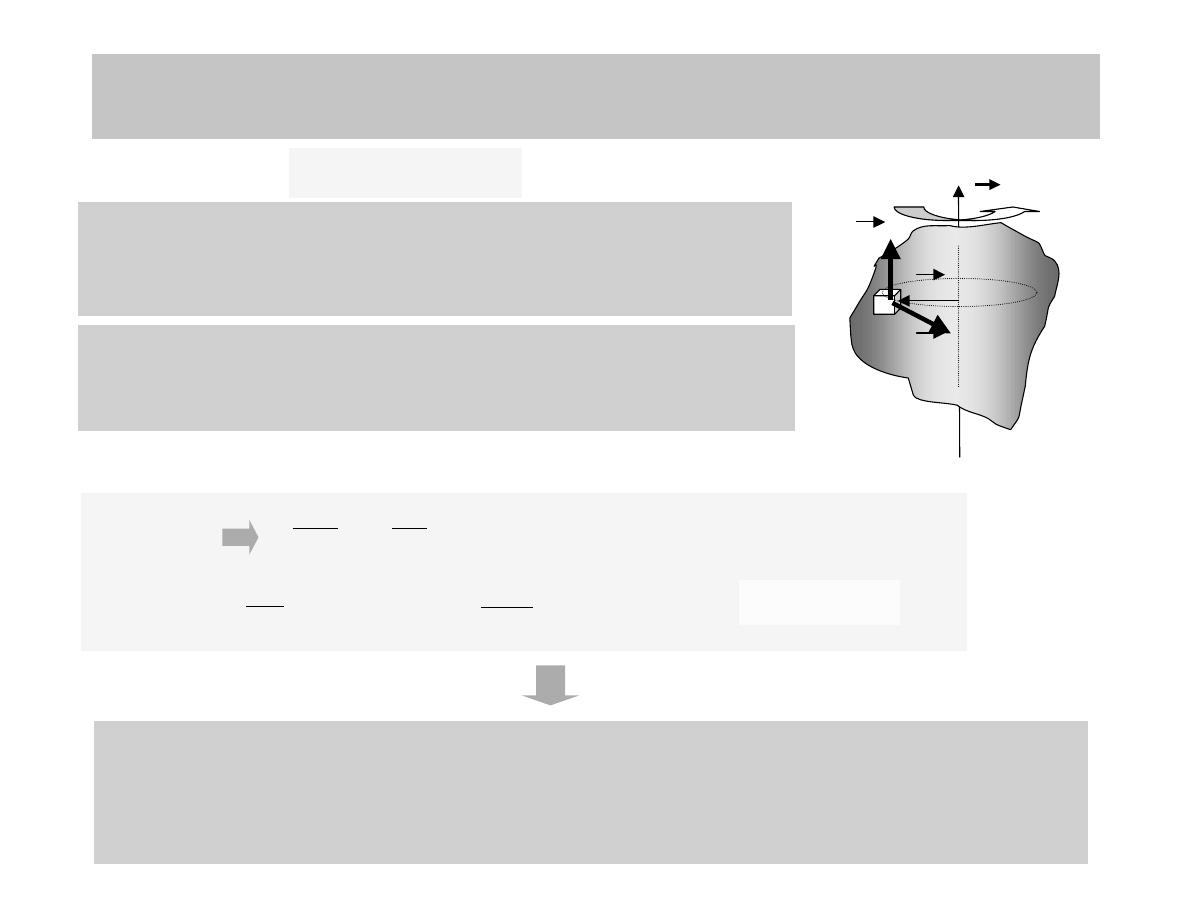
RUCH OBROTOWY BRYŁY SZTYWNEJ WZGLĘDEM 

NIERUCHOMEJ OSI

Jeśli bryła obraca się ze stałą prędkością kątową ω

ω

ω

ω

wokół 

stałej osi to składowa jej  momentu pędu wzdłuż tej osi wynosi

I

L

z

ω

=

r

r

Jeśli obracająca się bryła jest symetryczna względem 
osi obrotu, to jej całkowity momentu pędu wynosi

I

ω

L

r

r

=

Stąd:

I

L

z

ω

=

r

r

ω

ω

ω

ω

z

V

i

r

i⊥

L

z

w  jaki sposób można zmienić moment pędu takiej bryły?

ale ponieważ

ε

⋅

=

ω

⋅

=

r

r

r

I

dt

d

I

dt

L

d

z

zewn

N

dt

L

d

r

r

=

z

,

zewn

z

N

dt

dL

=

I

L

z

ω

=

r

r

czyli

ε

⋅

= I

N

z

,

zewn

więc:

Składowa przyśpieszenia kątowego wzdłuż osi obrotu ustalonej w  układzie inercjalnym 
(lub przechodzącej przez środek masy), zależy od składowej zewnętrznego momentu 
siły wzdłuż tej osi

ε

⋅

=

r

r

I

N

zewn

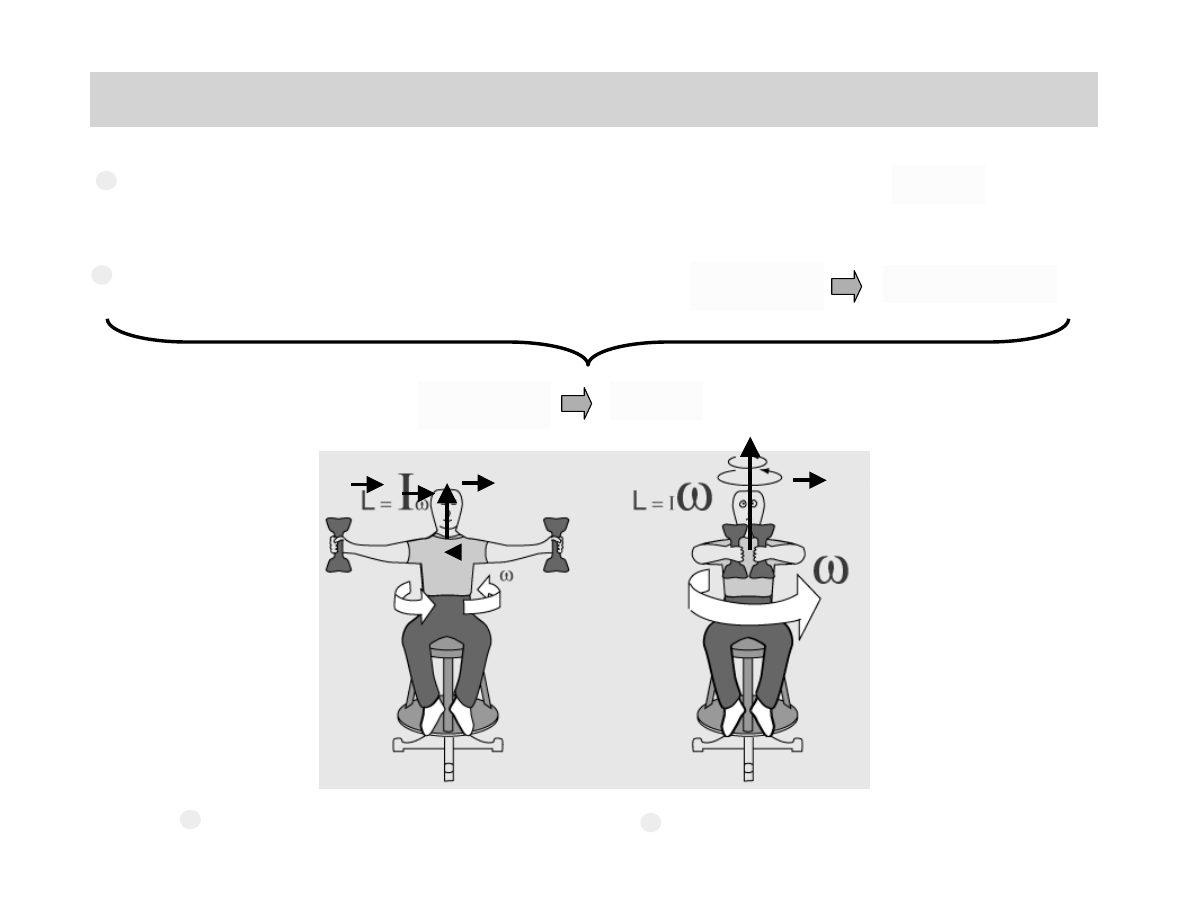
Jeśli obracająca się bryła jest symetryczna względem 
osi obrotu, to jej całkowity momentu pędu wynosi

I

ω

L

r

r

=

PRZYKŁAD: STOLIK OBROTOWY

Jeśli brak jest zewnętrznego momentu siły to 
moment pędu układu mas jest zachowany

0

N

zewn

=

r

const

L =

r

0

N

zewn

=

r

I

ω

L

r

r

=

ω

ω

ω

ω

ω

Ciężarki odległe od osi obrotu: 
mała prędkość kątowa

Ciężarki bliskie osi obrotu: duża 
prędkość kątowa

Rysunek skopiowane z 
http://hyperphysics.phy-astr.gsu.edu/

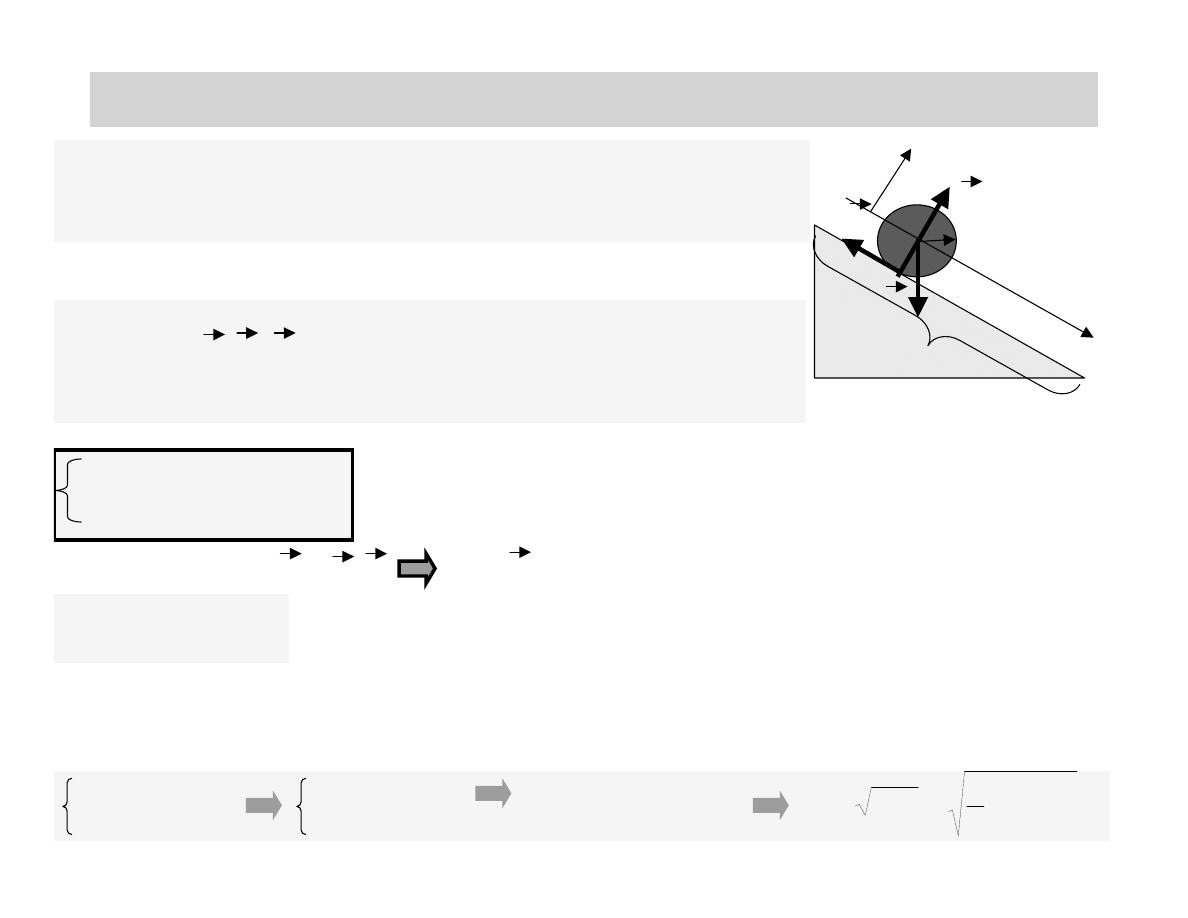
PRZYKŁAD: TOCZENIE PO RÓWNI

Pełny walec o masie M i promieniu r toczy się bez poślizgu po 
równi o dl. L nachylonej pod kątem α do poziomu. Ile wynosi 
prędkość środka masy walca w najniżej położonym punkcie równi?

T

G

R

N

N

N

I

T

G

R

M

a

r

r

r

r

r

r

r

r

+

+

=

ε

+

+

=

Opisuje ruch środka masy

Opisuje ruch obrotowy względem środka masy

Każdy z momentów N

F

to rXF        tylko T ma niezerowy moment siły względem osi obrotu. 

Ma=Mgsinα-T
Tr = Iε

Tr=(1/2)Mr*a  

T=(1/2)M*a 

a=2/3gsinα

Ma=Mgsinα-T

Ma=Mgsinα-T

Rzut sił i przyśpieszenia na kierunek x

Rzut momentów sił i przyśpieszenia kątowego na kierunek z

Ponieważ I dla walca wynosi I=(1/2)Mr

2

, dlatego Tr=(1/2)Mr

2

*ε. 

Jeśli toczenie bez poślizgu, to ruch postępowy środka masy i ruch obrotowy wokół osi obrotu 
walca są powiązane: a=ε*r⇒ ε=a/r. 

(Ponieważ V=at i L=at

2

/2) 

α

=

=

sin

gL

3

4

La

2

V

Środek masy walca będzie się poruszał tak, jakby wszystkie siły 
zewnętrzne (R, T i G) były do niego przyłożone, czyli będzie 
poruszał się ruchem jedn. przyśp. wzdłuż równi. Walec będzie się 
obracał względem osi przechodzącej przez ten środek masy. 

ROZWIĄZANIE

α

G

R

T

L

x

y

r

MOMENTY BEZWŁADNOŚCI: OBLICZANIE

ω

ω

ω

ω

r

i

Moment bezwładności względem osi obrotu, to suma mas i 
odległości od osi obrotu

∫

∑

=

∆

=

dm

r

m

r

I

2

i

2

i

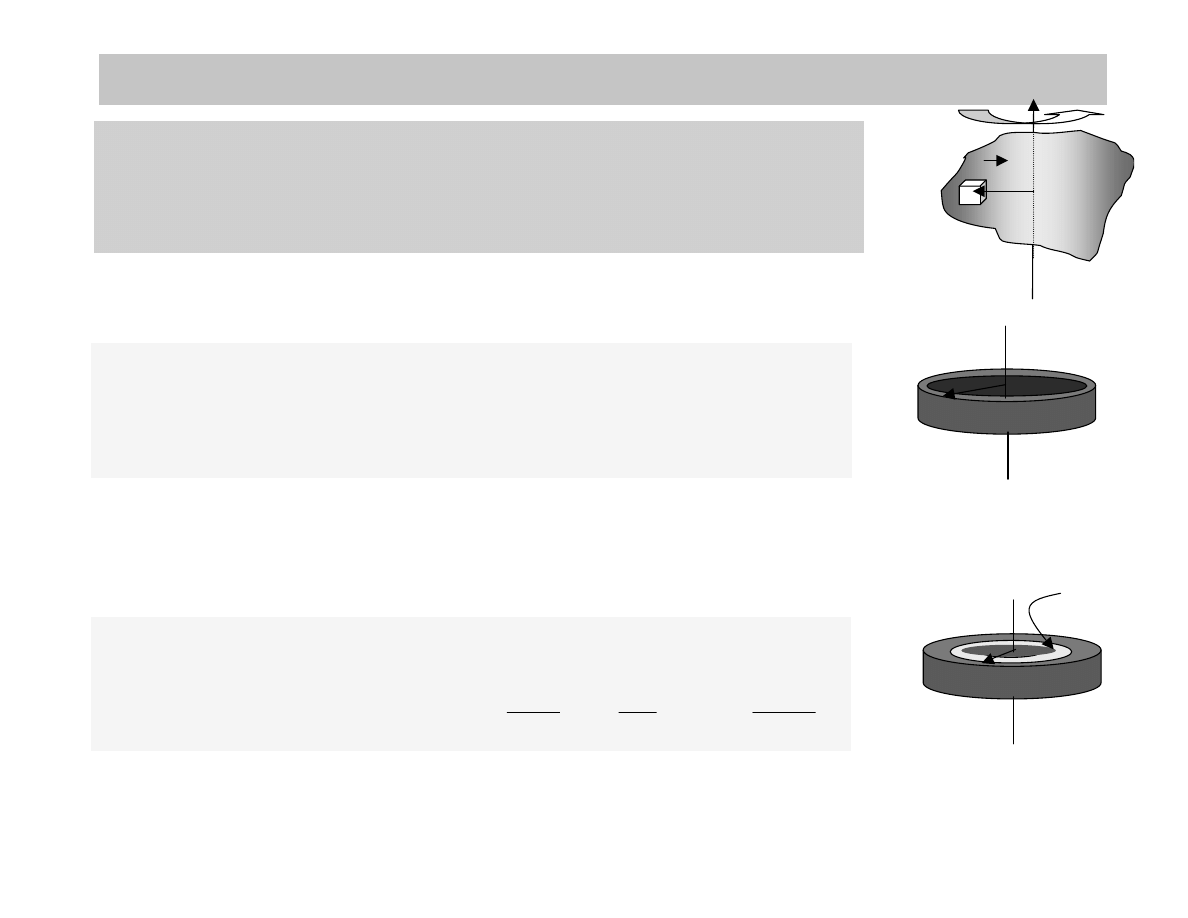
moment bezwładności obręczy

R

Ponieważ masa jest rozłożona symetrycznie i w  odległości R 
względem osi obrotu, to 

m

R

dm

r

I

2

2

=

=

∫

moment bezwładności walca

R

dm’

Walec składa się z pierścieni o masie dm’ i w  odległości r 
względem osi obrotu, to 

2

MR

dr

r

R

M

2

R

M

r

2

dr

r

'

dm

r

dm

r

I

2

R

0

3

2

2

R

0

2

2

2

=

⋅

=

π

⋅

π

⋅

=

=

=

∫

∫

∫

∫

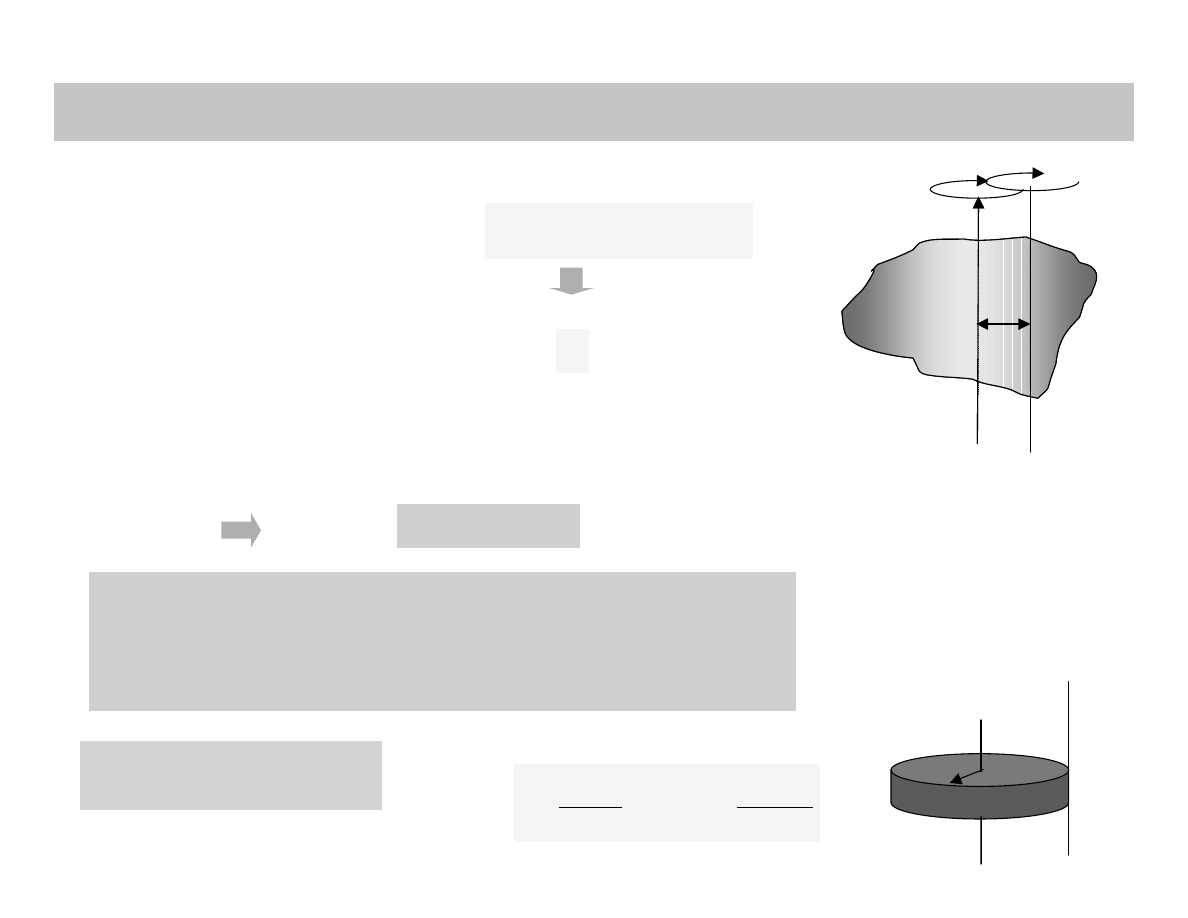
MOMENTY BEZWŁADNOŚCI: TWIERDZENIE STEINERA

Moment bezwładności względem osi 
obrotu, to suma mas i odległości od 
osi obrotu

∫

∑

=

∆

=

dm

r

m

r

I

2

i

2

i

Przykład: moment 
bezwładności walca

2

MR

3

MR

2

MR

I

2

2

2

=

+

=

R

oś obrotu

Moment bezwładności względem dowolnej osi jest równy 
momentowi bezwładności względem osi do niej równoległej i 
przechodzącej przez środek masy plus iloczyn masy przez 
kwadrat odległości między obiema osiami

∑

+

=

i

2

∆

m

a

I

0

I

śm

Oznaczmy przez I

0

moment 

bezwładności jeśli oś obrotu 
przechodzi przez środek masy

0

I

a

A jaki jest moment bezwładności względem innej osi, nie 
przechodzącej przez środek masy?

śm

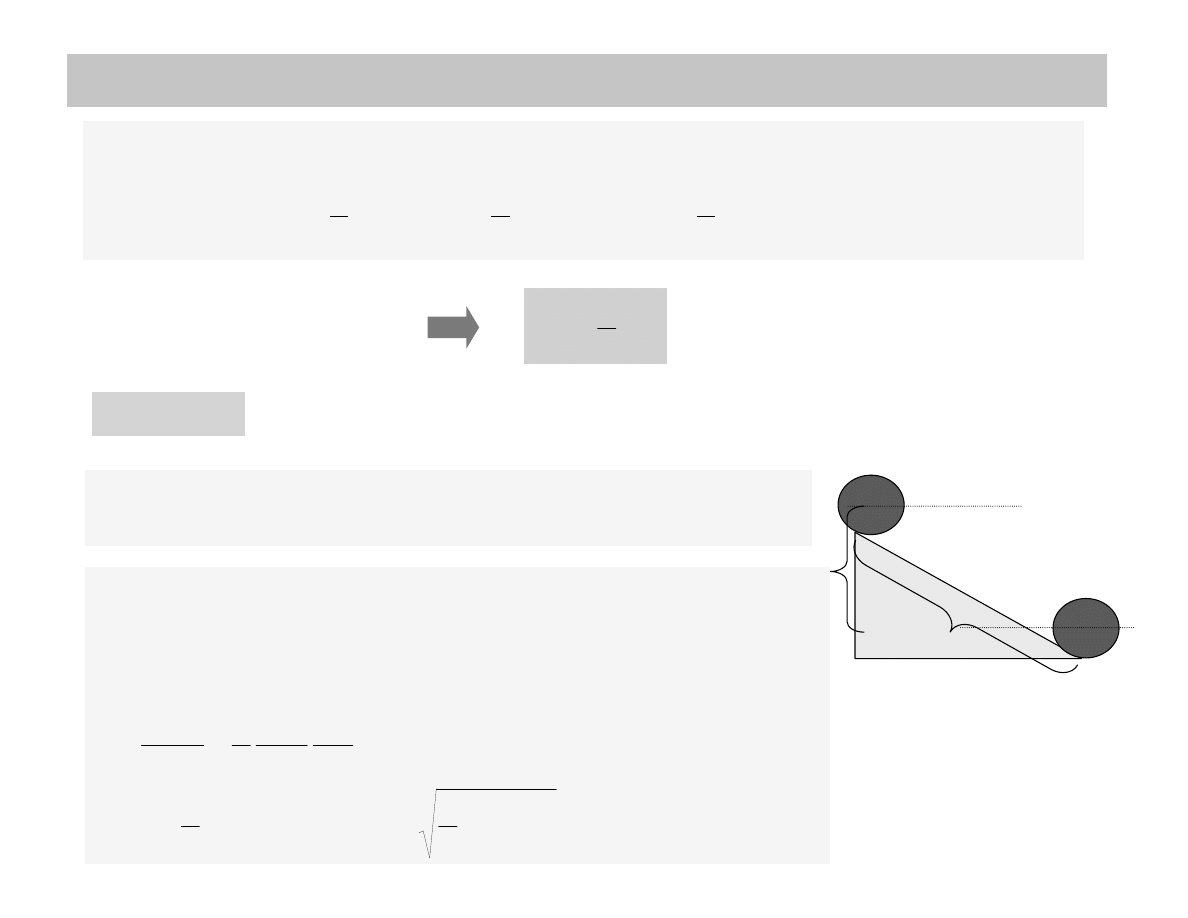
ENERGIA KINETYCZNA RUCHU OBROTOWEGO

Jeśli bryła obraca się wokół stałej osi to całkowita energia kinetyczna jest  sumą energii 
kinetycznych poszczególnych mas ∆m:

∑

∑

∑

∆

ω

=

ω

∆

=

∆

=

i

i

2

i

i

2

2

i

i

i

2

i

i

K

r

m

2

1

)

r

(

m

2

1

v

m

2

1

E

PRZYKŁAD:

α

h

T

L

E

p

=mgh

Korzystając z zasady zachowania energii obliczyć prędkość 
środka masy walca u podnóża równi

E

K

=(mV

2

+Iω

2

)/2

Energia potencjalna na szczycie przekształca się w energię 
kinetyczna ruchu postępowego i obrotowego 

E

p

=E

K

(mV

2

+Iω

2

)/2=mgh

Ale:
I=mr

2

/2 i ω=V/r, to 

α

=

⇒

α

=

α

=

+

sin

gL

3

4

V

sin

gL

4

3

V

sin

mgL

r

V

2

mr

2

1

2

mV

2

2

2

2

2

I

2

1

E

2

K

ω

=

Bąk  symetryczny  podparty  u  podstawy, 
wiruje  z  bardzo  dużą  prędkością  kątową  ω. 
Jego  chwilowy  moment  pędu  wynosi  L=Iω

ω

ω

ω

, 

czyli skierowany jest wzdłuż osi obrotu. Jaki 
będzie  ruch  bąka,  jeśli  przestanie  działać 
podtrzymująca go siła?

r

sm

L

PRECESJA

R

G

- siła reakcji R podłoża przyłożona do punktu podparcia (moment siły pochodzący od tej siły 
wynosi 0).

Na bąk działają dwie siły:
- ciężkości  G=mg,  (moment  siły  z  nią 
związany, 

obliczony 

względem 

punktu 

podparcia, wynosi N=r

sm

XG i jest skierowany 

ll do podłoża),

r

sm

N

dL

Całkowity moment siły N=r

sm

X G powoduje zmianę momentu pędu dL=Ndt, czyli w kierunku ⊥ do 

L (bo N jest ⊥ do r

sm

, a r

sm

ll L). ⇒ L  obraca się (precesuje) wokół kierunku równoległego do 

działającej siły. 

dθ

ω

=

=

θ

=

Ω

I

mgr

L

Gr

dt

d

sm

sm

α

Lsinα

dL=r

sm

Gsinα

Ponieważ     dL=r

sm

Gsin(α)dt, a kąt dθ wynosi:   

L

dt

r

G

sin

L

dt

sin

r

G

sin

L

dL

d

sm

sm

⋅

⋅

=

α

⋅

⋅

α

⋅

⋅

=

α

⋅

=

θ

więc prędkość kątowa 
precesji Ω: