Jacek Kabziński

Automatyka i sterowanie

————————————————————————————————————————

2

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

C(s)

P(s)

D(s)

R(s)

Y(s)

E(s)

U(s)

regulator

obiekt

N(s)

F(s)

v(s)

n(s)

F(s)=1 – sprz. od uchybu

3

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

6 transmitancji:

YN

T

,

YD

T

,

YR

T

;

N

PC

D

PC

P

R

PC

FPC

Y

+

+

+

+

+

=

1

1

1

1

,

N

PC

PC

D

PC

P

R

PC

FPC

n

+

−

+

+

+

+

=

1

1

1

,

N

PC

C

D

PC

R

PC

FC

v

+

−

+

+

+

+

=

1

1

1

1

,

UN

T

,

UD

T

,

UR

T

:

N

PC

C

D

PC

PC

R

PC

FC

U

+

−

+

+

−

+

+

=

1

1

1

,

N

PC

D

PC

P

R

PC

F

E

+

−

+

+

−

+

+

=

1

1

1

1

Na sygnał zadający

Na szum pomiarowy

Na zakłócenie

P(s)C(s) Transmitancja układu otwartego

1

1

S( s )

P( s )C( s )

=

+

funkcja wrażliwości

1

YR

S( s ) T ( s )

+

=

4

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

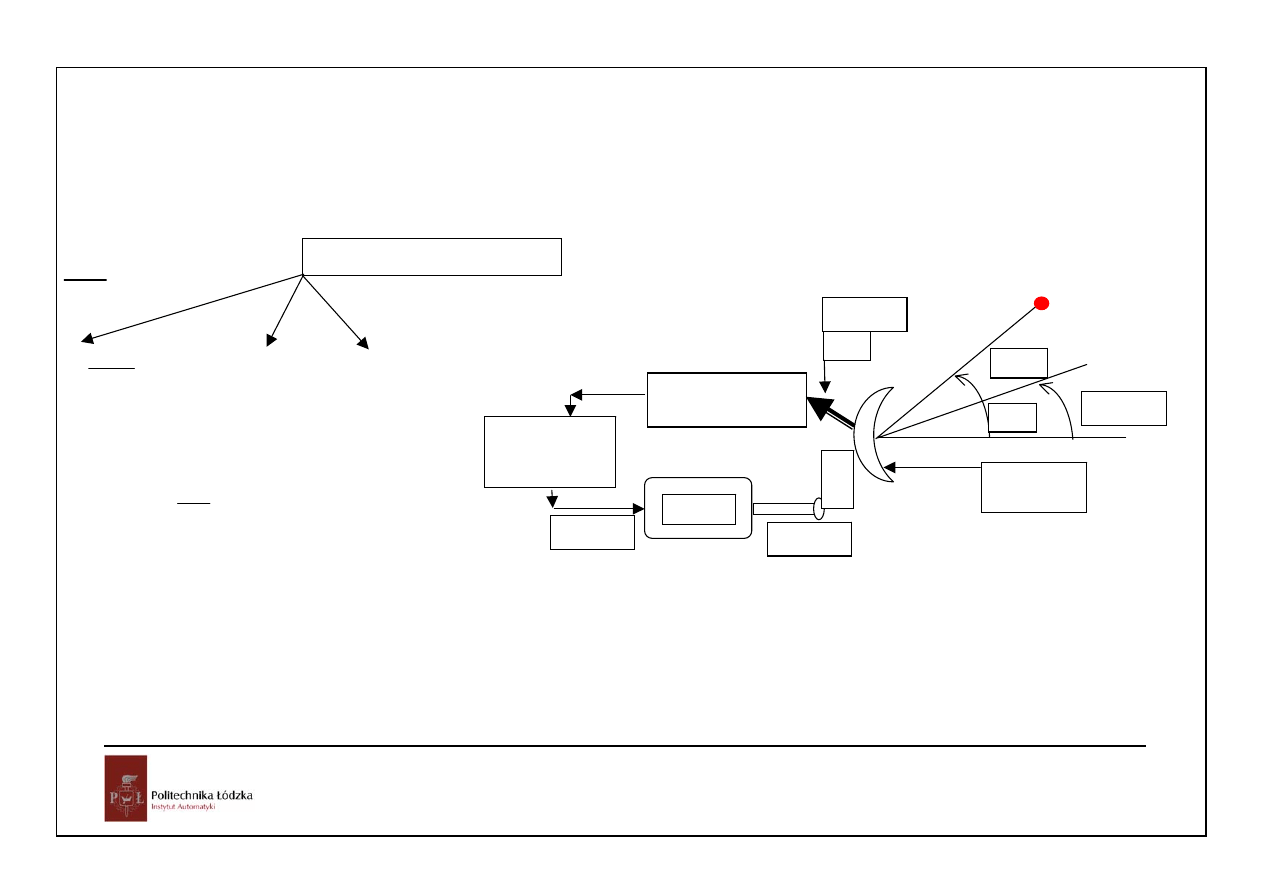
Silnik serwo

0

d

dt

d

J

( t ) B ( t ) M ( t )

dt

θ ω

ω τ

ω

=

=

−

−

( t ) K i( t ) K i( t )

τ

τ

ϕ

=

=

1

m

m

m

di

u( t ) L

Ri( t ) e ( t )

dt

e ( t ) K

( t ) K

( t )

ϕω

ω

=

+

+

=

=

silnik

Układ pomiaru i
sterowania

Wzmacniacz
mocy

θ

a

(t)

r(t)

e(t)

θ (t)

u(t)

r(t)

θ

a

(t)

zakłócenie

Uwzględnia maszynę roboczą

5

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

0

1

( s )

( s )

s

Js ( s ) K i( s ) B ( s ) M ( s )

τ

θ

ω

ω

ω

=

=

−

−

m

u( s ) Lsi( s ) Ri( s ) K

( s )

ω

=

+

+

(

)

(

)

1

1

1

m

m

R

i( s )

u( s ) K

( s )

u( s ) K

( s )

L

Ls R

s

R

ω

ω

=

−

=

−

+

+

(

)

(

)

0

0

1

1

1

B

( s )

K i( s ) M ( s )

K i( s ) M ( s )

J

Js B

s

B

τ

τ

ω

=

−

=

−

+

+

6

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

0

1

u

m

m

K

K

RB

L

T

J

K K

JRs RB K K

s

B

RB

τ

τ

ω

τ

τ

≈ ⇒

=

=

+

+

⎛

⎞

+ +

⎜

⎟

⎝

⎠

1

1

R

L

s

R

+

K

τ

1

1

B

J

s

B

+

0

M

−

m

K

−

1

s

θ

u

ω

7

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

(

)

1

1

1

1

1

1

1

1

1

1

1

1

u

m

m

m

R

B

K

L

J

K

s

s

K

R

B

RB

T

L

J

K K

L

s

s

s

JRs RB

K K

R

B

K

K

R

B

RB

R

L

J

s

s

R

B

τ

τ

τ

ω

τ

τ

τ

+

+

=

=

=

⎛

⎞⎛

⎞

⎛

⎞

+

+ +

+

+

+

⎜

⎟⎜

⎟

⎜

⎟

+

⎝

⎠⎝

⎠

⎝

⎠

+

+

(

)

0

u

m

K

L ~

T

JRs RB

K K

τ

ω

τ

≈

⇒

=

+

+

C( s )

m

K

JRs RB K K

τ

τ

+

+

0

M

K M

−

1

−

1

s

θ

u

p

K

a

θ

r

N

8

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

(

)

0

0

a

u

m

K

L

T

JRs RB K K s

θ

τ

≈ ⇒

=

+

+

C( s )

m

K

JRs RB K K

τ

τ

+

+

0

M

K M

−

1

−

1

s

θ

u

p

K

a

θ

r

N

9

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

(

)

0

2

4

4

1

2

3

2

1

a

u

m

K

T

s( s

)( s

)

s( s

s

)

L

s

JRs RB

K K

s

R

θ

τ

=

=

=

+

+

+ +

⎛

⎞

⎛

⎞

+

+

+

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

C( s )

(

)

1

m

K

L

s

JRs RB

K K

R

τ

τ

⎛

⎞

+

+

+

⎜

⎟

⎝

⎠

z

M

−

1

−

1

s

θ

u

p

K

a

θ

r

N

10

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

C(s)=1:

2

2

2

4

4

3

2

4

3

2

4

1

3

2

a

r

s( s

s

)

T

s( s

s

)

s( s

s

)

θ

+

+

=

=

+

+

+

+

+

+

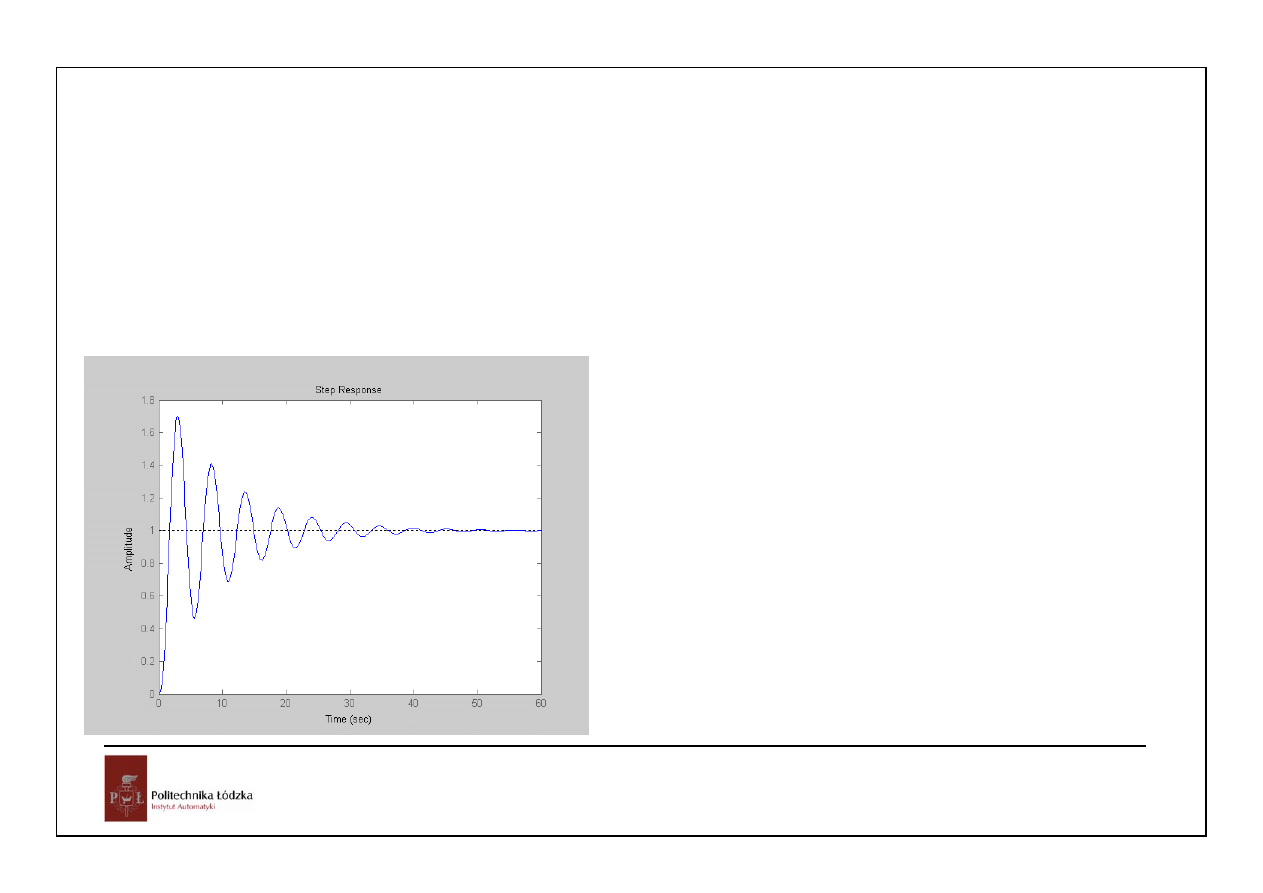
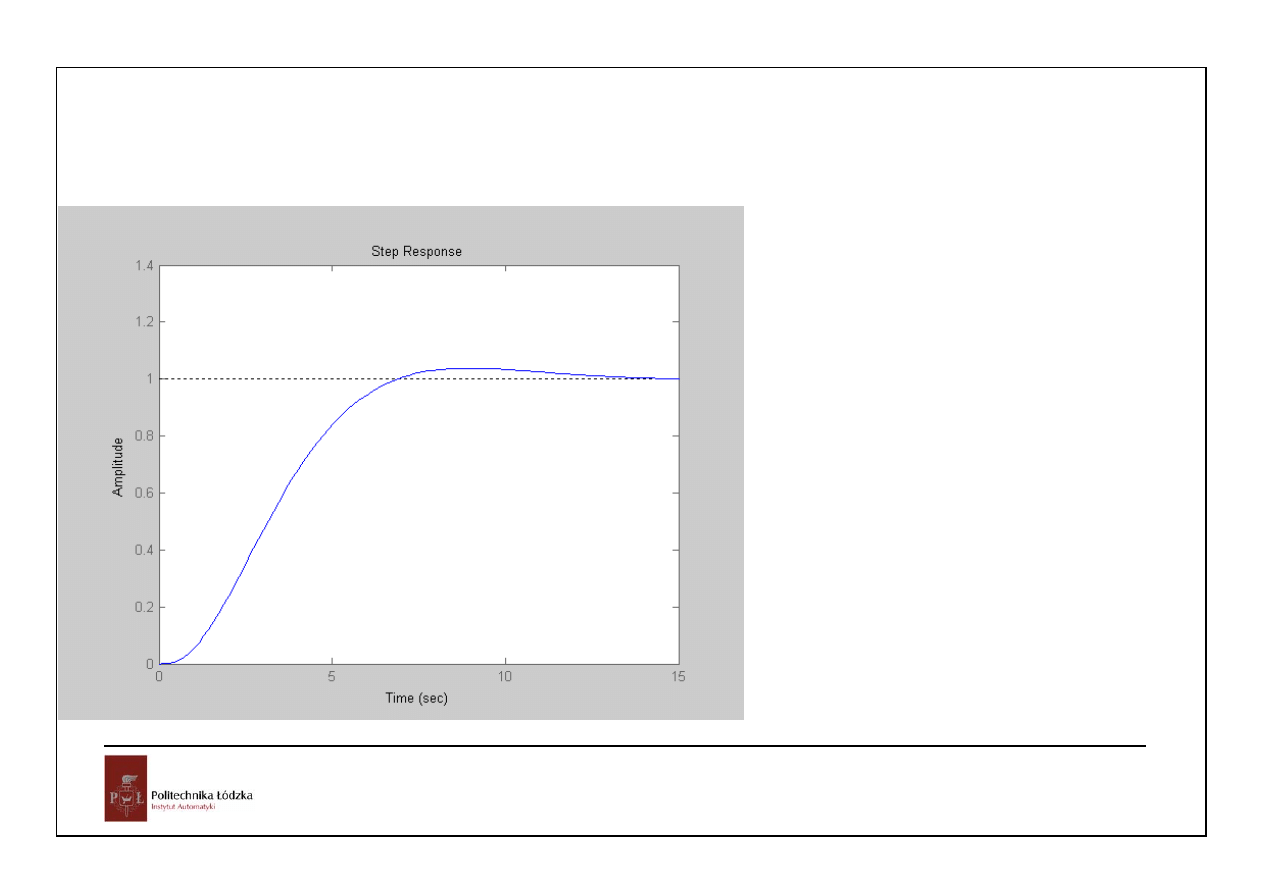
po zamknięciu stabilny,
małe zapasy stabilności,
przy wymuszeniu jednostkowym uchyb
ustalony zerowy,
przy wymuszeniu narastającym liniowo
uchyb ustalony=0.5
bieguny układu zamkniętego:

3

2

3

2

4 0

s

s

s

+

+

+ =

:

-2.7963
-0.1018 + 1.1917j
-0.1018 - 1.1917j

0

-45

-90

11

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

Taką transmitancję można przedstawić jako równoległe połączenie układu inercyjnego o biegunie

-2.7963 i oscylacyjnego o biegunach -0.1018 + 1.1917j i -0.1018 - 1.1917j. W odpowiedzi możemy

spodziewać się składowej aperiodycznej zanikającej jak exp(-2.7963t), czyli ze stałą czasową
1/2.7963=0.3576 i składowej oscylacyjnej o obwiedni zanikającej jak exp(-0.1018t), czyli ze stałą
czasową 1/0.1018=9.82, wypełnionej oscylacjami o okresie 2π/1.1917=5.27.
Dla tego układu można wyznaczyć opis w przestrzeni stanów:

a

równanie sta

d

x( t ) Ax( t ) Br( t )

dt

( t ) Cx( t ) Dr

nu

równanie wyjśc a

( t )

i

θ

=

+

=

+

np.

[

]

0

1

0

0

0

0

1

0

4 0 0

0

4

2 3

1

A

B

C

D

⎡

⎤

⎡ ⎤

⎢

⎥

⎢ ⎥

=

=

=

=

⎢

⎥

⎢ ⎥

⎢

⎥

⎢ ⎥

−

−

⎣

⎦

⎣ ⎦

wartości własne macierzy A są takie same jak bieguny transmitancji i

(

)

(

)

(

)

1

a

r

adj sI

A

T ( s ) C sI

A

B D C

B D

det sI

A

θ

−

−

=

−

+ =

+

−

.

12

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

Rozwiązanie równania stanu można otrzymać np. ze wzoru

( )

0

0

1

1

1

0

0

i

i

i

i

t

t

n

n

n

s t

s t

s t

s

T

T

T

i

i

i

i

i

i

i

i

i

x( t )

e v w x

e

v w Bu( )d

e v w x

e

Bu( )d

τ

τ

τ τ

τ τ

−

−

=

=

=

⎡

⎤

=

+

=

+

⎢

⎥

⎣

⎦

∑

∑

∑

∫

∫

13

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

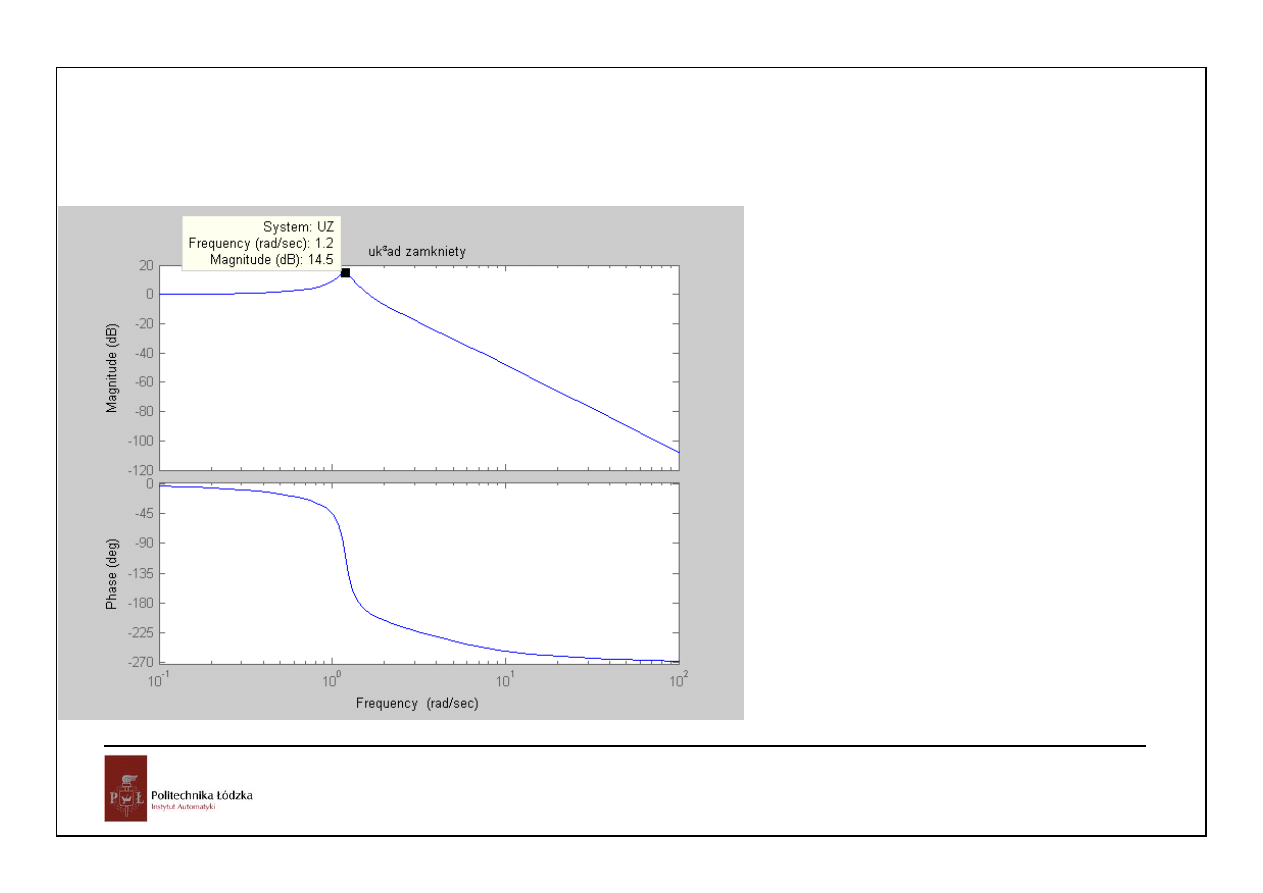
14

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

2

2

2

1

3

2

4

3

2

4

1

3

2

s( s

s

)

S

s( s

s

)

s( s

s

)

+

+

=

=

+

+

+

+

+

+

15

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

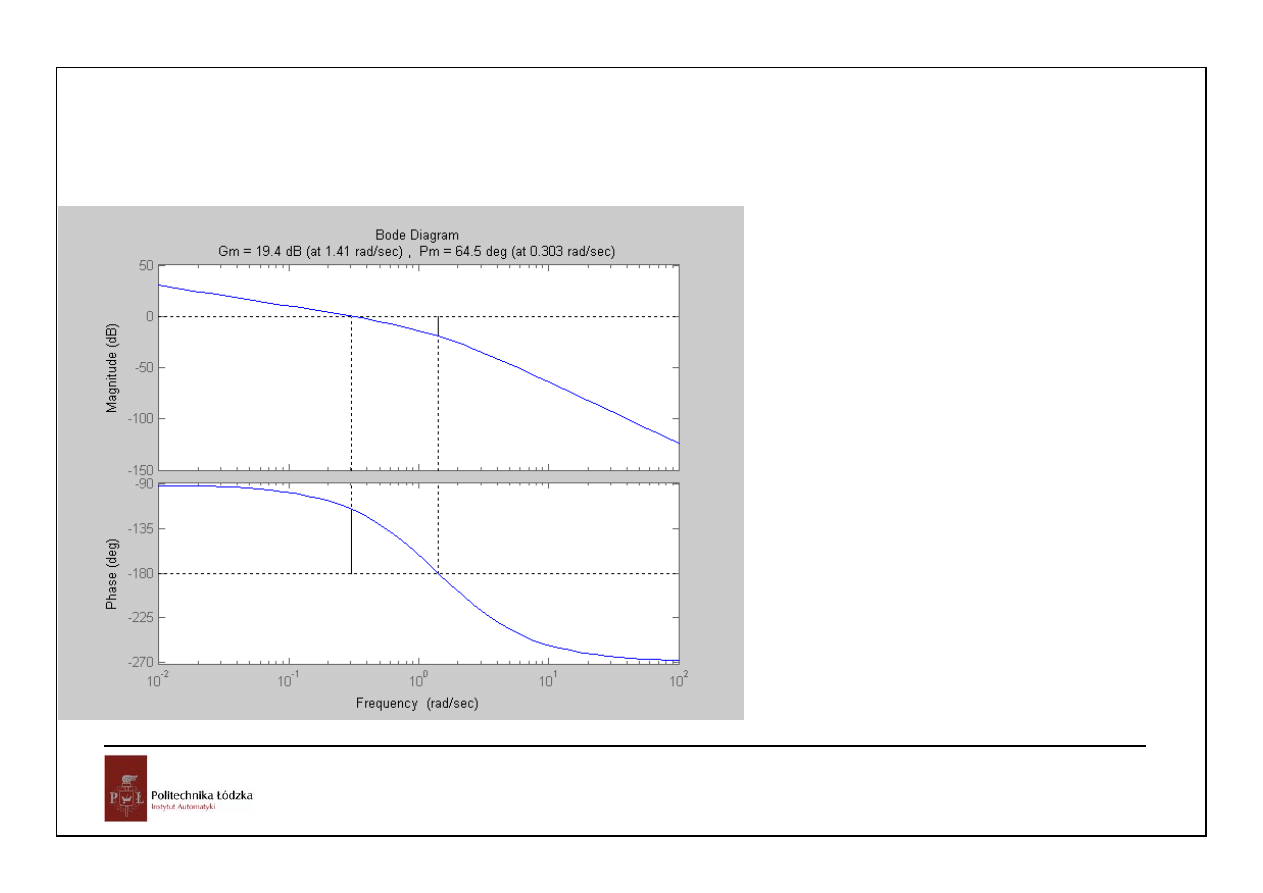
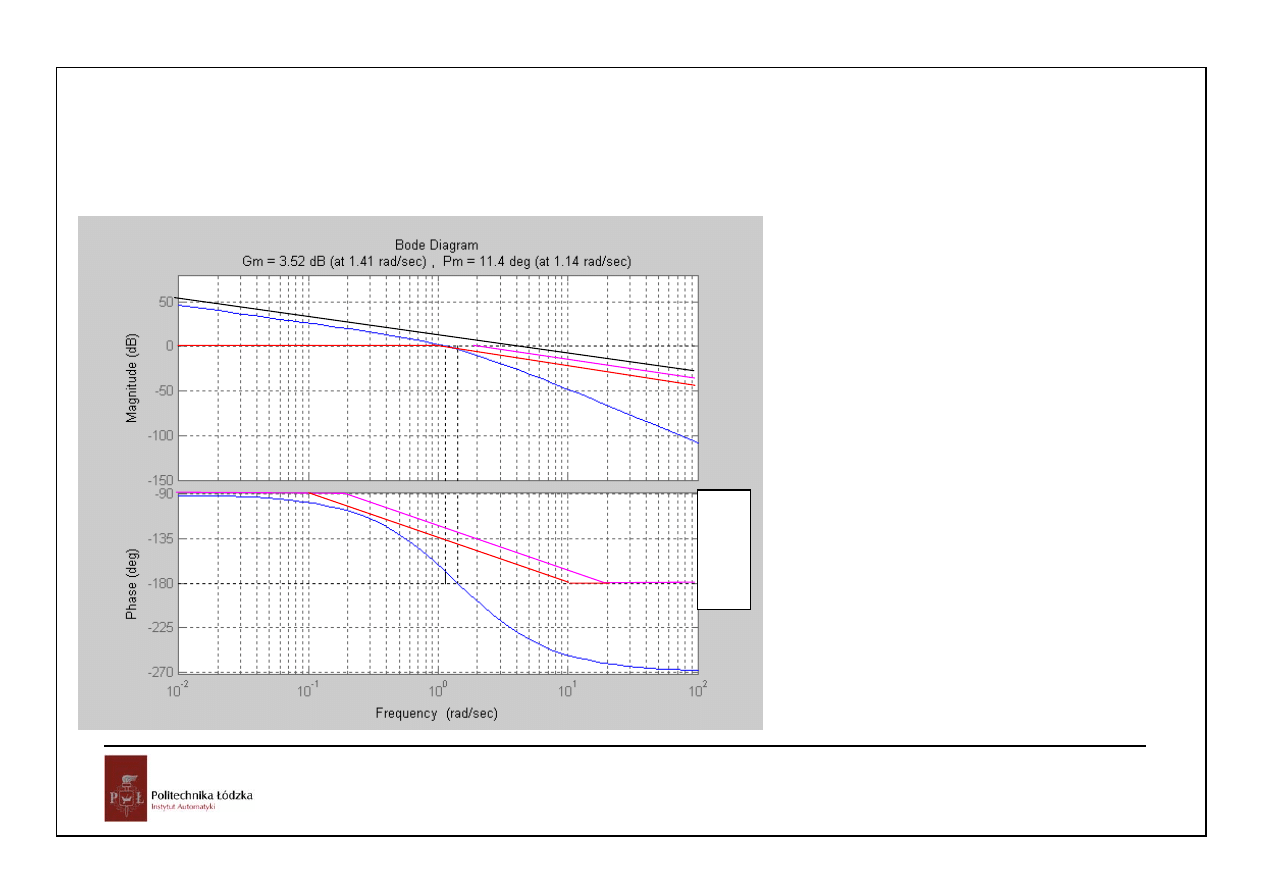
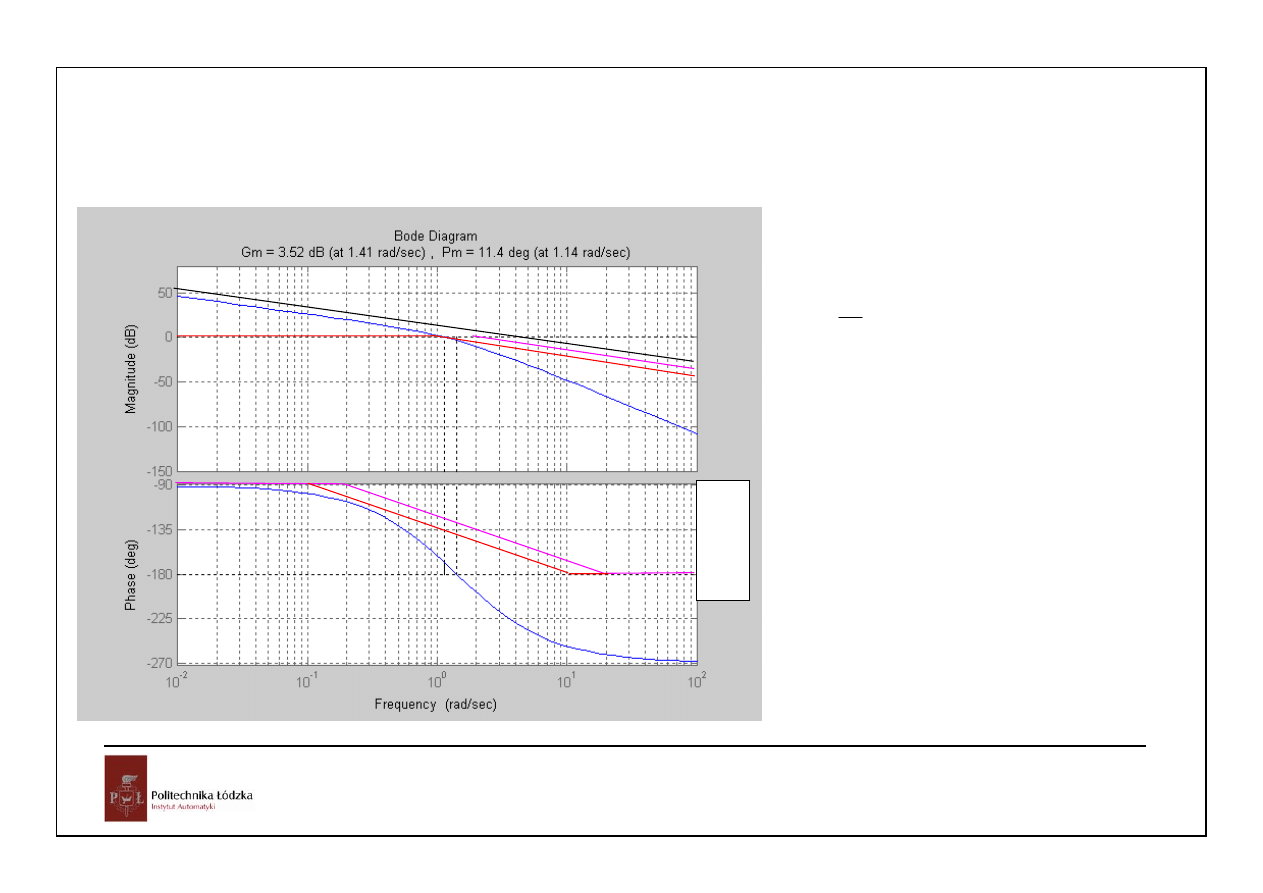
Zwiększenie współczynnika
wzmocnienia układu otwartego do
wartości 10^(3.52/20)=1.4997
doprowadzi do utraty stabilności.
Podobnie włączenie opóźnienia
dającego przesunięcie fazowe
11.4deg przy pulsacji 1.14 rad/sek
czyli 0.1745 sek.
Zmniejszając współczynnik
wzmocnienia układu otwartego
potrafimy powiększyć zapasy
stabilności kosztem zmniejszenia
pasma przenoszenia i wzrostu
uchybu ustalonego przy
wymuszeniu liniowym. Np. dla
C=0.16.

16

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

17

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

18

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

19

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

20

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

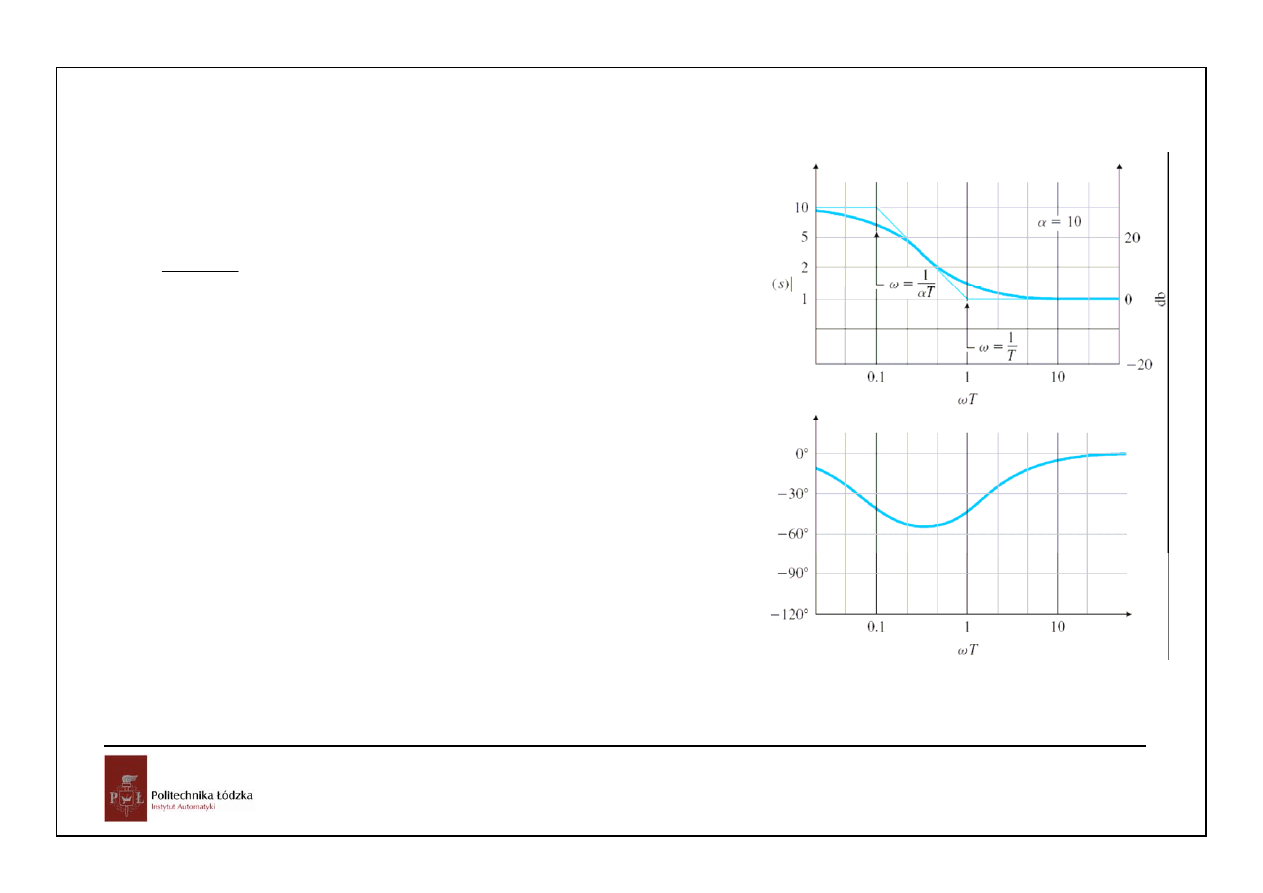
Kompensator opóźniający fazę:

1

1

1

Ts

C( s )

,

Ts

α

α

α

+

=

>

+

wzmocnienie dla małych częstotliwości, ale niekorzystne
opóźnienie fazy

21

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

T=1/0.04=25, alfa=4

0

-45

-90

22

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

23

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

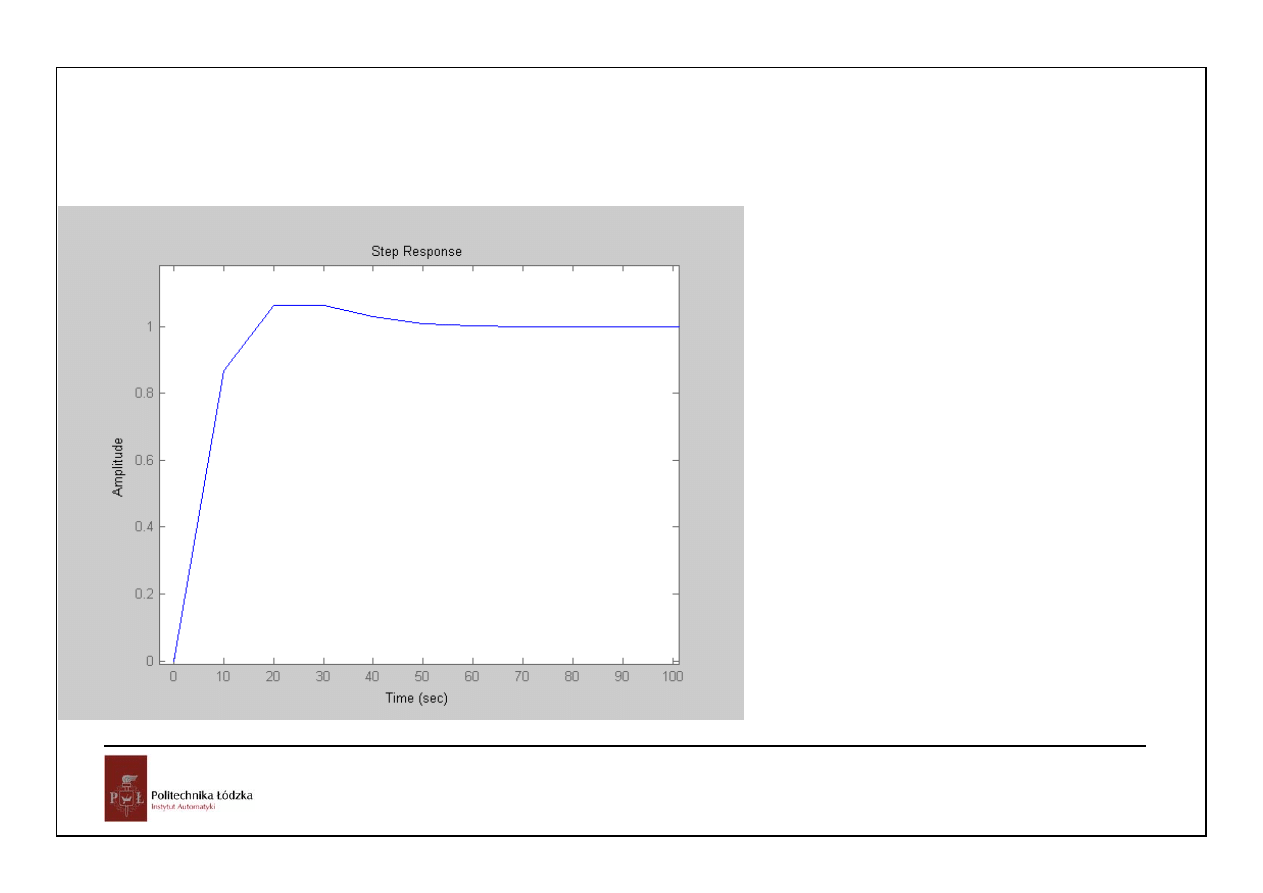
zapas stabilnosci jest mały

24

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

25

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

26

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

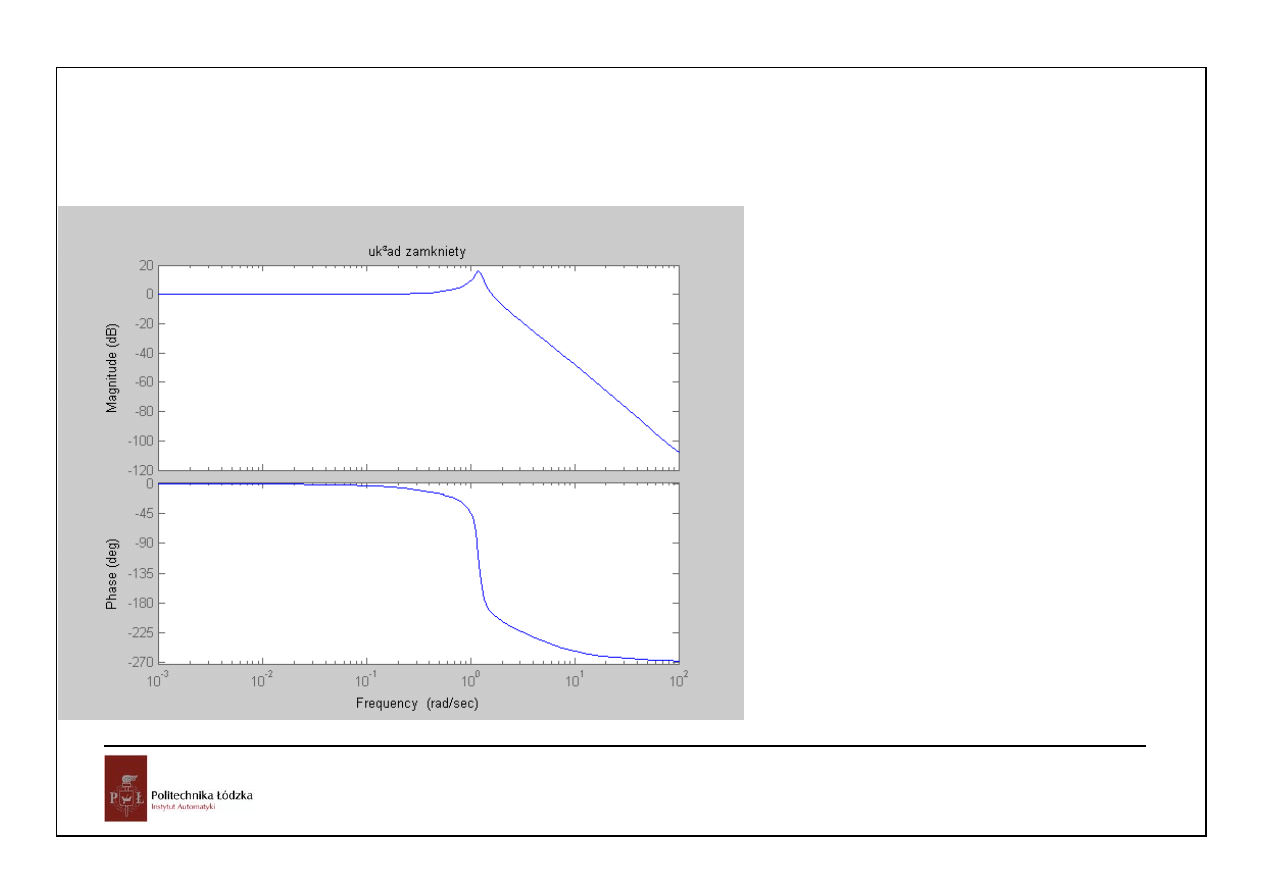
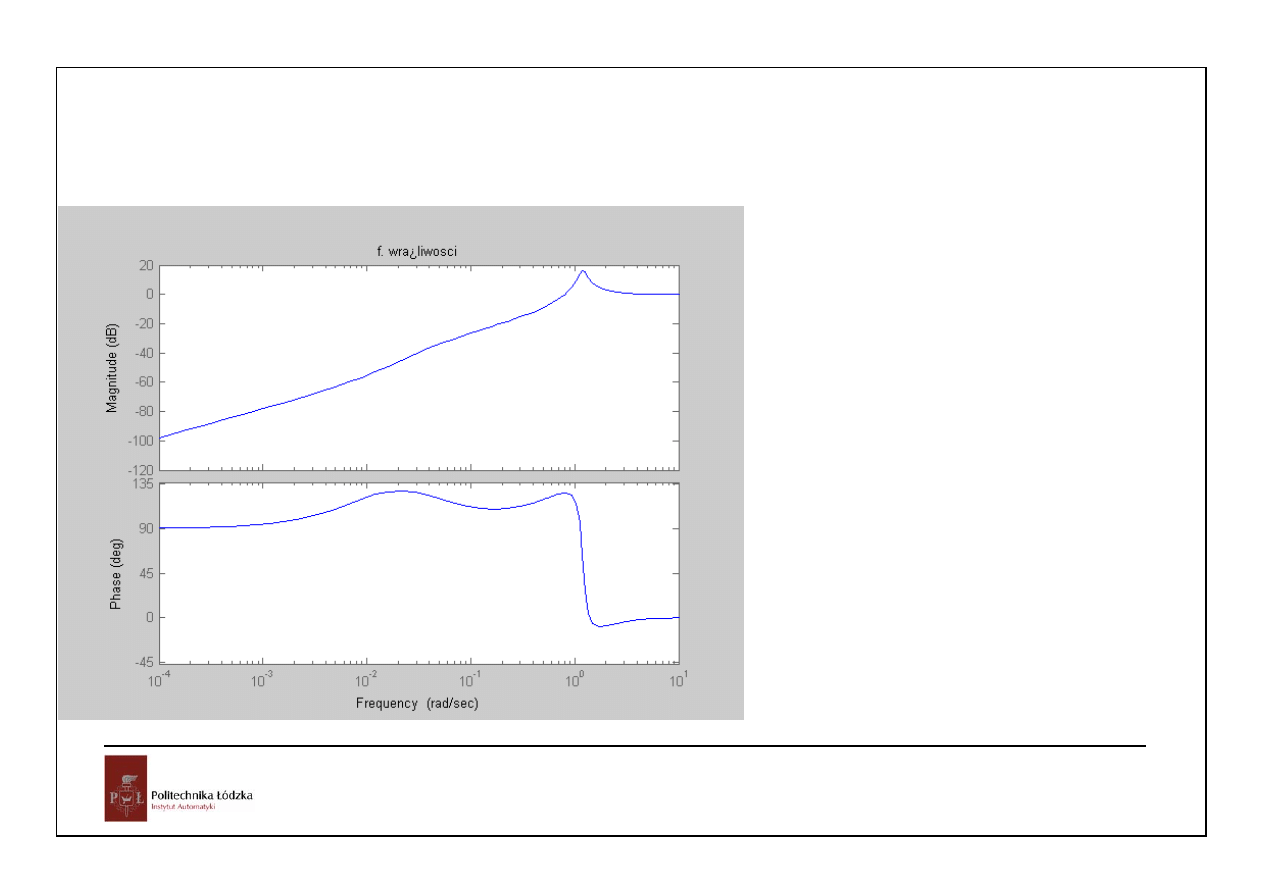
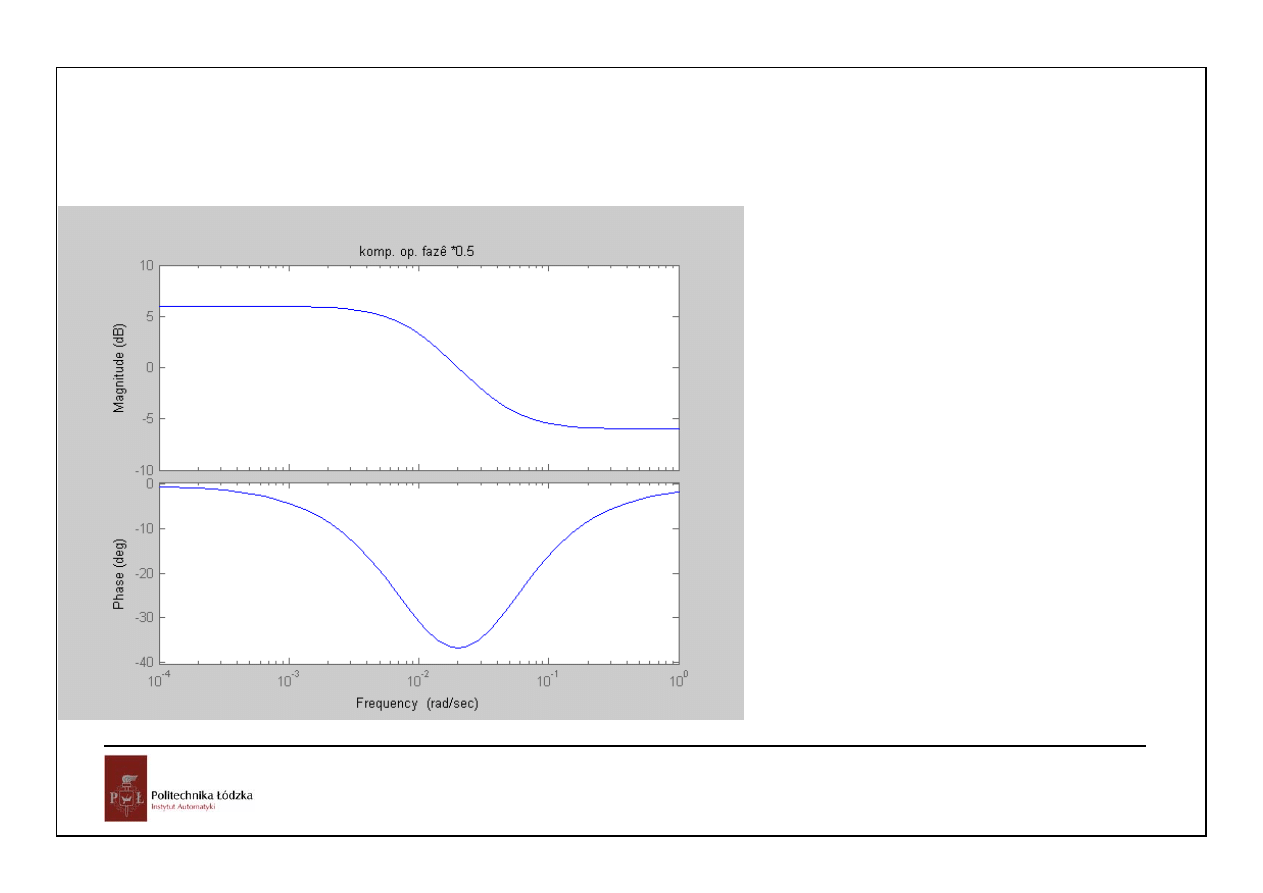
jeszcze obniżymy wzmocnienie:K=0.5

27

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

28

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

29

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

30

Automatyka i sterowanie 10 Przykłady

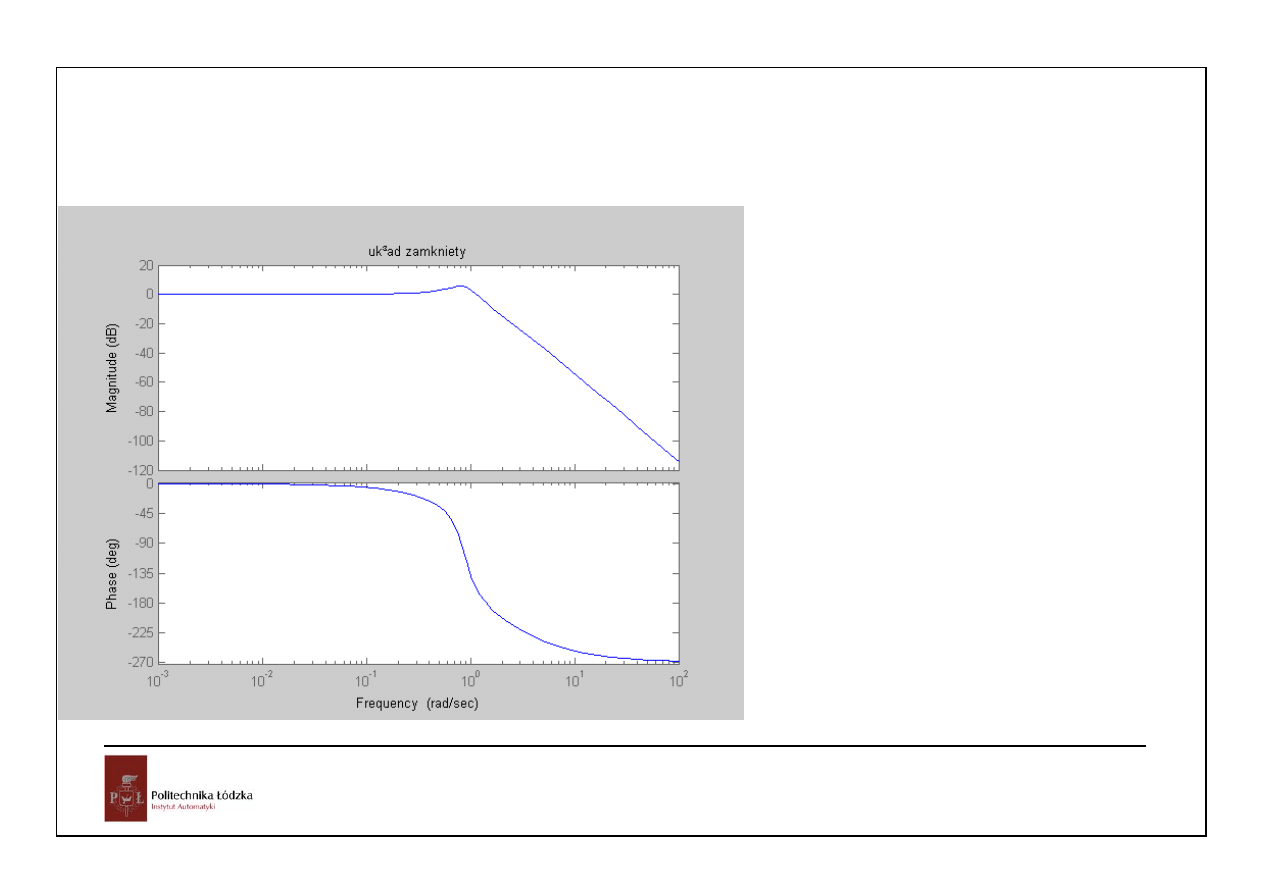
Układy czasu ciągłego

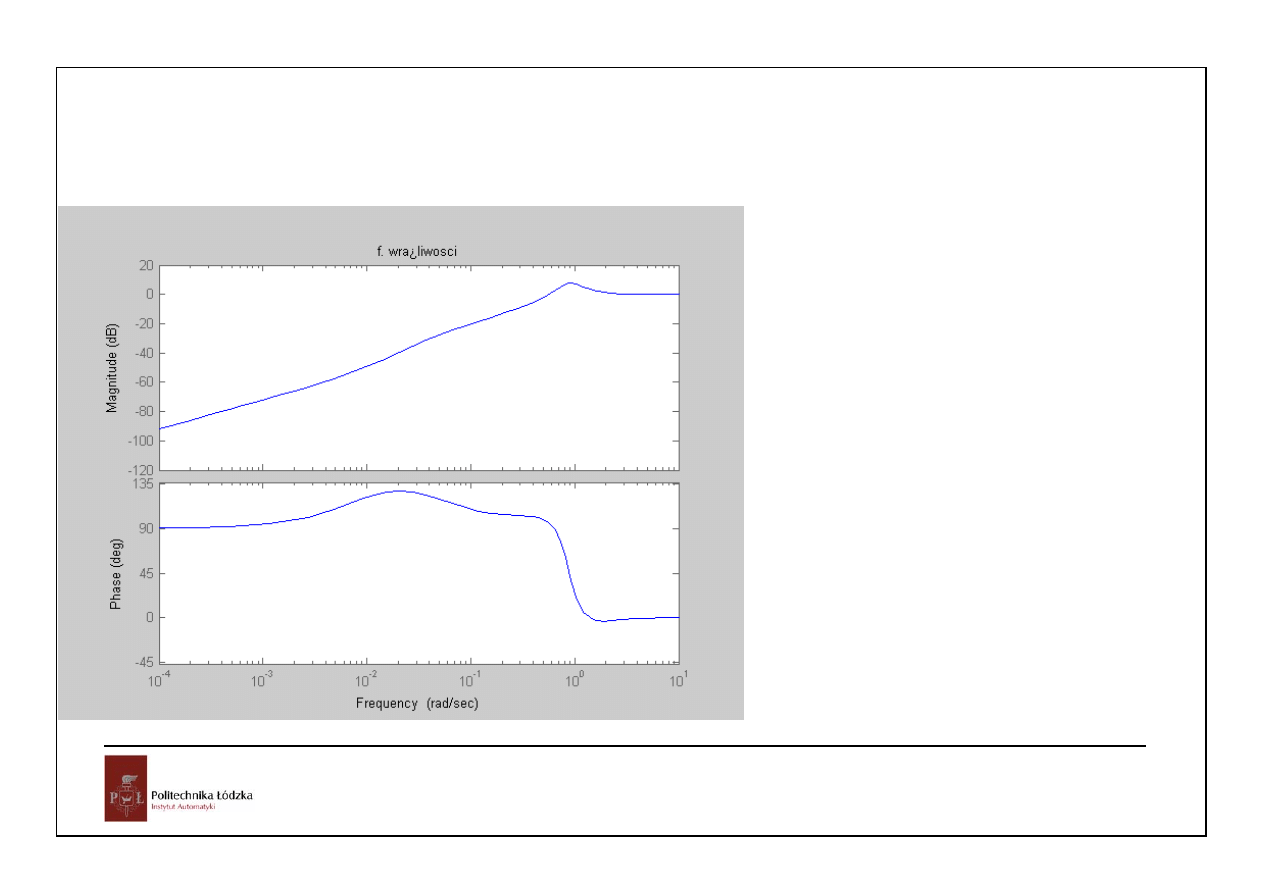
31

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

32

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

33

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

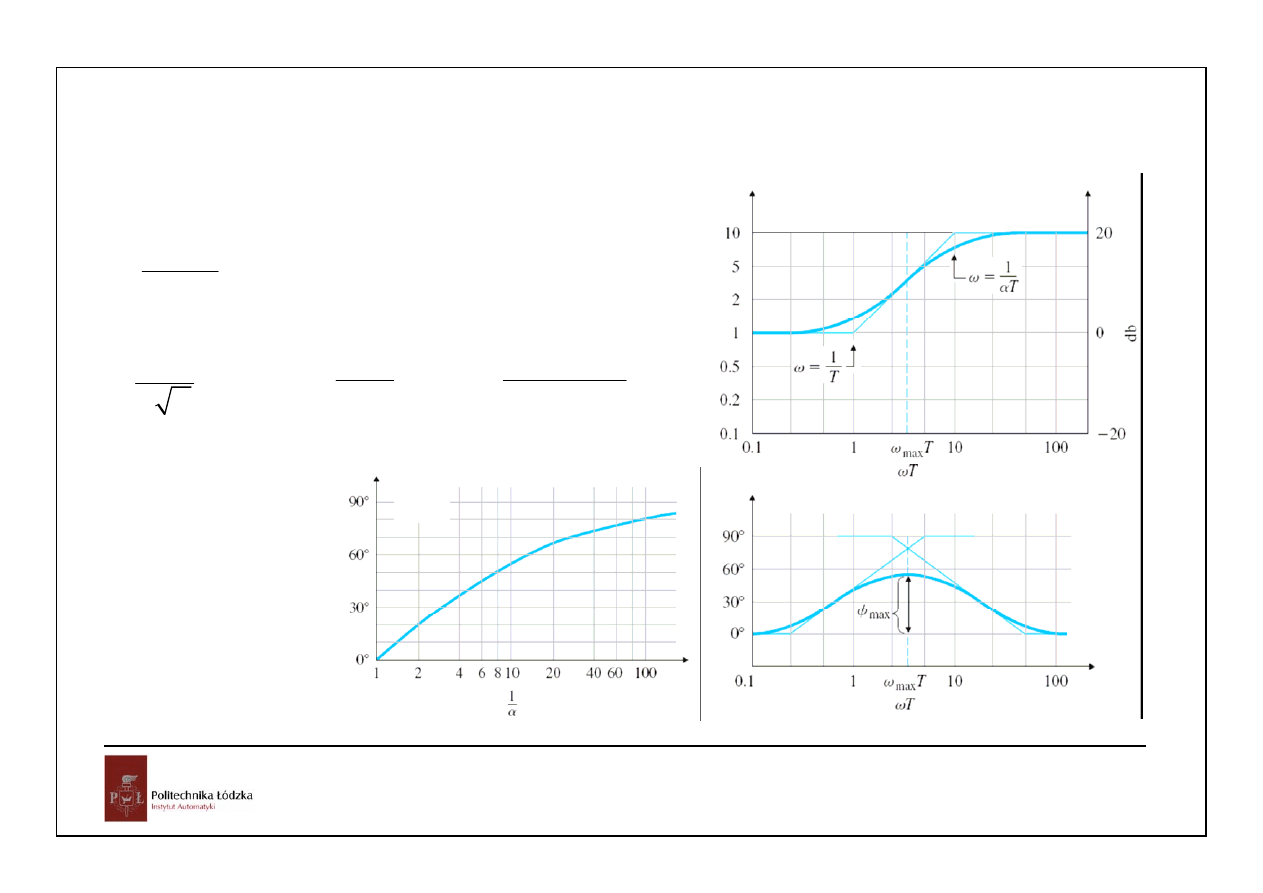
Kompensator przyśpieszający fazę:

1

1

1

Ts

C( s )

,

Ts

α

α

+

=

<

+

arctg( T ) arctg( T )

ϕ

ω

α ω

=

−

1

max

T

ω

α

=

1

1

1

1

max

max

max

sin

sin

sin

α

ϕ

ϕ

α

α

ϕ

−

−

=

⇒ =

+

+

mniejsze α – większe φ

max

- większe wzmocnienie dla

dużych częstotliwości
kompromis:

60

o

max

ϕ

<

max

ϕ

34

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

T=1/1.14=0.8772
alfa=(1-sin(pi/4))/(1+sin(pi/4))=
0.1716

0

-45

-90

35

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

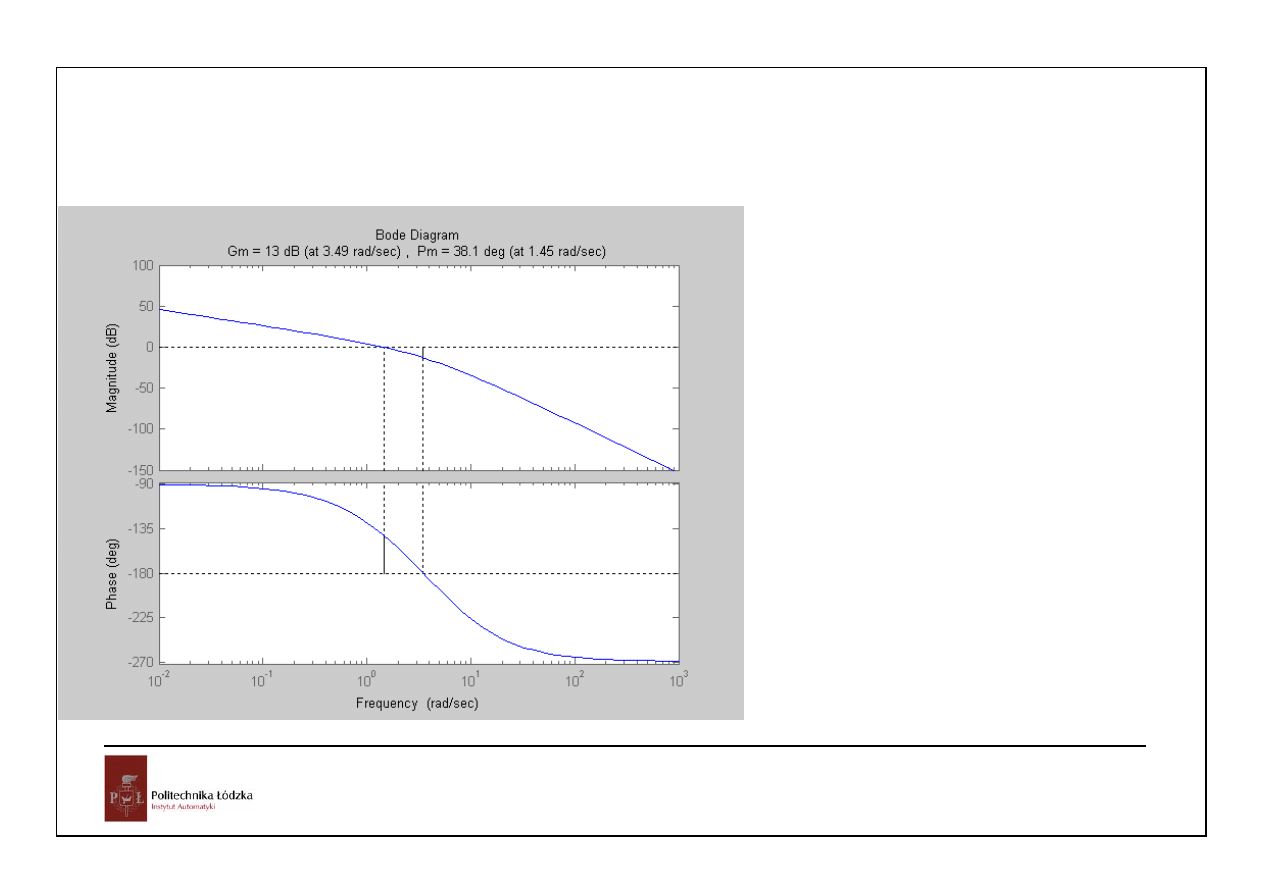
36

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

37

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

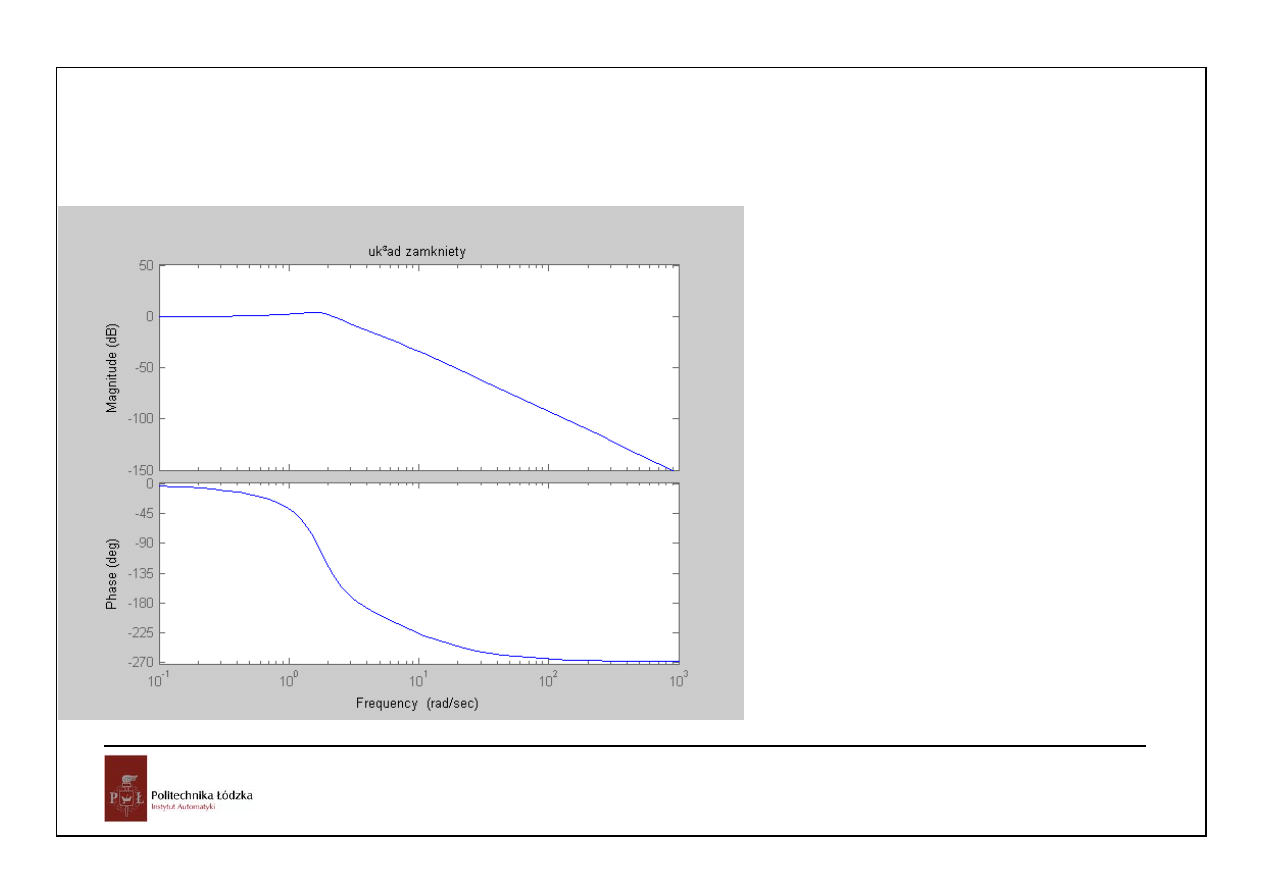
38

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

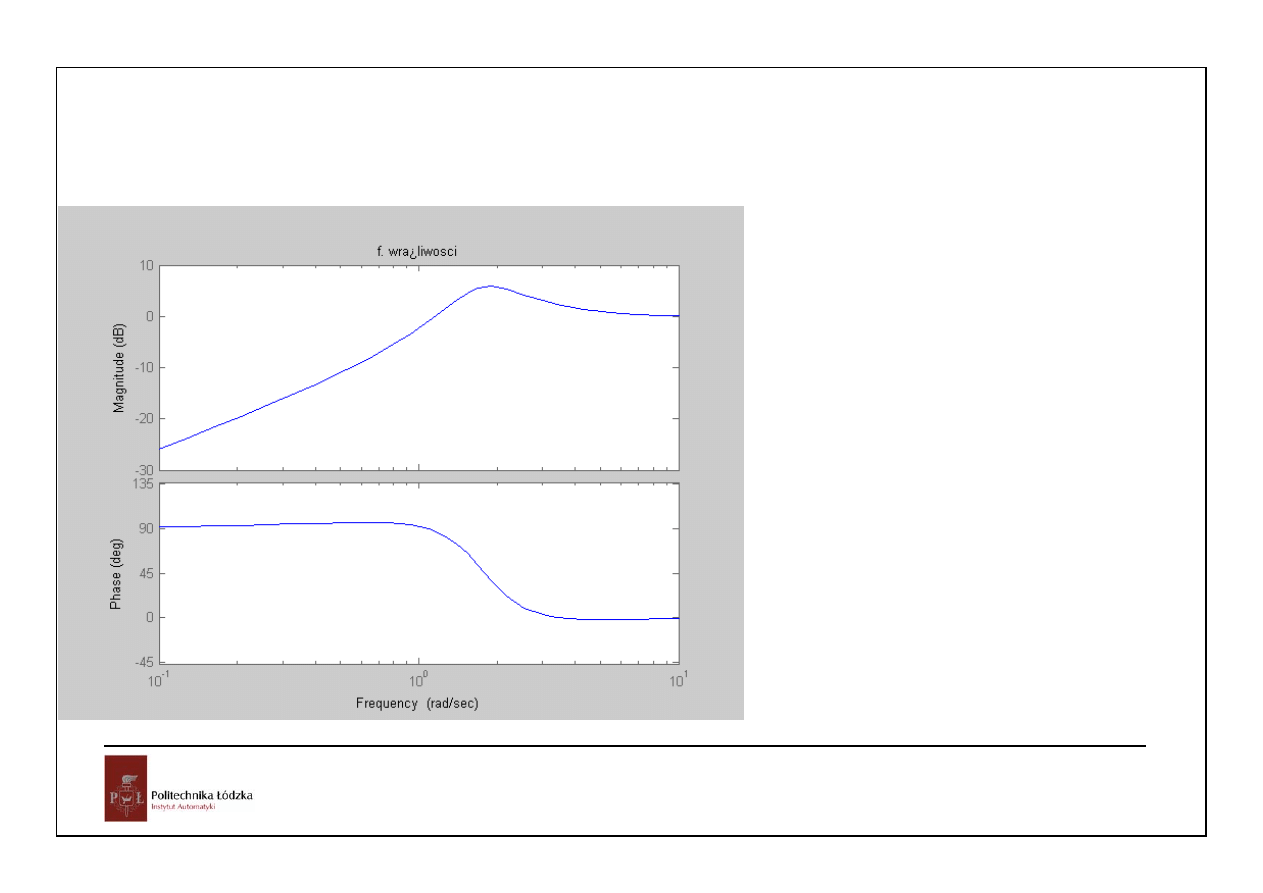
39

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

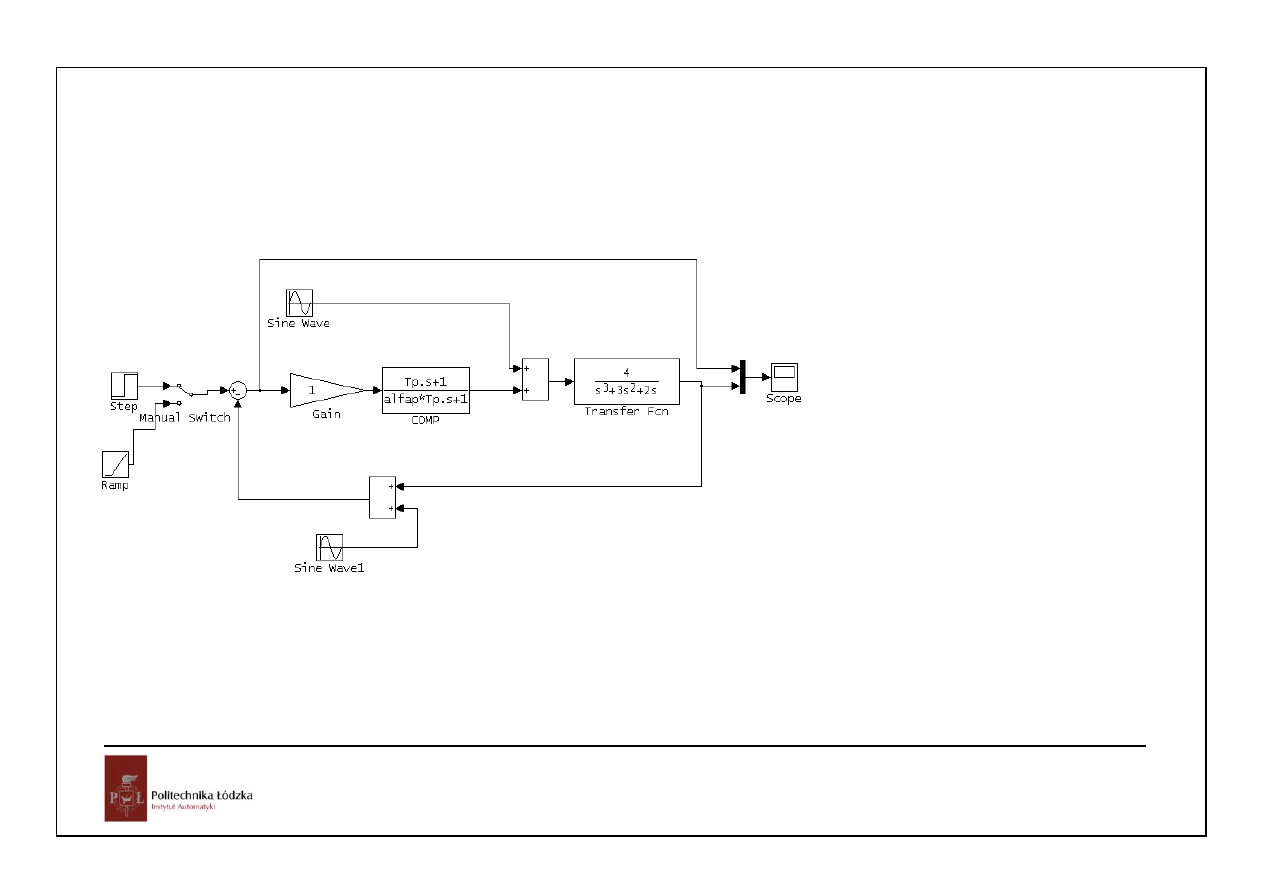
40

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

połączymy oba komp.

41

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

42

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

43

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

44

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

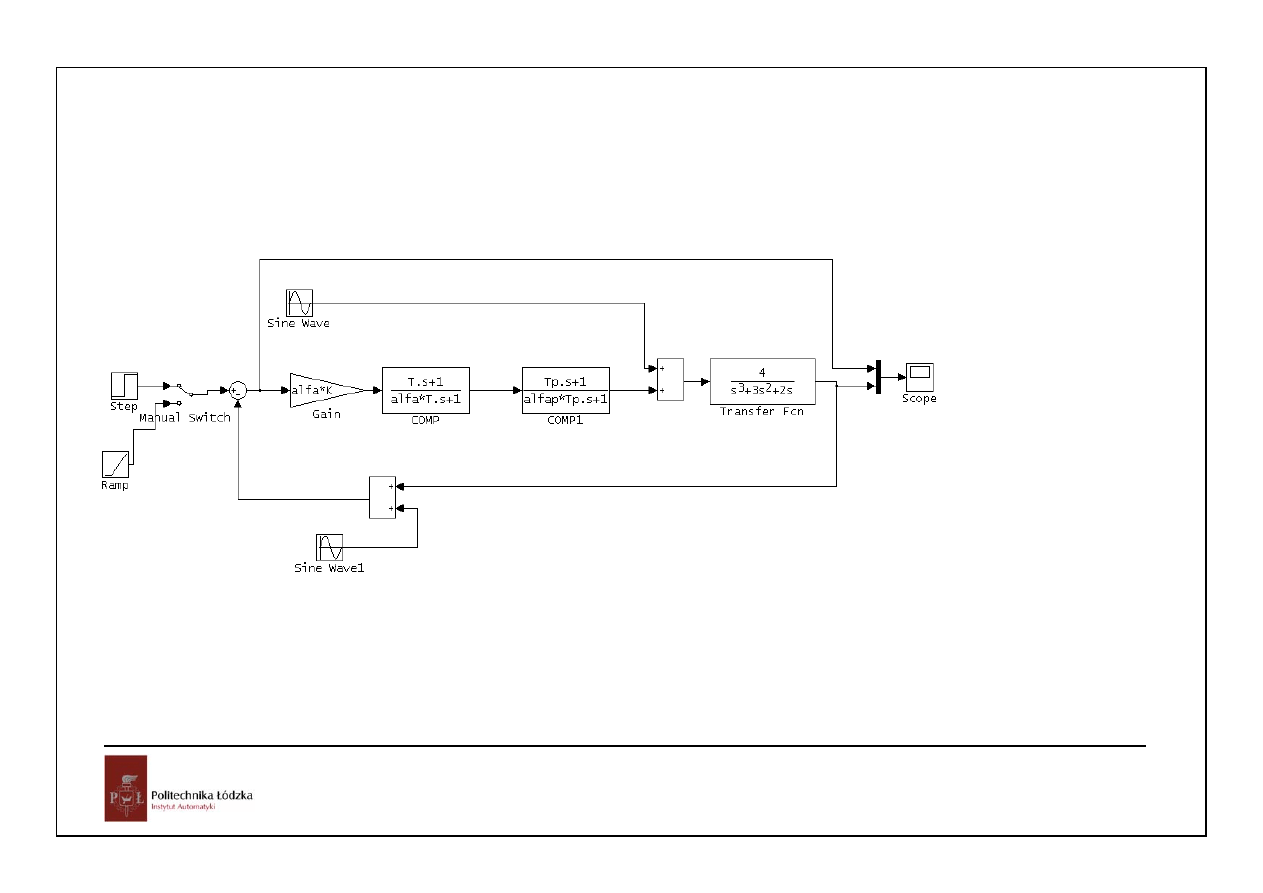
45

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

46

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

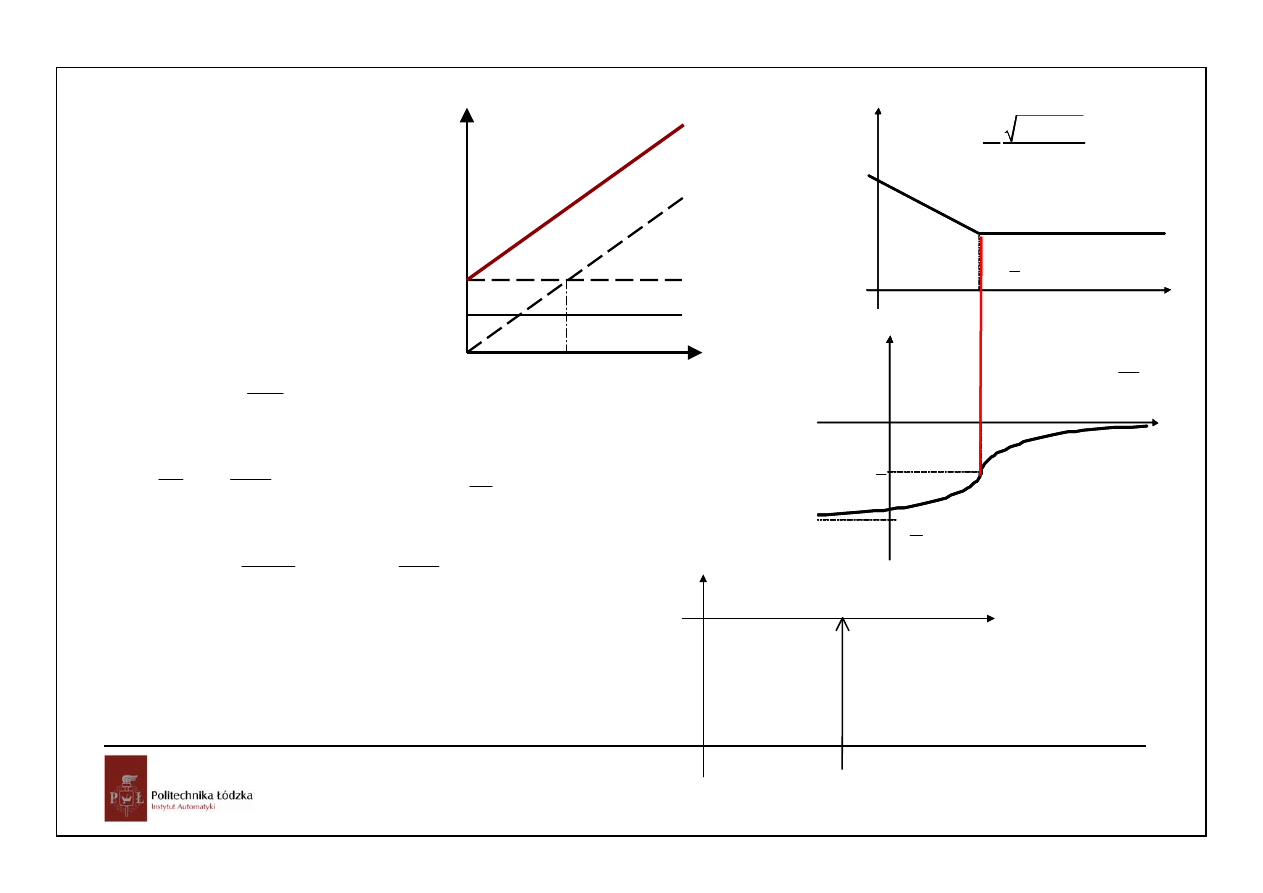
Regulator PI

1

( )

1

c

i

C s

k

sT

⎛

⎞

=

+

⎜

⎟

⎝

⎠

1

( )

1

1( )

c

i

h t

k

t

t

T

⎛

⎞

=

+

⎜

⎟

⎝

⎠

1

( )

1

c

i

k

H s

s

sT

⎛

⎞

=

+

⎜

⎟

⎝

⎠

1

(

)

1

( )

( )

c

c

c

i

i

k

C j

k

k

j

P

jQ

j T

T

ω

ω

ω

ω

ω

⎛

⎞

=

+

=

−

=

+

⎜

⎟

⎝

⎠

Q(

ω

)

P(

ω

)

0

ω

=

∝

ω

=0

k

c

Cz. całkująca

t

e(t)

u(t)

e(t)

T

i

Cz.

2

1 (

)

( ) 20 log

i

c

i

T

k

L

T

ω

ω

ω

+

=

1

1

i

T

ω

=

ω

( )

( )

2

π

ω

ω

ϕ

−

=

i

T

arctg

−

π

4

−

π

2

ω

2

1 (

)

( ) 20 log

i

c

i

T

k

L

T

ω

ω

ω

+

=

1

1

i

T

ω

=

ω

( )

( )

2

π

ω

ω

ϕ

−

=

i

T

arctg

−

π

4

−

π

2

ω

47

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

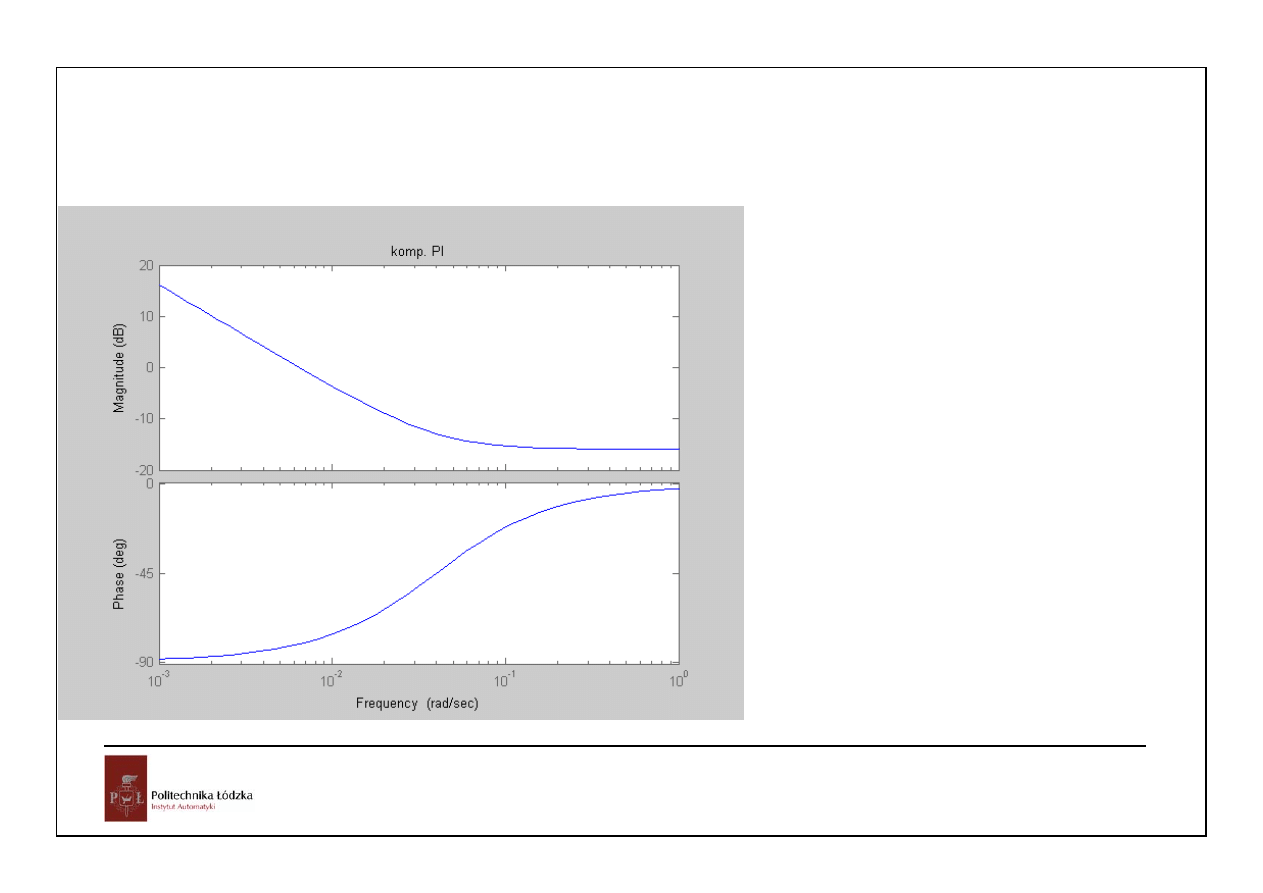
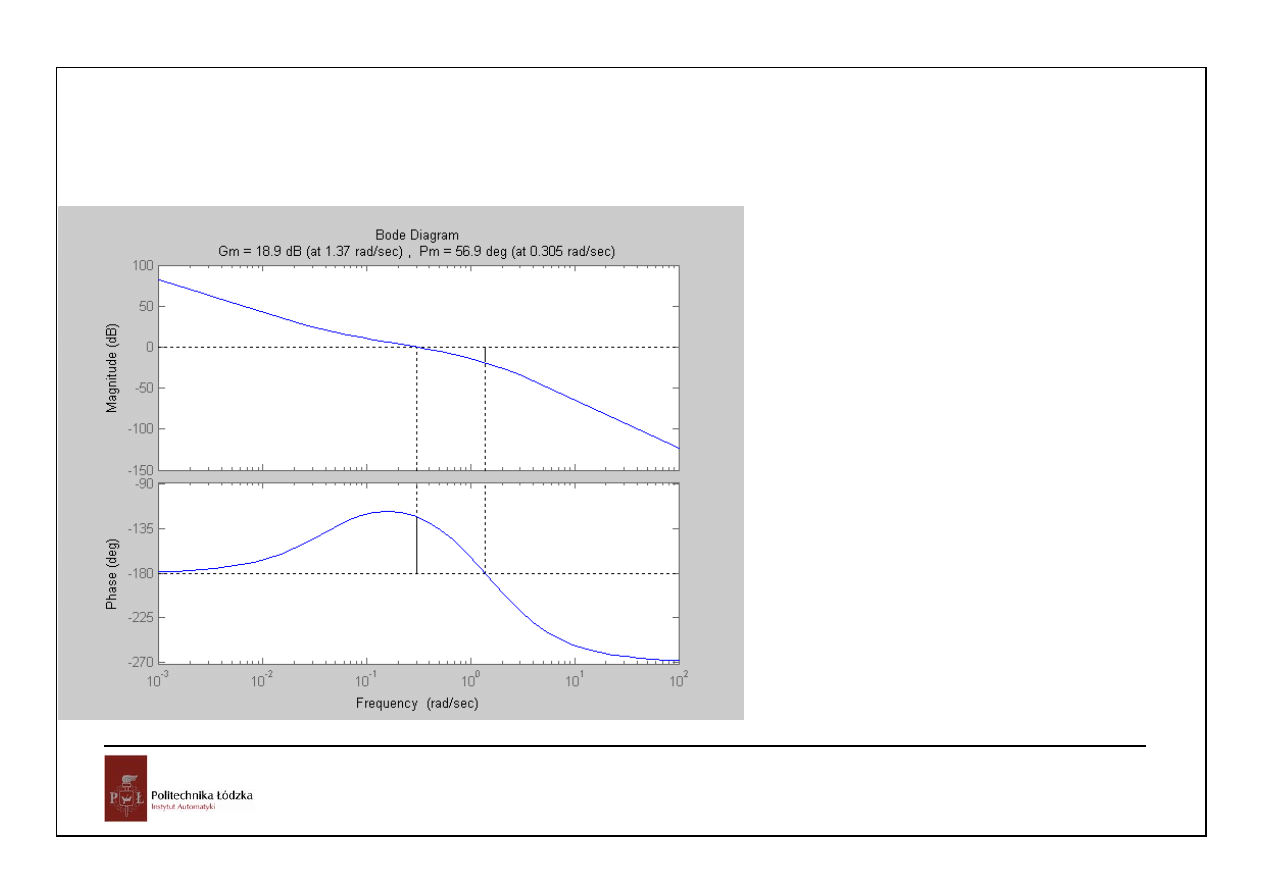
Ti=1/0.04, kc=0.16

0

-45

-90

1

1

10 ,

0.16

c

i

k

T

−

<

<

48

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

49

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

50

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

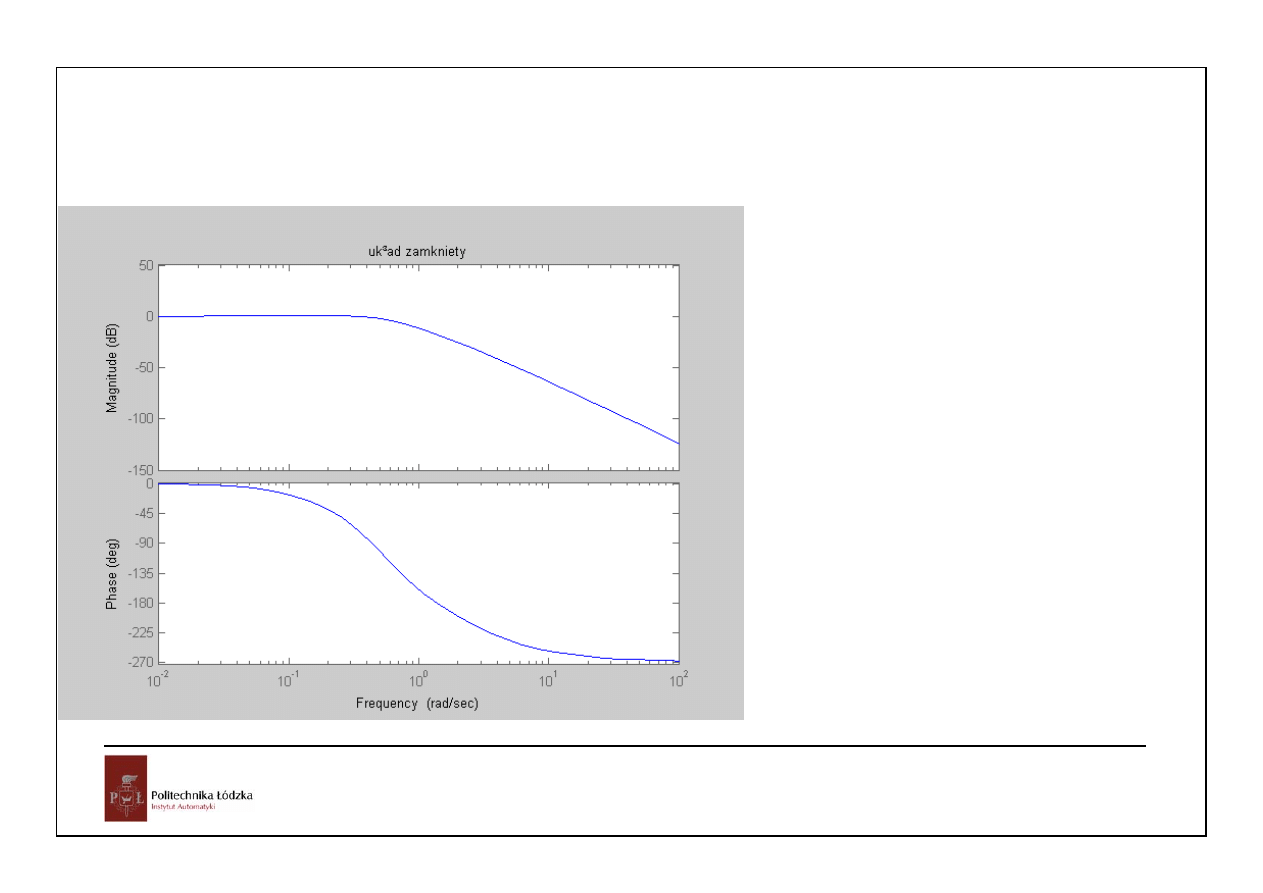
51

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

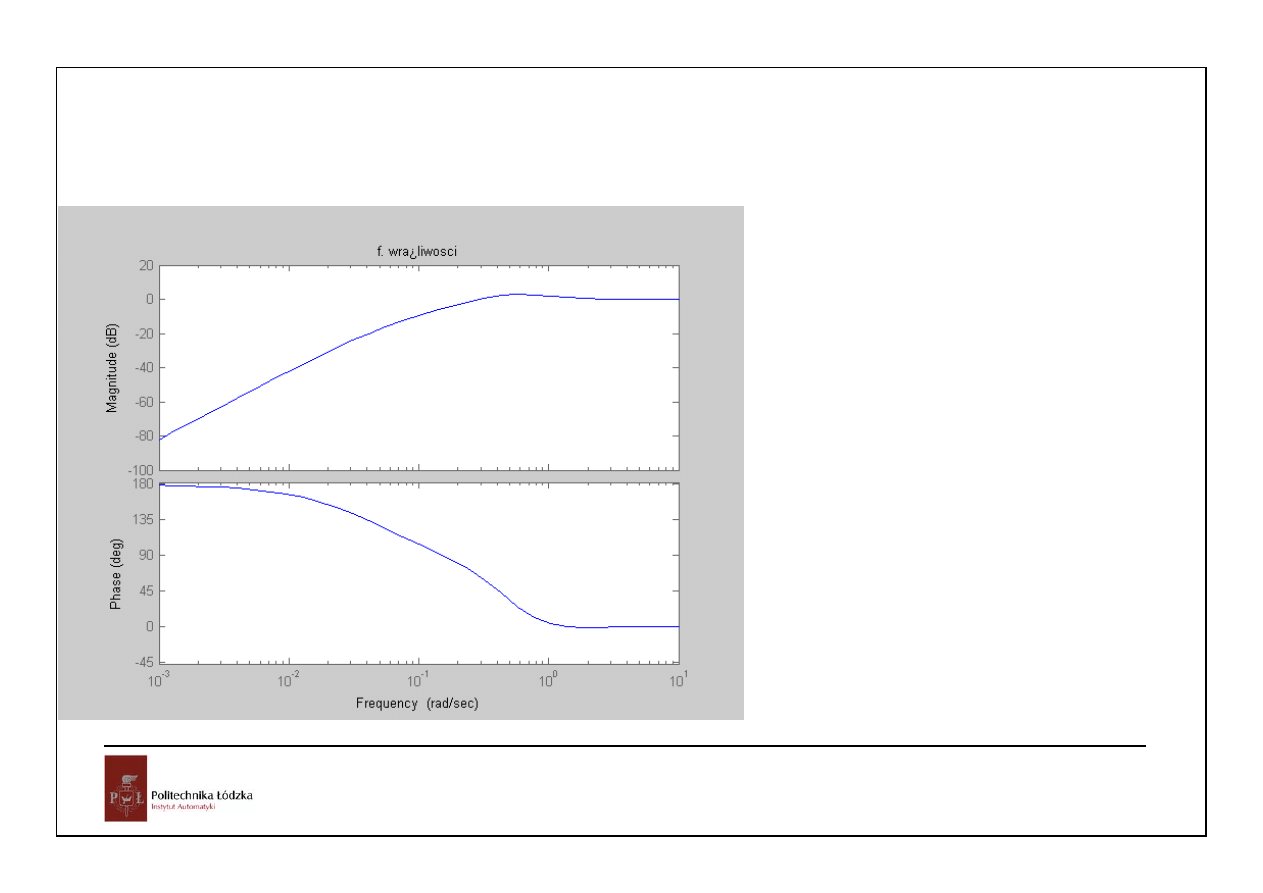
52

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

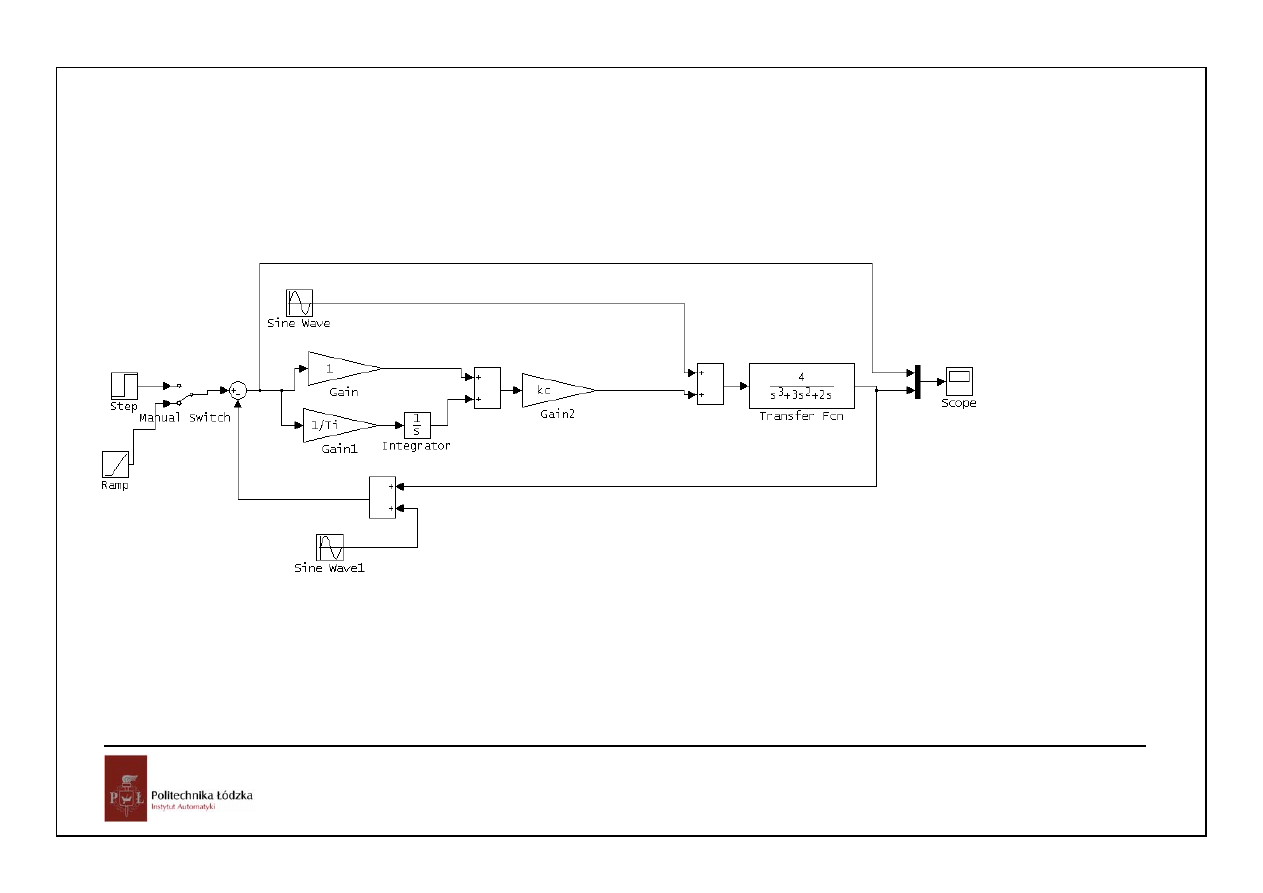
53

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

54

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

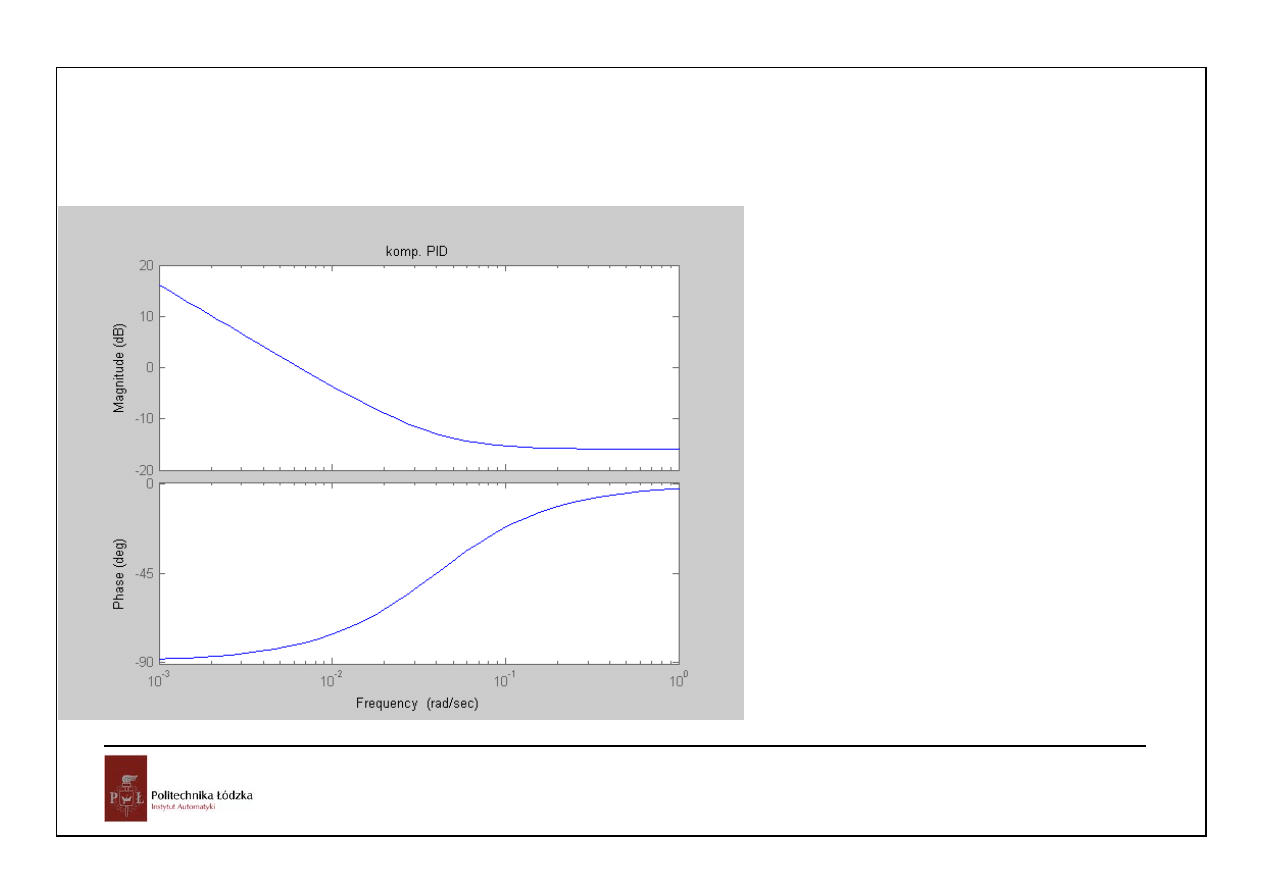
Regulator PID:

T

D

=1, kp=1.6, Ti =1/0.04

s

k

s

k

k

)

s

(

C

d

i

p

+

+

=

1

⎥

⎦

⎤

⎢

⎣

⎡

+

+

=

∫

)

t

(

e

dt

d

T

d

)

(

e

T

)

t

(

e

k

)

t

(

u

d

t

i

p

0

1

τ

τ

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+

=

d

i

p

sT

sT

k

)

s

(

C

1

1

)

t

(

e

dt

d

k

d

)

(

e

k

)

t

(

e

k

)

t

(

u

d

t

i

p

+

+

=

∫

0

τ

τ

π

2

−

π

2

1

T T

I

D

ω

1

T

D

1

T

I

ω

T

I

> T

D

π

2

−

π

2

1

T T

I

D

ω

1

T

D

1

T

I

ω

T

I

> T

D

20log k

p

2

1

( ) 20log

20log

1

p

D

I

L

k

T

T

ω

ω

ω

⎛

⎞

=

+

−

+

⎜

⎟

⎝

⎠

( )

(

)

1

arg

D

I

C j

arctg

T

T

ω

ω

ω

⎛

⎞

=

−

⎜

⎟

⎝

⎠

1

(

)

1

p

d

i

C j

k

j T

j T

ω

ω

ω

⎛

⎞

=

+

+

⎜

⎟

⎝

⎠

Q(

ω)

P(

ω)

0

ω=∝

ω=0

k

p

55

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

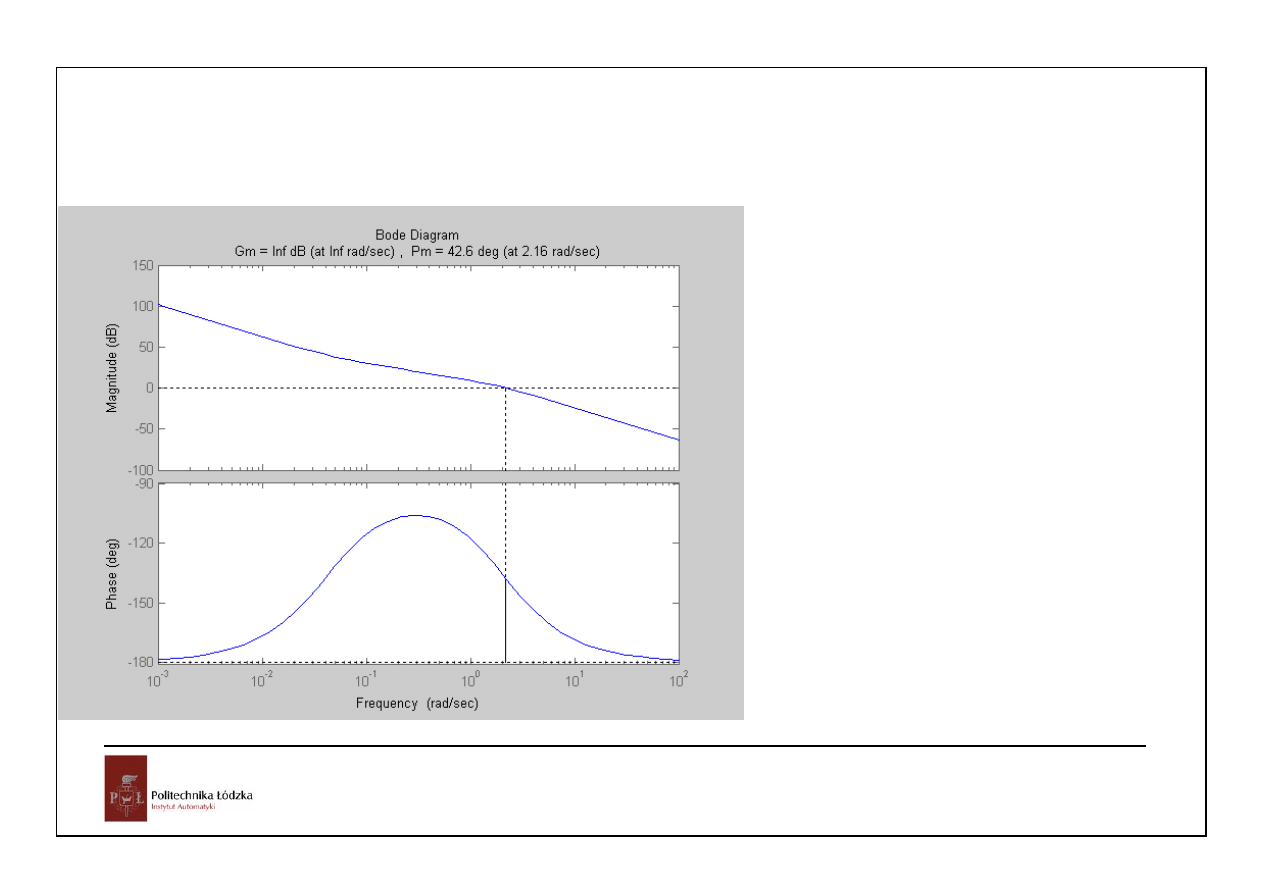
56

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

57

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

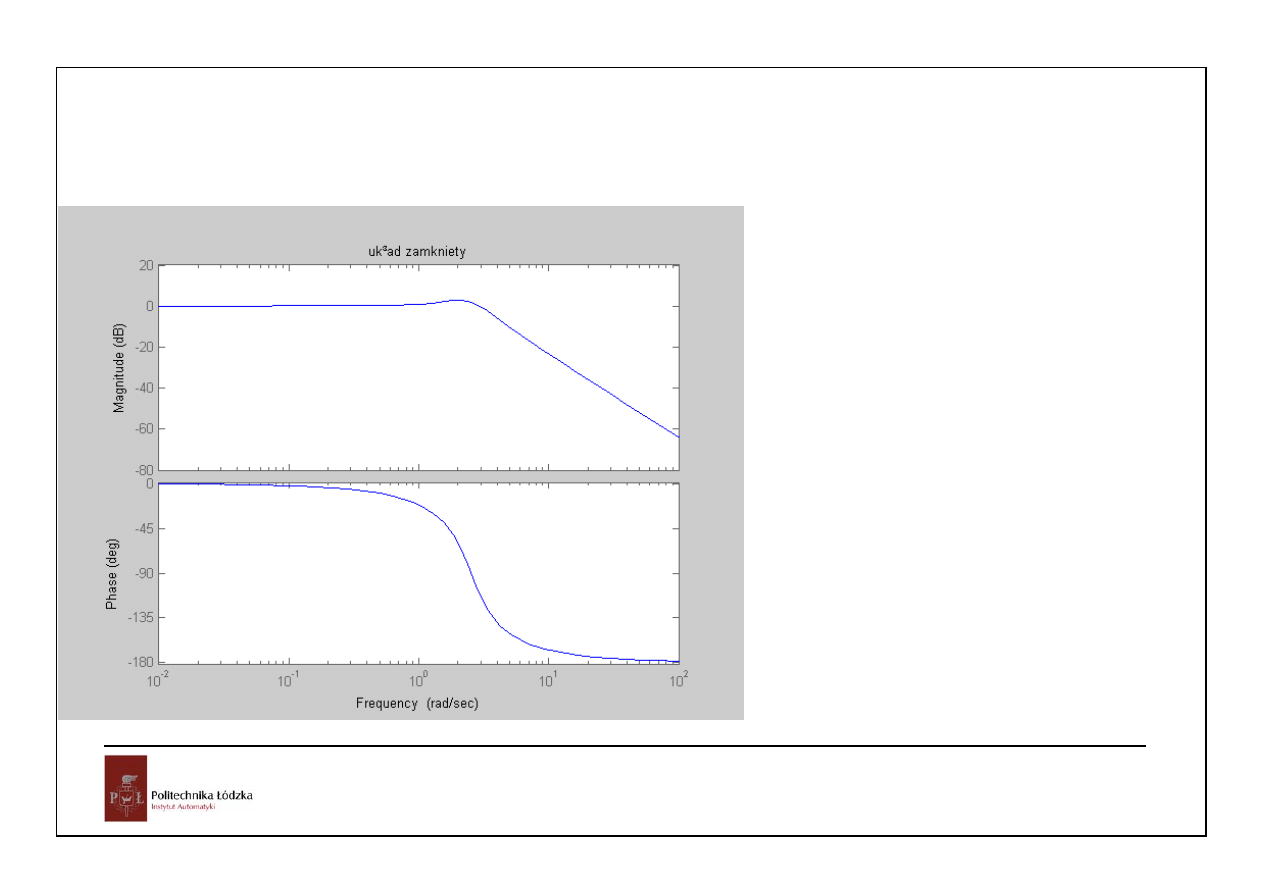
58

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

59

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

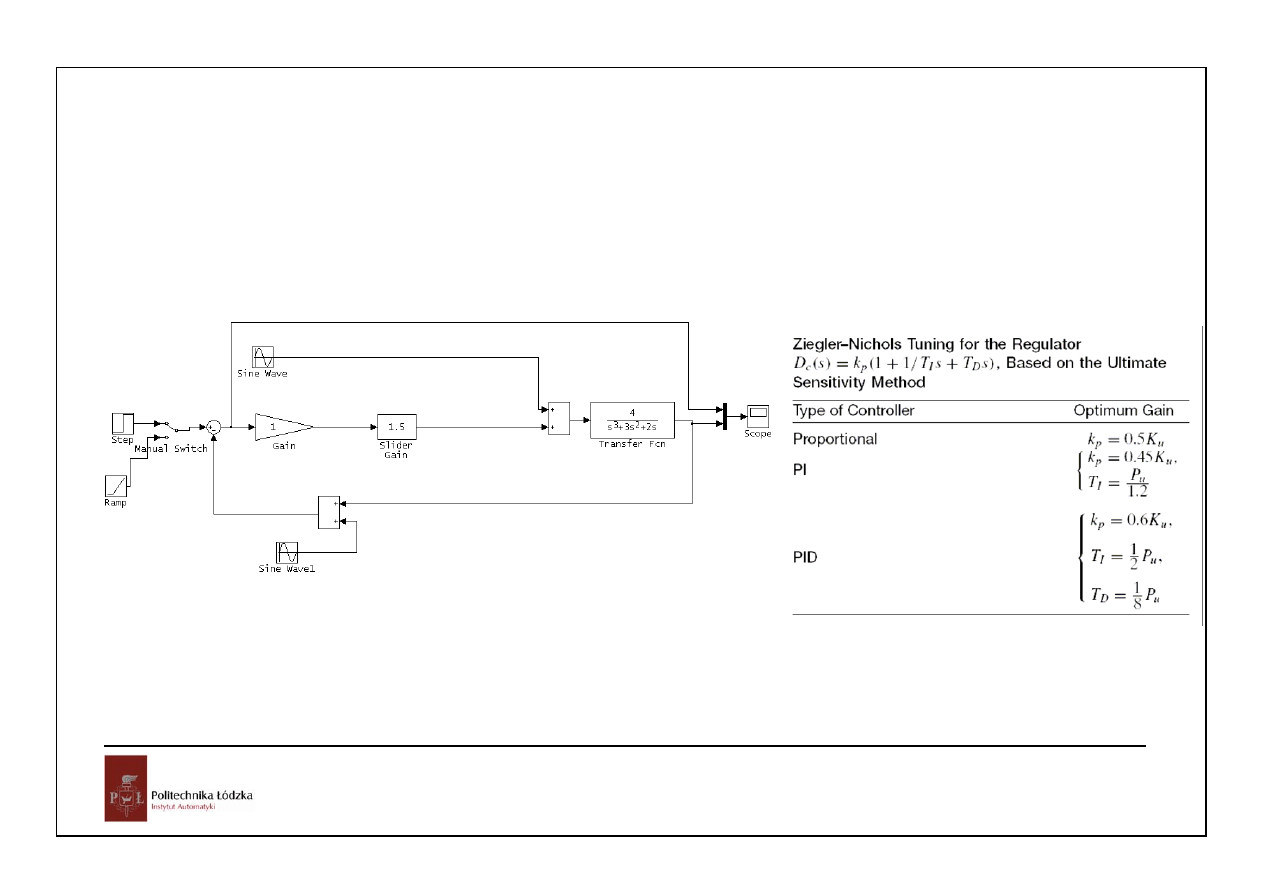
60

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

Metoda Zieglera-Nicholsa

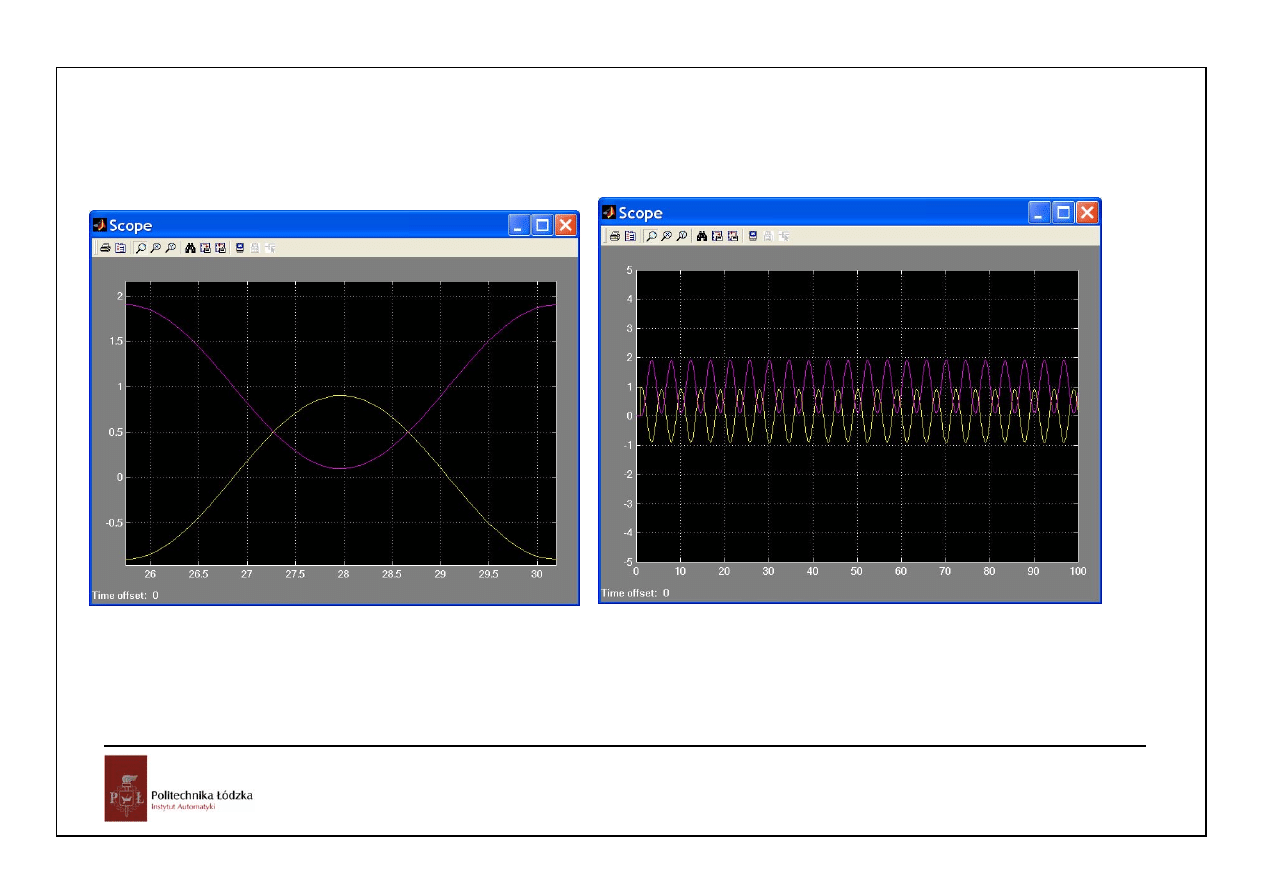
61

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

Ku=1.5, Pu=5
Kp=0.6Ku=0.9, Ti=0.5Pu=2.5, Td=Pu/8=5/8

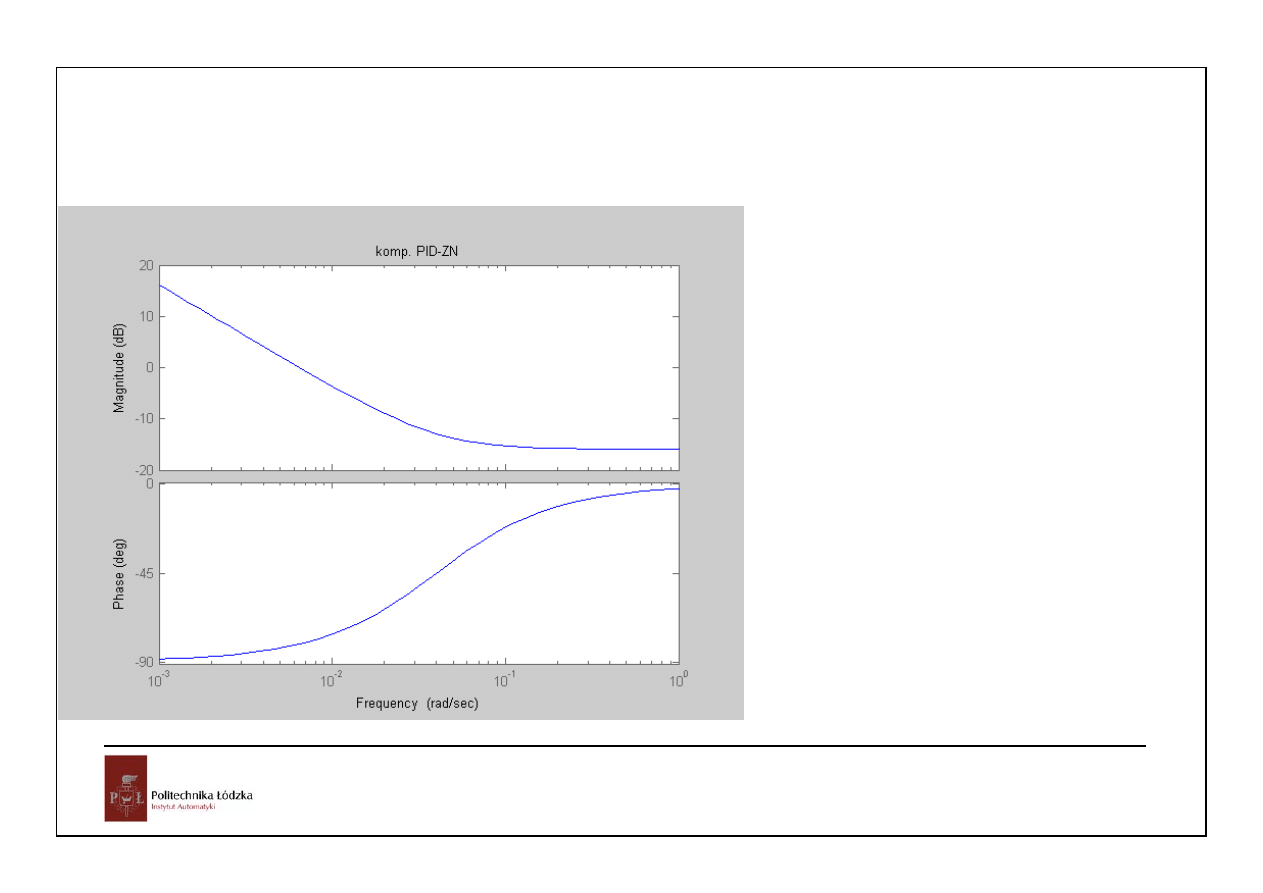
62

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

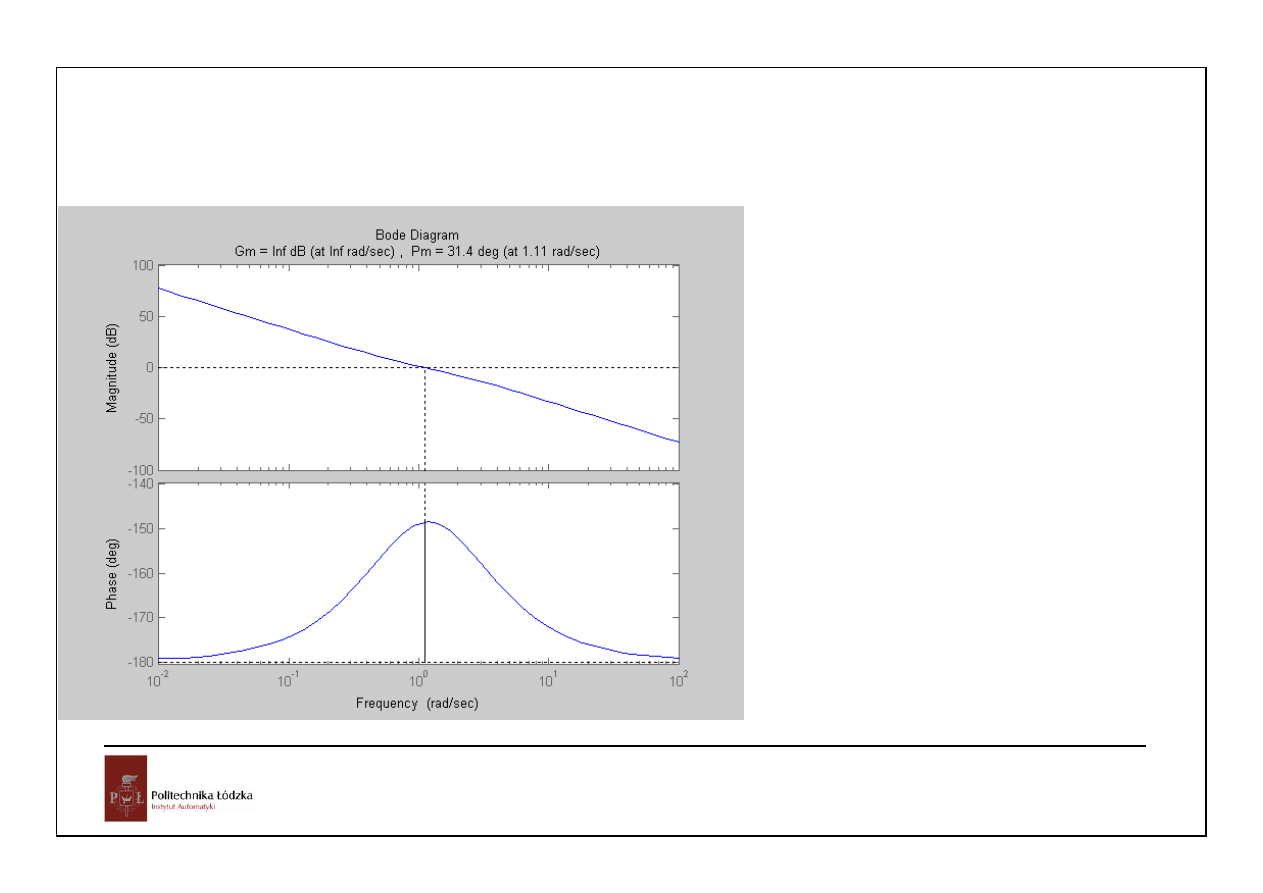
63

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

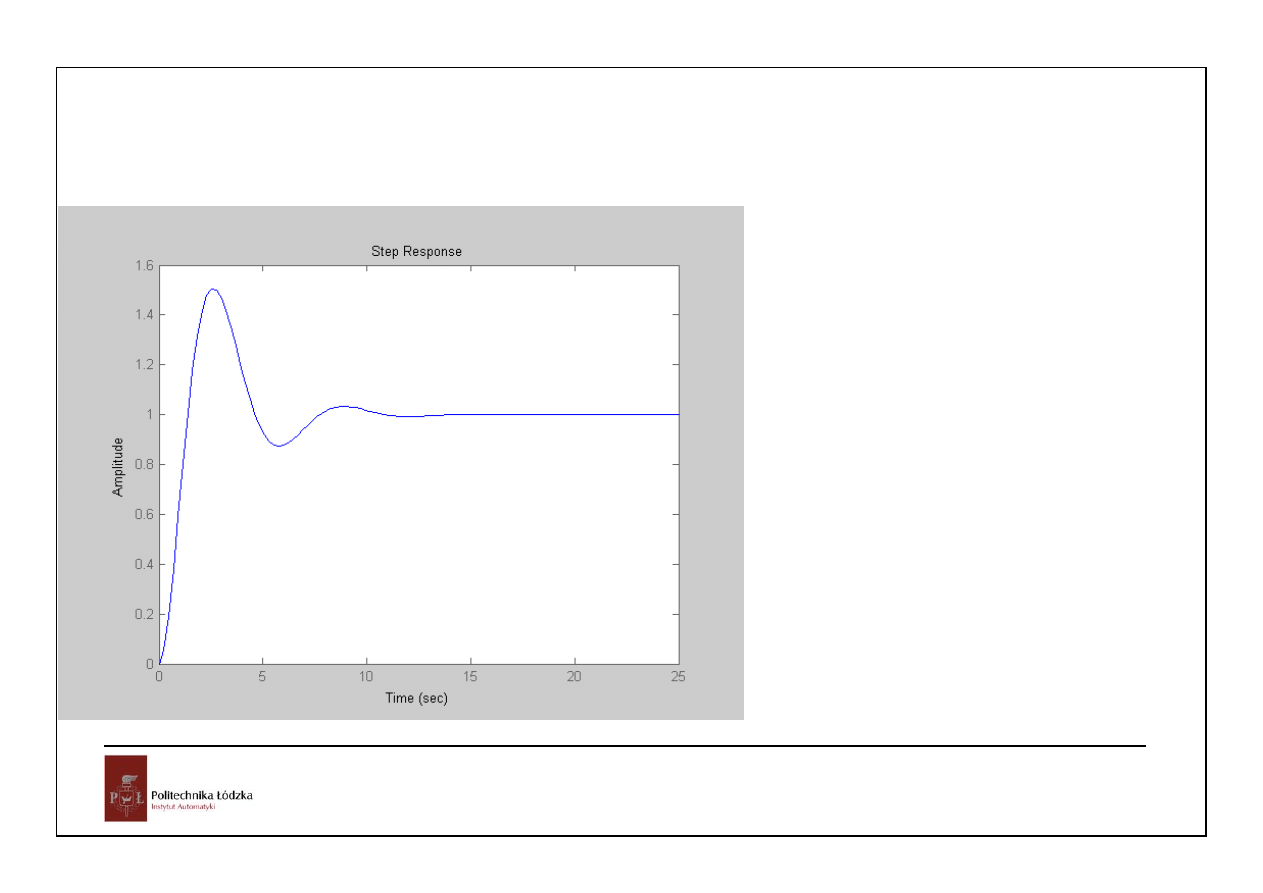
64

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

65

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

66

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego

67

Automatyka i sterowanie 10 Przykłady

Układy czasu ciągłego