WTŻ I, gr.10

2002-03-26

Ćwiczenie 42. Wyznaczanie oporu elektrycznego metodą mostka Wheatstone a.

Celem ćwiczenia jest wyznaczanie oporu elektrycznego wyżej wymienioną metodą

Opór elektryczny R danego przewodnika jest to stosunek napięcia U zmierzonego na końcach przewodnika, przez który płynie prąd o natężeniu I. Prawo Ohma mówi,że natężenie prądu płynącego przez przewodnik jest proporcjonalne do napięcia przyłożonego do jego końców i jest wyrażane wzorem

Jednostką oporu elektrycznego jest 1Ω=1V/A.

Opór elektryczny przewodników metalicznych jest wynikiem oddziaływania nośników prądu (elektronów) z jonami sieci krystalicznej. Zależy on od cech geometrycznych przewodnika, tzn od długości l i pola przekroju S oraz od rodzaju materiału z jakiego jest wykonany:

Współczynnik proporcjonalności ρ charakteryzujący rodzaj materiału nazyazmy oporem właściwym przewodnika. Jednostką oporu właściwego jest
.

W obwodach prądu występują układy oporów połączonych szeregowo tak jak to widać na rysunku, opór zastępczy n ma wtedy wartość:

W obwodach prądu występują również układy oporów połączonych równolegle co widać na rysunku, opór zastępczy n ma wtedy wartość:

I Prawo Kirchoffa.

Suma algebraicznych natężeń prądó wpływających i wypływających z węzła, czyli punktu obwodu, w którym zbiega się kilka przewodów
,równa się zeru
. Prądy wpływające do węzła uważamy za dodatnie, a prądy wypływające z węzła za ujemne.

II prawo Kirchoffa

W obwodziezamkniętym suma sił elektromotorycznych równa się sumie spadkó napięć na oporach.

Pomiar oporu elektrycznego za pomocą mostka Wheatstone a według rysunku 1.

Wyznaczany opór
, łączymy szeregowo z oporem wzorcowym
. Wolne końce połączonych oporników łączymy z punktami A i C, pomiędzy którymi rozpięty jest drut oporowy wzdłuż podziałki milimetrowej. Punkt B, współny dla oporów
łączymy poprzez miliamperomierz G z suwakiem D, który może swobodnie ślizgać się po drucie. Włączając zasilacz Z prąu stałego, przykładamy napięcie do punktów A i C. Szukamy teraz takiego położenia suwaka D na strunie, aby przez odcinek BD prąd nie płynął (galwanometr musi wskazywać zerową wartość natężenia prądu). Wóczas mostek jest zrównoważony, czyli potencjały punktów B i D są sobie równe i napięcie w poszczegółnych gałęziach obwodu spełniają warunek:
,

Z I Prawa Kirchoffa wynika, że jeśli przez odcinek BD prąd nie płynie, to:
,
.

Korzystając z prawa Ohma równości możemy wyrazić następująco:

Po podzieleniu tych równań stronami otrzymamy:
.

Ze względu na związek
, biorąc pod uwagę, że cała struna ma wszędzie jednakowe pole przekroju, stosunek oporów
możemy zastąpić stosunkiem ich długości
.

Z dwóch ostatnich równości otrzymujemy wzór na szukaną wartość oporu

Wykonanie pomiarów.

Zestawiamy obwód elektryczny tak jak to widać na rysunku powyżej, przy czym:
opornik wzorcowy dekadowy,
opornik badany, Z - źródło prądu stałego, G - galwanometr (miliamperomierz), W - wyłącznik z oporem zabezpieczającym. Przy otwartym wyłączniku W ustawiamy opornicę dekadową na wartość 10Ω i włączamy zasilacz Z (napięcie ok. 2V). Dobieramy położenie suwaka D na strunie tak, aby galwanometr wskazywał wartość 0. Po zamknięciu klucza W położenie to ustalamy bardziej precyzyjnie i odczytujemy wartość długości odcinków
Obliczamy ze wzoru
wartość szukanego oporu - jest to wartość orientacyjna, obciążona dość dużym błędem pomiarowym. Oznaczamy wyznaczoną wartość
jako
.

Z rozważań opartych na rachunku błędów wynika, że minimalny błąd pomiaru otrzymujemy wówczas, gdy zrównoważenie mostka zachodzi przy ustawieniu suwaka w połowie długości struny. W związku z tym, właściwe pomiary wykonujemy dobierając opór wzorcowy
tak, aby był on w przybliżeniu równy wartości
wyznaczonej wcześniej.

Następnie wykonujemy trzy pomiary oporu
. Ustawiamy na opornicy dekadowej kolejno trzy różne, ale bliskie
wartości oporu wzorcowego. Otrzymujemy w ten sposób trzy wartości
jako właściwą wartość oporu przyjmujemy średnią arytmetyczną: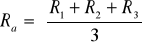
. Identycznie wyznaczamy nieznany opór następnego opornika -
.

Potem łączymy badane oporniki szeregowo i dokonujemy pomiaru oporu wypadkowego za pomocą mostka Wheatstone a. W ten sam sposób wykonujemy pomiary dla połączenia równoległego.

Zestawiamy układ według rysunku i badamy opór stali.

Dla otrzymanych wyników przedstawionych w załączonej tabelce obliczam opór dla stali

Wartość orientacyjna

Pomiar I

Pomiar II

Pomiar III

Średnia wartość badanego oporu wynosi:

Następnie badamy opór dla konstantanu.

Wartość orientacyjna

Pomiar I

Pomiar II

Pomiar III

Średnia wartość badanego oporu wynosi

Następnie oporniki łączymy szeregowo, a potem równolegle i otrzymujemy następujące wyniki:

Obliczam ukłąd oporników przy połączeniu szeregowym

Opór wzorcowy

Obliczam układ oporów przy połączeniu równoległym:

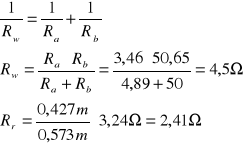
Obliczam opory właściwe:

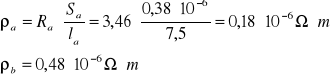
3